Коллоидный журнал, 2021, T. 83, № 5, стр. 532-539

ВВЕДЕНИЕ

Электродиспергирование жидкости весьма широко используется в технике и науке при создании ионно-кластерно-капельных пучков в жидкометаллических источниках ионов, в жидкометаллической эпитаксии и литографии, при получении порошков тугоплавких металлов, в жидкостной масс-спектрометрии (для анализа труднолетучих веществ и веществ органического происхождения). Оно применяется также в реактивной космической технике для точной регулировки орбит, для быстрого рассеяния оптически плотных аэродисперсных систем, при создании потоков монодисперсных капель для термоядерного синтеза, в каплеструйной печати, в ускорителях макрочастиц, при электрораспылении инсектицидов, лаков, красок и горюче-смазочных материалов. Явление диспергирования заряженных капель во внешних электрических полях используется для истолкования разнообразных геофизических феноменов, связанных с грозовым электричеством.

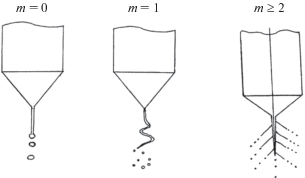
В связи с общим исследованием электрических разрядов с металлических остриев в конце 19-го и начале 20-го веков использовались острия из различных металлов с целью возможного получения каких-либо различий в форме разрядов (см., например, ссылки в [1]). Выяснилось, что критические условия зажигания разряда вокруг острия зависят от многих особенностей приготовленного острия: его вещества, особенностей обработки и, в частности, от порядкового номера разряда с одного и того же острия. Исследователи, выбирая лучшее из нескольких остриев, пришли к выводу, что следует исследовать сначала жидкие острия, вырастающие на полусферическом жидком мениске под влиянием электрического поля между электродами, а сами жидкости в разрядной ситуации отличаются от металлов и обладают по сравнению с ними рядом перспективных свойств [1]. С легкой руки Зелени [1] выяснили, что электрический разряд с жидких электродов отличается большим разнообразием наблюдаемых форм, зависящих от физико-химических свойств жидкостей, таких как коэффициенты вязкости и электропроводности жидкости, и геометрии разрядной системы и подаваемой на электроды разности потенциалов [1–4]. В частности, были зафиксированы формы электрических разрядов, схематически изображенные на рис. 1 и 2 (для более детальной визуальной информации см. работы [1, 2, 4]). Свечение, приведенное на рис. 1 (впоследствии названное “веерным”), наблюдалось при эмиссии капель прямо с мениска жидкости на торце капилляра, по которому жидкость подавалась в разрядную систему. Веерное свечение возникало у вершин менисков жидкостей, обладающих высокой электропроводностью: этилового спирта, растворов соляной кислоты и воды. Отметим, что электропроводность воды в зависимости от того какая она – морская, дождевая, озерная, дистиллированная, деионизованная или перегнанная в вакууме – различается на несколько порядков величины [5, стр. 326, 6, стр. 27, 531], но при описании экспериментов это, как правило, не указывается [4, 7, 8].

Рис. 1.

Схематическое изображение “веерного” свечения.

Рис. 2.

Схемы распада струи при возбуждении азимутальных мод с m = 0, 1 и ≥2.

Когда веерное свечение не возникало, из мениска выбрасывались струи. На рис. 2 схематически изображены примеры форм распада струй для разных значений азимутального параметра $m$, характеризующего осенесимметричность струи, при различных значениях прикладываемого напряжения и вязкости, зафиксированные в работах [1–4, 7–9]. Следует отметить, что струи распадаются на отдельные капли уже в силу капиллярной неустойчивости.

Напомним, что при электродиспергировании жидкости в “веерной” форме струи не образуются, а капли выбрасывает мениск. Формы распада струй, приведенные на рис. 2, – только примеры нескольких десятков форм распада, экспериментально наблюдавшихся, например, в [2] и других цитированных работах.

Интересна в связи с вышесказанным, приведенная в [9] фотография струйки сильно заряженных капель, вылетающей с конца капилляра. На ней зафиксированы капли, дважды распадающиеся из-за электростатической неустойчивости: прямо на срезе капилляра (где образуется облачко дочерних капелек) и на расстоянии нескольких сантиметров от среза капилляра, где распад повторяется. Такие распады и лежат в основе физической модели “веерного” свечения, но все начинается с электростатических распадов сильно заряженных капель.

Собственно говоря, работа [9] была первой работой, в которой производилась экспериментальная проверка критерия электростатической неустойчивости Рэлея сильно заряженной капли [10]. Впоследствии подобные экспериментальные проверки многократно повторялись (см., например, [11–15]) и повторяются до сих пор по мере усовершенствования экспериментальной техники и повышения точности измерений.

Теоретическим аналитическим путем критерий электростатического распада был выведен Рэлеем в конце 19-го века в весьма сжатой форме [10], и подробное изложение расчетов было воспроизведено почти через столетие другими авторами [16]. Само критическое условие электростатического распада сильно заряженной сферической капли идеальной несжимаемой идеально проводящей жидкости Рэлей вывел в виде безразмерного неравенства, составленного из радиуса капли $R$, ее заряда $Q$ и коэффициента поверхностного натяжения жидкости ${{\sigma }}$, имеющего в системе СИ вид

В связи со сказанным, в экспериментах [9, 11–15] капля заряжалась до рэлеевского предела ($W = 1$) так, чтобы выполнялось неравенство (1). Как показали эксперименты [17], при выполнении (1) “родительская” капля выбрасывает несколько сотен “дочерних” капелек на два порядка меньшего размера и еще меньшего заряда, теряя при этом 23% исходного заряда $Q$ и примерно 0.5% процента исходной массы $M$. Образующиеся дочерние капельки оказываются заряженными выше рэлеевского предела и, в свою очередь, распадаются по тому же закону, а родительская капля, сбросив примерно четверть заряда и ничтожную часть массы, становится устойчивой по отношению к оставшемуся заряду [18, 19].

В силу большой кривизны поверхности дочерних капель и значительного заряда на них, вокруг каждой из капель зажигается коронный разряд. Веерную форму он принимает вследствие движения дочерних капелек вдоль внешнего электростатического поля и их кулоновского расталкивания [20].

Утверждение, что дочерние капельки, образующиеся при электростатическом распаде, заряжены выше рэлеевского предела, не очевидно. Поэтому остановимся на этом вопросе отдельно.

ЭЛЕКТРОСТАТИЧЕСКАЯ УСТОЙЧИВОСТЬ ДОЧЕРНЕЙ КАПЕЛЬКИ

Примем, что образовавшаяся при электростатическом распаде исходно сферической (с радиусом $R$ и зарядом $Q$) капли идеальной несжимаемой электропроводной жидкости дочерняя капелька имеет заряд $q$, радиус $r$ и находится во внешнем электростатическом поле напряженностью $E$. Поле $E$ создается зарядом остатка родительской капли для распада заряженной капли или разрядной системой при электродиспергировании с мениска на торце капилляра. Поле $E$ в пределах объема, занимаемого отрывающейся капелькой, для предстоящей качественной оценки будем считать квазиоднородным на том основании, что характерный линейный размер дочерней капельки на два порядка меньше толщины капилляра или радиуса родительской капли [18, 19]. Свободная энергия дочерней капельки $F(r,q,E)$ есть сумма энергии капиллярных сил и электростатической энергии электрического заряда $q$ и энергии зарядов, индуцированных полем $E$ в дочерней капельке:

Здесь $C$ – размерная константа, зависящая от геометрии пространства, занятого электростатическим полем, ${{\varphi *}}$ – электростатический потенциал внешнего для капельки поля, в котором она находится. Речь идет об уже оторвавшейся от мениска капельке. Заряд $q$ она получила за время отрыва от мениска на торце капилляра, поддерживающегося при постоянном потенциале. Потенциал ${{\varphi *}}$ есть потенциал суммарного внешнего поля в том месте, где находится капелька, и от ее радиуса не зависит. Слагаемое $q{{{{\varphi }}}_{*}}$ в записанном выше выражении определяет энергию заряда капельки во внешнем поле. В том месте, где находится капелька, $E = \left| {\nabla {{\varphi *}}} \right|.$

Исследуем (2) на экстремум, для чего найдем первую производную от $F(r,q,E)$ по радиусу $r$ и приравняем ее нулю:

Если взять от $F(r,q,E)$ вторую производную по $r$, то получим, что $\left( {{{{{\partial }^{2}}F} \mathord{\left/ {\vphantom {{{{\partial }^{2}}F} {\partial r{}^{2}}}} \right. \kern-0em} {\partial r{}^{2}}}} \right) > 0$. Иначе говоря, экстремуму $F(r,q,E)$ по $r$ соответствует минимум, и наличие на дочерней капельке запредельного в смысле реализации электростатической неустойчивости заряда выгодно с термодинамической точки зрения.

ВЕЕРНОЕ СВЕЧЕНИЕ

Из всех физических характеристик процесса электродиспергирования на сам процесс должны влиять радиус струйки диспергируемой жидкости $r$, коэффициент поверхностного натяжения жидкости σ, ее коэффициент кинематической вязкости ν и удельная электропроводность ${{\chi }}$. В безразмерных переменных, в которых ${{\sigma }} = {{\rho }} = r = 1$ (здесь ${{\rho }}$ – массовая плотность жидкости), остаются только вязкость и электропроводность жидкости. В контексте сказанного и проведем дальнейшее изложение.

Итак, пусть в результате электростатического распада мениска на торце капилляра, по которому жидкость подается в разрядную систему, мениск выбросил капельку, заряженную выше рэлеевского предела. Она, в свою очередь, в результате реализации электростатической неустойчивости выбросит еще несколько сотен на два порядка более мелких и также сильно заряженных капелек и т.д. Естественно, возникает вопрос, когда наступит предел описанной серии последовательных распадов? Как показано в [22], предел серии последовательных электростатических распадов может положить вязкость жидкости. Когда коэффициент кинематической вязкости, обезразмеренный в системе, в которой ${{\sigma }} = {{\rho }} = r = 1$, и имеющий вид ${{\nu }}\sqrt {\frac{{{\rho }}}{{{{\sigma }}r}}} $, станет сравним с единицей, заряженные капельки из-за демпфирующего влияния вязкости станут делиться пополам, на капельки, устойчивые по отношению к собственному заряду (заряд не превысит рэлеевского предела).

Следует обратить внимание, что величина безразмерного коэффициента кинематической вязкости зависит от ${{\nu }}$, $r$, ${{\rho }}$, ${{\sigma }}$. Таким образом, безразмерный коэффициент кинематической вязкости для одной и той же жидкости может быть большим или малым в зависимости от размеров капли (ее радиуса $r$), плотности жидкости ${{\rho }}$ и коэффициента поверхностного натяжения ${{\sigma }}$ [22].

Как отмечалось выше, в случае маловязких заряженных капель, когда ${{\nu }}\sqrt {\frac{{{\rho }}}{{{{\sigma }}r}}} \ll 1$, каждая выброшенная мениском капля эмитирует около двух сотен существенно более мелких сильно заряженных капелек, вокруг каждой из которых загорится поддерживающийся за счет фотоионизации коронный разряд [20], феноменологически воспринимаемый как веерное свечение.

Следует отметить, что в экспериментальных работах [23, 24] реально наблюдаемое веерное свечение в окрестности вершин осевших на твердую подложку сильно заряженных капель воды положено в основу физической модели распространенного явления, известного как огни Св. Эльма.

Подчеркнем, что веерное свечение появляется только в случае хорошо проводящих жидкостей. Так, Зелени [1, 2] наблюдал его на вершине менисков воды, этилового спирта и раствора соляной кислоты, Инглиш [4] и Войцеховские [23, 24] – для воды, Дрозин [7] – для воды, метилового спирта, ацетона, этилнитрата и уксусной кислоты.

Электропроводность жидкости ${{\chi }}$ обеспечивает появление заряда на эмитируемой капельке. Чем больше электропроводность ${{\chi }}$, тем быстрее капелька накопит максимальный для ее размеров заряд. Проводившиеся ранее [18, 19] расчеты параметров электростатического распада сильно заряженных капель и жидких менисков, а также закономерностей образования монодисперсных капель жидкостей при электростатическом распаде струи на срезе капилляра [25] осуществлялись на модели идеально проводящей жидкости. В данном же рассмотрении мы берем реальную жидкость. В этой связи для того, чтобы дочерняя капля унесла максимально возможный для своего размера и потенциала заряд, необходимо, чтобы характерное время электрической релаксации ${{{{\tau }}}_{{{\chi }}}}$ было существенно меньше характерного времени отрыва капельки – обратной величины инкремента неустойчивости ${{\gamma }}$ заряженной перетяжки, связывающей вершину мениска с отрывающейся каплей (см. рис. 3).

Рис. 3.

Схема отрыва капельки от мениска и дальнейшего ее электростатического распада в процессе формирования “веерного” свечения.

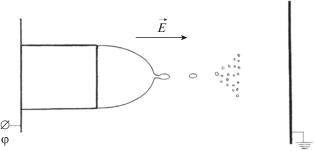
Как отмечалось выше, веерное свечение появляется только в окрестности вершин хорошо проводящих маловязких жидкостей. Иначе говоря, необходимо выделить по коэффициенту кинематической вязкости ν и удельной электропроводности ${{\chi }}$ область, в которой реализуется разряд с жидкого мениска именно в виде веерного свечения. Капелька должна успеть зарядиться до возможного предела, причем ее размер должен быть достаточно велик для реализации последующего электростатического распада, и только затем оторваться от мениска. Только в этом случае с гарантией будет обеспечена серия последовательных распадов дочерних капелек, которым не помешает вязкость.

Если коэффициент кинематической вязкости жидкости ν велик, то струя после вылета из сопла будет распадаться на капли медленно и до первого отрыва капли приобретет конечную длину, как и отмечается в многочисленных публикациях по диспергированию жидкостей и созданию эмпирической классификации экспериментально наблюдаемых режимов диспергирования [2, 26–30].

ОЦЕНКА ХАРАКТЕРНОГО ВРЕМЕНИ ЭЛЕКТРИЧЕСКОЙ РЕЛАКСАЦИИ ЖИДКОСТИ

Характерное время электрической релаксации ${{{{\tau }}}_{{{\chi }}}}$ – время, за которое амплитудное значение флуктуации электрического потенциала или заряда уменьшится за счет электропроводности в $e$ раз; ${{{{\tau }}}_{{{\chi }}}}$ имеет вид [6 (стр. 27), 31, 32 (стр. 642)]:

Из (3) следует, что характерное время электрической релаксации ${{{{\tau }}}_{{{\chi }}}}$ обратно пропорционально электропроводности и прямо пропорционально диэлектрической проницаемости. Учитывая, однако, диапазоны изменения указных физических величин, следует признать зависимость ${{{{\tau }}}_{{{\chi }}}}$ от электропроводности определяющей.

Оценим ${{{{\tau }}}_{{{\chi }}}}$ для пресной воды, с которой проводилось большинство экспериментов, количественно. Для оценки диэлектрическую проницаемость пресной воды примем ${{\varepsilon }} = 81$, а удельную электропроводность ([6], стр. 531) возьмем как χ = 9 × 10⁸ с^–1 и получим по (3) τ_χ = 9 × 10⁸ с ≈ 10⁷ с.

Чтобы обезразмерить время электрической релаксации ${{{{\tau }}}_{{{\chi }}}}$ при ${{\sigma }} = {{\rho }} = r = 1$, достаточно умножить ${{{{\tau }}}_{{{\chi }}}}$ на $\sqrt {\frac{{{\sigma }}}{{{{\rho }}{{r}^{3}}}}} $, и тогда характерное безразмерное время электрической релаксации примет вид

Напомним, что $R$ – радиус капли или мениска, а $r$ – радиус струйки или дочерней капельки, выбрасываемой мениском на вершине капилляра.

ОЦЕНКА ХАРАКТЕРНОГО ВРЕМЕНИ ОТРЫВА ЗАРЯЖЕННОЙ КАПЕЛЬКИ ОТ ЖИДКОГО ЗАРЯЖЕННОГО МЕНИСКА НА ТОРЦЕ КАПИЛЛЯРА, ПО КОТОРОМУ ЖИДКОСТЬ ПОДАЕТСЯ В РАЗРЯДНУЮ СИСТЕМУ

Необходимо, иначе говоря, оценить характерное время развития неустойчивости в перетяжке, связывающей торец мениска с отрывающейся каплей (см. рис. 3). Для этого найдем инкремент неустойчивости в перетяжке и возьмем обратную ему величину. Для качественной оценки перетяжку смоделируем отрезком струи и будем исходить из задачи об устойчивости цилиндрической струи вязкой жидкости по отношению к осесимметричным возмущениям, решение которой приведено в [33]. В отличие от [33] будем считать, что жидкость электропроводна, а струя заряжена так, что на единице длины невозмущенной капиллярным волновым движением поверхности струи находился заряд ${{\mu }_{0}}$. В итоге, к постановке задачи [33] об устойчивости цилиндрической струи вязкой жидкости необходимо добавить в динамическом граничном условии давление электрических сил на поверхность струи.

Математическая формулировка задачи

В связи со сказанным выше, рассмотрим задачу исследования на устойчивость осесимметричных капиллярных волн на однородно заряженной, с поверхностной плотностью заряда ${{\chi }}$, цилиндрической поверхности струи радиуса $r$. Жидкость примем несжимаемой, вязкой, проводящей, с коэффициентом поверхностного натяжения σ и плотностью ${{\rho }}$.

Задачу будем решать в цилиндрических координатах. Орт ${{{\mathbf{e}}}_{z}}$ совпадает по направлению с осью симметрии невозмущенной капиллярным волновым движением цилиндрической поверхности струи. Все рассмотрение проведем в безразмерных переменных, в которых ${{\sigma }} = {{\rho }} = r = 1$, а поверхность, возмущенная капиллярным волновым движением, описывается соотношением

$f(r,z,t) \equiv r - 1 - {{\xi }}(z,t) = 0,\,\,\,\,\left| {{\xi }} \right| \ll 1,$

где ${{\xi }}(z,t)$ – возмущение поверхности струи.

Полная математическая формулировка задачи имеет следующий вид:

$\nabla {\text{g}}{\mathbf{U}}({\mathbf{r}},t) = 0,\,\,\,\,{{\Delta \Phi }}({\mathbf{r}},t) = 0,$

${{\partial }_{t}}{\mathbf{U}}({\mathbf{r}},t) + \left( {{\mathbf{U}}({\mathbf{r}},t){\text{g}}\nabla } \right){\mathbf{U}}({\mathbf{r}},t) = - \nabla p({\mathbf{r}},t),$

$r \to 0:\,\,\,\,{\mathbf{U}}({\mathbf{r}},t) \to 0,$

$r \to \infty {\kern 1pt} :\,\,\,\,\nabla \Phi ({\mathbf{r}},t) \to 0,$

$\begin{gathered} r = {{\xi }}{\kern 1pt} :\,\,\,\,\frac{{df(r,z,t)}}{{dt}} = 0,\,\,\,\,p({\mathbf{r}},t) + {{p}_{{{\chi }}}}({\mathbf{r}},t) - {{p}_{{{\sigma }}}}({\mathbf{r}},t) = 0, \\ {{\Phi }}\left( {{\mathbf{r}},t} \right) = {{{{\Phi }}}_{{\text{s}}}}(t). \\ \end{gathered} $

Здесь ${\mathbf{U}}({\mathbf{r}},t)$ – поле скоростей течения жидкости в струе, генерируемое капиллярными волнами на поверхности струи, $p({\mathbf{r}},t)$ – гидродинамическое давление в струе, ${{p}_{{{\chi }}}}({\mathbf{r}},t)$ и ${{p}_{{{\sigma }}}}({\mathbf{r}},t)$ – давление электрических сил и давление сил поверхностного натяжения на поверхности струи, $\Phi \equiv \Phi ({\mathbf{r}},t)$ – потенциал электростатического поля, ${{{{\Phi }}}_{{\text{s}}}}(t)$ – потенциал поверхности струи.

В качестве дополнительных условий примем: условие постоянства объема струи $V$, приходящегося на одну длину волны ${{\lambda }}$,

$\begin{gathered} \int\limits_V {dV = {{\pi \lambda }}} , \\ V = \left\{ {0 \leqslant r \leqslant 1 + {{\xi }}(z,t),\,\,\,\,{{z}_{0}} \leqslant z \leqslant {{z}_{0}} + {{\lambda }}} \right\}, \\ \end{gathered} $

а также условие сохранения заряда на отрезке струи длиной ${{\lambda }}$,

$\begin{gathered} - \int\limits_S {\frac{1}{{4{{\pi }}}}{\mathbf{n}}({\mathbf{r}},t){\text{g}}\nabla {{\Phi }}dS = 2{{\pi \chi \lambda }}} , \\ S = \left\{ {r = 1 + {{\xi }}(z,t),\,\,\,\,{{z}_{0}} \leqslant z \leqslant {{z}_{0}} + {{\lambda }}} \right\}, \\ \end{gathered} $

где ${{z}_{0}}$ – фиксированная координата вдоль оси симметрии струи, от которой отсчитывается длина волны, ${\mathbf{n}}({\mathbf{r}},t)$ – орт нормали к поверхности струи.

Линеаризуя поставленную задачу возле невозмущенной поверхности струи, будем решать ее стандартными методами [33], отыскивая решения для электростатического ${{\Phi }}({\mathbf{r}},t)$ и гидродинамического ${{\psi }}({\mathbf{r}},t)$ потенциалов, функции тока f(r,t) и возмущения поверхности ${{\xi }}\left( {{{\varphi }},z,t} \right)$ в виде

(4)

$\begin{gathered} \Phi ({\mathbf{r}},t) = d\exp (ist)\exp (ikz + im\varphi ){{K}_{m}}\left( {kr} \right), \\ \psi ({\mathbf{r}},t) = c\exp (ist)\exp (ikz + im\varphi ){{I}_{m}}\left( {kr} \right) \\ f({\mathbf{r}},t) = b\exp (ist)\exp (ikz + im\varphi ){{K}_{m}}\left( {kr} \right) \\ \xi \left( {\varphi ,z,t} \right) = a\exp (ist)\exp (ikz + im\varphi ), \\ \end{gathered} $

где $s$ – частота (в общем случае комплексная), $k$ – волновое число, ${{I}_{m}}\left( x \right)$ и ${{K}_{m}}\left( x \right)$ – модифицированные функции Бесселя первого и второго рода порядка $m$, $m$ – азимутальный параметр. При $m = 0$ будем иметь осесимметричные волны, при $m = 1$ – изгибные, при $m \geqslant 2$ – изгибно-деформационные, что продемонстрировано рис. 2.

Подставляя (4) в систему граничных и дополнительных условий задачи, найдем дисперсионное уравнение задачи об устойчивости осесимметричных капиллярных волн на поверхности заряженной струи вязкой несжимаемой электропроводной жидкости. В безразмерных переменных, в которых ${{\sigma }} = {{\rho }} = r = 1$, для осесимметричных капиллярных волн ($m = 0$) это дисперсионное уравнение будет иметь вид

(5)

$\begin{gathered} {{s}^{2}} - \frac{{2{{\nu }}{{k}^{2}}s}}{{{{I}_{0}}\left( k \right)}}\left\{ {sI_{1}^{'}\left( k \right) - \frac{{2kl}}{{({{l}^{2}} + {{k}^{2}})}}\frac{{{{I}_{1}}\left( k \right)}}{{{{I}_{1}}\left( l \right)}}{{{I'}}_{1}}\left( l \right)} \right\} = \\ = G(k)\left( {1 - {{k}^{2}} - w(1 - H(k))} \right){{({{l}^{2}} - {{k}^{2}})} \mathord{\left/ {\vphantom {{({{l}^{2}} - {{k}^{2}})} {({{l}^{2}} + {{k}^{2}})}}} \right. \kern-0em} {({{l}^{2}} + {{k}^{2}})}}, \\ \end{gathered} $

$\begin{gathered} l \equiv \sqrt {{{k}^{2}} + {s \mathord{\left/ {\vphantom {s {{\nu }}}} \right. \kern-0em} {{\nu }}}} ,\,\,\,\,G(k) \equiv k\frac{{{{I}_{1}}\left( k \right)}}{{{{I}_{0}}\left( k \right)}},\,\,\,\,H(k) \equiv k\frac{{{{K}_{1}}\left( k \right)}}{{{{K}_{0}}\left( k \right)}}, \\ w \equiv 4\pi \mu _{0}^{2}. \\ \end{gathered} $

$w$ – зарядовый безразмерный параметр, характеризующий устойчивость струи к поверхностному заряду.

Вещественная часть частоты $s$ определяет реальную частоту капиллярных волн $\omega $, мнимая же часть частоты $s$ в зависимости от значений физических величин, входящих в (5), определяет инкремент неустойчивости волн ${{\gamma }}$ либо декремент их затухания ${{\eta }}$.

В соответствии с проведенным в [33] анализом рассмотрим случай маловязкой жидкости, когда выполняется условие l $ \gg $ k (напомним, что ${{l}^{2}} \equiv {{k}^{2}} + {s \mathord{\left/ {\vphantom {s \nu }} \right. \kern-0em} \nu }$, и значит, что в этом случае (s/ν) $ \gg $ k²). Тогда для длинных волн на струе, длина которых много больше ее радиуса ($k \ll 1$), выполняются соотношения [33, стр. 636]

$\begin{gathered} {{I}_{0}}\left( k \right) \approx 1,\,\,\,\,{{I}_{1}}\left( k \right) \approx \frac{k}{2},\,\,\,\,{{I}_{1}}\left( l \right) \approx \frac{l}{2}, \\ I_{1}^{'}\left( l \right) = I_{1}^{'}\left( k \right) \approx \frac{1}{2}, \\ \end{gathered} $

и уравнение (5) принимает вид

${{s}^{2}} + 3{{\nu }}{{k}^{2}}s - \frac{{{{k}^{2}}(1 - {{k}^{2}})}}{2} = 0,$

а его решения

(6)

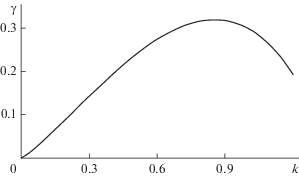
${{s}_{{1,2}}} = - \frac{{3{{\nu }}{{k}^{2}}}}{2} \pm \sqrt {\frac{{9{{{{\nu }}}^{2}}{{k}^{4}}}}{4} + \frac{{{{k}^{2}}(1 - {{k}^{2}})}}{2}} $.

На рис. 4 приведен график зависимости безразмерного инкремента неустойчивости капиллярных волн на струе от безразмерного волнового числа для безразмерного коэффициента кинематической вязкости жидкости 0.125 и зарядового параметра $w = 1.05$, рассчитанной по (6). Видно, что максимальное значение безразмерного инкремента ${{\gamma *}} \approx 0.3$, а размерное выражение для инкремента определится выражением

${{\gamma }} \approx 0.3\sqrt {\frac{{{\sigma }}}{{{{\rho }}{{R}^{3}}}}} \approx {{10}^{5}}\frac{1}{{\text{с}}}$.

Рис. 4.

Зависимость безразмерного инкремента γ капиллярных осесимметричных волн на поверхности струи маловязкой жидкости от безразмерного волнового числа k, рассчитанная при $w = 1.05$ и значении безразмерного коэффициента кинематической вязкости ${{\nu }} = 0.125$.

Характерное время отрыва заряженной капельки от жидкого заряженного мениска на торце капилляра, по которому жидкость подается в разрядную систему, запишется как

${{{{\tau }}}_{{{\gamma }}}} \equiv \frac{1}{{{\gamma }}} = {{10}^{{ - 5}}}{\text{с}}.$

ВЫДЕЛЕНИЕ ОБЛАСТИ РЕАЛИЗАЦИИ “ВЕЕРНОГО” СВЕЧЕНИЯ

Сравнивая ${{{{\tau }}}_{{{\chi }}}} = {{10}^{{ - 7}}}{\text{с}}$ и ${{{{\tau }}}_{{{\gamma }}}} \approx {{10}^{{ - 5}}}{\text{с}}$, получим, что в рассматриваемом случае пресной воды τ_χ$ \ll $ τ_γ (следует отметить, что для дождевой или морской воды ${{{{\tau }}}_{{{\chi }}}}$ будет еще меньше) и отрывающаяся капелька за характерное время отрыва успеет набрать максимально возможный заряд, превышающий согласно (2) критическое по Рэлею его значение.

Таким образом, область устойчивого существования “веерного” свечения в безразмерном виде можно обозначить в виде системы неравенств:

Если условие (7) не выполняется, то феноменологическая картина электродиспергирования будет совсем иной: с вершины мениска будут выбрасываться слабо либо сильно заряженные струи вязкой жидкости, которые будут распадаться (в силу присущей жидким струям капиллярной неустойчивости) на слабо либо сильно заряженные капли. Заряженные капли вязкой жидкости распадутся на две–три дочерних слабо заряженных, устойчивых по отношению к собственному заряду капелек, а коронный разряд возле них может как зажечься, так и не зажечься в зависимости от величины напряженности электрического поля в их окрестности (в зависимости от радиусов и зарядов дочерних капелек).

РОЛЬ ВЯЗКОСТИ ЖИДКОСТИ

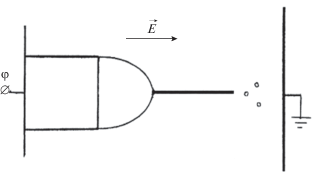
При увеличении вязкости жидкости ее влияние на распад заряженных струй определится снижением инкремента неустойчивости по сравнению с маловязкими жидкостями. Согласно [33] (стр. 637, формула (124.19)) величина инкремента вязкой жидкости обратно пропорциональна коэффициенту вязкости. Так, если вязкость увеличится в сто раз, то инкремент уменьшится примерно в сто раз и в сто раз увеличится характерное время отрыва капли от струи. При той же объемной скорости расхода жидкости через капилляр мениск превратится в струю, от торца которой и будут отрываться капли, как это показано на рис. 5.

Рис. 5.

Схематическое изображение выброса заряженным мениском жидкости на торце капилляра, по которому она подается в разрядную систему, струи вязкой жидкости.

На рис. 6 приведен график зависимости безразмерного инкремента осесимметричных волн на струе сильновязкой жидкости γ от безразмерного волнового числа $k$, рассчитанной по дисперсионному уравнению (5), взятому в пределе большой вязкости. При численных расчетах принималось: $w = 1.05$, ${{\nu }} = 125$, т.е. коэффициент кинематической вязкости стал в тысячу раз больше, чем на рис. 4, при прочих равных условиях. Сравнение рис. 4 и 6 показывает, что величина инкремента неустойчивости вязкой жидкости при увеличении ее коэффициента кинематической вязкости в тысячу раз уменьшилась примерно в тысячу раз.

Рис. 6.

Зависимость безразмерного инкремента капиллярных осесимметричных волн на струе сильновязкой жидкости γ от безразмерного волнового числа $k$, рассчитанная при $w = 1.05$ и значении безразмерного коэффициента кинематической вязкости ${{\nu }} = 125$.

Радиусы струй, принятые при проведении оценки характерных времен, получены из сравнения толщины капилляра, численное значение которого приведено в тексте работы [2], с диаметром струи по фотографиям режимов электродиспергирования, приведенных в [2]. Погрешность такой оценки значительна, и полученные таким образом данные могут быть использованы лишь по порядку величины.

ЗАКЛЮЧЕНИЕ

Подводя итог сказанному выше, отметим, что и вязкость, и электропроводность жидкости существенно влияют на ее электродиспергирование в электрическом поле и на феноменологию этого явления. В зависимости от численных величин указанных двух характеристик жидкости в этом процессе могут образовываться как высокодисперсные, так и грубодисперсные капли, причем как заряженные, так и незаряженные.

Из размерного вида критических параметров Рэлея $W$ (1) и Тейлора $w$ (2) видна их зависимость от величины коэффициента поверхностного натяжения диспергируемой жидкости и радиуса жидкого мениска.