Коллоидный журнал, 2021, T. 83, № 5, стр. 548-556
Охлаждение газа в облаке испаряющихся капель
1 Объединенный институт высоких температур РАН
125412 Москва, ул. Ижорская, д. 13, стр. 2, Россия
* E-mail: naumkor@yandex.ru
Поступила в редакцию 15.05.2021
После доработки 17.05.2021
Принята к публикации 19.05.2021
Аннотация
Представлена модель установления теплового равновесия в смеси горячего газа (азота) и холодных капель воды в замкнутом теплоизолированном объеме. Работоспособность принятой модели подтверждена совпадением вычисленных стационарных значений температуры газа и капель и плотности пара с равновесными значениями, следующими из законов сохранения массы и энергии для смеси газ–пар–капли. Проведено численное моделирование охлаждения газа при нагреве и испарении капель. Получены аппроксимационные выражения для времени охлаждения газа в заданном температурном интервале в зависимости от начального радиуса и массовой доли капель. В расчетах наряду с каплями рассмотрены неиспаряющиеся шарики, радиус которых равен начальному радиусу капель, а материал обладает плотностью и теплоемкостью воды. Выяснено, насколько снижается температура газа и сокращается время его охлаждения с учетом испарения.
ВВЕДЕНИЕ
Испарение капель является предметом изучения в течение длительного времени. Тем не менее, это направление исследований продолжает быть актуальным [1, 2], в том числе, в связи с возможными приложениями. Среди них – получение наночастиц методом LPSP (low-pressure spray pyrolysis), включающим испарительное охлаждение капель с образованием в них пересыщенного раствора и его последующим распадом по нуклеационному механизму [3, 4]. Капельные кластеры, образующиеся над локально нагретой поверхностью воды, имеют, по мнению авторов [5], потенциал использования в качестве уникальных биохимических микрореакторов. Результаты исследования процессов испарения–конденсации в таких кластерах представлены в [6]. Моделирование процесса горения в двигателях и топках котлов, работающих на жидком топливе, невозможно без корректного описания процессов нагрева и испарения капель применительно к указанным объектам [7–9]. Газокапельные потоки, в том числе импульсные, предлагается использовать для испарительного охлаждения поверхностей различных аппаратов, включая мощные светодиоды [10–12]. Способность испаряющихся капель охлаждать окружающий их газ используется в кондиционировании. По аналогии предлагается использовать этот эффект для пожаротушения с помощью “водяного тумана” (water mist fire suppression systems) [13–15], а также как способ охлаждения потока газа в многоступенчатых компрессорах [16]. В химической технологии зачастую возникает необходимость быстрого охлаждения продуктов реакции для предотвращения образования нежелательных побочных продуктов. В этом случае также может быть предложено охлаждение реакционного объема испаряющимися каплями. Результаты численного моделирования капельного охлаждения продуктов конверсии метана в синтез-газ представлены в [17]. Быстрое охлаждение в рассмотренном случае требуется для предотвращения образования сажи.
Объектом рассмотрения данной работы является смесь горячего газа (азота) и холодных капель воды в замкнутом теплоизолированном объеме. Цель работы – получить соотношения, связывающие время охлаждения газа в заданном температурном интервале, начальные значения радиуса и массовой доли капель. Будет использовано обобщение результатов численного моделирования. На основе указанных соотношений, полученных без привязки к конкретному объекту, можно будет оценивать возможности охлаждения газа испаряющимися каплями воды в различных практических приложениях.
В первой части данной работы описана использованная математическая модель исследуемого процесса, во второй – представлены результаты моделирования и их обсуждение, заключение содержит выводы по работе.
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
Рассматривается облако неподвижных капель, равномерно распределенных в замкнутом теплоизолированном объеме V, заполненном газом. В начальный момент времени температура газа выше температуры капель, что определяет тепло- и массообмен между каплями и газом в процессе установления термодинамического равновесия. В рассматриваемых условиях сохраняющимися величинами являются суммарная масса M и внутренняя энергия смеси газ/капли/пар U, а также удельные (на единицу объема смеси) значения массы и внутренней энергии
(1)
$\frac{M}{V} = {{\rho }_{{\text{g}}}} + {{\rho }_{{\text{d}}}} + {{\rho }_{{\text{v}}}} = {{\rho }_{{\text{g}}}} + \rho _{{\text{d}}}^{0} = {\text{const,}}$(2)
$\frac{U}{V} = {{\rho }_{{\text{g}}}}{{u}_{{\text{g}}}} + {{\rho }_{{\text{d}}}}{{u}_{{\text{d}}}} + {{\rho }_{{\text{v}}}}{{u}_{{\text{v}}}} = {\text{const}},$(3)
${{\rho }_{{\text{d}}}} = \frac{4}{3}\pi {{\rho }_{l}}\int\limits_{r_{{\text{d}}}^{{\min }}}^{r_{{\text{d}}}^{{\max }}} {r_{{\text{d}}}^{3}} f({{r}_{{\text{d}}}})d{{r}_{{\text{d}}}},$(4)
${{n}_{{\text{d}}}} = \int\limits_{r_{{\text{d}}}^{{{\text{min}}}}}^{r_{{\text{d}}}^{{\max }}} {f({{r}_{{\text{d}}}})d{{r}_{{\text{d}}}}} .$В процессе охлаждения газа число капель не изменяется. В данной работе будет рассмотрен случай монодисперсного распределения, для которого
(5)
${{{{\rho }}}_{{\text{d}}}} = \frac{4}{3}{{\pi }}{{{{\rho }}}_{{\text{l}}}}{{n}_{{\text{d}}}}r_{{\text{d}}}^{3}.$С учетом баланса массы компонентов смеси
(6)
$\frac{{d{{{{\rho }}}_{{\text{g}}}}}}{{dt}} = 0,\,\,\,\,\frac{{d{{{{\rho }}}_{{\text{v}}}}}}{{dt}} = - \frac{{d{{{{\rho }}}_{{\text{d}}}}}}{{dt}}$и быстрого выравнивания температур пара и газа в молекулярных столкновениях (${{{{\tau }}}_{{{\text{vg}}}}}$ ~ 10–8 с) из выражения (2) следуют уравнения энергии для смеси в целом
(7)
$\begin{gathered} ({{{{\rho }}}_{{\text{g}}}}{{c}_{{\text{g}}}} + {{{{\rho }}}_{{\text{v}}}}{{c}_{{\text{v}}}})\frac{{d{{T}_{{\text{g}}}}}}{{dt}} + {{{{\rho }}}_{{\text{d}}}}{{c}_{{\text{d}}}}\frac{{d{{T}_{{\text{d}}}}}}{{dt}} = \\ = \frac{{d{{{{\rho }}}_{{\text{d}}}}}}{{dt}}\left( {\Delta {{u}_{{{\text{vd}}}}}({{T}_{{\text{d}}}}) + {{c}_{{\text{v}}}}\left( {{{T}_{{\text{g}}}} - {{T}_{{\text{d}}}}} \right)} \right) \\ \end{gathered} $(8)
$({{{{\rho }}}_{{\text{g}}}}{{c}_{{\text{g}}}} + {{{{\rho }}}_{{\text{v}}}}{{c}_{{\text{v}}}})\frac{{d{{T}_{{\text{g}}}}}}{{dt}} = - {{Q}_{{{\text{gd}}}}},$(9)
${{{{\rho }}}_{{\text{d}}}}{{c}_{d}}\frac{{d{{T}_{{\text{d}}}}}}{{dt}} = \frac{{d{{{{\rho }}}_{{\text{d}}}}}}{{dt}}\left( {\Delta {{u}_{{{\text{vd}}}}}({{T}_{{\text{d}}}}) + {{c}_{{\text{v}}}}\left( {{{T}_{{\text{g}}}} - {{T}_{{\text{d}}}}} \right)} \right) + {{Q}_{{{\text{gd}}}}}.$Здесь ${{c}_{i}}$ – изохорная теплоемкость i-го компонента, T – температура, ${{Q}_{{{\text{gd}}}}}$ – количество тепла, передаваемое в единицу времени в единице объема от газа к каплям, $\Delta {{u}_{{{\text{vd}}}}}$ – изменение внутренней энергии в процессе испарения, связанное с теплотой испарения L и давлением $p_{{\text{v}}}^{{\text{s}}}$ и плотностью пара ${{\rho }}_{{\text{v}}}^{{\text{s}}}$ в состоянии насыщения соотношением
(10)
$\Delta {{u}_{{{\text{vd}}}}}(T) = L(T) - {{p_{{\text{v}}}^{{\text{s}}}(T)} \mathord{\left/ {\vphantom {{p_{{\text{v}}}^{{\text{s}}}(T)} {{{\rho }}_{{\text{v}}}^{{\text{s}}}(T)}}} \right. \kern-0em} {{{\rho }}_{{\text{v}}}^{{\text{s}}}(T)}}.$Теплообмен газа и капель в общем случае включает конвективную и радиационную составляющие,
(11)
${{Q}_{{{\text{gd}}}}} = Q_{{{\text{gd}}}}^{{\text{c}}}\left( {1 + \frac{{Q_{{{\text{gd}}}}^{{\text{R}}}}}{{Q_{{{\text{gd}}}}^{{\text{c}}}}}} \right).$Согласно оценкам по формулам нестационарной теплопроводности [18], в капле воды радиусом ~10 мкм относительная разность температур меньше 5% достигается за время t > ${{\tau }}_{{{\text{0}}{\text{.05}}}}^{{\text{c}}} \approx $ 5.5 мкс. Имея в виду рассматривать именно такие капли, при определении конвективной составляющей будем считать профиль температуры в каплях однородным и используем выражение
(12)
$Q_{{{\text{gd}}}}^{{\text{c}}} = \left( {\frac{{3{{{{\rho }}}_{{\text{d}}}}}}{{{{{{\rho }}}_{{\text{l}}}}r_{{\text{d}}}^{2}}}} \right)\frac{{{\text{Nu}}}}{2}{{{{\lambda }}}_{{\text{g}}}}\left( {{{T}_{{\text{g}}}} - {{T}_{{\text{d}}}}} \right),$Оценку сверху влияния теплообмена излучением на нагрев капель в случае прозрачного газа дает соотношение
(13)
$\begin{gathered} Q_{{{\text{gd}}}}^{{\text{R}}} = {{\sigma }}\left( {\frac{{3{{{{\rho }}}_{{\text{d}}}}}}{{{{{{\rho }}}_{{\text{l}}}}{{r}_{{\text{d}}}}}}} \right)\left( {{{T}_{{{\text{wal}}}}} - {{T}_{{\text{d}}}}} \right) \times \\ \times \,\,T_{{{\text{wal}}}}^{3}\left( {1 + \frac{{{{T}_{{\text{d}}}}}}{{{{T}_{{{\text{wal}}}}}}}} \right)\left( {1 + {{{\left( {\frac{{{{T}_{{\text{d}}}}}}{{{{T}_{{{\text{wal}}}}}}}} \right)}}^{2}}} \right), \\ \end{gathered} $(14)
$\frac{{Q_{{{\text{gd}}}}^{{\text{R}}}}}{{Q_{{{\text{gd}}}}^{{\text{c}}}}} = \frac{{{{r}_{{\text{d}}}}{{\sigma }}}}{{{{{{\lambda }}}_{{\text{g}}}}}}T_{{\text{g}}}^{{\text{3}}}\left( {1 + \frac{{{{T}_{{\text{d}}}}}}{{{{T}_{{\text{g}}}}}}} \right)\left( {1 + {{{\left( {\frac{{{{T}_{{\text{d}}}}}}{{{{T}_{{\text{g}}}}}}} \right)}}^{2}}} \right).$Для смеси азота ($T_{{\text{g}}}^{{\text{0}}} = $ 973 K, ${{{{\lambda }}}_{{\text{g}}}}$ = 0.055 Вт/(м K)) и капель воды ($T_{{\text{d}}}^{{\text{0}}} = $ 293 K) имеем ${{Q_{{{\text{gd}}}}^{{\text{R}}}} \mathord{\left/ {\vphantom {{Q_{{{\text{gd}}}}^{{\text{R}}}} {Q_{{{\text{gd}}}}^{{\text{c}}}}}} \right. \kern-0em} {Q_{{{\text{gd}}}}^{{\text{c}}}}} \approx {{10}^{3}}{{r}_{{\text{d}}}}$. Следовательно, для капель радиусом 10 мкм (10–5 м) вкладом радиационной составляющей можно пренебречь. Разумеется, такое утверждение не относится к модели, описывающей поведение капельного кластера под действием излучения лазера [6].
Предполагается, что имеет место независимое испарение отдельных капель. Данное предположение накладывает ограничение на плотность капель. Исходя из требования n-кратного превышения среднего расстояния между каплями по отношению к диаметру капли, имеем
(15)
${{\rho }}_{{\text{d}}}^{{\text{0}}} \leqslant \frac{{{\pi }}}{{\text{6}}}{{n}^{{ - 3}}}{{{{\rho }}}_{{\text{l}}}}.$Для капель воды при n = 10 ${{\rho }}_{{\text{d}}}^{{\text{0}}} \leqslant $ 0.52 кг/м3. Отметим, что накладываемое ограничение удовлетворяется для любых начальных размеров капель. В то же время размер капель определяет режим испарения. Для капель с начальным радиусом ~10 мкм, которые будут рассмотрены в данной работе, скорость испарения определяется процессом диффузии пара от капли. При этом квазистационарное изменение радиуса одиночной капли с учетом стефановского течения описывается выражением [19]
(16)
$\frac{{d{{r}_{{\text{d}}}}}}{{dt}} = - \frac{{{{{{\rho }}}_{{{\text{vg}}}}}D}}{{{{{{\rho }}}_{{\text{l}}}}{{r}_{{\text{d}}}}}}\left( {\ln \frac{{\left( {1 - {{{{\alpha }}}_{1}}} \right)}}{{\left( {1 - {{{{\alpha }}}_{2}}} \right)}}} \right).$Здесь
(17)
${{\alpha }_{1}} = \frac{{{{\rho }_{{\text{v}}}}}}{{{{\rho }_{{{\text{vg}}}}}}},\,\,\,{{\alpha }_{2}} = \frac{{\rho _{{\text{v}}}^{{\text{s}}}}}{{{{\rho }_{{{\text{vg}}}}}}},\,\,\,\,{{\rho }_{{{\text{vg}}}}} = {{\rho }_{{\text{v}}}} + {{\rho }_{{\text{g}}}}\frac{{{{\mu }_{{\text{v}}}}}}{{{{\mu }_{{\text{g}}}}}},$Скорость нестационарного испарения капли может быть определена следующим образом [19]:
(18)
$\frac{{d{{r}_{{\text{d}}}}}}{{dt}} = {{\left( {\frac{{d{{r}_{{\text{d}}}}}}{{dt}}} \right)}_{{{\text{st}}}}}\left( {1 + {{{{r}_{{\text{d}}}}} \mathord{\left/ {\vphantom {{{{r}_{{\text{d}}}}} {\sqrt {{{\pi }}Dt} }}} \right. \kern-0em} {\sqrt {{{\pi }}Dt} }}} \right).$Следуя [19], на основе (18) определяем значение ${{\tau }}_{{{\text{0}}{\text{.05}}}}^{{\text{D}}}$, обеспечивающее (при t > ${{\tau }}_{{{\text{0}}{\text{.05}}}}^{{\text{D}}}$) вклад нестационарности менее 5%:
(19)
${{\tau }}_{{{\text{0}}{\text{.05}}}}^{{\text{D}}} = {{400r_{{\text{d}}}^{{\text{2}}}} \mathord{\left/ {\vphantom {{400r_{{\text{d}}}^{{\text{2}}}} {{{\pi }}D}}} \right. \kern-0em} {{{\pi }}D}}.$Для капель воды радиусом 10 мкм и коэффициенте диффузии паров воды в азоте 0.26 × × 10–4 м2/с значение ${{\tau }}_{{{\text{0}}{\text{.05}}}}^{{\text{D}}}$ ≈ 0.49 мс. В дальнейшем будем использовать для определения скорости испарения капель выражение (16). Полученное в расчетах с использованием (16) время испарения капель будет сопоставлено со значением ${{\tau }}_{{{\text{0}}{\text{.05}}}}^{{\text{D}}}$ для выяснения допустимости предположения о квазистационарном испарении.
Согласно (5) и при условии ${{n}_{{\text{d}}}} = {\text{const}}$ уравнение материального баланса для капель в единице объема имеет вид
(20)
$\frac{{d{{{{\rho }}}_{{\text{d}}}}}}{{dt}} = \frac{{3{{{{\rho }}}_{{\text{d}}}}}}{{{{r}_{{\text{d}}}}}}\frac{{d{{r}_{{\text{d}}}}}}{{dt}}.$Решение системы уравнений (8), (9), (16), (20) с учетом (12) позволяет определить изменение температуры и массы компонентов смеси в зависимости от времени. В состоянии теплового равновесия указанные величины можно найти непосредственно из балансовых соотношений согласно (1) и (2). В частности, при неполном испарении капель, когда ${{{{\rho }}}_{{\text{v}}}} \leqslant {{\rho }}_{{\text{d}}}^{{\text{0}}}$, выражение для температуры смеси ${{\theta }}$ и распределение компонентов в состоянии теплового равновесия имеют вид
(21)
${{\theta }} = \frac{{{{{{\rho }}}_{{\text{g}}}}{{{\bar {c}}}_{{\text{g}}}}T_{{\text{g}}}^{0} + {{\rho }}_{{\text{d}}}^{{\text{0}}}{{c}_{{\text{d}}}}T_{{\text{d}}}^{{\text{0}}} + {{{{\rho }}}_{{\text{v}}}}\left( {({{{\bar {c}}}_{{\text{v}}}} - {{c}_{{\text{d}}}})T_{{\text{d}}}^{0} - \Delta {{u}_{{{\text{vd}}}}}(T_{{\text{d}}}^{{\text{0}}})} \right)}}{{{{{{\rho }}}_{{\text{g}}}}{{{\bar {c}}}_{{\text{g}}}} + {{\rho }}_{{\text{d}}}^{{\text{0}}}{{c}_{{\text{d}}}} + {{{{\rho }}}_{{\text{v}}}}({{{\bar {c}}}_{{\text{v}}}} - {{c}_{{\text{d}}}})}},$(22)
${{\rho }_{{\text{v}}}} = \rho _{{\text{v}}}^{{\text{s}}}(\theta ),\,\,\,{{\rho }_{{\text{d}}}} = \rho _{{\text{d}}}^{0} - \rho _{{\text{v}}}^{{\text{s}}}(\theta ).$При полном испарении капель до достижения теплового равновесия
(23)
${{\theta }} = \frac{{{{{{\rho }}}_{{\text{g}}}}{{{\bar {c}}}_{{\text{g}}}}T_{{\text{g}}}^{0} + {{\rho }}_{{\text{d}}}^{{\text{0}}}\left( {{{{\bar {c}}}_{{\text{v}}}}T_{{\text{d}}}^{0} - \Delta {{u}_{{{\text{vd}}}}}(T_{{\text{d}}}^{0})} \right)}}{{{{{{\rho }}}_{{\text{g}}}}{{{\bar {c}}}_{{\text{g}}}} + {{\rho }}_{{\text{d}}}^{{\text{0}}}{{{\bar {c}}}_{{\text{v}}}}}},$Здесь ${{\bar {c}}_{{\text{g}}}}$ и ${{\bar {c}}_{{\text{v}}}}$ – средне-интегральные значения теплоемкости газа и пара:
(25)
$\begin{gathered} {{{\bar {c}}}_{{\text{g}}}} = \int\limits_{{\theta }}^{T_{{\text{g}}}^{{\text{0}}}} {{{{{c}_{{\text{g}}}}(T)dT} \mathord{\left/ {\vphantom {{{{c}_{{\text{g}}}}(T)dT} {\left( {T_{{\text{g}}}^{0} - {{\theta }}} \right)}}} \right. \kern-0em} {\left( {T_{{\text{g}}}^{0} - {{\theta }}} \right)}}} , \\ {{{\bar {c}}}_{{\text{v}}}} = \int\limits_{T_{{\text{d}}}^{0}}^{{\theta }} {{{{{c}_{{\text{v}}}}(T)dT} \mathord{\left/ {\vphantom {{{{c}_{{\text{v}}}}(T)dT} {\left( {{{\theta }} - T_{{\text{d}}}^{0}} \right)}}} \right. \kern-0em} {\left( {{{\theta }} - T_{{\text{d}}}^{0}} \right)}}} . \\ \end{gathered} $РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
Представленная выше модель была применена для смеси азота ($T_{{\text{g}}}^{{\text{0}}} = $ 973 K, ${{{{\rho }}}_{{\text{g}}}}$ = 1.21 кг/м3) и капель воды ($T_{{\text{d}}}^{0} = $ 293 K). Варьируемыми величинами были начальные значения плотности и радиуса капель – ${{\rho }}_{{\text{d}}}^{{\text{0}}}$ и $r_{{\text{d}}}^{0}$. Для выяснения роли процесса испарения в расчетах наряду с каплями рассмотрены неиспаряющиеся шарики, радиус которых равен начальному радиусу капель, а материал, как и капли, обладает плотностью и теплоемкостью воды. Необходимые справочные данные о свойствах азота, водяного пара и воды взяты из [20].
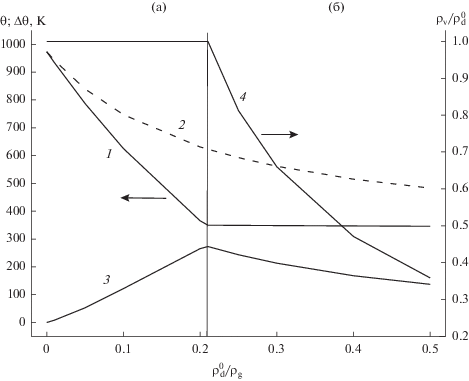
Результаты расчета параметров теплового равновесия в смеси согласно (21)–(24) представлены на рис. 1. Видно, что с точки зрения термодинамики влияние испарения проявляется в возможности достижения более низкой равновесной температуры газа. При увеличении суммарной массы вводимых частиц разность достижимых значений температуры в случае капель и шариков возрастает в области частичного испарения капель и падает в области полного испарения капель, достигая максимальной величины на границе областей. Увеличение массовой доли вводимых капель для снижения равновесной температуры в области полного испарения неэффективно: при увеличении ${{\rho }}_{{\text{d}}}^{{\text{0}}}{\text{/}}{{{{\rho }}}_{{\text{g}}}}$ вдвое снижение ${{\theta }}$ составляет менее 1%.
Рис. 1.
Температура газа (1, 2) и плотность пара (4), соответствующие тепловому равновесию при различных значениях ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$. Сплошные кривые – охлаждение газа испаряющимися каплями, штриховые – неиспаряющимися шариками. 3 – Разность равновесных температур. (a) Область полного испарения капель, (б) частичное испарение капель.
Результаты численного интегрирования системы уравнений (8), (9), (16), (20) с учетом (12) для указанных выше условий представлены на рис. 2–6. Использовалась авторская программа COND-KINET-1 [21].
Рис. 2.
Изменение температур газа (1), испаряющихся капель ($r_{{\text{d}}}^{0}$ = 10 мкм) и неиспаряющихся шариков радиусом 10 мкм (2) в процессе установления теплового равновесия. Сплошные кривые – охлаждение газа испаряющимися каплями, штриховые – неиспаряющимися шариками. ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$= 0.1.

Рис. 3.
Изменение температуры газа (1), испаряющихся капель ($r_{{\text{d}}}^{0}$ = 10 мкм) и неиспаряющихся шариков радиусом 10 мкм (2) в процессе установления теплового равновесия. Сплошные кривые – охлаждение газа испаряющимися каплями, штриховые – неиспаряющимися шариками. ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$ = 0.3.
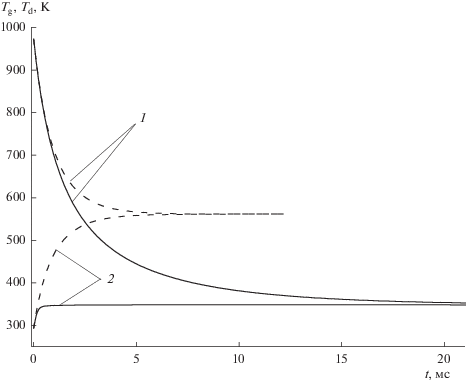
Рис. 4.
Изменение температуры газа в процессе охлаждения испаряющимися каплями ($r_{{\text{d}}}^{0}$ = 10 мкм) при различных значениях ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$: 1 – 0.1, 2 – 0.2, 3 – 0.3, 4 – 0.4.

Рис. 5.
Изменение температуры газа в процессе охлаждения испаряющимися каплями (${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$ = 0.3) при различных значениях $r_{{\text{d}}}^{0}$: 1 – 5, 2 – 10, 3 – 20 мкм. Сплошные кривые – зависимость от реального времени, значки – зависимость от нормированного времени.
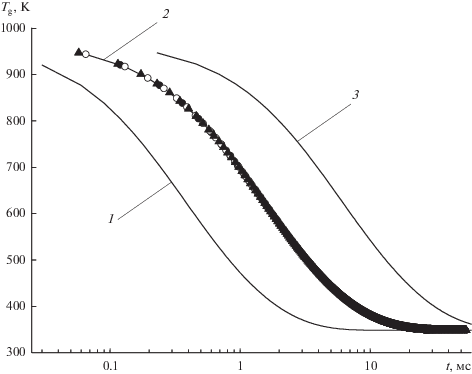
Рис. 6.
Изменение температуры (сплошные кривые) и плотности капель (штриховые кривые) в процессе охлаждения газа испаряющимися каплями ($r_{{\text{d}}}^{0}$= 10 мкм) при различных значениях ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$: 1 – 0.1, 2 – 0.2, 3 – 0.3, 4 – 0.4.

Изменения температуры газа и капель для случая полного (рис. 2) и частичного (рис. 3) испарения капель показаны на рис. 2, 3. Видно, что с учетом испарения не только достигается более низкая, чем для шариков, стационарная температура, но и охлаждение газа происходит быстрее. Указанный эффект имеет место и для полного испарения капель, и для частичного. В расчетах полное испарение капель моделировалось прекращением счета при уменьшении начального радиуса капли до размера ~1 мкм. Неиспарившаяся часть исходной массы капель (~0.1%) не влияла на близость результатов термодинамического (равновесная температура) и кинетического (стационарная температура) подходов. При этом оставалось неизменным количество капель, что было использовано при выводе уравнения (20), и сохранялась возможность использовать выражение для скорости испарения в виде (16).
Рисунки 4, 5 демонстрируют изменение температуры газа в процессе охлаждения испаряющимися каплями при различных начальных значениях массовой доли капель в смеси (рис. 4) и их радиуса (рис. 5). Согласно данным рис. 4, начальная массовая доля капель в смеси влияет на скорость охлаждения. Если значение величины ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$ соответствует области полного испарения капель, ее увеличение позволяет достичь более низкой температуры в конце охлаждения (рис. 4, кривые 1 и 2). Для значений ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$ области частичного испарения капель (рис. 4, кривые 3 и 4) температура в конце охлаждения слабо зависит от ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$. Из результатов расчетов выяснилось, что при перенормировке оси времени множителем ${{({{10} \mathord{\left/ {\vphantom {{10} {r_{{\text{d}}}^{{\text{0}}}}}} \right. \kern-0em} {r_{{\text{d}}}^{{\text{0}}}}})}^{2}}$ кривые ${{T}_{{\text{g}}}}(t)$ для различных значений $r_{{\text{d}}}^{{\text{0}}}$ совмещаются с соответствующей кривой для $r_{{\text{d}}}^{{\text{0}}}$ = 10 мкм (см. рис. 5). По-видимому, это отражает тот факт, что согласно (8) и (12) в начальный момент времени скорость охлаждения газа обратно пропорциональна квадрату начального радиуса капли.
Изменение температуры и плотности капель при охлаждении газа испаряющимися каплями представлено на рис. 6. Обращает на себя внимание, что нагрев капель происходит намного быстрее их испарения. Аналогичный эффект отмечен в [4, 17]. Стационарная температура капель слабо зависит от соотношения начальных масс капель и газа. Видно, что характерные времена процессов нагрева и испарения капель более чем на порядок превышают величины ${{\tau }}_{{{\text{0}}{\text{.05}}}}^{{\text{c}}}$ и ${{\tau }}_{{{\text{0}}{\text{.05}}}}^{{\text{D}}}$ соответственно, что подтверждает справедливость использованных допущений об однородном температурном профиле в каплях и квазистационарном испарении. Представленные результаты получены с использованием предположения о монодисперсном распределении капель. Результаты моделирования испарения полидисперсного ансамбля капель в работе [22] сопоставлены с аналогичными результатами для монодисперсного приближения и с экспериментальными данными [23]. Можно сказать, что три группы результатов достаточно близки. Аналогичный вывод сделан в [24] при сравнении результатов моделирования гетерогенной конденсации пара на моно- и полидисперсных центрах.
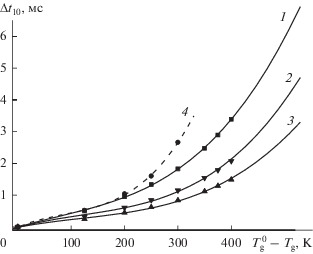
На основании проведенных расчетов получены данные о времени снижения температуры газа от начального значения $T_{{\text{g}}}^{{\text{0}}}$ до заданного значения ${{T}_{g}}$. Использованы различные значения массовой доли капель в смеси и их начального радиуса. Для случая $r_{{\text{d}}}^{{\text{0}}}$ = 10 мкм эти данные демонстрирует рис. 7. Видно, что испаряющиеся капли быстрее охлаждают газ, чем шарики, и до более низких температур. Время охлаждения газа уменьшается с ростом начального значения массовой доли капель ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$. Для каждого значения ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$ время охлаждения описывается полиномом третьей степени аргумента y = ($T_{{\text{g}}}^{{\text{0}}}$ − ${{T}_{g}}$)/1000. В целом полученные данные могут быть аппроксимированы выражением
(26)
$\Delta {{t}_{{\text{T}}}} = A{{\left( {\frac{{r_{{\text{d}}}^{0}}}{{10}}} \right)}^{2}}{{\left( {\frac{{{{\rho }}_{{\text{d}}}^{{\text{0}}}}}{{{{{{\rho }}}_{{\text{g}}}}}}} \right)}^{{ - n}}}.$Рис. 7.
Время охлаждения газа испаряющимися каплями ($r_{{\text{d}}}^{0}$ = 10 мкм, сплошные кривые) и неиспаряющимися шариками радиусом 10 мкм (штриховая кривая) в зависимости от величины температурного интервала при различных значениях ${{{{\rho }}_{{\text{d}}}^{{\text{0}}}} \mathord{\left/ {\vphantom {{{{\rho }}_{{\text{d}}}^{{\text{0}}}} {{{{{\rho }}}_{{\text{g}}}}}}} \right. \kern-0em} {{{{{\rho }}}_{{\text{g}}}}}}$: 1 – 0.2, 2 – 0.3, 3 – 0.4, 4 – 0.2. Значки – результаты расчета, кривые – аппроксимация полиномами третьей степени.
Здесь $\Delta {{t}_{T}}$ – время охлаждения газа от начального значения $T_{{\text{g}}}^{{\text{0}}}$ до заданного значения ${{T}_{g}}$, начальный радиус капель выражен в мкм, а величина A и время охлаждения выражены в мс. Найденные по результатам численного моделирования значения A и n представлены на рис. 8. Они также описываются полиномами третьей степени:
(27)
$\begin{gathered} A = - {\text{0}}{\text{.00143}} + {\text{0}}{\text{.880638}}y - \\ - \,\,{\text{1}}{\text{.45544}}{{y}^{{\text{2}}}} + {\text{6}}{\text{.07539}}{{y}^{{\text{3}}}}{\text{,}} \\ \end{gathered} $(28)
$\begin{gathered} n = {\text{0}}{\text{.99947}} + {\text{0}}{\text{.690143}}y - \\ - \,\,{\text{2}}{\text{.19456}}{{y}^{{\text{2}}}} + {\text{4}}{\text{.1189}}{{y}^{{\text{3}}}}{\text{.}} \\ \end{gathered} $Рис. 8.
Параметры степенной аппроксимации величины $\Delta {{t}_{T}}$ согласно выражению (26): 1 – n, 2 – A. Значки – результаты расчета, кривые – аппроксимация полиномами третьей степени.
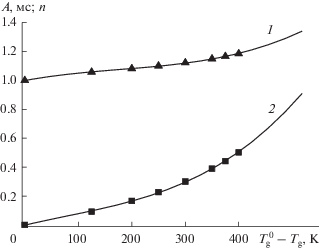
Видно, что с учетом погрешности вычислений при определении времени охлаждения выражения (27) и (28) обеспечивают правильное асимптотическое поведение параметров A и n: при условии ${{T}_{{\text{g}}}} \to T_{{\text{g}}}^{0}$ следует $A \to 0$, $n \to 1$, $\Delta {{t}_{T}} \sim {{\left( {r_{{\text{d}}}^{0}} \right)}^{2}}{{\left( {{{\rho }}_{{\text{d}}}^{{\text{0}}}} \right)}^{{ - 1}}}$, что соответствует уравнению энергии для газа (8) с учетом (12). Выражения (26)–(28) позволяют определить время охлаждения газа испаряющимися каплями в заданном температурном интервале в зависимости от начальных значений массовой доли и радиуса капель, что соответствует заявленной цели данной работы.
ЗАКЛЮЧЕНИЕ
Современные возможности численного моделирования позволяют, с одной стороны, дать детальное описание процессов в изучаемом объекте с получением результатов, зачастую применимых только к рассмотренной ситуации. С другой стороны, имеется возможность, упростив постановку задачи, на основе результатов численного моделирования получить обобщающие зависимости. В данной работе была реализована именно такая возможность.
Использована упрощенная модель процесса установления теплового равновесия в смеси горячего газа и холодных капель воды в замкнутом объеме. На основе компьютерной реализации модели определены температура газа, а также масса и температура капель в зависимости от времени. Обобщение данных численного моделирования позволило определить искомые зависимости для времени охлаждения газа. Справедливость принятых упрощающих предположений о квазистационарном испарении и однородном температурном профиле в каплях подтверждена результатами расчетов. Потенциальное влияние учета полидисперсного распределения капель оценено на основе сопоставления с литературными данными.
Можно предположить, что учет такого неучтенного в модели фактора, как обдув капель газом, привел бы к снижению времени охлаждения. Следовательно, результаты, полученные на основе (26)–(28), дают оценку сверху времени охлаждения газа испаряющимися каплями. Эта информация, полученная без привязки к конкретному объекту, может служить ориентиром при оценке возможностей охлаждения газа испаряющимися каплями воды в различных приложениях. Задачей дальнейших исследований является определение зависимости времени охлаждения от отношения теплоты испарения к начальному теплосодержанию газа, а также рассмотрение процесса охлаждения газа в газокапельном потоке.
Список литературы
Zang D., Tarafdar S., Tarasevich Y.Yu., Choudhury M.D., Dutta T. // Phys. Rep. 2019. V. 804. P. 1.
Кучма А.Е., Есипова Н.Е., Михеев А.А., Щекин А.К., Ицков С.В. // Коллоид. журн. 2019. Т. 81. С. 724.
Nandiyanto A. B. D., Okuyama K. // Adv. Powder Technol. 2011. V. 22. P. 1.
Фисенко С.П., Ходыко Ю.А. // Инж.-физ. журн. 2020. Т. 93. С. 1368.
Fedorets A.A., Bormashenko E., Dombrovsky L.A., Nosonovsky M. // Phil. Trans. R. Soc. A. 2019. V. 377. 20190121.
Dombrovsky L.A., Fedorets A.A., Levashov V.Yu., Kryukov A.P., Bormashenko E., Nosonovsky M. // Int. J. Heat Mass Transfer. 2020. V. 161. 120255.
Фролов С.М., Басевич В.Я., Посвянский В.С., Сметанюк В.А. // Хим. физика. 2004. Т. 23. № 7. С. 49.
Kryukov A.P., Levashov V. Yu., Sazhin S. S. // Int. J. Heat Mass Transfer. 2004. V. 47. P. 2541.
Sazhin S.S. // Fuel. 2017. V. 196. P. 69.
Gatapova E.Ya., Sahu G., Khandekar S., Hu R. // Appl. Therm. Eng. 2021. V. 184. 116270.
Terekhov V.I., Karpov P.N., Nazarov A.D., Serov A.F. // Int. J. Heat Mass Transfer. 2020. V. 158. 120057.
Saverchenko, V.I., Fisenko, S.P. Evaporative cooling of the substrate by pulse-periodic spray with femtoliter droplets. Preprint, March 2021. https://doi.org/10.13140/rg.2.2.23363.73766
Yao B., Chow W.K. // J. Appl. Fire Sci. 2001. V. 10. P. 277.
Zhdanova A.O., Volkov R.S., Voytkov I.S., Osipov K.Y., Kuznetsov G.V. // Int. J. Heat Mass Transf. 2018. V. 126. P. 703.
Kuznetsov G.V., Kralinova S.S., Voytkov I.S., Islamova A.G. // Appl. Sci. 2019. V. 9. 5190. https://doi.org/10.3390/app9235190
Беркович А.Л., Полищук В.Г., Назаренко А.В. // Научно-технические ведомости Санкт-Петербургского политехнического университета. 2015. № 2 (219). С. 33.
Деревич И.В., Фокина А.Ю. // Инженерный журнал: наука и инновации. 2013. Вып. 8. http://engjournal.ru/catalog/mathmodel/hidden/886.html.
Лыков А.В. Теория теплопроводности. М.: Высшая школа, 1967.
Fuchs N.A. Evaporation and Droplet Growth in Gaseous Media. New York: Pergamon Press, 1959.
Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука, 1972.
Корценштейн Н.М., Герасимов Г.Я., Петров Л.В., Шмельков Ю.Б. // Теплоэнергетика. 2020. № 9. С. 6.
Ягодников Д.А., Антонов Ю.В., Власов Ю.Н. // Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2011. № 4. С. 71.
Терехов В.И., Терехов В.В., Шишкин Н.Е., Би К.Ч. // Инж.-физ. журн. 2010. Т. 83. С. 829.
Корценштейн Н.М., Ястребов А.К. // Коллоид. журн. 2016. Т. 78. С. 444.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


