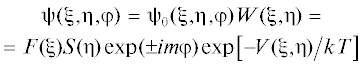1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 83, № 5, 2021

Коллоидный журнал, 2021, T. 83, № 5, стр. 557-571

Молекулярно-динамическое моделирование конформационных изменений макромолекул полиэлектролитов на поверхности заряженной или поляризованной вытянутой сфероидальной металлической наночастицы

Н. Ю. Кручинин 1, *, М. Г. Кучеренко 1

1 Центр лазерной и информационной биофизики Оренбургского государственного университета
460018 Оренбург, просп. Победы, 13, Россия

* E-mail: kruchinin_56@mail.ru

Поступила в редакцию 13.05.2021
После доработки 17.05.2021
Принята к публикации 18.05.2021

Полный текст (PDF)

Аннотация

Методом молекулярной динамики исследованы изменения конформационной структуры полиэлектролитных полипептидов, адсорбированных на поверхности заряженной, а также поляризованной вдоль большой оси вытянутой сфероидальной золотой наночастицы. Представлена аналитическая модель структуры гауссовой макроцепи, адсорбированной на сфероидальной наночастице. Модель отражает особенности формирования структуры адсорбированной макроцепи, связанные с геометрией незаряженной, неполяризованной вытянутой сфероидальной наночастицы, а при необходимости также учитывает поверхностный заряд или поляризацию частицы посредством введения больцмановского фактора для равновесных конфигураций макроцепи в потенциальном поле. На поверхности поляризованного вытянутого металлического наносфероида происходило набухание адсорбированных полиамфолитных полипептидов в приполярных областях, а также смещение звеньев однородно заряженных полипептидов в приполярную область, заряженную противоположно знаку заряда звеньев. На поверхности заряженной вытянутой сфероидальной золотой наночастицы макромолекула полиэлектролита обволакивала всю наночастицу и набухала при увеличении полного заряда наносфероида.

1. ВВЕДЕНИЕ

В настоящее время плазмонные наночастицы с адсорбированными на их поверхности макромолекулярными цепями находят широкое применение при создании различных сенсоров и нанозондов, а также и других устройств наноэлектроники [1–7]. При этом особый интерес вызывает использование металлических наночастиц, имеющих форму вытянутых или сжатых эллипсоидов вращения [8–12]. Такие нанообъекты занимают промежуточное положение между цилиндрическими и сферическими наночастицами.

Ранее в работах [13–21] нами были исследована адсорбция, а также электрически индуцированная перестройка конформационной структуры полиамфолитных и однородно заряженных полипептидов на металлических поверхностях различной формы: плоской поверхности кристалла [15, 17], поверхностях наночастиц сферической [13–16, 19, 21] и цилиндрической формы [18, 20]. Было показано, что конформационная структура адсорбированных на поверхности полиэлектролитов зависит от ее формы и от характера распределения электрических зарядов на поверхности металлического нанообъекта.

Форма вытянутой сфероидальной наночастицы существенно отличается от формы как сферической, так и цилиндрической наночастиц, а поэтому будет оказывать большое влияние на конформационную структуру адсорбированных на ней макромолекулярных цепей. На поверхности как заряженного, так и поляризованного вдоль большой оси вытянутого металлического сфероида распределение электрических зарядов будет значительно отличаться от их распределения на поверхности нанообъектов сферической и цилиндрической формы. Так, распределение поверхностной плотности зарядов ${{\sigma }_{Q}}$ на поверхности заряженного (с полным зарядом $Q$) вытянутого металлического сфероида, в отличие от однородного распределения на поверхности сферической наночастицы и цилиндрического нанопровода, неоднородно [22]:

(1)
${{\sigma }_{Q}} = \frac{Q}{{4\pi {{a}^{2}}b\sqrt {\left( {\frac{{{{x}^{2}} + {{z}^{2}}}}{{{{a}^{4}}}} + \frac{{{{y}^{2}}}}{{{{b}^{4}}}}} \right)} }},$
где $b$ – длина большой полуоси, направленной вдоль оси $y$, $a$ – длина малых полуосей.

На поверхности вытянутого сфероида, поляризованного во внешнем однородном электрическом поле, направленном вдоль большой оси, формируется распределение поверхностной плотности зарядов ${{{{\sigma }}}_{{\text{p}}}}$ [22]:

(2)
${{{{\sigma }}}_{{\text{p}}}} = \frac{{{{{{\sigma }}}_{{\max }}}y}}{{{{b}^{2}}\sqrt {\left( {\frac{{{{x}^{2}} + {{z}^{2}}}}{{{{a}^{4}}}} + \frac{{{{y}^{2}}}}{{{{b}^{4}}}}} \right)} }},$
где ${{\sigma }_{{\max }}} = \frac{{{{D}_{y}}}}{V}$ – значение поверхностной плотности заряда на полюсе такого сфероида, ${{D}_{y}}$ – дипольный момент сфероида, $V$ – объем сфероида. Видно, что распределение электрических зарядов на поверхности поляризованного вытянутого сфероида заметно отличается от распределения по закону косинуса поверхностной плотности зарядов поляризованной сферической наночастицы или поперечно поляризованного нанопровода.

Такие неоднородные распределения поверхностной плотности зарядов как на поверхности заряженной вытянутой сфероидальной металлической частицы, так и на поверхности вытянутого сфероида, поляризованного вдоль большой оси в однородном электрическом поле, будут оказывать существенное влияние на конформационную структуру адсорбированных макроцепей полиэлектролитов, и она будет значительно отличаться от случаев адсорбции на поверхности нанообъектов сферической и цилиндрической формы.

Таким образом, целью данной работы является исследование конформационных изменений макромолекул полиэлектролитов на поверхности заряженной, а также поляризованной вдоль большой оси вытянутой сфероидальной металлической наночастицы.

2. МОЛЕКУЛЯРНО-ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Молекулярно-динамическое (МД) моделирование было произведено для молекулярной системы, в которой полипептид, содержащий в своей структуре заряженные звенья, располагался на поверхности вытянутой сфероидальной золотой наночастицы. Атомы сфероидальной наночастицы в процессе МД-моделирования оставались зафиксированными.

Модель вытянутой сфероидальной золотой наночастицы была получена путем вырезания из кристалла золота эллипсоида вращения с большой полуосью длиной 6 нм и малыми полуосями длиной 1.5 нм. Были рассмотрены четыре в целом нейтральных полиамфолитных полипептида с разным порядком расположения заряженных аминокислотных остатков:

1) полипептид A400R100D100, состоящий из 600 аминокислотных остатков, а именно из 400 звеньев Ala (A) и равномерно распределенных 100 звеньев Asp (D, заряд –1e) и 100 звеньев Arg (R, заряд +1e) – (ADA2RA)100,

2) полипептид A480R60D60, состоящий из 600 аминокислотных остатков, а именно из 480 звеньев Ala и равномерно распределенных 60 звеньев Asp и 60 звеньев Arg – (A2DA4RA2)60,

3) полипептид A784R98D98, состоящий из 980 аминокислотных остатков, а именно из 784 звеньев Ala и равномерно распределенных 49 пар звеньев Asp и 49 пар звеньев Arg – (A4R2A8D2A4)49,

4) полипептид A880R54D54, состоящий из 988 аминокислотных остатков, а именно из 880 звеньев Ala и равномерно распределенных 27 пар звеньев Asp и 27 пар звеньев Arg – A8(A8D2A16R2A8)27A8.

Также были рассмотрены три отрицательно заряженных полипептида, состоящих из 800 аминокислотных остатков:

5) полипептид A760D40 (суммарный заряд макроцепи –40e), состоящий из 760 звеньев Ala и равномерно распределенных 40 звеньев Asp – (A10DA9)40,

6) полипептид A720D80 (суммарный заряд макроцепи –80e), состоящий из 720 звеньев Ala и равномерно распределенных 80 звеньев Asp – (A5DA4)80,

7) полипептид A640D160 (суммарный заряд макроцепи –160e), состоящий из 640 звеньев Ala и равномерно распределенных 160 звеньев Asp – (A2DA2)160.

МД-моделирование было произведено с использованием программного комплекса NAMD 2.14 [23] при постоянной температуре (термостат Берендсена) 900 К с последующим снижением до 300 К. Длина временнóй траектории достигала 15 нс. Для полипептидов было использовано силовое поле CHARMM22 [24]. Нековалентные взаимодействия со сфероидальной золотой наночастицей описывались потенциалом Леннард-Джонса, параметризованным в работе [25]. Потенциал Ван-дер-Ваальса обрезался на расстоянии 1.2 нм с помощью функции сглаживания между 1.0 и 1.2 нм. Электростатические взаимодействия рассчитывались непосредственно на расстоянии 1.2 нм, а на большем расстоянии использовался метод “частица–сетка” Эвальда (PME) [26] с шагом сетки 0.11 нм. Вся наносистема была помещена в куб с ребрами 24 нм, заполненный молекулами воды TIP3P [27]. Для контроля получения равновесных конформаций осуществлялось наблюдение за изменением среднеквадратичного расстояния между атомами полипептида в различных конформациях.

Были рассмотрены случаи адсорбции полипептидов на нейтральной поверхности вытянутой сфероидальной золотой наночастицы и на поверхности такой наночастицы, поляризованной во внешнем электрическом поле, направленном вдоль ее большой оси, а также на поверхности золотого сфероида, несущего положительный заряд. В случае поляризованного вдоль большой оси вытянутого сфероида заряды на его поверхности были распределены согласно формуле (2). Были получены следующие значения индуцированного дипольного момента сфероидальной наночастицы: ${{p}_{{0.25}}} \approx 9.8$, ${{p}_{{0.5}}} \approx 19.5$ и ${{p}_{{1.0}}} \approx 39$ кД. При этих значениях дипольного момента наносфероида атомы на его положительно заряженном полюсе имели парциальные заряды $ + 0.25e$, $ + 0.5e$ и $ + 1e$ соответственно. Также были рассмотрены вытянутые золотые сфероиды с различным полным положительным зарядом, у которых поверхностная плотность зарядов была распределена по формуле (1): ${{Q}_{{0.25}}} \approx 107e$, ${{Q}_{{0.5}}} \approx 214e$ и ${{Q}_{{1.0}}} \approx 426e$. При таких значениях полного заряда сфероида атомы на его заряженном полюсе имели парциальные заряды $ + 0.25e$, $ + 0.5e$ и $ + 1.0e$ соответственно, а в экваториальной области на участках, расположенных на концах малых полуосей, парциальные заряды были меньше в 4 раза согласно (1).

Сначала была исследована адсорбция первых четырех в целом нейтральных полиамфолитных полипептидов на нейтральной поверхности сфероидальной наночастицы, а полученные результирующие конформационные структуры были использованы в дальнейшем в качестве стартовых при МД-моделировании адсорбции на поверхностях поляризованного, а также заряженного наносфероидов. Для получения стартовых конформаций отрицательно заряженных полипептидов (под номерами 5–7) они предварительно адсорбировались на положительно заряженной поверхности золотого сфероида с полным зарядом ${{Q}_{{0.25}}}$ до формирования конформационной структуры, при которой макроцепь полностью обволакивала сфероидальную наночастицу. Были получены по три стартовых конформаций для каждого рассмотренного полипептида, при которых он обволакивал сфероидальную наночастицу.

По результатам МД-моделирования на поляризованной, а также положительно заряженной сфероидальной наночастице на конечном стационарном участке траектории по всем полученным конформациям рассчитывались радиальные распределения средней плотности атомов полипептидов вдоль большой оси сфероида по слоям с шагом 1 нм от центра, а также распределения линейной плотности их атомов вдоль большой оси вытянутого наносфероида.

3. АНАЛИТИЧЕСКАЯ МОДЕЛЬ СТРУКТУРЫ ГАУССОВОЙ МАКРОЦЕПИ, АДСОРБИРОВАННОЙ НА СФЕРОИДАЛЬНОЙ НАНОЧАСТИЦЕ

В предыдущих наших работах полимерные молекулы представлялись идеальными гауссовыми цепями без объемных взаимодействий, но учитывалось ван-дер-ваальсово притяжение звеньев макромолекулы к поверхности адсорбента либо в его нанопорах, либо когда он является сферической наночастицей или нанопроволокой [28–30]. Во всех этих случаях проявлялась специфика формы адсорбента, в том числе и кривизна его поверхности. В данной работе изучение этого вопроса продолжено. Теперь вместо сферических наночастиц и нанопроволок будут исследованы сфероидальные наночастицы, т.е. частицы, имеющие форму вытянутых эллипсоидов вращения. Очевидно, что такие объекты занимают промежуточное положение между цилиндром и сферой, поскольку характеризуются набором различных радиусов кривизны. На то, что конформационная структура адсорбированных макроцепей будет зависеть от особенностей формы частиц, указывает особый вид дифференциального оператора, определяющего основное уравнение для конформационной функции ψ(r) гауссовой макроцепи [31]. Эта функция определяет конформации полимерной молекулы в растворителе вблизи криволинейной поверхности адсорбента [28–30]. Плотность $n({\mathbf{r}}) = {{{{\psi }}}^{2}}({\mathbf{r}})$ звеньев адсорбированной макроцепи в поле заряженной или поляризованной частицы будет определять конформационную функцию ${{\psi }}({\mathbf{r}})$.

Дифференциальное уравнение – уравнение Гросберга–Хохлова для конформационной функции ψ гауссовой макроцепи имеет вид [31]

(3)
$\frac{{{{a}^{2}}kT}}{6}{{\nabla }^{2}}{{\psi }}({\mathbf{r}}) = [V({\mathbf{r}}) - {{\varepsilon }}]{{\psi }}({\mathbf{r}}),$
где a – размер звена цепи, kT – энергия теплового кванта. В отсутствие адсорбирующего потенциала (V = 0) уравнение (3) принимает вид уравнения на собственные значения оператора свободной диффузии, или уравнения Гельмгольца, записанного в некоторых криволинейных, в данном случае – сфероидальных, координатах для области вне сфероида.

В работах [13, 30] было предложено использовать потенциал $V(r)$ поля сферической наночастицы в виде ${{\delta }}$-функциональной ямы, моделирующей притяжение звеньев макромолекулы к поверхности наночастицы на сфере радиуса r0, и с барьером в виде твердой стенки при r = R:

(4)
$V\left( r \right) = \left\{ \begin{gathered} - \alpha \delta \left( {r - {{r}_{0}}} \right),\,\,\,\,r > R \hfill \\ \infty ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,r = R \hfill \\ \end{gathered} \right..$

В сфероидальных координатах ξ,η,φ потенциал (4) соответствующим образом модифицируется. Вытянутые сфероидальные координаты (ВСК) могут быть заданы соотношениями ${{\xi }} = {{({{r}_{1}} + {{r}_{2}})} \mathord{\left/ {\vphantom {{({{r}_{1}} + {{r}_{2}})} d}} \right. \kern-0em} d}$, ${{\eta }} = {{({{r}_{1}} - {{r}_{2}})} \mathord{\left/ {\vphantom {{({{r}_{1}} - {{r}_{2}})} d}} \right. \kern-0em} d}$ через фокальные радиусы ${{r}_{1}},\,\,{{r}_{2}}$ и фокусное расстояние d. Тогда ξ ∈ [1,∞], η ∈ [–1, 1], φ ∈ [0,2π] [32, 33]. Угол φ – полярный, лежащий в плоскости, перпендикулярной оси сфероида, потенциал (4) от этого угла не зависит.

Адсорбционный потенциал поверхности сфероидальной наночастицы, в случае ван-дер-ваальсовой адсорбции также может быть эффективно представлен комбинацией простейших модельных потенциалов “твердая стенка–дельта-функциональная яма”: ${{V}_{1}}({{\xi }}) = {{V}_{\infty }}(2a)$ – – ${{\alpha \delta }}({{\xi }} - (2a + {{\delta }}{{r}_{0}}))$ (a – длина большой полуоси сфероида).

В случае, когда частице сообщается избыточный электрический заряд q, или при помещении сфероидальной наночастицы в однородное электрическое поле E0, возникает поле, создаваемое соответственно заряженной или поляризованной частицей. Тогда к адсорбционному потенциалу ${{V}_{1}}({{\xi }})$ добавляется либо потенциал ${{V}_{2}}({{\xi }})$ заряженной частицы, либо потенциал ${{V}_{2}}({{\xi ,\eta }})$ внешнего поля E0r вместе с потенциалом Vp поля поверхности поляризованного сфероида. Суммарный потенциал поля для заряженного по поверхности сфероида в пространстве вне наночастицы может быть записан в виде

(5)
$\begin{gathered} V({{\xi }}) = {{V}_{1}}({{\xi }}) + {{V}_{2}}({{\xi }}) = \\ = {{V}_{\infty }}(2a) - {{\alpha \delta }}({{\xi }} - 2(a + {{\delta }}{{r}_{0}})) + {{V}_{q}}({{\xi }}), \\ \end{gathered} $
где потенциал статического поля [22]

(6)
${{V}_{2}}({{\xi }}) = {{V}_{q}}({{\xi }}) = \frac{{q{{e}_{1}}}}{{\sqrt {{{a}^{2}} - {{b}^{2}}} }}{\text{arth}}\left( {\frac{{2\sqrt {{{a}^{2}} - {{b}^{2}}} }}{{{{\xi }}d}}} \right).$

Для поляризованного сфероида в случае ориентации вектора E0 вдоль большой оси a > b можем записать

(7)
$\begin{gathered} V(\xi ,\eta ) = {{V}_{1}}(\xi ) + {{V}_{2}}(\xi ,\eta ) = \\ = {{V}_{\infty }}(2a) - \alpha \delta (\xi - 2(a + \delta {{r}_{0}})) - \\ - \,\,{{e}_{1}}{{E}_{0}}rcos\theta + {{V}_{{\text{p}}}}(\xi ,\eta ), \\ \end{gathered} $
где потенциал внешнего статического поля E0r вместе с потенциалом Vp поля поверхности поляризованного сфероида определен выражением [22, 34]

(8)
$\begin{gathered} {{V}_{2}}({{\xi ,\eta }}) = - {{e}_{1}}{{E}_{0}}\frac{{{{\xi \eta }}}}{{\sqrt {{{a}^{2}} - {{b}^{2}}} }}{{\left( {\frac{d}{2}} \right)}^{2}} \times \\ \times \,\,\left\{ {1 - \frac{{{\text{arth}}\left( {\frac{{2\sqrt {{{a}^{2}} - {{b}^{2}}} }}{{{{\xi }}d}}} \right) - \frac{{2\sqrt {{{a}^{2}} - {{b}^{2}}} }}{{{{\xi }}d}}}}{{{\text{arth}}\sqrt {1 - \frac{{{{b}^{2}}}}{{{{a}^{2}}}}} - \sqrt {1 - \frac{{{{b}^{2}}}}{{{{a}^{2}}}}} }}} \right\}. \\ \end{gathered} $

В случае малого заряда q и слабого внешнего поля E0 учет потенциалов (6) и (8) может быть произведен в рамках теории возмущений, как это было сделано в работах [14, 18, 19]. Если же поле E0 не мало, необходимо решать уравнение Гросберга–Хохлова (3) с потенциалами (6) или (8) в общем виде, что представляет собой сложную задачу в попытке получения аналитического решения. Поэтому в данной работе мы рассматриваем упрощенную модель формирования конформаций макроцепи при ее адсорбции на заряженной или поляризованной сфероидальной наночастице. В такой модели статическое поле (6) поверхностного заряда или поле поляризации (8) для равновесных конформаций макромолекулы учитывается в виде больцмановского фактора, а в уравнении (3) учитываются только ван-дер-ваальсов потенциал и потенциал твердой стенки ${{V}_{1}}({{\xi }})$.

Больцмановский фактор $W({{\xi ,\eta }})$ = = $exp\left[ {{{ - {{V}_{2}}({{\xi ,\eta }})} \mathord{\left/ {\vphantom {{ - {{V}_{2}}({{\xi ,\eta }})} {kT}}} \right. \kern-0em} {kT}}} \right]$ для цепи полиэлектролита с электрическим зарядом звена (группы звеньев) e1 в поле заряженного сфероида определяется потенциалом (6):

(9)
${{W}_{{e1}}}({{\xi }}) = exp\left\{ { - \frac{{q{{e}_{1}}}}{{kT\sqrt {{{a}^{2}} - {{b}^{2}}} }}{\text{arth}}\left( {\frac{{2\sqrt {{{a}^{2}} - {{b}^{2}}} }}{{{{\xi }}d}}} \right)} \right\}.$

Для макроцепи полиамфолита с характерным электрическим дипольным моментом p сегмента (единичного звена или группы звеньев) можем записать

(10)
$\begin{gathered} {{W}_{{\text{p}}}}({{\xi }}) = \\ = exp\left\{ { - \frac{{q{\mathbf{p}}{{{\mathbf{n}}}_{{{\xi }}}}}}{{kT{{h}_{1}}\sqrt {{{a}^{2}} - {{b}^{2}}} }}\frac{d}{{d{{\xi }}}}{\text{arth}}\left( {\frac{{2\sqrt {{{a}^{2}} - {{b}^{2}}} }}{{{{\xi }}d}}} \right)} \right\}, \\ \end{gathered} $
где ${{{\mathbf{n}}}_{{{\xi }}}}$ единичный орт ВСК, а h1 – масштабный параметр Ламе.

Факторы ${{W}_{{e1}}}({{\xi ,\eta }}),\,\,{{W}_{p}}({{\xi ,\eta }})$ в случае полиэлектролита и полиамфолита, аналогичные (9) и (10), получаем при использовании потенциала ${{V}_{2}}({{\xi ,\eta }})$, заданного выражением (8) для незаряженного сфероида в поляризующем поле.

Покажем, при каких условиях проявление поля V2 в формировании конформационной функции ${{\psi }}({\mathbf{r}}) = {{\psi (\xi ,\eta )}}$ редуцируется к больцмановскому фактору $W({{\xi ,\eta }}) = exp\left[ {{{ - {{V}_{2}}({{\xi ,\eta }})} \mathord{\left/ {\vphantom {{ - {{V}_{2}}({{\xi ,\eta }})} {kT}}} \right. \kern-0em} {kT}}} \right]$. Пусть функция ${{{{\psi }}}_{{\text{0}}}}({\mathbf{r}}) = {{{{\psi }}}_{{\text{0}}}}({{\xi ,\eta ,}}\varphi )$ представляет собой решение уравнения

(11)
$ - \frac{{{{a}^{2}}}}{6}{{\nabla }^{2}}{{{{\psi }}}_{0}}({\mathbf{r}}) = \frac{{{\varepsilon }}}{{kT}}{{{{\psi }}}_{0}}({\mathbf{r}}),$
то есть уравнения (3) при V = 0. Представляя функцию ${{\psi }}({\mathbf{r}}) = {{\psi }}({{\xi ,\eta ,}}\varphi )$ в виде
(12)
и подставляя (12) в (3), получаем, что функция (12) является решением уравнения (3) при выполнении следующего равенства для безразмерного потенциала ${{V({{\xi ,\eta }})} \mathord{\left/ {\vphantom {{V({{\xi ,\eta }})} {kT}}} \right. \kern-0em} {kT}}$:

(13)
$\begin{gathered} \frac{{{{a}^{2}}}}{6}{{\nabla }^{2}}{{{{\psi }}}_{{\text{0}}}}({\mathbf{r}})\left[ {exp\left( { - \frac{{V({\mathbf{r}})}}{{kT}}} \right) - 1} \right] = \\ = \frac{{V({\mathbf{r}})}}{{kT}}{{{{\psi }}}_{{\text{0}}}}({\mathbf{r}})exp\left( { - \frac{{V({\mathbf{r}})}}{{kT}}} \right). \\ \end{gathered} $

Если реальные потенциалы (6) или (8) не удовлетворяют условию (13), для оправдания использования аппроксимации решения в факторизованном виде (12) можно считать e1 и p (или температуру T) вариационными параметрами для наилучшего (хотя бы и приближенного) выполнения равенства (13).

3.1. Конформации адсорбированной макроцепи в случае незаряженного и неполяризованного сфероида

В отсутствие потенциального поля, т.е. при V = 0, аксиально-симметричное уравнение (3) (уравнение Гельмгольца) в вытянутых сфероидальных координатах принимает вид [32, 33]:

(14)

Индекс 0 у функции 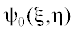в (14) отражает факт отсутствия потенциала ${{V}_{2}}({{\xi }})$ либо потенциала ${{V}_{2}}({{\xi ,\eta }})$.

Решения уравнения (14) могут быть представлены в факторизованном виде через радиальную $F({{\xi }})$ и угловую $S({{\eta }})$ вытянутые сфероидальные функции [32, 33]:

(15)
${{{{\psi }}}_{0}}({{\xi ,\eta ,}}\varphi ) = F({{\xi }})S({{\eta }})exp( \pm im\varphi ),\,\,\,\,m = 0,1,2 \ldots ~.~$

После разделения переменных (${{{{\lambda }}}_{{ml}}}$ – параметр разделения) для этих функций вытянутого сфероида [32] получаем два уравнения:

(16а)
$\begin{gathered} \frac{d}{{d{{\xi }}}}({{{{\xi }}}^{2}} - 1)\frac{d}{{d{{\xi }}}}{{F}_{{ml}}}(c,{{\xi }}) - \\ - \,\,\left[ {{{{{\lambda }}}_{{ml}}} - {{c}^{2}}({{{{\xi }}}^{2}} - 1) + \frac{{{{m}^{2}}}}{{({{{{\xi }}}^{2}} - 1)}}} \right]{{F}_{{ml}}}(c,{{\xi }}) = 0, \\ \end{gathered} $
(16б)
$\begin{gathered} \frac{d}{{d{{\eta }}}}(1 - {{{{\eta }}}^{2}})\frac{d}{{d{{\eta }}}}{{S}_{{ml}}}(c,{{\eta }}) + \\ + \,\,\left[ {{{{{\lambda }}}_{{ml}}} + {{c}^{2}}(1 - {{{{\eta }}}^{2}}) - \frac{{{{m}^{2}}}}{{(1 - {{{{\eta }}}^{2}})}}} \right]{{S}_{{ml}}}(c,{{\eta }}) = 0. \\ \end{gathered} $

В осесимметричном случае (m = 0) уравнения для радиальной и угловой функций вытянутого сфероида принимают вид

$\begin{gathered} \frac{d}{{d{{\xi }}}}\left[ {({{{{\xi }}}^{2}} - 1)\frac{d}{{d{{\xi }}}}{{F}_{{0l}}}(c,{{\xi }})} \right] - \\ - \,\,\left[ {{{{{\lambda }}}_{{0l}}} - {{c}^{2}}({{{{\xi }}}^{2}} - 1)} \right]{{F}_{{0l}}}(c,{{\xi }}) = 0, \\ \end{gathered} $
$\begin{gathered} \frac{d}{{d{{\eta }}}}\left[ {(1 - {{{{\eta }}}^{2}})\frac{d}{{d{{\eta }}}}{{S}_{{0l}}}(c,{{\eta }})} \right] + \\ + \,\,\left[ {{{{{\lambda }}}_{{0l}}} + {{c}^{2}}(1 - {{{{\eta }}}^{2}})} \right]{{S}_{{0l}}}(c,{{\eta }}) = 0. \\ \end{gathered} $

Угловые вытянутые сфероидальные функции (УВСФ) задаются в виде ряда [32]

(17)
${{S}_{{ml}}}(c,{{\eta }}) = \sum\limits_{r'\, = \,0,\,\,1}^\infty {d_{r}^{{ml}}(c)P_{{m + r}}^{m}({{\eta }})} ,$
где присоединенные полиномы Лежандра $P_{l}^{m}({{\eta }})$ удовлетворяют уравнению

$\begin{gathered} \frac{\partial }{{\partial {{\eta }}}}\left[ {(1 - {{{{\eta }}}^{2}})\frac{\partial }{{\partial {{\eta }}}}P_{l}^{m}({{\eta }})} \right] + \\ + \,\,\left[ {l(l + 1) - \frac{{{{m}^{2}}}}{{1 - {{{{\eta }}}^{2}}}}} \right]P_{l}^{m}({{\eta }}) = 0. \\ \end{gathered} $

После того как вычислены собственные значения ${{{{\lambda }}}_{{ml}}}$, коэффициенты $d_{r}^{{ml}}(c)$ находятся из рекуррентных соотношений [32].

Другая форма записи УВСФ удобна для использования при малых значениях параметра с (Приложение 1 . П1.1), т.е. при вырождении сфероида в сферу. В этом случае УВСФ ${{S}_{{ml}}}(c,{{\eta }})$ естественным образом трансформируются к виду с выделенным главным членом – присоединенным полиномом Лежандра $P_{l}^{m}({{\eta }})$.

3.2. Радиальная вытянутая сфероидальная функция

Вытянутые радиальные сфероидальные функции (ВРСФ) двух родов могут быть использованы для построения решения вблизи поверхности сфероида, а также в периферийной части адсорбированной макромолекулы, где плотность ее звеньев должна убывать с расстоянием. Возрастающую с ростом радиального аргумента функцию $F_{{ml}}^{{(1)}}(c,{{\xi }})$ можно выбрать в виде суперпозиции функций Бесселя ${{J}_{{m + r + 1/2}}}(c{{\xi }})$ мнимого аргумента с полуцелым индексом

(18)
$\begin{gathered} F_{{ml}}^{{(1)}}(c,{{\xi }}) = \sqrt {\frac{{{\pi }}}{{2c{{\xi }}}}} {{\left( {\frac{{{{{{\xi }}}^{2}} - 1}}{{{{{{\xi }}}^{2}}}}} \right)}^{{m/2}}} \times \\ \times \,\,{{\left[ {\sum\limits_{r' = 0,\,1}^\infty {d_{r}^{{ml}}(c)} \frac{{(2m + r)!}}{{r!}}} \right]}^{{ - 1}}} \times \\ \times \,\,\sum\limits_{r' = 0,\,1}^\infty {d_{r}^{{ml}}(c)} \frac{{(2m + r)!{{i}^{{r + m - l}}}}}{{r!}}{{J}_{{m + r + 1/2}}}(c{{\xi }}), \\ c = i\frac{d}{a}\sqrt {\frac{{3\left| {{\varepsilon }} \right|}}{{2kT}}} . \\ \end{gathered} $

Монотонно убывающую с ростом радиального аргумента функцию РВСФ $F_{{ml}}^{{(3)}}(c,{{\xi }})$ можно выбрать в виде суперпозиции функций Ханкеля $H_{{m + r + 1/2}}^{{(1)}}(c{{\xi }})$ первого рода мнимого аргумента с полуцелым индексом

(19)
$\begin{gathered} F_{{ml}}^{{(3)}}(c,{{\xi }}) = \sqrt {\frac{{{\pi }}}{{2c{{\xi }}}}} {{\left( {\frac{{{{{{\xi }}}^{2}} - 1}}{{{{{{\xi }}}^{2}}}}} \right)}^{{m/2}}} \times \\ \times \,\,{{\left[ {\sum\limits_{r' = 0,\,1}^\infty {d_{r}^{{ml}}(c)} \frac{{(2m + r)!}}{{r!}}} \right]}^{{ - 1}}} \times \\ \times \sum\limits_{r' = 0,\,1}^\infty {d_{r}^{{ml}}(c)} \frac{{(2m + r)!{{i}^{{r + m - l}}}}}{{r!}}H{{_{{m + r + 1/2}}^{{(1)}}}_{{}}}(c{{\xi }}), \\ c = i\frac{d}{a}\sqrt {\frac{{3\left| \varepsilon \right|}}{{2kT}}} \\ \end{gathered} $

При |c| → 0 сфероид вырождается в шар, и в качестве РВСФ вместо (18) и (19) можно использовать более простые выражения (П2.1) и (П2.2), приведенные в Приложении 2 .

В другом предельном случае больших значений параметра |c| $ \gg $ 1 сфероид превращается в цилиндр кругового сечения. Поведение радиальных сфероидальных функций при этом определяют функции Бесселя (П2.3) с целым индексом, но более сложным аргументом [32]. Выражениями (П2.4) определяется переход к общеупотребительным функциям Бесселя мнимого аргумента.

3.3. Осесимметричное решение краевой задачи

Решение уравнения (3) для осесимметричной конформационной функции ${{{{\psi }}}_{0}}({\mathbf{r}}) = {{{{\psi }}}_{0}}({{\xi ,\eta }})$ макроцепи для слоя ${{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d} \leqslant {{\xi }} \leqslant {{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}$ и снаружи этого слоя, т.е. при ${{\xi }} > {{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}$ может быть записано в виде

(20)
${{{{\psi }}}_{0}}({{\xi ,\eta }}) = \left\{ \begin{gathered} \sum\limits_l^\infty {\left[ {{{A}_{l}}F_{{0l}}^{{(1)}}(c,{{\xi }}) + {{B}_{l}}F_{{0l}}^{{(3)}}(c,{{\xi }})} \right]{{S}_{{0l}}}(c,{{\eta }}),\,\,\,\,{{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d} \leqslant {{\xi }} \leqslant {{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}} \hfill \\ \sum\limits_l^\infty {{{C}_{l}}F_{{0l}}^{{(3)}}(c,{{\xi }}){{S}_{{0l}}}(c,{{\eta }}),\,\,\,\,{{\xi }} > {{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}} \hfill \\ \end{gathered} \right..$

При этом граничные условия на поверхности сфероида и условие сшивки решений в точке разрыва первой производной (точке локализации дельта-функциональной адсорбционной ямы) определяются выражениями

$\begin{gathered} {{A}_{l}}F_{{0l}}^{{(1)}}(c,{{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d}) + {{B}_{l}}F_{{0l}}^{{(3)}}(c,{{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d}) = 0,{{{{\xi }}}_{a}} = {{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d}, \\ {{A}_{l}}F_{{0l}}^{{(1)}}(c,{{2(a + \delta {{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + \delta {{r}_{0}})} d}} \right. \kern-0em} d}) + {{B}_{l}}F_{{0l}}^{{(3)}}(c,{{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}) = \\ = {{C}_{l}}F_{{0l}}^{{(3)}}(c,{{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}){{{{\xi }}}_{{a + {{\delta }}}}} = {{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}. \\ \end{gathered} $

Коэффициенты Bl, Cl могут быть выражены через нормировочный коэффициент Al:

$\begin{gathered} {{B}_{l}} = - \frac{{F_{{0l}}^{{(1)}}(c,{{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d})}}{{F_{{0l}}^{{(3)}}(c,{{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d})}}{{A}_{l}}, \\ {{C}_{l}} = \left[ {1 - \frac{{F_{{0l}}^{{(3)}}(c,{{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d})F_{{0l}}^{{(1)}}(c,{{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d})}}{{F_{{0l}}^{{(1)}}(c,{{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d})F_{{0l}}^{{(3)}}(c,{{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d})}}} \right]{{B}_{l}}, \\ \end{gathered} $
а уравнение для собственных значений c получаем из условия конечного разрыва для первой производной РВСФ, вытекающего из уравнения (16а) в точке ${{{{\xi }}}_{{a + {{\delta }}}}} = {{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}$,

(21)
$\begin{gathered} F_{{{\text{II}}}}^{'}({{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}) - F_{{{\text{II}}}}^{'}({{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}) = \\ = - \frac{{3\alpha }}{{2{{a}^{2}}kT}}\frac{{{{F}_{{II}}}({{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d})}}{{{{{({{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d})}}^{2}} + 1}}. \\ \end{gathered} $

В случае заряженного или поляризованного металлического сфероида общее решение для конформационной функции получаем объединением “электронейтрального” решения (8) в суперпозиционной форме (16) решения краевой задачи с больцмановскими факторами (9) либо (10):

(22)
$\begin{gathered} {{\psi }}({{\xi ,\eta ,}}\phi ) = {{\psi }}_{0}^{S}({{\xi ,\eta ,}}\phi )W({{\xi ,\eta }}) = exp\left[ {{{ - {{V}_{2}}({{\xi ,\eta }})} \mathord{\left/ {\vphantom {{ - {{V}_{2}}({{\xi ,\eta }})} {kT}}} \right. \kern-0em} {kT}}} \right] \times \\ \times \,\,\left\{ {\begin{array}{*{20}{c}} {\sum\limits_l^\infty {\left[ {{{A}_{l}}F_{{0l}}^{{(1)}}(c,{{\xi }}) + {{B}_{l}}F_{{0l}}^{{(3)}}(c,{{\xi }})} \right]{{S}_{{0l}}}(c,{{\eta }}),} }&{{{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d} \leqslant {{\xi }} \leqslant {{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}} \\ {\sum\limits_l^\infty {{{C}_{l}}F_{{0l}}^{{(3)}}(c,{{\xi }}){{S}_{{0l}}}(c,{{\eta }}),} }&{{{\xi }} > {{2(a + {{\delta }}{{r}_{0}})} \mathord{\left/ {\vphantom {{2(a + {{\delta }}{{r}_{0}})} d}} \right. \kern-0em} d}} \end{array}} \right\}. \\ \end{gathered} $

Выражения (20)–(22) представляют полное решение задачи о конформациях гауссовой цепи полиэлектролита или полиамфолита, адсорбированной на электрически заряженном или поляризованном проводящем наносфероиде в стационарном внешнем поле.

4. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

4.1. МД-моделирование полиамфолитных полипептидов на поверхности поляризованной |или заряженной вытянутой сфероидальной золотой наночастицы

При МД-моделировании всех рассмотренных полиамфолитных полипептидов на нейтральной поверхности вытянутой сфероидальной золотой наночастицы происходила адсорбция макромолекул, а полиамфолитная макроцепь при этом обволакивала сфероид (рис. 1а) [35].

Рис. 1.

Полипептид A480R60D60 после МД-моделирования на незаряженной поверхности вытянутой сфероидальной золотой наночастицы (а), а также на поверхности наночастицы, поляризованной вдоль большой оси с дипольным моментом ${{p}_{{1.0}}}$, направленным снизу вверх (б). Полипептиды A480R60D60 (в) и A880R54D54 (г) на поверхности заряженной сфероидальной золотой наночастицы с полным зарядом ${{Q}_{{1.0}}}$. Светло-серая трубка – звенья Ala, черным цветом изображены звенья Arg, а серым – звенья Asp.

На рис. 2а (кривая 1) изображена зависимость средней линейной плотности атомов полипептида A480R60D60 вдоль большой оси вытянутого нейтрального золотого сфероида (положительные значения по оси абсцисс соответствуют верхней половине сфероида на рис. 1). Видно, что примерно на 4 нм в обе стороны от центра сфероида вдоль большой оси средняя линейная плотность атомов полипептида почти не изменяется, а при дальнейшем смещении к полюсам быстро снижается, что обусловлено резким уменьшением площади поверхности сфероида в приполярной области. На рис. 2б и 2в изображены радиальные зависимости средней плотности в центральной (на участке от –1 до +1 нм вдоль большой оси от центра сфероида) и в приполярной (на участке от 5 до 6 нм, вверху на рис. 1) областях нейтрального сфероида соответственно. В обоих случаях формируются характерные радиальные распределения средней плотности атомов с пиком у поверхности, которые схожи с ранее полученными распределениями при адсорбции полипептидов на плоской, цилиндрической и сферической поверхностях [13–20]. На рис. 2в (кривая 1) видно, что этот пик радиального распределения плотности атомов полипептида не такой острый в приполярной области в отличие от пика радиального распределения плотности атомов в центральной части нейтрального сфероида (рис. 2б). Это связано с резким изменением радиуса поперечного сечения сфероида в приполярной области, на участке от 5 до 6 нм, вдоль большой оси. Схожая картина наблюдалась и для остальных рассмотренных полиамфолитных полипептидов.

Рис. 2.

Распределение средней линейной плотности атомов полипептида A480R60D60 вдоль большой оси сфероидальной золотой наночастицы (а), а также радиальные зависимости средней плотности атомов полипептида в ее центральной области (б) и в области верхнего (рис. 1) полюса (в) при разных значениях дипольного момента, а также полного заряда наночастицы. Цифрами обозначены распределения: 1 – на нейтральной поверхности наночастицы, 2 и 3 – на поверхности поляризованной наночастицы с дипольным моментом ${{p}_{{0.5}}}$ и ${{p}_{{1.0}}}$, а 4 и 5 – заряженной наночастицы с полным зарядом ${{Q}_{{0.5}}}$ и ${{Q}_{{1.0}}}$.

При МД-моделировании на поверхности поляризованной вдоль большой оси (рис. 1б) сфероидальной золотой наночастицы происходила перестройка конформационной структуры всех рассмотренных полиамфолитов в большей степени в сильно заряженных приполярных областях (2), а в протяженной слабо заряженной центральной области сфероида конформационные изменения были незначительны. В заряженных приполярных областях наблюдалось выбрасывание петель макроцепи вдоль нормали к поверхности сфероида. При этом на поверхности был адсорбирован аминокислотный остаток со знаком заряда, противоположным знаку заряда поверхности (для положительно заряженной области это был остаток Asp), аминокислотный остаток другого знака максимально отдалялся от поверхности, а между ними находились нейтральные звенья Ala. Таким образом, плотность адсорбированной макромолекулы плавно изменялась от рыхлой на полюсах к плотной в центральной части сфероидальной наночастицы.

На рис. 2а (кривые 2 и 3) изображены распределения средней линейной плотности атомов полипептида A480R60D60 вдоль большой оси сфероида в зависимости от значения его дипольного момента (положительные значения по оси абсцисс соответствуют положительно заряженной половине сфероида). Видно, что они мало отличаются от распределения линейной плотности атомов макроцепи на поверхности нейтральной сфероидальной наночастицы. На рис. 2б (кривые 2 и 3) показаны радиальные распределения средней плотности атомов полипептида в центральной слабо заряженной области сфероида при различных значениях его дипольного момента, которые практически совпадают за исключением небольших флуктуаций. При этом в приполярных областях поляризованного сфероида радиальные распределения средней плотности атомов полипептида значительно отличаются от случая неполяризованной сфероидальной наночастицы (рис. 2в, кривые 2 и 3). На графиках видно, что по мере увеличения дипольного момента сфероида пиковое значение радиального распределения плотности атомов полипептида в приполярной области уменьшается, а сам пик смещается, удаляясь от поверхности. Это показывает, что в данной пространственной области адсорбированная макромолекула набухает.

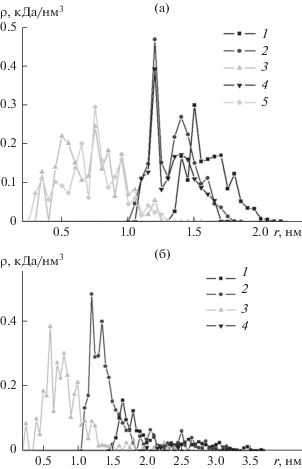
На рис. 3а изображены радиальные распределения плотности атомов аминокислотных остатков Asp полипептида A480R60D60 на поверхности поляризованного с дипольным моментом ${{p}_{{1.0}}}$ вытянутого золотого сфероида на разных участках вдоль большой оси: в экваториальной области (кривая 1), в области положительно (кривая 3) и отрицательно (кривая 5) заряженных полюсов, посередине между центром сфероида и его полюсами – положительным (кривая 2) и отрицательным (кривая 4). Видно, что в положительно заряженной половине сфероида (кривые 2 и 3) звенья Asp находятся у его поверхности, а в отрицательно заряженной половине отдалены от нее (кривые 4 и 5).

Рис. 3.

Радиальные зависимости средней плотности атомов аминокислотных остатков Asp полипептида A480R60D60 на поверхности поляризованного с дипольным моментом ${{p}_{{1.0}}}$ (а) и заряженного с полным зарядом ${{Q}_{{1.0}}}$ (б) наносфероида в разных областях вдоль его большой оси: 1 – в экваториальной области, посередине между центром сфероида и его полюсом – верхним (2) и нижним (4), в верхней (3) и нижней (5) приполярных областях.

Для остальных рассмотренных полиамфолитных полипептидов наблюдался сходный характер конформационных изменений с учетом того, что чем больше было расстояние между положительными и отрицательными звеньями в макроцепи, тем бóльшим был размер петель макроцепи, “выброшенных” по нормали к поверхности в раствор. Соответственно толщина адсорбированного макромолекулярного слоя в приполярных областях также становилась большей.

Другой характер конформационных изменений имел место при адсорбции полиамфолита на заряженной вытянутой сфероидальной металлической наночастице. На рис. 1в и 1г видно, что в отличие от случая поляризованного сфероида наблюдается выбрасывание петель полипептида вдоль нормали к поверхности сфероида не только в приполярных областях, но и по всей поверхности наночастицы. При этом, чем больше расстояние между разноименно заряженными звеньями в макроцепи рассмотренных полипептидов, тем сильнее эффект такого набухания (рис. 1г).

На рис. 2а (кривые 4 и 5) изображено распределение средней линейной плотности атомов полиамфолитного полипептида A480R60D60 вдоль большой оси сфероида в зависимости от значения его полного заряда. Как и в случае поляризованного сфероида, распределение средней линейной плотности макроцепи почти не отличается от случая адсорбции на нейтральной поверхности. На рис. 2б (кривые 4 и 5) изображены радиальные распределения плотности атомов полипептида в центральной области заряженного сфероида. Видно, что в отличие от случая поляризованного сфероида в центральной области заряженного сфероида по мере увеличения значения его полного заряда происходит все большее набухание адсорбированной макромолекулы. Это связано с отталкиванием положительно заряженных звеньев Arg от положительно заряженной поверхности сфероидальной наночастицы, что приводило к выбрасыванию петель макроцепи в раствор в центральной области сфероида. В приполярных областях (рис. 2в, кривые 4 и 5) характер радиальных распределений плотности атомов полипептида на заряженном сфероиде был схож со случаем адсорбции на поляризованной сфероидальной наночастице. При этом пиковые значения радиальных распределений плотности атомов полипептида в центральной и промежуточных (посередине между полюсом и центром сфероида вдоль большой оси) областях наносфероида с полным зарядом ${{Q}_{{1.0}}}$ почти не различались, а в приполярных областях они были лишь немногим меньше. На рис. 3б видно, что все звенья Asp находятся у поверхности сфероидальной наночастицы с полным зарядом ${{Q}_{{1.0}}}$ во всех ее областях в отличие от случая адсорбции на поверхности поляризованного сфероида (рис. 3а).

4.2. МД-моделирование отрицательно заряженных полипептидов на поверхности поляризованной или положительно заряженной вытянутой сфероидальной золотой наночастицы

На рис. 4а и 4б представлены результирующие конформации отрицательно заряженного полипептида A720D80 на поверхности вытянутой заряженной сфероидальной золотой наночастицы со значениями полного заряда ${{Q}_{{0.25}}}$ и ${{Q}_{{1.0}}}$ соответственно. Видно, что при увеличении значения полного заряда сфероида все отрицательно заряженные звенья Asp смещаются на положительно заряженную поверхность сфероида, а в раствор выбрасываются петли, состоящие из аминокислотных остатков Ala. Чем больше было расстояние между остатками Asp в макроцепи рассмотренных заряженных полипептидов, тем более длинные фрагменты макроцепи в виде петель выбрасывались в раствор. Кроме того, несмотря на неоднородное распределение плотности поверхностных зарядов на поверхности заряженного сфероида (1), перемещения звеньев макроцепи вдоль большой оси сфероида не происходило. Это видно на рис. 5а (кривые 1 и 2), где изображены зависимости линейной плотности адсорбированного полипептида A720D80 при различных значениях полного заряда сфероидальной наночастицы.

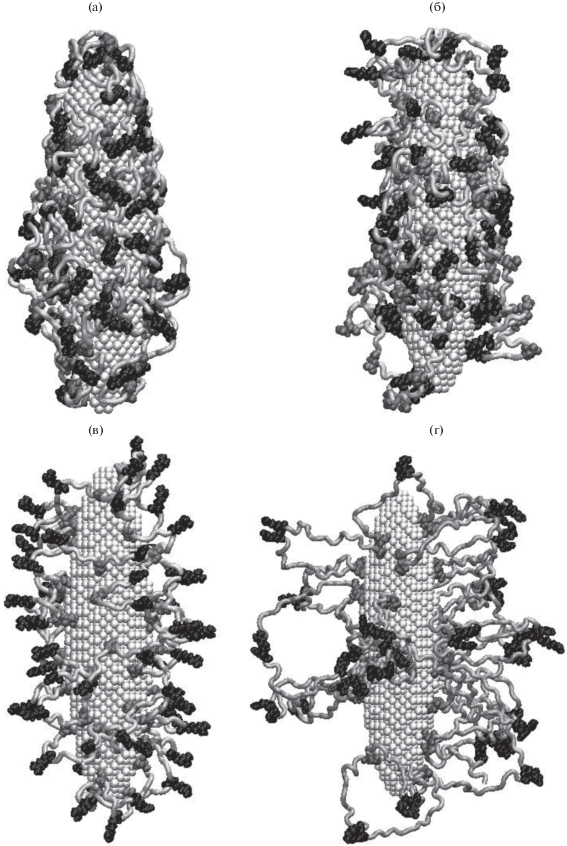
Рис. 4.

Полипептид A720D80 после МД-моделирования на поверхности заряженной вытянутой сфероидальной золотой наночастицы с полным зарядом ${{Q}_{{0.25}}}$ (а) и ${{Q}_{{1.0}}}$ (б) или поляризованной вдоль большой оси с направленным снизу вверх дипольным моментом ${{p}_{{0.5}}}$ (в) и ${{p}_{{1.0}}}$ (г). Светло-серая трубка – звенья Ala, черным цветом изображены звенья Asp.

Рис. 5.

Распределение средней линейной плотности атомов полипептида A720D80 вдоль большой оси сфероидальной золотой наночастицы (а), а также радиальные зависимости средней плотности атомов полипептида в центральной области (б) и в области верхнего (рис. 4) полюса (в) при различных значениях полного заряда, а также дипольного момента наночастицы. Цифрами обозначены распределения на заряженной наночастице с полным зарядом ${{Q}_{{0.25}}}$ (1) и ${{Q}_{{1.0}}}$ (2), а также на поляризованной наночастице с дипольным моментом ${{p}_{{0.25}}}$ (3), ${{p}_{{0.5}}}$ (4) и ${{p}_{{1.0}}}$ (5).

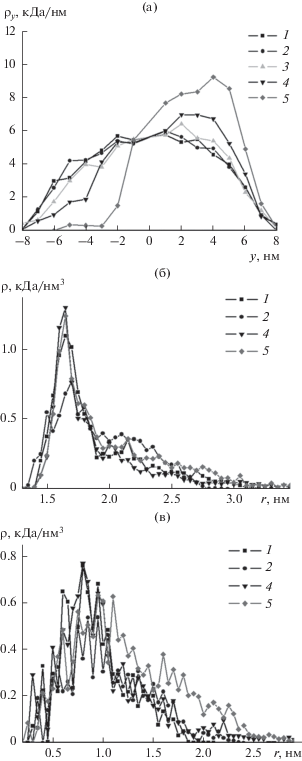
На рис. 5б и 5в (кривые 1 и 2) изображены радиальные распределения плотности атомов полипептида A720D80 в центральной и приполярной областях наносфероида при различных значениях его полного заряда. Видно, что пики радиальных зависимостей средней плотности атомов макроцепи в центральной (рис. 5б) и приполярной области (рис. 5в) при увеличении значения полного заряда наносфероида уменьшаются, что говорит о набухании адсорбированной макромолекулы. Как и в случае рассмотренных выше полиамфолитов, адсорбированных на поверхности заряженной сфероидальной наночастицы, пиковые значения радиальных распределений плотности атомов полипептида в центральной и промежуточных (посередине между полюсом и центром сфероида вдоль большой оси) областях заряженного наносфероида с полным зарядом ${{Q}_{{1.0}}}$ почти не различались, постепенно снижаясь в приполярных областях. На рис. 6а видно, что кривые радиальных распределений плотности атомов аминокислотных остатков Asp полипептида A720D80 схожи с аналогичными кривыми, построенными для макромолекулы полиамфолита на поверхности заряженного сфероида (рис. 3б).

Рис. 6.

Радиальные зависимости средней плотности атомов аминокислотных остатков Asp полипептида A720D80 на поверхности заряженного с полным зарядом ${{Q}_{{1.0}}}$ (а) и поляризованного с дипольным моментом ${{p}_{{1.0}}}$ (б) наносфероида в разных областях вдоль его большой оси: 1 – в экваториальной области, посередине между центром сфероида и его полюсом – верхним (2) и нижним (4), а также в верхней (3) и нижней (5) приполярных областях.

На поверхности поляризованной вдоль большой оси вытянутой сфероидальной золотой наночастицы по мере увеличения значения ее дипольного момента происходило смещение звеньев отрицательно заряженного полипептида в положительно заряженную половину сфероида. На рис. 4в и 4г видно, что при значении дипольного момента сфероида ${{p}_{{0.5}}}$ на поверхности отрицательно заряженной приполярной области звенья полипептида A720D80 отсутствуют, а при значении дипольного момента ${{p}_{{1.0}}}$ практически все звенья макроцепи сместились в верхнюю положительно заряженную половину сфероидальной наночастицы. Аналогичная картина наблюдалась и для полипептида A760D40, а в случае полипептида A640D160 с наибольшим полным зарядом макроцепи все ее звенья сместились в положительно заряженную половину сфероида уже при значении его дипольного момента ${{p}_{{0.5}}}$.

На графиках зависимости линейной плотности атомов полипептида A720D80 вдоль большой оси сфероидальной наночастицы от значения ее дипольного момента (рис. 5а, кривые 3–5) видно, что при увеличении значения дипольного момента происходит все большее смещение звеньев макроцепи в положительно заряженную область поляризованного сфероида. Пиковые значения радиальных распределений средней плотности атомов полипептида A720D80 в центральной области сфероида (рис. 5б, кривые 4 и 5) при различных значениях дипольного момента сфероида почти не различаются, а сами зависимости имеют схожий вид. На рис. 5в (кривые 4 и 5) изображены радиальные зависимости средней плотности атомов полипептида в положительно заряженной приполярной области поляризованной сфероидальной наночастицы. Видно, что при увеличении дипольного момента сфероида (кривая 5) происходит набухание адсорбированной макроцепи в этой области, что связано со смещением звеньев из нижней отрицательно заряженной области сфероида (рис. 4г) в положительно заряженную приполярную область. Радиальные зависимости средней плотности атомов аминокислотных остатков Asp полипептида A720D80 на поверхности поляризованного с дипольным моментом ${{p}_{{1.0}}}$ (рис. 6б) наносфероида в разных областях вдоль его большой оси также показывают, что произошло смещение звеньев отрицательно заряженной макромолекулы в положительно заряженную половину сфероида. Как следствие, в нижней отрицательно заряженной половине сфероида (рис. 4в) значения радиальных распределений плотности атомов аминокислотных остатков Asp полипептида A720D80 имеют значения, близкие к нулю.

5. ЗАКЛЮЧЕНИЕ

Таким образом, на поверхности заряженной, а также поляризованной вдоль большой оси вытянутой сфероидальной металлической наночастицы конформационная структура адсорбированных полиэлектролитов существенно отличается от структуры полиэлектролитов, адсорбированных как на поверхностях поляризованной сферической наночастицы и поперечно поляризованного цилиндрического нанопровода, так и на однородно заряженных металлических поверхностях плоской, цилиндрической и сферической формы [13–21].

В случае полиамфолитных полипептидов структура адсорбированной макромолекулы на поверхности поляризованного вытянутого металлического сфероида оказывается рыхлой в его приполярных областях сфероида и плотной в его центральной области. Такое набухание адсорбированных макромолекул в приполярной области сфероида обусловлено выбросом вдоль нормали к поверхности петель макроцепи, содержащих на концах заряженные звенья одного знака с зарядом на поверхности металлической сфероидальной наночастицы в ее приполярной области. При адсорбции однородно заряженных полипептидов на поляризованной сфероидальной наночастице происходит смещение макроцепи в противоположно заряженную по отношению к заряду макромолекулы приполярную область сфероида и ее набухание в этой области.

При адсорбции на поверхности заряженной вытянутой сфероидальной наночастицы как полиамфолитных, так и однородно заряженных полипептидов наблюдается набухание адсорбированных макромолекул по всей поверхности наносфероида. При этом в случае полиамфолитных полипептидов макромолекулярная “опушка” состоит из трех слоев: на поверхности находятся звенья макроцепи, противоположно заряженные по отношению к поверхности сфероида, далее идет слой нейтральных звеньев, а во внешнем слое находятся звенья, заряженные одноименно с поверхностью сфероида. Толщина такой опушки тем больше, чем больше расстояние между противоположно заряженными звеньями в полипептиде. В случае однородно заряженных полипептидов набухание адсорбированной макромолекулы на поверхности противоположно заряженной сфероидальной наночастицы связано с выбросом петель, образованных нейтральными звеньями.

Такие конформационные изменения на поверхности вытянутых сфероидальных нанообъектов могут быть использованы как при создании новых, так и модификации существующих сенсоров на основе эффекта гигантского комбинационного рассеяния, нанозондов с переключаемыми под воздействием электрического поля параметрами, а также в ближнепольной оптической микроскопии. Кроме того такие наноструктуры могут быть использованы в оптимизированном варианте люминесцентно-оптическго измерителя концентрации молекулярного (в том числе синглетного) кислорода в газах и жидких растворах [28, 29].

ПРИЛОЖЕНИЕ 1

Другая форма записи УВСФ (17) удобна для использования при малых значениях параметра с, т.е. при вырождении сфероида в шар. В этом случае УВСФ естественным образом трансформируются к виду с выделенным главным членом – присоединенным полиномом Лежандра:

(П1.1)
$\begin{gathered} {{S}_{{ml}}}(c,{{\eta }}) = P_{l}^{m}({{\eta }}) + \sum\limits_{k = 1}^\infty {{{c}^{{2k}}}{{{[S({{\eta }})]}}_{k}}} , \\ {{{{\lambda }}}_{{ml}}} = l(l + 1) + \sum\limits_{k = 1}^\infty {{{c}^{{2k}}}{{{[{{\lambda }}]}}_{{2k}}},} \\ {{[{{\lambda }}]}_{2}} = \frac{1}{2}\left[ {1 - \frac{{(2m - 1)(2m + 1)}}{{(2l - 1)(2l + 3)}}} \right], \\ {{[S({{\eta }})]}_{k}} = d_{{l - m}}^{{ml}}(c)\sum\limits_{r = l - m - 2k \geqslant 0}^{l - m + 2k} {{{{[{{d}_{r}}]}}_{k}}P_{{m + r}}^{m}({{\eta }})} . \\ \end{gathered} $

ПРИЛОЖЕНИЕ 2

Поведение радиальных сфероидальных функций (18) и (19) при |с| → 0 будут определяться следующими функциями Бесселя и Ханкеля с полуцелым индексом:

(П2.1)
$\begin{gathered} F_{{ml}}^{{(1)}}(c,{{\xi }}) = \\ = \,\,\sqrt {\frac{{{\pi }}}{{2c{{\xi }}}}} {{\left( {\frac{{{{{{\xi }}}^{2}} - 1}}{{{{{{\xi }}}^{2}}}}} \right)}^{{m/2}}}{{J}_{{m + r + 1/2}}}(c{{\xi }}) + O({{c}^{2}}), \\ c = i\frac{d}{a}\sqrt {\frac{{3\left| {{\varepsilon }} \right|}}{{2kT}}} , \\ \end{gathered} $
(П2.2)
$\begin{gathered} F_{{ml}}^{{(3)}}(c,{{\xi }}) = \\ = \,\,\sqrt {\frac{{{\pi }}}{{2c{{\xi }}}}} {{\left( {\frac{{{{{{\xi }}}^{2}} - 1}}{{{{{{\xi }}}^{2}}}}} \right)}^{{m/2}}}H_{{m + r + 1/2}}^{{(1)}}(c{{\xi }}) + O({{c}^{2}}), \\ c = i\frac{d}{a}\sqrt {\frac{{3\left| {{\varepsilon }} \right|}}{{2kT}}} \\ \end{gathered} $

Поведение радиальных сфероидальных функций при больших параметрах |c| $ \gg $ 1 определяют функции Бесселя с целым индексом, но сложным аргументом [32]:

(П2.3)
$\begin{gathered} {{F}_{{ml}}}(c,{{\xi }}) = \sqrt {\frac{{{\pi }}}{{2c{{\xi }}}}} \times \\ \times \,\,{{J}_{m}}\left( {c\sqrt {{{{{\xi }}}^{2}} - 1} - \frac{{2(l - m) + 1}}{2}{\text{arctg}}\sqrt {{{{{\xi }}}^{2}} - 1} } \right) \times \\ \times \,\,\left[ {1 + O\left( {\frac{1}{c}} \right)} \right]. \\ \end{gathered} $

Цилиндрические функции мнимого аргумента выражаются через обычные функции Бесселя и Ханкеля первого рода

(П2.4)
$\begin{gathered} {{I}_{{{\nu }}}}(x) = exp\left( { - \frac{{{\pi }}}{2}\nu i} \right){{J}_{{{\nu }}}}(ix), \\ {{K}_{{{\nu }}}}(x) = \frac{{{{\pi }}i}}{2}exp\left( {\frac{{{\pi }}}{2}{{\nu }}i} \right)H_{{{\nu }}}^{{(1)}}(ix), \\ \end{gathered} $
причем

$H_{{{\nu }}}^{{(1)}}(x) = \frac{i}{{sin({{\pi \nu }})}}\left[ {{{J}_{{{\nu }}}}(x)exp\left( { - i{{\pi \nu }}} \right) - {{J}_{{ - {{\nu }}}}}(x)} \right].$

Это дает возможность записать вытянутые радиальные сфероидальные функции через монотонно изменяющиеся функции Бесселя мнимого аргумента, удобные для построения решения краевой задачи уравнения (3).

Список литературы

  1. Tang M., Gandhi N.S., Burrage K., Gu Y. // Langmuir. 2019. V. 35. P. 4435.

  2. Walsh T.R. // Acc. Chem. Res. 2017. V. 50. P. 1617.

  3. Dahal U., Dormidontova E.E. // Macromolecules. 2020. V. 53. P. 8160.

  4. Sajib M.S.J., Sarker P., Wei Y., Tao X., Wei T. // Langmuir. 2020. V. 36. P. 13356.

  5. Chen Y., Cruz-Chu E.R., Woodard J., Gartia M.R., Schulten K., Liu L. // ACS Nano. 2012. V. 6. P. 8847.

  6. Ramezani F., Amanlou M., Rafii-Tabar H. // J. Nanoparticle Res. 2014. V. 16. P. 2512.

  7. Shao Q., Hall C.K. // Nanoscale. 2017. V. 9. P. 380.

  8. Klimov V.V., Ducloy M., Letokhov V.S. // Chem. Phys. Lett. 2002. V. 358. P. 192.

  9. Liaw J.-W., Wu H.-Y., Huang C.-C., Kuo M.-K. // Nanoscale Res. Lett. 2016. V. 11. Article 26.

  10. Chandra S., Doran J., McCormack S.J. // J. Colloid Interface Sci. 2015. V. 459. P. 218.

  11. Piralaee M., Asgari A., Siahpoush V. // Optik. 2018. V. 172. P. 1064.

  12. Norton S.J., Vo-Dinh T. // IEEE Trans. Nanotechnol. 2007. V. 6. P. 627.

  13. Кручинин Н.Ю., Кучеренко М.Г. // Коллоид. журн. 2019. Т. 81. С. 175.

  14. Кручинин Н.Ю., Кучеренко М.Г. // Коллоид. журн. 2020. Т. 82. С. 177.

  15. Kruchinin N.Yu., Kucherenko M.G. // Biophysics. 2020. V. 65. No. 2. P. 186.

  16. Кручинин Н.Ю., Кучеренко М.Г. // Коллоид. журн. 2020. Т. 82. С. 440.

  17. Kruchinin N.Yu., Kucherenko M.G. // Russ. J. Phys. Chem. A. 2020. V. 94. P. 1433.

  18. Кручинин Н.Ю., Кучеренко М.Г. // Коллоид. журн. 2021. Т. 83. С. 57.

  19. Kruchinin N.Yu., Kucherenko M.G., Neyasov P.P. // Russ. J. Phys. Chem. A. 2021. V. 95. P. 362.

  20. Kruchinin N.Yu., Kucherenko M.G. // Eurasian Physical Technical J. 2021. P. 16.https://doi.org/10.31489/2021No1/16-28

  21. Кручинин Н.Ю. // Коллоид. журн. 2021. Т. 83. С. 302.

  22. Ландау Л. Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982.

  23. Phillips J.C., Braun R., Wang W., Gumbart J., Tajkhor-shid E., Villa E., Chipot C., Skeel R.D., Kale L, Schul-ten  K. // J. Comput. Chem. 2005. V. 26. P. 1781.

  24. MacKerell A.D. Jr., Bashford D., Bellott M., Dunbrack R.L., Jr., Evanseck J.D., Field M.J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F.T.K., Mattos C., Michnick S., Ngo T., Nguyen D.T., Prodhom B., Reiher III W.E., Roux B., Schlenkrich M., Smith J.C., Stote R., Straub J., Watanabe M., Wiorkiewicz-Kuczera J., Yin D., Karplus M. // J. Phys. Chem. B. 1998. V. 102. P. 3586.

  25. Heinz H., Vaia R.A., Farmer B.L., Naik R.R. // J. Phys. Chem. C. 2008. V. 112. P. 17281.

  26. Darden T., York D., Pedersen L. // J. Chem. Phys. 1993. V. 98. P. 10089.

  27. Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., Klein M.L. // J. Chem. Phys. 1983. V. 79. P. 926.

  28. Kucherenko M.G., Rusinov A.P., Chmereva T.M., Ignat’ev A.A., Kislov D.A., Kruchinin N.Yu. // Optics and Spectroscopy. 2009. V. 107. P. 480.

  29. Kucherenko M.G., Izmodenova S.V., Kruchinin N.Yu., Chmereva T.M. // High Energy Chem. 2009. V. 43. P. 592.

  30. Кучеренко М.Г., Кручинин Н.Ю., Чмерева Т.М. // Вестник ОГУ. 2010. № 5. С. 124.

  31. Гросберг А.Ю., Хохлов А.P. Статистическая физика макромолекул. М.: Наука, 1989.

  32. Комаров И.В., Пономарев Л.И., Славянов С.Ю. Сфероидальные и кулоновские сфероидальные функции. М.: Наука, 1976.

  33. Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979.

  34. Смайт В. Электростатика и электродинамика. М.: Изд. ИЛ, 1954.

  35. Humphrey W., Dalke A., Schulten, K. // J. Mol. Graphics. 1996. V. 14. P. 33.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал