Коллоидный журнал, 2021, T. 83, № 6, стр. 634-643

ВВЕДЕНИЕ

Управление физическими свойствами жидкостей с помощью внешнего магнитного поля позволяет получить новые решения ряда технических и инженерных задач. Магнитные жидкости, как искусственно синтезированные материалы, легко управляются слабыми магнитными полями. Помещая магнитную жидкость во внешнее магнитное поле, можно легко изменять ее поведение и физические свойства, такие как вязкость, упругость, теплопроводность, оптическая проницаемость [1, 2].

Опубликовано достаточно большое число работ, посвященных исследованию вязкостных свойств магнитных жидкостей (см., например, [3–6]), которые позволяют решить задачи, связанные с их применением в качестве смазывающих материалов, измерительных приборов, герметизирующих устройств. Вместе с тем многие колебательные системы, созданные на основе магнитных жидкостей, такие как амортизаторы и демпфирующие устройства, датчики перемещения и акустические системы, основаны на упругих колебаниях магнитных жидкостей [6, 7]. Следовательно, требуется детальный теоретический анализ упругих свойств магнитных жидкостей.

В [8] теоретически исследованы магнитореологические свойства магнитных жидкостей с кластерными частицами и показано, что предложенная модель объясняет обнаруженные в экспериментах эффекты длительной релаксации напряжения с характерным временем и существованием остаточного напряжения, сохраняющегося после прекращения течения среды.

Механическая реакция эластомерных композитов с железными частицами на приложенное магнитное поле исследована в [9]. Показано, что модуль упругости композита под воздействием магнитного поля увеличивается на 30–40%. Также изучено влияние частоты на модуль упругости и показано, что возрастание частоты приводит к увеличению этого модуля композитного материала.

Упругие свойства магнитных гелей, представляющих собой намагничивающиеся частицы, распределенные в мягкой и упругой матрице, исследованы в [10, 11].

В [12] представлены результаты теоретического изучения эффективного модуля сдвига магнитного геля, состоящего из намагниченных частиц, изотропно распределенных в упругой матрице. Там же, на основе аналогии между решениями задач о вязком течении и упругих свойствах, а также известных результатов теории намагничиваемости макроскопическое напряжение композита представили в виде

где ${{\sigma }_{{{\text{el}}}}} = {{G}_{{{\text{el}}}}}\gamma $ – напряжение сдвига в упругом композите с твердыми частицами, ${{G}_{{{\text{el}}}}}$ – соответствующий модуль сдвига композита, ${{\sigma }_{{\text{m}}}} = \frac{1}{2}\varphi {{\mu }_{0}}\left\langle {{{M}_{x}}} \right\rangle $ – часть общего напряжения, создаваемая приложенным магнитным полем, $\left\langle {{{M}_{x}}} \right\rangle $ – соответствующая составляющая намагниченности, усредненная по всем относительным положениям частиц в композите, $\varphi $ – объемная концентрация частиц, ${{\mu }_{0}}$ – магнитная проницаемость вакуума.

На основе результатов работы Бэтчелора и Грина [13] эффективный модуль сдвига ${{G}_{{{\text{el}}}}}$ представлен в виде

где ${{G}_{0}}$ является модулем сдвига материала матрицы композита.

Как известно, формула (2) для обычных суспензий и композитных материалов хорошо описывает экспериментальные данные при концентрации частиц твердой фазы до 10–15%. Для более точного определения модуля сдвига феррожидкостей, магнитных суспензий и магнитных гелей, необходимо учесть магнитное взаимодействие между твердыми частицами.

В [12] при учете магнитного взаимодействия твердых частиц показано, что при незначительной магнитоиндуцированной анизотропии приложенное поле приводит к уменьшению модуля сдвига, тогда как сильная анизотропия может вызвать его увеличение с возрастанием напряженности магнитного поля.

Целью настоящей работы является теоретическое исследование упругих свойств магнитных жидкостей и влияния внешнего магнитного поля на сдвиговый и объемный модули упругости.

ФИЗИЧЕСКАЯ МОДЕЛЬ И УРАВНЕНИЯ

Одним из основных свойств жидкостей является их текучесть и способность к свободному изменению формы. При изменении формы в жидкости не возникает сил, стремящихся вернуть ее в первоначальное состояние, т.е. жидкости не обладают упругими свойствами по отношению к изменениям формы. В то же время жидкости проявляют идеальные упругие свойства по отношению к изменению объема. Следовательно, единственной упругой реакцией жидкости на медленное внешние воздействие является ее сопротивление всестороннему сжатию, характеризующееся коэффициентом изотермической сжимаемости ${{\beta }_{T}}$ или соответствующим адиабатическим объемным модулем упругости ${{K}_{{\text{S}}}}.$

Если жидкость подвергается очень быстрым внешним воздействиям, в ней обнаруживаются упругие свойства такого же рода, как в упругом твердом теле. В жидкостях, наряду с вязким течением, проявляется упругость, при этом жидкости, становясь неньютоновскими, подчиняются обобщенному закону Гука, а их реологическое уравнение является уравнением Кельвина–Фойгта или уравнением Максвелла. Тензор напряжения, возникающего в жидкости, складывается из упругого напряжения, пропорционального деформации среды ${\mathbf{u}},$ и вязкого напряжения, пропорционального скорости деформации ${\mathbf{\dot {u}}}$ [14]:

В этом случае каждому виду переноса соответствуют определенный модуль упругости, т.е. между уравнениями теории упругости и соответствующими уравнениями движения вязких жидкостей можно обнаружить аналогию, где кинетическим коэффициентам объемной ${{\eta }_{{\text{v}}}}$ и сдвиговой ${{\eta }_{{\text{s}}}}$ вязкости соответствуют объемный $K$ и сдвиговый $\mu $ модули упругости.

Ранее [15–17] были исследованы вязкостные свойства магнитных жидкостей для модели двухкомпонентной системы, состоящей из ферритной (далее обозначаемой индексом f) и молекулярной (индекс s) частей. На основе полученных аналитических выражений для динамических коэффициентов объемной ${{\eta }_{{\text{v}}}}(\omega )$ и сдвиговой ${{\eta }_{{\text{s}}}}(\omega )$ вязкости магнитных жидкостей были проведены численные расчеты зависимости коэффициентов переноса от частоты внешнего возмущения и термодинамических параметров системы. Полученные результаты показали удовлетворительное согласие с литературными данными.

В [15, 16] на основе кинетических уравнений для одночастичной ${{f}_{{1i}}}({{{\mathbf{q}}}_{1}},{{{\mathbf{p}}}_{1}},t)$ и двухчастичной ${{f}_{{2i}}}({{{\mathbf{q}}}_{1}},{{{\mathbf{q}}}_{2}},{{{\mathbf{p}}}_{1}},{{{\mathbf{p}}}_{2}},t)$ функций распределения частиц магнитной жидкости

получена система уравнений обобщенной гидродинамики, в которой микроскопическое выражение для тензора напряжения имеет вид где $K_{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ = ${{P}_{{{\text{k}}i}}}\left( {{{{\mathbf{q}}}_{1}},t} \right){{\delta }^{{\alpha \beta }}} + k_{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ – кинетическая часть тензора потока импульса $i$-ой подсистемы, ${{P}_{{{\text{k}}i}}}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ = $\frac{1}{3}\int {\frac{{p_{1}^{2}}}{{{{m}_{i}}}}{{f}_{{1i}}}\left( {{{{\mathbf{q}}}_{1}},{{{\mathbf{p}}}_{1}},t} \right)d{{{\mathbf{p}}}_{1}}} $ – кинетическая часть неравновесного давления, $k_{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ = = $\int {\frac{1}{{{{m}_{i}}}}{\kern 1pt} \left( {p_{1}^{\alpha }p_{1}^{\beta } - \frac{1}{3}p_{1}^{2}{{\delta }^{{\alpha \beta }}}} \right){\kern 1pt} {{f}_{{1i}}}\left( {{{{\mathbf{q}}}_{1}},{{{\mathbf{p}}}_{1}},t} \right)d{{{\mathbf{p}}}_{1}}} {\kern 1pt} {\kern 1pt} - $ кинетическая часть вязкого тензора напряжения, ${{n}_{{2i}}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t)$ – неравновесная бинарная плотность, ${{\sigma }_{i}}$ – диаметр частицы соответствующей подсистемы, r = $ = {{\left| {{{{\mathbf{q}}}_{2}} - {{{\mathbf{q}}}_{1}}} \right|} \mathord{\left/ {\vphantom {{\left| {{{{\mathbf{q}}}_{2}} - {{{\mathbf{q}}}_{1}}} \right|} \sigma }} \right. \kern-0em} \sigma } = {x \mathord{\left/ {\vphantom {x \sigma }} \right. \kern-0em} \sigma }$ – безразмерное расстояние между частицами. Уравнения для ${{P}_{{\text{k}}}}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ и ${{k}^{{\alpha \beta }}}\left( {{{{\mathbf{q}}}_{1}},t} \right),$ полученные на основе уравнения (4), приведены в [18], где найдены их решения.

Согласно (6) тензор напряжения магнитной жидкости определяется посредством функций бинарной плотности частиц ${{n}_{{2i}}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t),$ для которых необходимо иметь уравнение. Интегрируя уравнение (5) по импульсам ${{{\mathbf{p}}}_{1}}$ и ${{{\mathbf{p}}}_{2}},$ после некоторых преобразований получим обобщенное уравнение Смолуховского для возмущенной части неравновесной функции бинарной плотности частиц i-ой подсистемы магнитной жидкости в конфигурационном пространстве [16]:

где ${{R}_{{\text{s}}}}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right) = - {{\varphi }_{{\text{s}}}}\left( r \right){\text{div}}{\mathbf{\dot {u}}} - \varphi _{{\text{s}}}^{{\alpha \beta }}\left( r \right)\left\{ {\frac{{\partial {{{\dot {u}}}^{\alpha }}}}{{\partial q_{1}^{\beta }}}} \right\},$${{\hat {L}}_{i}} = - \frac{\partial }{{\partial {{r}^{\alpha }}}}\left[ {\frac{\partial }{{\partial {{r}^{\alpha }}}} - \frac{\partial }{{\partial {{r}^{\alpha }}}}ln{{g}_{i}}\left( r \right)} \right]$ – оператор Смолуховского в конфигурационном пространстве, ${{\omega }_{{0i}}} = {1 \mathord{\left/ {\vphantom {1 {{{\tau }_{{0i}}}}}} \right. \kern-0em} {{{\tau }_{{0i}}}}} = {{2kT} \mathord{\left/ {\vphantom {{2kT} {{{\beta }_{i}}\sigma _{i}^{2}}}} \right. \kern-0em} {{{\beta }_{i}}\sigma _{i}^{2}}},$ ${{n}_{i}},$ ${{\beta }_{i}},$ ${{C}_{{Vi}}},$ ${{P}_{i}}$ и ${{g}_{i}}$ – соответствующие i-ой подсистеме характерная частота, числовая плотность, коэффициент трения, теплоемкость, давление и радиальная функция распределения, $T$ – температура системы, $H$ – внешнее магнитное поле, ${\mathbf{m}}$ – магнитный момент магнитной частицы, ${\mathbf{u}}$ – вектор смещения.

Решение уравнения для $n_{{2i}}^{'}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t),$ приведенное в [16], имеет следующий вид:

Функция являясь функцией Грина или фундаментальным решением однородного уравнения Смолуховского, описывает пространственно-временнóе поведение неравновесной бинарной плотности ${{n}_{{2i}}}({{{\mathbf{q}}}_{1}},{\mathbf{r}},t)$ под действием приложенной гидродинамической силы ${{R}_{i}}\left( {{{{\mathbf{q}}}_{1}},{\mathbf{r}},t} \right).$

Из анализа (7) и (8) видно, что процесс перестройки структуры магнитной жидкости носит диффузионный характер и описывается непрерывным спектром времен релаксации.

Теперь, записывая неравновесную бинарную плотность в виде, состоящем из локально-равновесной и возмущенной частей:

где $n_{{2i}}^{0}\left( {\left| {\mathbf{r}} \right|,{{n}_{i}}({{{\mathbf{q}}}_{1}},t),T({{{\mathbf{q}}}_{1}},t)} \right)$ = $n_{{2i}}^{0}(\left| {\mathbf{r}} \right|) + {{\left( {\frac{{\partial n_{{2i}}^{0}(\left| {\mathbf{r}} \right|)}}{{\partial {{n}_{i}}}}} \right)}_{T}}$ × $ \times \,\,n_{i}^{'}({{{\mathbf{q}}}_{1}},t)$ + ${{\left( {\frac{{\partial n_{{2i}}^{0}(\left| {\mathbf{r}} \right|)}}{{\partial T}}} \right)}_{{{{n}_{i}}}}}T{\kern 1pt} '({{{\mathbf{q}}}_{1}},t),$ $n_{{2i}}^{0}(\left| {\mathbf{r}} \right|) = n_{i}^{{\text{2}}}{{g}_{i}}(\left| {\mathbf{r}} \right|)$ – равновесная бинарная плотность, далее подставляя решение (8) в определение (9) и учитывая его вместе с решениями ${{P}_{{{\text{k}}i}}}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ и $k_{i}^{{\alpha \beta }}\left( {{{{\mathbf{q}}}_{1}},t} \right)$ из [17] в (6), и совершив после этого в нем фурье-преобразование по времени, получим: где ${{G}_{{0i}}}(r,{{r}_{1}},\omega )$ = $\int_0^t {{{e}^{{i\omega (t - {{t}_{1}})}}}{{G}_{i}}(r,{{r}_{1}},t - {{t}_{1}})d{{t}_{1}}} .$

Используя в (10) термодинамические соотношения

${{P}_{i}}(0) = {{P}_{{{\text{k}}i}}}(0) - \frac{{n_{i}^{2}\sigma _{i}^{3}}}{6}\int_{ - \infty }^\infty {\frac{{\partial {{\Phi }_{i}}}}{{\partial r}}{{g}_{i}}rd{\mathbf{r}}} ,$ ${{\left( {\frac{{\partial {{P}_{i}}(0)}}{{\partial {{n}_{i}}}}} \right)}_{T}}$ = $ = kT - \frac{{n_{i}^{2}\sigma _{i}^{3}}}{6}\int_{ - \infty }^\infty {\frac{{\partial {{\Phi }_{i}}}}{{\partial r}}{{{\left( {\frac{{\partial {{g}_{i}}}}{{\partial {{n}_{i}}}}} \right)}}_{T}}rd{\mathbf{r}}} ,$ ${{\left( {\frac{{\partial {{P}_{i}}(0)}}{{\partial T}}} \right)}_{{{{n}_{i}}}}} = {{n}_{i}}T$ –$ - \,\,\frac{{n_{i}^{2}\sigma _{i}^{3}}}{6}\int_{ - \infty }^\infty {\frac{{\partial {{\Phi }_{i}}}}{{\partial r}}{{{\left( {\frac{{\partial {{g}_{i}}}}{{\partial T}}} \right)}}_{{{{n}_{i}}}}}rd{\mathbf{r}}} $ и фурье-образ ${{R}_{i}}({{{\mathbf{q}}}_{1}},{{{\mathbf{r}}}_{1}},\omega ),$ выражение для тензора напряжения приводим к следующему виду:

Из выражения (11) видно, что, как и в (1), в присутствии магнитного поля тензор напряжения в магнитной жидкости складывается из напряжения, возникающего в отсутствие поля, и напряжения, создаваемого приложенным полем.

Далее в (11), применяя к реальной и мнимой частям функции ${{G}_{{0i}}}(r,{{r}_{1}},\omega )$ косинус и синус преобразования Фурье соответственно и сравнивая полученное выражение с фурье-образом (3) для динамических релаксационного объемного ${{K}_{{\text{r}}}}(\omega ) = K(\omega ) - {{K}_{{\text{S}}}}$ и сдвигового $\mu (\omega )$ модулей упругости магнитной жидкости, получим:

Здесь

${{\varphi }_{{(1,2)i}}}\left( {r,{{r}_{1}},\omega } \right)$ = ${{\left( {\frac{{\omega {{\tau }_{{0i}}}}}{2}} \right)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}\left( {r \mp {{r}_{1}}} \right),$ ${{\tau }_{{1i}}} = \frac{{{{m}_{i}}}}{{2{{\beta }_{i}}}}$ – время трансляционной релаксации вязкого тензора напряжений, ${{\tau }_{{0i}}} = \frac{{{{\beta }_{i}}\sigma _{i}^{2}}}{{2kT}}$ – феноменологическое время структурной релаксации.

Выражения (12) позволяют определить динамические модули упругости магнитной жидкости в широком диапазоне изменения частоты и термодинамических параметров состояния. Первое слагаемое $\mu (\omega )$ учитывает трансляционную релаксацию в магнитной жидкости с характерными временами ${{\tau }_{{1i}}}.$ Потенциальные части $K(\omega )$ и $\mu (\omega )$ содержат функции ${{\Gamma }_{i}}\left( {r,{{r}_{1}},\omega } \right)$ с характерными временами ${{\tau }_{{0i}}}$ и определяют вклад структурной релаксации в модули упругости.

ЧИСЛЕННЫЕ РАСЧЕТЫ И ОБСУЖДЕНИЕ

Для проведения численных расчетов в (12) необходимо выбрать явный вид потенциальных энергий взаимодействия ${{\Phi }_{i}}$ между структурными единицами каждой подсистемы и соответствующие радиальные функции распределения ${{g}_{i}}.$

Энергию взаимодействия молекулярной подсистемы выбираем в виде модели Штокмайера

где $\Phi _{{\text{s}}}^{{{\text{L}} - {\text{J}}}}(r) = 4{{\varepsilon }_{{\text{s}}}}({{r}^{{ - 12}}} - {{r}^{{ - 6}}}),$ ${{\Phi }^{{{\text{pp}}}}}({\mathbf{r}})$ = $\frac{{{{p}^{2}}}}{{4\pi \varepsilon {{\varepsilon }_{0}}\sigma _{{\text{s}}}^{3}}}$ × × $\left[ {\frac{{({{{\mathbf{e}}}_{a}}{{{\mathbf{e}}}_{b}})}}{{r_{{ab}}^{3}}} - \frac{{3({{{\mathbf{e}}}_{a}}{{{\mathbf{r}}}_{{ab}}})({{{\mathbf{e}}}_{b}}{{{\mathbf{r}}}_{{ab}}})}}{{r_{{ab}}^{5}}}} \right].$

В магнитной подсистеме, считая феррочастицы сферическими однодоменными частицами, покрытыми слоем поверхностно-активного вещества, и находящимися под действием внешнего магнитного поля, представим их взаимодействие в виде

где $\Phi _{{\text{f}}}^{{{\text{L}} - {\text{J}}}}(r) = 4{{\varepsilon }_{{\text{f}}}}({{r}^{{ - 12}}} - {{r}^{{ - 6}}}),$ ${{\Phi }^{{{\text{mm}}}}}({\mathbf{r}}) = \frac{{{{\mu }_{0}}{{m}^{2}}}}{{4\pi \sigma _{{\text{f}}}^{{\text{3}}}}}$ × × $\left[ {\frac{{({{{\mathbf{e}}}_{a}}{{{\mathbf{e}}}_{b}})}}{{r_{{ab}}^{3}}} - \frac{{3({{{\mathbf{e}}}_{a}}{{{\mathbf{r}}}_{{ab}}})({{{\mathbf{e}}}_{b}}{{{\mathbf{r}}}_{{ab}}})}}{{r_{{ab}}^{5}}}} \right],$ ${{\Phi }^{{\text{H}}}}({\mathbf{H}}) = - {{\mu }_{0}}{\mathbf{mH}}.$

При переходе к сферической системе координат выражение для энергии диполь-дипольного взаимодействия примет вид:

где при $d = p$ и $d = m$ имеем соответственно ${{A}^{{\text{p}}}} = \frac{1}{{4\pi \varepsilon {{\varepsilon }_{0}}\sigma _{{\text{s}}}^{3}}}$ и ${{A}^{{\text{m}}}} = \frac{{{{\mu }_{0}}}}{{4\pi \sigma _{{\text{f}}}^{{\text{3}}}}}.$

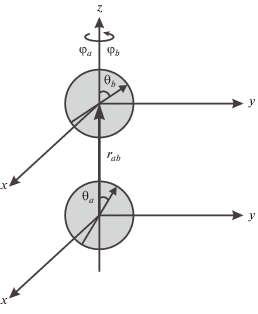
Непосредственная подстановка потенциалов (13)–(15) в выражении (12) приводит к сложным математическим трудностям. С целью упрощения задачи, следуя работам [19, 20], для двух ближайших частиц момент первой частицы принимаем направленным вдоль радиус-вектора, соединяющего ее со второй частицей, и, соответственно, в (15), положив ${{\theta }_{a}} = 0,$ ${{\theta }_{b}} = \theta $ (рис. 1), энергию взаимодействия двух диполей выражаем в виде

Аналогично, направляя вектор магнитного поля ${\mathbf{H}}$ параллельно оси $z$ системы, для потенциальной энергии магнитодипольного взаимодействия феррочастиц получим: Радиальные функции распределения в соответствии с [21] выбираем в виде где ${{y}_{{\text{s}}}}(\rho *) = {{(2 - \rho _{{\text{s}}}^{*})} \mathord{\left/ {\vphantom {{(2 - \rho _{{\text{s}}}^{*})} {2{{{(1 - \rho _{{\text{s}}}^{*})}}^{3}}}}} \right. \kern-0em} {2{{{(1 - \rho _{{\text{s}}}^{*})}}^{3}}}}$ – контактная функция Карнахана–Старлинга для молекулярной подсистемы, соответствующей системе с плотноупакованными твердыми частицами, $\rho _{{\text{s}}}^{*} = {{\pi {{\sigma }^{3}}{{n}_{{\text{s}}}}} \mathord{\left/ {\vphantom {{\pi {{\sigma }^{3}}{{n}_{{\text{s}}}}} 6}} \right. \kern-0em} 6}.$

Подставляя (13), (14) и (16) в выражение (12), приведем их к виду, удобному для проведения численных расчетов:

где ${{a}_{{\text{s}}}} = \frac{{{{p}^{2}}}}{{2\pi \varepsilon {{\varepsilon }_{0}}\sigma _{s}^{3}r_{1}^{3}kT}},$ ${{a}_{{\text{f}}}} = \frac{{{{\mu }_{0}}{{m}^{2}}}}{{2\pi \sigma _{{\text{f}}}^{3}r_{1}^{3}kT}} + \frac{{{{\mu }_{0}}mH}}{{kT}},$ $y{{_{{\text{s}}}^{'}}_{{}}}(\rho *)$ = = $\frac{{\rho _{{\text{s}}}^{*}(5 - 2\rho _{{\text{s}}}^{*})}}{{(1 - \rho _{{\text{s}}}^{*})(2 - \rho _{{\text{s}}}^{*})}},$ ${{\varepsilon }_{{\text{f}}}},$ ${{\varepsilon }_{{\text{s}}}}$ – глубины потенциальных ям для соответствующих подсистем, $l$ – характерный размер системы.

Учитывая в (17), что ${{n}_{{\text{f}}}} = \frac{{{{N}_{{\text{f}}}}}}{V} = \frac{{{{\rho }_{{\text{f}}}}{{N}_{{\text{A}}}}}}{{{{\mu }_{{\text{f}}}}}}\varphi {\text{,}}$ ${{n}_{{\text{s}}}} = \frac{{{{N}_{{\text{s}}}}}}{V}\frac{{{{\rho }_{{\text{s}}}}{{N}_{{\text{A}}}}}}{{{{\mu }_{{\text{s}}}}}}(1 - \varphi )$ и раскрывая суммы, получим:

Видно, что в пределе $\varphi \to {\text{0}}$ объемный и сдвиговый модули упругости магнитных жидкостей стремятся к значениям модулей упругости жидкости-основы ${{K}_{{\text{s}}}}$ и ${{\mu }_{{\text{s}}}}$ соответственно. Если в (18) при малых значениях концентрации не учитывать квадратичные зависимости по $\varphi ,$ выражения для модулей упругости принимают вид выражения, приведенного в [12, 13, 22], аналогичного выражению Эйнштейна для эффективной вязкости разбавленных суспензий.

Для определения области частотной дисперсии динамических модулей упругости ${{K}_{{\text{r}}}}(\omega )$ и $\mu (\omega )$ необходимо вычислить характерные времена ${{\tau }_{{1i}}} = {{{{m}_{i}}} \mathord{\left/ {\vphantom {{{{m}_{i}}} {2{{\beta }_{i}}}}} \right. \kern-0em} {2{{\beta }_{i}}}}$ и ${{\tau }_{{0i}}} = {{{{\beta }_{i}}\sigma _{i}^{2}} \mathord{\left/ {\vphantom {{{{\beta }_{i}}\sigma _{i}^{2}} {2kT,}}} \right. \kern-0em} {2kT,}}$ которые определяются через соответствующие коэффициенты внутреннего трения ${{\beta }_{i}}.$ Как известно, в статистической теории коэффициент трения определяется на основе обобщенной теории броуновского движения, в которой устанавливается его связь с межмолекулярными силами и параметрами состояния системы. Отметим, что исследователями для нахождения коэффициента трения на основе различных приближений предложены несколько моделей [23, 24], однако проблема его определения на основе статистических методов до сих пор остается нерешенной. Анализ, проведенный в [24], показал, что наиболее удовлетворительным для расчета коэффициентов внутреннего трения магнитной жидкости является полуфеноменологическое выражение, полученное Кирквудом в виде

С учетом выбранных потенциальных энергий и радиальных функций распределения последнее выражение приводится к виду где ${{g}_{{{\text{0s}}}}}(r) = {{y}_{{\text{s}}}}(\rho *)\exp \left[ {{{ - \Phi _{{\text{s}}}^{{{\text{L}} - {\text{J}}}}(r)} \mathord{\left/ {\vphantom {{ - \Phi _{{\text{s}}}^{{{\text{L}} - {\text{J}}}}(r)} {kT}}} \right. \kern-0em} {kT}}} \right],$ ${{g}_{{{\text{0f}}}}}(r)$ = $ = \exp \left[ {{{ - {\kern 1pt} \Phi _{{\text{f}}}^{{{\text{L}} - {\text{J}}}}(r)} \mathord{\left/ {\vphantom {{ - {\kern 1pt} \Phi _{{\text{f}}}^{{{\text{L}} - {\text{J}}}}(r)} {kT}}} \right. \kern-0em} {kT}}} \right].$

В табл. 1 приведены результаты численных расчетов коэффициентов трения, проведенных на основе (19), и соответствующие значения времен релаксации магнитных жидкостей, приготовленных на основе керосина (${{\sigma }_{{\text{s}}}} = 0.43\,\,{\text{нм,}}$ ${{\varepsilon }_{{\text{s}}}} = 0.6kT,$ $\varepsilon = 2.1,$ $p = 8.3 \times {{10}^{{ - 30}}}\,\,{\text{Кл}}\,{\text{м}}$) или воды (${{\sigma }_{{\text{s}}}} = 0.27\,\,{\text{нм,}}$ ${{\varepsilon }_{{\text{s}}}} = 1.27kT,$ ε = 81, p = 6.2 × $ \times \,\,{{10}^{{ - 30}}}\,\,{\text{Кл}}\,{\text{м}}$) и частиц Fe₃O₄, при m = $ = {{10}^{{ - 20}}}\,\,{{{\text{Дж}}} \mathord{\left/ {\vphantom {{{\text{Дж}}} {{\text{Тл}}}}} \right. \kern-0em} {{\text{Тл}}}}{\text{,}}$ ${{\sigma }_{{\text{f}}}} = 5\,\,{\text{нм,}}$ ${{\varepsilon }_{{\text{f}}}} = 0.37kT.$

Видно, что трансляционная релаксация в обеих подсистемах магнитных жидкостей протекает очень быстро. Времена структурной релаксации всегда на 2–3 порядка меньше времени трансляционной релаксации.

Далее на основе (17) были проведены численные расчеты частотных зависимостей релаксационного объемного и сдвигового модулей упругости магнитных жидкостей на основе керосина и воды. Результаты расчетов продемонстрированы на рис. 2 и 3. Кривые 1 и 3 соответствуют объемной концентрации $\varphi = {\text{0}}{\text{.03,}}$ кривые 2 и 4 – $\varphi = {\text{0}}{\text{.1}}{\text{.}}$

Данные, приведенные на рис. 2 и 3, показывают, что с увеличением частоты внешнего возмущения модули упругости возрастают и качественно согласуются с результатами экспериментов [9], проведенных для композитных материалов с частицами железа. Для обеих магнитных жидкостей дисперсия объемного и сдвигового модулей упругости начинается примерно с частоты ${{10}^{8}}{\text{ Гц}}$ и при высоких частотах стремится к постоянному значению, соответствуя теоретическим выводам [25, 26]. Согласно рис. 3, для магнитной жидкости на основе воды модули упругости в низкочастотной области возрастают с концентрацией магнитной фазы, напротив, при высоких частотах увеличение ее концентрации приводит к уменьшению модулей упругости. Такой эффект для магнитной жидкости на основе керосина не наблюдается.

На рис. 4 и 5 приведены зависимости величины ${{{{K}_{{\text{r}}}}(\omega )} \mathord{\left/ {\vphantom {{{{K}_{{\text{r}}}}(\omega )} {\mu (\omega )}}} \right. \kern-0em} {\mu (\omega )}}$ от частоты для магнитных жидкостей на основе керосина и воды. С увеличением частоты значение ${{{{K}_{{\text{r}}}}(\omega )} \mathord{\left/ {\vphantom {{{{K}_{{\text{r}}}}(\omega )} {\mu (\omega )}}} \right. \kern-0em} {\mu (\omega )}}$ для магнитной жидкости на основе керосина при $\varphi = {\text{0}}{\text{.1}}$ изменяется от 4 до 1.5, а для магнитной жидкости на основе воды при той же концентрации отношение ${{{{K}_{{\text{r}}}}(\omega )} \mathord{\left/ {\vphantom {{{{K}_{{\text{r}}}}(\omega )} {\mu (\omega )}}} \right. \kern-0em} {\mu (\omega )}}$ лежит в пределах 3.5–3, что обусловлено вкладом структурной релаксации и согласуется с выводами феноменологической релаксационной теории [27, 28]. Для обеих жидкостей в области высоких частот отношение модулей упругости остается постоянным. Согласно [28], отношение высокочастотных модулей упругости ${{{{K}_{\infty }}} \mathord{\left/ {\vphantom {{{{K}_{\infty }}} {{{\mu }_{\infty }}}}} \right. \kern-0em} {{{\mu }_{\infty }}}}$ для сильно ассоциированных жидкостей определенно больше, чем для углеводородных и полимерных жидкостей. Это различие, по-видимому, связано [28] со слабостью ван-дер-ваальсовых сил в углеводородных и полимерных жидкостях по сравнению с относительно сильными водородными связями, существующими в ассоциированных жидкостях. Такой же результат можно наблюдать на рис. 4 и 5: для магнитной жидкости на основе керосина ${{{{K}_{\infty }}} \mathord{\left/ {\vphantom {{{{K}_{\infty }}} {{{\mu }_{\infty }}}}} \right. \kern-0em} {{{\mu }_{\infty }}}} \approx 1.5,$ а для магнитной жидкости на основе воды ${{{{K}_{\infty }}} \mathord{\left/ {\vphantom {{{{K}_{\infty }}} {{{\mu }_{\infty }}}}} \right. \kern-0em} {{{\mu }_{\infty }}}} \approx 3.$

На рис. 6 и 7 продемонстрированы результаты численных расчетов зависимостей изочастотных ($\omega = {{10}^{{12}}}\,\,{\text{Гц}}$) релаксационного объемного и сдвигового модулей упругости магнитных жидкостей на основе керосина и воды от напряженности внешнего магнитного поля.

Согласно рис. 6 и 7, как объемный, так и сдвиговый модули упругости обеих магнитных жидкостей монотонно возрастают с увеличением $H$ магнитного поля. Также видно, что увеличение концентрации магнитных частиц приводит к более быстрому возрастанию модулей упругости с увеличением значения $H.$ Возрастание модулей упругости магнитных жидкостей в зависимости от приложенного магнитного поля аналогично магнитовязкому эффекту, наблюдаемому в экспериментах, и подтверждает правильность учета диполь-дипольного взаимодействия магнитных частиц и их взаимодействия с внешним магнитным полем. Проведенные расчеты зависимости модулей упругости от напряженности магнитного поля находятся в качественном согласии с результатами экспериментальных и теоретических исследований [8, 9, 11].

ЗАКЛЮЧЕНИЕ

На основе кинетических уравнений для одночастичных и двухчастичных функций распределения получены аналитические выражения для динамических релаксационного объемного ${{K}_{{\text{r}}}}(\omega )$ и сдвигового $\mu (\omega )$ модулей упругости магнитной жидкости, потенциальные части которых определены через равновесные потенциальные энергии межчастичного взаимодействия ${{\Phi }_{i}}({\mathbf{r}})$ и равновесные радиальные функции распределения ${{g}_{i}}(r,{{n}_{i}},T).$ Показано, что в пределе малых концентраций выражения для модулей упругости трансформируются в выражение для модуля сдвига, полученное Бэтчелером и Кристенсеном [13, 22].

Исследована частотная зависимость динамических модулей упругости магнитных жидкостей на основе керосина и воды, и установлено, что область дисперсии модулей упругости, как следствие учета структурной релаксации, является широкой, и при высоких частотах, как и в [25, 26], они стремятся к постоянным значениям высокочастотных модулей упругости ${{K}_{\infty }}$ и ${{\mu }_{\infty }}.$ Показано, что отношение модулей упругости для магнитных жидкостей при изменении частоты лежит в пределах интервала 1.5–4, который согласуется с интервалом 0.5–10, указанным в [27].

Проведенные численные расчеты зависимостей модулей упругости магнитных жидкостей от напряженности внешнего магнитного поля при различных значениях концентрации магнитной фазы показали их возрастание с увеличением напряженности внешнего поля, аналогичное магнитовязкому эффекту.

На основе полученных результатов можно заключить, что учет потенциала диполь-дипольного взаимодействия магнитных частиц и их взаимодействия с внешним магнитным полем в аналитических выражениях для модулей упругости позволяет адекватно описать упругие свойства магнитных жидкостей.