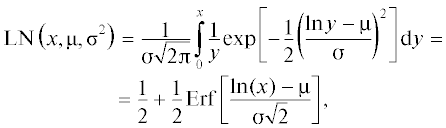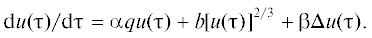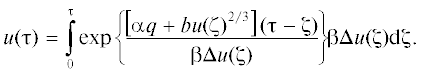Коллоидный журнал, 2022, T. 84, № 1, стр. 84-96

ВВЕДЕНИЕ

Как известно, металлические и полуметаллические порошки являются исходным сырьем для многих промышленных металлургических технологий [1, 2]. Такие технологии включают, как правило, стадию механической обработки (механоактивацию) порошковых материалов в мельницах различного типа [3]. Механообработка используется, в частности, для получения заранее заданных гранулометрических характеристик порошка, которые зависят от физико-химических условий и продолжительности процесса (см., например, [4–7]).

В научной литературе опубликовано достаточное количество исследований, в которых этому вопросу уделяется должное внимание (см., например, [4–15]). Однако в большинстве из них рассматриваются лишь конкретные порошковые системы, а анализ временнóго поведения статистических характеристик ансамблей микрочастиц носит узко эмпирический характер. Такой подход не позволяет заранее предсказать влияние условий механической обработки порошковых материалов в каждом новом случае и, в частности, оптимизировать длительность процесса, или заранее выбрать подходящую размольную среду.

Исключение составляет цикл работ Малышева с сотрудниками (см. статьи [16, 17] и ссылки в них на собственные работы группы). В этих статьях изложены результаты разработки вероятностно-статистической модели кинетики процесса измельчения руд, обладающей прогностическими возможностями. Такая модель позволяет успешно предсказывать временные изменения фракционного состава ансамбля упруго-хрупких частиц при их механообработке в мельницах различного типа. Однако физико-механические характеристики обрабатываемого материала, а, следовательно, и вероятностные параметры, определяющие гранулометрический состав отдельных фракций и межфракционные переходы в ансамбле частиц, предполагаются в данной модели не зависящими от времени). Такая модель не применима для описания процесса механической обработки металлических порошков, который включает пластической моду изменения формы частиц. Влияние этой моды на процесс механообработки порошка зачастую приводит к заметному изменению физико-механических характеристик материала частиц в этом процессе.

В данной работе для решения указанных выше проблем предлагается простейшая кинетическая модель процесса механообработки металлических и полуметаллических порошковых материалов, включающая в рассмотрение пластическую деформацию, а также учитывающая динамический и стохастический факторы. Модель позволяет на основе знания физико-химических, кинетических и граничных условий процесса механообработки описать и/или заранее предсказать вариации во времени статистических характеристик функций распределения порошковых частиц по их объемным, или линейным размерам. Модель построена на базе массива экспериментальных данных, полученных авторами.

МАТЕРИАЛЫ И МЕТОДЫ

В экспериментах использовали следующие кристаллические микропорошки промышленного производства: алюминий марки АСД-4 (средний объемно-взвешенный линейный размер (диаметр) частиц d_v = 20–30 мкм), вольфрам ПВ-2 (d_v = = 10–20 мкм), гафний ГФМ (d_v = 10–20 мкм), магний МПФ-4 (d_v = 150–250 мкм), никель ПНК-УТ3 (d_v = 8–15 мкм), титан ПТМ-1 (d_v = 50–60 мкм), цирконий ИМП (d_v = 10–20 мкм), а также аморфный бор Б-99В (d_v = 2–4 мкм).

Механообработка микропорошков проводилась в лабораторной планетарно-центробежной шаровой мельнице АГО-2У с водяным охлаждением. Мелющими телами служили изготовленные из сплава ШХ-15 шары диаметром 6 мм и общей массой М = 100 г. Масса порошковой пробы в индивидуальном эксперименте составляла m = 10 г. Круговая скорость орбитального вращения цилиндрических барабанов-контейнеров Ω = 1062 об./мин, частота этого вращения ν₀ = Ω/2π = 169 рад/мин. Продолжительность механообработки t индивидуальной порошковой пробы фиксировалась во временнóм интервале от 3 до 21 мин (в некоторых случаях – до 50 мин). В качестве размольной среды использовали очищенный неполярный гексан.

Гранулометрические характеристики порошков и их смесей определяли с помощью жидкофазного (в среде пропанола) трехлазерного дифрактометрического анализатора высокого разрешения Microtrac S3500. Для разрушения агрегатов слабосвязанных микрочастиц, образующихся в порошковом материале в результате его “слеживания”, проводилось предварительное ультразвуковое вибрационное диспергирование загруженных в рабочий объем анализатора порошковых проб в течение 3–6 мин.

Для каждой исследованной порошковой пробы были построены интегральные и дифференциальные функции распределения микрочастиц по размерам и определены их моменты: средний объемно-взвешенный диаметр 〈d_v〉 ≡ mv(t), средний поверхностно-взвешенный диаметр 〈d_s〉 ≡ ma(t), средний численно-взвешенный диаметр 〈d_n〉 ≡ ≡ mn(t), а также стандартное среднеквадратичное отклонение sd(t) = D(t)^0,5, где D(t) – дисперсия функции распределения. Вычисляли также временные зависимости медианы распределения Dia(t), а также асимметрию ski(t) и эксцесс kg(t) этой функции [18]. В рамках модели сферических микрочастиц рассчитывали удельную поверхность порошка cs(t).

РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ

Рассмотрим одномодальную двухпараметрическую интегральную функцию распределения логарифмически нормального вида LN(x,μ,σ²):

со случайной безразмерной переменной х > 0, количественно характеризующей индивидуальную микрочастицу (например, ее приведенный объем $v{\text{/}}{{v}_{0}}$ или приведенный диаметр d/d₀) и имеющей два безразмерных параметра: –∞ < μ < +∞, σ > 0) [18–20]. Здесь величины ${{v}_{0}}$ и d₀ – заранее выбранные масштабирующие единицы объема и диаметра микрочастиц.

Соответствующая ей дифференциальная функция lnN(x,μ,σ²) (плотность вероятности значений переменной x такого распределения) имеет следующий вид:

Наиболее информативными статистическими характеристиками этого распределения являются [18–21]: математическое ожидание (среднее значение) случайной переменной E[x] = 〈x〉 = exp(μ + + 0.5σ²), медиана этого распределения Dia[x] = = е^μ, его мода Mo[x] = exp(μ – σ²) и дисперсия .

Начальные моменты k-того порядка указанной функции распределения рассчитываются по общей формуле: ${\text{E[}}{{x}^{k}}{\text{]}} = \exp (k{{\mu }} + 0.5{{k}^{2}}{{{{\sigma }}}^{2}}),\,\,\,\,k \in [N].$

Для первичного анализа массива полученных экспериментальных данных проводили сопоставление их интервального ранжированного статистического ряда (выборки) с соответствующими значениями стандартной интегральной функции распределения (1).

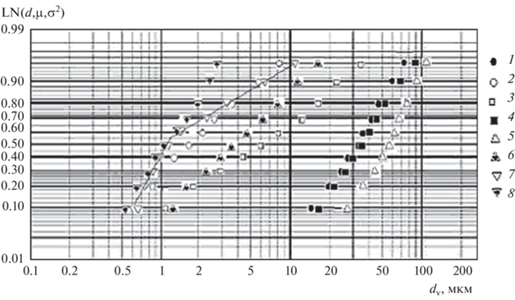
На рис. 1 представлены примеры зафиксированных в статистических экспериментах интегральных функций распределения микрочастиц по их объемно-взвешенным линейным размерам d_v = хd_v0 [мкм] для исходных микропорошков. Графики на рисунке построены в функциональных координатах, спрямляющих логарифмически нормальные интегральные функции распределения типа (1) (см. [22]). Соответствующие графоаналитические построения свидетельствуют о достаточной близости экспериментальных функций к логнормальной группе. На непротиворечивость этой гипотезы полученным экспериментальным данным указывают рассчитанные для каждого случая значения критериев согласия Колмогорова и χ²-Пирсона при уровне значимости 0.05 [19–21].

Опыты показали, что соответствующие функции распределения, как правило, являются логнормальными и одномодальными (в редких случаях – бимодальными). Такие их характеристики определяются методами промышленного получения указанных металлических порошков: физико-химическими – золь-гель технологиями, перекристаллизацией в пересыщенных растворах, или механическим – дроблением массивных полуфабрикатов. Теоретически доказано (см., например, [23, 24]), что при использовании этих методов получения порошков соответствующие функции распределения должны быть логнормальными и одномодальными.

Как показали наши многочисленные эксперименты, механообработка микропорошков в шаровой мельнице в размольной среде чистого гексана при разной длительности процесса не изменяет, вообще говоря, принятую для их статистического описания логнормальную математическую форму и структуру функций интегрального и дифференциального распределений частиц по их объемно-взвешенным линейным размерам. Вариации граничных условий и длительности могут влиять лишь на количество мод, наклон прямолинейной графической линии в спрямляющих координатах (функционально зависящий от дисперсии распределения), а также на значение медианы и среднее значение линейных размеров микрочастиц 〈d_v〉 (сравните рис. 1 и 2).

Так, например, в том случае, когда твердость порошковых микрочастиц существенно превышает твердость мелющих тел, при их механообработке возможно царапающее “квазишлифование” микрочастицами поверхности инструмента с выделением продуктов износа в размольную среду. В таких нештатных ситуациях исходная интегральная одномодальная функция распределения (1), полученная, например, для механически необработанных частиц порошкового бора (см. рис. 1), может стать бимодальной, как это показано на рис. 2. Бимодальность функции распределения в данном случае появляется благодаря присутствию в такой порошковой пробе новой фракции микрочастиц продуктов износа. Однако при проведении экспериментов по механообработке микропорошков в шаровых мельницах таких случаев следует избегать как артефактов.

Обобщая полученные экспериментальные результаты, можно заключить, что изменение физико-химических условий и длительности процесса механообработки микропорошковых материалов в шаровой планетарной мельнице может сводиться лишь к влиянию указанных факторов на параметры логнормальной функции распределения μ и σ или, что то же самое (согласно приведенным выше определениям статистических характеристик – моментов), на среднее значение E₁[x] = = 〈x〉 = $\left\langle {{{{(v{\text{/}}\theta )}}^{{1/3}}}} \right\rangle $ соответствующей функции распределения, на ее медиану Dia[х], дисперсию D[х] = (sd[x])²= E₂[x] = E[(x – 〈x〉)²], а также на приведенные центральные моменты более высокого порядка: коэффициенты асимметрии ski(x) = = Е₃[x] = E[(x – 〈x〉 )³]/(sd[х])³] и эксцесса Ex(x) = = kg(x) = Е₄[x] = {E[(x – 〈x〉)⁴]/(D[x]])²} – 3]. В приведенных формулах символом E обозначена операция усреднения по ансамблю микрочастиц, а коэффициент θ является фактором формы индивидуальной микрочастицы. Для микрочастиц анализируемых порошковых ансамблей значение θ по порядку величины близко к единице.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Для того чтобы выявить влияние длительности и физико-химических условий механообработки на указанные выше характеристики функций распределения, необходимо построить кинетическую модель этого процесса. При этом необходимо учесть физическое содержание процесса: вид, характер и последовательность элементарных актов механического воздействия на любую микрочастицу, приводящих к изменению ее состояния. Последовательность таких изменений формально можно представить как марковский процесс случайных блужданий выделенной i-той микрочастицы между фиксированными (дискретными) ее состояниями в обобщенной одномерной модели Изинга [25]. Эти блуждания характеризуются единственной стохастической переменной – объемом микрочастицы ${{v}_{i}}(t)$ или ее линейным размером – приведенным диаметром d_i(t). Простейшей математической моделью такого процесса может служить механохимический аналог уравнения Ланжевена – обобщенное кинетическое уравнение обратимой псевдохимической реакции, содержащее динамические и стохастические члены [26–29]. Для эвристической анзац-формулировки такого уравнения применительно к рассматриваемой задаче необходимо дать несколько дополнительных определений.

Пусть ${{v}_{i}}(t)$ – объем некоторой фиксированной (i-той) порошковой микрочастицы в момент времени t, τ_р – предел текучести материала этой микрочастицы, τ_s – предел его прочности, ν₁ – частота успешного (т.е. приводящего к изменению объема микрочастицы) квазирегулярного ударного воздействия инструмента (шаров) на выбранную микрочастицу, ν₂ – частота успешных (результативных) взаимных столкновений двух микрочастиц ансамбля, приводящих к их слипанию и обусловленных перемешиванием микропорошка при вращении мельницы, γ – поверхностная энергия материала микрочастицы, λ – нормирующий множитель, характеризующий максимально возможную энергонапряженность упругого контакта микрочастиц, ν₃ – основная частота в частотном спектре стохастического силового воздействия на микрочастицу, Δv_i(t) – флуктуирующая (стохастическая) добавка к объему ${{v}_{i}}(t)$ выбранной i-той микрочастицы, для изменения объема которой во времени выполняются условия винеровского типа: 1) $\left\langle {\Delta {{v}_{i}}(t)} \right\rangle $ = 0 и 2) ${{\left[ {\left\langle {\Delta {{v}_{i}}({{t}_{1}})\Delta {{v}_{i}}({{t}_{2}})} \right\rangle } \right]}^{{1/2}}}$ = Φ₀δ(t₁ – t₂) [29, 30]. В приведенных соотношениях величина Φ₀ – не зависящая от времени механообработки t характеристика стохастического процесса, имеющая размерность объема (м³) и носящая название интенсивности ланжевеновского источника, а δ(t₁ – t₂) – дельта-функция Дирака. Тогда обобщенное дифференциальное стохастическое уравнение для случая объемной переменной ${{v}_{i}}(t)$ при механообработке однокомпонентного порошка примет следующий вид:

Здесь первый (динамический) член справа от знака равенства представляет собой успешный результат регулярно действующей на микрочастицы внешней периодической (с частотой ν₁ ≠ ν₀) ударной силы. С формальной точки зрения этот член является аналогом обратимой псевдохимической реакции первого порядка, направление которой зависит от соотношения величин τ_р и τ_s.

Второй (тоже динамический) член в выражении (3) описывает процесс взаимного прилипания микрочастиц, обладающих поверхностной энергией γ [Дж/м²] и плотностью максимальной возможной упругой энергии λ [H/м²], запасенной в микрочастицах при их взаимном прилипании. Этот член по существу является термодинамическим аналогом удельной (т.е. отнесенной к величине максимально возможного контактного давления на микрочастицу λ ≈ τ_s) работы коньюгативной силы притяжения F ≈ $\gamma {{v}^{{1/3}}}$ > 0, действующей между соседними частицами на расстояниях порядка ${{v}^{{1/3}}}$ и меньше. Отношение γ/λ в этом члене играет роль условно линейной (с размерностью [м]) характеристики взаимного прилипания микрочастиц с частотой ν₂.

Третий (стохастический) член ${{\nu }_{3}}\Delta {{v}_{i}}$ отображает флуктуационный микроструктурный (микрообъемный) “шум”, возникающий в ансамбле микрочастиц при работе мельницы в результате их многочисленных случайных взаимных столкновений с основной (несущей) частотой ν₃. Размерность этого члена – м³/с, размерность сомножителей ν₁, ν₂ и ν₃ – 1/мин. В соответствии с общепринятой формулировкой ланжевеновского стохастического процесса ν₃ $ \gg $ ν₁ и ν₃$ \gg $ ν₂.

Сопоставительный анализ математической структуры членов уравнения (3) показывает, что его возможные решения не являются автомодельными. Поэтому для достижения масштабной инвариантности этих решений уравнение (3) следует привести к безразмерному виду [31, 32].

Для этой цели необходимо ввести новые безразмерные переменные: время τ = ν₀t, где ν₀ = = Ω/2π = 169 рад/мин – частота орбитального вращения барабанов мельницы вокруг ее оси, а также объем u(τ) = ${{v}_{i}}(\tau {\text{/}}{{\nu }_{0}}){\text{/}}{{v}_{{0i}}},$ где ${{v}_{{0i}}}$ – объем некоторой случайно выбранной i-той порошковой микрочастицы перед механообработкой ансамбля (т.е. при t = τ = 0), а ${{v}_{i}}(\tau {\text{/}}{{\nu }_{0}})$ – ее объем в момент времени τ. Тогда уравнение (3) в безразмерных переменных u(τ) и τ примет вид

Здесь введены следующие безразмерные критерии подобия: комплекс α = Мν₁/mν₀ > 0 и критерий Иоффе–Давиденкова–Фридмана (ИДФ): q = = f(τ_p/τ_s) = (1 – τ_p/τ_s). Знак последнего определяет тип (моду) разрушения материала микрочастицы (или характер изменения ее объема) – хрупкий (при q < 0) или пластический (при q > 0) [33–35]. Комплекс b и симплекс β также являются критериями подобия процесса и выражаются соответственно в виде $b = \left[ {{{{{\nu }_{2}}{{\gamma }}} \mathord{\left/ {\vphantom {{{{\nu }_{2}}{{\gamma }}} {\left( {{{\lambda }}v_{{0i}}^{{1/3}}{{\nu }_{0}}} \right)}}} \right. \kern-0em} {\left( {{{\lambda }}v_{{0i}}^{{1/3}}{{\nu }_{0}}} \right)}}} \right] > 0$ и β = (ν₃/ν₀) > 0.

Дифференциальное уравнение первого порядка (4) – это частный случай уравнения Бернулли со стохастическим членом. Его общее решение имеет следующий вид:

В решении (5) переменная ζ обозначает новое безразмерное время.

Вариативный анализ этого решения показывает, что направление изменения во времени объема u(τ) любой микрочастицы и, следовательно, его среднего значения по ансамблю микрочастиц 〈u(τ)〉 при механообработке заданной продолжительности τ будет определяться знаком и величиной параметрического критерия q, который управляет ходом процесса. Пусть τ_p < τ_s, т.е. значение критерия q > 0, и в процессе механообработки оно не изменяется. В этом случае при механообработке реализуется деформационно-пластическая мода процесса, сопровождающаяся укрупнением объема каждой микрочастицы u(τ). Тогда и средний объем микрочастиц в ансамбле 〈u(τ)〉 будет со временем возрастать. Иными словами, вместо измельчения микрочастиц в мельнице будет происходить их агломерация. Классическим примером, многократно описанным в научной литературе (см., например, [13]), является процесс механообработки в шаровой мельнице микропорошка достаточно чистого алюминия (см. рис. 3), для которого τ_p ≈ 20–50 МПа и τ_s ≈   150–160 МПа [36], а коэффициент деформационного упрочнения минимален: dτ_p/dε ≤ ≤ 0.005 МПа/% [37]. Столь малое его значение обусловлено тем обстоятельством, что в кристаллической ГЦК-решетке этого металла имеется 12 независимых систем легкого скольжения для дислокаций. Поэтому в данном случае критерий q ≈ 0.7–0.9 > 0, и при механообработке длительностью до 60 мин (или при деформации ε микрочастиц вплоть до ε_cr ≈ 0.25) его численное значение практически не изменяется.

Если же экспериментально найденная величина управляющего критерия q = const < 0, то в зависимости от соотношения коэффициентов, входящих в уравнение (5), временнáя эволюция характеристик ансамбля микрочастиц может происходить по разным траекториям. Чтобы качественно проанализировать их вид, следует записать решение (5) уравнения (4) при нормированных начальных условиях u(τ = 0) = 1 и Φ₀(τ = 0) = 0 в явном виде:

Если соблюдены оба винеровских темпоральных ограничения, последний член соотношения (6) при усреднении по времени обнуляется благодаря равной вероятности периодической смены знака (signΦ₀) у ланжевеновского источника Φ₀ с течением времени на противоположный. Однако в том случае, когда первое винеровское ограничение не выполняется и 〈Δu(τ)〉 = β(signΦ₀)|Φ₀| ≠ 0, процесс перестает быть марковским и последний член в соотношении (6), соответствующий стохастической “шумовой” функции какого либо одного знака (т.е. когда знак ланжевеновского источника Φ₀ оказывается в среднем устойчиво больше или меньше нуля), становится линейно зависящим от времени механообработки: ±β|Ф₀|τ. Тем не менее, если при механообработке порошка выполняется соотношение β|Ф₀|τ $ \ll $ b/(α|q|), последним членом в соотношении (6) в первом приближении можно пренебречь. В этом случае процесс механообработки порошковых микрочастиц становится полностью динамическим, и его направление будет по-прежнему определяться отрицательным знаком критерия ИДФ, приводя со временем к уменьшению средних размеров микрочастиц до минимального в данных условиях равновесного значения u_st = b/(α|q(τ_p,τ_s)|). На рис. 4 в качестве примера реализации такого процесса представлены в безразмерных координатах соответствующие зависимости основных статистических характеристик дифференциальной функции (2) от времени, полученные для микропорошкового гафния.

Однако для того, чтобы обеспечить непротиворечивую интерпретацию приведенных выше зависимостей, следует принять во внимание то обстоятельство, что для сверхчистых отожженных (деформационно не упрочненных) макрообразцов гафния τ_s = 230 МПа > τ_p = 180 МПа [38, 39] и q(τ_p/τ_s) = 0.83 > 0. Тем не менее, при механообработке ансамбля порошковых микрочастиц этого металла, имеющего кристаллическую ГПУ-решетку и всего 3 независимые системы скольжения для дислокаций [40], уже в течение первой минуты механического воздействия (при τ ≤ 5 × 10²) происходит быстрое деформационное упрочнение микрочастиц и достигаются условия τ_s < τ_p, и q(τ_p,τ_s) < 0 (рис. 4а).

Графоаналитическая обработка экспериментальных данных, приведенных на рис. 4, позволяет получить количественные оценки параметров, входящих в уравнение (4) и в его решение (6). При временах механообработки τ > 2 × 10³ процесс измельчения микрочастиц почти полностью прекращается и достигается стационарное значение их средних объемно-взвешенных размеров (mv/mv₀)_st = = u_st. В этом случае можно получить следующие параметрические оценки этого процесса: для критерия ИДФ – q = (1 – τ_p/τ_s) = –(0.01–0.1), для комплексов – α ≈ (1.5–15) × 10^–2 и b ≈ 5.2 × 10^–3, для частот – ν₁ ≈ 1.26–2.5 мин^–1 ≈ (0.71–1.4) × 10^–2ν₀ и ν₂ ≈ 1.9 × 10³ мин^–1 ≈ 11ν₀ при ν₀ = 169 мин^–1. Кажущееся на первый взгляд нереально малым найденное значение частоты ν₁, ответственной за взаимодействие отдельной микрочастицы с возникающим в порошке динамическим силовым полем, созданным мелющим инструментом, можно объяснить достаточно малой вероятностью этого события¹¹.

Действительно, в стандартной навеске металлического микропорошка, имеющего массу 10 г, перед механообработкой содержится порядка n_μ ≈ 10⁹–10¹⁰ микрочастиц гафния, причем в режиме измельчения порошка n_μ с увеличением длительности эксперимента τ значительно (на порядки) возрастает. В то же время количество стальных шаров общей массой 100 г, находящихся в одном барабане мельницы, не превышает 25–26 штук.

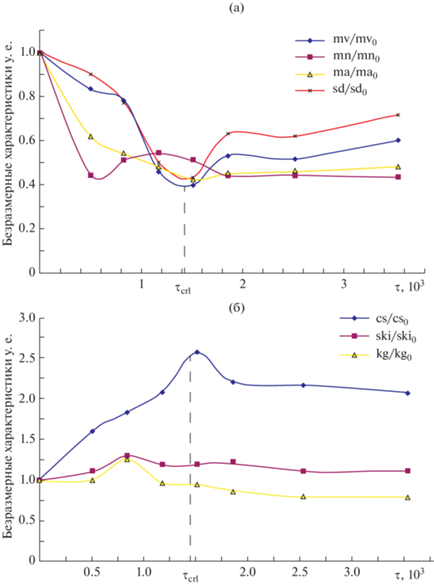
Предельные физико-механические характеристики приповерхностного слоя материала τ_p и τ_s, вообще говоря, являются нелинейными функциями его поверхностной энергии γ (эффект Ребиндера, см. [41, 42]). Поэтому квазиравновесное численное значение u_st можно варьировать, проводя механообработку порошка в технологических (размольных) средах, содержащих органические поверхностно-активные вещества в разной концентрации [42]. Однако при этом следует помнить, что стохастический член β(sign Φ₀)|Φ₀|τ в решении (6) при преобладании положительного знака интенсивности ланжевеновского источника Φ₀ > 0 со временем растет. Его включение при достаточно больших значениях τ ≥ τ_cr1 (или при реальных временах механообработки t ≥ t_cr1 = τ_cr1/ν₀ ≈ 15 мин для вольфрама и t_cr1 ≈ 8 мин для циркония) может прервать режим измельчения, переведя систему в режим агломерации микрочастиц (см. рис. 5 и 6).

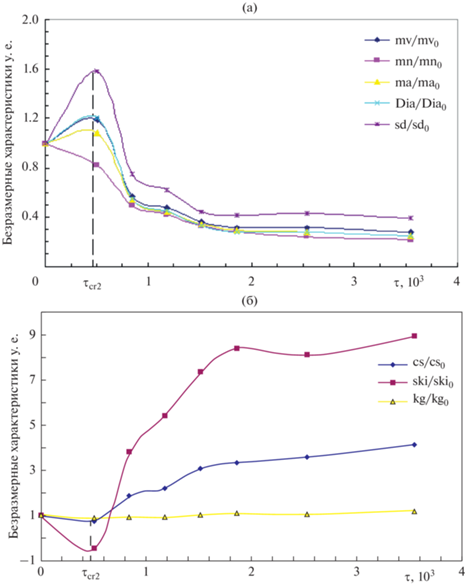
Вместе с тем, на практике часто встречаются ситуации, когда материал металлических микрочастиц в процессе механического воздействия, в отличие от случаев, приведенных на рис. 4–6, упрочняется достаточно медленно и постепенно, а его предел текучести τ_p зависит от деформации ε (или от безразмерного времени τ) по слабо выраженному степенному закону: τ_p = φ(ε) ~ τⁿ_, где 0 < n < 1 [35, 36]. При этом предел прочности τ_s материала микрочастиц практически не изменяется. В таких случаях, несмотря на первоначальные соотношения (τ_p/τ_s) < 1 и q(τ_p/τ_s) > 0, величина управляющего параметра q(τ_p/τ_s) при достижении некоторого критического значения τ_cr2 меняет знак: q(τ ≥ τ_cr2) < 0, и режим агломерации порошковых микрочастиц немедленно переходит в режим их измельчения. Так, для микропорошкового магния t_cr2 = τ_cr2/ν₀ = = 2.6 мин (рис. 7). Аналогичное поведение наблюдается и при механообработке микропорошкового никеля, для которого t_cr2 = 12 мин.

Очевидно, что чем больше величина коэффициента упрочнения металла dτ_p/dε ~ nτ^{(n– 1}), тем значительнее рост параметра |q(τ)| и тем быстрее начинается и заканчивается процесс измельчения порошка. При этом также уменьшается и равновесное значение u_st.

Особый случай реализуется, когда исходные порошковые микрочастицы достаточно велики (например, при <d_v0 ≥ 100–300 мкм) и разрушение их внешнего слоя сопровождается обнажением глубинных слоев материала, менее “наклепанных” (т.е. менее упрочненных), чем поверхностный слой микрочастиц. При многократном повторении этого процесса возможен периодический, или квазипериодический режим изменения управляющего параметра q(τ). Разлагая его в ряд Фурье по безразмерному времени τ в виде $q({{\tau }}){\text{ }} = \mathop q\nolimits_0 + \sum\nolimits_{k = 1}^\infty {\mathop C\nolimits_k } \exp (ik{{\omega \tau }})$, можно получить следующие выражения для объемной функции u(τ) и линейной функции x(τ) = [u(τ)]^1/3/θ в “бесшумном” приближении при экспериментально найденных условиях θ ≈ 1, q₀ < 0 и $\left| {{{q}_{0}}} \right| \equiv \left| {q({{\tau }} = 0)} \right| \gg \left| {\sum\nolimits_k {{{C}_{k}}} } \right|$:

В таком случае средние по ансамблю микрочастиц значения 〈u(τ)〉, 〈x(τ)〉, а также другие гомоморфные им характеристики соответствующей функции распределения также будут периодическими или квазипериодическими функциями от времени τ механообработки порошка. Очевидно, что эти характеристики будут менять знак скорости своего изменения (т.е. знак первой производной) на противоположный в точках $\mathop t\nolimits_{{\text{cr}}j}^i = \mathop {{\tau }}\nolimits_{{\text{cr}}j}^i {\text{/}}\mathop \nu \nolimits_{\text{0}} $, где j = 1 или 2.

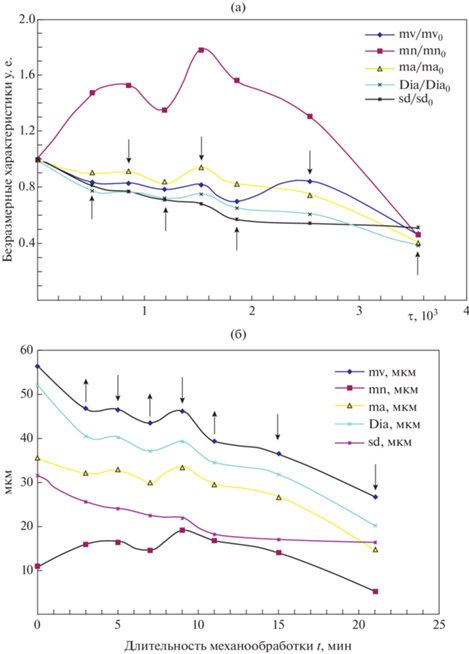
В качестве примера можно привести временные зависимости статистических характеристик дифференциальной функции распределения ансамбля изначально сравнительно крупных микрочастиц титана при их механообработке в размольной среде чистого гексана (рис. 8).

ВЫВОДЫ

1. Проведено экспериментальное исследование гранулометрического состава микропорошков ряда металлов 2-ой, 3-ей, 4-ой и 6-ой групп таблицы Менделеева, подвергнутых механической обработке в шаровой планетарной мельнице при различной длительности процесса.

2. Показано, что механообработка исследованных микропорошков не изменяет общую математическую форму и структуру соответствующих статистических функций распределения микрочастиц по размерам, характерную для необработанных микропорошков. Во всех случаях указанные функции принадлежат к группе логнормальных распределений.

3. Для всех исследованных металлических микропорошков рассчитаны основные статистические характеристики (моменты) логнормальных функций распределения микрочастиц по размерам, которые полностью определяют фракционный состав этих микропорошков.

4. Изучены вариации указанных статистических характеристик, наблюдающиеся при изменении времени механообработки микропорошков.

5. Построена эвристическая математическая анзац-модель процесса механической обработки металлических микропорошков в шаровой планетарной мельнице, позволяющая получить масштабно инвариантные временные и микроструктурные характеристики этого процесса при различных граничных и начальных условиях экспериментов.