1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 84, № 2, 2022

Коллоидный журнал, 2022, T. 84, № 2, стр. 171-185

Статистическое и молекулярно-динамическое моделирование электрически индуцированных изменений конформационной структуры полиамфолитов на поверхности сплюснутого металлического наносфероида

Н. Ю. Кручинин 1, *, М. Г. Кучеренко 1

1 Центр лазерной и информационной биофизики Оренбургского государственного университета
460018 Оренбург, пр. Победы 13, Россия

* E-mail: kruchinin_56@mail.ru

Поступила в редакцию 26.01.2022
После доработки 06.03.2022
Принята к публикации 07.03.2022

Полный текст (PDF)

Аннотация

Рассмотрена проблема формирования макромолекулярного опушечного слоя адсорбированной цепи полиамфолита на поверхности металлического сжатого наносфероида, несущего избыточный электрический заряд или поляризованного внешним однородным полем. Предложена математическая модель такой системы, учитывающая энтропийный эффект образования конформаций адсорбированной гауссовой цепи на криволинейной поверхности и взаимодействие диполей ее сегментов с полем заряженного или поляризованного проводящего наносфероида. Методом молекулярной динамики были исследованы электрически индуцированные конформационные изменения полиамфолитных полипептидов с различным расстоянием между разноименно заряженными звеньями в макроцепи, адсорбированной на поверхности заряженного или поляризованного вдоль оси вращения сплюснутого золотого наносфероида. Были рассчитаны распределения средней линейной плотности вдоль оси вращения, а также радиальные распределения средней плотности в экваториальной области наносфероида. На поверхности заряженного сплюснутого металлического наносфероида при увеличении расстояния между заряженными звеньями в макроцепи происходила преимущественная ориентация петель макроцепи в направлении оси вращения наносфероида. На поверхности сплюснутого наносфероида, поляризованного вдоль оси вращения во внешнем электрическом поле, происходило набухание макромолекулярной опушки как в приполярных областях наносфероида, так и в его экваториальной области, которое было обусловлено образованием макромолекулярных петель двух видов.

Ключевые слова: молекулярная динамика, сплюснутый металлический наносфероид, полиамфолитные полипептиды, конформационные изменения.

1. ВВЕДЕНИЕ

Плазмонные наночастицы, в том числе с адсорбированными на их поверхности полимерными молекулами, широко используются в сенсорах на основе эффектов гигантского комбинационного рассеяния и поверхностного плазменного резонанса, в качестве нанозондов в биомедицине, а также при создании различных элементов устройств наноэлектроники [1–6]. При этом большой интерес вызывает использование сфероидальных плазмонных наночастиц [7–12], при изменении анизотропии которых возможно получать наносистемы с различными плазмонными характеристиками.

Как было показано в работах [13–23], на поверхности заряженных и поляризованных металлических нанообъектов различной формы наблюдаются значительные конформационные изменения адсорбированных полиэлектролитов. При этом на поверхности вытянутого заряженного или поляризованного золотого наносфероида [22–23] конформационные структуры адсорбированных макромолекул значительно отличались от случаев адсорбции макроцепей на поверхности металлических нанообъектов сферической и цилиндрической формы [13–21]. При использовании заряженных или поляризованных металлических наночастиц в форме сплюснутых сфероидов распределение зарядов на их поверхности будет сильно отличаться от рассмотренных случаев нанообъектов как сферической и цилиндрической, так и вытянутой сфероидальной формы. Поэтому конформации адсорбированных на поверхности сплюснутого наносфероида полиамфолитов также будут сильно отличаться.

На поверхности заряженного с полным зарядом $Q$ сплюснутого металлического сфероида распределение поверхностной плотности зарядов ${{\sigma }_{Q}}$ описывается аналогичной формулой, что и для вытянутого наносфероида [24]:

(1)
${{\sigma }_{Q}} = \frac{Q}{{4\pi {{a}^{2}}c\sqrt {\left( {\frac{{{{x}^{2}} + {{y}^{2}}}}{{{{a}^{4}}}} + \frac{{{{z}^{2}}}}{{{{c}^{4}}}}} \right)} }},$
где $a$ – длина больших полуосей, а $c$ – длина малой полуоси, направленной вдоль оси $z$, которая совпадает с осью вращения сфероида. Но в отличие от заряженного вытянутого сфероида, где наиболее высокая поверхностная плотность заряда была сосредоточена на концах оси вращения, на поверхности заряженного сплюснутого сфероида максимальная плотность заряда находится в экваториальной области. При этом поверхностная плотность в экваториальной области во столько же раз больше поверхностной плотности на полюсах сплюснутого заряженного металлического сфероида, во сколько его длина большой полуоси больше длины малой полуоси.

Если поместить сплюснутый металлический сфероид во внешнее однородное электрическое поле, которое направленно вдоль его оси вращения, то на его поверхности будут индуцироваться заряды, поверхностная плотность которых ${{\sigma }_{p}}$ будет распределена по формуле [24]:

(2)
${{\sigma }_{p}} = \frac{{{{\sigma }_{{\max }}}z}}{{{{c}^{2}}\sqrt {\left( {\frac{{{{x}^{2}} + {{y}^{2}}}}{{{{a}^{4}}}} + \frac{{{{z}^{2}}}}{{{{c}^{4}}}}} \right)} }},$
где ${{\sigma }_{{\max }}} = \frac{{{{p}_{z}}}}{V}$ – значение поверхностной плотности заряда на полюсе вытянутого поляризованного сфероида, ${{p}_{z}}$ – дипольный момент сфероида, $V$ – объем сфероида. В отличие от поляризованного вдоль оси вращения вытянутого сфероида, у которого поверхностная плотность заряда медленно изменялась от экватора в сторону полюсов, достигая пиковых значений на концах большой оси около полюсов, на поверхности сплюснутого сфероида при смещении от его центра вдоль оси вращения поверхностная плотность заряда меняется резко, достигая значений близких к максимальным на небольшом расстоянии от нейтрального экватора.

Таким образом, целью данной работы является исследование электрически индуцированных изменений конформационной структуры полиамфолитных полипептидов на поверхности как заряженного, так и поляризованного вдоль оси вращения во внешнем электрическом поле сплюснутого металлического наносфероида.

2. ФОРМИРОВАНИЕ МАКРОМОЛЕКУЛЯРНОГО ОПУШЕЧНОГО СЛОЯ НА ПОВЕРХНОСТИ СЖАТОГО НАНОСФЕРОИДА. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

2.1. Заряженный или поляризованный во внешнем поле сфероид с адсорбированной цепью полиамфолита. Учет энтропийного эффекта и взаимодействия диполей сегментов гауссовой макроцепи с полем заряженного или поляризованного наносфероида

Для описания поля заряженных или поляризованных осесимметричных эллипсоидальных тел (эллипсоидов вращения, для которых полуоси $a = b \ne c$) часто используют связанные с эллипсоидальными сфероидальные координаты ξ1 = $ = {{{{{({{r}_{1}} + {{r}_{2}})}}^{2}}} \mathord{\left/ {\vphantom {{{{{({{r}_{1}} + {{r}_{2}})}}^{2}}} {4 - {{a}^{2}}}}} \right. \kern-0em} {4 - {{a}^{2}}}}$, ${{\eta }_{1}} = {{{{{({{r}_{1}} - {{r}_{2}})}}^{2}}} \mathord{\left/ {\vphantom {{{{{({{r}_{1}} - {{r}_{2}})}}^{2}}} {4 - {{a}^{2}}}}} \right. \kern-0em} {4 - {{a}^{2}}}}$, φ, [24] где ${{r}_{1}},{{r}_{2}}$ – минимальное и максимальное расстояния до окружности радиуса d/2, проходящей через фокусы, а d – расстояние между этими фокусами, a – длина большой оси сплюснутого эллипсоида вращения. Для сплюснутого эллипсоида вращения $a = b > c$. Эксцентриситет такого сфероида $e = \sqrt {{{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} {{{c}^{2}} - 1}}} \right. \kern-0em} {{{c}^{2}} - 1}}} $. Связанные с координатами ${{\xi }_{1}}$, ${{\eta }_{1}}$ безразмерные сплюснутые сфероидальные координаты (БССК) $\xi $, $\eta $ заданы соотношениями $\xi = {{({{r}_{1}} + {{r}_{2}})} \mathord{\left/ {\vphantom {{({{r}_{1}} + {{r}_{2}})} d}} \right. \kern-0em} d}$, $\eta = {{({{r}_{1}} - {{r}_{2}})} \mathord{\left/ {\vphantom {{({{r}_{1}} - {{r}_{2}})} d}} \right. \kern-0em} d}$ [25]. Тогда областями определения БССК будут $\xi \in [1,\infty ),\eta \in [ - 1,1],$ $\varphi \in [0,2\pi )$. Угол φ – полярный, в плоскости, перпендикулярной оси сфероида. В аксиально симметричном случае характеристики поля от этого угла не зависят. Связь между сфероидальными координатами двух типов определяется соотношениями ${{\xi }_{1}} = {{{{\xi }^{2}}{{d}^{2}}} \mathord{\left/ {\vphantom {{{{\xi }^{2}}{{d}^{2}}} {4 - {{a}^{2}}}}} \right. \kern-0em} {4 - {{a}^{2}}}}$, ${{\eta }_{1}} = {{{{\eta }^{2}}{{d}^{2}}} \mathord{\left/ {\vphantom {{{{\eta }^{2}}{{d}^{2}}} {4 - {{a}^{2}}}}} \right. \kern-0em} {4 - {{a}^{2}}}}$. Для точек поверхности сфероида, т.е. при $\xi = {{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d}$ получаем ${{\xi }_{1}} = 0$.

Точное решение задачи уравнения Лапласа для потенциала квазистационарного поля в случае сфероидов выражается через элементарные функции [24]. Незаряженный сфероид, помещенный в электрическое поле, поляризуется, сам становясь источником дополнительного поля во внешней области. В общем случае переменного поля E0(iωt), рассмотренного в [23], величина такой поляризации определяется диэлектрической проницаемостью металла на частоте ω изменения поля. В статическом случае при ω = 0 напряженность E0 = const.

Будем рассматривать в качестве модели макромолекулярной цепи полиамфолита, адсорбированного на поверхности наночастицы, идеальную гауссову цепь, т.е. полимерную молекулу без учета объемных взаимодействий пространственно удаленных звеньев друг с другом. В то же время дистанционное взаимодействие сегментов цепи с заряженной, либо поляризованной наночастицы будет приниматься во внимание и проявится в формировании больцмановского статистического фактора, определяющего характер распределения электродипольных звеньев в поле сфероида. Соседствующие звенья цепи определяют ее первичную структуру, а также связанную с ней специфику возникающих конформаций и связанной с ними энтропии [26]. В общем случае конфигурационная функция ψ(r) идеальной гауссовой макроцепи удовлетворяет уравнению шредингеровского типа [27]

(3)
$\frac{{a_{c}^{2}{{k}_{{\text{B}}}}T}}{6}{{\nabla }^{2}}\psi ({\mathbf{r}}) = [V({\mathbf{r}}) - \varepsilon ]\psi ({\mathbf{r}}),$
где ac – размер звена цепи, kBT – произведение постоянной Больцмана на абсолютную температуру (энергия теплового кванта). В отсутствие потенциала V(r) уравнение (3) принимает вид уравнения на собственные значения ε оператора свободной диффузии, или уравнения Гельмгольца, записанного в некоторых криволинейных координатах для области вне наночастицы. В работах [28, 29] было предложено использовать потенциал V(r) поля поверхности сферической наночастицы в виде δ-функциональной ямы, моделирующей ван-дер-ваальсово притяжение звеньев макромолекулы к поверхности наночастицы на сфере радиуса r0, вместе с барьером в виде отталкивающей твердой стенки при r = R:
(4)
$V(r) = \left\{ \begin{gathered} - \alpha \delta (r - {{r}_{0}}),\,\,\,\,r > R \hfill \\ \infty ,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,r = R. \hfill \\ \end{gathered} \right.$
Уравнение (3) при V = 0 в сплюснутых сфероидальных координатах принимает вид [25, 30]
(5)
$\begin{gathered} {{\nabla }^{2}}\psi (\xi ,\eta ) + \frac{{6{{d}^{2}}\varepsilon }}{{4a_{c}^{2}kT}}\psi (\xi ,\eta ) = \\ = \frac{\partial }{{\partial \xi }}\left[ {({{\xi }^{2}} + 1)\frac{{\partial \psi }}{{\partial \xi }}} \right] + \frac{\partial }{{\partial \eta }}\left[ {(1 - {{\eta }^{2}})\frac{{\partial \psi }}{{\partial \eta }}} \right] + \\ + \,\,\frac{{{{\xi }^{2}} + {{\eta }^{2}}}}{{({{\xi }^{2}} + 1)(1 - {{\eta }^{2}})}}\frac{{{{\partial }^{2}}\psi }}{{\partial {{\varphi }^{2}}}} + \\ + \,\,{{\kappa }^{2}}({{\xi }^{2}} + {{\eta }^{2}})\psi (\xi ,\eta ,\varphi ) = 0,\,\,\,\,\left( {\kappa = i\frac{d}{{{{a}_{c}}}}\sqrt {\frac{{3\left| \varepsilon \right|}}{{2kT}}} } \right). \\ \end{gathered} $
Решение (5) может быть представлено в виде произведения
$\psi (\xi ,\eta ,\varphi ) = F(\kappa ,\xi )S(\kappa ,\eta )\exp ( \pm im\varphi ),$
радиальных $F(\kappa ,\xi )$ и угловых $S(\kappa ,\eta )$ сплюснутых сфероидальных функций [25, 30], где m – целые числа, аналогично тому, как это было сделано в работе [22] для случая вытянутого сфероида. После разделения переменных для сплюснутого сфероида получаем
(6)
$\begin{gathered} \frac{d}{{d\xi }}\left[ {({{\xi }^{2}} + 1)\frac{d}{{d\xi }}{{F}_{{ml}}}(\kappa ,\xi )} \right] - \\ - \,\,\left[ {{{\lambda }_{{ml}}} - {{\kappa }^{2}}({{\xi }^{2}} + 1) - \frac{{{{m}^{2}}}}{{({{\xi }^{2}} + 1)}}} \right]{{F}_{{ml}}}(\kappa ,\xi ) = 0, \\ \frac{d}{{d\eta }}\left[ {(1 - {{\eta }^{2}})\frac{d}{{d\eta }}{{S}_{{ml}}}(\kappa ,\eta )} \right] + \\ + \,\,\left[ {{{\lambda }_{{ml}}} - {{\kappa }^{2}}(1 - {{\eta }^{2}}) - \frac{{{{m}^{2}}}}{{(1 - {{\eta }^{2}})}}} \right]{{S}_{{ml}}}(\kappa ,\eta ) = 0. \\ \end{gathered} $
Добавляя в (5) адсорбирующий потенциал V в виде дельта-функциональной ямы и решая полученное уравнение, можно получить распределение $n(\xi ,\eta ) = {{\psi }^{2}}(\xi ,\eta )$ плотности звеньев макроцепи, часть которых будет захвачена потенциальной ямой (4), что приводит к определенной конформации адсорбированного на поверхности наночастицы полимера. В отсутствие полей и зарядов конформации цепи будут определять только характеристиками дельта-функциональной ямы и формой поверхности наночастицы. Однако, такой подход, именно в силу его строгости, связан с получением сложных функциональных рядов для радиальных ${{F}_{{ml}}}(\kappa ,\xi )$ и угловых ${{S}_{{ml}}}(\kappa ,\eta )$ сплюснутых сфероидальных функций. Это приводит к очень громоздкой структуре получаемой математической модели как, например, в [22].

В целях получения более простой и удобной для использования модели в данной работе используем другой, приближенный метод. Не апеллируя к уравнениям (5)–(6), записанным в БССК, можем приближенно представить сжатый сфероид как аппроксимацию сплюснутого сфероида двумя соединенными сферическими сегментами с радиусами оснований равными a и высотами c. Угол ${{\theta }_{0}}$ “обзора” половины сферического сегмента равен ${{\theta }_{0}} = \arcsin ({a \mathord{\left/ {\vphantom {a R}} \right. \kern-0em} R})$ = $\arcsin \left[ {{{2ac} \mathord{\left/ {\vphantom {{2ac} {({{a}^{2}} + {{c}^{2}})}}} \right. \kern-0em} {({{a}^{2}} + {{c}^{2}})}}} \right]$, или ${{\theta }_{0}} \approx {a \mathord{\left/ {\vphantom {a R}} \right. \kern-0em} R} = {{2ac} \mathord{\left/ {\vphantom {{2ac} {({{a}^{2}} + {{c}^{2}})}}} \right. \kern-0em} {({{a}^{2}} + {{c}^{2}})}}$, если приближенно заменить дугу хордой. Полный угловой размер сферического сегмента $2{{\theta }_{0}} = 2\arcsin ({a \mathord{\left/ {\vphantom {a R}} \right. \kern-0em} R})$ = $ = 2\arcsin \left[ {{{2ac} \mathord{\left/ {\vphantom {{2ac} {({{a}^{2}} + {{c}^{2}})}}} \right. \kern-0em} {({{a}^{2}} + {{c}^{2}})}}} \right]$.

Сферически-симметричное решение уравнения (3) Гросберга−Хохлова [27] для сферической наночастицы и дельта- функционального потенциала притяжения с отталкивающей стенкой ${{V}_{1}}(r) = {{V}_{\infty }}(R) - \alpha \delta (r - {{r}_{0}})$ имеет вид [28–29] ($A = {\text{const}}$)

(7)
$\left\{ \begin{gathered} {{\psi }_{{\text{I}}}}(r) = A\frac{{\exp ( - qr)[\exp (2qr) - \exp (2qR)]}}{{2qr}}, \hfill \\ R < r < {{r}_{0}} \hfill \\ {{\psi }_{{{\text{II}}}}}(r) = A\frac{{\exp ( - qr)[\exp (2q{{r}_{0}}) - \exp (2qR)]}}{{2qr}}, \hfill \\ {{r}_{0}} < r < \infty \hfill \\ \end{gathered} \right.,$
где параметр q является корнем уравнения
(8)
$q = \frac{{3\alpha }}{{{{a}^{2}}{{k}_{{\text{B}}}}T}}[1 - \exp (2q(R - {{r}_{0}}))].$
Сферически-симметричные функции (7) могут быть представлены через функции Бесселя ${{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qr)$ и ${{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qr)$, в эквивалентной (7) форме
(9)
$\left\{ \begin{gathered} {{\psi }_{{\text{I}}}}(r) = A\frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qr)}}{{\sqrt r }} + B\frac{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qr)}}{{\sqrt r }},\,\,\,\,R < r < {{r}_{0}} \hfill \\ {{\psi }_{{{\text{II}}}}}(r) = C\frac{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qr)}}{{\sqrt r }},\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{{r}_{0}} < r < \infty \hfill \\ \end{gathered} \right.,$
которая более удобна для построения теории возмущений в задачах с малыми нарушениями сферической симметрии системы [13]. Учитывая, что ${{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(\xi ) = \sqrt {\frac{2}{{\pi \xi }}} {\text{sh}}\xi $, ${{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(\xi ) = \sqrt {\frac{\pi }{{2\xi }}} \exp ( - \xi )$ легко приходим от (9) к (7), с параметром q, определяемым уравнением (8).

Соотношения между константами A, B и C находим из условий сшивки решений (9) в точке ${{r}_{0}}$

(10)
$B = - A\frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}},\,\,\,\,C = A\left[ {\frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(q{{r}_{0}})}}{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(q{{r}_{0}})}} - \frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}} \right].$
Тогда (9) принимают вид [13]

(11)
$\left\{ \begin{gathered} {{\psi }_{{\text{I}}}}(r) = A\left[ {\frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qr)}}{{\sqrt r }} - \frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}\frac{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qr)}}{{\sqrt r }}} \right], \hfill \\ R < r < {{r}_{0}} \hfill \\ {{\psi }_{{{\text{II}}}}}(r) = A\left[ {\frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(q{{r}_{0}})}}{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(q{{r}_{0}})}} - \frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}} \right]\frac{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qr)}}{{\sqrt r }}, \hfill \\ {{r}_{0}} < r < \infty \hfill \\ \end{gathered} \right..$

Общее трансцендентное уравнение для собственных значений q совпадает с (8)

(12)
$\frac{{{{a}^{2}}kT}}{{6\alpha {{r}_{0}}}} = {{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(q{{r}_{0}}){{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(q{{r}_{0}}) - K_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}^{2}(q{{r}_{0}})\frac{{{{I}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}{{{{K}_{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}(qR)}}.$
Уравнения (8) и (12) для корня q обеспечивают такую его зависимость от радиуса R сферической наночастицы, что с уменьшением R величина q растет, а вместе с ее ростом уменьшается ширина распределения плотности $n(r) = {{\psi }^{2}}(r)$ звеньев макроцепи на радиусе r0 локализации ямы [18]. Таким образом, в случае малых наночастиц получаем более узкое радиальное распределение незаряженных звеньев адсорбированной цепи.

Зависимость от меридианального угла появляется лишь для обозначения границы сферического сегмента. Конечно, решение (7)–(11) не дает правильного поведения плотности звеньев на этой границе. Радиус максимальной кривизны эллипса в точке фокуса ${{r}_{m}} = a - {d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$. Эта величина определяет ширину экваториального пояса, в котором имеют место отклонения кривизны участка поверхности сфероида от его истинного значения. В этой области размером $s \sim {{r}_{m}} = a\left( {1 - \sqrt {1 - {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}} } \right)$ пользоваться выражениями для радиального распределения (7) или (11) уже нельзя. Но при достаточном удалении от нее функции ${{\psi }_{{\text{I}}}}(r)$ и ${{\psi }_{{{\text{II}}}}}(r)$ способны передать все особенности геометрии сфероида через радиус $R = {{({{a}^{2}} + {{c}^{2}})} \mathord{\left/ {\vphantom {{({{a}^{2}} + {{c}^{2}})} {(2c)}}} \right. \kern-0em} {(2c)}}$. Полный угловой размер $2{{\theta }_{0}}$ сферического сегмента при наблюдении из центра сферы радиуса R равен $2{{\theta }_{0}} = 2\arcsin ({a \mathord{\left/ {\vphantom {a R}} \right. \kern-0em} R}) = 2\arcsin \left[ {{{2ac} \mathord{\left/ {\vphantom {{2ac} {({{a}^{2}} + {{c}^{2}})}}} \right. \kern-0em} {({{a}^{2}} + {{c}^{2}})}}} \right]$. Для определения угла “обзора” сегмента без обращения к функции arcsin (a/R) можно воспользоваться приближенной формулой Гюйгенса для связи длины дуги сегмента окружности с ее хордой

(13)
$L = 2a\left[ {({4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3})\sqrt {1 + {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right].$
Выражению (13) можем придать форму, включающую в нее эксцентриситет e сфероида

$L = 2a\left[ {\frac{4}{3}\sqrt {\frac{{{{e}^{2}} + 2}}{{{{e}^{2}} + 1}}} - \frac{1}{3}} \right].$

В случае большого эксцентриситета, т.е. при a $ \gg $ c можем записать

(14)
$L \approx 2a\left[ {1 + ({2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0em} 3}){{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}} \right].$
Исходя из (13) угловой размер сферического сегмента в приближении Гюйгенса
(15)
$\begin{gathered} 2{{\theta }_{0}} = {L \mathord{\left/ {\vphantom {L R}} \right. \kern-0em} R} = \\ = 4ac{{\left[ {({4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3})\sqrt {1 + {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right]} \mathord{\left/ {\vphantom {{\left[ {({4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0em} 3})\sqrt {1 + {{{{c}^{2}}} \mathord{\left/ {\vphantom {{{{c}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}} - {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0em} 3}} \right]} {({{a}^{2}} + {{c}^{2}}).}}} \right. \kern-0em} {({{a}^{2}} + {{c}^{2}}).}} \\ \end{gathered} $
Пренебрегая в (15) малым слагаемым с множителем c2/a2 в подкоренном выражении приходим к ранее приведенной формуле для угла обзора $2{{\theta }_{0}} = {{2a} \mathord{\left/ {\vphantom {{2a} R}} \right. \kern-0em} R} = {{4ac} \mathord{\left/ {\vphantom {{4ac} {({{a}^{2}} + {{c}^{2}})}}} \right. \kern-0em} {({{a}^{2}} + {{c}^{2}})}}$.

2.2. Поле заряженного или поляризованного наносфероида

Потенциал электростатического поля вне сплюснутого сфероида (a = b > c) с зарядом Q можно определить, не прибегая к аппроксимации его формы частями сферического сегмента [24]

(16)
${{\varphi }_{Q}}({{\xi }_{1}}) = \frac{Q}{{\sqrt {{{a}^{2}} - {{c}^{2}}} }}{\text{arctg}}\sqrt {\frac{{{{a}^{2}} - {{c}^{2}}}}{{{{\xi }_{1}} + {{c}^{2}}}}} .$
Т.е. данное выражение для поля справедливо для всех точек пространства, включая и область с малым радиусом кривизны. Для сравнения с потенциалом поля вытянутого сфероида [24]
(15)
$\begin{gathered} \varphi _{{_{Q}}}^{{{\text{prol}}}}(\xi _{1}^{'}) = \frac{Q}{{\sqrt {{{a}^{2}} - {{c}^{2}}} }}\ln \frac{{\sqrt {\xi _{1}^{'} + {{a}^{2}}} + \sqrt {{{a}^{2}} - {{b}^{2}}} }}{{\sqrt {\xi _{1}^{'} + {{a}^{2}}} - \sqrt {{{a}^{2}} - {{b}^{2}}} }}, \\ \xi _{1}^{'} = {{\xi {\kern 1pt} {{'}^{2}}{{d}^{2}}} \mathord{\left/ {\vphantom {{\xi {\kern 1pt} {{'}^{2}}{{d}^{2}}} 4}} \right. \kern-0em} 4} - {{a}^{2}},\,\,\,\,e = \sqrt {{{1 - {{b}^{2}}} \mathord{\left/ {\vphantom {{1 - {{b}^{2}}} {{{a}^{2}}}}} \right. \kern-0em} {{{a}^{2}}}}} ,\,\,\,\,d = 2ae. \\ \end{gathered} $
Потенциал поля заряженного сплюснутого сфероида в БССК
${{\varphi }_{Q}}(\xi ) = \frac{Q}{{\sqrt {{{a}^{2}} - {{c}^{2}}} }}{\text{arctg}}\sqrt {\frac{{4({{a}^{2}} - {{c}^{2}})}}{{{{\xi }^{2}}{{d}^{2}} - 4({{a}^{2}} - {{c}^{2}})}}} ,\,\,\,\,\,\,\,\,\,\,\left( {16{\kern 1pt} '} \right)$
или, поскольку ${{d}^{2}} = 4({{a}^{2}} - {{c}^{2}})$
${{\varphi }_{Q}}(\xi ) = \frac{{2Q}}{d}{\text{arctg}}\left[ {{{{({{\xi }^{2}} - 1)}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right].\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( {16{\kern 1pt} ''} \right)$
Потенциал поля вне незаряженного (Q = 0) проводящего сплюснутого эллипсоида вращения во внешнем однородном поле E0 параллельном оси z [24]
(18)
$\varphi ({{\xi }_{1}},{{\eta }_{1}}) = - {{E}_{0}}z\left[ {1 - \frac{{\sqrt {\frac{{{{a}^{2}} - {{c}^{2}}}}{{{{c}^{2}} + {{\xi }_{1}}}}} - {\text{arctg}}\sqrt {\frac{{{{a}^{2}} - {{c}^{2}}}}{{{{c}^{2}} + {{\xi }_{1}}}}} }}{{\sqrt {\frac{{{{a}^{{\text{2}}}}}}{{{{c}^{2}}}} - 1} - {\text{arctg}}\sqrt {\frac{{{{a}^{{\text{2}}}}}}{{{{c}^{2}}}} - 1} }}} \right].$
Потенциал $\varphi (\xi ,\eta )$ поля вне поляризованного сплюснутого наносфероида в БССК
(19)
$\varphi (\xi ,\eta ) = - {{E}_{0}}z\left[ {1 - \frac{{\sqrt {\frac{{4({{a}^{2}} - {{c}^{2}})}}{{{{\xi }^{2}}{{d}^{2}} - 4({{a}^{2}} - {{c}^{2}})}}} - {\text{arctg}}\sqrt {\frac{{4({{a}^{2}} - {{c}^{2}})}}{{{{\xi }^{2}}{{d}^{2}} - 4({{a}^{2}} - {{c}^{2}})}}} }}{{\sqrt {\frac{{{{a}^{{\text{2}}}}}}{{{{c}^{2}}}} - 1} - {\text{arctg}}\sqrt {\frac{{{{a}^{{\text{2}}}}}}{{{{c}^{2}}}} - 1} }}} \right].$
или
$\begin{gathered} \varphi (\xi ,\eta ) = - {{E}_{0}}z \times \\ \times \,\,\left[ {1 - \frac{{{{{({{\xi }^{2}} - 1)}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {\text{arctg[}}{{{({{\xi }^{2}} - 1)}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{\text{]}}}}{{e - {\text{arctg}}e}}} \right],\,\,\,\,\,\,\,\,\,\,(19{\kern 1pt} ') \\ e = \sqrt {\frac{{{{a}^{2}}}}{{{{c}^{2}}}} - 1} . \\ \end{gathered} $
Поскольку связь БССК со сферическими координатами определяется формулами [25] $r = {{({{\xi }^{2}} - {{\eta }^{2}} + 1)}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}{d \mathord{\left/ {\vphantom {d 2}} \right. \kern-0em} 2}$, $\cos {\kern 1pt} \theta = \xi \eta {\kern 1pt} {{({{\xi }^{2}} - {{\eta }^{2}} + 1)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$, можем записать, что $r{\kern 1pt} \cos \theta = {{\xi \eta d} \mathord{\left/ {\vphantom {{\xi \eta d} 2}} \right. \kern-0em} 2}$, откуда следует ${{\eta }^{2}} = 4{{r}^{2}}{{{{{\cos }}^{2}}\theta } \mathord{\left/ {\vphantom {{{{{\cos }}^{2}}\theta } {({{\xi }^{2}}{{d}^{2}})}}} \right. \kern-0em} {({{\xi }^{2}}{{d}^{2}})}}$. Тогда для координаты $\xi = {{2a} \mathord{\left/ {\vphantom {{2a} d}} \right. \kern-0em} d}$ получаем следующее биквадратное уравнение
${{({{\xi }^{2}})}^{2}} - \left( {\frac{{4{{r}^{2}}}}{{{{d}^{2}}}} - 1} \right){{\xi }^{2}} - \frac{{4{{r}^{2}}{{{\cos }}^{2}}\theta }}{{{{d}^{2}}}} = 0,$
положительный квадрат корня которого
(20)
${{\xi }^{2}} = \frac{1}{2}\left( {\frac{{4{{r}^{2}}}}{{{{d}^{2}}}} - 1} \right) + \sqrt {\frac{1}{4}{{{\left( {\frac{{4{{r}^{2}}}}{{{{d}^{2}}}} - 1} \right)}}^{2}} + \frac{{4{{r}^{2}}{{{\cos }}^{2}}{\kern 1pt} \theta }}{{{{d}^{2}}}}} = 0,$
вместе с выражением для квадрата второй переменной $\eta $ БССК
(21)
$\begin{gathered} {{\eta }^{2}} = \frac{{4{{r}^{2}}{{{\cos }}^{2}}{\kern 1pt} \theta }}{{{{\xi }^{2}}{{d}^{2}}}} = \frac{{4{{r}^{2}}{{{\cos }}^{2}}{\kern 1pt} \theta }}{{{{d}^{2}}}} \times \\ \times \,\,{{\left[ {\frac{1}{2}\left( {\frac{{4{{r}^{2}}}}{{{{d}^{2}}}} - 1} \right) + \sqrt {\frac{1}{4}{{{\left( {\frac{{4{{r}^{2}}}}{{{{d}^{2}}}} - 1} \right)}}^{2}} + \frac{{4{{r}^{2}}{{{\cos }}^{2}}{\kern 1pt} \theta }}{{{{d}^{2}}}}} } \right]}^{{ - 1}}}, \\ \end{gathered} $
определяют зависимости потенциалов ${{\varphi }_{Q}}(\xi )$ и $\varphi (\xi ,\eta )$ от сферических координат $r,\theta $. Заметим, что потенциал ${{\varphi }_{Q}}(\xi )$ поля заряженного сфероида, определенный выражениями (16') или (16''), не зависит от второй переменной $\eta $ БССК. Потенциал $\varphi (\xi ,\eta )$ зависит от переменной $\eta $ формально через декартову координату z. Однако при переходе к сферическим координатам $r,\theta $ можем сразу записать $z = r{\kern 1pt} \cos {\kern 1pt} \theta $, минуя сложную зависимость (21). Тогда для потенциала $\varphi (r,\theta )$ поляризованного сфероида в окончательном виде получаем
(22)
$\begin{gathered} \varphi (r,\theta ) = - {{E}_{0}}r \times \\ \times \,\,\cos {\kern 1pt} \theta \left[ {1 - \frac{{{{{({{\xi }^{2}} - 1)}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}} - {\text{arctg}}\left[ {{{{({{\xi }^{2}} - 1)}}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}} \right]}}{{e - {\text{arctg}}e}}} \right], \\ e = \sqrt {\frac{{{{a}^{2}}}}{{{{c}^{2}}}} - 1} , \\ \end{gathered} $
с ${{\xi }^{2}} = {{\xi }^{2}}(r,\theta )$, определенной формулой (20).

В качестве примера проявления полевого влияния (22) на рис. 1 градациями серого представлено распределение плотности звеньев гауссовой цепи полиамфолита с учетом лишь больцмановского фактора $n(r,\theta ) \sim \exp [{{ - V(r,\theta )} \mathord{\left/ {\vphantom {{ - V(r,\theta )} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}]$, в опушечном слое на сфероидальной поверхности, охватывающей поверхность адсорбирующего цепь наносфероида. Показана верхняя половина незаряженного поляризованного сплюснутого наносфероида. Энтропийный фактор ${{\psi }^{2}}(r)$, подробно рассмотренный в [29], здесь в учет не принимался.

Рис. 1.

Радиально-угловое распределение плотности $n(r,\theta )$ звеньев гауссовой цепи полиамфолита в опушечном слое на сфероидальной поверхности, охватывающей граничную поверхность незаряженного поляризованного сплюснутого наносфероида (a = b > > c). Величина $n(r,\theta )$ плотности звеньев цепи представлена градациями серого различного затемнения в соответствии с логарифмической шкалой, полученной на основе цветной диаграммы (серый различной затемненности отвечает определенному цвету окрашенной логарифмической шкалы). Участки различной затемненности на сфероидальной поверхности отображают величину больцмановского фактора $n(r,\theta ) \sim \exp [{{ - V(r,\theta )} \mathord{\left/ {\vphantom {{ - V(r,\theta )} {{{k}_{{\text{B}}}}T}}} \right. \kern-0em} {{{k}_{{\text{B}}}}T}}]$ в различных областях опушечного макромолекулярного слоя. Показана верхняя половина сфероида. Горизонтальные оси x, y расположены в экваториальной плоскости сфероида. Вектор напряженности E0 внешнего электростатического поля направлен вдоль вертикальной оси z.

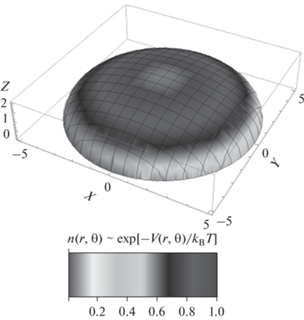
Потенциальная энергия взаимодействия сегмента (единичного звена или группы звеньев) полиамфолита с координатами $r,\theta $ и характерным электрическим дипольным моментом p может быть записана в виде ${{V}_{Q}}(r,\theta ) = - {\mathbf{p}}\nabla \varphi (r,\theta )$ или $V(r,\theta ) = - {\mathbf{p}}\nabla \varphi (r,\theta )$, в зависимости от того с каким сфероидом, заряженным или поляризованным, взаимодействует полиамфолитная цепь. Окончательно радиально-угловое распределение плотности $n(r,\theta )$ звеньев макроцепи, адсорбированной сплюснутым заряженным или поляризованным наносфероидом принимает следующий вид

(23)
${{n}_{{(Q)}}}(r,\theta ) = \left\{ \begin{gathered} \psi _{{\text{I}}}^{2}(r),R < r < {{r}_{0}} \hfill \\ \psi _{{{\text{II}}}}^{2}(r),{{r}_{0}} < r < \infty \hfill \\ \end{gathered} \right\}\exp \left[ { - \frac{{{{V}_{{(Q)}}}(r,\theta )}}{{{{k}_{{\text{B}}}}T}}} \right].$

3. МОЛЕКУЛЯРНО-ДИНАМИЧЕСКОЕ МОДЕЛИРОВАНИЕ

Молекулярно-динамическое (МД) моделирование полиамфолитных полипептидов на поверхности сплюснутого золотого наносфероида было произведено с использованием программного комплекса NAMD 2.14 [31].

Модель сплюснутого золотого наносфероида была получена путем вырезания из кристалла золота эллипсоида вращения с большими полуосями длиной 3 нм и малой полуосью длиной 1.5 нм. Такой способ построения модели наночастицы является упрощенным [32], однако, полученная структура наночастицы является удобной для описания неравномерного распределения зарядов на поверхности заряженного (1) или поляризованного (2) металлического наносфероида во внешнем электрическом поле. Атомы наносфероида в процессе МД-моделирования оставались зафиксированными. Были рассмотрены четыре в целом нейтральных полиамфолитных полипептида:

1) полипептид P1, состоящий из 402 аминокислотных остатков с 268 звеньями Ala (A) с равномерно распределенными 67 звеньями Asp (D, заряд –1e) и 67 звеньями Arg (R, заряд +1e) – (ADA2RA)67;

2) полипептид P2, состоящий из 400 аминокислотных остатков с 320 звеньями Ala с равномерно распределенными 40 звеньями Asp и 40 звеньями Arg – (A2DA4RA2)40;

3) полипептид P3, состоящий из 400 аминокислотных остатков с 320 звеньями Ala с равномерно распределенными 20 парами звеньев Asp и 20 парами звеньев Arg – (A4R2A8D2A4)20;

4) полипептид P4, состоящий из 412 аминокислотных остатков с 368 звеньями Ala с равномерно распределенными 11 парами звеньев Asp и 11 парами звеньев Arg – A8(A8D2A16R2A8)11A8.

МД-моделирование производилось при постоянной температуре (термостат Берендсена) при 900 К с последующим снижением до 300 К. Длина временной траектории достигала 15 нс. Для полипептидов было использовано силовое поле CHARMM36 [33, 34]. Нековалентные взаимодействия с золотым сплюснутым наносфероидом описывались потенциалом Леннард-Джонса, параметризованным в работе [35]: глубина потенциальной ямы для атома золота задавалась равной –5.29 ккал/моль, а минимум потенциала находился на расстоянии 2.951 Å. Потенциал Ван-дер-Ваальса обрезался на расстоянии 1.2 нм с помощью функции сглаживания между 1.0 и 1.2 нм. Электростатические взаимодействия рассчитывались непосредственно на расстоянии 1.2 нм, а на большем расстоянии использовался метод “частица–сетка” Эвальда (PME) [36] с шагом сетки 0.11 нм. Вся наносистема была помещена в куб с ребрами 22 нм, заполненный молекулами воды TIP3P [37]. Для контроля получения равновесных конформаций осуществлялось наблюдение за изменением среднеквадратичного расстояния между атомами полипептида в различных конформациях (RMSD).

Сначала была проведено МД-моделирование полиамфолитных полипептидов на нейтральной поверхности сплюснутого золотого наносфероида. Полученные конформационные структуры полипептидов были использованы в качестве стартовых при МД-моделировании на поверхности заряженного, а также поляризованного вдоль оси вращения во внешнем однородном электрическом поле сплюснутого наносфероида. Всего были получены по четыре стартовых конформаций для каждого рассмотренного полипептида, при которых он обволакивал сплюснутый наносфероид.

Были рассмотрены положительно заряженные сплюснутые золотые наносфероиды, в которых поверхностная плотность зарядов была распределена по формуле (1), а их полный заряд был равен: ${{Q}_{{0.125}}} \approx 187e$, ${{Q}_{{0.25}}} \approx 373e$ и ${{Q}_{{0.5}}} \approx 745e$. При таких значениях полного заряда сплюснутого наносфероида атомы, которые были расположены на поверхности на его полюсах, имели парциальные заряды $ + 0.125e$, $ + 0.25e$ и $ + 0.5e$ соответственно, а парциальные заряды атомов, расположенных на поверхности на экваторе наносфероида, были в 2 раза больше (1): $ + 0.25e$, $ + 0.5e$ и $ + 1.0e$.

На поверхности поляризованного во внешнем однородном электрическом поле вдоль оси вращения сплюснутого золотого наносфероида заряды были распределены согласно формуле (2). Были рассмотрены наносфероиды со значениями индуцированного дипольного момента: ${{p}_{{0.25}}} \approx 7.7\,\,{\text{кД}}$, ${{p}_{{0.5}}} \approx 15.4\,\,{\text{кД}}$ и ${{p}_{{1.0}}} \approx 30.8\,\,{\text{кД}}$. При этих значениях дипольного момента сплюснутого наносфероида атомы на поверхности его положительно заряженного полюса имели парциальные заряды: $ + 0.25e$, $ + 0.5e$ и $ + 1e$ соответственно.

По результатам МД-моделирования всех рассмотренных полиамфолитов на поверхности сплюснутого наносфероида на конечном стационарном участке траектории по всем полученным конформациям рассчитывались распределения средней линейной плотности атомов вдоль оси вращения с шагом 0.2 нм, а также радиальные распределения средней плотности атомов полипептидов в экваториальной области шириной 1 нм.

4. РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

4.1. МД-моделирование полиамфолитных полипептидов на поверхности нейтрального и заряженного сплюснутого металлического наносфероида

По результатам МД-моделирования полиамфолитных полипептидов на поверхности нейтрального сплюснутого золотого наносфероида макромолекулы адсорбировались на нем, полностью обволакивая его (рис. 2а и 2б) [38], как и в ранее рассмотренных случаях сферических, цилиндрических и вытянутых сфероидальных золотых наночастиц [13, 15, 17, 21–23].

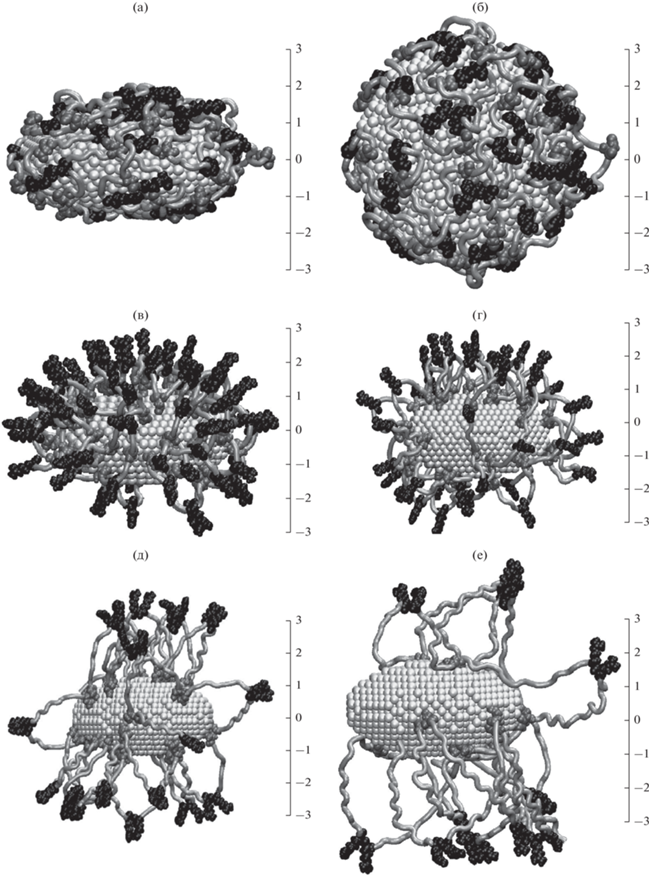
Рис. 2.

Полипептид P2 после МД-моделирования на незаряженной поверхности сплюснутого золотого наносфероида (а – вид сбоку, б – вид сверху). Полипептиды P1 (в), P2 (г), P3 (д) и P4 (е) после МД-моделирования на поверхности заряженного с полным зарядом ${{Q}_{{0.5}}}$ сплюснутого золотого наносфероида. На рисунке: светло-серая трубка – звенья Ala, черным цветом изображены звенья Arg, а серым – Asp, значения на линейке указаны в нанометрах.

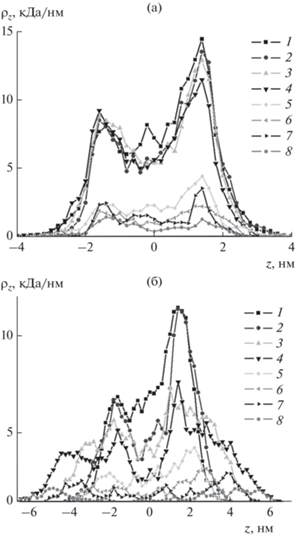
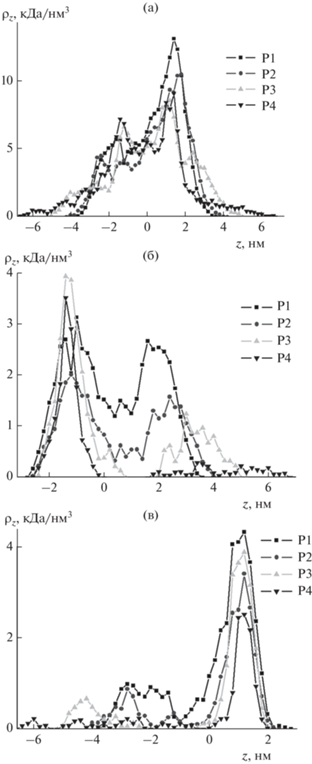
На рис. 3 изображены распределения средней линейной плотности атомов всех рассмотренных полипептидов вдоль оси вращения на поверхности электронейтрального сплюснутого золотого наносфероида (область отрицательных значений по оси $z$ соответствует атомам полипептида расположенным ниже (рис. 1а) от центра наносфероида). Видно, что распределения по всем атомам полипептида, а также по его заряженным звеньям Arg, имеют характерные пики линейной плотности по обе стороны от начала координат. Данные пики соответствуют адсорбции звеньев макромолекулы в верхней и нижней (рис. 2а) области наносфероида. Появление таких пиков связано с тем, что при в целом равномерном распределении звеньев по поверхности нейтрального сплюснутого наносфероида в расчетный слой линейной плотности вдоль оси вращения в приполярной области попадает больше атомов полипептида в отличие от случая вытянутого нейтрального наносфероида [22], где наоборот наблюдалось снижение линейной плотности в приполярных областях.

Рис. 3.

Распределения средней линейной плотности атомов полипептидов P1 (1, 5), P2 (2, 6), P3 (3, 7) и P4 (4, 8) вдоль направления оси вращения на поверхности нейтрального (а) и заряженного с полным зарядом ${{Q}_{{0.5}}}$ (б) сплюснутого золотого наносфероида по всем атомам полипептида (1–4) и по аминокислотным остаткам Arg (5–8).

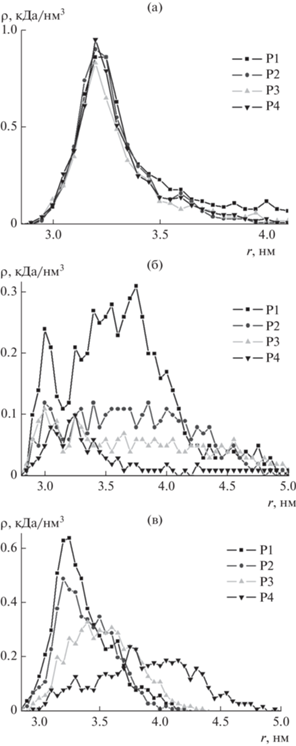
На рис. 4а изображены радиальные зависимости средней плотности атомов всех рассмотренных полипептидов в экваториальной области сплюснутого золотого наносфероида. Видно, что радиальные распределения атомов для полиамфолитных полипептидов близких по длине размеров с различным расстоянием между разноименно заряженными звеньями имеют схожий вид с образованием характерного пика [13, 16, 17, 21] у поверхности и с плавным снижением плотности при удалении от нее.

Рис. 4.

Радиальные зависимости средней плотности атомов полипептидов P1, P2, P3 и P4 в экваториальной области сплюснутого золотого наносфероида: а – на нейтральной поверхности, б – на поверхности наносфероида, заряженного с полным зарядом ${{Q}_{{0.5}}}$, в – на поверхности поляризованного наносфероида вдоль оси вращения с дипольным моментом ${{p}_{{1.0}}}$.

На поверхности заряженного сплюснутого золотого наносфероида при увеличения его полного заряда постепенно наблюдалось все большее смещение одноименно заряженных с наносфероидом звеньев Arg от поверхности с вытягиваем петель макроцепи. На рис. 2в–2е изображены конформационные структуры всех рассмотренных полипептидов после МД-моделирования на поверхности заряженного с полным зарядом ${{Q}_{{0.5}}}$ сплюснутого золотого наносфероида. Видно, что для полипептидов P1 (рис. 2в) и P2 (рис. 2г) с небольшим числом нейтральных аминокислотных остатков Ala между противоположно заряженными звеньями Arg и Asp наблюдается выбрасывание петель макроцепи вдоль нормали к поверхности по всей поверхности сплюснутого наносфероида как в экваториальной, так приполярных областях. Смещения звеньев в экваториальную область с большей поверхностной плотностью заряда или в приполярные области с более низкой поверхностной плотностью заряда не произошло. При этом непосредственно на поверхности наночастицы находятся звенья Asp, которые имеют заряд противоположный заряду сплюснутого наносфероида.

Другая картина наблюдалась для полипептидов P3 и P4 с наибольшим расстоянием между положительными и отрицательными звеньями в макроцепи. На рис. 2д и 2е видно, что бóльшая часть из петель макромолекулярной цепи направлены либо вдоль оси вращения, либо отклоняются в ее сторону, при этом в экваториальной области петель, вытянутых в направлении перпендикулярном оси вращения очень мало в отличие от случаев адсорбции полипептидов P1 (рис. 2в) и P2 (рис. 2г). Это связано с тем, что петли полиамфолитного полипептида, которые образуются на поверхности положительно заряженной наночастицы, образованы двумя отрицательно заряженными звеньями Asp, находящимися на поверхности, а также фрагментом полипептида между ними, состоящего из нейтральных звеньев Ala и отталкивающихся от поверхности звеньев Arg. В случае небольшой длины такого фрагмента между звеньями Asp образуется множество петель небольшой длины, которые распределены по всей поверхности (рис. 2в и 2г). В случае, когда этот фрагмент достаточно большой, как у полипептидов P3 (рис. 2д) и P4 (рис. 2е), концы петли (звенья Asp) могут находиться как рядом на поверхности, так и на достаточно большом расстоянии друг от друга, в том числе на противоположных полюсах сплюснутого наносфероида. Как видно из рис. 2д и 2е у большинства петель, один конец которых начинается на экваторе, второй конец находится в приполярной области, а поэтому лишь некоторые из петель направлены в направлении перпендикулярном к оси вращения наносфероида. Поэтому у полипептидов P3 и P4 макромолекулярная опушка на поверхности сплюснутого заряженного металлического наносфероида получается вытянутой вдоль оси вращения, в отличие от случаев заряженных сферической [14], цилиндрической [17, 21] и вытянутой сфероидальной наночастиц [22].

Это хорошо видно на графиках зависимостей средней линейной плотности атомов полипептидов вдоль оси вращения на поверхности заряженного с полным зарядом ${{Q}_{{0.5}}}$ сплюснутого золотого наносфероида (рис. 3б). Видно, что профиль распределения средней линейной плотности по всем атомам полипептидов P1 и P2 уширился незначительно по сравнению с нейтральной наночастицей (рис. 3а). При это для полипептидов P3 и P4 наблюдается значительное вытягивание макромолекулярной опушки вдоль оси вращения и профиль данного распределение был тем шире, чем больше расстояние между разноименно заряженными звеньями в макроцепи. Это уширение обусловлено смещением звеньев Arg (рис. 3б, кривые 5–8) от поверхности и вытягиванием макромолекулярной опушки вдоль оси вращения. Также видно, что по сравнению с нейтральным наносфероидом (рис. 3а, кривая 8) у полипептида P4 в экваториальной области положительно заряженного наносфероида (рис. 3б, кривая 8) практически не осталось звеньев Arg, что соответствует отклонению петель макроцепи в направлении оси вращения наносфероида. При этом звенья Asp находятся на поверхности наносфероида, в том числе в его экваториальной области.

На графиках радиальных зависимостей средней плотности атомов полипептида P2 в экваториальной области сплюснутого золотого наносфероида (рис. 5а, кривые 5–7) видно, что при увеличении полного заряда наносфероида происходит разрыхление макромолекулярной опушки, которое связано с выбрасыванием петель макроцепи. Также видно, что уже при полном заряде наносфероида ${{Q}_{{0.125}}}$ происходит очень сильное снижение значений радиальной плотности атомов полипептида по аминокислотным остаткам Arg (рис. 5б, кривая 5), которые отдалялись тем дальше, чем был выше полный заряд наносфероида (рис. 5б, кривые 6 и 7). При этом профиль радиального распределения атомов полипептида P2 по звеньям Asp (рис. 5в, кривые 5–7) все сильнее смещался в левую часть графика, что соответствует адсорбции всех аминокислотных остатков Asp на поверхности наносфероида.

Рис. 5.

Радиальные зависимости средней плотности атомов полипептида P2 в экваториальной области сплюснутого золотого наносфероида: а – по всем атомам полипептида, б – по аминокислотным остаткам Arg, в – по аминокислотным остаткам Asp. Цифрами обозначено: 1 – на нейтральной поверхности, на поверхности поляризованного наносфероида вдоль оси вращения с дипольным моментом ${{p}_{{0.25}}}$ (2), ${{p}_{{0.5}}}$ (3) и ${{p}_{{1.0}}}$ (4), а также на поверхности заряженного с полным зарядом ${{Q}_{{0.125}}}$ (5), ${{Q}_{{0.25}}}$ (6) и ${{Q}_{{0.5}}}$ (7) наносфероида.

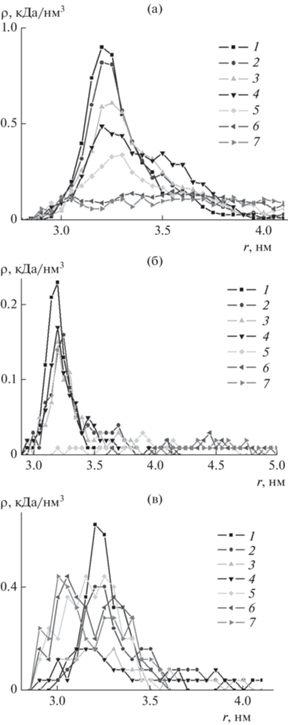
На рис. 4б показано сравнение радиальных зависимостей средней плотности атомов всех рассмотренных полипептидов в экваториальной области заряженного с полным зарядом ${{Q}_{{0.5}}}$ сплюснутого золотого наносфероида. Видно, что чем больше было расстояние между положительными и отрицательными звеньями в макроцепи, тем профиль радиального распределения плотности становился ниже. Это связано с описанным выше характером отклонения петель полипептидов P3 и P4 в сторону оси вращения наносфероида, а также с тем, что число адсорбированных звеньев Asp на поверхности у полипептидов P1 и P2 выше, вследствие их большего количества в макроцепи.

4.2. МД-моделирование полиамфолитных полипептидов на поверхности поляризованного сплюснутого золотого наносфероида

В случае адсорбции полиамфолитных полипептидов на поверхности поляризованного вдоль оси вращения сплюснутого наносфероида по мере увеличения его дипольного момента происходило вытягивание макромолекулярной опушки вдоль оси вращения (рис. 6), которое было тем сильнее, чем больше было нейтральных звеньев между противоположно заряженными аминокислотными остатками в макроцепи.

Рис. 6.

Полипептиды P1 (а), P2 (б), P3 (в) и P4 (г) после МД-моделирования на поверхности поляризованного вдоль оси вращения с дипольным моментом ${{p}_{{1.0}}}$ сплюснутого золотого наносфероида. На рисунке: светло-серая трубка – звенья Ala, черным цветом изображены звенья Arg, а серым – Asp, значения на линейке указаны в нанометрах.

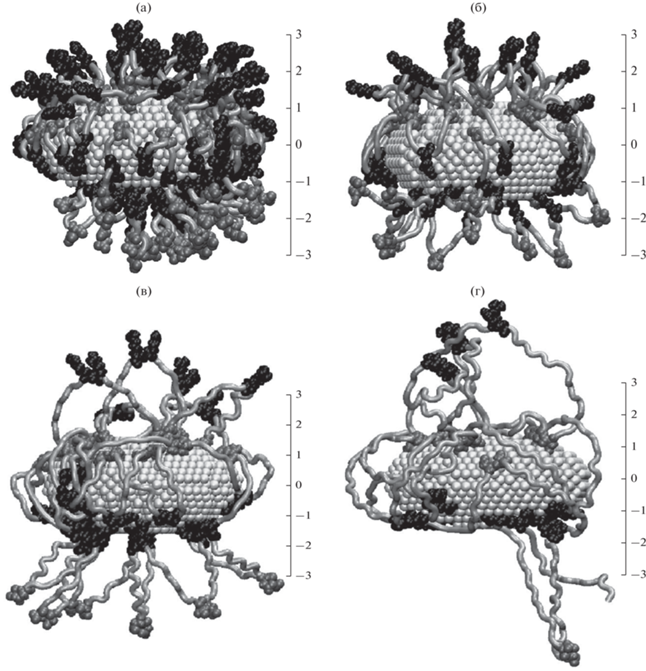
В приполярных областях поляризованного сплюснутого наносфероида, в которых парциальные заряды атомов на поверхности (2) были близкими по величине к зарядам непосредственно на полюсе поляризованного наносфероида, наблюдалось выбрасывание петель полиамфолита (рис. 6) по виду подобных макромолекулярным петлям на поверхности заряженного наносфероида. Данные петли образованы двумя аминокислотными остатками с зарядом противоположным заряду приполярной области и фрагментом полипептида, расположенного между ними из нейтральных звеньев и одноименно заряженных поверхности. Приполярные области сплюснутого наносфероида простираются более широко, чем в ранее рассмотренных случаях сферической [13–15] и вытянутой сфероидальной золотой наночастицы [22, 23]. Поэтому на поверхности поляризованного сплюснутого металлического наносфероида наблюдается значительно большее количество петель макроцепи, которые направлены вдоль его оси вращения.

На рис. 6 видно, что заряженные с разным знаком заряда аминокислотные остатки полиамфолитных полипептидов адсорбировались на противоположно заряженных приполярных областях полюсах сплюснутого наносфероида. При этом одноименно заряженные остатки по отношению к заряду верхней или нижней (рис. 6) приполярной области отталкиваясь отдалялись от поверхности, что и приводило к вытягиванию макромолекулярной опушки в направлении поляризации вдоль оси вращения. В сплюснутом наносфероиде слабо заряженная экваториальная область значительно уже, чем в сферической наночастице [13–15], а тем более в вытянутом наносфероиде [22, 23]. Поэтому переход от адсорбции отрицательных звеньев полипептида Asp в верхней (рис. 6) половине наносфероида к адсорбции положительных звеньев Arg в нижней половине очень резкий в отличие от поляризованного вытянутого наносфероида, где наблюдалась широкая плотная макромолекулярная опушка из адсорбированных аминокислотных остатков всех типов в его центральной области, которая постепенно набухала около полюсов [22, 23].

На рис. 7а изображены распределения средней линейной плотности атомов всех рассмотренных полипептидов вдоль оси вращения на поверхности поляризованного с дипольным моментом ${{p}_{{1.0}}}$ сплюснутого золотого наносфероида. Видно, что по сравнению с нейтральным наносфероидом (рис. 3а) произошло уширение профиля распределения линейной плотности полипептидов, что говорит о вытягивании опушки вдоль оси сплюснутого наносфероида. Как и в случае заряженного наносфероида (рис. 3б), чем больше было расстояние между положительными Arg и отрицательными Asp звеньями в полипептиде, тем больше была ширина профиля линейного распределения. Однако, в отличие от заряженного сплюснутого наносфероида (рис. 3б) распределение средней линейной плотности атомов полипептидов по аминокислотным остаткам Arg (рис. 7б) и Asp (рис. 7в) на поверхности поляризованного сплюснутого наносфероида значительно отличалось. На рис. 7б видно, что большое количество звеньев Arg сконцентрировано в области отрицательных значений вдоль оси вращения, то есть около отрицательно заряженного полюса наносфероида (рис. 6). А в области положительных значений наблюдается снижение линейной плотности атомов по остаткам Arg и смещение профиля распределения от поверхности. Для распределения средней линейной плотности атомов полипептида по остаткам Asp (рис. 7в) наблюдалась зеркальная картина по отношению к распределению по остаткам Arg.

Рис. 7.

Распределение средней линейной плотности атомов полипептидов P1, P2, P3 и P4 вдоль направления z оси вращения на поверхности поляризованного вдоль z с дипольным моментом ${{p}_{{1.0}}}$ сплюснутого золотого наносфероида: а – по всем атомам полипептида, б – по аминокислотным остаткам Arg, в – по аминокислотным остаткам Asp.

На графиках радиальных зависимостей средней плотности атомов полипептида P2 в экваториальной области поляризованного сплюснутого золотого наносфероида (рис. 5а, кривые 2–4) видно, что при увеличении дипольного момента наносфероида происходит постепенное уменьшение плотности атомов в экваториальной области. При этом кривые располагаются выше, чем для заряженного наносфероида (рис. 5а, кривые 4–7). Такое более слабое набухание опушки связано с тем, что в случае поляризованного наносфероида его атомы на поверхности в экваториальной области слабо заряжены или нейтральны. Поэтому выброса петель в этой области не происходит и в ней могут находиться аминокислотные остатки всех типов, в том числе положительно заряженные Arg (рис. 5б, кривые 2–4) или отрицательно заряженные Asp (рис. 5в, кривые 2–4).

Сравнивая радиальные зависимости средней плотности атомов всех рассмотренных полипептидов (рис. 4в), можно заметить, что чем больше число нейтральных аминокислотных остатков Ala находится между противоположно заряженными звеньями полипептида, тем сильнее происходит набухание опушки в экваториальной области, а пик профиля данного распределения смещается от поверхности (кривые для полипептидов P3 и P4). Такое набухание опушки в экваториальной области связано со перемещением заряженных звеньев из нее в приполярные области. При большом расстоянии между противоположно заряженными звеньями в полипептидах P3 и P4 все заряженные остатки Arg и Asp смещаются в приполярные области (рис. 6в и 6г), а петли из фрагментов макроцепи, состоящих из аминокислотных остатков Ala соединяют их. В то время как у полипептидов P1 и P2 петли из звеньев Ala небольшой длины, а часть заряженных звенья находятся в районе экватора (рис. 6а и 6б). Это приводит к тому, что для полипептидов P1 и P2 макромолекулярная опушка в экваториальной области более плотная.

Можно отметить, что имеет место согласованность между результатами, полученными с помощью математической модели (рис. 1) и по результатам проведенного МД-моделирования (рис. 4–7) на поверхности поляризованного сплюснутого наносфероида. По результатам, полученным на основе математической модели, на поверхности поляризованного наносфероида на его полюсах наблюдаются максимальные значения плотности звеньев полиамфолита. Результаты, полученные методом молекулярной динамики также говорят о том, что большая часть аминокислотных остатков полипептида сосредоточена в приполярных областях сплюснутого наносфероида.

5. ЗАКЛЮЧЕНИЕ

Таким образом, в работе исследована проблема формирования макромолекулярного опушечного слоя адсорбированной цепи полиамфолита на поверхности металлического сжатого наносфероида, несущего избыточный электрический заряд или электронейтрального, но поляризованного во внешнем постоянном электрическом поле. Предложена математическая модель такой системы, учитывающая энтропийный эффект образования конформаций адсорбированной гауссовой цепи на криволинейной поверхности наночастицы без обращения к формализму описания конформационных функций в сфероидальной системе координат. Вклад в формирование структуры макроцепной опушки взаимодействия дипольных сегментов цепи полиамфолита с полем заряженного или поляризованного проводящего наносфероида учтен в виде отдельного больцмановского фактора. Произведенная факторизация энтропийного и полевого вкладов позволяет осуществлять независимый анализ их влияния на формирование конформационной структуры макроопушки полиамфолитов. По мере удаления от поверхности сфероида эквипотенциальные поверхности поля все больше приближаются к слегка искаженным сферам – для заряженной наночастицы, и к эквипотенциальным поверхностям точечного диполя в поле – в случае поляризованного наносфероида.

Проведенное МД-моделирование для случая адсорбции полиамфолитных полипептидов на поверхности заряженного сплюснутого металлического наносфероида показало, что по мере увеличения его полного заряда происходит все большее вытягивание петель макроцепи. Данные макромолекулярные петли образованы двумя адсорбированными звеньями макромолекулы, заряженными со знаком заряда противоположным знаку заряду поверхности, а также находящимися между ними одноименно заряженными с поверхностью звеньями макроцепи, которые отталкиваясь от нее увлекает за собой две цепочки из нейтральных звеньев, которые соединяют положительные и отрицательные аминокислотные остатки полипептида. Поэтому толщина полиамфолитной опушки на поверхности заряженного сплюснутого наносфероида тем больше, чем больше расстояние между противоположно заряженными звеньями в макромолекуле. Кроме того, в отличие от случаев адсорбции на поверхностях заряженных металлических сферических [14], цилиндрических [21] и вытянутых сфероидальных нанообъектов [22], на поверхности заряженного сплюснутого наносфероида для полипептидов с большим расстоянием между разноименно заряженными звеньями в макроцепи наблюдается вытягивание макромолекулярной опушки в направлении оси вращения наносфероида.

В случае адсорбции полиамфолитных полипептидов на поверхности поляризованного вдоль оси вращения сплюснутого металлического наносфероида происходило вытягивание макромолекулярной опушки вдоль его оси. При этом опушка вытягивалась тем сильнее, чем больше было расстояние между положительными и отрицательными звеньями полипептида, а сама она была образована петлями макроцепи двух видов. В широких сильно заряженных приполярных областях они были схожими с петлями, которые образовывались на поверхности заряженной металлической наночастицы. А в экваториальной области они были образованы двумя разноименно заряженными звеньями, адсорбированными в противоположно заряженных половинах наносфероида, разделенных экватором, а также фрагментом из нейтральных звеньев макроцепи, который соединял их, пересекая экваториальную область. Поэтому опушка набухала не только в приполярных областях сплюснутого наносфероида, но и его экваториальной области.

Как уже было отмечено, МД-моделирование представляет собой по сути вычислительный эксперимент. Поэтому результирующие конформации адсорбированной полиамфолитной цепи в электрическом поле, полученные на основе МД-расчетов представляются максимально близкими к реализуемым в эксперименте макроцепным структурам. В частности МД-метод позволяет выявить петлевую структуру опушечного слоя и проследить за изменением параметров петель при изменении характеристик поля, температуры системы, типа растворителя. Представленная же в работе аналитическая модель, основанная на молекулярно-кинетических и статистических подходах, лишена этих возможностей, но, в свою очередь, она позволяет производить раздельный анализ значимости энтропийного и полевого вкладов в процессе формирования итоговых равновесных конформаций адсорбированной макромолекулы. Таким образом, два реализованных в работе подхода взаимно обогащают и дополняют друг друга.

Исследованные в данной работе электрически индуцированные изменения конформационной структуры полиамфолитов на поверхности сплюснутого металлического наносфероида могут найти применение при создании и модификации различных нанозондов, чувствительных к воздействию внешнего электрического поля, а также различных устройствах наноэлектроники и химических сенсорах на основе эффекта гигантского комбинационного рассеяния.

Список литературы

  1. Wang D., Cui M., Zhang X. // Acc. Chem. Res. 2021. V. 54. P. 4451.

  2. Lee J., Cho H., Choi H., Lee J., Choi J. // International Journal of Molecular Sciences. 2021. V. 19. P. ijms19072021.

  3. Franco D., De Plano L.M., Rizzo M.G., Scibilia S. Lentini G., Fazio E., Neri F., Guglielmino S.P.P., Mezzasalma A.M. // Spectrochimica Acta Part A: Molecular and Biomolecular Spectroscopy. 2020. V. 224. P. 117394.

  4. Samieegohar M., Sha F., Clayborne A.Z., Wei T. // Langmuir. 2019. V. 35. P. 5029.

  5. Su S., Yu T., Hu J., Xianyu Y. // Biosensors and Bioelectronics. 2022. V. 195. P. 113621.

  6. Pardehkhorram R., Alshawawreh F.A., Gonçales V.R., Lee N.A., Tilley R.D., Gooding J.J. // Anal. Chem. 2021. V. 93. P. 12954.

  7. Penninkhof J.J., Moroz A., van Blaaderen A., Polman A. // J. Phys. Chem. C. 2008. V. 112. P. 4146.

  8. Liaw J., Wu H., Huang C., Kuo M. // Nanoscale Research Letters. 2016. V. 11. No. 26.

  9. Alsawafta M., Wahbeh M., Truong V. // Journal of Nanomaterials. 2012. P. 457968.

  10. Chandra S., Doran J., McCormack S.J. // Journal of Colloid and Interface Science. 2015. V. 459. P. 218.

  11. Fedotov V.A., Emel’yanov V.I., MacDonald K.F., Zheludev N.I. // Journal of Optics A: Pure and Applied Optics. 2004. V. 6. P. 155.

  12. Piralaee M., Asgari A., Siahpoush V. // Optik. 2018. V. 172. P. 1064.

  13. Kruchinin N.Yu., Kucherenko M.G. // Colloid Journal. 2020. V. 82. № 2. P. 136.

  14. Kruchinin N.Yu., Kucherenko M.G. // Biophysics. 2020. V. 65. № 2. P. 186.

  15. Kruchinin N.Yu., Kucherenko M.G. // Colloid Journal. 2020. V. 82. №. 4. P. 392.

  16. Kruchinin N.Yu., Kucherenko M.G. // Russian Journal of Physical Chemistry A. 2020. V. 94. № 7. P. 1433.

  17. Kruchinin N.Yu., Kucherenko M.G. // Colloid Journal. 2021. V. 83. № 1. P. 79.

  18. Kruchinin N.Yu., Kucherenko M.G., Neyasov P.P. // Russian Journal of Physical Chemistry A. 2021. V. 95. № 2. P. 362.

  19. Kruchinin N.Yu., Kucherenko M.G. // Eurasian Physical Technical Journal. 2021. V. 18. № 1. P. 16.

  20. Kruchinin N.Yu. // Colloid Journal. 2021. V. 83. № 3. P. 326.

  21. Kruchinin N.Yu., Kucherenko M.G. // Surfaces and Interfaces. 2021. V. 27. P. 101517.

  22. Kruchinin N.Yu., Kucherenko M.G. // Colloid Journal. 2021. V. 83. № 5. P. 591.

  23. Kruchinin N.Yu., Kucherenko M.G. // High Energy Chemistry. 2021. V. 55. № 6. P. 442.

  24. Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред. М.: Наука, 1982.

  25. Комаров И.В., Пономарев Л.И., Славянов С.Ю. Сфероидальные и кулоновские сфероидальные функции. М.: Наука, 1976.

  26. Kruchinin N.Yu., Kucherenko M.G. // Polymer Science Series A. 2022. V. 64. № 3.

  27. Гросберг А.Ю., Хохлов А.P. Статистическая физика макромолекул. М.: Наука, 1989.

  28. Кучеренко М.Г., Кручинин Н.Ю., Чмерева Т.М. // Вестник ОГУ. 2010. № 5. С. 124.

  29. Kruchinin N.Yu., Kucherenko M.G. // Colloid Journal. 2019. V. 81. № 2. P. 110.

  30. Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979.

  31. Phillips J.C., Braun R., Wang W., Gumbart J., Tajkhorshid E., Villa E., Chipot C., Skeel R.D., Kale L., Schulten K. // J. Comput. Chem. 2005. V. 26. P. 1781.

  32. Mhashal A.R, Roy S. // PLoS One. 2014. V. 9. P. e114152.

  33. MacKerell A.D. Jr., Bashford D., Bellott M., Dunbrack Jr. R.L., Evanseck J.D., Field M.J., Fischer S., Gao J., Guo H., Ha S., Joseph-McCarthy D., Kuchnir L., Kuczera K., Lau F.T.K., Mattos C., Michnick S., Ngo T., Nguyen D.T., Prodhom B., Reiher W.E., III, Roux B., Schlenkrich M., Smith J.C., Stote R., Straub J., Watanabe M., Wiorkiewicz-Kuczera J., Yin D., Karplus M. // J. Phys. Chem. B. 1998. V. 102. P. 3586.

  34. Huang J., Rauscher S., Nawrocki G., Ran T., Feig M., de Groot B.L., Grubmuller H., MacKerell A.D., Jr. // Nature Methods. 2016. V. 14. P.71.

  35. Heinz H., Vaia R.A., Farmer B.L., Naik R.R. // J. Phys. Chem. C. 2008. V. 112. P. 17281.

  36. Darden T., York D., Pedersen L. // J. Chem. Phys. 1993. V. 98. P. 10089.

  37. Jorgensen W.L., Chandrasekhar J., Madura J.D., Impey R.W., Klein M.L. // J. Chem. Phys. 1983. V. 79. P. 926.

  38. Humphrey W., Dalke A., Schulten K. // J. Molec. Graphics. 1996. V. 14. P. 33.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал