Коллоидный журнал, 2022, T. 84, № 3, стр. 274-300

Обзор современного состояния исследований адгезионных явлений на границах твердых тел с твердыми и жидкими водными средами

К. А. Емельяненко^1, *, А. М. Емельяненко¹, Л. Б. Бойнович¹

¹ Институт физической химии и электрохимии им. А.Н. Фрумкина Российской академии наук
119071 Москва, Ленинский проспект, 31, корп. 4, Россия

^* E-mail: emelyanenko.kirill@gmail.com

Поступила в редакцию 25.03.2022
После доработки 30.03.2022
Принята к публикации 31.03.2022

EDN: BRKDDF
DOI: 10.31857/S002329122203003X

Полный текст (PDF)

Аннотация

Адгезия льда играет важную роль при эксплуатации технических сооружений и техники в открытой атмосфере, где накопление водных осадков может угрожать безопасному функционированию индустриальных объектов. В этом обзоре мы рассматриваем адгезию льда и воды к различным поверхностям и обсуждаем механизмы адгезии водных сред к твердым поверхностям. Отдельное внимание уделяется роли поверхностных сил и квази-жидкого водного слоя в адгезии льда к твердым поверхностям. Рассматриваются факторы, определяющие величину прочности адгезионного контакта к современным антиобледенительным покрытиям, и обсуждается ее температурная зависимость.

1. ВВЕДЕНИЕ

Адгезия, в наиболее широком смысле, может быть определена как количественная мера сопротивления разрыву контакта двух тел вдоль границы раздела [1]. Поскольку адгезия всегда является результатом межмолекулярных взаимодействий между двумя разнородными материалами, разделенными межфазной границей, то величина адгезии определяется как характером химической связи, так и физическими силами. Особый интерес вызывает изучение адгезионного контакта, возникающего за счет физических сил взаимодействия, таких, как вандерваальсовы силы, силы электрической природы и капиллярные силы. Именно такого рода силы ответственны за адгезию жидких и твердых водных сред к твердым поверхностям.

Для большого количества промышленных приложений адгезионные явления играют позитивную роль, определяя долговечность и эффективность контакта соединяемых элементов (см., например, [2]). В то же время часто возникает ситуация, когда высокая адгезия нежелательна. Например, для устройств, работающих в открытых атмосферных условиях, адгезия различных твердых или жидких сред, таких как органические и неорганические загрязнения, продукты биологической активности, а также жидкие и твердые водные осадки, приводит к нарушению штатных характеристик и нормального функционирования таких устройств. Здесь можно упомянуть адгезию пылевых частиц к электрическим проводам линий электропередач и к поверхности изоляторов, которая приводит к резкому возрастанию токов утечки по изоляторам или к развитию коронного разряда даже при не очень большом напряжении на проводе. Еще один яркий пример связан с адгезией капель атмосферных осадков, являющихся водными растворами с различным pH и химическим составом, на металлические поверхности. При контакте таких капель с металлами и сплавами развиваются интенсивные коррозионные процессы, ведущие к разрушению конструкций и деградации их свойств. Наконец, к негативным последствиям, напрямую зависящим от адгезионных свойств, можно отнести накопление льда, снега и воды на открытых поверхностях. В аэрокосмической отрасли, а также при передаче электроэнергии, адгезия льда приводит не только к многомиллиардным экономическим издержкам, но, в ряде случаев, и к человеческим жертвам. Поэтому задачи, стоящие перед исследователями, работающими в области создания адгезионных соединений, и исследующих возможности получения поверхностей с минимальной адгезией к атмосферным осадкам, решаются различными методами.

Анализ адгезии водных жидких сред к твердым поверхностям упрощается тем, что процесс разрыва контакта и образования новых поверхностей жидкость/газ и твердое тело/газ, как правило, термодинамически обратим. Это позволяет количественно характеризовать адгезию величиной работы адгезии. Качественно адгезия жидкости к поверхности может быть оценена по углу смачивания, который определяется межмолекулярными взаимодействиями в зоне трехфазного контакта. При этом углы смачивания, образуемые мениском жидкости с твердой поверхностью, могут быть использованы для расчета работы адгезии по уравнению Юнга−Дюпре [3–6].

Работа адгезии водных растворов к любым твердым поверхностям при комнатной температуре, как правило, довольно мала и изменяется в пределах от 0.16 Дж/м² до нуля. Наименьшие значения работы адгезии наблюдаются у супергидрофобных поверхностей, на которых капли водных сред имеют угол смачивания, близкий к 180°. На гидрофильных поверхностях с углом смачивания, близким к нулю, работа адгезии водной средой, в основном, определяется поверхностным натяжением водной среды, которое даже для концентрированных водных растворов поверхностно-инактивных веществ, как правило, не превышает 80 мН/м. Здесь нужно еще раз подчеркнуть, что работа адгезии характеризует затраты энергии именно на отрыв капли или мениска от поверхности. Если же рассматривать задачу движения капель вдоль поверхности, например при исследовании самопроизвольного удаления капель воды с твердой поверхности под действием силы тяжести или ветрового потока, то здесь определяющим физико-химическим фактором является гистерезис смачивания, т.е. разница между углами натекания и оттекания [7]. Чем ниже гистерезис смачивания, тем меньше пороговое значение касательной нагрузки, при котором начинается движение жидкости вдоль поверхности [7, 8].

Еще один способ оценки адгезии на границе твердой и жидкой сред, который активно развивается в последние годы, основан на измерении максимальной силы и силы отрыва сидящей капли с использованием электронных микровесов [8, 9].

На границе раздела двух твердых тел исследование и характеризация разрыва контакта оказывается гораздо более сложной задачей. Здесь, как и в случае контакта жидкости с твердым телом, основной вклад в величину адгезии дают поверхностные силы. В зависимости от природы соприкасающихся тел это могут быть как силы физической природы, например вандерваальсовы или электростатические взаимодействия, так и химической – водородные, ионные или ковалентные связи [1]. Поскольку химические силы очень короткодействующие, а радиус действия поверхностных сил физической природы составляет десятки, а иногда и сотни нанометров [10–12], т. е., часто сравним с характерным масштабом шероховатости поверхности, величина адгезии оказывается крайне чувствительна к шероховатости соприкасающихся тел. Кроме того, разрыв контакта твердых тел часто сопровождается большими диссипативными потерями энергии, связанными с локальным нагревом и пластическими деформациями вблизи границы раздела. Действие указанных факторов приводит к тому, что энергия, необходимая для разрыва контакта, оказывается зависящей от деталей конкретного процесса разделения тел. В этом случае работа адгезии, рассчитываемая в рамках приближения термодинамически обратимого процесса, должна рассматриваться как нижняя оценка энергии, затрачиваемой на разделение тел.

Трудности как в воспроизводимом измерении полной энергии, необходимой для разделения фаз, так и в аналитическом описании и интерпретации полученных данных, вызвали интерес к использованию силовых параметров адгезионного контакта, таких как прочность адгезионного контакта. В настоящее время прочность адгезионного контакта льда с твердой поверхностью, на практике, является основной характеристикой, определяющей накопление твердых водных осадков на такой поверхности. Исследования материалов, которые снижают адгезию льда и снега, активно ведутся на протяжении многих десятилетий и в последние годы переживают настоящий бум, связанный с появлением новых классов покрытий. К таким новым классам покрытий, демонстрирующих возможность удаления твердых водных осадков под действием собственного веса, ветра или вибраций [13–24], относятся супергидрофобные покрытия [14, 15, 25, 26], скользкие пористые покрытия с пропитками на основе водной или органической фазы [18–21], покрытия с низкой межфазной прочностью и межфазным проскальзыванием [13, 16], покрытия с низким модулем упругости на основе гидрогелей, органогелей, ионогелей и эластомеров [17, 22–24].

Исследования покрытий с низкой адгезией к твердым водным фазам показали, что величина прочности адгезионного контакта оказывается чувствительна к температуре окружающей среды и влажности, особенностям процесса замораживания, а также к методу измерения адгезионной прочности. В данном обзоре мы вкратце обсудим механизмы адгезии льда к твердым поверхностям, рассмотрим факторы, снижающие прочность адгезионного контакта к некоторым типам льдофобных поверхностей, обсудим влияние температуры кристаллизации капель и времени релаксации льда после кристаллизации воды на величину адгезии.

2. МЕЖФАЗНАЯ ГРАНИЦА ЖИДКОСТЬ–ТВЕРДОЕ ТЕЛО: ВЛИЯНИЕ МОРФОЛОГИИ ПОВЕРХНОСТИ НА РАБОТУ АДГЕЗИИ

Мы начнем наше рассмотрение с наиболее простого случая, соответствующего контакту капли водной среды на гладкой, однородной и инертной по отношению к жидкости твердой подложке. Как было сказано выше, угол смачивания, образуемый мениском жидкости или поверхностью капли с поверхностью твердого тела, является мерой адгезии жидкости к твердой поверхности и определяется поверхностными силами, действующими на межфазных границах и в области трехфазного контакта. И хотя целенаправленное изменение адгезии жидкости в системе жидкость–твердое тело потребует исследования и управления вкладами отдельных типов поверхностных сил, полное описание адгезии водных сред к тем или иным практически важным материалам может проводиться только на основе измерения угла смачивания и его поведения при изменении внешних условий. Таким образом, упрощение анализа адгезии жидкостей к твердым телам связано именно с возможностью использования легко измеримых в эксперименте интегральных характеристик трехфазного контакта.

Как отмечалось выше, для количественной оценки адгезии жидкости к гладкой поверхности используется величина работа адгезии $W_{{{\text{sl}}}}^{{{\text{smooth}}}}$, рассчитываемая на основе уравнения Юнга−Дюпре (1). При этом, как отмечалось в [12], предполагается нормальный к поверхности отрыв капли. Чтобы подчеркнуть характер отрыва жидкости от поверхности, в [12] было предложено ввести термин “практическая работа адгезии”. Как было показано в [3, 4], в этом случае в уравнении Юнга−Дюпре в качестве угла смачивания, следует использовать краевой угол оттекания, поскольку именно он характеризует поверхностные силы при квазиравновесном процессе отступления фронта жидкости по полностью или частично смоченной подложке:

(1)

$W_{{{\text{sl}}}}^{{{\text{smooth}}}} = {{\sigma }_{{{\text{lv}}}}}\left( {1 + {\text{cos}}{\kern 1pt} \theta _{{{\text{sl}}\left( r \right)}}^{{{\text{smooth}}}}} \right).$

Здесь σ_lv – поверхностное натяжение на границе жидкость-пар (которое определяется свойствами жидкости и поверхностными силами на межфазной границе жидкость−пар (так называемыми поверхностными силами первого рода [11, 27]), а $\theta _{{{\text{sl}}\left( r \right)}}^{{{\text{smooth}}}}$ – краевой угол оттекания, образованный жидким мениском и гладкой твердой поверхностью, индекс r указывает на угол оттекания. Этот краевой угол (или угол смачивания), в свою очередь, определяется свойствами всех трех фаз в зоне трехфазного контакта жидкость-пар-твердое тело. Соответственно, величина угла смачивания определяется поверхностными силами второго рода [11, 27]. Она может быть рассчитана для любой трехфазной системы на основе подхода Фрумкина−Дерягина [11, 27, 28] с применением изотерм расклинивающего давления, если известна толщина пленки жидкости, сосуществующей с отступающим мениском. В общем случае, изотерма расклинивающего давления определяется вкладами вандерваальсовых, ионно-электростатических, стерических, структурных и др. сил в расклинивающее давление [11, 27–29].

Из уравнения (1) следует, что для уменьшения работы адгезии для конкретной жидкости необходимо таким образом изменить свойства трехфазной системы, чтобы повысить угол смачивания. Этого можно добиться различными путями. Так, относительно небольшой вариацией состава или pH жидкой фазы можно регулировать величину или даже изменить знак заряда поверхности на границе жидкость/газ или жидкость/твердое тело, с соответствующим изменением вклада электростатических сил в изотерму расклинивающего давления. Другим способом является химическая модификация подложки. Например, осаждение даже монослоя низкополяризуемого диэлектрика с низкой поверхностной энергией приводит к возрастанию угла смачивания за счет изменения вандерваальсовых и/или структурных/гидрофобных сил, а также к изменению потенциала поверхности.

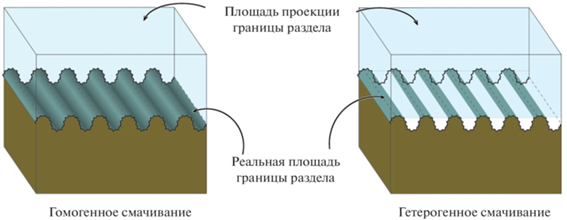
Наконец, одним из самых эффективных методов управления работой адгезии является изменение морфологии поверхности подложки. Для шероховатых поверхностей с величиной шероховатости r, смачиваемых в гомогенном режиме Венцеля-Дерягина, эффективная площадь контакта между жидкостью и твердым телом возрастает в r раз при сохранении проекции эффективной площади на горизонталь (см. рис. 1а). Тогда работа по разрыву контакта по межфазной границе, при сохранении эффективной площади для границ жидкость – пар и твердое тело-жидкость, приведенная к единице площади проекции межфазной границы, записывается следующим образом:

(2)

$W_{{{\text{sl}}}}^{W} = r{{\sigma }_{{{\text{lv}}}}}\left( {1 + {\text{cos}}{\kern 1pt} \theta _{{{\text{sl}}\left( r \right)}}^{{{\text{smooth}}}}} \right) = rW_{{{\text{sl}}}}^{{{\text{smooth}}}}.$

Рис. 1.

Схематичное изображение смачивания шероховатой поверхности в гомогенном и гетерогенном режимах смачивания.

Уравнение (2) представляет собой уравнение Юнга−Дюпре для работы адгезии $W_{{{\text{sl}}}}^{W}$ к шероховатой поверхности, смачиваемой в гомогенном режиме.

Поскольку по определению r > 1, из уравнения (2) следует, что шероховатость приводит к увеличению работы адгезии по сравнению с работой адгезии на гладкой поверхности, как для гидрофильных, так и для гидрофобных поверхностей при условии гомогенного режима смачивания. Однако, при некотором значении шероховатости гидрофобной поверхности гомогенный режим смачивания перестает быть термодинамически устойчивым и вместо него реализуется гетерогенный режим смачивания [30, 31]. В этом режиме реальная площадь границы раздела жидкость/твердое тело зависит не только от шероховатости, но и от доли смоченной площади (рис. 1б), и эффективный угол смачивания определяется уравнением Касси−Бакстера:

(3)

${\text{cos}}{\kern 1pt} \theta _{{\left( r \right)}}^{{{\text{эффект}}}} = {{r}_{l}}f{\text{cos}}{\kern 1pt} \theta _{{sl\left( r \right)}}^{{s{\text{mooth}}}} + f - 1,$

где f – отношение проекции площади подложки, смоченной жидкостью, к проекции всей подложки, а r_l – величина шероховатости площади твердого тела, смоченной жидкостью, угол $\theta _{{sl\left( r \right)}}^{{s{\text{mooth}}}}$ имеет смысл локального угла оттекания, который должен определяться в зоне трехфазного контакта с элементом текстуры.

При гетерогенном режиме смачивания уравнение Юнга-Дюпре для работы адгезии, приведенной к единице площади проекции межфазной границы, модифицируется к виду:

(4)

$W_{{{\text{sl}}}}^{{{\text{CB}}}} = {{r}_{l}}f{{\sigma }_{{lv}}}\left( {1 + {\text{cos}}\theta _{{sl\left( r \right)}}^{{s{\text{mooth}}}}} \right) = {{r}_{l}}fW_{{sl}}^{{s{\text{mooth}}}}.$

Из уравнения (4) следует, что в общем случае работа адгезии к шероховатой поверхности, смачиваемой в гетерогенном режиме смачивания, может оказаться как больше, так и меньше, чем для гладкой поверхности. В то же время, для хорошо приготовленных супергидрофобных поверхностей доля смоченной площади, как правило, имеет порядок f ≈ 0.01−0.05, а значение ${{r}_{l}}$ не превышает 10 [32]. Таким образом, работа адгезии для супергидрофобных шероховатых поверхностей оказывается значительно меньше, чем для гладких, имеющих ту же кажущуюся площадь (площадь проекции межфазной границы) и тот же химический состав поверхностного слоя.

Особый интерес представляет оценка работы адгезии для капель воды к супергидрофобным поверхностям при низких отрицательных температурах. Это связано с оценкой возможности самопроизвольного удаления капель переохлажденной воды с поверхностей, имеющих отрицательную температуру и, следовательно, к понижению накопления льда. Исследования, проведенные в [33, 34] на супергидрофобных покрытиях на алюминии показали, что несмотря на то, что поверхностное натяжение воды с понижением температуры растет, а угол смачивания несколько падает, величина работы адгезии переохлажденной воды к исследованным супергидрофобным поверхностям меняется незначительно и остается на уровне 0.8–1.2 мДж/м², что указывает на возможность самопроизвольного удаления таких капель с твердой поверхности воздушным потоком или вибрацией.

3. ВЛИЯНИЕ ПОВЕРХНОСТНЫХ СИЛ НА ВЕЛИЧИНУ АДГЕЗИИ ЛЬДА К ТВЕРДЫМ ПОВЕРХНОСТЯМ

3.1. Механизмы, определяющие адгезию льда

Поскольку для твердых тел времена, необходимые для установления равновесного состояния, на много порядков превышают времена установления равновесного контакта жидкость-твердое тело, создание и разрушение адгезионного контакта двух твердых сред, как правило, происходит в рамках термодинамически необратимого процесса. Именно поэтому особенности формы ледяного мениска в зоне трехфазного контакта определяются не только действием поверхностных сил и межмолекулярных взаимодействий и, следовательно, не могут рассматриваться, как характеристика межфазных взаимодействий. Поэтому, для характеризации и управления адгезией необходимо рассматривать, с одной стороны, механические и термодинамические свойства контактирующих тел, с другой стороны, форму контактирующих тел в зоне межфазной границы.

Как и для случая контакта твердых тел с жидкостями, при контакте двух твердых тел работают как химические взаимодействия между молекулами контактирующих фаз, так и физические механизмы адгезии.

Например, при адгезии льда к твердым подложкам, химические механизмы, которые включают в себя как собственно химические реакции, так и водородные связи между гидроксильными группами льда и соответствующими молекулярными группами на поверхности, в значительной степени определяются химической природой подложки. Оценить вклад химических механизмов в энергию адгезии можно по плотности химически активных центров подложки и вкладу в свободную энергию Гиббса каждой связи. Экспериментальные исследования вклада ковалентных и водородных связей в адгезию льда к чистым металлическим поверхностям и покрытым самоорганизованными монослоями, к стеклу и полимерам [35–37] подтвердили факт значительного увеличения адгезии за счет химических взаимодействий между льдом и подложкой.

Что касается вклада физических механизмов в величину адгезии льда к твердым поверхностям, то тут основными являются вклады вандерваальсовых и электростатических сил.

Вклад вандерваальсовых сил в адгезию льда к твердым поверхностям определяется диэлектрическим контрастом: разницей диэлектрических проницаемостей контактирующих фаз как функций мнимой частоты ε(iξ) [38, 39]. Численные расчеты для диэлектрических проницаемостей ε(iξ) для льда и воды [40, 41], а также различных твердых тел [40, 42] показали высокий диэлектрический контраст льда и металлов, и гораздо меньший для льда и различных полимеров. Соответственно, вклад в энергию адгезии вандерваальсовых взаимодействий в случае льда на металлах оказывается выше, чем для льда на полимерных материалах [40]. Важно отметить, что хотя в целом дисперсионные взаимодействия считаются дальнодействующими, введение даже тонкой, толщиной в несколько нанометров, прослойки между фазами с существенно отличными диэлектрическими свойствами может приводить к значительному изменению межфазной энергии. Так, введение слоя низкополяризуемого диэлектрика между высокополяризуемыми средами, например, адсорбционного монослоя углеводородов между льдом и металлом, может существенно ослабить величину взаимодействия. В частности, этот подход лежит в основе многих методов снижения адгезии льда [43] и активно используется при нанесении жидких смазок-антиадгезивов [7, 44]. Однако, как правило, значительная величина эффекта достигается за счет одновременного снижения величины как вандерваальсовых, так и электростатических взаимодействий.

Вклад электростатических взаимодействий в адгезию льда к твердым поверхностям может быть связан с несколькими механизмами. В одной из первых работ, рассматривающих эти взаимодействия [45], обсуждался эффект поляризации твердой поверхности зарядами, находящимися во льду вблизи межфазной границы. Такая поляризация приводит к возникновению сил изображения между реальными зарядами и поляризованной границей. Природу зарядов в [45] связывали с захватом в решетку льда носителей положительного заряда во время кристаллизации воды. Указанный механизм заряжения был предсказан теоретически [46–48], а факт заряжения был подтвержден экспериментально [49, 50].

Избыточная энергия, связанная с силами изображения на межфазной границе лед-подложка, определяется как плотностью зарядов в решетке льда, так и разницей статических диэлектрических проницаемостей контактирующих фаз. Теоретический анализ показывает, что, как и в случае вандерваальсовых сил, вклад сил изображения будет максимален в случае контакта с металлами, поскольку диэлектрическая проницаемость металлов стремится к бесконечности и поэтому взаимодействие единичного заряда с поляризованной им идеальной металлической поверхностью эквивалентно взаимодействию с отраженным противозарядом. Напротив, при взаимодействии с низкополяризуемыми подложками, взаимодействие льда с поверхностью за счет сил изображения может оказаться не только очень малым, но и способствовать снижению адгезии при определенном соотношении диэлектрических проницаемостей фаз, разделенных межфазной границей.

Однако, совместное действие поверхностных сил различной природы может приводить к тому, что система лед/жидкая водная пленка/подложка оказывается более энергетически выгодна, чем непосредственный контакт льда с подложкой, а обогащение межфазной зоны поверхностными зарядами, ионами и примесями приводит к кратному увеличению толщины такого квазижидкого слоя воды на межфазной границе [51, 52].

В результате в реальных системах вклад сил изображения между зарядами во льду и поляризованной подложкой может быть существенно ослаблен за счет формирования квазижидкого слоя воды между льдом и подложкой.

Диссоциация молекул воды в формирующемся квазижидком слое приводит к появлению свободных носителей зарядов, которые, в свою очередь, взаимодействуя со льдом и подложкой, формируют двойные электрические слои на каждой из межфазных границ. Например, на границе вода/воздух при нейтральных pH имеется преимущественная адсорбция гидроксилов [50]. Среди механизмов заряжения границы вода/лед можно выделить образование несвязанных гидроксилов в результате депротонирования молекул воды, адсорбцию ионов и несбалансированный захват ионов растущей границей льда [53]. Таким образом, образование жидкой или квазижидкой водной пленки между льдом и подложкой приводит к разнонаправленным эффектам [53–61]: с одной стороны, к дополнительному вкладу ионно-электростатических взаимодействий между границами лед/вода и вода/подложка, а с другой – к появлению экранирования вандерваальсовых сил и сил изображения за счет формирования двойных электрических слоев. Поскольку формирование квазижидкого водного слоя между льдом и твердой поверхностью оказывает существенное влияние на величину адгезии льда к различным поверхностям, мы рассмотрим причины появления квазижидкого слоя и механизм его влияния более подробно.

3.2. Квазижидкий слой на границе лед/воздух

Первые сообщения в научной литературе о существовании и свойствах водного слоя на поверхности льда при температурах слегка ниже тройной точки воды принадлежат Фарадею [62] и Томсону [63].

Как упоминалось выше, структура жидкого слоя вблизи поверхности раздела и, тем более, в пространственно-ограниченных системах, меняется под действием поверхностных сил [64, 65]. Это приводит к изменению плотности и к анизотропии тензора давления в приповерхностных слоях, и, как следствие, к сдвигу тройной точки T_tp для материалов вблизи межфазных границ, в тонких прослойках, в объеме наночастиц. В зависимости от свойств жидкости, а именно, от характера доминирующих поверхностных сил, температура T_tp может сдвигаться как в сторону более низких значений по отношению к величинам, характерным для объемных сред, приводя к появлению предплавленного слоя (как в случае со льдом), так и в сторону более высоких значений, приводя к предотверждению поверхностного слоя, как в случае со среднецепочечными углеводородами [66, 67]. Анализ, выполненный в [64], показал, что величина сдвига тройной точки на границе лед/воздух зависит от соотношения поверхностных энергий лед/воздух и вода/воздух, а также плотности воды и льда в поверхностном слое. Теоретический анализ предсказывает, что повышение радиуса действия поверхностных сил, ожидаемое для водных фаз вблизи гидрофобной поверхности [68], должно вести к утолщению предплавленного слоя. Кроме того, зависимость поверхностных сил различной природы от температуры должна приводить и к температурной зависимости толщины квазижидкого слоя на поверхности [64, 65].

Альтернативный теоретический подход, развитый в [40], объясняет появление предплавленного слоя на основе анализа избыточной энергии, связанной с дисперсионными взаимодействиям в системе лед-водный слой- подложка. Эта энергия в присутствии водной прослойки оказывается ниже, чем для границы лед−подложка. Однако, важно отметить, что низкая точность диэлектрических проницаемостей в широком спектре частот не позволяет сделать однозначные количественные оценки: в зависимости от используемых наборов данных, эти подходы могут предсказывать как устойчивость толстого жидкого слоя, так и его термодинамическую невыгодность [40, 41, 69]. Тем не менее, в целом в литературе имеется консенсус о необходимости учета ионно-электростатических взаимодействий на заряженных границах предплавленного слоя в дополнение к расчету вандерваальсовых взаимодействий [40, 61].

Наконец, можно рассматривать появление квазижидкого слоя на границе льда, как результат многократного повышения вблизи поверхности концентрации дефектов кристаллической решетки льда, таких, как вакансии, межузельные дефекты и несвязанные гидроксилы, формирующиеся в результате депротонирования молекул воды [70]. Неоднородное распределение дефектов по нормали к поверхности и скачкообразный рост их концентрации в процессе повышения температуры от абсолютного нуля к тройной точке T_tp, вызывает фазовый переход первого рода от льда к квазижидкому состоянию задолго до T_tp.

Хотя начиная с работ Фарадея [62] и Томсона [63] многочисленные экспериментальные исследования и численные расчеты подтвердили существование квазижидкого слоя на границе льда с воздухом [71–80] и твердыми телами различной химической природы [81–103], физические механизмы, отвечающие за появление квазижидкого слоя и его свойства, по-прежнему активно обсуждаются в литературе.

3.3. Квазижидкий слой на границе лед/твердое тело

Толщина, ее изменение с температурой и свойства квазижидкого слоя на границе лед/подложка непосредственно влияют на адгезию твердых водных сред к твердым поверхностям и поэтому должны быть рассмотрены более подробно. Наличие и свойства этого слоя исследовались широким спектром современных методов, таких как рентгеноструктурный анализ [81–83], ЯМР [84], рамановская спектроскопия [84], нейтронная дифракция [85], дифференциальная сканирующая калориметрия [86–88], термопорометрия [89], дилатометрия [90], нелинейная лазерная спектроскопия суммарных частот [84, 91, 92]. Основными объектами таких исследований были как квазижидкие прослойки на плоских подложках с различной геометрией поверхности и на гранях кристаллов льда, так и квазижидкие слои в микро- и нанопорах.

Значительное число работ было посвящено определению температур исчезновения квазижидкого слоя на подложках с разным смачиванием. Большое число экспериментальных данных, полученных для межфазной границы лед/оксид кремния, включает эксперименты с плоскими пластинами аморфного SiO₂ [83, 91, 92], с тонкими кварцевыми капиллярами [90], пористыми частицами [84], с пористыми материалами SBA15 и MCM-41, имеющими цилиндрические гексагонально упорядоченные поры [86–89, 93, 94]. Самая низкая температура появления квазижидкого слоя на границе воды и кремнезема была обнаружена ЯМР методами в нанопорах с диаметром 2–4 нм при −80°C [93, 94], при этом, для указанной температуры, толщина такого слоя была в интервале 0.35–0.54 нм. К сожалению, в этих работах не исследовалось влияние температуры на толщину пленки жидкости.

Калориметрические данные для фазовых переходов воды в гидрофильных порах SBA15 и MCM-41 материалов (диаметр пор от 2 до 12 нм) были получены разными авторами [88, 95] и хорошо воспроизводятся. В этих работах были получены следующие результаты. При охлаждении воды в поре, в зависимости от степени заполнения пор, наблюдается до четырех пиков выделения теплоты. Так, самый высокотемпературный пик (самый близкий к тройной точке) наблюдается при избытке воды и соответствует замерзанию воды снаружи пор. Второй пик соответствует кристаллизации воды в центральной части пор с сохранением пристеночной незамерзающей прослойки: этот пик наблюдается для достаточно широких пор (>5 нм) и степени заполнения пор более 60%. Интересно отметить, что температуры кристаллизации ядра пор соответствуют рассчитанным по уравнению Кельвина, если принять, что радиус кристаллизующейся части соответствует радиусу поры за вычетом толщины пристеночного незамерзающего слоя [96]. Было обнаружено, что при избытке воды пик выделения тепла сдвигается в область более высоких температур. Вероятно, обнаруженный эффект связан с тем, что лед снаружи пор играет роль инициатора кристаллизации для воды внутри поры. Третий и четвертый пики, по-видимому, связанные с кристаллизацией предплавленного слоя, наблюдаются при температурах порядка −37°С (236 К) и −40°С (233 К), соответственно. Последовательная кристаллизация пристеночной прослойки может быть объяснена двумя различными механизмами. Первый связан с фазовым переходом квазижидкого слоя в метастабильное кристаллическое состояние, которое затем вновь претерпевает фазовый переход в стабильное состояние. В качестве промежуточного или финального фазового состояния может выступать тип льда I_sd (stacking disordered ice). Для свободной границы лед-пар имеются данные [97] о том, что для нанодисперсной воды кристаллическое состояние, соответствующее I_sd, является более стабильным, чем гексагональный лед I_h, однако для воды в порах достоверной информации по стабильности этой кристаллической модификации льда в литературе не представлено. Отметим, что переход в другие фазовые состояния льда, а именно в I_III, I_IV и I_V, с учетом развивающегося в процессе кристаллизации в порах давления, маловероятен.

Второе возможное объяснение наличия третьего и четвертого пиков заключается в механизме поверхностно-индуцированной послойной кристаллизации. При этом более широкий и высокий (при условии избытка воды) третий пик соответствует кристаллизации второго и последующих слоев, в то время как четвертый пик соответствует кристаллизации первого слоя с наиболее отличающимися свойствами. Последовательная послойная кристаллизация пристеночной прослойки хорошо согласуется с теоретическими предсказаниями [64, 65] и связана с изменением плотности и структуры воды под действием поверхностных сил, которые затухают по мере удаления от межфазной границы. Важно отметить, что при нагреве не наблюдается множества пиков выделения теплоты, что, по-видимому, указывает на одновременное плавление льда по всему объему пор.

Следует отметить качественное, но не количественное совпадение результатов ЯМР и калориметрических измерений, касающихся кристаллизации пристеночного квазижидкого слоя в порах. Хотя оба метода фиксируют несколько фазовых переходов, температуры кристаллизации, получаемые при ЯМР исследованиях, оказываются на 30–40 градусов ниже, чем определенные калориметрически. В то же время, измерения в различных экспериментах по кристаллизации воды в центрах пор хорошо согласуются между собой, а также с результатами, предсказываемыми уравнением Кельвина при введении в это уравнение поправки на наличие незамерзающего слоя.

Для пористых частиц SiO₂ температурная зависимость толщины квазижидкого слоя тяжелой воды измерялась методом ²H ЯМР [84]. Было показано, что для достаточно крупных пор размером 190 нм, квазижидкий слой появляется при температуре −25°C, при этом его толщина оказывается порядка одного монослоя. Повышение температуры до 2.5°C, что на 1.5°C ниже температуры плавления тяжелой воды, вызывает, по данным ЯМР, повышение толщины слоя до 1.5 нм. Температура появления квазижидкого слоя между единичным монокристаллом льда и плоским листом аморфного SiO₂, измеренная методами рентгеноструктурного анализа, оказывается выше, около −17°C [83]. Приближение к температуре тройной точки тяжелой воды вызывает логарифмический рост толщины слоя, который достигает 5 нм для температуры на 0.1°C ниже тройной точки.

В целом, данные для пористого [84] и аморфного [83] оксида кремния хорошо согласуются между собой и показывают значительно более высокие температуры появления квазижидкого слоя, чем для мезопористого SiO₂ [86–89, 93, 94]. Следует отметить, что как большие толщины жидких пленок, так и значительно более низкие температуры их появления в нанометровых порах SBA15 и MCM-41, очевидно, связаны с перекрытием полей поверхностных сил от близкорасположенных стенок поры. Было показано, что подобное перекрытие играет значительную роль даже для неполярных жидкостей [100]. Ожидаемо, что для сильно поляризуемых жидкостей, таких как вода, перекрытие полей поверхностных сил будет определяющим образом влиять на свойства пристеночных слоев.

Важно отметить, что в обсуждаемых выше работах речь шла о не функционализированной поверхности кремнезема, который в отсутствии адсорбированных ПАВ является гидрофильным и имеет близкий к нулю угол смачивания. Для пористых кремниевых материалов с гидрофобной поверхностью [86] (фактически для таких материалов поверхностная группа Si–OH заменяется –O–Si(CH₃)₃) температура кристаллизации поверхностного слоя оказывается ниже, чем для гидрофильных пор того же диаметра, где диаметр определялся на основе изотерм адсорбции азота. Однако, влияние смачивания поверхности является неожиданно слабым. Смещение температуры появления квазижидкого слоя в область низких температур оказывается порядка 10 градусов для пор диаметром 2.5 нм и быстро падает с ростом ширины пор [86].

Появление квазижидкого слоя на границе раздела льда с гидрофильными материалами изучалось и на примере глин. Для исследований использовались два типа минералов [81]. Это имеющий слоистую структуру и заряжающийся при контакте с водными средами вермикулит, а также каолинит, относящийся к группе водных силикатов алюминия и практически не приобретающий заряд в водных средах. В указанной работе не приводятся значения угла смачивания для использованных глин, однако в литературе имеются данные, указывающие на гидрофильность обоих минералов с углом смачивания порядка 30° [102]. Рентгеновская дифракция показала, что при слабом переохлаждении толщины квазижидкого слоя для границы с вермикулитом и каолинитом несколько больше, чем для границы с кремнеземом [83, 84]. Данные по зависимости толщины квазижидкого водного слоя от величины переохлаждения относительно температуры объемной кристаллизации воды на разных подложках представлены на рис. 2. Анализ данных, полученных разными авторами для различных пористых материалов, показывает хорошее согласие в поведении толщины квазижидкого слоя с температурой. Для всех представленных систем характерен логарифмический рост толщины при приближении к тройной точке.

Рис. 2.

Зависимость толщины квазижидкого слоя на границе лед/подложка или лед/пора от переохлаждения относительно температуры объемной кристаллизации. Данные для мезопористого углерода с различным радиусом пор r_p [82] и глин [81] (вермикулита и каолинита) были оценены по рентгеновской дифракции; для плоского кремнезема – экспериментально по рентгеновскому отражению [83] и моделированием методом молекулярной динамики [103]; для пористого кремнезема – из ЯМР исследований для тяжелой воды [84].

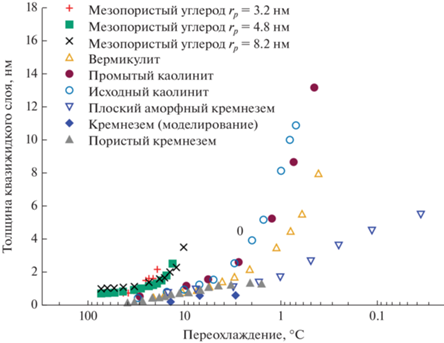
Температурная зависимость толщины квазижидкого слоя для более гидрофобных материалов была изучена на примере углеродных материалов: внутри цилиндрических пор упорядоченных мезопористого углерода с разным радиусом пор [82] и на базальной плоскости отслоенного графита [85]. Как и в случае гидрофильных материалов, температура появления квазижидкого слоя оказалась значительно ниже температуры кристаллизации воды. Так, на границе лед/графит квазижидкий слой образуется при температуре выше −30°C. Внутри пор мезопористого углерода квазижидкий слой наблюдается уже при −73°C, при этом доля жидкой воды оказывается больше 20%, образуя, как предполагается в работе [82], пленки толщиной 0.68, 0.71 и 0.98 нм в порах с радиусами 3.2, 4.8 и 8.2 нм соответственно. Эти значения несколько выше, чем полученные для более гидрофильных покрытий.

Таким образом, полученные до настоящего времени данные по квазижидким слоям воды между твердым телом и льдом позволяют сделать вывод, что смачивание поверхности влияет как на толщину, так и на температуру появления слоя воды между льдом и подложкой. Так, для гидрофобных подложек толщина квазижидкого слоя оказывается больше, а температура предплавления ниже, чем для подложек с гидрофильными свойствами. Эти выводы согласуются и с данными для предплавления на границе лед/воздух [82], если рассматривать воздух как идеальную гидрофобную среду.

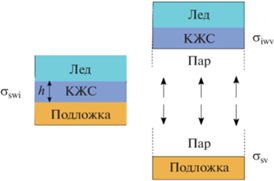
Из представленных выше данных следует, что при переохлаждениях, типичных для открытых атмосферных условий, квазижидкий слой воды существует как на границе лед/воздух, так и на границе лед/твердое тело. Таким образом, целесообразно оценить влияние предплавления на величину адгезии льда. Существование такой жидкой пленки позволяет предположить, что процесс разрушения адгезионного контакта может быть проведен в рамках термодинамически обратимого процесса через разрыв жидкого слоя. В этом случае величина работы адгезии может служить важным источником данных о величине и поведении поверхностных сил в такой трехфазной системе. Процесс разрушения контакта при наличии жидкой прослойки схематически показан на рис. 3. В начальном состоянии лед и подложка разделены квазижидким слоем воды толщиной h₀ с поверхностной энергией пленки σ_swi [11]:

(5)

${{\sigma }_{{swi}}} = {{\sigma }_{{sw}}} + {{\sigma }_{{wi}}} + \mathop \smallint \limits_{{{h}_{0}}}^\infty \Pi \left( h \right)dh,$

где индексы s, w, i при σ соответствуют твердому телу, воде и льду, соответственно; $\int_{{{h}_{0}}}^\infty {\Pi \left( h \right)dh} $ – избыточная энергия пленки, связанная с взаимодействием между льдом и подложкой через жидкую прослойку; П(h) – расклинивающее давление в жидкой прослойке.

Рис. 3.

Схема разрыва контакта лед−квазижидкий слой (КЖС)−подложка.

В конечном состоянии, после разрушения адгезионного контакта, поверхностная энергия системы равна сумме поверхностных энергий твердое тело/воздух σ_swv и лед/воздух σ_iwv, где как лед, так и твердое тело могут быть покрыты тонкой квазижидкой пленкой воды.

Таким образом, для гладкой поверхности при наличии квазижидкого слоя воды, работа адгезии (при условии термодинамической обратимости процесса) может быть рассчитана как:

(6)

${{W}_{{swi}}} = {{\sigma }_{{sv}}} + {{\sigma }_{{iwv}}} - {{\sigma }_{{sw}}} - {{\sigma }_{{wi}}} - \mathop \smallint \limits_{{{h}_{0}}}^\infty \Pi \left( h \right)dh.$

Используя уравнение Юнга для описания равновесия на межфазных границах твердое тело-объемная вода−пар и лед−объемная вода−пар, и полагая, что при сосуществовании льда с объемной водой на поверхности льда существует квазижидкий слой воды, т.е. σ_iv≡ σ_iwv, можно записать:

(7)

${{\sigma }_{{lv}}}{\text{cos}}{\kern 1pt} {{\theta }_{{iw}}} = {{\sigma }_{{iwv}}} - {{\sigma }_{{iw}}},$

(8)

${{\sigma }_{{lv}}}{\text{cos}}{\kern 1pt} {{\theta }_{{sw}}} = {{\sigma }_{{sv}}} - {{\sigma }_{{sw}}}.$

Тогда, используя уравнения (7) и (8) для работы адгезии льда к поверхности твердого тела при наличии квазижидкого слоя воды, уравнение (6) можно преобразовать в:

(9)

${{W}_{{swi}}} = {{\sigma }_{{wv}}}\left( {{\text{cos}}{\kern 1pt} {{\theta }_{{iw}}} + {\text{cos}}{\kern 1pt} {{\theta }_{{sw}}}} \right) - \mathop \smallint \limits_{{{h}_{0}}}^\infty \Pi \left( h \right)dh.$

Экспериментальные данные для углов смачивания льда переохлажденной водой θ_iw имеют широкий разброс значений от 0° до 12° [69, 104, 105]. Однако, для качественного анализа величины работы адгезии мы можем использовать аппроксимацию cosθ_iw ≈ 1. Таким образом, мы можем записать, что:

(10)

$\begin{gathered} {{W}_{{swi}}} = {{\sigma }_{{wv}}}\left( {1 + {\text{cos}}{\kern 1pt} {{\theta }_{{sw}}}} \right) - \mathop \smallint \limits_{{{h}_{0}}}^\infty \Pi \left( h \right)dh = \\ = \,\,{{W}_{{sw}}} - \mathop \smallint \limits_{{{h}_{0}}}^\infty \Pi \left( h \right)dh. \\ \end{gathered} $

Уравнение (8) позволяет заключить, что работа адгезии льда к гладкой поверхности при наличии квазижидкого слоя отличается от работы адгезии переохлажденной воды к той же подложке на величину − $\int_{{{h}_{0}}}^\infty {\Pi \left( h \right)dh} $. Для оценки интеграла $\int_{{{h}_{0}}}^\infty {\Pi \left( h \right)dh} $, который представляет собой избыточную энергию пленки воды между льдом и подложкой, можно использовать следующие соображения. Как обсуждалось ранее [11, 29], полное расклинивающее давление, а следовательно, и избыточная энергия в такой системе определяются вкладами разной природы. Помимо вандерваальсовых сил, значительную роль играют структурные и электростатические вклады, что подтверждается резким, на несколько порядков величины, ростом вязкости такой пленки, наблюдаемым в эксперименте [60, 106]. К сожалению, отсутствие точных данных для различных компонент расклинивающего давления не позволяет провести точные количественные расчеты рассматриваемого интеграла. Однако, качественная оценка интеграла в (10) может быть сделана на основе теории смачивания Дерягина−Фрумкина. Так, согласно этой теории, угол смачивания, образуемый каплей воды на твердой подложке в окружении льда ${{\theta }_{{sw\left( i \right)}}}$, связан с избыточной поверхностной энергией квазижидкой прослойки между льдом и твердой подложкой соотношением:

(11)

${\text{cos}}{\kern 1pt} {{\theta }_{{sw\left( i \right)}}} = 1 + \frac{1}{{{{\sigma }_{{wv}}}}}\mathop \smallint \limits_{{{h}_{0}}}^\infty \Pi \left( h \right)dh.$

В некоторых работах [107] интуитивно предполагается, что θ_sw(i) ≈ 90°, а ${\text{cos}}{{\theta }_{{sw\left( i \right)}}} = 0$ в силу сходства физико-химических характеристик льда и воды.

Однако такое предположение неверно, поскольку вандерваальсовы силы в системах воздух/лед/подложка и воздух/вода/подложка значительно различаются из-за различий в спектрах динамической диэлектрической проницаемости льда и воды [40, 41]. Кроме того, как отмечалось выше, плотности заряда на границах раздела лед/подложка и вода/подложка могут значительно отличаться, и для льда в игру также включаются силы изображения, что приводит к изменению электростатических сил при переходе от пленок льда к пленкам воды. Наконец, структурный вклад в устойчивость пленок воды может быть очень значительным. Однако, независимо от точной величины угла θ_sw(i), тот факт, что этот угол отличен от нуля, однозначно указывает на положительную величину члена −$\int_{{{h}_{0}}}^\infty {\Pi \left( h \right)dh} $.

Таким образом, можно заключить, что энергия адгезии льда к твердому телу через квазижидкую водную прослойку превосходит аналогичную энергию адгезии воды к подложке и зависит от избыточной энергии взаимодействия льда с подложкой через прослойку воды.

Если толщина водной прослойки между твердым телом и льдом велика по сравнению с радиусом действия поверхностных сил, то их вкладом в уравнение (6) можно пренебречь, так как $\int_{{{h}_{0}}}^\infty {\Pi \left( h \right)dh} = 0$, и для разрыва адгезионного контакта в термодинамически обратимом процессе внутри жидкой прослойки требуется только энергия образования двух новых поверхностей вода-пар. При этом, если после разрыва на подложке также остается толстый слой воды, то учитывая, что в этом случае ${{\sigma }_{{swv}}} = {{\sigma }_{{wv}}} + {{\sigma }_{{sw}}}$, работа адгезии переходит в работу по разрыву когезионного контакта ${{W}_{{swi}}} = 2{{\sigma }_{{wv}}}$.

Таким образом, исходя из представленного выше анализа, можно ожидать, что по мере приближения к тройной точке за счет утолщения предплавленного слоя работа адгезии на границе лед/твердое тело будет уменьшаться. Кроме того, наличие квазижидкого слоя существенно снижает диссипацию энергии на пластические деформации и нагрев при неравновесных процессах разрыва адгезионного контакта, поскольку разрыв по квазижидкой прослойки не требует большой энергии. Исчезновение же квазижидкого слоя приводит к скачкообразному росту адгезионной прочности. Например, в работе [108] было показано, что для шероховатого покрытия на основе частиц полиуретана с ковалентно пришитой диметилолпропионовой кислотой в интервале от −15 до −53°C значение прочности адгезионного контакта льда к покрытию было порядка 27 кПа и слабо менялось с температурой. Однако дальнейшее понижение температуры от −53 до −60°C приводило к быстрому возрастанию прочности адгезионного контакта до 200 кПа. Исследование прочности адгезионного контакта льда на нормальный отрыв от гидрофильных [84] и гидрофобных [4, 21] подложек показало снижение адгезионной прочности для случаев, когда между льдом и подложкой формировался квазижидкий слой. При этом была показана зависимость измеряемой прочности контакта от температуры.

Что касается зависимости сдвиговой прочности адгезионного контакта от толщины квазижидкого слоя, то в литературе обсуждалось два возможных механизма снижения этой прочности на границе лед/твердое тело.

Когда толщина предплавленного слоя мала по сравнению с характерной высотой шероховатости поверхности, как было показано в [109], квазижидкая пленка играет роль смазки, облегчая движение вдоль поверхности. При этом важным фактором оказывается то, что при сдвиговой нагрузке на область межфазного контакта, приводящей к тангенциальному движению, происходит существенный локальный нагрев, приводящий к плавлению вершин выступов на поверхности льда и, следовательно, к утолщению квазижидкого слоя. В случае же, когда толщина жидкого слоя больше размера шероховатости, сдвиговые нагрузки на адгезионное соединение сопровождаются течением, и основную роль в адгезионной прочности начинают играть вязкие характеристики квазижидкого слоя [106].

Значительное снижение адгезионной прочности за счет наличия незамерзающего слоя жидкости на границе лед/твердое тело, с одной стороны, и непостоянство величины этого эффекта, его высокая чувствительность к температуре и шероховатости поверхности, с другой, привели к развитию альтернативных родственных методов снижения адгезии. Тут можно выделить две группы таких методов, основанных на смазывающих свойствах жидких пленок на межфазной границе. К первой относится создание скользких пористых покрытий с пропиткой (slippery liquid infused porous surfaces, SLIPS) [20], где текстура поверхности пропитывается незамерзающей и нерастворимой в воде жидкостью до образования толстого слоя, сглаживающего шероховатость поверхности. Вторая группа методов использует образование слоя связанной воды за счет использования гидрогелей или гидрофильных полимерных щеток [21, 110], привитых к подложке.

Другой чрезвычайно перспективный подход по снижению адгезионной прочности, который будет подробно рассмотрен в следующем разделе, основывается на текстурировании и гидрофобизации поверхности для установления гетерогенного режима смачивания и супергидрофобного состояния поверхности.

4. АДГЕЗИЯ ЛЬДА К СУПЕРГИДРОФОБНЫМ ПОВЕРХНОСТЯМ

Недавние исследования показали, что адгезионная прочность льда на супергидрофобных покрытиях с низким гистерезисом смачивания и углами смачивания, превышающими 160°, оказывается значительно ниже, чем на гидрофобных поверхностях [15, 20, 25, 26, 111–114]. Как упоминалось выше, смачивание супергидрофобных поверхностей происходит в гетерогенном режиме, т.е. вода лишь частично смачивает текстуру подложки, а частично контактирует с воздушными пузырьками, захваченными в элементах текстуры. Чтобы количественно рассчитать адгезию к такой текстурированной поверхности, необходимо, с одной стороны, определить адгезионную прочность, приходящуюся на единицу площади контакта, а с другой – измерить истинную площадь адгезионного контакта, которая определяется как произведение доли смоченной площади f на величину шероховатости смоченной части поверхности r. Однако, измерение как площади, так и шероховатости смоченной поверхности, за исключением ряда специфических покрытий, является для супергидрофобных подложек весьма сложной задачей и, как правило, эти величины остаются неизвестны.

Поэтому обычно для характеризации адгезионных свойств супергидрофобных покрытий используют экспериментально измеренную прочность адгезионного контакта на единицу кажущейся площади (нормальной проекции реальной площади контакта). При этом, как показано в литературе [32, 115], истинная площадь адгезионного контакта может оказаться порядка процентов от проекции кажущейся площади контакта (f ~ 0.01–0.1), в то время как для гладких гидрофобных покрытий и для шероховатых покрытий в гомогенном режиме смачивания f = 1. Поэтому ожидалось, что величина прочности адгезионного контакта льда, приведенная на единицу площади нормальной проекции кажущейся площади контакта, для супергидрофобных покрытий должна быть на 1–2 порядка ниже аналогичной величины для гладких покрытий с тем же химическим составом поверхностного слоя.

Однако, анализ экспериментальных данных показывает, что хотя адгезионная прочность контакта льда с поверхностью супергидрофобных покрытий и ниже таковой для гидрофобных гладких материалов, часто она оказывается существенно выше, чем ожидалось по величине реальной площади контакта, оцениваемой на основании эффективных углов смачивания покрытий водой. Кроме того, в некоторых случаях прочность адгезии льда к таким покрытиям с высокими углами смачивания и низким гистерезисом смачивания демонстрирует значения выше, чем для гладких гидрофобных подложек с тем же составом поверхностного слоя [116]. Три механизма могут быть ответственны за такое явление.

Первый связан с неоднородным распределением слоя гидрофобного агента по глубине шероховатого поверхностного слоя. Поскольку толщина шероховатого слоя у супергидрофобных покрытий, как правило, превышает 1 мкм, неудачно подобранный метод нанесения гидрофобизатора может приводить как к тому, что внутренние поверхности микро и нанопор остаются непокрытыми гидрофобным агентом, так и к слабой привязке гидрофобного агента к поверхности. При этом измерение начальных углов оттекания и натекания часто не позволяет выявить подобную неоднородность поверхностной энергии, поскольку характерное время измерения углов смачивания (несколько минут) может оказаться существенно меньше времени жизни метастабильного состояния, при котором дефекты смачивания остаются в сухом состоянии. Однако, эти дефекты адсорбции гидрофобного агента достаточно легко выявить при продолжительном погружении образца с супергидрофобным покрытием в водную среду или при продолжительном контакте со льдом [117, 118]. В процессе контакта с водной фазой происходит как десорбция молекул гидрофобного агента, так и капиллярная конденсация воды и льда в поры с дефектами в гидрофобном слое (рис. 4а), что, в свою очередь, приводит к увеличению истинной площади контакта льда и поверхности. В результате, площадь контакта и прочность адгезионного контакта могут оказаться значительно выше, чем для гладкой гидрофобной поверхности. Таким образом, кажущееся противоречие высокой адгезионной прочности контакта льда с супергидрофобным покрытием для покрытий, которые проявляют лишь метастабильную супергидрофобность, может быть снято при должном предварительном тестировании устойчивости супергидрофобных покрытий.

Рис. 4.

(а) Смачивание супергидрофобного покрытия с дефектами (верхнее изображение) и без дефектов (нижнее изображение). (б) Образование метастабильных менисков в процессе кристаллизации воды (верхнее изображение) и их последующая сублимация (нижнее изображение).

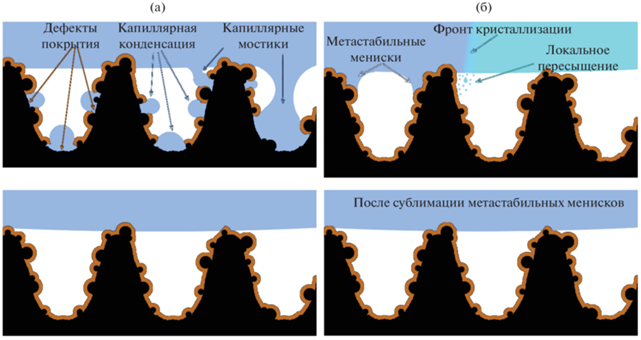
Вторая возможная причина повышенной адгезионной прочности связана с особенностями процесса кристаллизации, а именно, с не зависящим от свойств подложки выделением тепла кристаллизации. Поскольку продолжительность фазового перехода жидкости, контактирующей с поверхностью, значительно меньше характерного времени установления температурного равновесия в системе, кристаллизацию можно рассматривать как квазиадиабатический процесс, при котором выделение тепла приводит к локальному повышению температуры жидкости. Это явление было подтверждено в экспериментах [119–121] и приводит к кратковременному повышению давления паров вблизи мениска. По отношению к температуре шероховатой подложки пар оказывается пересыщенным, что приводит к неравновесной капиллярной конденсации и десублимации льда или инея, как на подложку, так и внутри пор текстуры под границей раздела жидкость−покрытие [26, 122] (рис. 4б.). Это, в свою очередь, приводит к увеличению адгезионной прочности, как за счет большей площади адгезионного контакта между подложкой и льдом, так и за счет взаимозацепления выступающих элементов текстуры и льда. Экспериментально образование метастабильных менисков наблюдалось в работах [26, 122], где было показано, что адгезионная прочность льда на пористой подложке, после кристаллизации при значительном переохлаждении, быстро падает в процессе выдержки за счет сублимации нестабильных ледяных мостиков из пор.

Как слабые льдофобные свойства дефектных супергидрофобных покрытий (рис. 4а), определяемые малой величиной барьера нуклеации льда на смачиваемых дефектах покрытия, так и десублимация льда в процессе кристаллизации воды (рис. 4б) приводят к значительному увеличению истинной площади контакта лед/подложка. При этом, чем выше супергидрофобные свойства у покрытия и, следовательно, выше барьер нуклеации [34], тем значительнее будет величина переохлаждения, при которой произойдет кристаллизация воды на подложке, и тем большее пересыщение паров на квазиадиабатическом этапе будет достигнуто в момент кристаллизации. Так, если задержка кристаллизации сидящей капли приведет к кристаллизации при −5°C, величина локального пересыщения будет порядка 140%, однако, если высокие водоотталкивающие свойства подложки позволят переохладить каплю до −20°C, локальное пересыщение при кристаллизации окажется гораздо выше, достигая 460%.

Таким образом, даже супергидрофобные покрытия, демонстрирующие устойчивость гетерогенного режима смачивания по отношению к переохлажденной воде, могут во время кристаллизации за счет кратковременного пересыщения претерпевать переход к гомогенному контакту лед/подложка, характеризующемуся на порядки большей площадью реального контакта. В то же время, как было показано в [122], для супергидрофобных покрытий, демонстрирующих стойкость к длительному контакту с водными средами, десублимированный иней и капиллярно сконденсировавшаяся вода существуют в метастабильном состоянии и после перехода давления паров к равновесному состоянию спонтанно испаряются как из гало вокруг капли, так и из элементов текстуры. Хотя этот процесс занимает несколько часов, он приводит к уменьшению величины адгезионного контакта и может успешно использоваться при эксплуатации льдофобных покрытий [25].

Наконец, третий механизм, способствующий завышенным значениям прочности адгезионного контакта на супергидрофобных покрытиях, связан с деградацией покрытия в процессе циклических нагрузок кристаллизации−отрыв льда. Кристаллизация воды сопровождается увеличением объема, при этом давление, создаваемое кристалликами льда на элементы текстуры в частично закрытых порах, может достигать сотен атмосфер [123]. Низкая механическая прочность многих супергидрофобных покрытий может приводить к отрыву отдельных элементов текстуры с обнажением поверхности, не покрытой гидрофобным агентом. Поскольку во многих случаях (исключение составляют в основном полимерные материалы) исходный материал подложки гидрофилен, новообразовавшиеся дефекты также гидрофильны, и адгезия к ним существенно больше, чем адгезия к соседним участкам, сохранившим супергидрофобное состояние. В целом для образца после появления дефектов текстуры, имеет место значительное увеличение прочности адгезионного контакта с превышением ожидаемого значения для супергидрофобной поверхности. При этом после плавления льда на обнаженную поверхность под действием градиента поверхностной энергии диффундирует гидрофобный агент, приводя к самозалечиванию и восстановлению супергидрофобного состояния [124]. Как показали исследования [124], процесс самозалечивания достаточно длителен и требует дни для восстановления исходного супергидрофобного состояния. Таким образом, покрытие, демонстрирующее низкую адгезию к воде до и через значительное время после кристаллизации, может характеризоваться высокой адгезией ко льду.

Остановимся теперь более подробно на влиянии квазижидкого слоя, формирующегося на межфазной границе лед/супергидрофобное покрытие, на адгезию льда к супергидрофобной поверхности.

5. ВЛИЯНИЕ КВАЗИЖИДКОГО СЛОЯ НА ВЕЛИЧИНУ СДВИГОВОЙ ПРОЧНОСТИ АДГЕЗИОННОГО КОНТАКТА

Для супергидрофобных поверхностей с иерархической шероховатостью толщина квазижидкого слоя при температурах значительно ниже нуля мала по сравнению с высотой текстуры поверхности. На участках контакта льда с твердой поверхностью нанорельеф с высотами, превышающими толщину квазижидкого слоя, создает энергетический барьер для скольжения льда относительно твердой поверхности по водному слою. В то же время, при непрерывном сдвиговом напряжении, даже незначительном по величине, взаимные смещения льда и твердого тела сопровождаются локальным плавлением выступающих участков льда и локальным увеличением толщины квазижидкого слоя. Последний фактор усиливает смазывающее действие квазижидкого слоя и приводит к снижению прочности сцепления льда с супергидрофобной поверхностью при сдвиге. В таких условиях, как было показано ранее [7], при длительном действии даже очень малых сдвиговых напряжений цилиндрический супергидрофобный образец медленно выскальзывал из ледяной муфты за счет последовательных процессов скольжения/плавления. О скольжении ледяной капли, находящейся под действием постоянно увеличивающегося напряжения сдвига, сообщалось и в работе [125]. Наконец, роль квазижидкой прослойки при отрыве льда от поверхности при очень низких сдвиговых напряжениях, была недавно показана в работе [26]. В этой работе сдвиговая прочность адгезии льда к супергидрофобным образцам определялась центробежным методом. На первом этапе исследования в процессе непрерывного увеличения частоты вращения тщательно определялась наименьшая частота, приводящая к отрыву льда от супергидрофобных подложек при Т = −5°С. На следующем этапе устанавливалась частота вращения образцов со льдом, вдвое меньшая, чем значение, определенное на первом этапе, т.е. необходимое для мгновенного отрыва льда. Далее частота вращения, а значит и сдвиговое напряжение, приложенное ко льду, поддерживались постоянными. Было обнаружено, что, несмотря на низкую частоту вращения, с увеличением времени вращения образцы начинали отрываться от супергидрофобных подложек. Распределение моментов отрыва льда по времени вращения при постоянном сдвиговом напряжении показано на рис. 5. Оказалось, что адгезионный контакт лед/супергидрофобная поверхность нарушился в течение 3 мин вращения с постоянной частотой для 12 идентичных супергидрофобных образцов, одновременно участвующих в эксперименте. Наблюдающийся самопроизвольный отрыв льда при касательных напряжениях значительно меньше требуемых для мгновенного отрыва, можно рассматривать как подтверждение механизма скольжения льда по поверхности за счет наличия квазижидкого водного слоя.

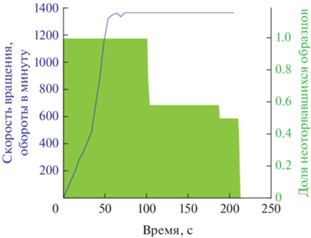
Рис. 5.

Распределение во времени событий отрыва льда от супергидрофобных образцов (закрашенная область), в условиях воздействия постоянной малой сдвиговой нагрузки при температуре –5°С [26]. Кривая показывает режим установления постоянной частоты вращения образцов. Последовательный отрыв образцов в этом эксперименте происходил при величине сдвиговой прочности адгезионного контакта льда с образцами, равной 13.6 ± 0.1 кПа.

Приведенный выше анализ позволяет заключить, что для супергидрофобных покрытий с малым количеством дефектов смачивания, малая истинная площадь контакта лед/подложка с одной стороны, и наличие более толстого по сравнению с гидрофильными подложками квазижидкого слоя на межфазной границе и внутри пор текстуры, облегчает удаление льда с поверхности. В частности, в рамках многолетних испытания таких покрытий в открытых атмосферных условиях [14, 15], было показано спонтанное удаление льда под действием гравитации, ветра и вибраций.

6. АДГЕЗИЯ ЛЬДА К СКОЛЬЗКИМ ПОКРЫТИЯМ С ПРОПИТКОЙ

Как отмечалось выше, к скользким покрытиям с пропиткой относятся три типа покрытий. К первому типу относятся покрытия, на которых формируется слой связанной воды [126] за счет использования гидрогелей или гидрофильных полимерных щеток [21, 110, 127] привитых к подложке. Поскольку температура кристаллизации связанной воды в таких слоях существенно ниже нуля, то до тех пор, пока гидратирующий слой воды остается в жидком состоянии, он работает как смазка, облегчающая удаление твердых водных осадков под действием внешних факторов.

Ко второму, наиболее многочисленному по применению и составам компонентов покрытия, относятся скользкие пористые покрытия с пропиткой [20, 128], где текстура поверхности пропитывается не замерзающей до требуемых температур и нерастворимой в воде жидкостью до образования толстого слоя, сглаживающего шероховатость поверхности. В значительном числе случаев для повышения устойчивости жидкого слоя поверхность текстуры покрывается гидрофобным веществом до нанесения пропитки. В качестве пропитывающих жидкостей используют, как правило, масла, фторированные органические жидкости и вакуумные смазки различных составов [128]. На сегодняшний день, применение именно этого типа скользких покрытий для борьбы с обледенением изучено наиболее полно. Показано, что в зависимости от степени заполнения пористой текстуры пропиткой, от типа самой текстуры, ее химической природы, прочность адгезионного контакта при низких отрицательных температурах может меняться в широких пределах от 6 до 50 кПа на свежеприготовленных покрытиях [129, 130]. Пример одной из зависимостей прочности адгезионного состава к скользкому покрытию от количества полидиметилсилоксана, импрегнированного в поры текстуры, представлен на рис. 6.

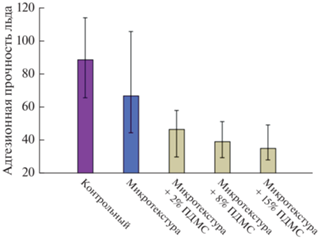
Рис. 6.

Зависимость прочности адгезионного контакта к скользкому покрытию от количества полидиметилсилоксана (указано в весовых процентах), импрегнированного в поры текстуры [129].

При этом для поверхностей с эластомерной текстурой [13] были обнаружены два фактора, а именно, плотность поперечных связей и межфазное проскальзывание, которые позволяют гибко управлять прочностью адгезионного контакта поверхностей со льдом. Было показано, что межфазное проскальзывание оказывает наибольшее влияние на адгезионную прочность льда к эластомерам с низкой плотностью поперечных связей. Именно для материалов с межфазным проскальзыванием были получены рекордные значения сдвиговой прочности адгезионного контакта 6 кПа при Т = −10°C.

Однако, как показали многочисленные исследования скользких покрытий [128], в том числе на металлах [25, 26], такие скользкие пропитанные жидкостями пористые поверхности очень недолговечны. К деградации таких покрытий при эксплуатации ведут следующие факторы. В первую очередь, это самопроизвольное стекание жидкой пропитки или ее удаление под действием внешних факторов, захват удаляющимся льдом или стекающими каплями воды, ведущие к снижению смазывающих свойств [128, 131–133]. Другой фактор, способствующий разрушению скользких пористых покрытий на основе смазывающей жидкости с низким поверхностным натяжением, состоит в механическом разрушении текстуры пористого покрытия под действием эффекта Ребиндера [25]. Суть явления заключается в том, что любая трещина или дефект, появляющийся в текстуре пористого слоя, начинает быстро расти благодаря низкой поверхностной энергии пропитывающей жидкости, контактирующей с трещиной и работающей как ПАВ для твердой текстуры. Поэтому при воздействии механических нагрузок, такие пористые покрытия с пропиткой будут разрушаться существенно быстрее, чем, например, супергидрофобные покрытия с близкой морфологией поверхности. В свою очередь, деградация покрытий приведет к быстрому ухудшению противообледенительных свойств в целом, и росту прочности адгезионного контакта в частности.

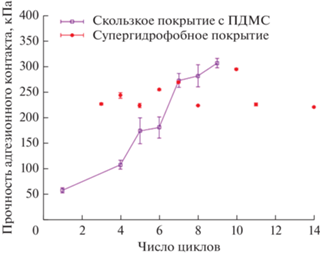
Пример эволюции прочности адгезионного контакта льда с лазерно-текстурированными супергидрофобными покрытиями и такими же покрытиями, пропитанными полидиметилсилоксановой жидкостью, с увеличением числа циклов кристаллизации/отрыва льда при температуре −25°С показан на рис. 7. Хотя для свежепропитанного скользкого покрытия сдвиговая прочность значительно ниже, чем для свежеприготовленного супергидрофобного покрытия, но уже через 6 циклов кристаллизации и отрыва льда от скользкого покрытия прочность адгезии становится значительно больше, чем для супергидрофобного покрытия. Заметим, что в последнем случае (для супергидрофобного покрытия), прочность контакта льда с покрытием остается практически постоянной на протяжения большого числа циклов кристаллизации льда и его последующего отрыва.

Рис. 7.

Зависимость прочности адгезионного контакта льда с супергидрофобным покрытием и скользким покрытием с ПДМС пропиткой на алюминии в зависимости от количества циклов кристаллизации/отрыва льда. Пропитывающая жидкость между не циклами не пополнялась.

Наконец, следующий фактор, способствующий потере смазывающих свойств покрытия – это потеря устойчивости тонких смачивающих слоев смазки при ее частичном удалении с поверхности и из впадин рельефа. Недавно проведенные расчеты на основе теории вандерваальсовых сил [134] показали, что для определенных комбинаций диэлектрических свойств текстуры и пропитывающей жидкости, смачивающие пленки пропитки на поверхности элементов текстуры прорываются и происходит стягивание жидкости внутрь впадин рельефа с обнажением участков твердой поверхности. Такие участки, свободные от смазки, создают энергетические барьеры для движения воды и льда вдоль поверхности покрытия, т.е. снижают ее смазочные свойства.

Для устранения этих недостатков скользких покрытий недавно был предложен новый тип смазывающих покрытий с твердой смазкой [130], потенциально обладающий повышенной механической стабильностью и устойчивостью к обледенению. Однако требуются еще детальные исследования, чтобы подтвердить перспективность этого типа покрытий для долговечного снижения адгезии ко льду.

Рассмотрим теперь температурную зависимость адгезионной прочности льда для систем, где верхний слой текстуры пропитан слоем масла, или между льдом и поверхностью имеется толстый слой гидратированной воды. В первом случае толщина слоя масла определяется геометрическими параметрами текстуры, количеством масла и изотермой расклинивающего давления пленки масла на поверхности, во втором устойчивость и кристаллизация слоя гидратированной воды определяется химическими и водородными связями воды с функциональными группами гидрофильного полимера [19, 108, 110, 125, 135]. Для таких систем необходимо упомянуть два механизма, влияющих на сдвиговую прочность адгезионного контакта лед/жидкая прослойка/подложка. Во-первых, это наличие связанного с разницей в углах натекания и оттекания неравномерного распределения капиллярных сил по периметру ледяного образца на подложке. Поскольку угол оттекания ниже угла натекания, капиллярные силы оказываются дополнительным фактором, увеличивающим пороговое напряжение, требующееся для начала движения.

Вклад в сдвиговую адгезионную прочность со стороны капиллярных сил можно оценить как:

(12)

${{\tau }_{{{\text{capillary}}}}} = {{\sigma }_{{li}}}\left( {{{P}_{{{\text{rec}}}}}{\text{cos}}\left( {{{\theta }_{{{\text{rec}}}}}} \right) - {{P}_{{{\text{adv}}}}}{\text{cos}}\left( {{{\theta }_{{{\text{adv}}}}}} \right)} \right){\text{/}}S,$

где P_rec, θ_rec, P_adv, θ_adv – периметр и угол оттекания, периметр и угол натекания, соответственно, σ_li – поверхностное натяжение на границе лед/материал пропитки, а S – кажущаяся площадь контакта. Для грубой оценки сверху вклада гистерезиса угла смачивания в сдвиговую адгезионную прочность можно рассмотреть квадратный столбик льда площадью в 1 см² на покрытии с масляной пропиткой на основе супергидрофобной поверхности и руководствоваться следующими соображениями. Отношение реального к кажущемуся периметру примем порядка 10, θ_rec = 0, θ_adv = 120°, σ_li = 30 мН/м. Тогда для τ_capillary получим величину порядка 45 Па. Сравнение этой оценки капиллярного вклада с экспериментальными данными показывает, что вклад капиллярных сил, как правило, на 2–3 порядка ниже экспериментально измеряемой величины прочности адгезионного контакта.

Второй механизм связан с переходом от внешнего трения в режиме граничной смазки к режиму смешанного трения, включающему гидродинамическую компоненту трения в жидкой пленке. В последнем случае, для объяснения порогового значения сдвигового напряжения, измеряемого в экспериментах по сдвиговой адгезионной прочности, необходимо привлекать гипотезу о вязко-пластичном поведении пленки масла или слоя гидратированной воды. Такая трактовка, впервые предложенная в работе [106], учитывает наличие порогового значения начала течения жидкости, впоследствии была развита рядом авторов [136–139]. В частности, подход по оптимизации передачи касательных напряжений к образцу для более подробного изучения механических свойств жидкости обнаружил твердообразное поведение тонких пленок жидкой воды и вязких алканов. Низкие величины порогового напряжения сдвига для льда, контактирующего с супергидрофобной подложкой, пропитанной силиконовым маслом [19, 25] и для слоя гидратированной воды, зажатого между льдом и полиуретаном [108], обнаруженные в эксперименте, хорошо согласуются с гипотезой о наличии порога течения переохлажденной жидкости, как механизма, ответственного за сдвиговую адгезионную прочность льда при наличии толстой жидкой прослойки на границе раздела. Действительно, измеренные величины адгезионной прочности оказываются порядка десятков кПа и в широком интервале температур плавно растут по мере уменьшения температуры, что, по-видимому, связано с уменьшением толщины квазижидкого слоя и увеличением его вязкости. Однако, в случае квазижидкого слоя на полиуретане, где исследовались и очень низкие температуры, наблюдался резкий рост величины адгезии в интервале от −50 до −65°C с последующим выходом на плато. Такое поведение может быть объяснено сначала переходом трения в режим смазки и потом в режим сухого трения при полном или частичном исчезновении квазижидкого слоя.

7. ВЛИЯНИЕ ВРЕМЕНИ РЕЛАКСАЦИИ ОБЛАСТИ МЕЖФАЗНОГО КОНТАКТА ПРИ НИЗКИХ ОТРИЦАТЕЛЬНЫХ ТЕМПЕРАТУРАХ НА ПРОЧНОСТЬ АДГЕЗИОННОГО КОНТАКТА

Для многих практических приложений противообледенительных покрытий большое значение имеет изменение во времени величины прочности адгезионного контакта льда к покрытию при нахождении льда на поверхности длительное время. Такое изменение может происходить по целому ряду причин. С одной стороны, быстрая кристаллизация льда сопровождается накоплением различных дефектов в поверхностном слое и приводит к временному повышению как поверхностной энергии льда [140], так и межфазной энергии на границе лед/твердое тело. Последующая выдержка льда при температуре кристаллизации с установлением однородной температуры по всему объему льда ведет к медленной релаксации неравновесной структуры поверхностного и межфазного слоев. При этом, из-за достаточно высокого давления паров надо льдом, релаксация структуры поверхностного слоя должна проходить быстрее, чем межфазного. Такая релаксация может вызывать изменение прочности адгезионного контакта. Данные, полученные в работе [141], позволили автору сделать вывод о небольшом росте прочности адгезионного контакта нержавеющей стали со льдом при длительной выдержке/старении образцов при отрицательных температурах. Такое возрастание прочности контакта со льдом при автор связал с упрочнением межфазного слоя за счет снижения концентрации дефектов структуры льда. Данные работы [142], также полученные при Т = −10°С, указывают на отсутствие значимого влияния времени релаксации на прочность адгезионного контакта льда с гладкими гидрофильной и гидрофобизованной поверхностями алюминиевого сплава при временах релаксации 15 часов. Напротив, старение контакта между шероховатой поверхностью и льдом приводит к очень значительному снижению прочности адгезионного контакта [25, 26] как для супергидрофобных так и для скользких пористых поверхностей, пропитанных вакуумной смазкой Критокс.

На гистограмме, представленной на рис. 8а, показаны значения прочности адгезионного контакта для супергидрофобного и скользкого покрытия с Критоксом при отрыве столбика льда от образцов через два часа выдержки при температуре Т = = −15°С. Для сравнения также представлены данные для тех же образцов, выдержанных после кристаллизации льда в течение 15 часов при температуре −15°С. Физический механизм наблюдающегося снижения прочности адгезионного контакта при длительной выдержке при постоянной температуре после кристаллизации воды связан с явлением, обсуждавшимся выше. Так, процесс кристаллизации переохлажденной капли воды может быть условно разделен на две стадии. Первая, с длительностью несколько секунд, соответствует квазиадиабатическому процессу, в котором тепло кристаллизации при формировании зародышей льда идет на одновременный нагрев капли и на повышение давления паров вокруг капли [119, 120, 122]. Перегретый по отношению к шероховатой подложке пар приводит к десублимации льда внутри текстуры под каплей или столбиком льда (см. рис. 4б). На втором этапе фронт кристаллизации распространяется внутри капли и теплообмен между каплей, окружающей средой и подложкой способствует выравниванию температуры в системе. При этом весь процесс кристаллизации для капель объемом 5–30 мкл занимает от 30 до 90 секунд. Из-за десублимации льда в элементы текстуры и в гало вокруг капли или ледяного столбика возрастает эффективная площадь контакта льда с покрытием, приводящая к росту адгезии льда к поверхности.

Рис. 8.

(а) Прочность адгезионного контакта льда к супергидрофобному и скользкому покрытиям на алюминии в зависимости от времени выдержки после кристаллизации [26]. (б) Прочность адгезионного контакта льда к супергидрофобному покрытию при различных температурах в зависимости от времени выдержки [26].

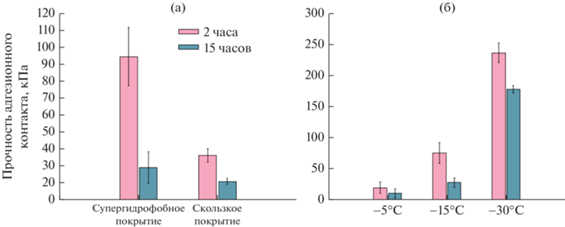
Поскольку образовавшиеся внутри текстуры и вокруг капли ледяные мениски сформировались на этапе перегрева паров вокруг капли, после установления однородного поля температур в системе такие мениски оказываются метастабильными. Выдержка образцов покрытия в контакте со льдом при постоянной температуре будет сопровождаться сублимацией льда из ледяных менисков и гало, как процессом, приводящим к снижению свободной энергии системы. Несмотря на достаточно высокое давление паров над льдом, как было показано в [122], такой процесс сублимации оказывается очень длительным. Поскольку он приводит к снижению эффективной площади контакта лед/образец, одновременно падает и прочность адгезионного контакта, что подтверждается данными, представленными на рис. 8а.

Прочности адгезионного контакта льда к супергидрофобному покрытию, полученные при разных температурах кристаллизации и двух временах выдержки льда после кристаллизации, представлены на рис. 8б. Анализ этих данных показывает, что в соответствии с вышеописанным механизмом, понижение температуры кристаллизации приводит к большему пересыщению пара при кристаллизации воды. Отметим, что пересыщение паров определяется относительно температуры подложки. Это, в свою очередь, способствует более значительному возрастанию адгезии, по сравнению со значением, соответствующим более равновесному состоянию системы через 15 часов релаксации межфазного слоя. Таким образом, представленные здесь данные подчеркивают необходимость указания времени выдержки льда после его формирования до момента отрыва одновременно с самой величиной прочности адгезионного контакта.

8. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА ПРОЧНОСТЬ АДГЕЗИОННОГО КОНТАКТА НА РАЗЛИЧНЫХ МАТЕРИАЛАХ И ПОКРЫТИЯХ

Хотя адгезионная прочность контакта лед/твердое тело измерялась различными методами [143–157] с 1930-х годов [141], долгое время оставался невыясненным вопрос о температурной зависимости этой характеристики. Экспериментальные исследования в этой области до недавнего времени не позволяли сделать достоверные выводы о характере температурной зависимости в силу ряда причин. Во-первых, точность измерения и статистическая достоверность получаемых результатов были не очень высоки, поскольку используемые ранее установки позволяли работать в одном эксперименте с одним или парой образцов. Большая длительность эксперимента по измерению прочности адгезионного контакта, как на отрыв, так и на сдвиг, сильно ограничивала возможности экспериментаторов по накоплению данных. Данные, полученные различными методами и на разных установках, даже для однотипных покрытий иногда отличаются в разы. Кроме того, температура и условия кристаллизации воды являются определяющими факторами для структуры, плотности и механических свойств образовавшегося льда [158]. В то же время, чтобы оценить способность материала к самопроизвольной или под действием внешнего воздействия очистки ото льда для широкого интервала условий эксплуатации, необходимо исследовать температурную зависимость адгезионной прочности в соответствующем интервале температур.

Анализ проблемы показывает, что в общем случае зависимость адгезионной прочности контакта льда с твердыми поверхностями от температуры связана с целым рядом факторов, такими как плотность и распределение поверхностных и объемных напряжений во льду, температурная зависимость отдельных типов поверхностных сил, которые, в свою очередь, определяют углы смачивания и толщину квазижидкого водного слоя на границе льда. Имеющиеся в литературе данные дают несколько противоречивые результаты по зависимости адгезии от температуры [143, 159]. Большая часть данных свидетельствует о снижении прочности адгезионного контакта по мере приближения температуры к тройной точке воды. В обзоре [143], собравшем данные из множества источников, было высказано предположение, что для металлов (см. рис. 34 и 35 в [143]) характерен экспоненциальный рост адгезионной прочности по мере снижения температуры. Однако, как обсуждалось выше, сравнение данных, полученных в разных экспериментах, а тем более лабораториях, зачастую некорректно. Свидетельством этого является как разброс на порядок величин адгезионной прочности, так и чрезвычайно низкий коэффициент корреляции R < 0.35 для зависимостей, полученных из сборных данных. Результаты, полученные в рамках одной серии экспериментов по исследованию температурных зависимостей сдвиговой адгезионной прочности льда к гладким поверхностям гидрофильного диоксида кремния и гидрофобизированного алкилдиметилалкоксисиланами алюминия, говорят скорее в пользу линейной зависимости [84, 125, 160]. Определенность в этом вопросе, как для полированного гидрофильного и гидрофобизованного алюминия, так и для супергидрофобного и скользкого пропитанного вакуумным маслом пористого алюминиевого образцов, дали недавние работы, в которых была набрана большая статистика для измеренной адгезионной прочности для широкого интервала температур [26, 142]. Так, было показано, что в интервале от −1 до −20°C воспроизводимо проявляется линейная зависимость адгезионной прочности от температуры.

Некоторые примеры температурного изменения прочности адгезионного контакта прозрачного льда с подложкой, полученные для супергидрофобных подложек, приготовленных различными методами текстурирования и функционализированных различными гидрофобными молекулами, представлены на рис. 9.

Рис. 9.

Температурные зависимости сдвиговой адгезионной прочности контакта лед/подложка для: 1 – полированного кремнезема [84], 2 – гидрофобизованной двуокиси кремния [110], 3 – гидрофобизованного алюминия [142], 4, 5, 6 – супергидрофобные покрытия на алюминии, гидрофобизованном различными фтороксисиланами [19, 26] и полидиметилсилоксаном [19], 7 – покрытие на супергидрофобном полидиметилсилоксане, пропитанное силиконовым маслом [19], 8 – покрытие на супергидрофобном алюминии, пропитанное фторорганическим маслом [26], 9 – композитное покрытие на основе диметилпропионовой кислоты и полиуретана с водным квазижидким слоем [108]. Для покрытий с пропиткой, перед каждым испытанием пропитывающая жидкость пополнялась.

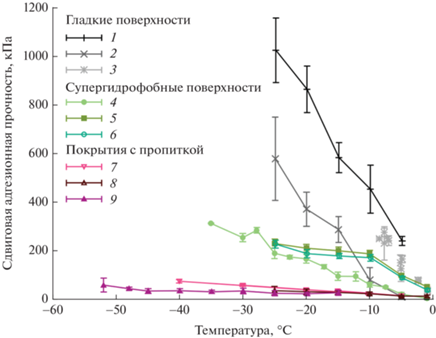
Что касается абсолютных значений, полученных в разных лабораториях для различных супергидрофобных покрытий, то для прозрачного льда при −10°C прочность адгезионного контакта меняется в широких пределах от 9 кПа для текстурированного тефлона [114], 50–70 кПа для силиконовой резины и алюминия, текстурированных лазером и гидрофобизированных фтороксисиланами [15, 26], до 200 кПа для анодированного алюминия с монослоем фтороксисилана [157].

Как следует из представленных на рисунке и других литературных данных о величине прочности адгезионного контакта лед/покрытие с пропиткой, эти покрытия, сразу после внесения жидкости в пористую структуру, демонстрируют самую низкую прочность адгезионного контакта со льдом, по сравнению с другими типами противообледенительных покрытий. Так, по данным работы [161], при температуре −34°C для материала с пропиткой из магнитной жидкости (при приложении магнитного поля) величина прочности адгезионного контакта составляет всего 2 Па. На различных покрытиях с масляной пропиткой характерная величина прочности адгезионного контакта при температурах –0–15°C составляет 1−40 кПа [18, 26, 162–164]. Однако, подходить к анализу этих данных следует с большой осторожностью. Действительно, ко всем проблемам, характерным для измерения адгезионной прочности на твердых поверхностях, для покрытий с пропиткой добавляются факторы, подробно обсужденные выше и вносящие неопределенность в состояние поверхности. Таким образом, практическое значение полученных низких величин адгезионной прочности остается неясным: обнадеживающие результаты лабораторных испытаний могут не проявиться при реальных условиях эксплуатации без частых и дорогостоящих операций повторного заполнения пористой текстуры смазывающей жидкостью.

9. ЗАКЛЮЧЕНИЕ

В этом обзоре мы проанализировали механизмы адгезии жидких и твердых водных сред к твердым поверхностям и обсудили влияние смачиваемости этих поверхностей на адгезионные явления. Представленный анализ показал, что адгезия жидкой воды к подложкам в основном определяется характером смачивания. В то же время анализ механизмов адгезии льда к тем же поверхностям показывает более сложное поведение. Толщина квазижидкого водного слоя, спонтанно образующегося на границе лед/твердое тело, оказывается одной из ключевых величин, определяющих прочность адгезионного контакта и работу адгезии к подложке. Отмечено многоплановое влияние гидрофобности поверхностного слоя подложки на снижение адгезии. С одной стороны, это изменение величины поверхностных сил, ответственных за адгезию, включая вандерваальсовы и электростатические силы изображения. С другой стороны, это расширение интервала существования квазижидкого слоя в область отрицательных температур и увеличение толщины квазижидкого слоя по сравнению с таковым на негидрофобизованных подложках. Кроме того, нанесение слоя гидрофобного агента, например фторорганической природы, способствует улучшению трибологических свойств поверхности, а значит, также приводит к увеличению эффективности удаления льда с поверхности. Также на многочисленных литературных примерах показано, что для химически и механически устойчивых супергидрофобных поверхностей дополнительным фактором, облегчающим отрыв снега и льда, является на один−два порядка меньшая площадь реальной границы раздела подложка/твердая водная среда.

В то же время, представленные здесь данные и анализ показали, что требуется дополнительная работа по созданию новых типов противообледенительных покрытий, для которых особый характер взаимодействия со льдом будет приводить к самопроизвольному отрыву льда и снега под действием гравитационной или ветровой нагрузки даже при очень низких отрицательных температурах.

Список литературы

Deryagin, B.V., Krotova, N.A., Smilga, V.P. Adhesion of Solids; Springer US: Boston, MA, 1978, ISBN 978-1-4615-8191-8.
Aronovich, D.A., Boinovich, L.B. Structural Acrylic Adhesives: A Critical Review. In Progress in Adhesion and Adhesives; 2021, V. 6. P. 65–122.
Gao, L., McCarthy, T.J. Wetting 101°^†. Langmuir. 2009, 25, 14105–14115, https://doi.org/10.1021/la902206c
Meuler, A.J., Smith, J.D., Varanasi, K.K., Mabry, J.M., McKinley, G.H., Cohen, R.E. Relationships between Water Wettability and Ice Adhesion. ACS Appl. Mater. Interfaces. 2010, 2, 3100–3110. https://doi.org/10.1021/am1006035
Drelich, J.W., Boinovich, L., Chibowski, E., Della Volpe, C., Hołysz, L., Marmur, A., Siboni, S. Contact Angles: History of over 200 Years of Open Questions. Surf. Innov. 2020, 8, 3–27. https://doi.org/10.1680/jsuin.19.00007
Voïtchovsky, K., Kuna, J.J., Contera, S.A., Tosatti, E., Stellacci, F. Direct Mapping of the Solid–Liquid Adhesion Energy with Subnanometre Resolution. Nat. Nanotechnol. 2010, 5, 401–405.https://doi.org/10.1038/nnano.2010.67
Boinovich, L.B., Emelyanenko, A.M. Anti-Icing Potential of Superhydrophobic Coatings. Mendeleev Commun. 2013, 23, 3–10.https://doi.org/10.1016/j.mencom.2013.01.002
He, Z., Vågenes, E.T., Delabahan, C., He, J., Zhang, Z. Room Temperature Characteristics of Polymer-Based Low Ice Adhesion Surfaces. Sci. Rep. 2017, 7, 42181. https://doi.org/10.1038/srep42181
Sun, Y., Jiang, Y., Choi, C.-H., Xie, G., Liu, Q., Drelich, J.W. Direct Measurements of Adhesion Forces for Water Droplets in Contact with Smooth and Patterned Polymers. Surf. Innov. 2017, 1–52. https://doi.org/10.1680/jsuin.17.00049
Klimchitskaya, G., Mohideen, U., Mostepanenko, V. The Casimir Force between Real Materials: Experiment and Theory. Rev. Mod. Phys. 2009, 81, 1827.
Derjaguin, B.V., Churaev, N.V., Muller, V.M. Surface Forces, Springer US: Boston, MA, 1987, ISBN 978-1-4757-6641-7.
Mittal, K. Adhesion Measurement: Recent Progress, Unsolved Problems, and Prospects. In Adhesion Measurement of Thin Films, Thick Films, and Bulk Coatings, Mittal, K., Ed., ASTM International: 100 Barr Harbor Drive, PO Box C700, West Conshohocken, PA 19428-2959, 1978, pp. 5-5–13 ISBN 978-0-8031-0272-9.
Golovin, K., Kobaku, S.P.R., Lee, D.H., DiLoreto, E.T., Mabry, J.M., Tuteja, A. Designing Durable Icephobic Surfaces. Sci. Adv. 2016, 2, e1501496, https://doi.org/10.1126/sciadv.1501496
Boinovich, L.B., Emelyanenko, A.M., Emelyanen-ko, K.A., Modin, E.B. Modus Operandi of Protective and Anti-Icing Mechanisms Underlying the Design of Longstanding Outdoor Icephobic Coatings. ACS Nano. 2019, 13, 4335–4346, https://doi.org/10.1021/acsnano.8b09549
Emelyanenko, A.M., Boinovich, L.B., Bezdomni-kov, A.A., Chulkova, E.V., Emelyanenko, K.A. Reinforced Superhydrophobic Coating on Silicone Rubber for Longstanding Anti-Icing Performance in Severe Conditions. ACS Appl. Mater. Interfaces. 2017, 9, 24210–24219, https://doi.org/10.1021/acsami.7b05549
Golovin, K., Dhyani, A., Thouless, M.D., Tuteja, A. Low–Interfacial Toughness Materials for Effective Large-Scale Deicing. Science. 2019, 364, 371–375. https://doi.org/10.1126/science.aav1266
Urata, C., Nagashima, H., Hatton, B.D., Hozumi, A. Transparent Organogel Films Showing Extremely Efficient and Durable Anti-Icing Performance. ACS Appl. Mater. Interfaces. 2021, 13, 28925–28937.
Coady, M.J., Wood, M., Wallace, G.Q., Nielsen, K.E., Kietzig, A.-M., Lagugné-Labarthet, F., Ragogna, P.J. Icephobic Behavior of UV-Cured Polymer Networks Incorporated into Slippery Lubricant-Infused Porous Surfaces: Improving SLIPS Durability. ACS Appl. Mater. Interfaces 2018, 10, 2890–2896. https://doi.org/10.1021/acsami.7b14433
Barthwal, S., Lee, B., Lim, S.-H. Fabrication of Robust and Durable Slippery Anti-Icing Coating on Textured Superhydrophobic Aluminum Surfaces with Infused Silicone Oil. Appl. Surf. Sci. 2019, 496, 143677. https://doi.org/10.1016/j.apsusc.2019.143677
Kreder, M.J., Alvarenga, J., Kim, P., Aizenberg, J. Design of Anti-Icing Surfaces: Smooth, Textured or Slippery? Nat. Rev. Mater. 2016, 1, 15003. https://doi.org/10.1038/natrevmats.2015.3
Chen, D., Gelenter, M.D., Hong, M., Cohen, R.E., McKinley, G.H. Icephobic Surfaces Induced by Interfacial Nonfrozen Water. ACS Appl. Mater. Interfaces. 2017, 9, 4202–4214. https://doi.org/10.1021/acsami.6b13773
Zhuo, Y., Chen, J., Xiao, S., Li, T., Wang, F., He, J., Zhang, Z. Gels as Emerging Anti-Icing Materials: A Mini Review. Mater. Horiz. 2021.
He, Z., Wu, C., Hua, M., Wu, S., Wu, D., Zhu, X., Wang, J., He, X. Bioinspired Multifunctional Anti-Icing Hydrogel. Matter. 2020, 2, 723–734. https://doi.org/10.1016/j.matt.2019.12.017
Liu, F., Wang, Z., Pan, Q. Intelligent Icephobic Surface toward Self-Deicing Capability. ACS Sustain. Chem. Eng. 2020, 8, 792–799. https://doi.org/10.1021/acssuschemeng.9b04570
Boinovich, L.B., Chulkova, E.V., Emelyanenko, K.A., Domantovsky, A.G., Emelyanenko, A.M. The Mechanisms of Anti-Icing Properties Degradation for Slippery Liquid-Infused Porous Surfaces under Shear Stresses. J. Colloid Interface Sci. 2022, 609, 260–268. https://doi.org/10.1016/j.jcis.2021.11.169
Boinovich, L.B., Emelyanenko, K.A., Emelyanenko, A.M. Superhydrophobic versus SLIPS: Temperature Dependence and the Stability of Ice Adhesion Strength. J. Colloid Interface Sci. 2022, 606, 556–566. https://doi.org/10.1016/j.jcis.2021.08.030
Boinovich, L., Emelyanenko, A. Wetting and Surface Forces. Adv. Colloid Interface Sci. 2011, 165, 60–69. https://doi.org/10.1016/j.cis.2011.03.002
Churaev, N.V., Sobolev, V.D. Prediction of Contact Angles on the Basis of the Frumkin−Derjaguin Approach. Adv. Colloid Interface Sci. 1995, 61, 1–16. https://doi.org/10.1016/0001-8686(95)00257-Q
Boinovich, L.B. Long-Range Surface Forces and Their Role in the Progress. Russ. Chem. Rev. 2007, 76, 471–488. https://doi.org/10.1070/RC2007v076n05ABEH003692
Marmur, A. Wetting on Hydrophobic Rough Surfaces: To Be Heterogeneous or Not to Be? Langmuir 2003, 19, 8343–8348.
Boinovich, L., Emelyanenko, A. Principles of Design of Superhydrophobic Coatings by Deposition from Dispersions. Langmuir. 2009, 25, 2907–2912.
Boinovich, L.B., Emelyanenko, A.M. The Behaviour of Fluoro- and Hydrocarbon Surfactants Used for Fabrication of Superhydrophobic Coatings at Solid/Water Interface. Colloids Surf. Physicochem. Eng. Asp. 2015, 481, 167–175. https://doi.org/10.1016/j.colsurfa.2015.05.003
Chulkova, E.V., Emelyanenko, A.M., Emelyanenko, K.A., Boinovich, L.B. Parameters of Supercooled Droplets of Water and Aqueous Solutions of Chlorides of Alkali Metals in the Temperature Range of +25 to −19°C. Russ. J. Phys. Chem. A 2020, 94, 564–569. https://doi.org/10.1134/S0036024420030061
Boinovich, L., Emelyanenko, A.M., Korolev, V.V., Pashinin, A.S. Effect of Wettability on Sessile Drop Freezing: When Superhydrophobicity Stimulates an Extreme Freezing Delay. Langmuir. 2014, 30, 1659–1668.
Sonwalkar, N., Sunder, S.S., Sharma, S.K. Ice/Solid Adhesion Analysis Using Low-Temperature Raman Microprobe Shear Apparatus. Appl. Spectrosc. 1993, 47, 1585–1593. https://doi.org/10.1366/0003702934334606
Petrenko, V.F., Peng, S. Reduction of Ice Adhesion to Metal by Using Self-Assembling Monolayers (SAMs). Can. J. Phys. 2003, 81, 387–393. https://doi.org/10.1139/p03-014
Matsumoto, K., Tsubaki, D., Sekine, K., Kubota, H., Minamiya, K., Yamanaka, S. Influences of Number of Hydroxyl Groups and Cooling Solid Surface Temperature on Ice Adhesion Force. Int. J. Refrig. 2017, 75, 322–330. https://doi.org/10.1016/j.ijrefrig.2016.12.007
Lifshitz, E.M., Hamermesh, M. The Theory of Molecular Attractive Forces between Solids. In Perspectives in Theoretical Physics, Elsevier, 1992, pp. 329–349 ISBN 978-0-08-036364-6.
Dzyaloshinskii, I.E., Lifshitz, E.M., Pitaevskii, L.P. The General Theory of van Der Waals Forces. Adv. Phys. 1961, 10, 165–209. https://doi.org/10.1080/00018736100101281
Wilen, L.A., Wettlaufer, J.S., Elbaum, M., Schick, M. Dispersion-Force Effects in Interfacial Premelting of Ice. Phys. Rev. B 1995, 52, 12426–12433. https://doi.org/10.1103/PhysRevB.52.12426
Fiedler, J., Boström, M., Persson, C., Brevik, I., Corkery, R., Buhmann, S.Y., Parsons, D.F. Full-Spectrum High-Resolution Modeling of the Dielectric Function of Water. J. Phys. Chem. B. 2020, 124, 3103–3113. https://doi.org/10.1021/acs.jpcb.0c00410
Moazzami Gudarzi, M., Aboutalebi, S.H. Self-Consistent Dielectric Functions of Materials: Toward Accurate Computation of Casimir–van Der Waals Forces. Sci. Adv. 2021, 7, eabg2272.
Saleema, N., Farzaneh, M., Paynter, R.W., Sarkar, D.K. Prevention of Ice Accretion on Aluminum Surfaces by Enhancing Their Hydrophobic Properties. J. Adhes. Sci. Technol. 2011, 25, 27–40. https://doi.org/10.1163/016942410X508064
Menini, R., Farzaneh, M. Advanced Icephobic Coatings. J. Adhes. Sci. Technol. 2011, 25, 971–992. https://doi.org/10.1163/016942410X533372
Ryzhkin, I.A., Petrenko, V.F. Physical Mechanisms Responsible for Ice Adhesion. J. Phys. Chem. B 1997, 101, 6267–6270. https://doi.org/10.1021/jp9632145
Ryzhkin, I.A., Petrenko, V.F. Proton Ordering in Ice at an Ice-Metal Interface. J. Exp. Theor. Phys. 2005, 101, 317–321. https://doi.org/10.1134/1.2047797
Sugimoto, T., Aiga, N., Otsuki, Y., Watanabe, K., Matsumoto, Y. Emergent High-Tc Ferroelectric Ordering of Strongly Correlated and Frustrated Protons in a Heteroepitaxial Ice Film. Nat. Phys. 2016, 12, 1063–1068. https://doi.org/10.1038/nphys3820
Ryzhkin, I.A. Not Obeying the Rules. Nat. Phys. 2016, 12, 996–997. https://doi.org/10.1038/nphys3853
Takahashi, T. Electric Surface Potential of Growing Ice Crystals. J. Atmospheric Sci. 1970, 27, 453–462. https://doi.org/10.1175/1520-0469(1970)027<0453: ESPOGI>2.0.CO;2
Beattie, J.K., Djerdjev, A.M., Warr, G.G. The Surface of Neat Water Is Basic. Faraday Discuss 2009, 141, 31–39. https://doi.org/10.1039/B805266B
Wettlaufer, J. Impurity Effects in the Premelting of Ice. Phys. Rev. Lett. 1999, 82, 2516.
Mitsui, T., Aoki, K. Fluctuation Spectroscopy of Surface Melting of Ice with and without Impurities. Phys. Rev. E 2019, 99, 010801.
Inagawa, A., Harada, M., Okada, T. Charging of the Ice/Solution Interface by Deprotonation of Dangling Bonds, Ion Adsorption, and Ion Uptake in an Ice Crystal As Revealed by Zeta Potential Determination. J. Phys. Chem. C 2019, 123, 6062–6069. https://doi.org/10.1021/acs.jpcc.8b12435
Kallay, N., Čakara, D. Reversible Charging of the Ice–Water Interface. J. Colloid Interface Sci. 2000, 232, 81–85. https://doi.org/10.1006/jcis.2000.7193
Nikola Kallay, Tajana Preočanin, Davor Kovačević, Johannes Lützenkirchen, Emil Chibowski Electrostatic Potentials at Solid/Liquid Interfaces. Croat. Chem. Acta 2010, 83, 357–370.
Čop, A., Kallay, N. Surface Potential of Ice in Aqueous Electrolyte Solutions. In Trends in Colloid and Interface Science XVII, Springer Berlin Heidelberg: Berlin, Heidelberg, 2004, pp. 83–85. ISBN 978-3-540-20073-4.
Lee, A.J., Rick, S.W. Characterizing Charge Transfer at Water Ice Interfaces. J. Phys. Chem. Lett. 2012, 3, 3199–3203. https://doi.org/10.1021/jz301411q
Bryk, Haymet Profiles of Electrostatic Potential across the Water-Vapor, Ice-Vapor and Ice-Water Interfaces. Condens. Matter Phys. 2016, 19, 13607. https://doi.org/10.5488/CMP.19.13607
Lyklema, J. Fundamentals of Interface and Colloid Science, Academic Press: San Diego, 2000, ISBN 978-0-12-460523-7.
Lecadre, F., Kasuya, M., Harano, A., Kanno, Y., Kurihara, K. Low-Temperature Surface Forces Apparatus to Determine the Interactions between Ice and Silica Surfaces. Langmuir. 2018, 34, 11311–11315. https://doi.org/10.1021/acs.langmuir.8b01902
Thiyam, P., Fiedler, J., Buhmann, S.Y., Persson, C., Brevik, I., Boström, M., Parsons, D.F. Ice Particles Sink below the Water Surface Due to a Balance of Salt, van Der Waals, and Buoyancy Forces. J. Phys. Chem. C. 2018, 122, 15311–15317. https://doi.org/10.1021/acs.jpcc.8b02351
Faraday, M. On Certain Conditions of Freezing Water. A Discourse. In Experimental Researches In Chemistry And Physics., 2003, p. 264 ISBN. 978-0-203-21069-7.
James Thomson III. Note on Professor Faraday’s Recent Experiments on “Regelation.” Proc. R. Soc. Lond. 1862, 11, 198–204. https://doi.org/10.1098/rspl.1860.0041
Boinovich, L., Emelyanenko, A. To the Problem of First Order Phase Transition at the Fluid–Fluid Interface. Colloids Surf. Physicochem. Eng. Asp. 2007, 300, 321–326. https://doi.org/10.1016/j.colsurfa.2007.02.031
Boinovich, L., Emelyanenko, A. Shift of Triple Point in Confined Systems with Curved Interfaces. Mol. Phys. 2009, 107, 1745–1753. https://doi.org/10.1080/00268970903048776
Sloutskin, E., Bain, C.D., Ocko, B.M., Deutsch, M. Surface Freezing of Chain Molecules at the Liquid–Liquid and Liquid–Air Interfaces. Faraday Discuss 2005, 129, 339–352. https://doi.org/10.1039/B405969G
Gang, O., Wu, X.Z., Ocko, B.M., Sirota, E.B., Deutsch, M. Surface Freezing in Chain Molecules. II. Neat and Hydrated Alcohols. Phys. Rev. E 1998, 58, 6086–6100. https://doi.org/10.1103/PhysRevE.58.6086
Boinovich, L.B., Emelyanenko, A.M. Forces Due to Dynamic Structure in Thin Liquid Films. Adv. Colloid Interface Sci. 2002, 96, 37–58. https://doi.org/10.1016/S0001-8686(01)00074-4
Elbaum, M., Schick, M. Application of the Theory of Dispersion Forces to the Surface Melting of Ice. Phys. Rev. Lett. 1991, 66, 1713–1716. https://doi.org/10.1103/PhysRevLett.66.1713
Ryzhkin, I.A., Ryzhkin, M.I., Sinitsyn, V.V., Klyuev, A.V. Model of a Surface Liquid-Like Layer of Ice. JETP Lett. 2017, 106, 760–764. https://doi.org/10.1134/S0021364017230114
Golecki, I., Jaccard, C. Intrinsic Surface Disorder in Ice near the Melting Point. J. Phys. C Solid State Phys. 1978, 11, 4229–4237. https://doi.org/10.1088/0022-3719/11/20/018
Döppenschmidt, A., Butt, H.-J. Measuring the Thickness of the Liquid-like Layer on Ice Surfaces with Atomic Force Microscopy. Langmuir 2000, 16, 6709–6714. https://doi.org/10.1021/la990799w
Petrenko, V.F. Study of the Surface of Ice, Ice/Solid and Ice/Liquid Interfaces with Scanning Force Microscopy. J. Phys. Chem. B 1997, 101, 6276–6281. https://doi.org/10.1021/jp963217h
Dosch, H., Lied, A., Bilgram, J.H. Glancing-Angle X-Ray Scattering Studies of the Premelting of Ice Surfaces. Surf. Sci. 1995, 327, 145–164. https://doi.org/10.1016/0039-6028(94)00801-9
Maeno, N., Nishimura, H. The Electrical Properties of Ice Surfaces. J. Glaciol. 1978, 21, 193–205. https://doi.org/10.3189/S0022143000033402
Mazzega, E., del Pennino, U., Loria, A., Mantovani, S. Volta Effect and Liquidlike Layer at the Ice Surface. J. Chem. Phys. 1976, 64, 1028–1031. https://doi.org/10.1063/1.432311
Furukawa, Y., Yamamoto, M., Kuroda, T. Ellipsometric Study of the Transition Layer on the Surface of an Ice Crystal. J. Cryst. Growth. 1987, 82, 665–677. https://doi.org/10.1016/S0022-0248(87)80012-X
Sazaki, G., Zepeda, S., Nakatsubo, S., Yokomine, M., Furukawa, Y. Quasi-Liquid Layers on Ice Crystal Surfaces Are Made up of Two Different Phases. Proc. Natl. Acad. Sci. 2012, 109, 1052–1055. https://doi.org/10.1073/pnas.1116685109
Slater, B., Michaelides, A. Surface Premelting of Water Ice. Nat. Rev. Chem. 2019, 3, 172–188. https://doi.org/10.1038/s41570-019-0080-8
Dash, J.G., Fu, H., Wettlaufer, J.S. The Premelting of Ice and Its Environmental Consequences. Rep. Prog. Phys. 1995, 58, 115–167. https://doi.org/10.1088/0034-4885/58/1/003
Li, H., Bier, M., Mars, J., Weiss, H., Dippel, A.-C., Gutowski, O., Honkimäki, V., Mezger, M. Interfacial Premelting of Ice in Nano Composite Materials. Phys. Chem. Chem. Phys. 2019, 21, 3734–3741. https://doi.org/10.1039/C8CP05604H
Morishige, K. Influence of Pore Wall Hydrophobicity on Freezing and Melting of Confined Water. J. Phys. Chem. C. 2018, 122, 5013–5019. https://doi.org/10.1021/acs.jpcc.8b00538
Engemann, S., Reichert, H., Dosch, H., Bilgram, J., Honkimäki, V., Snigirev, A. Interfacial Melting of Ice in Contact with SiO 2. Phys. Rev. Lett. 2004, 92, 205701. https://doi.org/10.1103/PhysRevLett.92.205701
Liljeblad, J.F.D., Furó, I., Tyrode, E.C. The Premolten Layer of Ice next to a Hydrophilic Solid Surface: Correlating Adhesion with Molecular Properties. Phys. Chem. Chem. Phys. 2017, 19, 305–317. https://doi.org/10.1039/C6CP05303C
Gay, J.-M., Suzanne, J., Dash, J.G., Fu, H. Premelting of Ice in Exfoliated Graphite, a Neutron Diffraction Study. J. Cryst. Growth 1992, 125, 33–41. https://doi.org/10.1016/0022-0248(92)90317-C
Deschamps, J., Audonnet, F., Brodie-Linder, N., Schoeffel, M., Alba-Simionesco, C. A Thermodynamic Limit of the Melting/Freezing Processes of Water under Strongly Hydrophobic Nanoscopic Confinement. Phys. Chem. Chem. Phys. 2010, 12, 1440–1443. https://doi.org/10.1039/B920816J
Schreiber, A., Ketelsen, I., Findenegg, G.H. Melting and Freezing of Water in Ordered Mesoporous Silica Materials. Phys. Chem. Chem. Phys. 2001, 3, 1185–1195. https://doi.org/10.1039/b010086m
Findenegg, G.H., Jähnert, S., Akcakayiran, D., Schreiber, A. Freezing and Melting of Water Confined in Silica Nanopores. ChemPhysChem. 2008, 9, 2651–2659. https://doi.org/10.1002/cphc.200800616
Endo, A., Yamamoto, T., Inagi, Y., Iwakabe, K., Ohmori, T. Characterization of Nonfreezable Pore Water in Mesoporous Silica by Thermoporometry. J. Phys. Chem. C 2008, 112, 9034–9039. https://doi.org/10.1021/jp8016248
Бардасов, С.А., Соболев, В.Д., Чураев, Н.В. Зависимость толщин незамерзающих прослоек воды от кривизны поверхности частиц кремнезема и температуры. Коллоидный Журнал 1991, 53, 996–1002.
Wei, X., Miranda, P.B., Zhang, C., Shen, Y.R. Sum-Frequency Spectroscopic Studies of Ice Interfaces. Phys. Rev. B. 2002, 66, 085401. https://doi.org/10.1103/PhysRevB.66.085401
Yamaguchi, S., Suzuki, Y., Nojima, Y., Otosu, T. Perspective on Sum Frequency Generation Spectroscopy of Ice Surfaces and Interfaces. Chem. Phys. 2019, 522, 199–210. https://doi.org/10.1016/j.chemphys.2019.03.005
Schmidt, R., Hansen, E.W., Stoecker, M., Akporiaye, D., Ellestad, O.H. Pore Size Determination of MCM-51 Mesoporous Materials by Means of 1H NMR Spectroscopy, N₂ Adsorption, and HREM. A Preliminary Study. J. Am. Chem. Soc. 1995, 117, 4049–4056. https://doi.org/10.1021/ja00119a021
Hansen, E.W., Stöcker, M., Schmidt, R. Low-Temperature Phase Transition of Water Confined in Mesopores Probed by NMR. Influence on Pore Size Distribution. J. Phys. Chem. 1996, 100, 2195–2200. https://doi.org/10.1021/jp951772y
Takamuku, T., Yamagami, M., Wakita, H., Masuda, Y., Yamaguchi, T. Thermal Property, Structure, and Dynamics of Supercooled Water in Porous Silica by Calorimetry, Neutron Scattering, and NMR Relaxation. J. Phys. Chem. B. 1997, 101, 5730–5739. https://doi.org/10.1021/jp9631238
Christenson, H.K. Confinement Effects on Freezing and Melting. J. Phys. Condens. Matter 2001, 13, R95.
Lupi, L., Hudait, A., Peters, B., Grünwald, M., Gotchy Mullen, R., Nguyen, A.H., Molinero, V. Role of Stacking Disorder in Ice Nucleation. Nature. 2017, 551, 218–222. https://doi.org/10.1038/nature24279
Boinovich, L.B., Emel’yanenko, A.M. Surface-Induced Shift of Melting/Freezing Temperatures at Interfaces between Two Semi-Infinite Media. Russ. Chem. Bull. 2007, 56, 14–19. https://doi.org/10.1007/s11172-007-0003-6
Boinovich, L.B., Emel’yanenko, A.M. Triple Point in Spatially Limited Systems: Small Particles and Pores. Prot. Met. Phys. Chem. Surf. 2010, 46, 403–410. https://doi.org/10.1134/S2070205110040027
Boinovich, L.B. Boundary Layers and Surface Forces in Pure Nonaqueous Liquids. Curr. Opin. Colloid Interface Sci. 2019, 44, 85–93. https://doi.org/10.1016/j.cocis.2019.10.002
Williams, R., Goodman, A.M. Wetting of Thin Layers of SiO₂ by Water. Appl. Phys. Lett. 1974, 25, 531–532. https://doi.org/10.1063/1.1655297
Kholodov, V.A., Milanovskiy, E.Y., Konstantinov, A.I., Tyugai, Z.N., Yaroslavtseva, N.V., Perminova, I.V. Irreversible Sorption of Humic Substances Causes a Decrease in Wettability of Clay Surfaces as Measured by a Sessile Drop Contact Angle Method. J. Soils Sediments 2018, 18, 1327–1334. https://doi.org/10.1007/s11368-016-1639-3
Uchida, S., Fujiwara, K., Shibahara, M. Structure of the Water Molecule Layer between Ice and Amorphous/Crystalline Surfaces Based on Molecular Dynamics Simulations. J. Phys. Chem. B. 2021, 125, 9601–9609. https://doi.org/10.1021/acs.jpcb.1c03763
Knight, C.A. Experiments on the Contact Angle of Water on Ice. Philos. Mag. 1971, 23, 153–165, https://doi.org/10.1080/14786437108216369
Thiévenaz, V., Josserand, C., Séon, T. Retraction and Freezing of a Water Film on Ice. Phys. Rev. Fluids 2020, 5, 041601. https://doi.org/10.1103/PhysRevFluids.5.041601
Barer, S.S., Churaev, N.V., Derjaguin, B.V., Kiseleva, O.A., Sobolev, V.D. Viscosity of Nonfreezing Thin Interlayers between the Surfaces of Ice and Quartz. J. Colloid Interface Sci. 1980, 74, 173–180. https://doi.org/10.1016/0021-9797(80)90180-0
Bahadur, V., Mishchenko, L., Hatton, B., Taylor, J.A., Aizenberg, J., Krupenkin, T. Predictive Model for Ice Formation on Superhydrophobic Surfaces. Langmuir 2011, 27, 14143–14150.
Dou, R., Chen, J., Zhang, Y., Wang, X., Cui, D., Song, Y., Jiang, L., Wang, J. Anti-Icing Coating with an Aqueous Lubricating Layer. ACS Appl. Mater. Interfaces. 2014, 6, 6998–7003. https://doi.org/10.1021/am501252u
Budnevich, S.S., Derjaguin, B.V. On the Slip of Solids on Ice. Prog. Surf. Sci. 1994, 45, 262–276. https://doi.org/10.1016/0079-6816(94)90059-0
Heydari, G., Tyrode, E., Visnevskij, C., Makuska, R., Claesson, P.M. Temperature-Dependent Deicing Properties of Electrostatically Anchored Branched Brush Layers of Poly(Ethylene Oxide). Langmuir. 2016, 32, 4194–4202. https://doi.org/10.1021/acs.langmuir.6b00671
Janjua, Z.A., Turnbull, B., Choy, K.-L., Pandis, C., Liu, J., Hou, X., Choi, K.-S. Performance and Durability Tests of Smart Icephobic Coatings to Reduce Ice Adhesion. Appl. Surf. Sci. 2017, 407, 555–564. https://doi.org/10.1016/j.apsusc.2017.02.206
Nguyen, T.-B., Park, S., Lim, H. Effects of Morphology Parameters on Anti-Icing Performance in Superhydrophobic Surfaces. Appl. Surf. Sci. 2018, 435, 585–591. https://doi.org/10.1016/j.apsusc.2017.11.137
Idriss, H., Guselnikova, O., Postnikov, P., Kolska, Z., Haušild, P., Čech, J., Lyutakov, O., Švorčík, V. Versatile and Scalable Icephobization of Airspace Composite by Surface Morphology and Chemistry Tuning. ACS Appl. Polym. Mater. 2020, 2, 977–986. https://doi.org/10.1021/acsapm.9b01185
Vazirinasab, E., Maghsoudi, K., Jafari, R., Momen, G. A Comparative Study of the Icephobic and Self-Cleaning Properties of Teflon Materials Having Different Surface Morphologies. J. Mater. Process. Technol. 2020, 276, 116415. https://doi.org/10.1016/j.jmatprotec.2019.116415
Boinovich, L., Emelyanenko, A.M. The Analysis of the Parameters of Three-Phase Coexistence in the Course of Long-Term Contact between a Superhydrophobic Surface and an Aqueous Medium. Chem. Lett. 2012, 41, 1241–1243. https://doi.org/10.1246/cl.2012.1241
Chen, J., Liu, J., He, M., Li, K., Cui, D., Zhang, Q., Zeng, X., Zhang, Y., Wang, J., Song, Y. Superhydrophobic Surfaces Cannot Reduce Ice Adhesion. Appl. Phys. Lett. 2012, 101, 111603. https://doi.org/10.1063/1.4752436
Kulinich, S.A., Honda, M., Zhu, A.L., Rozhin, A.G., Du, X.W. The Icephobic Performance of Alkyl-Grafted Aluminum Surfaces. Soft Matter 2015, 11, 856–861. https://doi.org/10.1039/C4SM02204A
Boinovich, L., Emelyanenko, A.M., Pashinin, A.S. Analysis of Long-Term Durability of Superhydrophobic Properties under Continuous Contact with Water. ACS Appl. Mater. Interfaces. 2010, 2, 1754–1758. https://doi.org/10.1021/am100241s
Jung, S., Tiwari, M.K., Poulikakos, D. Frost Halos from Supercooled Water Droplets. Proc. Natl. Acad. Sci. 2012, 109, 16073–16078. https://doi.org/10.1073/pnas.1206121109
Alizadeh, A., Yamada, M., Li, R., Shang, W., Otta, S., Zhong, S., Ge, L., Dhinojwala, A., Conway, K.R., Bahadur, V., et al. Dynamics of Ice Nucleation on Water Repellent Surfaces. Langmuir. 2012, 28, 3180–3186. https://doi.org/10.1021/la2045256
Yin, L., Xia, Q., Xue, J., Yang, S., Wang, Q., Chen, Q. In Situ Investigation of Ice Formation on Surfaces with Representative Wettability. Appl. Surf. Sci. 2010, 256, 6764–6769. https://doi.org/10.1016/j.apsusc.2010.04.086
Boinovich, L., Emelyanenko, A.M. Role of Water Vapor Desublimation in the Adhesion of an Iced Droplet to a Superhydrophobic Surface. Langmuir. 2014, 30, 12596–12601. https://doi.org/10.1021/la503447f
Zaleski, A., Florensky, B. On Some Basic Prerequisites for Testing Stone Building Materials for Frost Resistance. Proc. Inst. Geol. Sci. Acad. Sci. USSR 1952, 146, 39–50.
Sataeva, N.E., Boinovich, L.B., Emelyanenko, K.A., Domantovsky, A.G., Emelyanenko, A.M. Laser-Assisted Processing of Aluminum Alloy for the Fabrication of Superhydrophobic Coatings Withstanding Multiple Degradation Factors. Surf. Coat. Technol. 2020, 397, 125993. https://doi.org/10.1016/j.surfcoat.2020.125993
Höhne, S., Hoch, C., Böhm, C., Winkler, R., Bittrich, E., Uhlmann, P. A New Measuring System for the Determination of the Ice Adhesion Strength on Smooth Surfaces. Langmuir. 2020, 36, 4465–4476. https://doi.org/10.1021/acs.langmuir.9b03791
Wolfe, J., Bryant, G., Koster, K.L. What Is’ Unfreezable Water’, How Unfreezable Is It and How Much Is There? CryoLetters. 2002, 23, 157–166.
Lee, H., Alcaraz, M.L., Rubner, M.F., Cohen, R.E. Zwitter-Wettability and Antifogging Coatings with Frost-Resisting Capabilities. ACS Nano. 2013, 7, 2172–2185.
Peppou-Chapman, S., Hong, J.K., Waterhouse, A., Neto, C. Life and Death of Liquid-Infused Surfaces: A Review on the Choice, Analysis and Fate of the Infused Liquid Layer. Chem. Soc. Rev. 2020, 49, 3688–3715.
Yeong, Y.H., Wang, C., Wynne, K.J., Gupta, M.C. Oil-Infused Superhydrophobic Silicone Material for Low Ice Adhesion with Long-Term Infusion Stability. ACS Appl. Mater. Interfaces. 2016, 8, 32050–32059.
Donadei, V., Koivuluoto, H., Sarlin, E., Niemelä-Anttonen, H., Varis, T., Vuoristo, P. The Effect of Mechanical and Thermal Stresses on the Performance of Lubricated Icephobic Coatings during Cyclic Icing/Deicing Tests. Prog. Org. Coat. 2022, 163, 106614.
Niemelä-Anttonen, H., Koivuluoto, H., Tuominen, M., Teisala, H., Juuti, P., Haapanen, J., Harra, J., Stenroos, C., Lahti, J., Kuusipalo, J., et al. Icephobicity of Slippery Liquid Infused Porous Surfaces under Multiple Freeze-Thaw and Ice Accretion-Detachment Cycles. Adv. Mater. Interfaces 2018, 5, 1800828. https://doi.org/10.1002/admi.201800828
Subramanyam, S.B., Rykaczewski, K., Varanasi, K.K. Ice Adhesion on Lubricant-Impregnated Textured Surfaces. Langmuir 2013, 29, 13414–13418.
Goodband, S.J., Armstrong, S., Kusumaatmaja, H., Voïtchovsky, K. Effect of Ageing on the Structure and Properties of Model Liquid-Infused Surfaces. Langmuir. 2020, 36, 3461–3470.
Emelyanenko, K.A., Emelyanenko, A.M., Boinovich, L.B. Disjoining Pressure Analysis of the Lubricant Nanofilm Stability of Liquid-Infused Surface upon Lubricant Depletion. J. Colloid Interface Sci. 2022.
Chen, J., Dou, R., Cui, D., Zhang, Q., Zhang, Y., Xu, F., Zhou, X., Wang, J., Song, Y., Jiang, L. Robust Prototypical Anti-Icing Coatings with a Self-Lubricating Liquid Water Layer between Ice and Substrate. ACS Appl. Mater. Interfaces. 2013, 5, 4026–4030. https://doi.org/10.1021/am401004t
Derjaguin, B.V., Bazaron, U.B., Zandanova, K.T., Budaev, O.R. The Complex Shear Modulus of Polymeric and Small-Molecule Liquids. Polymer 1989, 30, 97–103, https://doi.org/10.1016/0032-3861(89)90389-3
Derjaguin, B.V., Bazaron, U.B., Lamazhapova, Kh.D., Tsidypov, B.D. Shear Elasticity of Low-Viscosity Liquids at Low Frequencies. Phys. Rev. A 1990, 42, 2255–2258. https://doi.org/10.1103/PhysRevA.42.2255
Badmaev, B., Dembelova, T., Damdinov, B., Makarova, D., Budaev, O. Influence of Surface Wettability on the Accuracy of Measurement of Fluid Shear Modulus. Colloids Surf. Physicochem. Eng. Asp. 2011, 383, 90–94. https://doi.org/10.1016/j.colsurfa.2011.03.036
Noirez, L., Baroni, P. Identification of a Low-Frequency Elastic Behaviour in Liquid Water. J. Phys. Condens. Matter 2012, 24, 372101. https://doi.org/10.1088/0953-8984/24/37/372101
Епифанов, В.П., Глазовский, А.Ф. Акустическе характеристики как индикатор особенностей движения льда в ледниках. Криосфера Земли 2010, 14, 42–55.
Work, A.H. A Statistical Analysis of Impact Ice Adhesion Strength Data Acquired with a Modified Lap Joint Test. In Proceedings of the AIAA AVIATION 2020 FORUM, 2020, p. 2801.
Чулкова, Е.В., Емельяненко, К.А., Емельяненко, А.М., Бойнович, Л.Б. Исследование Прочности Адгезионного Контакта Льда На Поверхностях с Различным Смачиванием. Коллоидный Журнал 2022, 84.
Work, A., Lian, Y. A Critical Review of the Measurement of Ice Adhesion to Solid Substrates. Prog. Aerosp. Sci. 2018, 98, 1–26. https://doi.org/10.1016/j.paerosci.2018.03.001
Rønneberg, S., Zhuo, Y., Laforte, C., He, J., Zhang, Z. Interlaboratory Study of Ice Adhesion Using Different Techniques. Coatings 2019, 9, 678. https://doi.org/10.3390/coatings9100678
Schulz, M., Sinapius, M. Evaluation of Different Ice Adhesion Tests for Mechanical Deicing Systems., June 15 2015, pp. 2015-01–2135.
Kasaai, M.R., Farzaneh, M. A Critical Review of Evaluation Methods of Ice Adhesion Strength on the Surface of Materials. In Proceedings of the 23rd International Conference on Offshore Mechanics and Arctic Engineering, Volume 3, ASMEDC: Vancouver, British Columbia, Canada, January 1 2004, pp. 919–926.
Rønneberg, S., He, J., Zhang, Z. The Need for Standards in Low Ice Adhesion Surface Research: A Critical Review. J. Adhes. Sci. Technol. 2020, 34, 319–347. https://doi.org/10.1080/01694243.2019.1679523
Laroche, A., Grasso, M.J., Dolatabadi, A., Bonaccurso, E. Tensile and Shear Test Methods for Quantifying the Ice Adhesion Strength to a Surface. In Ice Adhesion, Mittal, K.L., Choi, C. -H., Eds., Wiley, 2020, pp. 237–284. ISBN 978-1-119-64052-3.
Bleszynski, M., Clark, E. Current Ice Adhesion Testing Methods and the Need for a Standard: A Concise Review. Standards. 2021, 1, 117–133, https://doi.org/10.3390/standards1020011
Mirshahidi, K., Alasvand Zarasvand, K., Luo, W., Golovin, K. A High Throughput Tensile Ice Adhesion Measurement System. HardwareX. 2020, 8, e00146. https://doi.org/10.1016/j.ohx.2020.e00146
Regulagadda, K., Gerber, J., Schutzius, T.M., Poulikakos, D. Microscale Investigation on Interfacial Slippage and Detachment of Ice from Soft Materials. Mater. Horiz. 2022. https://doi.org/10.1039.D1MH01993G
Laforte, C., Beisswenger, A. Icephobic Material Centrifuge Adhesion Test. Proc. 11th Int. Workshop Atmospheric Icing Struct. 2005.
Гольдштейн, Р.В., Епифанов, В.П. К измерению адгезии льда к другим материалам. Вестник Пермского национального исследовательского политехнического университета 2011, 2, 28–40.
Tetteh, E., Loth, E. Reducing Static and Impact Ice Adhesion with a Self-Lubricating Icephobic Coating (SLIC). Coatings. 2020, 10, 262. https://doi.org/10.3390/coatings10030262
Yeong, Y.H., Milionis, A., Loth, E., Sokhey, J., Lambourne, A. Atmospheric Ice Adhesion on Water-Repellent Coatings: Wetting and Surface Topology Effects. Langmuir. 2015, 31, 13107–13116. https://doi.org/10.1021/acs.langmuir.5b02725
Psarski, M., Pawlak, D., Grobelny, J., Celichowski, G. Relationships between Surface Chemistry, Nanotopography, Wettability and Ice Adhesion in Epoxy and SU-8 Modified with Fluoroalkylsilanes from the Vapor Phase. Appl. Surf. Sci. 2019, 479, 489–498. https://doi.org/10.1016/j.apsusc.2019.02.082
Boinovich, L.B., Zhevnenko, S.N., Emel’yanenko, A.M., Gol’dshtein, R.V., Epifanov, V.P. Adhesive Strength of the Contact of Ice with a Superhydrophobic Coating. Dokl. Chem. 2013, 448, 71–75. https://doi.org/10.1134/S0012500813020079
Petrovic, J.J. Review Mechanical Properties of Ice and Snow. J. Mater. Sci. 2003, 38, 1–6. https://doi.org/10.1023/A:1021134128038
Work, A. The Measurement of the Adhesion of Glaze Ice., University of Louisville, 2018.
Smith, J.G., Whol, C.J., Kreeger, R.E., Palacios, J., Hernandez, M. Effects of Hydrogen Bonding and Molecular Chain Flexibility of Substituted N-Alkyldimethylsilanes On Impact Ice Adhesion Shear Strength. 2020.
Irajizad, P., Hasnain, M., Farokhnia, N., Sajadi, S.M., Ghasemi, H. Magnetic Slippery Extreme Icephobic Surfaces. Nat. Commun. 2016, 7, 13395. https://doi.org/10.1038/ncomms13395
Liang, Z.-H., Wu, S.-L., Liu, C., Yang, H.-C., Darling, S.B., Xu, Z.-K. When SLIPS Meets TIPS: An Endogenous Lubricant-Infused Surface by Taking the Diluent as the Lubricant. Chem. Eng. J. 2021, 425, 130600. https://doi.org/10.1016/j.cej.2021.130600
Bottone, D., Donadei, V., Niemelä, H., Koivuluoto, H., Seeger, S. Coral-like Silicone Nanofilament Coatings with Extremely Low Ice Adhesion. Sci. Rep. 2021, 11, 20427. https://doi.org/10.1038/s41598-021-98215-1
Yuan, Y., Wang, L., Liu, G., Liao, R. Fabrication of Ultralow Ice-Adhesion Slippery Liquid Infused Porous Surfaces on Aluminum Alloy (7075-T651). Coatings. 2020, 10, 1025. https://doi.org/10.3390/coatings10111025

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал