Коллоидный журнал, 2022, T. 84, № 3, стр. 301-310
Дифракция и ослабление света в магнитных эмульсиях с низким межфазным натяжением
К. В. Ерин 1, *, С. С. Белых 1
1 Северо-Кавказский федеральный университет, Физико-технический факультет
355017 Ставрополь,
ул. Пушкина, 1, Россия
* E-mail: exiton@inbox.ru
Поступила в редакцию 24.03.2022
После доработки 11.04.2022
Принята к публикации 11.04.2022
- EDN: OXDMXF
- DOI: 10.31857/S0023291222030041
Аннотация
Исследованы эффекты дифракции и ослабления света в магнитных эмульсиях с низким межфазным натяжением на основе масла гидросистем АМГ-10 при воздействии магнитного и гидродинамического полей. Предложена интерпретация эффектов на основе известного в оптике дисперсных систем приближения аномальной дифракции. При анализе поворота дифракционной картины во вращающейся эмульсии учтены особенности вращательной подвижности жидких микрокапель. Расчеты по такой модели позволили получить согласующуюся с экспериментом нелинейную зависимость угла поворота дифракционной картины от скорости вращения эмульсии.
ВВЕДЕНИЕ
Магниточувствительные эмульсии были синтезированы на рубеже к 70–80-х годов XX века [1]. Первоначально они предназначались для визуализации магнитных записей и контроля качества магнитных головок [2]. В последнее время спектр применения подобных систем существенно расширился за счет развития микрофлюидики [3] и биомедицинских технологий [4]. С использованием магниточувствительных эмульсий предложены методы измерения вязкости и поверхностного натяжения жидкостей [5], определения содержания метилового спирта [6] и др.
Обычно выделяют два типа магнитных эмульсий, исходя из величины межфазного натяжения между каплей и окружающей дисперсионной средой [7]. Это различие в значительной степени определяет физические механизмы эффектов, наблюдающихся в магнитных эмульсиях при воздействии внешнего поля. В магнитных эмульсиях на водной основе межфазное натяжение высокое, деформация капель в поле затруднена, но при этом легко образуются различного рода агрегативные структуры. При малом межфазном натяжении, что обычно бывает при диспергировании магнитной жидкости на углеводородной основе в различных маслах, капли легко могут менять форму в поле даже небольшой напряженности. Наиболее известны подобные эмульсии, полученные путем смешивания магнитной жидкости на основе керосина с гидравлическим маслом АМГ-10. Исследованию магнитных, реологических и электрофизических свойств таких эмульсий, а также структурным образованиям в них посвящен ряд исследований [8–10]. Деформированные капли создают в дисперсной системе анизотропию, приводящую, в том числе и к оптическим эффектам [11].
Магнитные эмульсии чрезвычайно чувствительны к магнитному полю даже самой малой напряженности (оптические эффекты в них можно наблюдать в полях, начиная с 300–500 А/м). В связи с этим, оптические свойства магнитных эмульсий представляют существенный интерес как с чисто научной, так и с практической точек зрения. В статье [12] исследовалась дифракция света на микроскопических каплях магнитной жидкости во вращающемся магнитном поле. Авторами [12] теоретический анализ движения одиночной капли распространен на случай систем микрокапель. При этом во вращающемся магнитном поле обнаружен режим нестационарного вращения, а также сложная S-образная деформация микрокапель. В [13] обнаружен эффект изменения прозрачности в магнитных эмульсиях в продольном магнитном поле, величиной которого можно управлять магнитным полем. Этот эффект делает магнитные эмульсии перспективными материалами для магнитоуправляемых оптических элементов. В настоящей работе мы приводим результаты исследования эффекта дифракционного рассеяния света в магнитных эмульсиях с низким межфазным натяжением, синтезированных на основе масла гидросистем АМГ-10.
ЭКСПЕРИМЕНТ
Эмульсии для экспериментальных исследований синтезировались с использованием магнитной жидкости типа магнетит в керосине (производитель – НИПИ Газпереработки, г. Краснодар, Россия) с объемной концентрацией твердой фазы около 5%, намагниченностью насыщения Ms = = 24.4 кАм, начальной магнитной восприимчивостью при комнатной температуре χ = 1.5 и размером частиц в диапазоне 8–20 нм. Намагниченность насыщения и начальная магнитная восприимчивость определялись из кривой намагничивания, измеренной на вибрационном магнитометре LakeShore Cryotronics VSM 7000 series в лаборатории магнитных наноматериалов СКФУ. Распределение частиц по размерам было определено методом динамического рассеяния света с помощью спектрометра Photocor Complex. Эмульсия магнитной жидкости в авиационном масле гидросистем АМГ-10 изготавливалась путем продавливания магнитной жидкости через тонкий капилляр и последующего механического перемешивания. Стабильность системы в значительной степени достигалась за счет вязкости масла и близости значений плотности масла и магнитной жидкости. Объемная концентрация магнитной жидкости в образцах эмульсий составляла от 2 до 7%, а размер капель находился в пределах 1–7 мкм. На рис. 1 приведены фотографии микрокапель магнитной эмульсии при воздействии магнитного поля и в его отсутствие. Величина межфазного натяжения в эмульсии оценивалась по деформации сравнительно крупной капли под действием магнитного поля и составила σ ≈ 10–6 Н/м [14].
Рис. 1.
Схема экспериментальной установки для исследования дифракционного рассеяния и ослабления света в магнитных эмульсиях и фотографии микрокапель магнитной эмульсии.
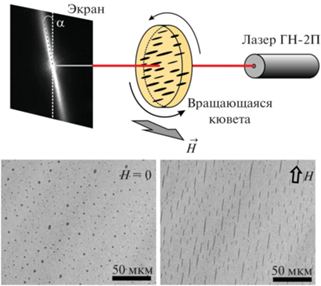
Для исследования оптических эффектов в магнитных эмульсиях использовалась оптическая установка (рис. 1), состоящая из гелий-неонового лазера с длиной волны излучения 633 нм. Изображение дифракционной картины регистрировалось КМОП-матрицей фотоаппарата с разрешением 4272 × 2848 пикселей. Обработка изображений производилась с помощью специализированного программного обеспечения ImageJ. Регистрация прошедшего через образец света производилась при помощи фотоэлектронного умножителя ФЭУ-27, подключенного к цифровому запоминающему осциллографу AURIS-B423. В этом случае экран демонтировался. Магнитное поле создавалось катушками Гельмгольца, установленными так, чтобы вся кювета находилась в области однородного поля. Ток в цепи катушек создавался источником питания АКТАКОМ ATH-2335 с компьютерным управлением, что позволяло создавать поля с напряженностью до 9 кА/м. Для исследований дифракции света при воздействии гидродинамического поля использовался метод вращающейся кюветы [15]. В этом случае кювета для образца представляла собой стеклянный цилиндр с внутренним диаметром 35 мм и высотой 1 мм, закрепленный на фторопластовой трубке, приводимой во вращение электродвигателем постоянного тока с помощью ременной передачи. Диапазон частот вращения составлял 9–200 об./мин. Луч лазера направлялся строго по оси вращения кюветы.
Исследования спектров пропускания магнитной эмульсии производились с помощь спектрального эллипсометра ЭЛЛИПС-1891 в режиме спектрофотометра в диапазоне длин волн 400–1050 нм.
Изменение прозрачности магнитной эмульсии под действием поля оценивали по значению величины $\delta T = ({{T}_{H}} - {{T}_{0}}){\text{/}}{{T}_{0}}$, где ${{T}_{H}} = {{I}_{H}}{\text{/}}I_{0}^{i}$ – прозрачность системы при воздействии поля и ${{T}_{0}} = {{I}_{0}}{\text{/}}I_{0}^{i}$ в его отсутствие соответственно ($I_{0}^{i}$ – интенсивность света, падающего на кювету). Связь между оптической плотностью эмульсии и прозрачностью можно интерпретировать на основе закона Бугера−Ламберта:
где ${{D}_{H}}$ и ${{D}_{0}}$ – оптическая плотность системы в магнитном поле и без него соответственно. В приближении однократного рассеяния оптическую плотность можно выразить через сечение ослабления света частицей (σe), концентрацию частиц (N) и длину пути света l:Поскольку точное определение числовой концентрации микрокапель в магнитной эмульсии затруднительно, а параметр $\delta T$ зависит от нее сложным образом, то для сопоставления результатов эксперимента с оптическими моделями рассчитывалось относительное изменение оптической плотности:
В ряде работ [16, 17] этот параметр используется для описания эффекта изменения прозрачности в дисперсных системах (ориентационного турбидиметрического эффекта). Он удобен тем, что при неизменной концентрации частиц определяется только соотношением сечений ослабления света вследствие ориентации частиц полем или, как в нашем случае, вытяжением микрокапель вдоль направления поля:
Отметим, что параметры $\delta T$и $\delta D$ имеют противоположные знаки, т.е. при увеличении прозрачности системы в поле $\delta T > 0,\,\,\delta D < 0$, а при уменьшении –$\delta T < 0,\,\,\delta D > 0$.
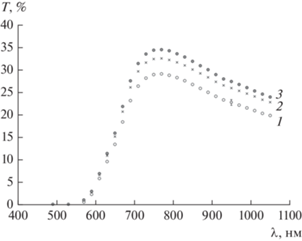
Воздействие магнитного поля приводит к существенному изменению прозрачности магнитной эмульсии (рис. 2). Наиболее выраженный эффект изменения прозрачности (относительное изменение прозрачности δT достигает 25–30%) достигается в магнитном поле, направленном вдоль луча света (так называемом продольном поле). При этом величиной изменения прозрачности можно управлять не только величиной напряженности поля, но и его ориентацией относительно луча света. Спектры пропускания магнитной эмульсии при воздействии поля и при его отсутствии подобны. Изменения максимума пропускания, приходящегося на 760–780 нм, нами обнаружено не было, в отличие от данных [18], в которых было показано изменение цвета структурированного магнитного коллоида при воздействии поля. Эффект изменения прозрачности имеет выраженное насыщение при напряженности магнитного поля свыше 5 кА/м. Для света с длиной волны менее 550 нм магнитная эмульсия практически непрозрачна, что обуславливает ее характерный желто-коричневый цвет.
Рис. 2.
Спектры пропускания магнитной эмульсии в продольном магнитном поле различных напряженностей (1 – H = 0, 2 – H = 1.5 кА/м, 3 – H = 3 кА/м).
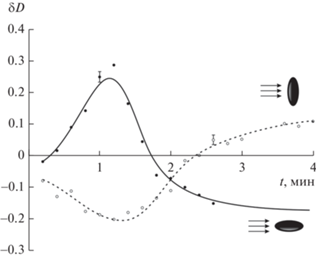
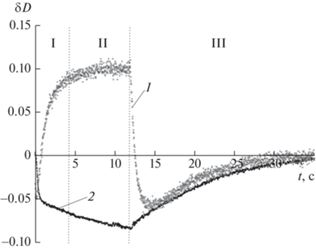
Эксперимент по определению влияния времени воздействия магнитного поля на эффект изменения оптической плотности проводили следующим образом. Величина и знак параметра изменения оптической плотности δD измерялись при воздействии импульсов магнитного поля напряженностью Н = 4.5 кА/м длительностью 12 секунд с периодом следования 40 c. Магнитное поле было как продольной, так и поперечной конфигурации. В импульсном магнитном поле кривая изменения эффекта достаточно типична для электро- и магнитооптических эффектов и состоит из трех участков: нарастания эффекта (I), области близкой к насыщению (II) и релаксации после выключения поля (III) (рис. 3). При этом релаксация эффекта для определенного диапазона размеров частиц может носить немонотонный характер с переходом величины эффекта через нуль. Установлено, что при последовательном воздействии импульсов магнитного поля величина и знак изменения оптической плотности меняются. На рис. 3 показаны два изменения оптической плотности в импульсном поле третьего импульса (общее время действия поля 36 c) и после многократного воздействия импульсов. Под действием первых нескольких импульсов поля оптическая плотность системы в продольном поле увеличивается, затем величина эффекта уменьшается, а после воздействия поля в течение примерно 100 с знак эффекта меняется на противоположный. Аналогичный результат наблюдается и в поперечном поле, но знак эффекта меняется в этом случае с отрицательного на положительный. На рис. 4 представлены экспериментальные результаты изменения оптического эффекта от продолжительности экспозиции в продольном и поперечном полях. Отметим, что релаксация оптического эффекта в магнитных эмульсиях может меняться немонотонным образом (рис. 3, кривая 1). Ранее мы обсуждали причины такой немонотонности в агрегированных магнитных коллоидах [19] и магнитных эмульсиях [20].
Рис. 3.
Эффект изменения оптической плотности в магнитной эмульсии в импульсном магнитном поле (1 – отклик на действие третьего импульса (36 с после включения поля), 2 – после многократного действия импульсов (120 с после включения поля).
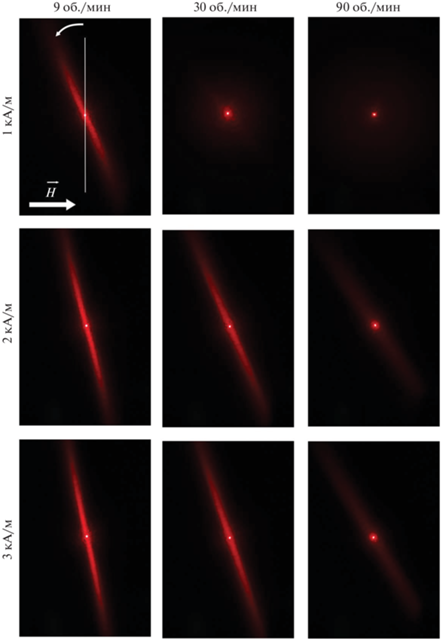
При воздействии магнитного поля, перпендикулярного направлению распространения света, в магнитных эмульсиях возникает выраженный эффект дифракции света на вытянутых иглообразных микрокаплях. Дифракционная полоса ориентирована в направлении, перпендикулярном длинным осям вытянутых микрокапель. Поскольку капли имеют различные размеры, а также расположены в эмульсии хаотично, то дифракционная картина представляет собой полосу без выраженных максимумов и минимумов, характерных для строго упорядоченных структур (дифракционных решеток). Дифракционная картина в магнитной эмульсии с низким межфазным натяжением принципиально не отличается описанной нами ранее картины в магнитной эмульсии на водной основе с высоким межфазным натяжением [7]. Дополнительное действие гидродинамических сил во вращающейся эмульсии приводит к отклонению осей капель от направления магнитного поля, в результате чего дифракционная полоса поворачивается относительно первоначального направления. На рис. 5 представлены фотографии дифракционной картины, возникающей при прохождении света через образец магнитной эмульсии при различных напряженностях магнитного поля и скоростях вращения кюветы. Угол отклонения зависит как от скорости вращения кюветы, так и от напряженности магнитного поля. На рис. 6 и 7 показаны зависимости угла поворота полосы от частоты вращения кюветы при постоянной напряженности магнитного поля и угла поворота от напряженности поля при постоянной скорости вращения.
Рис. 5.
Фотографии дифракционных полос при различных напряженностях магнитного поля и частотах вращения кюветы.
ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Интерпретация оптических эффектов в магнитных эмульсиях возможна с использованием, так называемого приближения аномальной дифракции. Приближение было сформулировано Ван де Хюлстом [21, 22]. Это приближение справедливо для частиц, существенно крупнее длины волны света, но при этом оптически “мягких”, т.е. таких, у которых показатель преломления мало отличается от окружающей среды, $x = 2\pi {{r}_{0}}{\text{/}}\lambda \gg 1$ и $\left| {m - 1} \right| \ll 1$, где m = n/n0. Оба условия выполняются для микрокапель магнитной эмульсии, так как у исследованных нами образцов на основе АМГ-10 $x \approx 10 - 50$, а $\left| {m - 1} \right| = 0.06$.
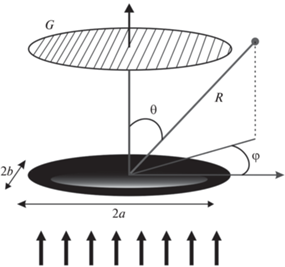
Рассмотрим рассеяние света в приближении аномальной дифракции на вытянутой сфероидальной частице со значениями длинной и короткой полуосей a и b (рис. 8). Сечение ослабления света микрокаплей в приближении аномальной дифракции можно записать как [23]:
где S(p,α) – площадь тени, зависящая от степени вытянутости микрокапли (p = a/b) и ее ориентации по отношению к свету, а Q(ρ) – фактор эффективности ослабления света. Выражение для Q(ρ) поглощающей частицы (показатель преломления капель использованной нами магнитной жидкости для длины волны 633 nm составляет ${{n}_{{mf}}} = 1.57 - 0.02i$) приведено в [22]:(6)
$\rho = \frac{{4\pi {{r}_{0}}}}{\lambda }\frac{{m - 1}}{{\sqrt[3]{p}\sqrt {1 + ({{p}^{{ - 2}}} - 1){{{\cos }}^{2}}{\kern 1pt} \alpha } }}.$Тогда, с учетом (4), (5) и простых геометрических соображений, можно получить выражение для сечения ослабления света:
(7)
${{\sigma }_{e}} = \pi r_{0}^{2}Q\left( \rho \right)\sqrt[3]{p}\sqrt {1 + ({{p}^{{ - 2}}} - 1){{{\cos }}^{2}}{\kern 1pt} \alpha } .$Использование приближения аномальной дифракции позволяет объяснить большинство особенностей эффекта изменения прозрачности в магнитных эмульсиях под действием магнитного поля. В частности, расчеты по формулам (4)–(7) показывают, что при изменении радиуса r0 эквивалентного объема микрокапли свыше 1.5–2 мкм знак эффекта изменения оптической плотности меняется на противоположный. Так для системы микрокапель с радиусом эквивалентного объема r0 = 1 мкм при вытяжении вдоль направления распространения света величина $\delta D = 0.1$, т.е. при воздействии поля эмульсия становится менее прозрачной, чем в отсутствие поля. Однако при увеличении радиуса до r0 = 2 мкм величина относительного изменения оптической плотности становится отрицательной $\delta D = - 0.4$, т.е. прозрачность системы при включении поля возрастает. При ориентации микрокапель поперек направления распространения света относительное изменение оптической плотности также меняет знак с ростом размера микрокапель, но с отрицательного при относительно малых размерах (r0 < 2 мкм) на положительный для более крупных частиц. Необходимо отметить, что переход знака эффекта через нуль происходит при несколько отличающихся значениях радиуса эквивалентного объема для частиц различно ориентированных по отношению к лучу света. Это очень хорошо согласуется с экспериментом (рис. 4). Таким образом, изменение формы оптического отклика магнитной эмульсии при длительном воздействии поля (рис. 3) можно интерпретировать частичной коалесценцией микрокапель, сопровождающейся увеличением их среднего размера до 4–6 мкм. Также расчеты в приближении аномальной дифракции позволяют объяснить необычную для коллоидных систем немонотонную релаксацию эффектов при включении и выключении поля. Эту особенность можно объяснить тем, что для микрокапель определенных размеров максимальная или минимальная величина оптического эффекта может достигаться не в случае сферической или максимально вытянутой формы микрокапли, а в некотором промежуточном состоянии. Такая немонотонная релаксация наблюдается в эксперименте для образца со сравнительно малым средним размером капель (рис. 3, кривая 1). Подробнее о возможных механизмах релаксации магнитооптического эффекта в магнитных эмульсиях мы сообщали в [20, 24].
Приближение аномальной дифракции может быть использовано и для интерпретации дифракционного рассеяния света в магнитных эмульсиях. Интенсивность света в любой точке экрана (рис. 8), удаленной на расстояние R и задаваемой углами $\theta ,\varphi $, может быть записана [22, 23] как:
(8)
$I\left( {\theta ,\phi } \right) = I_{0}^{i}\frac{{{{G}^{2}}}}{{{{\lambda }^{2}}{{R}^{2}}}}{{\left| {D\left( {\theta ,\varphi } \right)} \right|}^{2}},$(9)
$D\left( {\theta ,\varphi } \right) = \frac{{{{\lambda }^{2}}}}{{{{\pi }^{2}}}}\frac{{\sin \left( {\frac{{\pi a}}{\lambda }{\kern 1pt} \sin {\kern 1pt} \theta \cos {\kern 1pt} \varphi } \right)}}{{a{\kern 1pt} \sin {\kern 1pt} \theta \cos {\kern 1pt} \varphi }}\frac{{\sin \left( {\frac{{\pi b}}{\lambda }{\kern 1pt} \sin {\kern 1pt} \theta \sin {\kern 1pt} \varphi } \right)}}{{b{\kern 1pt} \sin {\kern 1pt} \theta \sin {\kern 1pt} \varphi }}.$Расчеты по формулам (8) и (9) показывают дифракционную картину, вполне согласующуюся с экспериментом. Полоса дифракционного рассеяния на сильно вытянутых полидисперсных частицах ориентирована в направлении, перпендикулярном их длинным осям. Если предположить, что в процессе вытяжения объем микрокапель эмульсии не меняется, то параметры сфероида a и b могут быть выражены через радиус сферы эквивалентного объема r0 и соотношение осей p = a/b ($a = {{r}_{0}}\sqrt[3]{{{{p}^{2}}}}$ и $b = {{r}_{0}}\sqrt[3]{{{{p}^{{ - 1}}}}}$).
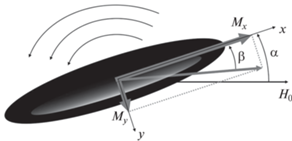
Воздействие гидродинамических сил со стороны вращающейся жидкости приводит к повороту вытянутой микрокапли на некоторый угол α и, соответственно, повороту дифракционной полосы на такой же угол [25]. Равновесное положение микрокапли может быть в этом случае найдено исходя из баланса моментов магнитных сил Tm и сил вязкого трения Th [2, 25, 26].
Момент гидродинамических сил, возникающих в жидкости с градиентом скорости течения, определяется угловой скоростью вращения ${{\omega }} = 2\pi n$:
где B – вращательная подвижность микрокапли. Сложность заключается в том, что подвижность жидкой микрокапли может существенно отличаться от известного выражения для твердой вытянутой частицы [26]:(11)
$B = \frac{3}{{6{{\eta }_{2}}{{V}_{0}}}}\frac{{{{a}^{2}}{{N}_{a}} + {{b}^{2}}{{N}_{b}}}}{{{{a}^{2}} + {{b}^{2}}}},$Особенности определения вращательного трения для жидких капель рассмотрены в работах [26, 27], в которых показано, что наиболее существенное отличие во вращательных подвижностях жидкой и твердой капель наблюдается в случае, когда капля имеет незначительную вытянутость. Это связано с характером движения жидкости внутри капли при ее вращении. Для оценки движения жидкости в капле в [26] предложено использовать параметр завихренности $\zeta (p)$. С учетом этого параметра вращательная подвижность жидкой микрокапли имеет вид:
(12)
$B = \frac{3}{{6{{\eta }_{2}}{{V}_{0}}}}\frac{{{{a}^{2}}{{N}_{a}} + {{b}^{2}}{{N}_{b}}}}{{{{a}^{2}} + {{b}^{2}} + 2ab{{\zeta (p)} \mathord{\left/ {\vphantom {{\zeta (p)} \omega }} \right. \kern-0em} \omega }}}.$Параметр внутрикапельной завихренности, выраженный в единицах угловой скорости ${{\zeta (p)} \mathord{\left/ {\vphantom {{\zeta (p)} \omega }} \right. \kern-0em} \omega }$, зависит в общем случае от вытянутости капли и соотношения вязкостей сред внутри η1 и снаружи η2 капли. В предельных случаях сильно вытянутой (с эксцентриситетом e → 1) и практически сферической капли (при e → 0) параметр внутрикапельной завихренности имеет вид:
Для произвольных значений вытянутости в [26] приведены численные решения для параметра ${{\zeta (p)} \mathord{\left/ {\vphantom {{\zeta (p)} \omega }} \right. \kern-0em} \omega }$. Для сильно вытянутой капли завихренностью движения жидкости внутри капли можно пренебречь ${{\zeta (p)} \mathord{\left/ {\vphantom {{\zeta (p)} \omega }} \right. \kern-0em} \omega } \approx 0$, и капля ведет себя как твердый сфероид таких же размеров. Аналогичный результат для сфероидов получается при условии ${{{{\eta }_{1}}} \mathord{\left/ {\vphantom {{{{\eta }_{1}}} {{{\eta }_{2}}}}} \right. \kern-0em} {{{\eta }_{2}}}} \gg 1$, но уже при достаточно слабой вытянутости p > 1.5. При этом для исследуемых нами систем вязкости магнитной жидкости и масла АМГ-10 близки, т.е. ${{{{\eta }_{1}}} \mathord{\left/ {\vphantom {{{{\eta }_{1}}} {{{\eta }_{2}}}}} \right. \kern-0em} {{{\eta }_{2}}}} \approx 1$. В этом случае для микрокапель, близких по форме к сферическим (это реализуется либо в случае слабых полей, либо при значительном отклонении оси капли от направления поля), требуется учет внутрикапельной завихренности. С учетом этого выражение для момента сил вязкого трения, действующего на жидкую вытянутую каплю, имеет вид:
(13)
${{T}_{{\text{h}}}} = \frac{{4\eta {{V}_{0}}\omega \left( {1 + {{p}^{2}} + 2p{{\zeta (p)} \mathord{\left/ {\vphantom {{\zeta (p)} \omega }} \right. \kern-0em} \omega }} \right)}}{{1 + 2{{p}^{2}}{{N}_{a}} - {{N}_{a}}}},$Выражение для момента магнитных сил имеет вид [2]:
(14)
${{T}_{{\text{m}}}} = \frac{1}{2}\frac{{{{\mu }_{0}}{{V}_{0}}{{\chi }^{2}}{{H}^{2}}\left| {1 - 3{{N}_{a}}} \right|}}{{(1 + \chi {{N}_{a}})(2 + \chi - \chi {{N}_{a}})}}\sin {\kern 1pt} 2\alpha .$Соотношение между углом отклонения оси капли от направления поля α и углом между осью капли и направлением ее намагничивания β можно записать в виде:
Из (15) видно, что для несферической капли Na < Nb направление намагниченности отклоняется от направления поля на угол α – β. Для сферической капли Na = Nb и из (15) логично следует, что α = β, т.е. направление намагниченности совпадает с направлением поля. Оценки зависимости $\alpha - \beta = f(\alpha )$ показывают ее немонотонный характер с максимумом, смещающимся в область больших углов с ростом напряженности поля. Свободную энергию капли c межфазным натяжением γ, эксцентриситетом e, отклоненной от направления поля на угол α, можно записать в виде:
(16)
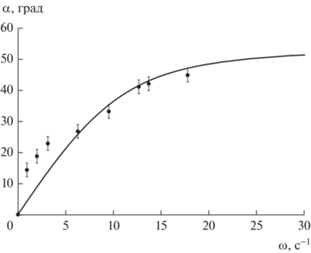
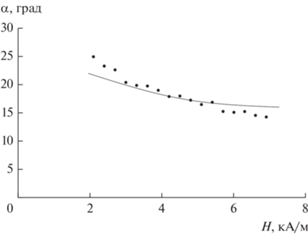
$\begin{gathered} W = 2\pi r_{0}^{2}\gamma \sqrt[3]{{1 - {{e}^{2}}}}\left[ {1 + \frac{{\arcsin {\kern 1pt} e}}{{e\sqrt {1 - {{e}^{2}}} }}} \right] - \\ - \,\,\frac{1}{2}{{\mu }_{0}}{{V}_{0}}{{H}^{2}}\left[ {\frac{{\chi {\kern 1pt} {{{\cos }}^{2}}{\kern 1pt} \alpha }}{{1 + \chi {{N}_{a}}}} + \frac{{\chi {\kern 1pt} {{{\sin }}^{2}}{\kern 1pt} \alpha }}{{1 + \chi {{N}_{b}}}}} \right]. \\ \end{gathered} $Путем численного решения уравнения ${{dW} \mathord{\left/ {\vphantom {{dW} {de}}} \right. \kern-0em} {de}} = 0$ при условии ${{{{d}^{2}}W} \mathord{\left/ {\vphantom {{{{d}^{2}}W} {d{{e}^{2}}}}} \right. \kern-0em} {d{{e}^{2}}}} > 0$ можно получить зависимость эксцентриситета (или соотношения осей капли) от угла ее отклонения от направления поля заданной напряженности. Результаты расчета представлены на рис. 10 в сопоставлении с экспериментальными данными. Рис. 10 подтверждает простые физические соображения о том, что при отклонении от направления поля у вытянутой микрокапли уменьшается соотношение осей. В этом случае компонента намагниченности, перпендикулярная длинной оси, увеличивается, растет величина магнитного давления вдоль этого направления, что приводит к уменьшению соотношения осей. Используя рассчитанную таким образом функцию $p = f(\alpha )$ и условие равенства моментов магнитных сил и сил вязкого трения Tm = Th (формулы 13 и 14), была получена зависимость угла отклонения микрокапли от скорости вращения кюветы, показанная сплошной линией на рис. 11. Из рис. 11 видно, что расчет в целом подтверждает обнаруженную экспериментально нелинейную зависимость угла поворота микрокапли от скорости вращения. Ранее этот факт интерпретировался разрушением микрокапель в магнитной жидкости в процессе увеличения скорости вращения [15]. На рис. 12 показано сопоставление зависимости угла отклонения от напряженности магнитного поля при постоянной скорости вращения. В данном случае расчет хорошо описывает ход экспериментальной зависимости на качественном уровне (рис. 7), хотя точного соответствия экспериментальным данным и не наблюдается. Различие между экспериментом и расчетом может быть объяснено не учтенной в расчетах полидисперсностью эмульсии, а также сложными S-образными деформациями концов вытянутых микрокапель при высоких скоростях вращениях, о которых сообщалось в [12]. Отметим, что близкая по форме нелинейная зависимость угла поворота дифракционной картины от скорости вращения кюветы наблюдалась нами также и для магнитной эмульсии на водной основе [7]. Существенным отличием эффекта в магнитной эмульсии с низким межфазным натяжением являются существенно большие углы отклонения вытянутых микрокапель от направления поля при тех же скоростях вращения кюветы.
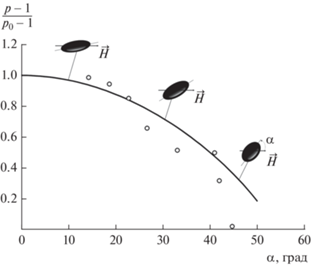
Рис. 10.
Зависимость соотношения осей сфероида от угла отклонения его большой оси от направления поля (точки – эксперимент, кривая – расчет для микрокапли с r0 = 2 мкм и H = 3 кА/м).
ВЫВОДЫ
Деформация капель магнитной эмульсии в магнитном поле создает в эмульсии ориентированную структуру, в которой наблюдаются ярко выраженные эффекты дифракционного рассеяния света. Магнитное поле также изменяет прозрачность эмульсии без изменения спектра пропускания. Величиной и знаком изменения прозрачности можно управлять как направлением приложенного поля, так и длительностью его воздействия. Интерпретация как эффектов ослабления света при различных ориентациях внешнего поля по отношению к лучу света, так и дифракционного рассеяния, построенная на основе приближения аномальной дифракции дает результаты, хорошо согласующиеся с экспериментальными данными, в том числе и с учетом частичной коалесценции микрокапель магнитной эмульсии при длительном воздействии поля. Это позволяет использовать магнитные эмульсии с низким межфазным натяжением в качестве нейтральных фильтров с тонкой регулировкой светопропускания магнитным полем.
Исследование дифракционных картин, возникающих при прохождении света через магнитные эмульсии, позволяет не только качественно оценивать структурное состояние таких систем, но и определять параметры микрокапель и их изменение под действием магнитного и гидродинамического полей. При интерпретации дифракционных эффектов, возникающих во вращающейся магнитной эмульсии, необходимо учитывать особенности вращательной подвижности жидких микрокапель. Это позволяет добиться хорошего согласия с экспериментальными данными без привлечения гипотез о разрушении микрокапель при вращении. Эффект дифракции на вытянутых микрокаплях может быть использован в магнитооптических датчиках для определения ориентации и напряженности магнитного поля.
Работа выполнена при поддержке государственного задания Минобрнауки России на выполнение научно-исследовательских работ (проект № 0795-2020-007).
Список литературы
Romankiw L.T. and Briachift N.Y. U.S. Patent 3981844, 1976.
Диканский Ю.И. Эффекты взаимодействия частиц и структурно-кинетические процессы в магнитных коллоидах: Дис. … д-ра физ.-мат. наук. Ставрополь, 1999. 305 с.
Torres-Diaz I. and Rinaldi C. // Soft Matter. 2014. V. 10. P. 8584.
Dailey J.P., Phillips J.P., Li C., Riffle J.S. // J. Magn. Magn. Mater. 1999. V. 194. P. 140.
Backholm M., Vuckovac M., Schreier J., Latikka M., Hummel M., Linder M. B., Ras R.H.A. // Langmuir. 2017. V. 33. P. 6300.
Mahendran V., Philip J. // Sensors and Actuators. 2013. V. B 185. P. 488.
Ерин К.В., Белых С.С. // Колл. журн. 2020. Т. 82. № 6. С. 689.
Диканский Ю.И., Нечаева О.А., Закинян А.Р. // Колл. журн. 2006. Т. 68. № 2. С. 161.
Диканский Ю.И., Нечаева О.А., Закинян А.Р., Константинова Н.Ю. // Колл. журн. 2007. Т. 69. № 6. С. 737.
Zakinyan A.R., Dikansky Y.I. // J. Magn. Magn. Mater. 2017. V. 431. P. 103.
Ерин К.В., Куникин С.А. // Опт. и спектр. 2008. Т. 104. № 2. С. 319.
Sandre O., Browaeys J., Perzynski R., Bacri J.-C., Cabuil V., and Rosensweig R.E. // Physical Review E. 1999. V. 59. P.1736.
Zakinyan A.A., Belykh S.S., Zakinyan A.R., Yerin K.V. // Journal of Optical Technology. 2021. V. 88. № 3. P. 158.
Закинян А., Диканский Ю. Магнитные и электрические свойства магнитных эмульсий. Саарбрюккен–Москва: LAP Lambert Academic Publishing, 2011. 146 с.
Skibin Yu.N. and Chekanov V.V. // Magnetohydrodynamics. 1979. V. 15. No. 1. P. 15.
Оптическая биомедицинская диагностика. Т. 1 / Перевод под ред. В.В. Тучина. М.: Физматлит, 2006. С. 36.
Khlebtsov N.G., Melnikov A.G., Bogatyrev V.A. // Colloid and Surface A. 1999. V. 148. № 1–2. P. 17.
Jianping Ge, Yongxing Hu, Yadong Yin // Angewandte Chemie Int. Ed. 2007. V. 46. P. 1.
Ерин К.В. // Опт. и спектр. 2016. Т. 120. № 2. С. 333.
Белых С.С., Ерин К.В. // Опт. и спектр. 2021. Т. 129. № 9. С. 1166.
Лопатин В.Н., Приезжев А.В. Апонасенко А.Д. и др. Методы светорассеяния в анализе водных дисперсных биологических сред. М.: Физматлит, 2004. 384 с.
Ван де Хюлст Г. Рассеяние света малыми частицами. М.: ИИЛ, 1961. 536 с.
Yerin C., Belykh S. // IEEE Trans. Magn. 2022. V. 58(2). 4600704.
Belykh S.S., Yerin C.V. // Magnetohydrodynamics. 2018. V. 54. № 1–2. P. 5.
Yerin C.V., Belykh S.S. // AIP Advances. 2022. V. 12 (3). 035329.
Морозов К.И. // ЖЭТФ. 1997. Т. 112, Вып. 4 (10). С. 1340.
Engel A., Lebedev A.V., Morozov K.I. // Zeitschrift für Naturforschung. 2003. V. 58a. P. 703.
Afkhami S., Tyler A., Renardy Y., Renardy M., St Pierre T., Woodward R., Riffle J.S. // J. Fluid Mech. 2010. V. 663. P. 358.
Блум Э.Я., Майоров М.М., Цеберс А.О. Магнитные жидкости. Рига: Зинатне, 1989. 387 с.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал