Коллоидный журнал, 2022, T. 84, № 3, стр. 311-317
Релаксационные процессы в супрамолекулярной структуре поливиниловый спирт–йод–йодид калия
В. А. Ломовской 1, *, Н. А. Абатурова 1, Н. Ю. Ломовская 1, Т. Б. Галушко 1
1 ФГБУН Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский просп. 31, корп. 4, Россия
* E-mail: n5123@mail.ru
Поступила в редакцию 16.03.2022
После доработки 29.03.2022
Принята к публикации 30.03.2022
- EDN: BKIDZR
- DOI: 10.31857/S0023291222030089
Аннотация
Путем сравнительного анализа спектров внутреннего трения исследован диссипативный α-процесс релаксации в пленках поливинилового спирта (ПВС) и в супрамолекулярной композитной структуре, образующейся при формировании упорядоченных областей в системе ПВС–I2–KI. Показано, что структурные изменения в образцах поливинилового спирта, происходящие при введении йода, вызывают увеличение релаксационной микронеоднородности всей системы в области температур α-процесса релаксации.
ВВЕДЕНИЕ
Исследования в области супрамолекулярной химии вызывают значительный интерес и в последнее время интенсивно развиваются [1]. Соединения включения – класс веществ, занимающий промежуточное положение между твердыми растворами внедрения и химическими соединениями. Эти соединения интересны как с практической, так и с теоретической точки зрения.
В частности, известно такое соединение включения, которое формируется в водных растворах поливинилового спирта (ПВС) с йодом в составе комплекса ПВС−I2−KI. Соединения включения в системе ПВС–йод формируются при внедрении молекул одного индивидуального химического вещества в свободные имеющиеся или образующиеся полости. Такие структуры можно называть нанокомпозитами. Рядом авторов был сделан вывод о нековалентном характере взаимодействия входящих в состав структуры компонентов [2–4].
Как показали исследования методом мало- и широкоугольного рассеяния рентгеновских лучей, компьютерного моделирования для кристаллической структуры комплекса ПВС−йод, полийодные цепочки йода формируются внутри каналов, образуемых закручивающимися в спираль макромолекулами ПВС. Скоординированный анализ данных рентгеновской дифракции и нейтронной дифракции, введение структурного беспорядка в ранее предложенные модели регулярной структуры синтетического полимера позволили сделать вывод о способе образовании структуры ПВС−I2−KI.
Наблюдается несколько стадий образования структуры. Сначала образуется неупорядоченная структура упаковки ионов ПВС−йод (форма I), а затем она развивается в форму (II) с более или менее регулярно упакованными слоями ПВC-йод, достигая наконец структуры формы (III) с равномерно расположенными слоями ПВС−йод [5].
Установлено, что процесс формирования кристаллической структуры ПВС−йод происходит по мере обезвоживания студнеобразной системы ПВС−йод. Упорядоченные области образуются при удалении молекул воды, внедренных между полимерными цепями и препятствующих структурообразованию [6–8]. Цвик М.М. нашел, что на одну молекулу I2 приходится 24 мономерных звена ПВС, и это составляет 2 витка спирали [9].
Йод, включенный в макромолекулу полимера, обнаруживает высокий антимикробный эффект. Подобные системы могут представлять интерес как антисептические лекарственные препараты широкого спектра направленного воздействия на живой организм человека и животных [10].
Цель нашего исследования изучить влияние внедрения молекул йода в ПВС и остаточной воды в системе на образование упорядоченных областей в процессе формирования супрамолекулярной нанокомпозитной структуры и на диссипативный процесс, связанный с температурным размягчением сегментов макромолекул.
ОБЪЕКТЫ И МЕТОДЫ ИССЛЕДОВАНИЯ
В работе исследовался поливиниловый спирт марки Mowiol Kurrary Specialities Europe со степенью гидролиза 88% и молекулярной массой 68 × 103 Да. Раствор полимера готовили из предварительно набухшей в дистиллированной воде навески с последующим нагреванием в течение нескольких часов до 90°С при тщательном перемешивании. Пленки для исследования готовили путем полива 8% раствора на стеклянную подложку с последующим высушиванием при комнатной температуре до постоянного веса с конечным содержанием воды ~ 4–5%. Из приготовленных пленок толщиной 0.4 мм вырезали полоски размером 65 × 5 мм и пропитывали их спиртовым раствором йода в присутствии йодида калия в течение 2 часов. При этом получались студнеобразные образцы, которые подвергались последующему досушиванию с термошкафу при 40°С в течение часа. Содержание влаги в них составляло ~ 4–7%. Механические свойства подготовленных таким образом образцов исследовали на горизонтальном крутильном маятнике в режиме свободно затухающих колебаний в диапазоне температур от –150 до +150°С с шагом нагрева в 1°С, как подробно описано в работе [11]. Таким образом были получены спектры внутреннего трения λ = f(T) и температурные зависимости частоты колебательного процесса ν = f(T). Принцип работы прибора изложен в статье [12].
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В представленной работе путем сравнительного анализа спектров внутреннего трения исследован диссипативный α-процесс релаксации в пленках ПВС и в супрамолекулярной структуре, образующейся при формировании упорядоченных областей в системе ПВС−I2−KI. Для каждого образца было проведено по три цикла измерений логарифмического декремента затухания (обозначенного λ) λ = f(T), и температурной зависимости частоты колебательного процесса (обозначенного ν) ν = f(T), возбужденного в твердом материале, в диапазоне температур от –150°С до +150°С. После каждого цикла измерения определялась потеря влаги в исследуемом образце, после чего он снова подвергался нагреванию в приборе. На рис. 1 и 2 (а, б) показаны спектры внутреннего трения и температурно-частотные зависимости для индивидуального ПВС и для композитной супрамолекулярной системы ПВС−I2−KI. Для наглядности на рисунках, представляющих спектры внутреннего трения, выделена только область проявления α-пика релаксации от –20°С (полный спектр в интервале температур от –150 до +150°С представлен в доп. материалах).
Рис. 1.
Спектры внутреннего трения (а) λ = f(T) и температурно-частотные зависимости (б) ν = f(T) образцов ПВС в процессе трех циклов измерения 1,2,3 –последовательно. Точками и пунктиром отмечена полувысота λ.
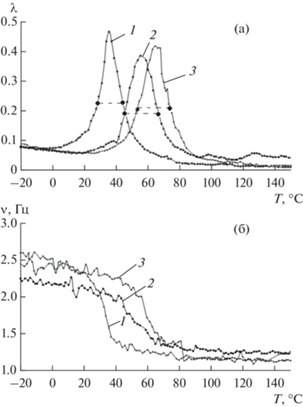
Рис. 2.
Спектры внутреннего трения (а) λ = f(T) и температурно-частотные зависимости (б) ν = f(T) образцов ПВС−I2−KI калия в процессе трех циклов измерения 1,2,3 – последовательно. Точками и пунктиром отмечена полувысота λ. Пересечение пунктирных линий на рисунке (б) обозначает точки νн и νк для процессов α-релаксации.
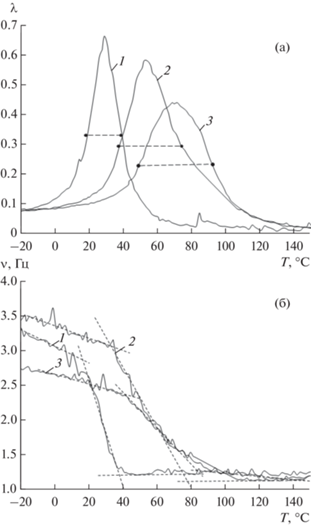
Очевидно, что α-процесс релаксации, проявляемый на спектрах внутреннего трения в виде интенсивного диссипативного процесса, а на температурно-частотных зависимостях в виде дефекта модуля [13, 14], претерпевает существенные изменения при модификации пленок ПВС введением йода в присутствии йодида калия. Эти явления обусловлены изменениями физико-химических свойств материала и отчетливо проявляются в увеличении ширины Δτ непрерывного спектра времен релаксации, как приведено, после математических вычислений в таблицах (табл. 1, 2).
Таблица 1.
Экспериментально полученные и теоретически рассчитанные физико-химические и физико-механические характеристики для образцов, приготовленных из ПВС
| Цикл нагрева |
Содержание воды в образце вес. % | Тαmax, °C | λmax | τα max, c | ΔT при λ = λmax/2 | νн | νк | ΔG | Uα, кДж/моль | Δτ, с |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 4.5 | 36 | 0.46 | 0.101 | 15 | 2.3 | 1.2 | 0.73 | 60.88 | 0.15 |
| 2 | 4 | 55 | 0.44 | 0.102 | 21 | 2.4 | 1.25 | 0.73 | 64.81 | 0.20 |
| 3 | 0.5 | 65 | 0.42 | 0.105 | 21 | 2.3 | 1.2 | 0.73 | 66.69 | 0.19 |
Таблица 2.
Физико-химические и физико-механические характеристики для образцов ПВС, пропитанных спиртовым раствором йода, в составе комплекса I2−KI
| Цикл нагрева |
Содержание воды в образце вес. % | Тαmax, °C | λmax | τα max, c | ΔT при λ = λmax/2 | νн | νк | ΔG | Uα, кДж/моль | Δτ, с |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 7 | 29 | 0.66 | 0.07 | 19 | 3.0 | 1.2 | 0.84 | 58.6 | 0.12 |
| 2 | 4 | 53 | 0.59 | 0.07 | 38 | 3.16 | 1.2 | 0.86 | 63.2 | 0.23 |
| 3 | 0.5 | 70 | 0.44 | 0.09 | 44 | 2.6 | 1.2 | 0.79 | 67.2 | 0.43 |
Первоначально содержание остаточной воды в исследуемых пленках до первого цикла измерения составляло приблизительно 4–7%.
При повторных измерениях спектров внутреннего трения в ходе нагревания до 120°С содержание воды в образцах уменьшалось до 4 и 0.5%, температура Тαmax смещалась в сторону повышения (табл. 1, 2). Кроме того, ширина α-пика значительно увеличивалась в образцах ПВС−I2−KI калия при каждом последующем цикле (рис. 2а). Подобное расширение пика диссипативных потерь свидетельствует о расширении непрерывного спектра времени релаксации, увеличении Δτ при определении этой величины на уровне λmax/2 и, соответственно релаксационной микронеоднородности в структурной подвижности элементов данного процесса при их стремлении к возврату в положение механического и термодинамического равновесия. Такая неоднородность, в свою очередь, обусловлена структурированием макромолекул ПВС в присутствии введенного в систему йода при удалении влаги из пленок ПВС в процессе повторных нагреваний в ходе эксперимента до 120°С. По данным рентгеновской спектроскопии и компьютерного моделирования известно, что ПВС образует кристаллические комплексы с ионами йода, в которых линейные ионы I3 превращаются в столбчатые массивы и связываются с соседними цепями ПВС плоско-зигзагообразной конформации посредством переноса заряда между ОН группами и I3 ионами. Эти процессы происходят именно при удалении воды, молекулы которой внедряясь между полимерными цепями препятствуют их упорядочиванию. В пленке, состоящей из чистого ПВС, мы не наблюдаем эффекта существенного расширения области проявления α-пика релаксации (рис. 1а, табл. 1).
Наиболее широкий спектр времен релаксации характерен для системы ПВС−I2−KI в третьем цикле измерения (табл. 2.).
Математическая постановка
Расчет физико-химических характеристик наблюдаемого процесса в рамках феноменологического модельного представления о возникновении локальных диссипативных явлений на спектрах внутреннего трения проведен исходя из модели стандартного линейного тела [15]. Данная модель позволяет описать пик потерь, налагаемый на фон спектра λ = f(T) с использованием дифференциального уравнения [16] в виде:
(1)
$\frac{{d\sigma }}{{dt}} + \frac{{{{G}_{1}}}}{\eta }\sigma = \left[ {\left( {{{G}_{1}} + {{G}_{2}}} \right)i\omega + \frac{{{{G}_{1}}{{G}_{2}}}}{\eta }} \right]{{\gamma }_{0}}{{e}^{{i\omega t}}},$Решение данного дифференциального уравнения для затухающего колебательного процесса приводит к соотношению вида:
(2)
${{\lambda }_{i}} = 2{{\lambda }_{{\max }}}\frac{{\omega \tau }}{{1 + {{{\left( {\omega \tau } \right)}}^{2}}}},$Из соотношения (2) следует, что текущее по температуре λi достигает своего максимума в пике потерь при таком значении температуры, при котором выполняется следующее условие:
где время релаксации есть функция температуры, т.е. U – энергия активации диссипативного процесса; τ0 ~ 5 × 10–12 с – теоретическое значение предэкспоненциального коэффициента, характеризующего колебательный процесс релаксирующей частицы на дне потенциальной ямы.Учитывая связь частоты ω с частотой затухающего колебательного процесса ν в виде ω = 2πν, соотношение (3) позволяет определить время релаксации τmax в пике локальных диссипативных потерь по соотношению вида:
(5)
$2\pi \nu {{\tau }_{{\max }}} = 1 \to {{\tau }_{{\max }}} = \frac{1}{{2\pi {{\nu }_{{\left( {T\,\, = \,\,{{T}_{{\max }}}} \right)}}}}}.$Рассчитанные по соотношению (5) дискретные значения времени α-релаксации для изучаемых систем (табл. 1, 2) показывают некоторое увеличение τα max c проведением трех циклов измерений.
Энергию активации данного процесса возможно определить из Аррениусовской зависимости времени релаксации τ от температуры (соотношение (4)) с учетом (5) в виде
Величина энергии активации Uα увеличивается для системы ПВС−йод в зависимости от циклов термообработки коррелируя по изменению с изменениями величины Тα max и τmax (табл. 2) и изменением массы остаточной воды в структуре исследуемой системы.
Таким образом, теоретический анализ пиков локальных диссипативных потерь, обнаруженных на спектрах внутреннего трения, позволяет рассмотреть влияние введения в ПВС молекул йода и рассчитать физико-химические характеристики полученных супрамолекулярных композитных структур.
Кроме того, может быть качественно дана оценка степени релаксационной микронеоднородности α-процесса релаксации в системе ПВС−I2−KI, как в зависимости от наличия в структуре молекул йода, так и от трехкратного повторения эксперимента.
Физико-механические характеристики системы ПВC−I2−KI определяются из экспериментальных температурных зависимостей частоты свободно затухающего колебательного процесса, возбужденного в исследуемой системе (рис. 2б).
Именно эти физико-механические характеристики позволяют выявить упругую и неупругую реакцию исследуемой системы на внешнее воздействие, выводящее все структурно-кинетические элементы системы из состояния механического и термодинамического равновесия.
Кроме того, трехкратное нагревание исследуемой системы в процессе эксперимента, позволяет определять изменения температурных интервалов и соотношения упругого и вязкоупругого состояния системы.
В динамическом режиме внешнего воздействия связь между частотой колебательного процесса, возбуждаемого в исследуемой системе, геометрическими характеристиками исследуемого образца и модулем сдвига материала, из которого состоит исследуемый образец, определяется в виде следующего соотношения [12]:
(7)
$\nu = \frac{1}{4}{{\left[ {G\frac{{{{I}_{a}}}}{{l\left( {{{I}_{s}} + 2I} \right)}}} \right]}^{{1/2}}},$В первом приближении температурными изменениями геометрических характеристик исследуемого образца можно пренебречь ввиду относительной малости их изменений относительно первоначальных значений.
В этом случае соотношение (7) может быть представлено в виде:
где ${{k}_{1}} = \frac{{{{I}_{a}}}}{{16l\left( {{{I}_{s}} + 2I} \right)}}$ – постоянный коэффициент.Температурная зависимость модуля сдвига G(T) должна быть линейной (для образца в кристаллическом состоянии) и повышение температуры на 100 градусов соответствует снижению модуля G на 2–4% [17].
В этом случае и частота ν является функцией температуры, т.е. ν = f(T) = ν(T) и будет изменяться пропорционально температурному изменению модуля G(T), т.е.
где k1 и k2 – постоянные коэффициенты.В безразмерной относительной форме соотношение (9) может быть представлено в видe:
(10)
$\frac{{{{k}_{2}}{{G}_{i}}\left( {{{T}_{i}}} \right)}}{{{{k}_{2}}{{G}_{0}}\left( {{{T}_{0}}} \right)}} = \frac{{{{k}_{1}}\nu _{i}^{2}\left( {{{T}_{i}}} \right)}}{{{{k}_{1}}\nu _{0}^{2}\left( {{{T}_{0}}} \right)}} \Rightarrow \Delta G\left( T \right) \approx \Delta {{\nu }^{2}}\left( T \right),$Таким образом, температурное изменение частоты ν колебательного процесса, возбужденного в исследуемом образце, позволяет определить и температурное изменение модуля сдвига G материала, из которого изготовлен исследуемый образец.
Однако, экспериментальные данные (рис. 1, 2) показывают, что в определенных температурных интервалах, где на спектре λ = f(T) (рис. 1, 2а) наблюдаются пики диссипативных потерь, частота ν (рис. 1, 2б) на температурной зависимости ν = = f(T), а следовательно и значения модуля G отклоняются от пропорциональной температурной зависимости. Это отклонение или дефект модуля определяется в виде:
(11)
$\Delta G\left( T \right) = \frac{{{{G}_{0}}\left( {{{T}_{0}}} \right) - {{G}_{i}}\left( {{{T}_{i}}} \right)}}{{{{G}_{0}}\left( {{{T}_{0}}} \right)}} = \frac{{\nu _{0}^{2}\left( {{{T}_{0}}} \right) - \nu _{i}^{2}\left( {{{T}_{i}}} \right)}}{{\nu _{0}^{2}\left( {{{T}_{0}}} \right)}}.$Рассчитанные величины ΔG(T) для системы ПВС−I2−KI (табл. 1, 2) показывают повышенные значения по сравнению с чистым ПВС при одновременном расширении температурного интервала ΔТ на половине высоты пика потерь λ = λmax/2 (рис. 3).
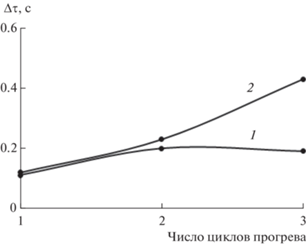
Рис. 3.
Температурная область проявления α-пика релаксации ΔТ на высоте λ/2 в процессе трех циклов измерения для образцов ПВС (кривая 1) и для композитной структуры ПВС−I2−KI (кривая 2).
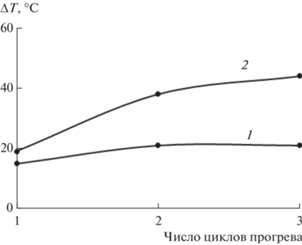
Повышение значений ΔТ также качественно указывает на увеличение релаксационной микронеоднородности диссипативного α-процесса при увеличении циклов термообработки.
Для количественного описания увеличения релаксационной микронеоднородности процесса необходимо рассчитать изменение непрерывного спектра времен релаксации Н(τ) исходя из полученных физико-химических и физико-механических характеристик процесса в данной системе. Расчет Н(τ) возможно провести несколькими методами:
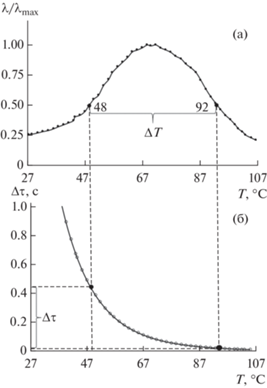
1 – расчет температурной зависимости времени релаксации по арренисовскому соотношению (4) и определение величины абсолютного времени релаксации Δτ, соответствующего интервалу температур ΔТ для пика потерь на спектре λ = f(T);
2 – определение вида функции, описывающей температурное изменение дефекта модуля и используемой в качестве ядра релаксации в уравнении наследственной вязкоупругости Больцмана−Вольтерра;
3 – теоретический расчет приведенных зависимостей для различных значений ширины непрерывного спектра времени релаксации Н(τ) и сопоставление этих кривых с экспериментальными данными.
Во втором и третьем случае требуется определение аналитического вида функции релаксации, удовлетворяющей требованиям ее применения в динамическом режиме в широком частотном диапазоне внешних воздействий, выводящих структурные элементы исследуемой системы из равновесного состояния.
В данной работе рассмотрен первый случай. Рассчитано Δτ = f(ΔT) для системы чистый ПВС и ПВС−I2−KI c различным числом циклов термообработки (табл. 1, 2). На рис. 4 показан пример определения релаксационной микронеоднородности α‑процесса релаксации по приведенным спектрам внутреннего трения (а) и температурной зависимости времени релаксации (б) для третьего цикла нагрева образца ПВС−I2−KI на полувысоте α-пика λ/2. Результаты проведенных расчетов можно видеть в табл. 1, 2 и на рис. 5. Обнаружено значительное расширение области времен релаксации Δτ, для системы, содержащей йод, тогда как для пленки из чистого ПВС мы не наблюдаем увеличение Δτ.
ЗАКЛЮЧЕНИЕ
Полученные экспериментальные результаты и математические расчеты количественно показывают расширение Δτ спектра времени релаксации с каждым циклом термообработки, т.е. циклическое температурное воздействие на систему ПВС−I2−KI приводит к структурным изменениям в этой системе. Структурные изменения вызывают увеличение релаксационной микронеоднородности всей системы в области температур α-процесса релаксации.
Работа выполнена в рамках Государственного задания.
Список литературы
Лен Ж.-М. // Супрамолекулярная химия. Концепции и перспективы. Новосибирск: Наука. 1998.
Гойхман А.Ш., Соломко В.П. // Высокомолекулярные соединения включения. Киев.: Наукова думка, 1982. С. 192.
Година Д.А., Файерман Г.П. // Журн. общ. химии. 1967. Т. 37. № 4. С. 945.
Божко Н.Н., Столяров В.П., Волков В.В., Назаров В.Г. // Перспективные материалы. 2013. № 3. С. 35.
Tashiro Kohji, Kusaka Katsuhiro, Yamamoto Hiroko, et al. // Macromolecules. 2020. V. 53. № 15. P. 6656.
Tashiro Kohji, Kitai Hideyuki, Munirah Siti Saharin, Shimazu Akira, and Takahiko Itou // Macromolecules. 2015. V. 48. P. 2138.
Zhang Rui, Zhang Qianlei, Ji Youxin et al. // Soft Matter. 2018. V. 1. № 13. P. 2546.
Божко Н.Н., Столяров В.П., Баблюк Е.Б., Назаров В.Г., Волков В.В., Амаронтов С.В., Дембо К.А. // Высокомолек. соединения А. 2011. Т. 53. № 9. С. 1537.
Zwick M.M. // J. Appl. Polym. Sci. A-1. 1966. V. 9. № 7. P. 2393.
Dorota Kida, Olimpia Gładysz, Małgorzata Szulc, Jacek Zborowski, Adam Junka, Maciej Janeczek, Anna Lipi’nska, Aleksandra Skalec, and Bo˙zena Karolewicz // Polymers. 2020. V. 12. P. 1271.
Lomovskoy V.A., Abaturova N.A., Lomovskaya N.Y., Khlebnikova O.A., Galushko T.B. // Polymer Science Series A. 2018. T. 60. № 3. C. 284.
Lomovskoy V.A., Abaturova N.A., Lomovskaya N.Yu., Galushko T.B. // Mechanics of Composite Materials. 2020. T. 56. № 1. C. 27.
Ломовской В.А. // Научное приборостроение. 2019. Т.29. № 1. С. 33.
Lomovskoy V.A., Nekrasova N.V., Lomovskaya N.Yu, Khlebnikova O.A., Abaturova N.A., Galushko T.B., Gorbunov M.A. // Mechanics of Composite Materials. 2020. V. 56. № 5. P. 685.
Механизмы внутреннего трения в твердых телах // Всесоюзное совещание АН СССР Отд. Физико-химии и технологии неорганических материалов. Под ред. Тавадзе Ф.Н., Постников В.С., Гордиенко Л.К. . М.: Наука, 1976. С. 256
Гольдберг И.И. // Механическое поведение полимерных материалов (математическое описание) М.: Химия. 1970. С. 192.
Физическая энциклопедия М.: Научное издательство “Большая Российская энциклопедия” 1992. Т. 3. С. 176–177.
Дополнительные материалы
- скачать ESM.docx
- Спектры внутреннего трения
(а) λ=f(T) и температурно-частотные зависимости
(б) ν=f(T) образцов ПВС в процессе трех циклов измерения 1,2,3- последовательно
Инструменты
Коллоидный журнал