1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 84, № 3, 2022

Коллоидный журнал, 2022, T. 84, № 3, стр. 338-349

Слабая адгезия между контактирующими шероховатыми поверхностями применительно к микро/нанотехнологиям

В. Б. Световой 1, *, И. А. Солдатенков 2

1 Институт физической химии и электрохимии им. А.Н. Фрумкина, РАН
119071 Москва, Ленинский проспект, д. 31-4, Россия

2 Институт проблем механики им. А.Ю. Ишлинского, РАН
119526 Москва, проспект Вернадского, д. 101-1, Россия

* E-mail: svetovoy@yandex.ru

Поступила в редакцию 17.03.2022
После доработки 13.04.2022
Принята к публикации 13.04.2022

Полный текст (PDF)

Аннотация

Залипание отдельных элементов микроэлектромеханических систем является серьезной проблемой, которая может проявляться на этапе изготовления или эксплуатации таких устройств. Для контроля этого процесса исследуется равновесное расстояние и энергия адгезии между поверхностями с нормальным распределением шероховатости. Обсуждаются характеристики исследуемых материалов, необходимые для расчетов, такие, как диэлектрические функции, шероховатость, пластические свойства материалов, а также кратко изложено базовое уравнение баланса сил. Проведены детальные расчеты для системы Si–Au в воздухе. Показано, что пластические свойства золота очень слабо влияют на энергию адгезии как функцию расстояния, но играют заметную роль для установления равновесного расстояния между поверхностями. Дальнодействующие дисперсионные силы доминируют в энергии адгезии для шероховатости со среднеквадратичным отклонением более 1 нм, поэтому энергия может быть рассчитана в рамках теории Лифшица.

Ключевые слова: дисперсионные силы, шероховатость, энергия адгезии, контактная задача, равновесное расстояние

1. ВВЕДЕНИЕ

В современном мире заметную роль играют микроэлектромеханические системы (МЭМС), которые встречаются во многих бытовых приборах (например, смартфонах), химических и биологических лабораториях. Развитие микротехнологий приводит к тому, что расстояния между отдельными элементами МЭМС становятся настолько малыми, что при изготовлении или функционировании этих систем заметную роль начинают играть дисперсионные силы (ДС) (силы ван-дер-Ваальса и Казимира). Спонтанное залипание [1, 2] отдельных элементов МЭМС выводит их из строя и является серьезным препятствием для более широкого распространения этих систем. Особенностью ДС является то, что их невозможно “выключить” как, например, капиллярные или электростатические силы, поскольку природа ДС связана с фундаментальными свойствами электромагнитного поля (квантовыми флуктуациями) [3]. По этой причине контроль ДС и глубокое понимание их природы приобретает особое значение.

Поскольку ДС играют заметную роль на расстояниях, не превышающих 100 нм, то дополнительное осложнение в анализ взаимодействия твердых тел вносит шероховатость поверхностей, которая может быть сравнима с такими расстояниями. Действительно, подложки, которые используются в микротехнологии, обычно очень гладкие (среднеквадратичное отклонение шероховатости 0.2–0.3 нм), но функциональные материалы, наносимые на подложку в виде покрытий, могут иметь значительную шероховатость, которая определяется процессом их нанесения. Чаще всего пики шероховатости описываются нормальным (гауссовым) распределением [4, 5]. Однако имеется немало свидетельств того, что шероховатость покрытий описывается негауссовым распределением и характеризуется значительным числом пиков, существенно превышающих среднеквадратичное отклонение [6–8].

При контактном взаимодействии шероховатых тел, ДС и другие поверхностные силы обуславливают существование энергии адгезии между поверхностями тел. Расчету этой энергии и равновесного расстояния между контактирующими шероховатыми телами посвящено много работ. Впервые концепция энергии адгезии использовалась в известных моделях Джонсона, Кендалла, Робертса [9] и Дерягина, Муллера, Топорова [10] для описания контактного взаимодействия гладких тел. Строгая формулировка контактной проблемы в присутствии межмолекулярных сил предполагает существование некоторого зазора между контактирующими телами, который обеспечивает равновесие между деформационными и межмолекулярными силами на контакте (самосогласованный по Дерягину подход [11]). Этот подход развивался в ряде более поздних работ [12–14]. В классической модели шероховатого контакта Гринвуда и Вильямсона [15] поверхность описывается ансамблем упругих пиков с одинаковой кривизной вершин и случайной высотой. Фуллер и Тэйбор [16] учли влияние адгезии на контакт и показали, что адгезия становится важным фактором при малых нагрузках. Позже модель одиночных пиков была обобщена на случай поверхностей с фрактальной топографией [17, 18] и, в частности, было предложено описание контакта для самоподобной шероховатости [5, 19]. Было установлено, что даже для тел, находящихся в состоянии, близком к контакту, шероховатость дает заметный вклад в силу взаимодействия между телами [6, 8].

Следует отметить, что предложенные ранее теории обычно применимы для энергий адгезии ~ ~ 0.1 Дж/м2, подразумевают нормальное распределение шероховатости и упругие деформации поверхности. Однако для материалов, фактически используемых в МЭМС, подобные условия нарушаются. Действительно, типичные значения энергии адгезии оказываются на три порядка меньше вышеуказанной ($ \lesssim $100 мкДж/м2) [20, 21], при том, что адгезия по-прежнему играет ключевую роль при контакте. Столь низкие значения энергии адгезии связаны с тем, что при изготовлении МЭМС отсутствует внешняя нагрузка, что приводит к заметно большему расстоянию между поверхностями при контакте. Кроме того, важную роль играет шероховатость и тщательный контроль капиллярных сил. Как указывалось выше, используемые в МЭМС покрытия часто имеют негауссовую шероховатость со значительным числом высоких пиков [6, 7, 22], которые необратимо деформируются при контакте (пластическое течение или хрупкое разрушение).

Модель адгезионного контакта, способная адекватно описать контакт шероховатых поверхностей, созданных с помощью микротехнологий, была предложена в работах [23, 24]. В настоящей работе кратко формулируются базовые принципы этой модели, и основное внимание уделяется расчету равновесного расстояния между контактирующими поверхностями c нормальной функцией распределения шероховатости по высотам при отсутствии внешней нагрузки. Кроме того, проводится анализ поверхностного и дальнодействующего вкладов в энергию адгезии для различных среднеквадратичных отклонений шероховатости. Показано, что малый поверхностный вклад в энергию адгезии позволяет надежно вычислять эту энергию, используя для ДС хорошо разработанную теорию Лифшица [3, 25, 26].

Работа организована следующим образом. В Разделе 2 формулируется проблема и обсуждаются ее основные составляющие, такие, как действующие силы, шероховатость поверхностей, пластические деформации пиков шероховатости. Кратко описано основное уравнение баланса сил, позволяющее решить проблему. В Разделе 3 приводится решение задачи контакта гладкой поверхности кремния и шероховатой поверхности напыленного слоя золота. Вычислены равновесные расстояния между телами при контакте и энергии адгезии для разных среднеквадратичных шероховатостей.

2. ФОРМУЛИРОВКА ПРОБЛЕМЫ И ПОДХОДЫ К ЕЕ РЕШЕНИЮ

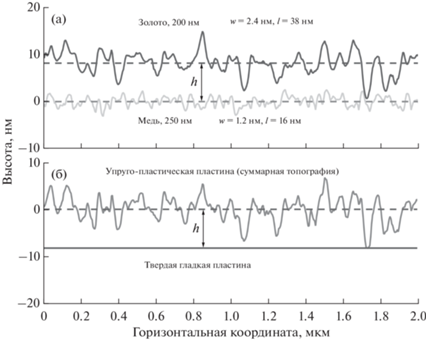
Рассмотрим две шероховатые параллельные пластины, вступающие в механический контакт. Пластины могут быть сделаны из разных или одинаковых материалов. Эту проблему можно упростить, если учесть, что пики шероховатости на разных пластинах не совпадают, поэтому задачу эффективно можно свести к контакту гладкой твердой пластины и упругой пластины с эффективной шероховатостью равной сумме топографий каждой пластины [27]. Схематически исходная и эффективная конфигурации пластин показаны на рис. 1а и 1б соответственно. Шероховатая пластина имеет эффективный модуль упругости, а ее пластические свойства определяются самым мягким материалом. Номинальная поверхность пластины определена как средняя плоскость, а расстояние между пластинами $h$ определено как расстояние между средними плоскостями.

Рис. 1.

(а) Исходная конфигурация: шероховатое покрытие из золота (толщина 200 нм, темная кривая) приближается к шероховатму покрытию из меди (толщина 250 нм, светлая кривая). Штриховыми линиями показаны положения средних плоскостей для каждого покрытия. Указаны среднеквадратичные отклонения шероховатостей и корреляционные длины (по данным [7 и 22]). (б) Эффективная конфигурация: упруго-пластическая пластина с эффективной шероховатостью приближается к твердой и гладкой пластине.

2.1. Сила между гладкими поверхностями

Шероховатость приводит к тому, что локальный зазор между пластинами заметно варьируется. Когда локальное расстояние стремится к нулю, силы притяжения, обусловленные дисперсионным взаимодействием, должны смениться отталкиванием, связанным с перекрытием электронных облаков. Условием равновесия тел при контакте является равенство притягивающих и отталкивающих сил. Для элементов МЭМС характерное равновесное расстояние составляет $h\sim 10~\,\,{\text{нм}}$, поэтому слабое дисперсионное взаимодействие, действующее на большой площади, уравновешивает сильное отталкивание, действующее в местах локального контакта с малой площадью.

Несколько упрощая реальную ситуацию, представим силу между параллельными гладкими пластинами, приходящуюся на единицу площади, как обобщение закона взаимодействия Леннарда-Джонса на объемные тела:

(1)
$P\left( h \right) = {{P}_{{\text{L}}}}\left( h \right)\left[ {1 - {{{\left( {\frac{{{{h}_{c}}}}{h}} \right)}}^{6}}} \right]~,$
где ${{P}_{{\text{L}}}}\left( h \right)$ – ДС, вычисленная по теории Лифшица, ${{h}_{c}}$ – равновесное расстояние между гладкими поверхностями без приложения внешних сил. Строго говоря, уравнение (1) справедливо, пока расстояние $h$ сравнимо с ${{h}_{c}}$, а ${{P}_{{\text{L}}}}\left( h \right)$ сводится к силе ван-дер-Ваальса ${{P}_{{\text{L}}}}\left( h \right) = - {{A}_{{\text{H}}}}{\text{/}}6\pi {{h}^{3}}$, где ${{A}_{{\text{H}}}}$ – константа Гамакера. Однако, поскольку отталкивающая компонента в (1) бысто убывает с увеличением $h$, соотношение (1) можно использовать для произвольных расстояний. Упрощение состоит в том, что на расстояниях порядка ${{h}_{c}}$ мы свели поверхностные силы лишь к дисперсионным и отталкивающим. Реальная ситуация может оказаться более сложной, особенно для полимерных материалов, но (1) можно применять для большинства микротехнологических материалов в атмосфере. Кроме того, как будет показано выше, для шероховатых поверхностей вклад малых расстояний в полную энергию адгезии достаточно мал. Следует отметить, что при нормальных атмосферных условиях на поверхности тел может адсорбироваться тонкий слой воды, который способен сильно изменить энергию адгезии. В МЭМС устройствах такие эффекты стараются исключать, чему способствует малая площадь реального контакта между телами. Низкие энергии адгезии, наблюдаемые, например, в [20, 21], свидетельствуют о незначительной роли капиллярных сил пока тела разделены расстояниями порядка 10 нм.

Ввиду неаддитивности ДС [6, 26], формулу (1), строго говоря, нельзя использовать для вычисления силы между шероховатыми поверхностями. Однако в нашем случае можно воспользоваться приближением Дерягина [28], предполагающим вычисление силы между локально плоскими участками. Справедливость этого приближения основана на том, что длина корреляции шероховатости $l$ (половина характерного расстояния между пиками на рис. 1а) заметно больше, чем равновесное значение $h$, поэтому профиль шероховатой поверхности можно считать плавным.

2.2. Шероховатость напыленных слоев в МЭМС

Для вычисления силы с помощью формулы (1) необходимо задать шероховатость поверхности. Наиболее детальная информация о шероховатости может быть получена с помощью атомно-силового микроскопа (АСМ). Изображения (сканы) поверхности, полученные на АСМ, позволяют представить реальную шероховатость как набор колонн с высотой ${{z}_{{ij}}}$ и поперечным сечением, равным квадрату размера пикселя, где индексы $i$ и $j$ задают положение пикселя на плоскости. Вершина каждой колонны считается плоской. При этом высоты ${{z}_{{ij}}}$ можно отсчитывать от средней плоскости. Каждый пиксель представляет собой локально плоскую поверхность, для которой применима формула (1). В результате силу между гладкой и шероховатой пластинами можно вычислить как сумму по всем пикселям.

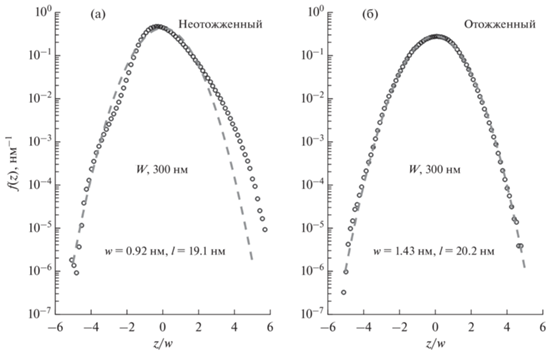
Может оказаться удобным представлять шероховатую поверхность как функцию распределения пикселей по высотам $f\left( z \right)$, которая задает вероятность обнаружить пиксель с высотой $z$ в интервале $dz$. Как пример, на рис. 2а и 2б показаны функции распределения для пленок из вольфрама, напыленного на кремниевую подложку магнетронным способом. Исходные АСМ сканы были получены в [7] по площади 20 × 20 мкм2 с разрешением 4096 пикселей на линию. На левом рисунке функция распределения показана для пленки, напыленной на подложку при температуре $T = 25~^\circ {\text{С}}$, а на правом – для образца, отожженного после напыления в течение 30 мин при температуре $T = 600^\circ {\text{С}}$. Для сравнения показаны также нормальные распределения

(2)
${{f}_{n}}\left( z \right) = \frac{1}{{w\sqrt {2\pi } }}{\text{exp}}\left( { - {{z}^{2}}{\text{/}}2{{w}^{2}}} \right),$
отвечающие такому же значению $w$ среднеквадратичного отклонения шероховатости. Как можно видеть из рисунка, для пленки, напыленной на холодную подложку, количество высоких пиков гораздо больше, чем предсказывается нормальным распределением. В случае же отожженного образца, распределение пиков по высотам хорошо согласуется с нормальным. Аналогичная ситуация наблюдается для пленок из Au и SiO2, а для пленок из Pt и Cu наблюдается даже большее число высоких пиков. Поскольку контакт поверхностей осуществляется по высоким пикам, это обстоятельство может существенно влиять на оценку адгезии между пластинами.

Рис. 2.

Функции распределения пикселей по высотам (кружки), полученные из АСМ сканов вольфрамовых покрытий [7]. Штриховые кривые показывают нормальные распределения с таким же среднеквадратичным отклонением шероховатости $w$. (а) Пленка, напыленная на Si подложку при комнатной температуре. (б) Такая же пленка, но отожженная после напыления при температуре $T = 600~^\circ {\text{С}}$ в течение 30 минут.

2.3. Деформации высоких пиков

Если две поверхности вступают в контакт без внешней нагрузки, т.е. под действием притягивающих ДС, то высокие пики могут деформироваться пластически, причем такие деформации значительно превышают упругие. Действительно, предположим, что на площади ${{L}^{2}}$ имеется один самый высокий пик с поперечной площадью ${{l}^{2}}$ и высотой $h\sim 10\,\,~{\text{нм}}$. На таких расстояниях ДС вида (1) имеет порядок $P\left( h \right) = {{10}^{4}}{\kern 1pt} - {\kern 1pt} {{10}^{5}}\,\,~{\text{Па}}$. Давление на одиночный пик будет составлять $P\left( h \right){{\left( {L{\text{/}}l} \right)}^{2}}\sim 10{\kern 1pt} - {\kern 1pt} 100{\text{ }}~{\text{ГПа}}$, если для оценки выбрать $L = 20~\,\,{\text{мкм}}$ и характерную корреляционную длину $l = 20\,\,~{\text{нм}}$. При столь высоких давлениях практически все материалы будут подвержены пластическим или хрупким деформациям. Ниже мы рассматриваем лишь пластические деформации, которые становятся существенными, когда давление превышает предел текучести для данного материала ${{P}_{f}}$. Высокие пики будут деформироваться пластически до тех пор, пока полная площадь контакта (по многим пикам) не вырастет настолько, что давление станет равным ${{P}_{f}}$.

Следует отметить, что величина упругой деформации для неполимерных материалов мала по сравнению с пластическими деформациями. Действительно, упругую деформацию пика высоты $h$ можно оценить как $\delta h = ({{P}_{f}}{\text{/}}E)h$, где $E$ – модуль Юнга. Для неполимерных материалов, используемых в МЭМС, $E\sim 100~\,\,{\text{ГПа}}$, поэтому $\delta h{\text{/}}h = {{10}^{{ - 3}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 2}}}$, что в абсолютных величинах составляет $\delta h = 0.01{\kern 1pt} - {\kern 1pt} 0.1{\text{\;нм}}$. В силу малости упругих деформаций мы будем ими пренебрегать, считая основные деформации пластическими.

Как указывалось выше, шероховатость представляется набором колонн с поперечным сечением равным квадрату размера пикселя АСМ. Это справедливо до тех, пока колонны не начинают деформироваться. Каждый пик состоит из нескольких колонн и деформацию пика, вообще говоря, нельзя свести к деформации составляющих его колонн. В работе [29] было показано, что пики шероховатости покрытия из напыленного золота наилучшим образом описываются половиной сфероида. Вопрос о пластических деформациях сфероида анализировался численно в [24], где было показано, что представление пиков в виде набора колонн адекватно описывает реальную ситуацию, если в контакте принимает участие несколько и более пиков. Это условие нарушается только для очень маленьких номинальных площадей ${{L}^{2}}$ (менее 1 мкм2). Отметим, что похожая модель шероховатого контакта рассматривалась в работе [30], где, однако, не учитывались пластические деформации. Для мягких материалов такая модель является адекватной, но для материалов, используемых в МЭМС, она может приводить к заметно заниженным значениям энергии адгезии. В отличие от нашей работы, в [30] силы притяжения уравновешивались распределенными в объеме упругими силами отталкивания. Эти упругие силы генерируются поверхностным отталкиванием, связанным с перекрытием электронных облаков (параметр ${{h}_{c}}$ в (1)), поэтому такие подходы эквивалентны (см., например [14]).

2.4. Уравнение баланса сил

В этом разделе представлен краткий вывод уравнения баланса сил между контактирующими пластинами, одна из которых принимается гладкой, а другая – шероховатой [24]. Пусть ${{h}_{0}}$ представляет собой расстояние (равновесное) между пластинами, находящимися в состоянии статического равновесия под действием притягивающих и отталкивающих сил вида (1) (схематическое представление контакта показано на рис. 3). В местах прямого контакта пика локальное расстояние достигает некоторого минимального значения ${{h}_{{0с}}}$, которое должно быть меньше, чем ${{h}_{с}}$, поскольку ДС здесь обеспечивают положительное контактное давление. В рассматриваемом случае пластического деформирования пиков это давление должно совпадать с пределом текучести, поэтому величина ${{h}_{{0с}}}$ определяется из уравнения

(3)
$P\left( {{{h}_{{0c}}}} \right) = {{P}_{f}},$
левая часть которого вычисляется по формуле (1).

Рис. 3.

Схематическое представление контакта гладкой (1) и шероховатой (2) пластин в модели колонн. Указаны расстояния, с которыми оперирует модель. Часть колонн, показанных штриховыми линиями, деформируются пластически (помечены знаком “+”). Колонны, помеченные знаком “—”, не вступают в контакт. Средняя плоскость шероховатой пластины показана пунктирной горизонтальной линией.

Относительную площадь пиков, которые находятся в прямом контакте с гладкой пластиной, можно представить в виде:

(4)
$R\left( {{{h}_{0}}} \right) = \mathop \smallint \limits_{{{h}_{{0p}}}}^\infty dzf\left( z \right),\,\,\,\,{{h}_{{0p}}} = {{h}_{0}} - {{h}_{{0c}}}.$

Отметим, что эта величина совпадает с долей площади, занимаемой пикселями АСМ изображения с высотой больше ${{h}_{{0p}}}$. Уравнение баланса сил можно тогда записать в следующем виде

(5)
$\mathop \smallint \limits_{ - \infty }^{{{h}_{{0p}}}} dzf\left( z \right)P\left( {{{h}_{0}} - z} \right) = - {{P}_{f}}R\left( {{{h}_{0}}} \right).$

Интеграл в левой части равенства (5) представляет собой силу притяжения, просуммированную по всем пикселям с локальным расстоянием ${{h}_{0}} - z$, а выражение в правой части (5) – отталкивающую силу (с обратным знаком), совпадающую с произведением контактного давления ${{P}_{f}}$ на соответствующую долю площади контакта $R\left( {{{h}_{0}}} \right)$. Отметим, что использование бесконечных пределов в (4) и (5) оправдывается быстрым затуханием функции $f\left( z \right)$ на бесконечности.

Рассмотрим пластины, расположенные на расстоянии $h$, и определим работу

(6)
$W\left( h \right) = \mathop \smallint \limits_h^\infty dxP\left( x \right),$
которую нужно совершить, чтобы развести эти пластины на бесконечность.

Тогда энергию адгезии между пластинами можно представить как [24]

(7)
${{\Gamma }}\left( {{{h}_{0}}} \right) = - \mathop \smallint \limits_{ - \infty }^{{{h}_{{0p}}}} dzf\left( z \right)W\left( {{{h}_{0}} - z} \right) - R\left( {{{h}_{0}}} \right)W\left( {{{h}_{{0c}}}} \right),$
причем расстояния ${{h}_{{0c}}}$ и ${{h}_{0}}$ находятся из уравнений (3) и (5). Равенство (7) позволяет найти величину энергии адгезии, располагая известной зависимостью $P\left( h \right)$ и функцией $f\left( z \right)$ распределения шероховатости по высотам.

3. РАСЧЕТ РАВНОВЕСНОГО РАССТОЯНИЯ ПРИ КОНТАКТЕ И ЭНЕРГИИ АДГЕЗИИ ДЛЯ СИСТЕМЫ Si–Au

Энергия адгезии и равновесное расстояние между пластинами представляют значительный практический интерес. В работе [24] уравнения (5) и (7) применялись для анализа ситуации в случае металлических покрытий, напыленных на холодную подложку. Как указывалось выше, такие покрытия содержат заметно больше высоких пиков шероховатости, чем предсказывается нормальным распределением. Важным следствием этого факта является то, что энергия адгезии слабо зависит от поверхностных сил, действующих на расстояниях порядка или менее 1 нм [23, 24]. Кроме того, она практически не зависит от пластических характеристик материала, в отличие от равновесного расстояния.

При напылении на горячую подложку или при отжиге напыленных пленок, статистика шероховатости хорошо описывается нормальным распределением [7]. Дальнейшие расчеты посвящены именно этому случаю с использованием описанной выше модели. Представляет интерес проследить за относительным вкладом контактного взаимодействия в энергию адгезии, а также выяснить влияние среднеквадратичного отклонения шероховатости на энергию адгезии и равновесное расстояние.

3.1. Входные параметры задачи

Рассмотрим взаимодействие шероховатого покрытия из золота и гладкой кремниевой пластины. Для такого покрытия, варьируя время его напыления, можно получить шероховатость с существенно различными значениями среднеквадратичого отклонения [22]. Диэлектрические свойства золота и кремния детально изучены в широком диапазоне частот электромагнитного поля, что необходимо для надежного расчета ДС по теории Лифшица. Кроме того, имеется ряд работ, в которых экспериментально исследуются пластические свойства золота на наноуровне.

Сила. Для расчета ДС по теории Лифшица необходимо знать диэлектрические функции материалов на мнимой оси частот [3]. Эти функции не могут быть непосредственно измерены, но могут быть вычислены по мнимой части диэлектрической функции на действительных частотах с помощью соотношения Крамерса−Кронига. Диэлектрическая функция кремния в широком диапазоне частот может быть взята из справочника [31]. Однако для золота диэлектрическая функция в этом справочнике описывается на основе данных из разных литературных источников. В качестве альтернативы следует указать работу [32], в которой свойства напыленных золотых пленок с разными толщинами исследовались эллипсометрическими методами в диапазоне длин волн от 0.14 до 33 мкм. В дальнейшем используются оба этих источника. На рис. 4а показаны диэлектрические функции Si и Au как функции мнимой частоты $\omega = i\zeta $. Отметим, что разные литературные источники приводят к несколько отличающимся диэлектрическим функциям, что связано с разными условиями приготовления образцов. Дисперсионная сила между гладкими параллельными пластинами вычисляется по формуле Лифшица [3]. Хотя процедура вычисления не вполне тривиальная, она детально описана в литературе (см., например, [33, 34]). Результаты расчета ДС с диэлектрическими функциями золота, взятыми из разных источников, показаны на рис. 4б. Как видно, значения ДС, вычисленные по данным для золота из [31] (сплошная кривая) и из [32] (кружки) отличаются не более чем на 4%.

Рис. 4.

(а) Диэлектрические функции взаимодействующих материалов на мнимых частотах. Указаны источники исходных данных (на действительных частотах). (б) Сила как функция расстояния между параллельными гладкими пластинами кремния и золота, рассчитанная по формуле Лифшица. Сплошная кривая отвечает диэлектрической функции золота согласно [31], а кривая, показанная кружками, – согласно [32].

Минимальное расстояние. Равновесное расстояние ${{h}_{c}}$ между гладкими поверхностями присутствует в качестве параметра в формуле (1), которая получается путем суммирования межмолекулярных взаимодействий, исходя из парного потенциала Леннард-Джонса:

(8)
${{u}_{{{\text{LJ}}}}}\left( r \right) = - 4{{\epsilon }_{0}}\left[ {{{{\left( {\sigma {\text{/}}r} \right)}}^{6}} - {{{\left( {\sigma {\text{/}}r} \right)}}^{{12}}}} \right],$
где ${{\epsilon }_{0}}$ – энергетический параметр, а $\sigma $ – размер молекулы. Поскольку ДС не являются аддитивными, то константа Гамакера не может быть получена из попарного суммирования молекулярных взаимодействий и должна вычисляться по теории Лифшица. С другой стороны, когда молекулы образуют сплошную среду, эффективные диаметры молекул изменяются незначительно. По этой причине параметр $\sigma $ имеет прямой смысл и может быть выбран так, как это принято в молекулярной динамике. Таким образом, суммирование межмолекулярных взаимодействий приводит к выражению

(9)
${{h}_{c}} = {{\left( {2{\text{/}}15} \right)}^{{1/6}}}\sigma .$

Для взаимодействия двух различных молекул 1 и 2 в молекулярной динамике используется правило Лоренца: $\sigma = \left( {{{\sigma }_{1}} + {{\sigma }_{2}}} \right){\text{/}}2$. В нашем случае для кремния используется значение ${{\sigma }_{{{\text{Si}}}}} = 0.392\,\,~{\text{нм}}$, а для золота – ${{\sigma }_{{{\text{Au}}}}} = 0.293~\,\,{\text{нм}}$ [35], поэтому для взаимодействия Si–Au находим по формуле (9): ${{h}_{c}} = 0.245\,\,~{\text{нм}}$.

Предел текучести. Этот параметр не поддается точному определению и может заметно варьироваться в зависимости от способа приготовления материала. Необходимо отметить, что здесь речь идет о пластических свойствах наноразмерных пиков шероховатости, для которых предел текучести ${{P}_{f}}$ заметно отличается от объемного материала [36]. Как указывалось выше, для контакта Si–Au следует использовать свойства золота, как более мягкого материала. Для наноразмерных образцов золота кривая напряжение – деформация была измерена в целом ряде работ [37–40]. Предел текучести оказался весьма чувствительным к деталям наноструктуры образца, что позволяет дать для этого предела лишь грубую оценку: ${{P}_{f}} \approx 1~\,\,{\text{ГПа}}$, с точностью 50%. Подобная оценка характерна для масштабов ~ 100 нм. Отметим, что указанное значение ${{P}_{f}}$ в несколько раз выше предела текучести объемного золота.

Шероховатость. Расчеты проводились для нормального распределения шероховатости. Это подразумевает, что покрытия из золота были напылены на горячую подложку или отожжены после напыления. В этом случае шероховатость вполне описывается функцией распределения пикселей изображения АСМ по высотам вида (2) и характеризуется среднеквадратичным отклонением $w$.

3.2. Равновесное расстояние при контакте

Уравнение баланса сил (5) позволяет найти равновесное расстояние между телами и выражает равенство притягивающих и отталкивающих сил. Для дальнейшего рассмотрения представляется целесообразным разложить притягивающую силу на поверхностную и дальнодействующую составляющие следующим образом. Несколько условно, к поверхностным силам мы отнесем силы, действующие на локальных расстояниях менее ${{h}_{s}} = 1~\,\,{\text{нм}}$. До тех пор, пока ${{h}_{s}}\sim 1~\,\,{\text{нм}}$, конкрентое значение этой величины не сильно влияет на результат. Тогда уравнение (5) можно представить следующим образом:

(10)
$\begin{gathered} \mathop \smallint \limits_{{{h}_{s}}}^\infty dxf\left( {{{h}_{0}} - x} \right)P\left( x \right) + \\ + \,\,\mathop \smallint \limits_{{{h}_{{0c}}}}^{{{h}_{s}}} dxf\left( {{{h}_{0}} - x} \right)P\left( x \right) = - {{P}_{f}}R\left( {{{h}_{0}}} \right), \\ \end{gathered} $
где в качестве переменной интегрирования выбрано локальное расстояние $x = {{h}_{0}} - z$. Здесь первый член слева, который обозначим как ${{P}_{{la}}}$, описывает дальнодействующую составляющую притягивающей силы, а второй – поверхностную составляющую, которую обозначим через ${{P}_{{sa}}}$. Таким образом, полную притягивающую силу можно представить в виде разложения ${{P}_{a}} = {{P}_{{la}}} + {{P}_{{sa}}}$. Отметим, что в нашем случае обе составляющие ${{P}_{{la}}}$ и ${{P}_{{sa}}}$ обусловлены ДС, однако в ${{P}_{{sa}}}$ формально можно включить и другие поверхностные силы.

На рис. 5а полная притягивающая сила показана сплошной темной кривой, а отталкивающая сила показана для трех разных значений предела текучести ${{P}_{f}}$ (светлые кривые). Составляющая ${{P}_{a}}$ тоже зависит от величины ${{P}_{f}}$, но эта зависимость очень слабая, поскольку проявляется только через параметр ${{h}_{{0c}}}$ (для ${{P}_{f}} = 1.0~\,\,{\text{ГПа}}$ имеем ${{h}_{{0c}}} = 0.225\,\,~{\text{нм}}$) и поэтому практически незаметна на графике. Точки пересечения светлых кривых с темной соответствуют равновесным значениям ${{h}_{0}}$. Естественно, что с уменьшением предела текучести равновесное расстояние между пластинами уменьшается. На рис. 5б показана доля поверхностной составляющей ${{P}_{{sa}}}$ в полной силе притяжения для трех различных значений среднеквадратичного отклонения $w$ шероховатости. Для малых величин $w$ эта доля весьма значительна (37% для $w = 1.5~\,\,{\text{нм}}$) и заметно уменьшается с увеличением $w$. Здесь равновесные значения расстояния и поверхностной составляющей также показаны светлыми штриховыми линиями. На врезке можно видеть зависимость равновесного расстояния от величины $w$. Это расстояние плавно растет от $3w$ до $5w$ с увеличением $w$. Следует отметить, что равновесное расстояние оказывается чувствительным к точному значению предела текучести ${{P}_{f}}$, что было отмечено и для распределения с избытком высоких пиков [23, 24].

Рис. 5.

(а) Определение равновесного расстояния ${{h}_{0}}$ для $w = 2.5~{\text{нм}}$. Темная кривая показывает полную притягивающую силу. Светлые кривые показывают отталкивающую силу для трех значений предела текучести золота ${{P}_{f}} = 1.5~\,\,{\text{ГПа}}$ (штриховая), ${{P}_{f}} = 1.0~\,\,{\text{ГПа}}$ (сплошная) и ${{P}_{f}} = 0.5~\,\,{\text{ГПа}}$ (штрихпунктирная). Тонкие штриховые линии указывают на равновесные значения ${{h}_{0}}$. (б) Доля поверхностной составляющей в полной притягивающей силе для трех значений $w$: 1.5 нм (штрихпунктирная), 2.5 нм (штриховая) и 3.5 нм (сплошная). Светлые штриховые линии показывают равновесные значения для ${{P}_{f}} = 1.0~\,\,{\text{ГПа}}$. На врезке представлена зависимость относительного равновесного расстояния от среднеквадратичного отклонения $w$.

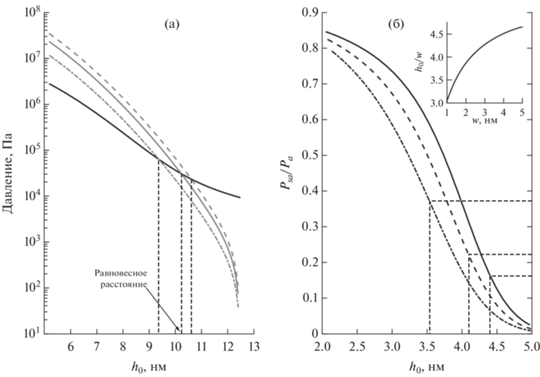
Обращает на себя внимание, что поверхностная составляющая ДС дает ощутимый вклад в полную силу притяжения, хотя среднее расстояние между поверхностями значительно превышает область действия этих сил. Причина состоит в том, что из-за шероховатости имеются области, где локальное расстояние сравнимо с ${{h}_{{0c}}}$ и локальная сила достигает очень больших значений (порядка $1~\,\,{\text{ГПа}}$). Роль поверхностных сил ограничивается малой площадью таких областей. В этом отношении шероховатость с нормальным распределением заметно отличается от шероховатости с избытком высоких пиков, для которой равновесное расстояние больше, а площадь контакта меньше [23, 24].

3.3. Энергия адгезии

Энергия адгезии определена равенством (7). Так же, как и для ДС, здесь целесообразно выделить поверхностный и дальнодействующий вклады:

(11)
$\begin{gathered} {{\Gamma }} = {{{{\Gamma }}}_{l}} + {{{{\Gamma }}}_{s}}, \\ {{{{\Gamma }}}_{l}}\left( {{{h}_{0}}} \right) = - \mathop \smallint \limits_{{{h}_{s}}}^\infty dxf\left( {{{h}_{0}} - x} \right)W\left( x \right), \\ {{{{\Gamma }}}_{s}}\left( {{{h}_{0}}} \right) = - \mathop \smallint \limits_{{{h}_{{0c}}}}^{{{h}_{s}}} dxf\left( {{{h}_{0}} - x} \right)W\left( x \right) - R\left( {{{h}_{0}}} \right)W\left( {{{h}_{{0c}}}} \right). \\ \end{gathered} $

Отметим, что здесь, в отличие от разложения ДС (предыдущий раздел), поверхностный вклад включает также и вклад $R\left( {{{h}_{0}}} \right)W\left( {{{h}_{{0c}}}} \right)$ от прямого контакта пика. В разложении (10) это не имело смысла, поскольку привело бы значительному взаимному сокращению членов в поверхностной составляющей.

На рис. 6а показана энергия адгезии ${{\Gamma }}$ как функция среднего расстояния между пластинами для среднеквадратичного отклонения $w = 2.5\,\,~{\text{нм}}$. Важно, что величина ${{\Gamma }}$ очень слабо зависит от предела текучести ${{P}_{f}}$. Неопределенность этого параметра в интервале ${{P}_{f}} = 0.5{\kern 1pt} - {\kern 1pt} 1.5\,\,~{\text{ГПа}}$ на графике показана узкой серой полоской с уменьшающейся шириной. Как видно, эта неопределенность гораздо меньше, чем для силы (рис. 5а). Причина столь слабой зависимости в том, что предел текучести ${{P}_{f}}$ появляется в уравнении (11) только через расстояние ${{h}_{{0c}}}$ на прямом контакте пика, которое меняется очень слабо. Аналогичное поведение отмечалось в работе [23], где анализировалась статистика шероховатости с избыточным количеством высоких пиков. Штриховая кривая на рис. 6а описывает поверхностный вклад в энергию адгезии согласно (11).

Рис. 6.

(а) Энергия адгезии как функция расстояния между пластинами для $w = 2.5{\text{\;нм}}$. Серая полоса с уменьшающейся шириной показывает полную энергию ${{\Gamma }}$. Ширина полосы соответствует изменению энергии при вариации предела текучести ${{P}_{f}}$ от 0.5 до 1.5 ГПа. Штриховая кривая представляет величину ${{{{\Gamma }}}_{s}}$. Тонкие штриховые линии отмечают положение равновесных расстояний для ${{P}_{f}} = \left( {0.5,~\,\,1.0,~\,\,1.5} \right)~\,\,{\text{ГПа}}$. (б) Левая ось – энергия адгезии как функция среднеквадратичного отклонения $w$ шероховатости. Сплошная и штриховая темные кривые соответствуют величинам ${{\Gamma }}$ и ${{{{\Gamma }}}_{{\text{s}}}}$. Правая ось – равновесное расстояние между пластинами как функция величины $w$.

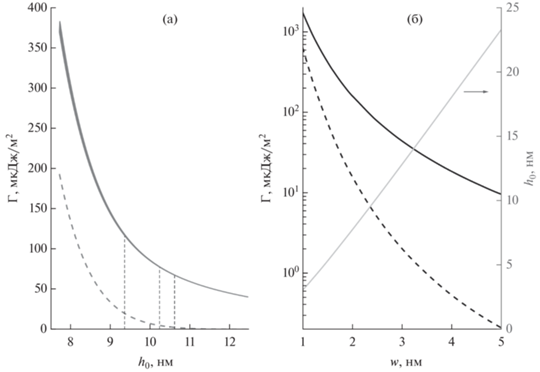
Хотя кривая ${{\Gamma }}\left( {{{h}_{0}}} \right)$ очень слабо зависит от предела текучести ${{P}_{f}}$, влияние этого параметра на равновесное значение ${{h}_{0}}$ является ощутимым. Тонкие штриховые линии на рис. 6а показывают положение равновесных расстояний на кривой ${{\Gamma }}\left( {{{h}_{0}}} \right)$ для трех значений ${{P}_{f}} = \left( {0.5,~\,\,1.0,~\,\,1.5} \right)~\,\,{\text{ГПа}}$. Этим значениям отвечают равновесные расстояния ${{h}_{0}} = \left( {9.36,~\,\,10.24,\,\,~10.62} \right)\,\,~{\text{нм}}$ и энергии адгезии Γ = $ = \left( {117.7,~\,\,77.9,~~\,\,67.7} \right)\,\,~{\text{мкДж/}}{{{\text{м}}}^{2}}$, соответственно, причем поверхностный вклад в энергию адгезии составляет ${{{{\Gamma }}}_{{\text{s}}}} = \left( {20.0,~\,\,5.0,~\,\,2.6} \right)~\,\,{\text{мкДж/}}{{{\text{м}}}^{2}}$. Следует отметить, что относительный поверхностный вклад в энергию адгезии остается малым, но растет с уменьшением предела текучести и среднеквадратичного отклонения шероховатости – это объясняется увеличением относительной площади реального контакта $R\left( {{{h}_{0}}} \right)$.

На рис. 6б показаны зависимости равновесных ${{\Gamma }}$ и ${{{{\Gamma }}}_{s}}$ от среднеквадратичного отклонения $w$ шероховатости (темные сплошная и штриховая кривые, относящиеся к левой вертикальной оси). На интервале изменения $w$ от 1 до 5 нм энергия адгезии уменьшается от 1750 до 9.6 мкДж/м2. Поверхностный вклад в энергию адгезии при этом убывает еще быстрее – от 643 до 0.2 мкДж/м2. Для среднеквадратичного отклонения порядка 1 нм роль поверхностного вклада оказывается значительной. Светлая кривая относится к правой вертикальной оси и показывает равновесное значение ${{h}_{0}}$ как функцию величины $w$. Эта функция проявляет незначительную нелинейность: отношение ${{h}_{0}}{\text{/}}w$ растет от 3.04 до 4.67 с ростом $w$.

3.4. Обсуждение результатов

Одним из результатов данной работы является выявление слабой зависимости энергии адгезии от предела текучести. Рассмотрение было выполнено для золота, которое является мягким металлом. Для материалов с более высоким пределом текучести эта зависимость будет еще более слабой. Поскольку предел текучести, как указывалось выше, не поддается точному определению, слабая зависимость энергии адгезии от него является важным выводом. Фактически это означает, что для данной пары материалов (в нашем случае Si–Au) зависимость ${{\Gamma }}\left( {{{h}_{0}}} \right)$ описывается некоторой универсальной кривой, причем равновесное состояние адгезии представляется точкой на этой кривой. Измерить величину ${{\Gamma }}$ значительно проще, чем определить равновесное расстояние $\sim {\kern 1pt} 10\,\,~{\text{нм}}$ между телами при контакте, поэтому такую универсальную кривую можно использовать для определения равновесного расстояния ${{h}_{0}}$.

Еще один важный результат данной работы заключается в том, что поверхностный вклад в адгезию является небольшим и можно даже утверждать, что для реальных шероховатостей он пренебрежимо мал. Здесь следует отметить, что расчеты были проведены для упрощенной модели поверхностных сил, которая, тем не менее, воспроизводит правильный порядок величин. До тех пор, пока можно считать, что ${{{{\Gamma }}}_{s}} \ll {{\Gamma }}$, кривую ${{\Gamma }}\left( {{{h}_{0}}} \right)$ можно рассчитать по теории Лифшица, для которой методика расчета хорошо разработана.

Данный результат имеет первостепенное значение для измерения ДС на расстояниях порядка 10 нм. Трудностью таких экспериментов является определение абсолютного расстояния [41, 42], поскольку даже точность ±1 нм приводит к ошибке в ДС около 30%. Однако для определения абсолютного расстояния целесообразно использовать расчетную кривую ${{\Gamma }}\left( {{{h}_{0}}} \right)$, т.к. измеряя величину ${{\Gamma }}$, можно определить значение ${{h}_{0}}$ с точностью, заметно превышающей 1 нм. Этот метод можно использовать для недавно предложенного эксперимента [43], в котором сила измеряется по форме тонкой упругой балки, один конец которой жестко фиксирован на некоторой высоте, а другой удерживается на подложке за счет адгезии без приложения внешних сил.

4. ЗАКЛЮЧЕНИЕ

В работе выполнены расчеты энергии адгезии и равновесного расстояния между гладкой поверхностью кремниевой пластины и шероховатым покрытием из золота, напыленного на кремниевую подложку, в предположении, что поверхностная шероховатость описывается нормальным распределением. Это дополняет анализ, проделанный в работах [23, 24], где использовалась статистика шероховатости с избыточным количеством высоких пиков. Подобные допущения отвечают реальным условиям изготовления и функционирования МЭМС.

Как показали расчеты, для нормального распределения наблюдается похожее поведение системы, однако имеется ряд количественных отличий. Например, для нормального распределения равновесное расстояние между телами при контакте меньше, а энергия адгезии больше, чем для статистики с избыточным количеством высоких пиков. Зависимость энергии адгезии от предела текучести очень слабая, как и в случае статистики с избыточным количеством высоких пиков. В энергии адгезии доминирует дальнодействующее дисперсионное взаимодействие, хотя роль поверхностного вклада становится заметной для малых шероховатостей. Методы расчета, использованные в данной работе, могут быть непосредственно перенесены на другие материалы (кроме мягких полимерных материалов).

Проведенный анализ имеет практическую ценность для контроля эффекта залипания в МЭМС. Результаты работы планируется использовать и для эксперимента по измерению ДС на расстояниях порядка 10 нм [43], что позволит заметно улучшить точность измерений.

Работа поддержана Российским научным фондом, грант № 20-19-00214.

Список литературы

  1. Tas N., Sonnenberg T., Jansen H., Legtenberg R., Elwenspoek M. // J. Micromech. Microeng. 1996 V. 6. № 4. P. 385.

  2. Maboudian R., Howe R.T. // J. Vacuum Sci. Technol. B. 1997. V. 15. P. 1.

  3. Лифшиц Е.М., Питаевский Л.П. // Статистическая физика. Часть 2. М.: Наука, 1978.

  4. Krim J, Palasantzas G. // Int. J. Mod. Phys. B. 1995. V. 9. P. 599.

  5. Persson B. // Surf. Sci. Rep. 2006. V. 61. P. 201.

  6. Svetovoy V.B., Palasantzas G. // Adv. Colloid Interface Sci. 2016. V. 216. P. 1–19.

  7. Muravyeva T.I., Uvarov I.V., Naumov V.V., Palasantzas G., Svetovoy V.B. // Phys. Rev. B. 2021 V. 104. P. 035415.

  8. Broer W, Palasantzas G, Knoester J, Svetovoy V.B. // Europhys. Lett. 2011. V. 95. P. 30001.

  9. Johnson K.L., Kendall K., Roberts A.D. // Proc. R. Soc. A. 1971. V. 324. P. 301.

  10. Derjaguin B., Muller V., Toporov Y.J. // Colloid Interface Sci. 1975. V. 53. P. 314.

  11. Muller V., Yushchenko V., Derjaguin B. // J. Colloid Interface Sci. 1980. V. 77. P. 91.

  12. Attard P. Parker J.L. // Phys. Rev. A. 1992. V. 46. P. 7959.

  13. Greenwood J. // Philos. Mag. 2009. V. 89. P. 945.

  14. Soldatenkov I. // J. Appl. Math. Mech. 2012. V. 76. P. 597.

  15. Greenwood J.A., Williamson J.B.P. // Proc. R. Soc. A. 1966. V. 295. P. 300.

  16. Fuller K.N.G. Tabor D. // Proc. R. Soc. A. 1975. V. 345. P. 327.

  17. Whitehouse D.J., Archard J.F., Tabor D. // Proc. R. Soc. A. 1970. V. 316. P. 97.

  18. Bush A., Gibson R., Thomas T. // Wear. 1975. V. 35. P. 87.

  19. Persson B.N.J. // Phys. Rev. Lett. 2007. V. 99. P. 125502.

  20. Knapp J.A., de Boer M.P. // J. Microelectromech. Syst. 2002. V. 11. P. 754.

  21. DelRio F.W., de Boer M.P., Knapp J.A., Reedy E.D., Clews P.J., Dunn M.L. // Nat. Mater. 2005. V. 4. p. 629.

  22. van Zwol P.J., Svetovoy V.B., Palasantzas G. // Phys. Rev. B. 2009. V. 80. P. 235401.

  23. Soldatenkov I.A., Palasantzas G., Svetovoy V.B. // Phys. Rev. B. 2021. V. 104. P. L121404.

  24. Soldatenkov I.A., Stepanov F.I., Svetovoy V.B. // Phys. Rev. B. 2022. V. 105. P. 075401.

  25. Лифшиц Е.М. // ЖЭТФ. 1955. Т. 29. С. 94.

  26. Дзялошинский И.Е., Лифшиц Е.М., Питаевский Л.П. УФН. 1961. Т. 73. № 3. С. 381.

  27. Greenwood J.A. Tripp J.H. // Proc. Inst. Mech. Eng. 1970. V. 185. P. 625.

  28. Derjaguin B. // Kolloid-Zeitschrift. 1934. V. 69. P. 155–164.

  29. Broer W., Palasantzas G., Knoester J., Svetovoy V.B. // Phys. Rev. B. 2012. V. 85. P. 155410.

  30. Parsons D.F., Walsh R.B., Craig V.S.J. // J. Chem. Phys. 2014. V. 140. P. 164701.

  31. Handbook of Optical Constants of Solids. Ed. by Palik E.D. New York: Academic Press, 1995. P. 804.

  32. Svetovoy V.B., von Zwol P.J., Palasantzas G., De Hosson J.Th.M. // Phys. Rev. B. 2008. V. 77. P. 035439.

  33. Lambrecht A., Reynaud S. // Eur. Phys. J. D. 2000. V. 8. P. 309.

  34. Klimchitskaya G.L., Mohideen U., Mostepanenko V.M. // Rev. Mod. Phys. 2009. V. 81. P. 1827.

  35. Munaò G., Correa A., Pizzirusso A., Milano G. // Eur. Phys. J. E. 2018. V. 41. P. 38.

  36. Hahn E.N., Meyers M.A. // Mater. Sci. Eng. A. 2015. V. 646. P. 101.

  37. Kim J.-Y., Greer J.R. // Acta Mater. 2009. V. 57. P. 5245.

  38. Sedlmayr A., Bitzek E., Gianola D. S., Richter G., Mönig R., Kraft O. // Acta Mater. 2012. V. 60. P. 3985.

  39. Wang J., Sansoz F., Huang J., Liu Y., Sun S., Zhang Z., Mao S. X. // Nat. Commun. 2012. V. 4. P. 1742.

  40. Islam A.A., Klassen R.J. // J. Mater. Res. 2017. V. 32. P. 3507.

  41. van Zwol P.J., Palasantzas G., van de Schootbrugge M., De Hosson J.T.M. // Appl. Phys. Lett. 2008. V. 92. P. 054101.

  42. Sedighi M., Svetovoy V.B., Palasantzas G. // Phys. Rev. B. 2016. V. 93. P. 085434.

  43. Svetovoy V.B., Postnikov A.V., Uvarov I.V., Stepanov F.I., Palasantzas G. // Phys. Rev. Applied. 2020. V. 13. P. 064057.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал