Коллоидный журнал, 2022, T. 84, № 3, стр. 328-337

Квазистационарное испарение малой капли жидкости на плоской подложке: аналитическое решение в биполярных координатах

О. А. Савенко¹, П. В. Лебедев-Степанов^1, 2, *

¹ Федеральный научно-исследовательский центр “Кристаллография и фотоника” Российской академии наук
119333 Москва, Ленинский проспект 59, Россия

² Национальный исследовательский ядерный университет МИФИ
115409 Москва, Каширское шоссе 31, Россия

^* E-mail: lebstep.p@crys.ras.ru

Поступила в редакцию 29.03.2022
После доработки 08.04.2022
Принята к публикации 08.04.2022

EDN: NZPWOT
DOI: 10.31857/S0023291222030119

Полный текст (PDF)

Аннотация

Исследование испаряющейся капли жидкости, нанесенной на плоскую поверхность, имеет большое значение для физико-химических, технических и медицинских приложений. Предложены новые аналитические выражения для плотности пара, плотности потока испарения и полного потока испарения в единицу времени для медленно испаряющейся малой осесимметричной капли, установленной на плоскую подложку с произвольным значением контактного угла в диапазоне от 0 до 180°. При выводе использовалось известное в электростатике решение уравнения Лапласа для плоского клина, преобразованное методом инверсии на сфере в решение для линзы в биполярных координатах. Новые выражения математически эквивалентны формулам в тороидальных координатах, предложенным ранее [Yu.O. Popov, Phys. Rev. E. 71 (2005), 036313], однако плотность потока испарения в биполярных координатах имеет более простую форму однократного интеграла от комбинации элементарных функций, что дает преимущества с вычислительной точки зрения. Предложено также новое выражение плотности потока испарения в полярных координатах и выполнены графические построения зависимости плотности потока испарения от полярного угла при разных значениях контактного угла капли.

ВВЕДЕНИЕ

Испаряющаяся на плоской подложке капля жидкости – важный объект как теоретического моделирования (динамика испарения, гидродинамика, самоорганизация растворенного вещества и др.) [1–4], так и многичисленных приложений (технологии печати, функционализированные покрытия, медицинская диагностика и т.д.) [5–12]. Можно выделить три основные задачи при описании испаряющейся капли раствора: [13–14]: 1) испарение растворителя с поверхности капли в окружающий воздух (внешняя задача), 2) гидродинамические течения в объеме капли (внутренняя задача), 3) динамика частиц (молекулярных или колллоидных) в капле с учетом межчастичных взаимодействий, взаимодействия частица-поверхность, частица-растворитель. Первая из этих задач, испарение, имеет первостепенное значение, поскольку является исходной движущей силой процесса самоорганизации вещества в капле.

Равновесная форма капли на плоской подложке, характерный размер которой (высота) много меньше капиллярной постоянной ${{\lambda }_{C}} = \sqrt {\eta {\text{/}}\rho g} $ ($\eta $ – коэффициент поверхностного натяжения, ρ – плотность жидкости, g – ускорение свободного падения), приблизительно описывается шаровым сегментом [14]. Капиллярная постоянная для большинства жидкостей имеет порядок нескольких мм.

Согласно Дж.К. Максвеллу, медленное (квазистационарное) испарение капли жидкости в воздушную среду определяется дифузией пара с поверхности капли в окружающий воздух. При этом концентрация пара n описывается уравнением Лапласа

(1)

${{\nabla }^{2}}n = 0,$

причем концентрация пара на поверхности капли удовлетворяет условию $n = {{n}_{S}}$_, где ${{n}_{S}}$ – концентрация насыщенного пара (которая в модели Максвелла считается много меньшей, чем концентрация молекул воздуха), а вдали от капли концентрация пара принимает некоторое асимптотическое значение $n = {{n}_{\infty }}$. В данной модели также предполагается, что температурные градиенты, связанные с испарением, пренебрежимо малы.

Такая постановка задачи позволяет воспользоваться электростатической аналогией. Действительно, электростатический потенциал проводящей (металлической) поверхности постоянен, а вне поверхности, где нет зарядов, удовлетворяет уравнению Лапласа.

Используя общее решение электростатической задачи, предложенное в монографии Н.Н. Лебедева [15], Р.Д. Диган с соавторами [1], Х. Хью и Р. Ларсон [16], а также О.Ю. Попов [2], воспользовавшись аналогией с электростатикой, получили выражение для концентрации пара в пространстве около капли в тороидальных координатах $(\alpha ,\beta )$ (рис. 1a):

(2)

$\begin{gathered} n(\alpha ,\beta ) = {{n}_{\infty }} + ({{n}_{s}} - {{n}_{\infty }})\sqrt {2(\operatorname{ch} {\kern 1pt} \alpha - \cos {\kern 1pt} \beta )} \times \\ \times \,\,\int\limits_0^\infty {\frac{{\operatorname{ch} {\kern 1pt} \theta \tau {\kern 1pt} \operatorname{ch} (2\pi - \beta )\tau }}{{\operatorname{ch} {\kern 1pt} \pi \tau {\kern 1pt} \operatorname{ch} (\pi - \theta )\tau }}} {{P}_{{ - 1/2i\tau }}}(\operatorname{ch} {\kern 1pt} \alpha )d\tau , \\ \end{gathered} $

где $\theta $ ̶ контактный угол (рис. 1б, 1в), ${{P}_{{ - 1/2 + i\tau }}}(\operatorname{ch} {\kern 1pt} \alpha ) = \frac{2}{\pi }\operatorname{ch} {\kern 1pt} \pi \tau $ $\int_0^\infty {\frac{{\cos {\kern 1pt} \tau t{\kern 1pt} }}{{2(\operatorname{ch} {\kern 1pt} t + \operatorname{ch} {\kern 1pt} \alpha )}}d\tau } $ – сферическая функция Лежандра [2, 15]. Тороидальные координаты $(\alpha ,\beta )$ связаны с цилиндрическими координатами r и z (рис. 1б и 1в) в соответствии с формулами

(3)

$r = \frac{{R{\kern 1pt} \operatorname{sh} {\kern 1pt} \alpha }}{{\operatorname{ch} {\kern 1pt} \alpha - \cos {\kern 1pt} \beta }},\,\,\,\,z = \frac{{R{\kern 1pt} \sin {\kern 1pt} \beta }}{{\operatorname{ch} {\kern 1pt} \alpha - \cos {\kern 1pt} \beta }}.$

Рис. 1.

(a) Тороидальные координаты $(\alpha ,\beta )$. Геометрия капель с контактными углами $\theta < 90^\circ $ (б) и $\theta > 90^\circ $ (в).

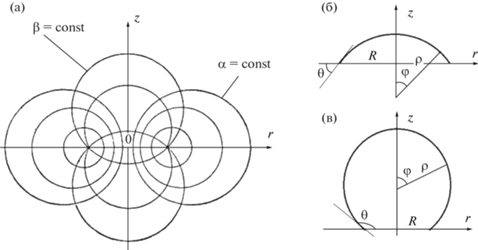
Заметим, что в случае капли с контактным углом, большим 90° (рис. 1в), преобразование (3) не является однозначным: может существовать два значения z для одного и того же r на поверхности капли. Поэтому более удобно использовать полярные координаты $(\rho ,\varphi )$, в которых такой неоднозначности не возникает.

Плотность потока испарения (среднее количество молекул, покидающее единицу площади поверхности капли за единицу времени в направлении, нормальном к поверхности в данной точке) при этом определяется формулой [2]

(4)

$\begin{gathered} J(\alpha ) = D\frac{{{{n}_{s}} - {{n}_{\infty }}}}{R} \times \\ \times \,\,\left[ {\frac{{\sin {\kern 1pt} \theta }}{2} + \sqrt 2 {{{(\operatorname{ch} {\kern 1pt} \alpha + \cos {\kern 1pt} \theta )}}^{{3/2}}}\,\,_{{_{{}}^{{_{{^{{}}}}^{{}}}}}}^{{_{{_{{}}^{{^{{}}}}}}^{{}}}}} \right. \times \\ \left. { \times \,\,\int\limits_0^\infty {\frac{{\operatorname{ch} {\kern 1pt} \theta \tau }}{{\operatorname{ch} {\kern 1pt} \pi \tau }}\operatorname{th} \left[ {(\pi - \theta )\tau } \right]{{P}_{{ - 1/2i\tau }}}(\operatorname{ch} {\kern 1pt} \alpha )\tau d\tau } } \right], \\ \end{gathered} $

где D коэффициент диффузии пара в окружающем воздухе. Здесь тороидальная координата $\alpha $ изменяется в интервале значений от 0 (вершина капли) до ∞ (контактная линия).

Аналитическое решение для интегральной скорости испарения капли (количество молекул, покидающее каплю в единицу времени) предложено О.Ю. Поповым [2]

(5)

$\begin{gathered} W = \pi RD({{n}_{s}} - {{n}_{\infty }}) \times \\ \times \,\,\left[ {\frac{{\sin {\kern 1pt} \theta }}{{1 + \cos {\kern 1pt} \theta }} + 4\int\limits_0^\infty {\frac{{1 + \operatorname{ch} {\kern 1pt} 2\theta \tau {\kern 1pt} }}{{\operatorname{sh} {\kern 1pt} 2\pi \tau }}} \operatorname{th} \left[ {(\pi - \theta )\tau } \right]d\tau } \right]. \\ \end{gathered} $

Оно получено интегрированием потока (4) по поверхности капли. Наряду с этим, широко используется приближенная формула, предложенная Р. Пикнеттом и Р. Бэксоном [17]

(6)

$W = 2\pi D({{n}_{s}} - {{n}_{\infty }})С = 2\pi \rho D({{n}_{s}} - {{n}_{\infty }})g(\theta ),$

где “емкость” капли $C = g(\theta )\rho $ определяется формулой

(7)

$\begin{gathered} g(\theta ) = 0.6366\theta + 0.09591{{\theta }^{2}} - 0.06144{{\theta }^{3}}, \\ 0 \leqslant \theta \leqslant 0.175; \\ g(\theta ) = 0.00008957 + 0.6333\theta + 0.1160{{\theta }^{2}} - \\ - \,\,0.08878{{\theta }^{3}} + 0.01033{{\theta }^{4}},\,\,\,\,0.175 \leqslant \theta \leqslant \pi . \\ \end{gathered} $

Ошибка приближения (7) не превышает 0.2%.

Из (4) следует, что плотность потока испарения пленки в виде диска радиуса R, лежащей на плоской поверхности, определяется формулой

(8)

$J(r) = D\frac{{\partial n}}{{\partial z}} = \frac{{2D({{n}_{s}} - {{n}_{\infty }})}}{{\pi R}}{{\left( {1 - \frac{{{{r}^{2}}}}{{{{R}^{2}}}}} \right)}^{{ - 1/2}}}.$

Интегрируя поток (8) по кругу радиуса R, получаем полную скорость испарения:

(9)

$W = 4DR({{n}_{s}} - {{n}_{\infty }}).$

Результат (9) был получен другим способом Н.А. Фуксом [18].

Для полусферы ($\theta = 0.5\,\pi $) имеем W = 2πD × × $({{n}_{s}} - {{n}_{\infty }})\rho $ (здесь $\rho $ –̶ радиус шарового сегмента, отвечающий капле (рис. 1б, 1в), а для сферы, установленной на подложку ($\theta = \pi $), скорость испарения дается формулой $W = 4\pi D({{n}_{s}} - {{n}_{\infty }})\rho {\kern 1pt} \ln {\kern 1pt} 2$.

Существует еще одно аналитическое решение задачи (1), опирающееся на формулу Г.М. Макдональда для электростатического потенциала плоского проводящего клина [19] и метод инверсии на сфере Дж.К. Максвелла [20], позволяющий преобразовать решение для клина в решение, соответствующее проводящей линзе. Этот путь в общем виде был рассмотрен Г.А. Гринбергом в монографии [21]. В препринте [22] одним из авторов этой статьи данный подход впервые применен к задаче об испаряющейся капле с учетом электростатической аналогии, а также опубликован в материалах Droplets 2021 [23].

В следующей части представлен вывод выражения для потока испарения капли в биполярных координатах. Показано, что этот поток можно выразить как явную функцию полярного угла φ (рис. 1б, 1в), имеющую вид однократного интеграла от выражения, состоящего только из элементарных функций, тогда как выражение (4) представляет фактически двукратный интеграл (с учетом интегрального представления функции Лежандра), зависящий от тороидальной координаты $\alpha \,$, неудобной для непосредственного использования и требующей пересчета в цилиндрическую систему по уравнениям (3).

ПОТОК ИСПАРЕНИЯ В БИПОЛЯРНЫХ И ПОЛЯРЫХ КООРДИНАТАХ

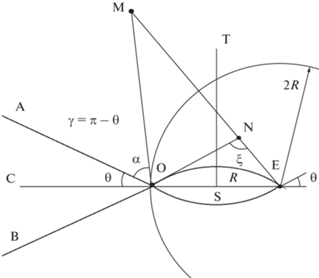
Рассмотрим следующую задачу электростатики. Пусть AO и BO две пересекающиеся проводящие плоскости, перпендикулярные плоскости рис 2. Они образуют клин с внутренним углом $2\theta $. Заряд e помещен в точку E, находящуюся на расстоянии 2R от ребра клина O на продолжении биссектрисы угла AOB. Требуется найти потенциал. Точка M характеризуется цилиндрическими координатами (r, α, 0) с центром в точке O, где r = |OM|, а полярный угол отсчитывается от луча OA вправо. Ось z проходит нормально плоскости данного рисунка. Потенциал проводящей поверхности постоянен, и его можно принять равным нулю. Требуется найти потенциал $\phi $ вне клина в произвольной точке $(r,\alpha ,z)$. Согласно Г.М. Макдональду, решение имеет вид [19]:

(10)

$\begin{gathered} \phi (r,\alpha ,z) = \frac{e}{{4\gamma \sqrt {Rr} }} \times \\ \times \,\,\int\limits_\eta ^\infty {\left[ {\frac{{\operatorname{sh} \frac{{\pi \varsigma }}{{2\gamma }}}}{{\operatorname{ch} {\kern 1pt} \frac{{\pi \varsigma }}{{2\gamma }} - \cos \frac{{\pi (\alpha - \gamma )}}{{2\gamma }}}} - \frac{{\operatorname{sh} {\kern 1pt} \frac{{\pi \varsigma }}{{2\gamma }}}}{{\operatorname{ch} {\kern 1pt} \frac{{\pi \varsigma }}{{2\gamma }} - \cos {\kern 1pt} \frac{{\pi (\alpha + \gamma )}}{{2\gamma }}}}} \right]} \times \\ \times \,\,\frac{{d\varsigma }}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \eta } }}, \\ \end{gathered} $

где $\operatorname{ch} {\kern 1pt} \eta = \frac{{4{{R}^{2}} + {{r}^{2}} + {{z}^{2}}}}{{4Rr}}$, $\gamma = \pi - \theta $.

Рис. 2.

Проводящий клин AOB, преобразуемый инверсией в проводящую линзу OE.

Учитывая, что из геометрии имеет место соотношение $\alpha = \gamma - \xi $ (см. рис. 2), так что $\cos \frac{{\pi (\alpha - \gamma )}}{{2\gamma }} = $ $ = \pm \sin {\kern 1pt} \frac{{\pi \alpha }}{{2\gamma }}$, выражение (10) может быть переписано в виде

(11)

$\begin{gathered} \phi (r,\alpha ,z) = \frac{e}{{2\gamma \sqrt {Rr} }}\sin {\kern 1pt} \frac{{\pi \alpha }}{{2\gamma }} \times \\ \times \,\,\int\limits_\eta ^\infty {\operatorname{sh} {\kern 1pt} \frac{{\pi \varsigma }}{{2\gamma }}{{{\left( {{{{\cosh }}^{2}}{\kern 1pt} \frac{{\pi \varsigma }}{{2\gamma }} - {{{\sin }}^{2}}{\kern 1pt} \frac{{\pi \alpha }}{{2\gamma }}} \right)}}^{{ - 1}}}} \times \\ \times \,\,\frac{{d\varsigma }}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \eta } }}. \\ \end{gathered} $

Сделаем преобразование инверсии относительно центра в точке E для сферы радиусом 2R. В результате преобразования получена линза OE, геометрия которой показана на рис. 2. Потенциал отраженной системы (эквипотенциальной линзы) в отраженной точке N с координатами (r', α', 0), где r' = |ON|, α' – угол AON определяется выражением

(12)

$\psi (r{\kern 1pt} ',\alpha {\kern 1pt} ',0) = - \frac{e}{{2R}} + \frac{{2R}}{{{\text{|}}{\kern 1pt} {\text{EN}}{\kern 1pt} {\text{|}}}}\varphi (r,\alpha ,0).$

По определению

(13)

$|{\kern 1pt} {\text{EN}}{\kern 1pt} | \cdot |{\kern 1pt} {\text{EM}}{\kern 1pt} | = 4{{R}^{2}},$

где 2R – радиус сферы, в которой точка M отражается в точку N.

Учитывая (11), получаем

(14)

$\begin{gathered} \psi (r{\kern 1pt} ',\alpha {\kern 1pt} ',0) = V - \frac{V}{{{\text{|}}{\kern 1pt} {\text{EN}}{\kern 1pt} {\text{|}}}}\frac{{2{{R}^{{1.5}}}}}{{\gamma \sqrt r }}\sin \frac{{\pi \alpha }}{{2\gamma }} \times \\ \times \,\,\int\limits_\eta ^\infty {\operatorname{sh} \frac{{\pi \varsigma }}{{2\gamma }}{{{\left( {{{{\operatorname{ch} }}^{2}}\frac{{\pi \varsigma }}{{2\gamma }} - {{{\sin }}^{2}}\frac{{\pi \alpha }}{{2\gamma }}} \right)}}^{{ - 1}}} \times } \\ \times \,\,\frac{{d\varsigma }}{{\sqrt {\operatorname{ch} \varsigma - \operatorname{ch} \eta } }}, \\ \end{gathered} $

где $V = - \frac{e}{{2R}}$.

Введем биполярные координаты (ξ, ω) с центрами в точках O и E (рис. 2), так что точка N имеет координаты:

(15)

$\xi = \angle {\text{ONE}},\,\,\,\,\omega = \ln {\kern 1pt} \frac{{{\text{|ON|}}}}{{{\text{|EN|}}}}.$

Уравнение (13) переписывается в виде

(16)

$\frac{{|{\kern 1pt} {\text{EN}}{\kern 1pt} |}}{{2R}} = \frac{{2R}}{{|{\kern 1pt} {\text{EM}}{\kern 1pt} |}}.$

Отсюда следует, что треугольники OME и NOE подобны: один угол общий, две стороны пропорциональны. Тогда $\angle {\text{MOE}} = \xi $. Следовательно

(17)

$\alpha = \gamma - \xi {\text{ и }}r = 2R{{e}^{\omega }}.$

По теореме косинусов

(18)

$\frac{1}{{|{\kern 1pt} {\text{EN}}{\kern 1pt} {{|}^{2}}r}} = \frac{{\operatorname{ch} {\kern 1pt} \omega - \cos {\kern 1pt} \xi }}{{4{{R}^{3}}}}.$

(19)

$\begin{gathered} {\text{Если }}z = 0,{\text{ то }}\operatorname{ch} {\kern 1pt} {\kern 1pt} \eta = \frac{{4{{R}^{2}} + {{r}^{2}}}}{{4Rr}} = \operatorname{ch} {\kern 1pt} {\kern 1pt} \rho {\text{ }} \\ {\text{отсюда }}\eta = \pm \omega {\text{.}}~~~~~~~~~~~~~~~~~~~~~~~~ \\ \end{gathered} $

С учетом этого потенциал определяется выражением

(20)

$\begin{gathered} \psi (\omega ,\xi ) = V - \frac{{2V}}{\gamma }{{(\operatorname{ch} {\kern 1pt} \omega - \cos {\kern 1pt} \xi )}^{{1/2}}}\cos \frac{{\pi \xi }}{{2\gamma }} \times \\ \times \,\,\int\limits_\omega ^\infty {{{{\left( {\operatorname{ch} \frac{{\pi \varsigma }}{\gamma } - \cos \frac{{\pi \xi }}{\gamma }} \right)}}^{{ - 1}}}\frac{{\operatorname{sh} \frac{{\pi \varsigma }}{{2\gamma }}d\varsigma }}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \omega } }}} . \\ \end{gathered} $

Поверхностная плотность заряда на поверхности линзы

(21)

$\sigma = - \frac{{\operatorname{ch} {\kern 1pt} \omega - \cos {\kern 1pt} \xi }}{R}\frac{{\partial \psi (\omega ,\xi )}}{{\partial \xi }}.$

Подчеркнем, что области определения потенциала (20) и поверхностной плотности заряда (21) отличаются: первый определен во всем пространстве вне линзы и на ее поверхности, а вторая – только на поверхности линзы.

Обозначим как P произвольную точку на поверхности линзы (рис. 3). По аналогии с точкой N на рис. 2, см. формулу (15), она характеризуется биполярными координатами (ξ, ω) с центрами в точках O и E:

(22)

$\xi = \angle {\text{OPE}},\,\,\,\,\omega = \ln \frac{{{\text{|OP|}}}}{{{\text{|EP|}}}}.$

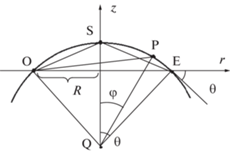
Угол $\xi $ на поверхности линзы имеет одну и ту же величину для всех точек дуги окружности с данным контактным углом $\theta $. Рассматривая равнобедренный треугольник OQS (рис. 3), легко показать, что на поверхности линзы равенство (17) приобретает вид:

(23)

$\xi = \gamma ,{\text{ где}}~{\text{ }}\gamma = \pi - \theta .$

Рис. 3.

Геометрия сферического сегмента, отвечающая верхней части линзы OE (см. также рис. 2) с заданным контактным углом $\theta $.

Принимая во внимание формулы (20)–(22), получаем

(24)

$\begin{gathered} \sigma (\omega ) = \frac{{\pi V}}{{2{{{(\pi - \theta )}}^{2}}R}}{{(\operatorname{ch} {\kern 1pt} \omega - \cos (\pi - \theta ))}^{{3/2}}} \times \\ \times \,\,\int\limits_\omega ^\infty {\frac{{\operatorname{sh} \frac{{\pi \varsigma }}{{2(\pi - \theta )}}}}{{{{{\operatorname{ch} }}^{2}}\frac{{\pi \varsigma }}{{2(\pi - \theta )}}}}\frac{{d\varsigma }}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \omega } }}} , \\ \end{gathered} $

или

(25)

$\begin{gathered} \sigma (\omega ) = \frac{V}{{(\theta - \pi )R}}{{(\operatorname{ch} {\kern 1pt} \omega - \cos (\pi - \theta ))}^{{3/2}}} \times \\ \times \,\,\int\limits_{\varsigma = \omega }^\infty {\frac{{d\operatorname{sech} \frac{{\pi \varsigma }}{{2(\pi - \theta )}}}}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \omega } }}} . \\ \end{gathered} $

Имеют место следующие соотношения для $\varphi $, ω и $\xi $ (рис. 3):

(26)

$r = \frac{{R{\kern 1pt} \operatorname{sh} {\kern 1pt} \omega }}{{\operatorname{ch} {\kern 1pt} \omega - \cos {\kern 1pt} \xi }},$

(27)

$z = \frac{{R{\kern 1pt} \sin {\kern 1pt} \xi }}{{\operatorname{ch} {\kern 1pt} \omega - \cos {\kern 1pt} \xi }},$

(28)

$\operatorname{ch} {\kern 1pt} \omega = \frac{{{{{\sin }}^{2}}{\kern 1pt} \theta }}{{\cos {\kern 1pt} \varphi - \cos {\kern 1pt} \theta }} - \cos {\kern 1pt} \theta ,$

(29)

$\omega (\varphi ) = \frac{1}{2}\ln \frac{{1 - \cos (\theta + \varphi )}}{{1 - \cos (\theta - \varphi )}},{\text{ где }}\varphi \in [0,\theta ].$

Используя (26)–(29), можно определить координату ω, соответствующую произвольной точке P, характеризуемой полярным углом φ на поверхности сегмента. Тогда поверхностная плотность заряда в данной точке поверхности сегмента может быть определена по формуле (24). Таким образом, можно найти явную зависимость $\sigma $ от $\varphi $ (рис. 1б, 1в):

(30)

$\begin{gathered} \sigma (\varphi ) = \frac{{\pi V}}{{{{{(\pi - \theta )}}^{2}}R}}\frac{{{{{\sin }}^{3}}{\kern 1pt} \theta }}{{\cos {\kern 1pt} \varphi - \cos {\kern 1pt} \theta }} \times \\ \times \,\,\int\limits_\varphi ^\theta {\frac{{{{{(1 - \cos (\theta + \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}} - {{{(1 - \cos (\theta - \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}}}}{{{{{\left( {{{{(1 - \cos (\theta + \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}} + {{{(1 - \cos (\theta - \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}}} \right)}}^{2}}}}} \times \\ \times \,\,\frac{{{{{(\cos {\kern 1pt} \beta - \cos {\kern 1pt} \theta )}}^{{\frac{\pi }{{2(\pi - \theta )}} - \frac{1}{2}}}}d\beta }}{{\sqrt {\cos {\kern 1pt} \varphi - \cos {\kern 1pt} \beta } }}. \\ \end{gathered} $

Полный заряд на выпуклой поверхности сегмента дается формулой

(31)

$Q = 2\pi {{R}^{2}}\int\limits_1^\infty {\frac{{\sigma {\kern 1pt} \operatorname{sih} {\kern 1pt} \omega }}{{{{{(\operatorname{ch} {\kern 1pt} \omega - \cos (\pi - \theta ))}}^{2}}}}d\omega } ,$

откуда

(32)

$\begin{gathered} Q = \frac{{{{\pi }^{2}}RV}}{{{{{(\pi - \theta )}}^{2}}}}\int\limits_{\omega = 1}^\infty {\frac{{\operatorname{sh} \omega }}{{\sqrt {\operatorname{ch} {\kern 1pt} \omega - \cos (\pi - \theta )} }}} \times \\ \times \,\,\left[ {\int\limits_\omega ^\infty {\frac{{\operatorname{sh} \frac{{\pi \varsigma }}{{2(\pi - \theta )}}}}{{{{{\operatorname{ch} }}^{2}}\frac{{\pi \varsigma }}{{2(\pi - \theta )}}}}\frac{{d\varsigma }}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \omega } }}} } \right]d\omega . \\ \end{gathered} $

Потенциал проводящей линзы $\psi (\omega ,\xi )$, определяемый формулой (20), вне линзы удовлетворяет уравнению Лапласа, а на поверхности линзы принимает постоянное значение. Таким образом, такой потенциал формально является решением задачи (1) с учетом замены $\psi (\omega ,\xi )$ на $n(\omega ,\xi )$. Используя эту аналогию, можно применить уравнение (20) для описания плотности пара

(33)

$\begin{gathered} n(\omega ,\xi ) = {{n}_{S}} - \frac{{2({{n}_{S}} - {{n}_{\infty }})}}{{\pi - \theta }} \times \\ \times \,\,{{(\operatorname{ch} {\kern 1pt} \omega - \cos {\kern 1pt} \xi )}^{{1/2}}}\cos \frac{{\pi \xi }}{{2(\pi - \theta )}} \times \\ \times \,\,\int\limits_{\varsigma = \omega }^\infty {{{{\left( {\operatorname{ch} \frac{{\pi \varsigma }}{{(\pi - \theta )}} - \cos \frac{{\pi \xi }}{{(\pi - \theta )}}} \right)}}^{{ - 1}}}\frac{{\operatorname{sh} \frac{{\pi \varsigma }}{{2(\pi - \theta )}}d\varsigma }}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \omega } }}} . \\ \end{gathered} $

Плотность потока испарения, отвечающая формуле (4), может быть записана с учетом выражений (24), (25) и (30)

(34)

$\begin{gathered} J(\omega ) = \frac{{D({{n}_{S}} - {{n}_{\infty }})}}{{(\pi - \theta )R}}{{(\operatorname{ch} {\kern 1pt} \omega - \cos (\pi - \theta ))}^{{3/2}}} \times \\ \times \,\,\int\limits_{\varsigma = \omega }^\infty {\frac{{d{\kern 1pt} \operatorname{sh} \frac{{\pi \varsigma }}{{2(\pi - \theta )}}}}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \omega } }}} . \\ \end{gathered} $

Или, переходя из биполярных в полярные координаты,

(35)

$\begin{gathered} J(\varphi ) = \frac{{\pi D({{n}_{S}} - {{n}_{\infty }})}}{{{{{(\pi - \theta )}}^{2}}R}}\frac{{{{{\sin }}^{3}}\theta }}{{\cos {\kern 1pt} \varphi - \cos {\kern 1pt} \theta }} \times \\ \times \,\,\int\limits_\varphi ^\theta {\frac{{{{{(1 - \cos (\theta + \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}} - {{{(1 - \cos (\theta - \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}}}}{{{{{\left( {{{{(1 - \cos (\theta + \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}} + {{{(1 - \cos (\theta - \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}}} \right)}}^{2}}}}} \times \\ \times \,\,\frac{{{{{(\cos {\kern 1pt} \beta - \cos {\kern 1pt} \theta )}}^{{\frac{\pi }{{2(\pi - \theta )}} - \frac{1}{2}}}}d\beta }}{{\sqrt {\cos {\kern 1pt} \varphi - \cos {\kern 1pt} \beta } }}. \\ \end{gathered} $

Интегральная скорость испарения, соответствующая формулам (5)–(7), представляющая собой интеграл от плотности потока пара по поверхности капли, имеет вид

(36)

$\begin{gathered} W = \frac{{{{\pi }^{2}}RD({{n}_{S}} - {{n}_{\infty }})}}{{{{{(\pi - \theta )}}^{2}}}}\int\limits_0^\infty {\frac{{\operatorname{sh} {\kern 1pt} \omega }}{{\sqrt {\operatorname{ch} {\kern 1pt} \omega - \cos (\pi - \theta )} }} \times } \\ \times \,\,\left[ {\int\limits_\omega ^\infty {\frac{{\operatorname{sh} \frac{{\pi \varsigma }}{{2(\pi - \theta )}}}}{{{{{\operatorname{ch} }}^{2}}\frac{{\pi \varsigma }}{{2(\pi - \theta )}}}}\frac{{d\varsigma }}{{\sqrt {\operatorname{ch} {\kern 1pt} \varsigma - \operatorname{ch} {\kern 1pt} \omega } }}} } \right]d\omega . \\ \end{gathered} $

Уравнение (35) удобно переписать в виде

(37)

$J(\varphi ) = \frac{{D({{n}_{S}} - {{n}_{\infty }})}}{R}f(\varphi ),$

где

(38)

$\begin{gathered} f(\varphi ) = \frac{\pi }{{{{{(\pi - \theta )}}^{2}}}}\frac{{{{{\sin }}^{3}}{\kern 1pt} \theta }}{{\cos {\kern 1pt} \varphi - \cos {\kern 1pt} \theta }} \times \\ \times \,\,\int\limits_\varphi ^\theta {\frac{{{{{(1 - \cos (\theta + \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}} - {{{(1 - \cos (\theta - \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}}}}{{{{{\left( {{{{(1 - \cos (\theta + \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}} + {{{(1 - \cos (\theta - \beta ))}}^{{\frac{\pi }{{2(\pi - \theta )}}}}}} \right)}}^{2}}}}} \times \\ \times \,\,\frac{{{{{(\cos {\kern 1pt} \beta - \cos {\kern 1pt} \theta )}}^{{\frac{\pi }{{2(\pi - \theta )}} - \frac{1}{2}}}}d\beta }}{{\sqrt {\cos {\kern 1pt} \varphi - \cos {\kern 1pt} \beta } }}. \\ \end{gathered} $

Напомним, что в этих формулах R – радиус круга, который занимает капля на подложке. Иногда (в случае контактных углов больше 90°) бывает удобнее использовать радиус сегмента, описывающего кривизну поверхности капли: $\rho = R{\text{/}}{\kern 1pt} \sin {\kern 1pt} \theta $.

Таким образом, формула (35) дает поток испарения капли как явную функцию полярного угла $\varphi $ (рис. 3), что с вычислительной точки зрения является принципиальным преимуществом этой формулы по сравнению с применявшимся ранее аналитическим выражением (4).

ОБСУЖДЕНИЕ

Введем безразмерную скорость испарения капли в соответствии с формулой

(39)

$\tilde {W}(\theta ) = \frac{{W(\theta )}}{{\pi D({{n}_{S}} - {{n}_{\infty }})\rho ,}}$

и сравним скорости испарения, вычисленные полном в диапазоне контактных углов $\theta \in [0,\pi ]$ по формулам Попова (5), Пикнетта и Бэксона (6), а также по формуле (36), впервые предложенной в [22].

Рис. 4 показывает, что три указанные формулы во всем диапазоне изменения контактного угла дают тождественный результат с точностью до погрешности расчета, за исключением узкой области около контактного угла $\theta \to \pi $ на самом краю области определения, где формула Попова имеет разрыв, не имеющий физического смысла.

Рис. 4.

Графики безразмерной скорости испарения капли (39), вычисленные по формулам Попова (5), Пикнетта и Бэксона (6), а также по новой формуле (36). Вплоть до области около $\theta = \pi $ три графика неразличимы. На врезке дана увеличенная область вблизи $\theta = \pi $, где сплошной линией, резко спадающей от значения $4{\kern 1pt} \ln {\kern 1pt} 2$ до значения 2, представлен график (5), а не имеющий такой особенности пунктир соответствует формулам (6) и (36).

Действительно, формула Пикнетта и Бэксона при $\theta = \pi $ дает (рис. 4)

(40)

$\tilde {W}(\pi ) = 4{\kern 1pt} \ln {\kern 1pt} 2,$

как и должно быть согласно точному решению, приведенному в [17]. Формула Попова (5) при $\theta = \pi $ дает

(41)

${{\tilde {W}}_{P}}(\pi ) = 2,$

что является ложным результатом. Однако на небольшом расстоянии от $\theta = \pi $ в сторону меньших контактных углов (рис. 4) формула Попова имеет правильное значение

(42)

$\mathop {\lim }\limits_{\theta \to \pi - } {{\tilde {W}}_{P}}(\theta ) = 4{\kern 1pt} \ln {\kern 1pt} 2,$

совпадающее с (40).

Причина такого поведения формулы (5) связана, очевидно, не с исходной математической моделью, поскольку формулы (6) и (36), основанные той же самой модели, ведут себя плавно вблизи $\theta = \pi $, а с процедурой интегрирования плотности потока (4). Действительно, для получения формулы (5) из (4) необходимо найти интеграл $\int_1^\infty {{{{(x + \cos {\kern 1pt} \theta )}}^{{ - 1/2}}}{{P}_{{ - 1/2 + i\tau }}}(x)dx} $. Попов в своей работе [2], где впервые опубликована формула (5), использует решение (2.17.1.10), приведенное в справочнике [24]. Можно убедиться, что применение указанного решения для взятия вышеприведенного интеграла происходит с нарушением указанных в [24] условий применимости. Это делает формулу (5) в целом не вполне корректной, хотя, как показывают непосредственные расчеты, практически пригодной в широком диапазоне контактных углов, не слишком близких к $\pi $.

Таким образом, формула Попова имеет ограничение в применимости со стороны больших контактных углов, и ее область определения должна быть скорректирована исключением области $\theta \to \pi $ из области определения: $\theta \in [0,\pi ]$. Численный расчет по формуле (36) при этом вполне соответствует расчету по выражению (6) во всем диапазоне контактных углов, однако нельзя не признать, что с практической точки зрения формула (6) гораздо удобнее, чем (36).

Дополнительная проверка новых формул может быть проведена расчетом асимптотической плотности потока испарения в пределе $\theta \to 0$, отвечающем приближению теории смазки (lubrication approximation). При этом уравнение (38) имеет вид

(43)

$f(\varphi ) \approx \frac{{2\theta }}{\pi }{{({{\theta }^{2}} - {{\varphi }^{2}})}^{{ - \frac{1}{2}}}},$

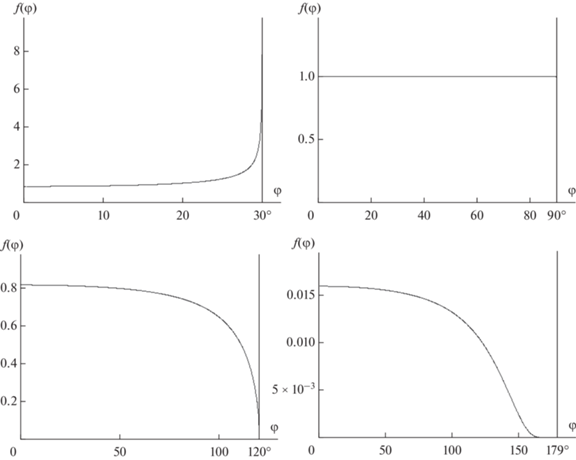
или, с учетом $r \approx \rho \varphi $ и $R \approx \rho \theta $, где r – цилиндрическая координата, отвечающая данному полярному φ (рис. 1), получаем

(44)

$J(r) \approx \frac{{2D({{n}_{s}} - {{n}_{\infty }})}}{{\pi R}}{{\left( {1 - \frac{{{{r}^{2}}}}{{{{R}^{2}}}}} \right)}^{{ - 1/2}}},$

т.е. в точности имеет место соотношение (8), как должно быть в соответствии с формулой (4).

Графики функции (38) для различных значений краевых углов $\theta $, представлены на рис. 5. Поведение этой функции определяет зависимость плотности потока испарения (35) от полярного угла $\varphi $, который указан на рис. 1б и 1в. Вид этих кривых эквивалентен соответствующим выражениям [1, 2, 16], но имеет другое формальное представление $J(\varphi )$, более удобное для построения.

Рис. 5.

Графики функции$f(\varphi )$, определяемой формулой (38), при различных значениях контактного угла ($\theta $ = 30°, 90°, 120°, 179°) описывают безразмерную плотность потока испарения с поверхности капли в зависимости от полярного угла φ, который изменяется в пределах от 0° до $\theta $.

Действительно, уравнение (35) содержит явную зависимость плотности потока от полярного угла $\varphi $, тогда как формула (4), предлагаемая О.Ю. Поповым и соавторами, имеет вид $J(\alpha )$и пересчитывается по формулам (3) в функцию $J(\alpha (r))$, зависящую от цилиндрической координаты r. Это приводит к неоднозначности значений потока в капле с контактным углом, большим 90°, что очевидно из рис. 1б: одному и тому же r могут отвечать две разные точки на поверхности, характеризуемые двумя разными значениями полярного угла $\varphi $.

Поведение плотности потока испарения при контактных углах, меньших 90°, вблизи края капли заслуживает специального обсуждения. Согласно формулам (4) и (3357), дающим эквивалентные результаты, плотность потока испарения на краю капли имеет бесконечное значение. Это следует также и из формулы (44). Данная особенность является интегрируемой, т.е. интеграл плотности потока по поверхности капли при этом имеет конечное значение, что, в частности, удостоверяется рис. 4. Однако, наличие указанной математической особенности плотности потока, полученной в диффузионном приближении, указывает на ограничения этого приближения с физической точки зрения.

Действительно, согласно молекулярно-кинетической теории, максимальная плотность потока испарения при данной температуре лимитируется скоростью испарения с единицы площади поверхности капли в вакуум, определяемой уравнением Герца−Кнудсена:

(45)

${{J}_{{\max }}} = \frac{{{{p}_{s}}}}{{\sqrt {2\pi m{{k}_{B}}T} }},$

где ${{p}_{s}} = {{n}_{s}}{{k}_{B}}T$ – давление насыщенного пара, ${{k}_{B}}$ – постоянная Больцмана, T – температура поверхности капли, m – масса молекулы пара.

Из этих же соображений можно оценить минимальный размер капли, который можно рассматривать в диффузионном приближении. Приравняем поток испарения сферической капли радиуса R в газе среднего давления, а именно, величину $W = 4\pi {{R}_{0}}D{{n}_{s}}$ [14, 18], среднему потоку вещества той же капли, покидающему ее в единицу времени в силу теплового движения молекул на границе капли и окружающей среды $W{\kern 1pt} ' = 4\pi R_{0}^{2}{{J}_{{\max }}}$.

Отсюда получаем выражение для критического радиуса (при котором скорость диффузионного испарения сравнялась бы со скоростью испарения в вакуум):

(46)

${{R}_{0}} = D\sqrt {\frac{{2\pi m}}{{{{k}_{B}}T}}} .$

С учетом того, что коэффициент диффузии пара в воздухе

(47)

$D \propto \tilde {l}\sqrt {\frac{{{{k}_{B}}T}}{m}} ,$

где $\tilde {l}$ – средняя длина свободного пробега молекулы пара в воздухе, оценка радиуса приобретает вполне ожидаемый вид: ${{R}_{0}} \propto \tilde {l}$. Очевидно, что диффузионное приближение справедливо при медленном испарении: $W \ll W{\kern 1pt} '$, т.е. при размерах, много больших чем длина свободного пробега. Отсюда для минимальной длины усреднения в диффузионном приближении L будем иметь:

(48)

$L \gg \tilde {l}.$

Практически речь идет о длинах, больших 1 мкм. Эта величина устанавливает, в частности, и порядок минимальной дистанции отступа от края капли, на которой плотность потока испарения с поверхности капли при краевом угле, меньшем 90°, в диффузионном приближении все еще имеет достоверные значения.

Строго говоря, обсуждаемая модель применима для капель простых медленно испаряющихся жидкостей, форму которых можно описать шаровым сегментом, т.е. достаточно малых по сравнению с капиллярной постоянной, но и достаточно больших по сравнению с длиной свободного пробега молекулы пара в окружающем воздухе. Описание капель меньшего размера нарушает диффузионное приближение и требует учета кинетических эффектов [18, 25]. Высокие скорости испарения могут нарушать условие квазистационарности, а также делают необходимым учет температурных градиентов, связанных с теплоообменом между каплей и окружающей средой. Наличие высоких градиентов температуры может привести к возникновению термокапиллярных потоков Марангони [26, 27], влияющих как на теплообмен, так и на форму капли. Рассмотрение бинарных и более сложных растворов жидкостей [28], применение поверхностно активных веществ, модифицирующих свойства поверхности капли [29], требует учета диффузионных, тепловых и конвективных процессов в объеме капли и в окружающей воздушной среде.

ВЫВОДЫ

Предложены новые аналитические выражения для плотности пара, плотности потока испарения и полного потока испарения в единицу времени для квазистационарно медленно испаряющейся малой осесимметричной капли на плоской подложке с произвольным значением контактного угла в рамках приближения малости температурных градиентов во всех частях системы. При выводе использовалось известное в электростатике решение уравнения Лапласа для плоского клина, преобразованное методом инверсии на сфере в решение для линзы в биполярных координатах. Новые выражения математически эквивалентны формулам в тороидальных координатах, предложенным ранее, однако плотность потока испарения в биполярных координатах имеет более простую форму однократного интеграла от комбинации элементарных функций, что дает преимущества с вычислительной точки зрения.

Проведена валидация новых формул путем сравнения скорости испарения (36) с ранее предложенными аналогами, а также установлена асимптотика плотности потока испарения (35) при малых контактных углах. Показана эквивалентность новых формул их аналогам.

Новые выражения справедливы для капли с любым контактным углом в диапазоне $\theta \in [0,\pi ]$. Показано, что плотность потока испарения, выведенную в биполярных координатах, можно выразить как явную функцию полярного угла φ (рис. 1б, 1в), имеющую вид однократного интеграла от выражения, состоящего только из элементарных функций, тогда как ранее предложенное выражение (4) представляет фактически двукратный интеграл (с учетом интегрального представления для функции Лежандра ${{P}_{{ - 1/2 + i\tau }}}(\operatorname{ch} {\kern 1pt} \alpha )$), зависящий от тороидальной координаты $\alpha \,$, неудобной для непосредственного использования и требующей пересчета в цилиндрическую систему.

Таким образом, для исследования плотности потока испарения более удобно использовать новую формулу (35), чем ее аналог (4). Однако если говорить об интегральной скорости испарения, то формула Пикнетта и Бэксона (6), являясь очень точной аппроксимацией аналитического решения, имеет преимущества перед ее аналитическими аналогами (5) и (36), оставаясь непревзойденной в практически значимых расчетах интегральной скорости испарения.

Вклады авторов: П.В. Лебедев-Степанов – вывод основных соотношений и асимптотики, О.А. Савенко – численные расчеты и построение графиков.

Список литературы

Deegan R.D., Bakajin O., Dupont T.F., Huber G., Nagel S.R., Witten T.A. // Phys. Rev. E 2000, V. 62. P. 756.
Popov Yu.O. // Phys. Rev. E. 2005. V. 71. P. 036313.
Brutin D., Starov V. // Chem. Soc. Rev. 2018. V. 47. P. 558.
Schnall-Levin M., Lauga E., Brenner M.P. // Langmuir. 2006. V. 22. P. 4547.
Zang D., Tarafdar S., Tarasevich Yu.Yu., Choudhury M.D., Dutta T. // Phys. Rep. 2019. V. 804. P. 1.
Talbot E.L., Yow H.N., Yang L., Berson A., Biggs S.R., Bain C.D. // ACS Appl. Mater. Interfaces. 2015. V. 7. P. 3782.
Gambaryan-Roisman T. // Eng Math. 2012. V. 73. P. 39.
Hamadeh L., Imran S., Bencsik M., Sharpe G.R., Johnson M.A., Fairhurst D.J. // Sci. Rep. 2020. V. 10. P. 3313.
Lebedev-Stepanov P.V., Buzoverya M.E., Vlasov K.O., Potekhina Yu.P. // J. of Bioinformatics and Genomics. 2018. V. 4. P. 1.
Kolegov K., Barash L. // Adv. Colloid and Interface Sci. 2020. V. 285. P. 102271.
Hoath. S.D. Fundamentals of Inkjet Printing. The Science of Inkjet and Droplets. Weinheim: Wiley-VCH Verlag GmbH & Co, 2016.
Kokornaczyk M.O., Bodrova N.B., Baumgartner S. // Coll. and Surf. B: Biointerfaces. 2021. V. 208. P. 112092.
Lebedev-Stepanov P., Vlasov K. // Coll. and Surf. A: Physicochem. Eng. Aspects. 2013. V. 432. P. 132.
Лебедев-Степанов П.В. Введение в самоорганизацию и самосборку ансамблей наночастиц. М.: НИЯУ МИФИ, 2015.
Лебедев Н.Н. Специальные функции и их приложения. М.: Физматгиз, 1963.
Hu H., Larson R.G.J. // J. Phys. Chem. B. 2002. V. 106. P. 1334.
R. G. Picknett, R. Bexon, J. Colloid Interface Sci. 1977. V. 61. P. 336.
Фукс Н.А. Испарение и рост капель в газообразной среде. М.: Изд-во АН СССР, 1958.
Macdonald H.M. // Proc. Lond. Math. Soc. 1895. V. S.1-26(1), P. 156.
Maxwell J.C. A Treatise on Electricity and Magnetism. V. 1. Oxford: Clarendon Press, 1873.
Гринберг Г.А. Избранные вопросы математической теории электрических и магнитных явлений. М.: Изд-во АН СССР, 1948.
Lebedev-Stepanov P. // arXiv:2103.15582v3. 2021.
Lebedev-Stepanov P. // Proc. 5th Int. Conf. on Droplets. Darmstadt. 2021. P. 231.
Prudnikov A.P., Brychkov Y.A., Marichev O.I. Integrals and Series. V. 3. London: Gordon and Breach, 1986.
Vlasov V.A. // Int. J. Heat Mass Transfer. 2021.V. 178. P 121597.
Hu H., Larson R.G.J. // J. Phys. Chem. B. 2006. V. 110. № 14. P.
Lebedev-Stepanov P., Kobelev A., Efimov S. // Proc. Int. Symposium “Interfacial Phenomena and Heat Transfer” (IPHT 2016). MATEC Web of Conferences. 2016. V. 84. P. 22(1–4).
Бородулин Ю.В., Летушко В.Н., Низовцев М.И., Стерлягов А.Н. // Коллоид. журн. 2021. Т. 83. № 3. С. 251.
Терехов В.И., Шишкин Н.Е. // Коллоид. журн. 2021. Т. 83. № 1. С. 107.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал