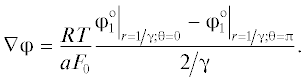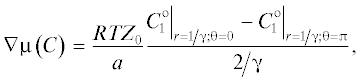1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 84, № 3, 2022

Коллоидный журнал, 2022, T. 84, № 3, стр. 350-362

Ячеечная модель ионообменной мембраны. Капиллярно-осмотический и обратноосмотический коэффициенты

А. Н. Филиппов *

РГУ нефти и газа (НИУ) имени И.М. Губкина
119991 Москва, Ленинский просп., 65, корп. 1, Россия

* E-mail: filippov.a@gubkin.ru

Поступила в редакцию 02.03.2022
После доработки 18.03.2022
Принята к публикации 21.03.2022

Полный текст (PDF)

Аннотация

В рамках термодинамики неравновесных процессов, на основе ранее предложенной автором ячеечной модели заряженного пористого слоя, вычислены капиллярно-осмотический и обратноосмотический коэффициенты ионообменной мембраны, рассматриваемые как кинетические коэффициенты матрицы Онзагера. Предполагается, что мембрана состоит из упорядоченной совокупности полностью пористых заряженных частиц сферической формы, помещенных в сферические оболочки, заполненные раствором бинарного электролита. Аналитически решены краевые задачи для определения капиллярно-осмотического и обратноосмотического коэффициентов такой мембраны в случае граничного условия Кувабары на поверхности ячейки. Рассмотрение ведется в рамках малого отклонения параметров системы от своих равновесных значений при наложении внешних полей. Исследованы различные частные случаи полученных точных аналитических формул, в том числе бинарного симметричного электролита и идеально-селективной мембраны. Показано, что для рассматриваемой ячеечной модели ионообменной мембраны нарушается принцип взаимности Онзагера – найденные перекрестные кинетические коэффициенты не равны между собой. Нарушение связывается с тем обстоятельством, что принцип взаимности работает только для систем в рамках линейной термодинамики необратимых процессов, для которых обобщенные потоки равны нулю при отличных от нуля термодинамических силах.

СПИСОК ОБОЗНАЧЕНИЙ

Латинские символы

a                        Радиус частицы

b                        Радиус ячейки

d                        Толщина ДЭС

$k$                       Константа Бринкмана

${{k}_{{\text{D}}}} = {{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} k}} \right. \kern-0em} k}$     Удельная гидродинамическая проницаемость ионитового зерна по Бринкману

$C$                      Концентрация электролита

${{C}_{0}}$                   Эквивалентная концентрация рав                             новесного с мембраной электролита

D, D0             Коэффициент диффузии, характер-                             ный коэффициент диффузии

$I$                      Плотность потока подвижных заря                                 дов  (плотность электрического тока)

$J$                     Плотность диффузионного потока

j                       Безразмерная плотность диффузион-                           ного потока

F0                    Постоянная Фарадея

h                 Толщина мембраны

$m = {{{{{{\mu }}}^{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{i}}}}} {{{{{\mu }}}^{{\text{o}}}}}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{o}}}}}}$              Отношение вязкостей жидко-                                       сти в среде Бринкмана и                                            чистой жидкости

${{m}_{0}} = {\text{1 - }}{{{{\gamma }}}^{3}}$                Макроскопическая пористость                                           мембраны

Lij                             Кинетические коэффициенты                                           матрицы Онзагера

r                                  Радиальная координата

$R$                              Универсальная газовая посто-                                      янная

$T$                                Абсолютная температура

p                                 Давление

${{p}_{0}} = RT{{C}_{0}}$     Характерное осмотическое                                          давление

${\text{Pe}} = \frac{{a{{U}_{0}}}}{{{{D}_{0}}}}$                Число Пекле

${{R}_{{\text{b}}}} = \sqrt {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} k}} \right. \kern-0em} k}} = \sqrt {{{k}_{{\text{D}}}}} $ Радиус Бринкмана (ширина                                              зоны фильтрации в пористой                                              среде)

${{s}^{2}} = {{{{a}^{2}}k} \mathord{\left/ {\vphantom {{{{a}^{2}}k} {{{{{\mu }}}^{{\text{i}}}}}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{i}}}}}}$               Безразмерный параметр

${{s}_{0}}^{2} = m{{s}^{2}} = {{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} {R_{{\text{b}}}^{2}}}} \right. \kern-0em} {R_{{\text{b}}}^{2}}}$  Безразмерный параметр

${{U}_{0}} = {{a{{p}_{0}}} \mathord{\left/ {\vphantom {{a{{p}_{0}}} {{{{{\mu }}}^{{\text{o}}}}}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{o}}}}}}$             Характерная скорость филь-                                             трации

$U$                                  Плотность потока раствори-                                         теля (воды)

v                                     Вектор скорости

Z±                                 Зарядовые числа ионов (без                                              знака)

Греческие символы

${{\gamma }} = {a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}$       Безразмерный параметр

${{\delta }} = {d \mathord{\left/ {\vphantom {d a}} \right. \kern-0em} a}$       Безразмерная толщина ДЭС

$\nabla $                   Оператор градиента

ε0 и ε            Диэлектрическая постоянная и отно-                          сительная диэлектрическая проница-                             емость среды

${{{{\mu }}}^{{\text{o}}}}$                  Вязкость чистой жидкости

${{{{\mu }}}^{{\text{i}}}}$                Вязкость жидкости в среде Бринк-                          мана

μ                     Химический потенциал

μ0                    Стандартный химический потенциал

φ                    Электрический потенциал

–ρV                Объемная плотность фиксированно-                           го заряда пористого скелета (катио-                           нообменника)

${{\bar {\rho }}} = \frac{{{{{{\rho }}}_{{\text{V}}}}}}{{{{F}_{0}}}}\,\,$         Обменная емкость ионитового зерна                               (абсолютная величина)

${{\sigma }} = \frac{{{{{{\rho }}}_{{\text{V}}}}}}{{{{F}_{0}}{{C}_{0}}}}$      Безразмерная обменная емкость

${{{{\bar {\rho }}}}_{0}} = \frac{{{{{{\mu }}}^{{\text{o}}}}{{D}_{ + }}}}{{{{k}_{{\text{D}}}}RT}}\,$ Характерная обменная емкость

Φi                Градиенты внешних сил, действующих                           на ячейку и мембрану

Индексы

“1”       Указывает на физическую величи-                           ну отклонения от ее равновесного зна-                           чения

“e”              Указывает на равновесное значение

“o”             Указывает на величину, относящуюся                            к жидкой оболочке ячейки

“I”             Указывает на величину, относящуюся                            к пористой частице в ячейке

~                 Тильда указывает на безразмерную ве-                        личину

“1” и “2” Указывают на левую и правую стороны                           мембраны, находящейся в измери-                          тельной ячейке

m               Указывает на величину, относящуюся                           к мембране

±                 Указывает на величину, относящуюся                            к катионам/анионам

ВВЕДЕНИЕ

Для исследования концентрированных дисперсных систем, в том числе мембран широко и эффективно применяется ячеечный метод, подробно изложенный Хаппелем и Бреннером в их известной монографии [1]. Ячеечная модель, например, ионообменной мембраны предполагает, в частности, замену реальной системы хаотически расположенных зерен ионита периодической решеткой одинаковых пористых заряженных сфер, заключенных в концентрические сферические оболочки, заполненные электролитом и образующие пористый слой. В ячеечном методе воздействие соседних частиц учитывается с помощью задания специальных граничных условий на поверхности жидкой оболочки. При этом предполагается, что градиенты действующих на пористый слой внешних сил совпадают с локальными градиентами на ячейке. Преимущество описанного подхода состоит в том, что все входящие в уравнения переноса через пористый слой величины – термодинамические потоки и силы можно непосредственно измерить в экспериментах. В работе [2] была построена ячеечная модель ионообменной мембраны, поставлена и решена в общем виде задача нахождения кинетических коэффициентов, а также впервые получена точная алгебраическая формула для гидродинамической проницаемости ${{L}_{{11}}}$ заряженной мембраны. Впоследствии c помощью разработанной в [2] модели были определены электроосмотическая проницаемость ${{L}_{{12}}}$ и удельная электропроводность ${{L}_{{22}}}$ катионообменной мембраны, а в работе [3] – диффузионная проницаемость ${{L}_{{33}}}$, а также электродиффузионный коэффициент ${{L}_{{23}}}$. Предложенная ячеечная модель была успешно верифицирована на экспериментальных данных, полученных для литой перфторированной мембраны МФ-4СК и ее модификаций нанотрубками галлуазита, функционализированными наночастицами платины и железа в водных растворах HCl, а также экструзионной мембраны МФ-4СК на ряде 1:1 электролитов (HCl, NaCl, KCl, LiCl, CsCl). Для определения физико-химических и геометрических параметров модели был создан специальный алгоритм и программа в вычислительной среде Mathematica® с целью одновременной оптимизации по экспериментальным зависимостям удельной электропроводности и электроосмотической проницаемости.

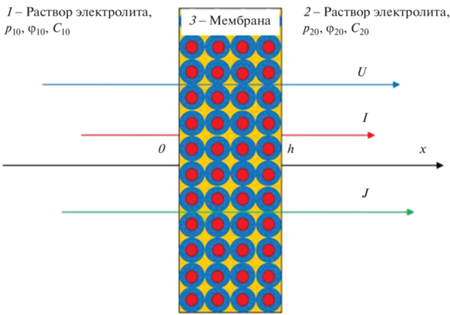
В данном исследовании в качестве независимых термодинамических сил, задаваемых в процессе проведения эксперимента, выберем градиенты давления, электрического потенциала и химического потенциала $\mu \left( C \right) = {{\mu }_{0}} + RT\ln \left( {{C \mathord{\left/ {\vphantom {C {{{C}_{0}}}}} \right. \kern-0em} {{{C}_{0}}}}} \right)$, соответственно: ${{{{\Phi }_{1}} = \nabla p \approx \left( {{{p}_{{20}}} - {{p}_{{10}}}} \right)} \mathord{\left/ {\vphantom {{{{\Phi }_{1}} = \nabla p \approx \left( {{{p}_{{20}}} - {{p}_{{10}}}} \right)} h}} \right. \kern-0em} h}$, ${{\Phi }_{2}} = \nabla {{\varphi }} \approx $ ${{ \approx \left( {{{{{\varphi }}}_{{20}}} - {{{{\varphi }}}_{{10}}}} \right)} \mathord{\left/ {\vphantom {{ \approx \left( {{{{{\varphi }}}_{{20}}} - {{{{\varphi }}}_{{10}}}} \right)} h}} \right. \kern-0em} h}$, ${{\Phi }_{3}} = \nabla \mu \left( C \right) \approx RT\left( {{{C}_{{20}}} - {{C}_{{10}}}} \right){\text{/(}}{{{\text{C}}}_{0}}h)$. Здесь ${{C}_{0}}$ – эквивалентная концентрация равновесного с мембраной электролита, μ0 – стандартный химический потенциал, h – толщина мембраны, $R$ – универсальная газовая постоянная, $T$ – абсолютная температура, а индексы “1” и “2” указывают на левую и правую стороны мембраны, находящейся в измерительной ячейке, заполненной раствором бинарного электролита (рис. 1). Для корректного вывода формул для кинетических коэффициентов, связанных с наличием перепада концентраций на мембране, в отличие от работы [2], вместо градиента концентрации здесь используется градиент химического потенциала, как и в работе [3].

Рис. 1.

Мембранная ячейка для исследования неравновесных процессов: 1 и 2 – отдающая и принимающая камеры, 3 – мембрана.

В качестве зависимых термодинамических параметров, определяемых в эксперименте, возьмем плотности потоков: $U$ – растворителя (воды, например), $I$ – подвижных зарядов (плотность электрического тока), $J$ – растворенного вещества (плотность диффузионного потока электролита). Тогда феноменологические транспортные уравнения в случае изотермических процессов могут быть записаны в виде следующей системы линейных уравнений:

(1)
$\left\{ \begin{gathered} U = - \left( {{{L}_{{11}}}\nabla p + {{L}_{{12}}}\nabla {{\varphi }} + {{L}_{{13}}}\nabla \mu } \right), \hfill \\ I = - \left( {{{L}_{{21}}}\nabla p + {{L}_{{22}}}\nabla {{\varphi }} + {{L}_{{23}}}\nabla \mu } \right), \hfill \\ J = - \left( {{{L}_{{31}}}\nabla p + {{L}_{{32}}}\nabla {{\varphi }} + {{L}_{{33}}}\nabla \mu } \right). \hfill \\ \end{gathered} \right.$

В соответствии с принципом взаимности Онзагера, матрица кинетических коэффициентов должна быть симметричной: ${{L}_{{ik}}} = {{L}_{{ki}}}\,\,\left( {i \ne k} \right)$. Однако, как будет показано ниже, это свойство в нашем случае перестает быть справедливым. Здесь мы будем обсуждать вычисление капиллярно-осмотического ${{L}_{{13}}}$ и обратноосмотического ${{L}_{{31}}}$ коэффициентов ионообменной мембраны, которые могут быть найдены по формулам, вытекающим из (1):

(2а)
${{L}_{{13}}} = - {{\left. {\frac{U}{{\nabla {{\mu }}}}} \right|}_{{\nabla p = 0,\nabla {{\varphi }} = 0}}},$
(2б)
${{L}_{{31}}} = - {{\left. {\frac{J}{{\nabla p}}} \right|}_{{\nabla {{\mu }} = 0,\nabla {{\varphi }} = 0}}}.$

Соотношения (2) означают, что корректное измерение коэффициента ${{L}_{{13}}}$ возможно только при отсутствии перепадов давления и электрического потенциала и заданном постоянном перепаде химического потенциала ${{{{\mu }}}_{{20}}} - {{{{\mu }}}_{{10}}} \approx h\nabla {{\mu }} = {\text{const}}$ на мембране, а коэффициента ${{L}_{{31}}}$ – при отсутствии перепадов химического и электрического потенциалов и заданном постоянном перепаде давления ${{p}_{{20}}} - {{p}_{{10}}} \approx h\nabla p = {\text{const}}$.

ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ

Будем моделировать заряженную мембрану периодической решеткой пористых заряженных сферических частиц одного и того же радиуса $a$, заключенных в жидкие сферические оболочки радиуса $b$, который выбирается таким образом, чтобы отношение объема частицы к объему ячейки равнялось объемной доле частиц в дисперсной системе:

(3)
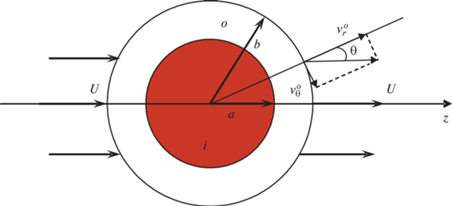
${{{{\gamma }}}^{3}} = {{\left( {{a \mathord{\left/ {\vphantom {a b}} \right. \kern-0em} b}} \right)}^{3}} = 1 - {{m}_{0}},$
где ${{m}_{0}}$ – макроскопическая пористость, зависящая от способа упаковки пористых частиц в заряженном слое (мембране) – рис. 2.

Рис. 2.

Единичная ячейка мембраны: o – внешняя область (раствор электролита), i – внутренняя область (заряженная пористая частица).

Математическая постановка задачи дана в работе [2] и здесь для краткости не повторяется. Обозначения переменных и параметров полностью совпадают с таковыми в статье [2]. Для удобства читателя список основных обозначений представлен в начале статьи. Движение несжимаемой жидкости (электролита) во внешней области $\left( {a < r < b} \right)$ описывается векторным дифференциальным уравнением Стокса при малых числах Рейнольдса (“ползущее течение”), дополненным пространственной электрической силой. Движение жидкости во внутренней области $\left( {0 \leqslant r < a} \right)$ подчиняется векторному дифференциальному уравнению Бринкмана [4], осложненному такой же пространственной электрической силой. Традиционно “жидкость Бринкмана” предполагается несжимаемой [5]. Электрический потенциал удовлетворяет уравнению Пуассона внутри и вне частиц, а для плотности потоков ионов используется представление Нернста–Планка. При этом в системе отсутствуют источники и стоки зарядов, а задача рассматривается в стационарной постановке. Пусть, как и ранее в работе [2], ${{{{\rho }}}_{{\text{V}}}}$ – объемная плотность фиксированного заряда пористого скелета. Для определенности примем заряд частицы отрицательным (моделируем катионообменную мембрану), тогда ${{{{\rho }}}_{{\text{V}}}} > 0$. Для удобства анализа используем те же безразмерные переменные и величины, что и в статье [2]:

(4)
$\begin{gathered} \tilde {r} = {r \mathord{\left/ {\vphantom {r {a,\,\,\,\,{\mathbf{\tilde {v}}} = {{\mathbf{v}} \mathord{\left/ {\vphantom {{\mathbf{v}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}}}} \right. \kern-0em} {a,\,\,\,\,{\mathbf{\tilde {v}}} = {{\mathbf{v}} \mathord{\left/ {\vphantom {{\mathbf{v}} {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}}},\,\,\,\,\tilde {p} = {p \mathord{\left/ {\vphantom {p {{{p}_{0}},\,\,\,\,{{{{{\tilde {\sigma }}}}}_{{r{{\theta }}}}} = {{{{{{\sigma }}}_{{r{{\theta }}}}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{r{{\theta }}}}}} {{{p}_{0}},}}} \right. \kern-0em} {{{p}_{0}},}}}}} \right. \kern-0em} {{{p}_{0}},\,\,\,\,{{{{{\tilde {\sigma }}}}}_{{r{{\theta }}}}} = {{{{{{\sigma }}}_{{r{{\theta }}}}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{r{{\theta }}}}}} {{{p}_{0}},}}} \right. \kern-0em} {{{p}_{0}},}}}} \\ {{{{{\tilde {\sigma }}}}}_{{rr}}} = {{{{{{\sigma }}}_{{rr}}}} \mathord{\left/ {\vphantom {{{{{{\sigma }}}_{{rr}}}} {{{p}_{0}},}}} \right. \kern-0em} {{{p}_{0}},}}\,\,\,\,{{{\tilde {C}}}_{ \pm }}{\text{ = }}{{{{C}_{ \pm }}} \mathord{\left/ {\vphantom {{{{C}_{ \pm }}} {{{C}_{0}}}}} \right. \kern-0em} {{{C}_{0}}}}{\text{,}}\,\,\,\,{{\tilde {\varphi }}} = \frac{{{{\varphi }}{{F}_{0}}}}{{RT}}, \\ {{{\mathbf{j}}}_{ \pm }} = \frac{{{{{\mathbf{J}}}_{ \pm }}}}{{{{U}_{0}}{{C}_{0}}}},\,\,\,\,{{\nu }_{ \pm }} = {{{{D}_{0}}} \mathord{\left/ {\vphantom {{{{D}_{0}}} {{{D}_{ \pm }},}}} \right. \kern-0em} {{{D}_{ \pm }},}}\,\,\,\,{{\nu }_{{{\text{m}} \pm }}} = {{{{D}_{0}}} \mathord{\left/ {\vphantom {{{{D}_{0}}} {{{D}_{{{\text{m}} \pm }}},}}} \right. \kern-0em} {{{D}_{{{\text{m}} \pm }}},}} \\ {\text{Pe}} = \frac{{a{{U}_{0}}}}{{{{D}_{0}}}},\,\,\,\,{{\sigma }} = \frac{{{{{{\rho }}}_{{\text{V}}}}}}{{{{F}_{0}}{{C}_{0}}}},\,\,\,\,{{p}_{0}} = RT{{C}_{0}}, \\ {{U}_{0}} = {{a{{p}_{0}}} \mathord{\left/ {\vphantom {{a{{p}_{0}}} {{{{{\mu }}}^{{\text{o}}}},\,\,\,\,{{\delta }} = {d \mathord{\left/ {\vphantom {d {a,}}} \right. \kern-0em} {a,}}}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{o}}}},\,\,\,\,{{\delta }} = {d \mathord{\left/ {\vphantom {d {a,}}} \right. \kern-0em} {a,}}}}\,\,\,\,m = {{{{{{\mu }}}^{{\text{i}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{i}}}}} {{{{{\mu }}}^{{\text{o}}}},}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{o}}}},}} \\ {{s}^{2}} = {{{{a}^{2}}k} \mathord{\left/ {\vphantom {{{{a}^{2}}k} {{{{{\mu }}}^{{\text{i}}}},}}} \right. \kern-0em} {{{{{\mu }}}^{{\text{i}}}},}}\,\,\,\,s_{0}^{2} = m{{s}^{2}} = {{{{a}^{2}}} \mathord{\left/ {\vphantom {{{{a}^{2}}} {R_{{\text{b}}}^{2}}}} \right. \kern-0em} {R_{{\text{b}}}^{2}}}, \\ \end{gathered} $
где ${{R}_{{\text{b}}}} = \sqrt {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} k}} \right. \kern-0em} k}} $ – характерная толщина фильтрационного слоя (радиус Бринкмана), ${{D}_{0}}$ – масштаб коэффициентов диффузии, $d = {{\left( {\frac{{{{C}_{0}}F_{0}^{2}}}{{\varepsilon {{\varepsilon }_{0}}RT}}} \right)}^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0em} 2}}}}$ – дебаевский радиус, Pe – число Пекле, ${{F}_{0}}$ – постоянная Фарадея. В дальнейшем тильда над безразмерными переменными будет для удобства опущена. Предполагая дебаевский радиус исчезающее малым по сравнению с радиусом частицы, двойные электрические слои (ДЭС) эффективно заменим скачками электрического потенциала и концентраций ионов при переходе через геометрическую межфазную границу $r = 1$ [2, 3]. При отсутствии внешних сил ${{\Phi }_{i}}$ $\,\,\left( {i = 1,2,3} \right)$ каждая ячейка мембраны находится в состоянии равновесия с окружающим ее покоящимся раствором электролита, т.е. скорости и плотности потоков ионов в этом состоянии равны нулю. При этом в системе устанавливаются равновесные распределения концентраций ионов $C_{{{\text{e}} \pm }}^{{\text{o}}},\,\,C_{{{\text{e}} \pm }}^{{\text{i}}}$ и электрического потенциала ${{\varphi }}_{{\text{e}}}^{{\text{o}}},\,\,{{\varphi }}_{{\text{e}}}^{{\text{i}}}$. Задача нахождения равновесных концентраций и потенциала была решена в работе [2] – см. формулы (28)–(32). Предполагая, что наложение внешнего поля приводит к малому отклонению искомых функций от их равновесных значений, и линеаризуя все уравнения и граничные условия краевой задачи на ячейке по этим малым отклонениям (имеют нижний индекс 1), приходим к справедливым всюду в ячейке уравнениям Лапласа для неизвестных потенциала и эквивалентной неравновесной концентрации электролита ${{C}_{1}} = {{Z}_{ + }}{{C}_{{1 + }}} = {{Z}_{ - }}{{C}_{{1 - }}}$ [2]:

(5)
$\Delta {{{{\varphi }}}_{1}} = 0,\,\,\,\,\Delta {{C}_{1}} = 0.$

Общее решение уравнений (5) представлено в работе [2]:

(6)
$\begin{gathered} {{\varphi }}_{1}^{{\text{o}}} = \left( {{{G}^{{\text{o}}}}r + \frac{{{{H}^{{\text{o}}}}}}{{{{r}^{2}}}}} \right)\cos {\kern 1pt} {{\theta }},\,\,\,\,C_{1}^{{\text{o}}} = \left( {{{L}^{{\text{o}}}}r + \frac{{{{M}^{{\text{o}}}}}}{{{{r}^{2}}}}} \right)\cos {\kern 1pt} {{\theta }} \\ {\text{при }}1 < r \leqslant {1 \mathord{\left/ {\vphantom {1 {{{\gamma ,}}}}} \right. \kern-0em} {{{\gamma ,}}}} \\ \end{gathered} $
(7)
$\begin{gathered} {{\varphi }}_{1}^{{\text{i}}} = {{G}^{{\text{i}}}}r\cos {\kern 1pt} {{\theta }},\,\,\,\,C_{1}^{{\text{i}}} = {{L}^{{\text{i}}}}r\cos {\kern 1pt} {{\theta ,}} \\ {\text{при }}0 \leqslant r < 1, \\ \end{gathered} $
где константы интегрирования ${{G}^{{{\text{o,i}}}}},\,\,{{L}^{{{\text{o,i}}}}},\,\,{{H}^{{\text{o}}}},\,\,{{M}^{{\text{o}}}}$ подлежат определению из граничных условий.

ОПРЕДЕЛЕНИЕ КАПИЛЛЯРНО-ОСМОТИЧЕСКОГО КОЭФФИЦИЕНТА

Сформулируем сначала граничные условия на единичной ячейке для этой краевой задачи. Линеаризация условий равенства электрохимических потенциалов ионов на межфазной границе позволяет записать [2, 3]:

(8)
$C_{1}^{{\text{o}}} = {{{{\alpha }}}^{{\text{o}}}}\left( {{{\varphi }}_{1}^{{\text{i}}} - {{\varphi }}_{1}^{{\text{o}}}} \right),\,\,\,\,C_{1}^{{\text{i}}} = {{{{\alpha }}}^{{\text{i}}}}\left( {{{\varphi }}_{1}^{{\text{i}}} - {{\varphi }}_{1}^{{\text{o}}}} \right){\text{ при }}r = 1,$
где обозначено
(9)
$\begin{gathered} {{{{\alpha }}}^{{\text{o}}}} = \frac{{{{Z}_{ + }}{{{{\beta }}}_{ + }} + {{Z}_{ - }}{{{{\beta }}}_{ - }}}}{{{\sigma }}},\,\,\,\,{{{{\alpha }}}^{{\text{i}}}} = \frac{{{{Z}_{ + }} + {{Z}_{ - }}}}{{{\sigma }}}{{{{\beta }}}_{ + }}{{{{\beta }}}_{ - }}, \\ {{{{\beta }}}_{ \pm }} = \frac{{\exp \left( { \mp {{Z}_{ \pm }}{{\varphi }}_{{\text{e}}}^{{\text{i}}}} \right)}}{{{{{{\gamma }}}_{ \pm }}}}, \\ \end{gathered} $
а ${{{{\gamma }}}_{ \pm }},\,\,\,\,{{{{\gamma }}}_{{\text{m}}}} = \sqrt {{{{{\gamma }}}_{ + }}{{{{\gamma }}}_{ - }}} $ – коэффициенты равновесного распределения ионов и молекул электролита в зерне ионита (геле), ${{\varphi }}_{{\text{e}}}^{{\text{i}}}$ – равновесный безразмерный электрический потенциал в нем, который находится из уравнения ${{{{\beta }}}_{ + }} - {{{{\beta }}}_{ - }} = {{\sigma }}$ [2].

На межфазной границе $r = 1$ должны выполняться условия равенства радиальных составляющих потоков ионов, которые приводят к следующей системе уравнений относительно неизвестных констант (см. (43а) в [2]):

(10)
$\begin{gathered} {\text{Pe}}{{u}_{{11}}}\left( {{{{{\beta }}}_{ + }} - 1} \right) = \frac{{{{L}^{{\text{i}}}} + {{Z}_{ + }}{{{{\beta }}}_{ + }}{{G}^{{\text{i}}}}}}{{{{\nu }_{{{\text{m}} + }}}}} - \\ - \,\,\frac{{{{L}^{{\text{o}}}} - 2{{M}^{{\text{o}}}} + {{Z}_{ + }}\left( {{{G}^{{\text{o}}}} - 2{{H}^{{\text{o}}}}} \right)}}{{{{\nu }_{ + }}}}, \\ {\text{Pe}}{{u}_{{11}}}\left( {{{{{\beta }}}_{ - }} - 1} \right) = \frac{{{{L}^{{\text{i}}}} - {{Z}_{ - }}{{{{\beta }}}_{ - }}{{G}^{{\text{i}}}}}}{{{{\nu }_{{{\text{m}} - }}}}} - \\ - \,\,\frac{{{{L}^{{\text{o}}}} - 2{{M}^{{\text{o}}}} - {{Z}_{ - }}\left( {{{G}^{{\text{o}}}} - 2{{H}^{{\text{o}}}}} \right)}}{{{{\nu }_{ - }}}}. \\ \end{gathered} $
Здесь, с учетом вида общего решения для радиальной компоненты скорости ${{u}_{1}}$, обозначено

(11)
${{u}_{{11}}} \equiv \frac{{{{{\left. {{{u}_{1}}} \right|}}_{{r = 1}}}}}{{\cos {\kern 1pt} {{\theta }}}}.$

Ячеечный градиент давления ${{\Phi }_{1}}$ был ранее определен как $\nabla p = {{ - F} \mathord{\left/ {\vphantom {{ - F} V}} \right. \kern-0em} V}$, где $V = {{4{{\pi }}{{b}^{3}}} \mathord{\left/ {\vphantom {{4{{\pi }}{{b}^{3}}} 3}} \right. \kern-0em} 3}$ – объем ячейки, а $F = - 4{{\pi }}Ba{{{{\mu }}}^{{\text{o}}}}{{U}_{0}}$ – сила, действующая со стороны жидкости на пористую заряженную частицу [1, 2], что приводит к формуле

(12)
${{\Phi }_{1}} = \nabla p = 3B{{{{\gamma }}}^{3}}\frac{{{{{{\mu }}}^{{\text{o}}}}{{U}_{0}}}}{{{{a}^{2}}}}.$

Ячеечный градиент электрического потенциала ${{\Phi }_{2}}$ был определен в [3]:

(13)

Аналогично работе [3] введем ячеечный градиент химического потенциала ${{\Phi }_{3}}$ на ячейке:

(14)
где ${{Z}_{0}} = {{\left( {{{Z}_{ + }} + {{Z}_{ - }}} \right)} \mathord{\left/ {\vphantom {{\left( {{{Z}_{ + }} + {{Z}_{ - }}} \right)} {{{Z}_{ + }}{{Z}_{ - }}}}} \right. \kern-0em} {{{Z}_{ + }}{{Z}_{ - }}}}$. При вычислении капиллярно-осмотического коэффициента ${{L}_{{13}}}$, как это следует из (2а), градиенты электрического потенциала и давления на мембране должны отсутствовать, а градиент химического потенциала быть постоянным,

(15)
${{\Phi }_{3}} = \frac{{RT{{Z}_{0}}}}{a}{\text{cons}}{{{\text{t}}}_{3}}.$

Первое условие ${{\Phi }_{2}} = 0$ с учетом (13) приводит к обнулению электрического потенциала на поверхности ячейки:

(16)
${{\varphi }}_{1}^{{\text{o}}} = 0\,\,{\text{при}}\,\,r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}.$

Подставляя общее решение (6) для потенциала в уравнение (16), имеем

(17)
${{G}^{{\text{o}}}} = - {{{{\gamma }}}^{3}}{{H}^{{\text{o}}}}.$

Второе условие ${{\Phi }_{1}} = 0$ с учетом (12) дает $B = 0$, что позволяет из системы алгебраических уравнений (45а) и (47а), полученной в работе [2] при задании на поверхности ячейки условия Кувабары (отсутствия завихренности), определить часть констант, необходимых для построения решения гидродинамической задачи – см. соотношения (23), (24) в [2]:

(18)
$A = B = D = E = 0,\,\,\,\,C = F = - \frac{{{{\sigma }}{{G}^{{\text{i}}}}}}{{m{{s}^{2}}}} = {{u}_{{11}}}.$

Третье условие (15) с учетом (14) дает граничное условие на концентрацию:

(19)
${{\left. {C_{1}^{{\text{o}}}} \right|}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}} = \frac{{{\text{cons}}{{{\text{t}}}_{3}}}}{{{\gamma }}}\cos {\kern 1pt} {{\theta ,}}$
которое при подстановке в (6) приводит к соотношению

(20)
${{L}^{{\text{o}}}} = {\text{cons}}{{{\text{t}}}_{3}} - {{{{\gamma }}}^{3}}{{M}^{{\text{o}}}}.$

Граничные условия (8), (17) и (19) с учетом вида решений (6) и (7) приводят к двум алгебраическим уравнениям для констант интегрирования:

(21)
$\begin{gathered} {{G}^{{\text{i}}}} = \frac{{{\text{cons}}{{{\text{t}}}_{3}}}}{{{{{{\alpha }}}^{{\text{o}}}}}} + \left( {1 - {{{{\gamma }}}^{3}}} \right)\left( {{{H}^{{\text{o}}}} + {{{{M}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{M}^{{\text{o}}}}} {{{{{\alpha }}}^{{\text{o}}}}}}} \right. \kern-0em} {{{{{\alpha }}}^{{\text{o}}}}}}} \right), \\ {{L}^{{\text{i}}}} = \frac{{{{{{\alpha }}}^{{\text{i}}}}}}{{{{{{\alpha }}}^{{\text{o}}}}}}\left( {{\text{cons}}{{{\text{t}}}_{3}} + \left( {1 - {{{{\gamma }}}^{3}}} \right){{M}^{{\text{o}}}}} \right). \\ \end{gathered} $

Подставляя (17), (18), (20) и (21) в систему (10), находим явные выражения для постоянных ${{H}^{{\text{o}}}},\,\,{{M}^{{\text{o}}}}$:

${{H}^{{\text{o}}}} = - \frac{{3{\text{cons}}{{{\text{t}}}_{3}}}}{{{{{{\alpha }}}^{{\text{o}}}}{{\Delta }_{{\text{0}}}}}}{{h}^{{\text{o}}}},\,\,\,\,{{M}^{{\text{o}}}} = - \frac{{{\text{cons}}{{{\text{t}}}_{3}}}}{{{{{{\alpha }}}^{{\text{o}}}}{{\Delta }_{{\text{0}}}}}}{{m}^{{\text{o}}}},\,\,{\text{где}}$
(22)
$\begin{gathered} {{h}^{{\text{o}}}} = \frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}} + {{{{\alpha }}}^{{\text{i}}}}\left( {\frac{1}{{{{{{\nu }}}_{ - }}{{{{\nu }}}_{{{\text{m}} + }}}}} - \frac{1}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}}} \right), \\ {{m}^{{\text{o}}}} = \left( {1 - {{{{\gamma }}}^{3}}} \right)\left( {{{\alpha }^{{\text{i}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{{{\text{m + }}}}}}}} \right) - {{\alpha }^{{\text{o}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right)} \right) + \\ + \,\,\left( {2 + {{{{\gamma }}}^{3}}} \right)\left( {\frac{{{{Z}_{ - }}{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} - \frac{{{{Z}_{ + }}{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}} + {{\alpha }^{{\text{i}}}}_{{_{{}}^{{}}}}^{{_{{_{{}}^{{}}}}^{{}}}}} \right. \times \\ \times \,\,\left. {\left( {\frac{{{{Z}_{ + }}}}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{Z}_{ - }}}}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}}} \right) - \frac{{{{\alpha }^{{\text{o}}}}}}{{{{\nu }_{ + }}{{\nu }_{ - }}}}\left( {{{Z}_{ + }} + {{Z}_{ - }}} \right)} \right), \\ \end{gathered} $
(23)
$\begin{gathered} {{\Delta }_{0}} = \left( {2 + {{{{\gamma }}}^{3}}} \right)\left( {1 - {{{{\gamma }}}^{3}}} \right) \times \\ \times \,\,\left( {\frac{1}{{{{\alpha }^{{\text{o}}}}}}\left( {\frac{{{{Z}_{ - }}{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} - \frac{{{{Z}_{ + }}{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right) + \left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right)} \right) + \\ + \,\,\frac{{\left( {{{Z}_{ + }} + {{Z}_{ - }}} \right){{{\left( {2 + {{{{\gamma }}}^{3}}} \right)}}^{2}}}}{{{{\nu }_{ - }}{{\nu }_{ + }}}} + \frac{{{{{{\alpha }}}^{{\text{i}}}}}}{{{{{{\alpha }}}^{{\text{o}}}}}}\left( {1 - {{{{\gamma }}}^{3}}} \right) \times \\ \times \,\,\left( {\left( {1 - {{{{\gamma }}}^{3}}} \right)\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{{{\text{m}} + }}}}}} \right) + } \right. \\ \left. { + \,\,\left( {2 + {{{{\gamma }}}^{3}}} \right)\left( {\frac{{{{Z}_{ + }}}}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{Z}_{ - }}}}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}}} \right)} \right). \\ \end{gathered} $
Здесь и далее обозначено:

(24)
$\begin{gathered} {{{{\delta }}}_{ \pm }} = \frac{{{{Z}_{ \pm }}{{{{\beta }}}_{ \pm }}}}{{{{{{\nu }}}_{{{\text{m}} \pm }}}}} \pm \frac{{{{\sigma Pe}}\left( {{{{{\beta }}}_{ \pm }} - 1} \right)}}{{m{{s}^{2}}}}{\text{,}} \\ \nu = \frac{{{{Z}_{ + }}{{\nu }_{ - }} + {{Z}_{ - }}{{\nu }_{ + }}}}{{{{\nu }_{ + }} - {{\nu }_{ - }}}},\,\,\,\,Z = \frac{{{{Z}_{ + }}}}{{{{\nu }_{ + }}}} + \frac{{{{Z}_{ - }}}}{{{{\nu }_{ - }}}}. \\ \end{gathered} $

Капиллярно-осмотический коэффициент ${{L}_{{13}}}$ (2а) найдем как отношение ячеечной скорости фильтрации $U$ к ячеечному градиенту химического потенциала (14):

(25)
$\begin{gathered} {{L}_{{13}}} = - \frac{U}{{{{\Phi }_{3}}}} = - \frac{{aU}}{{RT{{Z}_{0}}{\text{cons}}{{{\text{t}}}_{3}}}} = \\ = - \frac{{a{{u}_{{11}}}{{U}_{0}}}}{{RT{{Z}_{0}}{\text{cons}}{{{\text{t}}}_{3}}}} = \frac{{a{{\sigma }}{{G}^{i}}{{U}_{0}}}}{{s_{0}^{2}RT{{Z}_{0}}{\text{cons}}{{{\text{t}}}_{3}}}}, \\ \end{gathered} $
где ${{u}_{{11}}} = {U \mathord{\left/ {\vphantom {U {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}$ – безразмерная скорость фильтрации, значение которой находится из соотношений (18), (21)–(24):

(26)
${{u}_{{11}}} = - \frac{{\sigma {{G}^{{\text{i}}}}}}{{m{{s}^{2}}}} = - \frac{{{{\sigma }}{{{\operatorname{const} }}_{3}}}}{{m{{s}^{2}}{{\alpha }^{{\text{o}}}}}}\left( {1 - \frac{{1 - {{{{\gamma }}}^{3}}}}{{{{\Delta }_{0}}}}\left( {3{{h}^{{\text{o}}}} + \frac{{{{m}^{{\text{o}}}}}}{{{{\alpha }^{{\text{o}}}}}}} \right)} \right).$

Из соотношений (25) и (26) следует точная формула для капиллярно-осмотического коэффициента:

(27)
${{L}_{{13}}} = \frac{{R_{{\text{b}}}^{2}{{{{\rho }}}_{{\text{V}}}}}}{{{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}{{Z}_{0}}{{\alpha }^{{\text{o}}}}}}\left( {1 - \frac{{\left( {{\text{1}} - {{{{\gamma }}}^{3}}} \right)}}{{{{{{\alpha }}}^{{\text{o}}}}{{\Delta }_{0}}}}\left( {{\text{3}}{{\alpha }^{{\text{o}}}}{{h}^{{\text{o}}}} + {{m}^{{\text{o}}}}} \right)} \right).$

АНАЛИЗ КАПИЛЛЯРНО-ОСМОТИЧЕСКОГО КОЭФФИЦИЕНТА И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Переход к важным частным случаям позволяет упростить полученную точную формулу для капиллярно-осмотического коэффициента (27), одинаково применимую как для пористой заряженной мембраны, так и для концентрированной дисперсии заряженных частиц. Этот коэффициент определяет осмотический перенос растворителя (воды) через поры мембраны, возникающий в мембранной системе при наложении на нее внешнего перепада концентраций. В случае высококонцентрированной дисперсии пористых заряженных частиц выражение для капиллярно-осмотического коэффициента (27) существенно упрощается:

(28)
${{\left. {{{L}_{{13}}}} \right|}_{{{{\gamma }} = 1}}} = \frac{{R_{{\text{b}}}^{2}{{{{\rho }}}_{{\text{V}}}}}}{{{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}{{Z}_{0}}{{\alpha }^{{\text{o}}}}}} = \frac{{R_{{\text{b}}}^{2}{{\rho }}_{{\text{V}}}^{2}}}{{{{{{\mu }}}^{{\text{o}}}}{{Z}_{0}}F_{0}^{2}\left( {{{Z}_{ + }}{{{{\beta }}}_{ + }} + {{Z}_{ - }}{{{{\beta }}}_{ - }}} \right){{C}_{0}}}}.$

В случае 1:1 электролита и идеально селективных зерен ионита $\left( {{{{{\gamma }}}_{{\text{m}}}} = + \infty } \right)$ выражение (28) дает в размерном виде капиллярно-осмотический коэффициент дисперсии, не зависящий от концентрации электролита:

(29)
${{\left. {{{L}_{{13}}}} \right|}_{{{{\gamma }} = 1}}} = \frac{{{{k}_{{\text{D}}}}{{{{\rho }}}_{{\text{V}}}}}}{{{\text{2}}{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}}},$
где ${{k}_{{\text{D}}}} = {{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} k}} \right. \kern-0em} k}$ – удельная гидродинамическая проницаемость ионитового зерна по Бринкману.

Симметричный 1:1-электролит

Это – наиболее интересный случай, так как в эксперименте чаще всего используют именно 1:1-электролит. Тогда из формул (32а) работы [2], соотношений (9) и (24) получим:

(30)
$\begin{gathered} {{{{\alpha }}}^{{\text{o}}}} = \frac{{\sqrt {{{{{\sigma }}}^{2}} + {4 \mathord{\left/ {\vphantom {4 {{{\gamma }}_{{\text{m}}}^{2}}}} \right. \kern-0em} {{{\gamma }}_{{\text{m}}}^{2}}}} }}{{{\sigma }}},\,\,\,\,{{\alpha }^{{\text{i}}}} = \frac{2}{{{{\sigma \gamma }}_{{\text{m}}}^{2}}}{\text{,}} \\ \nu = \frac{{{{\nu }_{ + }} + {{\nu }_{ - }}}}{{{{\nu }_{ + }} - {{\nu }_{ - }}}},\,\,\,\,Z = \frac{1}{{{{\nu }_{ + }}}} + \frac{1}{{{{\nu }_{ - }}}}, \\ {{{{\delta }}}_{ \pm }} = \nu \frac{{{{{{\beta }}}_{ \pm }}}}{{{{{{\nu }}}_{{{\text{m}} \pm }}}}} \pm \frac{{\sigma {\text{Pe}}\left( {{{{{\beta }}}_{ \pm }} - 1} \right)}}{{m{{s}^{2}}}}{\text{,}}\,\,\,\,{{{{\beta }}}_{ \pm }} = \frac{{\sqrt {{{\sigma }^{2}} + {4 \mathord{\left/ {\vphantom {4 {{{\gamma }}_{{\text{m}}}^{2}}}} \right. \kern-0em} {{{\gamma }}_{{\text{m}}}^{2}}}} \pm \sigma }}{2}. \\ \end{gathered} $

Подставляя выражения (30) в формулу (27), с учетом определения (23) и (24) после преобразований, имея в виду обозначения (3) и (4), приходим к выражениям

(31)
${{L}_{{13}}} = \frac{{{{k}_{{\text{D}}}}{{{{\rho }}}_{{\text{V}}}}}}{{{\text{2}}{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}{{\alpha }^{{\text{o}}}}}}\left( {1 - \frac{{{{m}_{0}}}}{{{{\Delta }_{0}}}}\left( {\frac{{{{m}^{{\text{o}}}}}}{{{{\alpha }^{{\text{o}}}}}} + {\text{3}}{{h}^{{\text{o}}}}} \right)} \right),$
где

(32)
$\begin{gathered} \frac{{{{m}^{{\text{o}}}}}}{{{{\alpha }^{{\text{o}}}}}} + 3{{h}^{{\text{o}}}} = \left( {3 - {{m}_{0}}} \right) \times \\ \times \,\,\left[ {\frac{1}{{{{\alpha }^{{\text{o}}}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} - \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right) + \frac{{{{{{\alpha }}}^{{\text{i}}}}}}{{{{{{\alpha }}}^{{\text{o}}}}}}\left( {\frac{1}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}} + \frac{1}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}}} \right) - \frac{{\text{2}}}{{{{\nu }_{ + }}{{\nu }_{ - }}}}} \right] + \\ + \,\,3\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}} + {{\alpha }^{{\text{i}}}}\left( {\frac{1}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}} - \frac{1}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}}} \right)} \right) + \\ + \,\,{{m}_{0}}\left[ {\frac{{{{{{\alpha }}}^{{\text{i}}}}}}{{{{{{\alpha }}}^{{\text{o}}}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{{{\text{m + }}}}}}}} \right) - \left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right)} \right], \\ \end{gathered} $
(33)
$\begin{gathered} {{\Delta }_{0}} = \left( {3 - {{m}_{0}}} \right){{m}_{0}}\left( {\frac{1}{{{{\alpha }^{{\text{o}}}}}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} - \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right) + \left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{ - }}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{ + }}}}} \right)} \right) + \\ + \,\,\frac{{2{{{\left( {3 - {{m}_{0}}} \right)}}^{2}}}}{{{{\nu }_{ - }}{{\nu }_{ + }}}} + \frac{{{{\alpha }^{{\text{i}}}}}}{{{{\alpha }^{{\text{o}}}}}}{{m}_{0}} \times \\ \times \,\,\left( {{{m}_{0}}\left( {\frac{{{{{{\delta }}}_{ + }}}}{{{{\nu }_{{{\text{m}} - }}}}} + \frac{{{{{{\delta }}}_{ - }}}}{{{{\nu }_{{{\text{m}} + }}}}}} \right) + \left( {3 - {{m}_{0}}} \right)\left( {\frac{1}{{{{\nu }_{ + }}{{\nu }_{{{\text{m}} - }}}}} + \frac{1}{{{{\nu }_{ - }}{{\nu }_{{{\text{m}} + }}}}}} \right)} \right). \\ \end{gathered} $

Идеально-селективная мембрана для баромембранных процессов. В этом случае имеем,

(30а)
$\begin{gathered} {{{{\gamma }}}_{{\text{m}}}}{\text{ = + }}\infty {\text{,}}\,\,\,\,{{{{\beta }}}_{ - }} = 0,\,\,\,\,{{{{\beta }}}_{ + }} = {{\sigma ,}}\,\,\,\,{{{{\alpha }}}^{{\text{o}}}} = 1, \\ {{{{\alpha }}}^{{\text{i}}}} = 0,\,\,\,\,{{{{\delta }}}_{ + }} = \frac{{{\sigma }}}{{{{{{\nu }}}_{{{\text{m}} + }}}}} + \frac{{{{\sigma Pe}}\left( {{{\sigma }} - 1} \right)}}{{s_{0}^{2}}},\,\,\,\,{{{{\delta }}}_{ - }} = \frac{{{{\sigma Pe}}}}{{s_{0}^{2}}}. \\ \end{gathered} $

При этом выражения (31)–(33) существенно упрощаются и дают в размерном виде следующую формулу для коэффициента ${{L}_{{13}}}$:

(34)
${{L}_{{13}}} = \frac{{3{{k}_{{\text{D}}}}{{{{\rho }}}_{{\text{V}}}}}}{{2{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}}}\frac{1}{{{{m}_{0}}{{{{\delta }}}_{ + }}{{\nu }_{ + }} + \left( {3 - {{m}_{0}}} \right)}},$
или
(35)
${{L}_{{13}}} = \frac{{3{{k}_{{\text{D}}}}}}{{2{{{{\mu }}}^{{\text{o}}}}}}\frac{{{{\bar {\rho }}}{{C}_{0}}}}{{{{m}_{0}}{{\bar {\rho }}}\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right) + \left( {3 - {{m}_{0}}\left( {1 + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)} \right){{C}_{0}}}},$
где учтено, что ${{\sigma Pe = }}\frac{{s_{0}^{2}{{\bar {\rho }}}}}{{{{{{\nu }}}_{ + }}{{{{{\bar {\rho }}}}}_{0}}}}{\text{,}}\,\,\,\,{{\bar {\rho }}} = \frac{{{{{{\rho }}}_{{\text{V}}}}}}{{{{F}_{0}}}},$ а ${{{{\bar {\rho }}}}_{0}} = \frac{{{{{{\mu }}}^{{\text{o}}}}{{D}_{ + }}}}{{{{k}_{{\text{D}}}}RT}}$ – характерный масштаб обменной емкости. В случае нулевой макропористости (m0 = 0) из (35) получаем постоянное значение для капиллярно-осмотического коэффициента ${{\left. {{{L}_{{13}}}} \right|}_{{{{m}_{0}} = 0}}} = \frac{{{{k}_{{\text{D}}}}{{\bar {\rho }}}}}{{2{{{{\mu }}}^{{\text{o}}}}}}$, совпадающее с (29).

Видно, что выражение для капиллярно-осмотического коэффициента (35) прямо пропорционально гидродинамической проницаемости катионитового зерна (геля) и обратно пропорционально вязкости раствора. Отметим, что знак коэффициента L13, это следует из формулы (35), всегда положительный при физически приемлемых значениях определяющих параметров системы, т.е. осмотический поток растворителя направлен против градиента концентрации электролита и жидкость пытается разбавить более концентрированный раствор, проникая через мембрану.

Отметим также, что выражение для удельной электропроводности, которое было ранее получено для рассматриваемого случая, имеет структурно схожий с (35) вид:

(36)
$\begin{gathered} {{L}_{{22}}} = \frac{{F_{0}^{2}{{D}_{ + }}{{C}_{0}}}}{{RT\left( {3 - {{m}_{0}}} \right)}}\left( {2{{m}_{0}}\left( {1 + \frac{{{{D}_{ - }}}}{{{{D}_{ + }}}}} \right) + _{{_{{_{{}}^{{}}}}^{{_{{_{{}}^{{}}}}^{{}}}}}}^{{_{{_{{}}^{{_{{_{{}}^{{}}}}^{{}}}}}}^{{}}}}} \right. \\ + \,\,\left. {\frac{{9\left( {1 - {{m}_{0}}} \right)\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right){{\bar {\rho }}}}}{{{{m}_{0}}{{\bar {\rho }}}\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right) + \left( {3 - {{m}_{0}}\left( {1 + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)} \right){{C}_{0}}}}} \right). \\ \end{gathered} $

Из формулы (35) следует, что все характерные кривые для капиллярно-осмотического коэффициента идеально-селективной катионообменной мембраны имеют прямолинейную асимптоту при малых концентрациях электролита:

(37)
${{\left. {{{L}_{{13}}}} \right|}_{{{{C}_{0}} \to 0}}} \simeq \frac{{3{{k}_{{\text{D}}}}}}{{2{{{{\mu }}}^{{\text{o}}}}}}\frac{{{{C}_{0}}}}{{{{m}_{0}}\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)}} \equiv {{b}_{0}}{{C}_{0}},\,\,\,\,{{m}_{0}} \ne 0,$
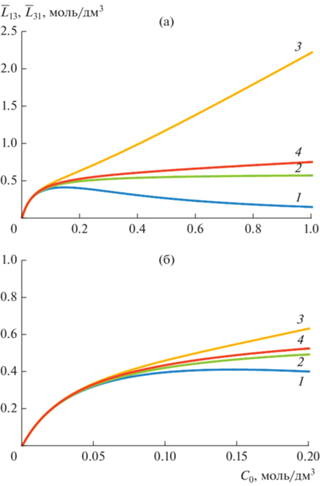
и выходят на константу – при больших концентрациях электролита:

(38)
${{\left. {{{L}_{{13}}}} \right|}_{{{{C}_{0}} \to \infty }}} \simeq \frac{{3{{k}_{{\text{D}}}}}}{{2{{{{\mu }}}^{{\text{o}}}}}}\frac{{{{\bar {\rho }}}}}{{3 - {{m}_{0}}\left( {1 + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)}} \equiv {{a}_{\infty }}.$

Из выражений (37) и (38) видно, что тангенс угла наклона прямой (37) всегда положительный, т.е. ${{b}_{0}} > 0$. В то же время величина ${{a}_{\infty }} > 0,$ если ${{{{\bar {\rho }}}} \mathord{\left/ {\vphantom {{{{\bar {\rho }}}} {{{{{{\bar {\rho }}}}}_{0}}}}} \right. \kern-0em} {{{{{{\bar {\rho }}}}}_{0}}}} < {3 \mathord{\left/ {\vphantom {3 {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}} - 1$ и ${{a}_{\infty }} < 0,\,$ если ${{{{\bar {\rho }}}} \mathord{\left/ {\vphantom {{{{\bar {\rho }}}} {{{{{{\bar {\rho }}}}}_{0}}}}} \right. \kern-0em} {{{{{{\bar {\rho }}}}}_{0}}}} > {3 \mathord{\left/ {\vphantom {3 {{{m}_{0}}}}} \right. \kern-0em} {{{m}_{0}}}} - 1 > 2$. Причем последний случай не реализуется на практике, так как ${{{{\bar {\rho }}}}_{0}} > {{\bar {\rho }}}$. Это означает, что зависимость ${{L}_{{13}}}\left( {{{С}_{0}}} \right)$ в случае идеально-селективной мембраны является монотонно возрастающей от нуля до асимптотической величины, представленной формулой (38). Не идеальность ионообменной мембраны качественно “деформирует” зависимость ${{L}_{{13}}}\left( {{{C}_{0}}} \right)$ и на ней появляется максимум. На рис. 3 показано поведение нормализованного капиллярно-осмотического коэффициента ${{\bar {L}}_{{13}}} \equiv \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{13}}}$, вычисленного по точной формуле (31) (кривая 1, ${{{{\gamma }}}_{{\text{m}}}} = 0.527$) и по приближенной формуле (35) (кривая 2, ${{{{\gamma }}}_{{\text{m}}}} = + \infty $) для идеально-селективной катионитовой мембраны при одних и тех же значениях физико-химических параметров, характерных для перфторированной литой мембраны МФ-4СК в растворе NaCl, исследованной в нашей работе [11 ] : ${{D}_{{{\text{m}} + }}} = {{D}_{{{\text{m}} - }}} = 23.68$ мкм2/с, ${{\bar {\rho } = 1}}{\text{.08}}$ моль/дм3, ${{{{\bar {\rho }}}}_{0}} = 2.18$ моль/дм3, ${{m}_{0}} = 0.2$. Видно, что при С0 = 0.15 моль/дм3 наблюдается экстремум на точной кривой 1. Это означает падение осмотической проницаемости системы при концентрациях электролита, превышающих указанную, что может быть связано со значительным (в полтора раза) превышением подвижности аниона хлора над подвижностью катиона натрия. В то же время, если бы существовала такая же по свойствам идеально-селективная мембрана, то падение L13 отсутствовало бы вовсе и наблюдался бы выход этого коэффициента на заметное положительное значение (кривая 2). Это может быть объяснено тем, что поток коионов через идеальную мембрану отсутствует.

Рис. 3.

Расчетные зависимости нормализованного капиллярно-осмотического ${{\bar {L}}_{{13}}} = \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{13}}}$ – 1, 2 (моль/дм3) и обратноосмотического ${{\bar {L}}_{{31}}} = $ = $\left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{31}}}$ – 3, 4 (моль/дм3) коэффициентов для литой перфторированной мембраны МФ-4СК от концентрации ${{C}_{0}}$ (моль/дм3) водного раствора NaCl при ${{\gamma = 0}}{\text{.527}}$ – 1, 3; ${{\gamma = + }}\infty $ – 2, 4: идеально-селективная катионообменная мембрана. Остальные параметры приведены в тексте.

Идеальная катионитовая мембрана (случай исключенных коионов – ${{\gamma }_{m}} = 0$).

В этом случае капиллярно-осмотический коэффициент равен нулю: ${{\left. {{{L}_{{13}}}\left( {{{C}_{0}}} \right)} \right|}_{{{{{{\gamma }}}_{{\text{m}}}}{\text{ = 0}}}}} = 0$. Это интуитивно понятно, поскольку в этом случае нет переноса коионов через мембрану, а значит они не могут переносить через нее и молекулы растворителя при отсутствии перепада давления.

ОПРЕДЕЛЕНИЕ ОБРАТНООСМОТИЧЕСКОГО КОЭФФИЦИЕНТА КАТИОНООБМЕННОЙ МЕМБРАНЫ И АНАЛИЗ РЕЗУЛЬТАТОВ

При вычислении обратноосмотического коэффициента ${{L}_{{31}}}$, как это следует из (2б), градиенты электрического и химического потенциалов должны отсутствовать $\left( {{{\Phi }_{2}} = {{\Phi }_{3}} = 0} \right)$, а градиент давления ${{\Phi }_{1}} = \nabla p = 3B{{{{\gamma }}}^{3}}\frac{{{{{{\mu }}}^{{\text{o}}}}{{U}_{0}}}}{{{{a}^{2}}}}$ поддерживаться постоянным. Это приводит к той же самой краевой задаче для ячейки, решение которой было найдено ранее при вычислении коэффициента ${{L}_{{11}}}$ [2] и которым теперь можно воспользоваться для вычисления коэффициента ${{L}_{{31}}}$. Плотность ячеечного потока соли определим стандартным способом [3]:

(39)
$J = {{C}_{0}}{{U}_{0}}\frac{{{{{\left. {j_{{1r}}^{{\text{o}}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}}}}{{\cos {\kern 1pt} {{\theta }}}},$
где $j_{{1r}}^{{\text{o}}} = \frac{1}{{{{Z}_{0}}}}\left( {j_{{1r + }}^{{\text{o}}} + j_{{1r - }}^{{\text{o}}}} \right)$ – радиальная компонента безразмерной локальной плотности потока соли, которую на поверхности ячейки найдем из выражений (34а) для плотности потоков ионов, приведенных в работе [2], с учетом выражений (6), (11), (17) и соотношения ${{L}^{{\text{o}}}} = - {{{{\gamma }}}^{3}}{{M}^{{\text{o}}}}$, являющегося следствием условия ${{\Phi }_{3}} = 0$:
(40)
$\begin{gathered} \frac{{{{{\left. {j_{{1r}}^{{\text{o}}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}}}}{{\cos {\kern 1pt} {{\theta }}}} = {{u}_{{1{{\gamma }}}}} - \frac{1}{{{{Z}_{0}}{\text{Pe}}\cos {\kern 1pt} {{\theta }}}} \times \\ \times \,\,\left( {\left( {\frac{1}{{{{{{\nu }}}_{ + }}{{Z}_{ + }}}} + \frac{1}{{{{{{\nu }}}_{ - }}{{Z}_{ - }}}}} \right){{{\left. {\frac{{\partial C_{1}^{{\text{o}}}}}{{\partial r}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}} + \left( {\frac{1}{{{{{{\nu }}}_{ + }}}} - \frac{1}{{{{{{\nu }}}_{ - }}}}} \right){{{\left. {\frac{{\partial {{\varphi }}_{1}^{{\text{o}}}}}{{\partial r}}} \right|}}_{{r = {1 \mathord{\left/ {\vphantom {1 {{\gamma }}}} \right. \kern-0em} {{\gamma }}}}}}} \right) = \\ = \frac{U}{{{{U}_{0}}}} + \frac{{3{{{{\gamma }}}^{3}}}}{{{{Z}_{0}}{\text{Pe}}}}\left( {\left( {\frac{1}{{{{{{\nu }}}_{ + }}{{Z}_{ + }}}} + \frac{1}{{{{{{\nu }}}_{ - }}{{Z}_{ - }}}}} \right){{M}^{{\text{o}}}} + \left( {\frac{1}{{{{{{\nu }}}_{ + }}}} - \frac{1}{{{{{{\nu }}}_{ - }}}}} \right){{H}^{{\text{o}}}}} \right). \\ \end{gathered} $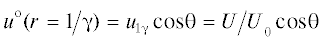
Здесь учтено выражение для радиальной скорости на границе ячейки r = 1/γ, которое можно найти в работе [2]: , т.е. .

Из условий равенства нормальных составляющих потоков ионов на межфазной границе при расчете коэффициента электроосмотической проницаемости были найдены константы Mo и Ho:

(41)
$\begin{gathered} {{M}^{{\text{o}}}} = \frac{{{\text{Pe}}{{u}_{{11}}}}}{{{{Z}_{ - }} + {{Z}_{ + }}}}\left( {\frac{{{{Z}_{ - }}\left( {{{{{\beta }}}_{ + }} - 1} \right){{\nu }_{{{\text{m}} + }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ + }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ + }}}} + } \right. \\ + \,\,\left. {\frac{{{{Z}_{ + }}\left( {{{{{\beta }}}_{ - }} - 1} \right){{\nu }_{{{\text{m}} - }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ - }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ - }}}}} \right), \\ {{H}^{{\text{o}}}} = \frac{{{\text{Pe}}{{u}_{{11}}}}}{{{{Z}_{ - }} + {{Z}_{ + }}}}\left( {\frac{{\left( {{{{{\beta }}}_{ + }} - 1} \right){{\nu }_{{{\text{m}} + }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ + }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ + }}}} - } \right. \\ - \left. {\frac{{\left( {{{{{\beta }}}_{ - }} - 1} \right){{{{\nu }}}_{{{\text{m}} - }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ - }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ - }}}}} \right). \\ \end{gathered} $

Подставим (41) в (40) и учтем при этом выражение для скорости u11 на межфазной границе r = 1, которое тоже было найдено в работе [2]:

(42)
$ - {{{{u}_{{11}}}} \mathord{\left/ {\vphantom {{{{u}_{{11}}}} B}} \right. \kern-0em} B} = {3 \mathord{\left/ {\vphantom {3 {\left( {m{{s}^{2}} + n{{\sigma Pe}}\left( {1 - {{{{\gamma }}}^{3}}} \right)} \right)}}} \right. \kern-0em} {\left( {m{{s}^{2}} + n{{\sigma Pe}}\left( {1 - {{{{\gamma }}}^{3}}} \right)} \right)}},$
где

(43)
$B = - \frac{{{U \mathord{\left/ {\vphantom {U {{{U}_{0}}}}} \right. \kern-0em} {{{U}_{0}}}}}}{{f\left( {{{\gamma }};s} \right) + \frac{3}{{m{{s}^{2}} + n{{\sigma Pe}}\left( {1 - {{{{\gamma }}}^{3}}} \right)}}}},$
(44)
$\begin{gathered} f\left( {{{\gamma }};s} \right) \equiv 1 - \frac{{6{{\gamma }}}}{5} + \frac{{{{{{\gamma }}}^{6}}}}{5} - \\ - \,\,\frac{{m{{{{\omega }}}_{3}}\left( s \right){{{\left( {1 - {{{{\gamma }}}^{3}}} \right)}}^{2}}}}{{3\left( {2{{{{\omega }}}_{1}}\left( s \right) - 4{{{{\omega }}}_{2}}\left( s \right) + m{{{{\omega }}}_{3}}\left( s \right)} \right)}}, \\ \end{gathered} $
(45)
$\begin{gathered} n = \frac{1}{{{{Z}_{ + }}{{{{\beta }}}_{ + }} + {{Z}_{ - }}{{{{\beta }}}_{ - }}}}\left[ {\frac{{{{{{\beta }}}_{ + }}\left( {{{{{\beta }}}_{ + }} - 1} \right){{\nu }_{{{\text{m}} + }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ + }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ + }}}} - } \right. \\ \left. { - \,\,\frac{{{{{{\beta }}}_{ - }}\left( {{{{{\beta }}}_{ - }} - 1} \right){{\nu }_{{{\text{m}} - }}}}}{{\left( {1 - {{{{\gamma }}}^{3}}} \right){{{{\beta }}}_{ - }} + \left( {2 + {{{{\gamma }}}^{3}}} \right){{m}_{ - }}}}} \right],\,\,\,\,{{m}_{ \pm }} = \frac{{{{\nu }_{{{\text{m}} \pm }}}}}{{{{\nu }_{ \pm }}}}, \\ \end{gathered} $
(46)
$\begin{gathered} {{{{\omega }}}_{1}}(x) = 30\left( {\frac{{ch{\kern 1pt} x}}{{{{x}^{4}}}} - \frac{{sh{\kern 1pt} x}}{{{{x}^{5}}}} - \frac{1}{{3{{x}^{2}}}}} \right), \hfill \\ {{{{\omega }}}_{2}}(x) = - \frac{{15}}{2}\left( {\frac{{ch{\kern 1pt} x}}{{{{x}^{4}}}} - \frac{{sh{\kern 1pt} x}}{{{{x}^{5}}}}\left( {1 + {{x}^{2}}} \right) + \frac{2}{{3{{x}^{2}}}}} \right), \hfill \\ {{{{\omega }}}_{3}}(x) = - 90\left( {\frac{{ch{\kern 1pt} x}}{{{{x}^{4}}}}\left( {1 + \frac{{{{x}^{2}}}}{6}} \right) - \frac{{sh{\kern 1pt} x}}{{{{x}^{5}}}}\left( {1 + \frac{{{{x}^{2}}}}{2}} \right)} \right). \hfill \\ \end{gathered} $

Выражение (44) в случае равных вязкостей жидкостей (m = 1) с учетом (46) приобретает более простой вид:

(47)
$\begin{gathered} {{\left. {f\left( {{{\gamma }};s} \right)} \right|}_{{m = 1}}} \equiv 1 - \frac{{6{{\gamma }}}}{5} + \frac{{{{{{\gamma }}}^{6}}}}{5} - \\ - \,\,2\left( {\frac{1}{{s_{0}^{2}}} + \frac{1}{6} + \frac{1}{3}\frac{{\operatorname{th} {\kern 1pt} {{s}_{0}}}}{{\operatorname{th} {\kern 1pt} {{s}_{0}} - {{s}_{0}}}}} \right){{\left( {1 - {{{{\gamma }}}^{3}}} \right)}^{2}}. \\ \end{gathered} $

Можно показать, что коэффициент при ${{\left( {1 - {{{{\gamma }}}^{3}}} \right)}^{2}}$ в выражении (44а) убывает от значения –1/5 при s0 = a/Rb = 0 до значения –1/3 при s0 → ∞, т. е. изменяется незначительно. Случай s0 = 0 соответствует высокой проницаемости пористого зерна (большому радиусу Бринкмана), а s0 → ∞, наоборот, низкой проницаемости (малому радиусу Бринкмана). Тогда из (44а) получим:

(44б)
$\begin{gathered} {{\left. {\mathop {\lim }\limits_{s = {{s}_{0}} \to 0} f\left( {{{\gamma }};s} \right)} \right|}_{{m = 1}}} \equiv 1 - \frac{{6{{\gamma }}}}{5} + \frac{{{{{{\gamma }}}^{6}}}}{5} - \frac{1}{5}{{\left( {1 - {{{{\gamma }}}^{3}}} \right)}^{2}} = \\ = \,\,\frac{4}{5} - \frac{{6{{\gamma }}}}{5} + \frac{{2{{{{\gamma }}}^{3}}}}{5} \in \left[ {0;\frac{4}{5}} \right], \\ \end{gathered} $
(44в)
$\begin{gathered} {{\left. {\mathop {\lim }\limits_{s = {{s}_{0}} \to \infty } f\left( {{{\gamma }};s} \right)} \right|}_{{m = 1}}} \equiv 1 - \frac{{6{{\gamma }}}}{5} + \frac{{{{{{\gamma }}}^{6}}}}{5} - \frac{1}{3}{{\left( {1 - {{{{\gamma }}}^{3}}} \right)}^{2}} = \\ = \,\,\frac{2}{3} - \frac{{6{{\gamma }}}}{5} + \frac{{2{{{{\gamma }}}^{3}}}}{3} - \frac{{2{{{{\gamma }}}^{6}}}}{{15}} \in \left[ {0;\frac{2}{3}} \right]. \\ \end{gathered} $

Отметим, что обе функции (44б) и (44в) являются монотонно убывающими. Из (2б) с учетом (39) и (12), а также (42)–(46), находим обратноосмотический коэффициент:

(47)
$\begin{gathered} {{L}_{{31}}} = \\ = \,\,\frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}}\left( \begin{gathered} \frac{{m{{s}^{2}}f\left( {\sqrt[3]{{1 - {{m}_{0}}}};s} \right)}}{{3\left( {1 - {{m}_{0}}} \right)}} + \frac{1}{{1 + n\frac{{{{m}_{0}}{{\bar {\rho }}}}}{{{{{{\nu }}}_{ + }}{{{{{\bar {\rho }}}}}_{0}}}}}} \times \hfill \\ \times \,\,\left( {\frac{1}{{1 - {{m}_{0}}}} + \frac{3}{{{{Z}_{0}}}}\left( {\frac{{{{m}_{ + }}}}{{{{Z}_{ + }}}}\frac{{\left( {{{{{\beta }}}_{ + }} - 1} \right)}}{{{{m}_{0}}{{{{\beta }}}_{ + }} + \left( {3 - {{m}_{0}}} \right){{m}_{ + }}}} + } \right.} \right. \hfill \\ \left. {\left. { + \,\,\frac{{{{m}_{ - }}}}{{{{Z}_{ - }}}}\frac{{\left( {{{{{\beta }}}_{ - }} - 1} \right)}}{{{{m}_{0}}{{{{\beta }}}_{ - }} + \left( {3 - {{m}_{0}}} \right){{m}_{ - }}}}} \right)} \right) \hfill \\ \end{gathered} \right). \\ \end{gathered} $

Первое слагаемое в (47) определяет транспорт соли через мембрану за счет конвективного переноса воды, а второе – за счет электродиффузии ионов. Если проницаемость зерен ионита достаточно высока (${{k}_{{\text{D}}}} \gg {{a}^{2}}$, т.е. s → 0), то первым слагаемым в (47) можно пренебречь, если же низка (${{k}_{{\text{D}}}} \ll {{a}^{2}}$, т.е. s → ∞), то, наоборот, пренебречь можно вторым слагаемым.

В случае нулевой макропористости (${{m}_{0}}\,{\text{ = }}\,{\text{1}}$) из (47) получаем формулу:

${{\left. {{{L}_{{31}}}} \right|}_{{{{\gamma = }}1}}} = \frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}{{Z}_{0}}}}\left( {\frac{{{{{{\beta }}}_{ + }}}}{{{{Z}_{ + }}}} + \frac{{{{{{\beta }}}_{ - }}}}{{{{Z}_{ - }}}}} \right) = \frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}}\left( {\frac{{{{{{\beta }}}_{ + }}{{Z}_{ - }} + {{{{\beta }}}_{ - }}{{Z}_{ + }}}}{{{{Z}_{ - }} + {{Z}_{ + }}}}} \right).$

Для сравнения приведем формулу для капиллярно-осмотического коэффициента при тех же условиях:

${{\left. {{{L}_{{13}}}} \right|}_{{{{\gamma }} = 1}}} = \frac{{{{k}_{{\text{D}}}}{{{{\rho }}}_{{\text{V}}}}}}{{{{{{\mu }}}^{{\text{o}}}}{{F}_{0}}{{Z}_{0}}{{{{\alpha }}}^{{\text{o}}}}}} = \frac{{{{k}_{{\text{D}}}}{{{{{\bar {\rho }}}}}^{2}}}}{{{{{{\mu }}}^{{\text{o}}}}{{Z}_{0}}\left( {{{Z}_{ + }}{{{{\beta }}}_{ + }} + {{Z}_{ - }}{{{{\beta }}}_{ - }}} \right){{C}_{0}}}}.$

Видно, что они существенно различаются. Таким образом, принцип взаимности Онзагера здесь не выполняется. Данный факт подтверждается результатами работы [6], в которой было феноменологически доказано, что в случае линейной неравновесной термодинамики симметричность матрицы кинетических коэффициентов наблюдается только в частном случае равенства нулю обобщенных термодинамических потоков и не равных нулю термодинамических силах. Отметим, что нами установлено неравенство ${{L}_{{ij}}} \ne {{L}_{{ji}}}$ для всех перекрестных коэффициентов, вычисленных по ячеечной модели ионообменной мембраны. Более подробно данный вопрос будет рассмотрен в следующей работе автора.

В случае идеально-селективной мембраны для баромембранных процессов (${{{{\gamma }}}_{{\text{m}}}} = + \infty $) и 1:1 электролита имеем:

(48)
$\begin{gathered} {{L}_{{31}}} = \\ = \,\,\frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}}\left( \begin{gathered} \frac{{m{{s}^{2}}f\left( {\sqrt[3]{{1 - {{m}_{0}}}};s} \right)}}{{3\left( {1 - {{m}_{0}}} \right)}} + \hfill \\ + \,\,\frac{1}{{1 + \frac{{\left( {{{\sigma }} - 1} \right){{{{\nu }}}_{{{\text{m}} + }}}}}{{{{m}_{0}}{{\sigma }}{{{{\nu }}}_{ + }} + \left( {3 - {{m}_{0}}} \right){{{{\nu }}}_{{{\text{m}} + }}}}}\frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}{{m}_{0}}}} \times \hfill \\ \times \,\,\left( {\frac{1}{{1 - {{m}_{0}}}} + } \right. \hfill \\ + \left. {\frac{3}{2}\left( {\frac{{\left( {{{\sigma }} - 1} \right){{{{\nu }}}_{{{\text{m}} + }}}}}{{{{m}_{0}}{{\sigma }}{{{{\nu }}}_{ + }} + \left( {3 - {{m}_{0}}} \right){{{{\nu }}}_{{{\text{m}} + }}}}} - \frac{1}{{\left( {3 - {{m}_{0}}} \right)}}} \right)} \right) \hfill \\ \end{gathered} \right). \\ \end{gathered} $

В случае нулевой макропористости из (48) получаем: ${{\left. {{{L}_{{31}}}} \right|}_{{{{m}_{0}} = 0}}} = \frac{{{{k}_{{\text{D}}}}{{\bar {\rho }}}}}{{{\text{2}}{{{{\mu }}}^{{\text{o}}}}}}$, что совпадает с формулой (29). После тождественных преобразований выражение (48) приобретает следующий вид:

(49)
$\begin{gathered} {{L}_{{31}}} = \frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}} \times \\ \times \,\,\left( \begin{gathered} \frac{{m{{s}^{2}}f\left( {\sqrt[3]{{1 - {{m}_{0}}}};s} \right)}}{{3\left( {1 - {{m}_{0}}} \right)}} + \hfill \\ + \,\,\frac{{{{m}_{0}}\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \left( {3 - {{m}_{0}}} \right)\frac{{{{C}_{0}}}}{{{{\bar {\rho }}}}}}}{{{{m}_{0}}\left( {\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{ + }}}} + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right) + \left( {3 - {{m}_{0}}\left( {1 + \frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)} \right)\frac{{{{C}_{0}}}}{{{{\bar {\rho }}}}}}} \times \hfill \\ \times \,\,\left( {\frac{1}{{1 - {{m}_{0}}}} + \frac{3}{2}} \right. \times \hfill \\ \left. { \times \,\,\left( {\frac{{\left( {1 - \frac{{{{C}_{0}}}}{{{{\bar {\rho }}}}}} \right)}}{{{{m}_{0}}\frac{{{{D}_{{{\text{m}} + }}}}}{{{{D}_{{\text{ + }}}}}} + \left( {3 - {{m}_{0}}} \right)\frac{{{{C}_{0}}}}{{{{\bar {\rho }}}}}}} - \frac{1}{{\left( {3 - {{m}_{0}}} \right)}}} \right)} \right) \hfill \\ \end{gathered} \right). \\ \end{gathered} $

В случае идеальной катионитовой мембраны (случай исключенных коионов – ${{\gamma }_{m}} = 0$), 1:1 электролита и совпадающей вязкости жидкостей – m = 1, имеем:

(50)
${{L}_{{31}}} = \frac{{{{k}_{{\text{D}}}}{{C}_{0}}}}{{{{{{\mu }}}^{{\text{o}}}}}}\left( \begin{gathered} \frac{{\left( {1 - \frac{{6\sqrt[3]{{1 - {{m}_{0}}}}}}{5} + \frac{{{{{\left( {1 - {{m}_{0}}} \right)}}^{2}}}}{5}} \right)s_{0}^{2} - 2\left( {1 + \frac{{s_{0}^{2}}}{6} + \frac{1}{3}\frac{{s_{0}^{2}\operatorname{th} {{s}_{0}}}}{{\operatorname{th} {{s}_{0}} - {{s}_{0}}}}} \right)m_{0}^{2}}}{{3\left( {1 - {{m}_{0}}} \right)}} + \hfill \\ \frac{{2{{m}_{0}} + 3\left( {1 - {{m}_{0}}} \right)\left( {\frac{{{{D}_{ + }}}}{{{{D}_{{{\text{m}} + }}}}} + \frac{{{{D}_{ - }}}}{{{{D}_{{{\text{m}} - }}}}}} \right)}}{{{{m}_{0}}\left( {1 - {{m}_{0}}} \right)\left( {2 + \left( {\frac{{{{D}_{ + }}}}{{{{D}_{{{\text{m}} + }}}}} - \frac{{{{D}_{ + }}}}{{{{D}_{{{\text{m}} - }}}}}} \right)\frac{{{{\bar {\rho }}}}}{{{{{{{\bar {\rho }}}}}_{0}}}}} \right)}} \hfill \\ \end{gathered} \right).$

Из формулы (50) следует, что обратноосмотический коэффициент идеальной катионитовой мембраны прямо пропорционален концентрации электролита. На рис. 3 показано изменение нормализованного обратноосмотического коэффициента ${{\bar {L}}_{{13}}} \equiv \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{13}}}$ катионообменной мембраны с ростом концентрации электролита для тех же параметров системы мембрана-электролит, для которых построены кривые 1 и 2. Кривая 3 построена для ${{\bar {L}}_{{13}}}$ по точной формуле (47), а кривая 4 – по формуле (48) для идеально-селективной мембраны при m = 1 (равные вязкости) и s0 = 0 (бесконечно малый размер зерна ионита). Рисунки 3а и 3б отличаются областью изменения концентрации электролита. Из рис. 3б видно, что перекрестные коэффициенты мало различаются только при небольших концентрациях электролита (до 0.1 М). При больших концентрациях наблюдается существенное как количественное, так и качественное расхождение между L13 и L31: обратноосмотический коэффициент (кривая 3) растет с ростом концентрации электролита, а капиллярно-осмотический (кривая 1) – убывает. В то же время между этими коэффициентами, вычисленными для идеально-селективных мембран, наблюдается не такое существенное различие (кривые 2 и 4).

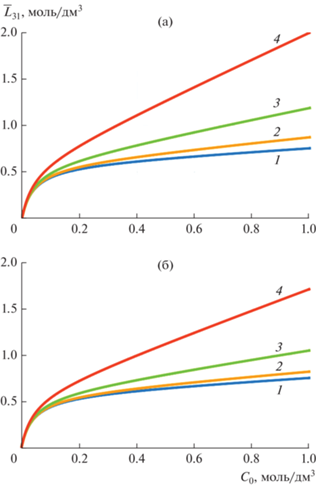
На рис. 4 показано поведение нормализованного обратноосмотического коэффициента ${{\bar {L}}_{{31}}} \equiv \left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{31}}}$ с ростом концентрации электролита C0 при разных отношениях вязкостей жидкости внутри пористого слоя и внутри жидкой оболочки: m = 1 4а и 4б. Значение m = 5 соответствует 20% пористости зерна ионита, что совпадает с выбранным для построения приведенных графиков значением макропористости m0 = 0.2. Кривые 1, 2, 3 и 4 на обоих рисунках соответствуют значениям параметра ${{s}_{0}} \equiv {a \mathord{\left/ {\vphantom {a {\sqrt {{{k}_{{\text{D}}}}} }}} \right. \kern-0em} {\sqrt {{{k}_{{\text{D}}}}} }} = 0.1;\,\,\,\,1;{\text{ }}10{\text{ и }}50$ соответственно. Сравнивая рис. 4а и 4б, заключаем, что увеличение эффективной вязкости среды Бринкмана ведет к падению коэффициента L31 при прочих равных условиях. Причем это падение усиливается с ростом параметра s0 (ростом размера зерна ионита). При этом рост размера зерна приводит к росту обратноосмотической проницаемости среды. Удельную проницаемость kD пористой оболочки зерна ионита изменять на рис. 3 и 4 нельзя, так как на нее нормированы оба коэффициента L13 и L31. Поскольку кривые 1 и 2 на рис. 4 практически совпадают, а кривая 3 расположена близко к ним, то это говорит о слабой зависимости коэффициента L31 от параметра s0 в диапазоне его значений от 0 до 10 и концентрации электролита меньше 1 М. Дальнейшее увеличение этого параметра на полпорядка приводит уже к заметному росту обратноосмотической проницаемости, которая во всех случаях растет также и от концентрации электролита.

Рис. 4.

Расчетные зависимости нормализованного обратноосмотического коэффициента ${{\bar {L}}_{{31}}} = $ = $\left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{31}}}$ (моль/дм3) для литой перфторированной мембраны МФ-4СК от концентрации ${{C}_{0}}$ (моль/дм3) водного раствора NaCl при ${{\gamma = 0}}{\text{.527}}$, ${{s}_{0}}{\text{ = 0}}{\text{.1}}\,\,{\text{(}}1{\text{);}}\,\,1\,(2);\,\,10\,(3);\,\,50\,(4)$, m = 1 (а); 5 (б). Остальные параметры приведены в тексте.

На рис. 5 показано поведение обратноосмотического коэффициента ${{\bar {L}}_{{31}}}$ с ростом концентрации электролита C0 при разных отношениях вязкостей жидкости внутри пористого слоя и внутри жидкой оболочки: m = 1 5а и 5б для виртуальной мембраны МФ-4СК, как если бы она имела коэффициент равновесного распределения, характерный для обратноосмотических мембран – ${{\gamma = 100}}$. Легко заметить, что обратноосмотическая проницаемость такой мембраны ниже при прочих равных условиях и эта разность достигает двухкратного значения при концентрации NaCl равной 1 М. Эффект связан с разным знаком адсорбции ионов внутри матрицы мембраны. В первом случае (рис. 4) имеет место положительная сорбция, т.е., концентрация ионов в порах повышена по сравнению с равновесной. Во втором случае (рис. 5) – сорбция ионов отрицательна, т.е. их концентрация в порах понижена. Это вполне естественно, так как обратноосмотические мембраны должны по максимуму задерживать растворенную соль. Отметим также, что и разница между кривыми 1–3 на рис. 5 более значительная, чем на рис. 4.

Рис. 5.

Расчетные зависимости нормализованного обратноосмотического коэффициента ${{\bar {L}}_{{31}}} = $ = $\left( {{{{{{{\mu }}}^{{\text{o}}}}} \mathord{\left/ {\vphantom {{{{{{\mu }}}^{{\text{o}}}}} {{{k}_{{\text{D}}}}}}} \right. \kern-0em} {{{k}_{{\text{D}}}}}}} \right){{L}_{{31}}}$ (моль/дм3) для виртуальной мембраны МФ-4СК от концентрации ${{C}_{0}}$ (моль/дм3) водного раствора NaCl при ${{\gamma = 100}}$, ${{s}_{0}}{\text{ = 0}}{\text{.1(}}1{\text{);}}\,\,1\,(2);\,\,10\,(3);\,\,50\,(4)$, m = 1 (а); 5 (б). Остальные параметры приведены в тексте.

Отметим, как и в предыдущих работах, что при очень малых значениях концентрации электролита, когда толщины внешнего и внутреннего ДЭС, примыкающих к межфазным границам, становятся сравнимыми с радиусом зерен ионита, формулы, полученные в данной и предыдущих работах для кинетических коэффициентов могут давать неточные результаты. Здесь мы пренебрегали толщинами ДЭС с целью получения аналитического решения краевой задачи для отдельной ячейки. Такой подход вполне оправдан при работе ионообменной мембраны в допредельных токовых режимах, когда концентрация электролита вблизи межфазной границы не является предельно низкой. В случае проведения электродиализа в сверхпредельных токовых режимах, когда внутри диффузионных слоев возникают области пространственного заряда и необходимо учитывать сопряженные эффекты электроконвекции, а также диссоциацию молекул воды, задача в точной постановке может быть решена только численно. Такие модели известны и опубликованы, например, в работах [7, 8]. Следует отметить, что существуют и другие модели ионообменной мембраны, например, микрогетерогенная [9, 10], активно развиваемая представителями кубанской научной школы мембранной электрохимии. Сравнение микрогетерогенной и ячеечной моделей ионообменной мембраны предполагается выполнить в одной из последующих работ автора.

Отметим также, что для того, чтобы получить формулы для капиллярно-осмотического и обратноосмотического коэффициентов анионообменной мембраны, необходимо в формулах, полученных для этих величин заменить знак ${{\sigma }}$ (или ${{\bar {\rho }}}$) на противоположный.

ЗАКЛЮЧЕНИЕ

В данной работе в рамках линейной термодинамики необратимых процессов, на основе разработанной нами ранее ячеечной модели ионообменной мембраны, рассчитаны ее капиллярно-осмотический и обратноосмотический коэффициенты. Мембрана рассматривается как упорядоченная совокупность пористых заряженных частиц сферической формы, помещенных в сферические оболочки, заполненные раствором бинарного электролита. Рассмотрение ведется в рамках малого отклонения параметров мембранной системы от своих равновесных значений при наложении внешнего концентрационного поля и поля давления. На поверхности жидких ячеек ставится граничное условие Кувабары (отсутствие завихренности жидкости). Течение в пористой частице описывается уравнением Бринкмана, а вне ее – уравнением “ползущего течения” Стокса с учетом пространственной электрической силы. Исследованы различные предельные случаи, в частности случай симметричного 1:1-электролита и идеально-селективной катионообменной мембраны. Показано, что для рассматриваемой ячеечной модели ионообменной мембраны нарушается принцип взаимности Онзагера – найденные перекрестные кинетические коэффициенты не равны между собой. Нарушение связывается с тем обстоятельством, что принцип взаимности работает только для неравновесных систем в рамках линейной термодинамики необратимых процессов, для которых обобщенные потоки равны нулю при отличных от нуля термодинамических силах. Результаты данного исследования, помимо процессов электродиализа и электрофильтрования на заряженных мембранах, могут найти применение также для учета переноса воды в топливных элементах, который определяет продолжительность работы этих устройств. Разработанная модель применима к любым мембранам, несущим объемный заряд (в частности, обратноосмотическим, нано-, ультра- и микрофильтрационным).

Список литературы

  1. Хаппель Д., Бреннер Г. Гидродинамика при малых числах Рейнольдса. М.: Мир, 1976.

  2. Филиппов А.Н. // Коллоид. журн. 2018. Т. 80. С. 745.

  3. Филиппов А.Н. // Коллоид. журн. 2021. Т. 83. С. 360.

  4. Brinkman H.C. // Appl. Sci. Res. A1. 1947. P. 27.

  5. Saffman P.G. // Stud. Appl. Math. 1971. V. 50. P. 93.

  6. Мамедов М.М. // Письма в ЖТФ. 2003. Т. 29. Вып. 16. С. 39.

  7. Uzdenova A., Kovalenko A., Urtenov M., Nikonenko V. // Membranes. 2018. V. 8(3). № 84.

  8. Nikonenko V., Urtenov M., Mareev S., Pourcelly G. // Membranes. 2020. V. 10(2). № 22.

  9. Ничка В.С., Мареев С.А., Порожный М.В., Шкирская С.А., Сафронова Е.Ю., Письменская Н.Д., Никоненко В.В. // Мембраны и мембранные технологии. 2019. Т. 9(3). С. 222.

  10. Davidov D.V., Nosova E.N., Loza S.A., Achoh A.R., Korzhov A.N., Melnikov S.S. // Chimica Techno Acta. 2021. V. 8(2). № 20218205.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал