Коллоидный журнал, 2023, T. 85, № 3, стр. 263-276
О некоторых особенностях преобразования энергии капиллярных волн на поверхности жидкости при наличии динамического поверхностного натяжения
А. И. Григорьев 1, *, Н. Ю. Колбнева 2, С. О. Ширяева 2
1 Институт проблем механики им. А.Ю. Ишлинского РАН
119526 Москва, просп. Вернадского, д. 101, к. 1, Россия
2 Ярославский государственный университет им. П.Г. Демидова
150000 Ярославль, ул. Советская д. 14, Россия
* E-mail: grigorai@mail.ru
Поступила в редакцию 15.03.2023
После доработки 13.04.2023
Принята к публикации 13.04.2023
- EDN: ZPFCCA
- DOI: 10.31857/S0023291223600128
Аннотация
В теоретических асимптотических расчетах первого порядка малости по безразмерной амплитуде осцилляций заряженных капель полярной жидкости исследуется влияние эффекта динамического поверхностного натяжения на капиллярные осцилляции капли. Расчеты проводятся на модели идеальной несжимаемой электропроводной жидкости. Показано, что учет эффекта динамического поверхностного натяжения приводит к повышению порядка дисперсионного уравнения, у которого появляется еще один затухающий корень, обязанный разрушению приповерхностного двойного электрического слоя (разрушению упорядоченности молекул в приповерхностном слое). В обнаруженном затухании интересно то, что оно имеет место в идеальной жидкости, а характерное время затухания совпадает с экспериментально измеряемым. Преобразования свободной энергии происходят между механической, тепловой, электромагнитной и снова механической, и все это обязано эффекту динамического поверхностного натяжения. Показано, что на низкочастотные осцилляции капель эффект динамического поверхностного натяжения влияет слабо, а на высокочастотные осцилляции существенно, заставляя такие осцилляции быстро затухать.
ВВЕДЕНИЕ
Теоретическое и экспериментальное исследование капиллярных осцилляций сферических и сфероидальных капель, заряженных собственными или индуцированными внешним электростатическим полем зарядами, незаряженных, неподвижных в разного вида подвесах или свободно падающих, начало развиваться с начала 20-го века. Тем не менее, первая строгая теоретическая работа появилась еще в конце 19-го века [1].
Капиллярные осцилляции капель и в настоящее время интенсивно исследуются, поскольку такой физический объект как капля встречается в массе академических, технических и технологических приложений [2–5].
В связи со сказанным представляет интерес посмотреть, какое влияние на осцилляции капель окажет давно известное динамическое поверхностное натяжение, всегда присутствующее в полярных жидкостях [6–9].
Суть эффекта динамического поверхностного натяжения заключается в следующем. Рассмотрим, к примеру, молекулу воды, которая представляет собой электрический диполь. Приповерхностные диполи воды ориентированы таким образом, что их отрицательно заряженные концы направлены наружу в окружающую среду, а положительно заряженные направлены внутрь жидкости [10]. Другими словами, поверхность раздела вода–воздух оказывает ориентирующее действие на диполи воды, и это экспериментальный факт [11, с. 46−47]. Следует отметить еще и тот факт, что в упорядочивании диполей в приповерхностном слое существенную роль играют электрические, квадрупольные взаимодействия. Согласно [11, с. 47], “взаимодействие квадрупольного момента молекулы с дипольными моментами соседних молекул может вызвать наблюдаемую параллельную ориентацию дипольных моментов”. “Взаимодействие дипольных моментов друг с другом приводило бы к антипараллельной ориентации соседних молекул”.
Электрическое поле слоя поверхностных диполей будет действовать на ионы примесей и ионы воды таким образом, что отрицательно заряженные ионы будут концентрироваться у положительно заряженных концов приповерхностных диполей и, в свою очередь, вытягивать из объема воды положительно заряженные ионы. В итоге у поверхности образуется двойной электрический слой, у которого верхнюю неподвижную обкладку будут составлять отрицательно заряженные концы диполей с сильно связанными с ними положительно заряженными ионами. Нижняя подвижная (диффузная) обкладка двойного слоя сформируется из слабо связанных подвижных ионов.
Двойной электрический слой образуется самопроизвольно, поскольку при возникновении упорядоченности диполей на поверхности воды система переходит в состояние с меньшей потенциальной энергией. Этот переход осуществляется за весьма малое время, называемое временем релаксации. При этом уменьшается и коэффициент поверхностного натяжения, ибо поверхностное натяжение жидкости измеряется свободной энергией поверхности жидкости, приходящейся на единицу площади поверхности [12, с. 351]. Это будет стационарное состояние.
Предположим теперь, что на поверхность жидкости оказывается кратковременное силовое воздействие вследствие процессов столкновений капель, их дробления, коагуляции или трения о воздух и т.п. Разрушению упорядоченности способствуют и капиллярные волны большой амплитуды, которые также разрушают упорядоченность диполей, т.к. известно, что при волновом движении частицы воды движутся по окружностям. В итоге разрушится существующая в равновесном состоянии упорядоченность диполей и двойной электрический слой расплывется. Свободная энергия поверхности жидкости увеличится, а с ней и коэффициент поверхностного натяжения. Затем упорядоченность диполей восстановится, поверхностная энергия уменьшится, и коэффициент поверхностного натяжения понизится.
Таким образом, величина коэффициента поверхностного натяжения будет колебаться между равновесным значением (при упорядоченности приповерхностных диполей) и максимальным (при полной разупорядоченности диполей).
Представляется интересным и целесообразным рассмотреть на качественном уровне вопрос того, какие последствия будет иметь периодическое изменение величины коэффициента поверхностного натяжения. Интересно, в частности, посмотреть, какие взаимопереходы энергии имеют место при реализации эффекта динамического поверхностного натяжения.
Ориентироваться для конкретности будем на капли воды естественного происхождения: облачные и дождевые [13–15]. Их счетные характеристики: концентрация, функция распределения по размерам и зарядам, скорость падения в зависимости от размеров хорошо изучены.
1. ФИЗИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Пусть имеется неподвижная сферическая капля радиуса $R$ идеальной несжимаемой электропроводной жидкости с массовой плотностью ${{\rho }_{1}}$, несущая электрический заряд $Q$. Коэффициент поверхностного натяжения жидкости обозначим $\sigma $. В качестве внешней среды примем идеальную несжимаемую диэлектрическую среду с диэлектрической проницаемостью ${{\varepsilon }_{{{\text{ex}}}}}$ и массовой плотностью ${{\rho }_{2}}$.
Вследствие теплового движения молекул жидкости на поверхности капли создается капиллярное волновое движение весьма малой амплитуды, не превышающей 1 Å. Однако из-за внешних силовых воздействий (коагуляция, дробление, столкновение, трение о воздух и т.д.) амплитуда может быть порядка десятков процентов от радиуса капли [16].
Рассмотрение задачи естественно провести в сферической системе координат $\left( {r,\;\theta ,\;\varphi } \right)$ с началом в центре масс сферы. Чтобы упростить следующие ниже математические выкладки, примем осевую симметрию задачи, т.е. зависимостью всех физических величин от азимутального угла $\varphi $ будем пренебрегать и будем решать упрощенную задачу в пренебрежении аксиально асимметричными модами.
Движение жидкости в капле и движение внешней среды будем считать потенциальными, выражая поле скоростей ${{{\mathbf{V}}}_{j}}(r,\theta ,t)$ через градиент гидродинамических потенциалов ${{\psi }_{j}}(r,\theta ,t)$ [17]:
Здесь величины с индексом $j = 1$ характеризуют каплю, а с $j = 2$ – среду.Искажение равновесной сферической формы $\xi (\theta ,t)$, вызванное капиллярным тепловым движением, будем считать малым вместе с величинами ${{{\mathbf{V}}}_{j}}(r,\theta ,t)$, ${{\psi }_{j}}(r,\theta ,t)$.
Уравнение границы раздела сред в любой момент времени $t$ запишем в виде:
где амплитуда волнового движения поверхности капли много меньше ее равновесного радиуса: $\max \left| \xi \right|{\text{/}}R \ll 1$.Моделируя каплю проводником, получим, что скорость перераспределения поверхностного заряда превосходит гидродинамические скорости течений жидкости в капле (в реальности вода в капле является электролитом). Тогда электрическое поле в окрестности капли, создаваемое ее равномерно распределенным зарядом, будем полагать квазистационарным, описываемым электрическим потенциалом $\Phi \left( {r,\theta ,t} \right)$, связанным с напряженностью поля ${\mathbf{E}}\left( {r,\theta ,t} \right)$ соотношением:
Потенциал вдоль возмущенной поверхности обозначим ${{\Phi }_{{\text{s}}}}$.
2. МАТЕМАТИЧЕСКАЯ ПОСТАНОВКА ЗАДАЧИ
Математическая формулировка задачи о капиллярных осцилляциях заряженной капли состоит из уравнений движения внутренней и внешней сред капли (уравнения Эйлера):
(3)
$\begin{gathered} \frac{{\partial {{{\mathbf{V}}}_{j}}(r,\theta ,t)}}{{\partial t}} + \left( {{{{\mathbf{V}}}_{j}}(r,\theta ,t)\nabla } \right){{{\mathbf{V}}}_{j}}(r,\theta ,t) = \\ = \,\, - \frac{1}{{{{\rho }_{j}}}}\nabla {{P}_{j}}\left( {r,\theta ,t} \right);\,\,\,\,(j = 1,2); \\ \end{gathered} $(5)
${\text{rot}}{\kern 1pt} {\mathbf{E}}\left( {r,\theta ,t} \right) = 0;\,\,\,\,{\text{div}}{\kern 1pt} {\mathbf{E}}\left( {r,\theta ,t} \right) = 0.$Использование уравнения (1) позволяет привести равенство (4) к уравнениям Лапласа для гидродинамических потенциалов ${{\psi }_{j}}(r,\theta ,t)$:
Подставляя (2) в (5), находим, что первое из уравнений системы (5) удовлетворяется тождественно, а второе уравнение сводится к уравнению Лапласа для потенциала электростатического поля $\Phi \left( {r,\theta ,t} \right)$:
Из уравнений (3) с учетом (1) получим соотношения для давлений в капле ${{P}_{1}}\left( {r,\theta ,t} \right)$ и во внешней среде ${{P}_{2}}\left( {r,\theta ,t} \right)$:
Кроме того, необходимо, чтобы искомые потенциалы ${{\psi }_{j}}(r,\theta ,t)$, $\Phi \left( {r,\theta ,t} \right)$ удовлетворяли условиям ограниченности (естественным граничным условиям) в начале координат и на бесконечном удалении от капли:
(9)
$r \to \infty {\kern 1pt} :\,\,\,\,{{\psi }_{2}}(r,\theta ,t) \to 0;\,\,\,\,\Phi (r,\theta ,t) \to 0.$На границе раздела сред $r = R + \xi \left( {\theta ,t} \right)$ должны выполняться гидродинамические и электростатические граничные условия: равенства нормальных компонент скоростей движения внутренней и внешней сред:
(10)
$\begin{gathered} {{n}_{1}}\nabla {{\psi }_{1}}\left( {r,\theta ,t} \right) = {{n}_{2}}\nabla {{\psi }_{2}}\left( {r,\theta ,t} \right) \equiv \\ \equiv \,\,n\nabla {{\psi }_{j}}\left( {r,\theta ,t} \right);\,\,\,\,{\mathbf{n}} = {{{\mathbf{n}}}_{1}} = - {{{\mathbf{n}}}_{2}}; \\ \end{gathered} $(11)
$\frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial t}} = n\left( {\theta ,t} \right)\nabla {{\psi }_{j}}\left( {r,\theta ,t} \right);$(12)
$\begin{gathered} {{P}_{1}}\left( {r,\theta ,t} \right) - {{P}_{2}}\left( {r,\theta ,t} \right) + {{P}_{q}}\left( {r,\theta ,t} \right) - {{P}_{\sigma }}\left( {r,\theta ,t} \right) = 0; \\ {{P}_{q}}\left( {r,\theta ,t} \right) = \frac{{{{\varepsilon }_{{{\text{ex}}}}}}}{{8\pi }}{{\left( {\nabla \Phi \left( {r,\theta ,t} \right)} \right)}^{2}}; \\ {{P}_{\sigma }}\left( {r,\theta ,t} \right) = \sigma {\kern 1pt} {\text{div}}{\kern 1pt} {\mathbf{n}}\left( {\theta ,t} \right); \\ \end{gathered} $Зададим дополнительные интегральные условия сохранения объема капли, отсутствия движения ее центра масс:
(14)
$\begin{gathered} \int\limits_V {{{r}^{2}}dr{\kern 1pt} \sin {\kern 1pt} \theta d\theta d\varphi = \frac{4}{3}\pi } {{R}^{3}};\,\,\,\,\int\limits_V {{\mathbf{r}}{{r}^{2}}dr{\kern 1pt} \sin {\kern 1pt} \theta d\theta d\varphi = 0;} \\ V = [0 \leqslant r \leqslant R + \xi (\theta ,t),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]; \\ \end{gathered} $(15)
$\begin{gathered} - \frac{{{{\varepsilon }_{{{\text{ex}}}}}}}{{4\pi }}\mathop \oint \limits_S n\left( {\theta ,t} \right)\nabla \Phi \left( {r,\theta ,t} \right)dS = Q; \\ S = [r = R + \xi (\theta ,t),0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]. \\ \end{gathered} $В выписанных выражениях ${{{\mathbf{n}}}_{1}}(\theta ,t)$ – внешний орт нормали по отношению к капле, ${{{\mathbf{n}}}_{2}}(\theta ,t)$ – внешний орт нормали по отношению к внешней среде, ${{P}_{q}}\left( {r,\theta ,t} \right)$ – давление электрических сил, ${{P}_{\sigma }}\left( {r,\theta ,t} \right)$ – давление сил поверхностного натяжения.
Решение сформулированной задачи (6)–(11) будем искать классическими методами теории возмущений [18] в линейном приближении по малому параметру $\varepsilon $, в качестве которого выберем отношение амплитуды капиллярных осцилляций капли к ее радиусу $\varepsilon \equiv \left| {\xi (\theta ,t)} \right|{\text{/}}R \ll 1$. В рамках метода прямого разложения возмущение равновесной формы $\xi (\theta ,t)$, потенциалы ${{\psi }_{j}}(r,\theta ,t)$, $\Phi \left( {r,\theta ,t} \right)$ и давления ${{P}_{j}}\left( {r,\theta ,t} \right)$, ${{P}_{q}}\left( {r,\theta ,t} \right)$, ${{P}_{\sigma }}\left( {r,\theta ,t} \right)$ представим в виде асимптотических разложений:
(16)
$\begin{gathered} \xi (\theta ,t) = {{\xi }^{{\left( 1 \right)}}}(\theta ,t) + {\rm O}({{\varepsilon }^{2}}); \\ {{\psi }_{j}}(r,\theta ,t) = \psi _{j}^{{\left( 1 \right)}}(r,\theta ,t) + {\rm O}({{\varepsilon }^{2}});\,\,\,\,\left( {j = 1,2} \right); \\ \Phi (r,\theta ,t) = {{\Phi }^{{\left( 0 \right)}}}(r,\theta ) + {{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t) + {\rm O}({{\varepsilon }^{2}}); \\ {{P}_{j}}(r,\theta ,t) = P_{j}^{{\left( 0 \right)}}(r,\theta ,t) + P_{j}^{{\left( 1 \right)}}(r,\theta ,t) + {\rm O}({{\varepsilon }^{2}}); \\ {{P}_{q}}(r,\theta ,t) = P_{q}^{{\left( 0 \right)}}(r,\theta ) + P_{q}^{{\left( 1 \right)}}(r,\theta ,t) + {\rm O}({{\varepsilon }^{2}}); \\ {{P}_{\sigma }}(r,\theta ,t) = P_{\sigma }^{{\left( 0 \right)}}(r,\theta ) + P_{\sigma }^{{\left( 1 \right)}}(r,\theta ,t) + {\rm O}({{\varepsilon }^{2}}), \\ \end{gathered} $3. ПРОЦЕДУРА ОТЫСКАНИЯ РЕШЕНИЯ. ВЫВОД ДИСПЕРСИОННОГО УРАВНЕНИЯ БЕЗ УЧЕТА РЕЛАКСАЦИИ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
Используя данные разложения, исходную систему уравнений (6), (7), (8), (9), (10) разделим по порядкам малости по $\varepsilon $.
В нулевом приближении по $\varepsilon $ имеем задачу для расчета равновесного состояния системы:
(19)
$\begin{gathered} r = R{\kern 1pt} :\,\,\,\,P_{1}^{{\left( 0 \right)}}\left( {r,\theta } \right) - P_{2}^{{\left( 0 \right)}}\left( {r,\theta } \right) + \\ + \,\,P_{q}^{{\left( 0 \right)}}\left( {r,\theta } \right) - P_{\sigma }^{{\left( 0 \right)}}\left( {r,\theta } \right) = 0; \\ \end{gathered} $(20)
$\begin{gathered} P_{1}^{{\left( 0 \right)}} = {{P}_{{01}}};\,\,\,\,P_{2}^{{\left( 0 \right)}} = {{P}_{{02}}};\,\,\,\,P_{q}^{{\left( 0 \right)}} = \frac{{{{\varepsilon }_{{{\text{ex}}}}}{{{\left( {\nabla {{\Phi }^{{\left( 0 \right)}}}} \right)}}^{2}}}}{{8\pi }}; \\ P_{\sigma }^{{\left( 0 \right)}} = \sigma {\kern 1pt} {\text{div}}{\kern 1pt} {{{\mathbf{n}}}_{0}}(\theta );\,\,\,\,{{{\mathbf{n}}}_{0}}(\theta ) = {{{\mathbf{e}}}_{r}};\,\,\,\,{{\Phi }^{{\left( 0 \right)}}}(r,\theta ) = \Phi _{{\text{s}}}^{{\left( 0 \right)}}; \\ \end{gathered} $(21)
$\begin{gathered} \int\limits_V {{{r}^{2}}dr{\kern 1pt} \sin {\kern 1pt} \theta d\theta d\varphi = \frac{4}{3}\pi } {{R}^{3}};\,\,\,\,\int\limits_V {{\mathbf{r}}{{r}^{2}}dr{\kern 1pt} \sin {\kern 1pt} \theta d\theta d\varphi = 0} ; \\ V = [0 \leqslant r \leqslant R,0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ]; \\ \end{gathered} $(22)
$\begin{gathered} - \frac{{{{\varepsilon }_{{{\text{ex}}}}}}}{{4\pi }}\mathop \oint \limits_S {{n}_{0}}\left( \theta \right)\nabla {{\Phi }^{{\left( 0 \right)}}}\left( {r,\theta } \right)dS = Q; \\ S = [r = R,0 \leqslant \theta \leqslant \pi ,0 \leqslant \varphi \leqslant 2\pi ], \\ \end{gathered} $В результате решения уравнения Лапласа (17) при удовлетворении граничным и дополнительным условиям (18), (20), (22) получим электрический потенциал в окрестности равновесной сферы:
Используя (23), из баланса давлений на границу раздела сред $r = R$ найдем перепад постоянных давлений $\Delta P$ в капле и во внешней среде:
Сформулируем отдельно электрогидродинамическую задачу первого порядка малости по $\varepsilon $:
(24)
$\Delta {{\psi }_{j}}(r,\theta ,t) = 0;\,\,\,\,\left( {j = 1,2} \right);\,\,\,\,\Delta {{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t) = 0;$(26)
$r \to \infty {\kern 1pt} :\,\,\,\,{{\psi }_{2}}(r,\theta ,t) \to 0;\,\,\,\,{{\Phi }^{{\left( 1 \right)}}}(r,\theta ,t) \to 0;$(27)
$r = R{\kern 1pt} :\,\,\,\,\frac{{\partial \xi \left( {\theta ,t} \right)}}{{\partial t}} = \frac{{\partial {{\psi }_{j}}(r,\theta ,t)}}{{\partial r}};\,\,\,\,\left( {j = 1,2} \right);$(28)
$\begin{gathered} P_{1}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right) - P_{2}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right) + \\ + \,\,P_{q}^{{\left( 1 \right)}}\left( {r,\theta } \right) - P_{\sigma }^{{\left( 1 \right)}}\left( {r,\theta ,t} \right) = 0; \\ \end{gathered} $(29)
${{\Phi }^{{\left( 1 \right)}}}\left( {r,\theta ,t} \right) - \frac{Q}{{{{\varepsilon }_{{{\text{ex}}}}}{{R}^{2}}}}\xi \left( {\theta ,t} \right) = \Phi _{{\text{s}}}^{{\left( 1 \right)}};$(30)
$\begin{gathered} 3{{R}^{2}}\int\limits_0^\pi {\xi \left( {\theta ,t} \right)\sin {\kern 1pt} \theta d\theta = 0} ; \\ 4{{R}^{3}}\int\limits_0^\pi {\xi \left( {\theta ,t} \right)\cos {\kern 1pt} \theta {\kern 1pt} \sin {\kern 1pt} \theta d\theta = 0} ; \\ \end{gathered} $(31)
$\int\limits_0^\pi {\frac{{\partial {{\Phi }^{{\left( 1 \right)}}}\left( {r,\theta ,t} \right)}}{{\partial r}}\sin {\kern 1pt} \theta d\theta = 0} .$Возмущение сферической формы капли $\xi (\theta ,t)$, связанное с капиллярным волновым движением в ней, запишем в виде ряда по осесимметричным полиномам Лежандра, принимая следующую зависимость от времени амплитудных коэффициентов ${{M}_{n}}\left( t \right)\sim \exp \left( {i{{\omega }_{n}}t} \right)$:
(32)
$\xi (r,\theta ,t) = \sum\limits_{n = 2}^\infty {{{M}_{n}}} {\kern 1pt} \exp \left( {i{{\omega }_{n}}t} \right){{P}_{n}}\left( \mu \right);\,\,\,\,\mu \equiv \cos {\kern 1pt} \theta .$Из (32) следует, что осесимметричные капиллярные осцилляции капли $n$-ой колебательной моды аналитически описываются полиномами Лежандра ${{P}_{n}}\left( \mu \right)$ $n$-ого порядка.
В силу осевой симметрии решения уравнений Лапласа (24) для потенциалов скоростей ${{\psi }_{j}}(r,\theta ,t)$ при выполнении условий ограниченности (25), (26) представим в виде разложений с учетом гармонической временной зависимости амплитуд ${{A}_{n}}\left( t \right),\;{{B}_{n}}\left( t \right)\sim \exp \left( {i{{\omega }_{n}}t} \right)$:
При помощи кинематического граничного условия (27) свяжем постоянные коэффициенты ${{A}_{n}}$, ${{B}_{n}}$ с амплитудами капиллярных осцилляций ${{M}_{n}}$ соотношениями:
Используя эти выражения, выпишем окончательный вид гидродинамических потенциалов:
(33)
${{\psi }_{1}}(r,\theta ,t) = R\sum\limits_{n = 2}^\infty {{{{\left( {\frac{r}{R}} \right)}}^{n}}\frac{{i{{\omega }_{n}}}}{n}{{M}_{n}}{\kern 1pt} \exp \left( {i{{\omega }_{n}}t} \right){{P}_{n}}\left( \mu \right)} ;$(34)
${{\psi }_{2}}(r,\theta ,t) = - R\sum\limits_{n = 2}^\infty {{{{\left( {\frac{r}{R}} \right)}}^{{n + 1}}}\frac{{i{{\omega }_{n}}}}{{\left( {n + 1} \right)}}{{M}_{n}}{\kern 1pt} \exp \left( {i{{\omega }_{n}}t} \right){{P}_{n}}\left( \mu \right)} .$Чтобы воспользоваться динамическим граничным условием (28), необходимо найти в явном виде добавки к давлениям $P_{j}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right)$, $P_{q}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right)$, $P_{\sigma }^{{\left( 1 \right)}}\left( {r,\theta ,t} \right)$, связанные с искажением равновесной сферы.
В первом порядке малости давления внутренней и внешней сред капли $P_{j}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right)$ определяются выражениями:
После подстановки в них решений (33), (34) найдем:
(35)
$P_{1}^{{\left( 1 \right)}} = {{\rho }_{1}}R\sum\limits_{n = 2}^\infty {\frac{{\omega _{n}^{2}}}{n}{{M}_{n}}{\kern 1pt} \exp \left( {i{{\omega }_{n}}t} \right){{P}_{n}}\left( \mu \right)} ;$(36)
$P_{2}^{{\left( 1 \right)}} = - {{\rho }_{2}}R\sum\limits_{n = 2}^\infty {\frac{{\omega _{n}^{2}}}{{\left( {n + 1} \right)}}{{M}_{n}}{\kern 1pt} \exp \left( {i{{\omega }_{n}}t} \right){{P}_{n}}\left( \mu \right)} .$Для нахождения поправки к давлению сил поверхностного натяжения $P_{\sigma }^{{\left( 1 \right)}}\left( {r,\theta ,t} \right)$ выпишем с учетом осевой симметрии задачи орт нормали ${\mathbf{n}}(\theta ,t)$ к свободной поверхности капли $F\left( {r,\theta ,t} \right) = r - R - $ $ - \,\,r\left( {\theta ,t} \right) = 0$, вычисляемый в первом порядке малости по общей формуле ${\mathbf{n}}\left( {\theta ,t} \right) = \nabla F{\text{/}}\left| {\nabla F} \right|$, в виде:
Тогда в первом же порядке малости давление $P_{\sigma }^{{\left( 1 \right)}}\left( {r,\theta ,t} \right)$ определится выражением:
(37)
$P_{\sigma }^{{\left( 1 \right)}} = \frac{\sigma }{{{{R}^{2}}}}\sum\limits_{n = 2}^\infty {\left( {n - 1} \right)\left( {n + 2} \right){{M}_{n}}{\kern 1pt} \exp \left( {i{{\omega }_{n}}t} \right){{P}_{n}}\left( \mu \right)} .$Пользуясь асимптотическим разложением (16) электрического потенциала, будем искать поправку к давлению сил электрического поля $P_{q}^{{\left( 1 \right)}}\left( {r,\theta ,t} \right)$, выписанную в первом порядке по амплитуде $\varepsilon $, в виде:
(38)
$\begin{gathered} r = R{\kern 1pt} :P_{q}^{{\left( 1 \right)}} = \\ = \,\,\frac{{{{\varepsilon }_{{{\text{ex}}}}}}}{{8\pi }}{{\left( {\frac{\partial }{{\partial r}}{{{\left( {\nabla {{\Phi }^{{\left( 0 \right)}}}} \right)}}^{2}}\xi \left( {\theta ,t} \right) + 2\nabla {{\Phi }^{{\left( 0 \right)}}}\nabla {{\Phi }^{{\left( 1 \right)}}}} \right)}^{2}}, \\ \end{gathered} $Для отыскания явного вида давления (38) необходимо найти компоненту потенциала ${{\Phi }^{{\left( 1 \right)}}}$, связанную с возмущением капли $\xi (\theta ,t)$, из решения электрической задачи (24), (26), (29), (31).
Решение уравнения (24), удовлетворяющее условию убывания потенциала ${{\Phi }^{{\left( 1 \right)}}}$ на бесконечности ($r \to \infty $), может быть представлено в виде:
При этом поправка к поверхностному потенциалу равна $\Phi _{{\text{s}}}^{{\left( 1 \right)}} = 0$.
Для возмущенного электрического потенциала несложно записать:
(39)
${{\Phi }^{{\left( 1 \right)}}}(r,\theta ) = \frac{Q}{{{{\varepsilon }_{{{\text{ex}}}}}{{R}^{2}}}}\sum\limits_{n = 1}^\infty {{{{\left( {\frac{R}{r}} \right)}}^{{n + 1}}}{{M}_{n}}{\kern 1pt} \exp \left( {i{{\omega }_{n}}t} \right){{P}_{n}}\left( \mu \right)} .$В итоге, пользуясь решениями (37), (32), (39), равенство (38) преобразуем к виду:
(40)
$P_{q}^{{\left( 1 \right)}} = \frac{{{{Q}^{2}}}}{{4\pi {{\varepsilon }_{{{\text{ex}}}}}{{R}^{5}}}}\sum\limits_{n = 2}^\infty {\left( {n - 1} \right){{M}_{n}}{\kern 1pt} \exp \left( {i{{\omega }_{n}}t} \right){{P}_{n}}\left( \mu \right)} .$Подставляя в баланс давлений (28) линейные по $\varepsilon $ поправки к давлениям (35), (36), (37), (40) и используя ортогональность полиномов Лежандра, придем к дисперсионному уравнению, определяющему связь частоты капиллярных осцилляций ${{\omega }_{n}}$ заряженной капли с номером колебательной моды $n$:
(41)
$\begin{gathered} \omega _{n}^{2} = \frac{\sigma }{{{{R}^{3}}}}\frac{{n\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)}}{{\left( {{{\rho }_{1}}\left( {n + 1} \right) + {{\rho }_{2}}n} \right)}}\left[ {1 - \frac{W}{{\left( {n + 2} \right)}}} \right]; \\ (n \geqslant 2);\,\,\,\,W = \frac{{{{Q}^{2}}}}{{4\pi {{\varepsilon }_{{{\text{ex}}}}}\sigma {{R}^{3}}}}. \\ \end{gathered} $Из уравнения (41) можно видеть, что для положительных значений выражения в квадратных скобках поверхность капли устойчива по отношению к величине ее нескомпенсированного заряда: $W < \left( {n + 2} \right)$ [1].
4. УЧЕТ РЕЛАКСАЦИИ ПОВЕРХНОСТНОГО НАТЯЖЕНИЯ
Экспериментально обнаружено, что характерное время релаксации τr поверхностного натяжения различных жидкостей, включая воду, составляет ${{10}^{{ - 5}}}{\kern 1pt} - {\kern 1pt} {{10}^{{ - 3}}}$ с [6–8], а максимальное значение динамического поверхностного натяжения ${{\sigma }_{\infty }}$ на 25% выше его равновесного значения ${{\sigma }_{0}}$ [9]. В связи с этим для численных оценок водяных капель (при ${{\sigma }_{0}} = 73$ дин/см) приняты средние характеристики: ${{\tau }_{{\text{r}}}} = 1 \times {{10}^{{ - 4}}}$ с, ${{\sigma }_{\infty }} = 91$ дин/см, ${{\sigma }_{*}} = {{\sigma }_{\infty }} - {{\sigma }_{0}} = 18$ дин/см.
Принимая во внимание, что в результате разрушения двойного электрического слоя коэффициент поверхностного натяжения изменяется от максимального до равновесного значений, динамический коэффициент $\sigma \left( t \right)$ естественно представить в виде суперпозиции коэффициента поверхностного натяжения равновесной структуры капли и добавки, связанной с разрушением упорядоченности полярных молекул в приповерхностном слое жидкости:
(42)
$\sigma \left( t \right) = {{\sigma }_{0}} + {{\sigma }_{*}}\exp \left( { - \frac{t}{{{{\tau }_{r}}}}} \right).$Следует отметить, что в общем случае релаксация поверхностного натяжения характеризуется отклонением структуры мгновенно деформированной поверхности от ее равновесной структуры. Известно, что лапласовское давление определяет связь между изменением давления под искривленным капиллярным волновым движением поверхности капли (что аналогично нормальному напряжению) с кривизной поверхности. Иначе говоря, эффект релаксации приповерхностной структуры капли можно связать с положением вязкоупругости, при котором нормальное напряжение зависит от истории деформации. В этом случае имеет место соотношение (аналогичное принципу суперпозиции Больцмана), выражающее мгновенное изменение давления на поверхности капли $\Delta {{P}_{1}}\left( t \right)$ через историю изменения кривизны ее поверхности $u\left( t \right)$ [20, 21]:
(43)
$\Delta {{P}_{1}}\left( t \right) = \int\limits_{ - \infty }^t {\sigma \left( {t - \tau } \right)\frac{{du\left( \tau \right)}}{{d\tau }}d\tau } .$Аналогично тому, как в случае твердотельного поведения жидкости его напряжение связывается с деформацией, согласно принципу суперпозиции Больцмана определим мгновенное изменение давления на поверхности капли $\Delta {{P}_{1}}\left( t \right)$ через историю изменения кривизны ее поверхности $u\left( t \right)$ [20, 21].
Подстановка (42) в (43) и применение прямого преобразования Фурье к (43) позволяет перейти от временной зависимости величины $\sigma $ к частотной. В результате комплексный коэффициент поверхностного натяжения $\sigma $ запишем в соответствии с известной формулой Максвелла [20]:
(44)
$\begin{gathered} \sigma = {{\sigma }_{\infty }} - \frac{{{{\sigma }_{*}}}}{{1 - i{{\omega }_{n}}{{\tau }_{{\text{r}}}}}} = {{\sigma }_{0}} - \frac{{i{{\omega }_{n}}{{\sigma }_{*}}{{\tau }_{{\text{r}}}}}}{{1 - i{{\omega }_{n}}{{\tau }_{{\text{r}}}}}}; \\ {{\sigma }_{*}} = {{\sigma }_{\infty }} - {{\sigma }_{0}}. \\ \end{gathered} $В (42), (44) введены обозначения: $i$ – мнимая единица, τr – характерное время релаксации (время, за которое мгновенно деформированный приповерхностный слой жидкой капли возвращается в равновесное состояние), ${{\sigma }_{0}}$ – значение коэффициента поверхностного натяжения равновесной структуры капли (для нулевой частоты), ${{\sigma }_{\infty }}$ – максимальное значение коэффициента поверхностного натяжения капли для весьма высоких частот (при разрушенной упорядоченной структуре двойного электрического слоя), отвечающих неравенству ${{\omega }_{n}}{{\tau }_{{\text{r}}}} \gg 1$, ${{\sigma }_{*}}$ – поправка к величине ${{\sigma }_{0}}$, связанная с отклонением приповерхностного слоя капли от равновесного состояния в результате эффекта релаксации.
Подставляя (44) в (41), легко выпишем окончательное дисперсионное уравнение для капиллярных осцилляций заряженной капли, порождаемых релаксацией поверхностного натяжения:
(45)
$\begin{gathered} \omega _{n}^{3} + i\frac{{\omega _{n}^{2}}}{{{{\tau }_{{\text{r}}}}}} - {{\omega }_{n}}\left( {\omega _{{n0}}^{2} + \frac{{{{\sigma }_{*}}}}{{{{\sigma }_{0}}}}\omega _{{n0}}^{{'2}}} \right) - i\frac{{\omega _{{n0}}^{2}}}{{{{\tau }_{{\text{r}}}}}} = 0;\,\,\,\,(n \geqslant 2); \\ \omega _{{n0}}^{{'2}} = \frac{{{{\sigma }_{0}}}}{{{{R}^{3}}}}\frac{{n\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)}}{{\left( {{{\rho }_{1}}\left( {n + 1} \right) + {{\rho }_{2}}n} \right)}}; \\ \omega _{{n0}}^{2} = \frac{{{{\sigma }_{0}}}}{{{{R}^{3}}}}\frac{{n\left( {n - 1} \right)\left( {n + 1} \right)\left( {n + 2} \right)}}{{\left( {{{\rho }_{1}}\left( {n + 1} \right) + {{\rho }_{2}}n} \right)}}\left[ {1 - \frac{{{{W}_{0}}}}{{\left( {n + 2} \right)}}} \right]; \\ {{W}_{0}} = \frac{{{{Q}^{2}}}}{{4\pi {{\sigma }_{0}}{{R}^{3}}}}, \\ \end{gathered} $Несложно видеть, что второй и четвертый коэффициенты дисперсионного уравнения являются мнимыми, и что включение механизма релаксации сказывается на увеличении порядка дисперсионного уравнения по сравнению с уравнением (41), выписанным без учета релаксации. Это происходит за счет появления затухания капиллярных осцилляций капли, связанных с релаксацией поверхностной энергии (коэффициента поверхностного натяжения) к их равновесным значениям в процессе восстановления двойного электрического слоя.
Решениями дисперсионного кубического уравнения (формула (45)), имеющего комплексные коэффициенты, являются три комплексных корня: первый корень содержит только мнимую часть, а два других имеют одинаковую комплексную часть и отличающуюся знаком реальную часть. При этом положительная вещественная компонента комплексной частоты интерпретируется как собственная частота осцилляций капли, а отрицательная вещественная часть не имеет физического смысла.
Решения уравнения (45), полученные в пакете аналитических вычислений MATHEMATICA, с использованием средних по облаку характеристик водяной капли и внешней среды (воздуха), принимают окончательный вид трех комплексных решений: одно – чисто мнимое и два других – с одинаковой мнимой частью и противоположной по знаку реальной частью:
(46)
$\begin{gathered} \omega _{n}^{{\left( 1 \right)}} = - i\left( {\frac{{{{l}_{1}}}}{3} + {{\alpha }_{0}} + {{\alpha }_{1}}} \right); \\ \omega _{n}^{{\left( 2 \right)}} = - \frac{{\sqrt 3 }}{2}{{\alpha }_{0}} + \frac{{\sqrt 3 }}{2}{{\alpha }_{1}} - i\left( {\frac{{{{l}_{1}}}}{3} + \frac{{{{\alpha }_{0}}}}{2} + \frac{{{{\alpha }_{1}}}}{2}} \right); \\ \omega _{n}^{{\left( 3 \right)}} = \frac{{\sqrt 3 }}{2}\alpha _{0}^{'} - \frac{{\sqrt 3 }}{2}\alpha _{1}^{'} - i\left( {\frac{{{{l}_{1}}}}{3} + \frac{{{{\alpha }_{0}}}}{2} + \frac{{{{\alpha }_{1}}}}{2}} \right). \\ \operatorname{Im} {\kern 1pt} \omega _{n}^{{\left( 2 \right)}} = \eta _{n}^{{\left( 2 \right)}} = - \left( {\frac{{{{l}_{1}}}}{3} + \frac{{\alpha _{0}^{'}}}{2} + \frac{{\alpha _{1}^{'}}}{2}} \right);\,\,\,\,{{\alpha }_{0}} = \frac{{\sqrt[3]{2}{{\beta }_{0}}}}{{3{{{\left( {{{\beta }_{1}} + {{\beta }_{3}}} \right)}}^{{\frac{1}{3}}}}}}; \\ {{\alpha }_{1}} \equiv \frac{{{{{\left( {{{\beta }_{1}} + {{\beta }_{2}}} \right)}}^{{\frac{1}{3}}}}}}{{3\sqrt[3]{2}}};\,\,\,\,{{l}_{1}} = \frac{1}{{{{\tau }_{{\text{r}}}}}};\,\,\,\,{{l}_{2}} = \omega _{{n0}}^{2} + \frac{{{{\sigma }_{*}}}}{{{{\sigma }_{0}}}}\omega _{{n0}}^{{'2}}; \\ {{l}_{3}} = \frac{{\omega _{{n0}}^{2}}}{{{{\tau }_{{\text{r}}}}}};\,\,\,\,{{\beta }_{0}} = l_{1}^{2} - 3{{l}_{2}};\,\,\,\,{{\beta }_{1}} = 2l_{1}^{3} - 9{{l}_{1}}{{l}_{2}} + 27{{l}_{3}}; \\ {{\beta }_{2}} = 3\sqrt {3\left| {l_{1}^{2}l_{2}^{2} - 4l_{2}^{3} - 4l_{1}^{3}{{l}_{3}} + 18{{l}_{1}}{{l}_{2}}{{l}_{3}} - 27l_{3}^{2}} \right|} . \\ \end{gathered} $Аналитические выражения (46) являются окончательным решением дисперсионного уравнения (45). При этом вещественная часть $\operatorname{Re} \omega _{n}^{{\left( j \right)}}$ комплексной величины $\omega _{n}^{{\left( j \right)}}$ определяет собственную частоту осцилляций капли, а мнимая – декремент затухания $\eta _{n}^{{\left( j \right)}} \equiv \operatorname{Im} {\kern 1pt} \omega _{n}^{{\left( j \right)}}$, связанный с релаксацией поверхностного натяжения, ${{\omega }_{n}}$ – частота осцилляций $n$-ой моды, ${{\omega }_{{n0}}}$, $\omega _{{n0}}^{'}$ – частоты осцилляций $n$-ой моды заряженной и незаряженной капель, имеющих равновесную структуру приповерхностного слоя жидкости.
Согласно данным натурных измерений [15], характерные размеры внутриоблачных капель, составляющих кучево-дождевые облака, приходятся на диапазон от 3 до 30 мкм с максимальной концентрацией при $R = 3{\kern 1pt} - {\kern 1pt} 7$ мкм. На стадии развития конвективных облаков в результате коагуляции облачных капель образуются мелкие дождевые капли радиусами $0.01 \leqslant R \leqslant 0.025\;{\text{см}}$, называемые моросью, и укрупненные дождевые капли с типичными размерами $0.025 \leqslant R \leqslant 0.35\;{\text{см}}$. Более крупные капли радиусами от 0.35 см разбиваются при падении в воздухе из-за аэродинамического сопротивления [13].
Появление нескомпенсированных зарядов на отдельных осциллирующих каплях вызывается процессами электризации при захвате каплями воздушных ионов, перераспределения зарядов из-за разрушения, слияния с другими каплями [14]. В соответствии со справочными данными [15], при характерных средних зарядах рассматриваемых капель величина параметра Релея, определяющая электрогидродинамическую устойчивость капли по отношению к ее собственному заряду, много меньше критического значения ${{W}_{{{\text{кр}}}}}{\text{/}}4 = 1$ [1], при котором наблюдается распад капли.
Расчеты показывают, что эффект релаксации поверхностного натяжения слабо влияет на параметры низкочастотных осцилляций капли (на основной моде и на соседних модах), он существенно проявляется, когда период осцилляций становится примерно равным характерному времени релаксации поверхностного натяжения. Для капли воды это происходит, когда номер моды осцилляций примерно на порядок величины превышает номер основной моды, поэтому нижеследующие вычисления проведем для $n = 10$.
Для отыскания численных решений примем, что осцилляции капель связаны с модой $n = 10$. Примем средние характеристики водяных капель: ${{\sigma }_{0}} = 73$ дин/см, ${{\rho }_{1}} = 1$ г/м3, $Q = 2 \times {{10}^{{ - 5}}}$ СГСЭ ($\sim {\kern 1pt} 0.04{{Q}_{{{\text{кр}}}}}$ при $R = 3$ мкм и $\sim {\kern 1pt} 0.001{{Q}_{{{\text{кр}}}}}$ приR = = 30 мкм), где ${{Q}_{{{\text{кр}}}}}$ – критическое для реализации электростатической неустойчивости значение заряда. Кроме того, примем ${{\varepsilon }_{{{\text{ex}}}}} = 1$, ${{\sigma }_{\infty }} = 91$ дин/см, ${{\sigma }_{*}} = 18$ дин/см, ${{\rho }_{2}} = 1.3 \times {{10}^{{ - 3}}}$ г/м3, ${{\tau }_{{\text{r}}}} = 1 \times {{10}^{{ - 4}}}$ с.
Анализируя численные решения, получаем, что первый корень $\omega _{{10}}^{{\left( 1 \right)}}$ определяет чисто апериодическое затухание, а второй и третий корни $\omega _{{10}}^{{\left( 2 \right)}}$, $\omega _{{10}}^{{\left( 3 \right)}}$ соответствуют медленно затухающим осцилляциям облачных капель (в этом случае декремент затухания на четыре порядка ниже частоты собственных осцилляций) и весьма быстрым затухающим осцилляциям мелких дождевых капель ($\eta _{{10}}^{{\left( j \right)}}$ на один-два порядка меньше $\operatorname{Re} \omega _{{10}}^{{\left( j \right)}}$). Одновременно с этим увеличение размера капли приводит к увеличению отношения $\left| {\eta _{{10}}^{{\left( j \right)}}} \right|{\text{/}}\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( j \right)}}$ так, что осцилляции крупных дождевых капель имеют апериодический характер. Из полученных численных решений выясняется, что при снижении размеров капель включение эффекта динамического поверхностного натяжения приводит к возрастанию собственных частот осцилляций по сравнению с частотами, определяемыми уравнением (41) без учета релаксации [13]. Отсюда можно сделать вывод, что вызванные релаксацией поверхностного натяжения затухающие осцилляции облачных капель соответствуют высоким частотам $\operatorname{Re} {\kern 1pt} {{\omega }_{{10}}}{{\tau }_{{\text{r}}}} \gg 1$.
Для того чтобы иметь возможность проиллюстрировать зависимости характеристик затухающих осцилляций капли, выделим в аналитических выражениях (46) вещественную $\operatorname{Re} {\kern 1pt} \omega _{n}^{{\left( j \right)}}$ и мнимую $\operatorname{Im} {\kern 1pt} \omega _{n}^{{\left( j \right)}}$ компоненты:
(47)
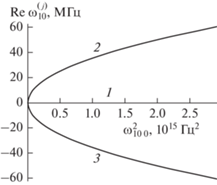
$\begin{gathered} \operatorname{Re} {\kern 1pt} \omega _{n}^{{\left( 1 \right)}} = 0;\,\,\,\,\operatorname{Re} {\kern 1pt} \omega _{n}^{{\left( 2 \right)}} = - \frac{{\sqrt 3 }}{2}\alpha _{0}^{'} + \frac{{\sqrt 3 }}{2}\alpha {\kern 1pt} '; \\ \operatorname{Re} {\kern 1pt} \omega _{n}^{{\left( 3 \right)}} = \frac{{\sqrt 3 }}{2}\alpha _{0}^{'} - \frac{{\sqrt 3 }}{2}\alpha {\kern 1pt} ';\,\,\,\,\operatorname{Im} {\kern 1pt} \omega _{n}^{{\left( 1 \right)}} = \\ = \,\, - \left( {\frac{{{{l}_{1}}}}{3} + \alpha _{0}^{'} + \alpha _{1}^{'}} \right);\,\,\,\,\operatorname{Im} {\kern 1pt} \omega _{n}^{{\left( 2 \right)}} = \operatorname{Im} {\kern 1pt} \omega _{n}^{{\left( 3 \right)}} = \\ = \,\, - \left( {\frac{{{{l}_{1}}}}{3} + \frac{{\alpha _{0}^{'}}}{2} + \frac{{\alpha _{1}^{'}}}{2}} \right). \\ \end{gathered} $На рис. 1 представлены зависимости вещественной части комплексных частот $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( j \right)}}$, описываемых соотношениями (4.9), от величины квадрата частоты $\omega _{{10\,\,0}}^{2}$ для равновесной структуры капли. В анализируемом случае радиус внутриоблачной капли R меняется от 3 до 30 мкм, поэтому $\omega _{{10\,\,0}}^{2}$ изменяется в диапазоне от 2.9 × 1012 рад до 2.9 × 1015 рад2/c2. Кривая 1 соответствует $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 1 \right)}} = 0$, кривая 2 построена для положительной частоты $\operatorname{Re} \omega _{{10}}^{{\left( 2 \right)}}$, кривая 3 определяет отрицательную $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 3 \right)}}$. Как показывают графики, с ростом параметра $\omega _{{10\,\,0}}^{2}$ частоты $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( j \right)}}$, связанные с релаксационным процессом, быстро увеличиваются по абсолютной величине.
Рис. 1.
Зависимость вещественной компоненты $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( j \right)}}$ комплексных частот осцилляций заряженной облачной капли от величины квадрата частоты $\omega _{{10\,\,0}}^{2}$ для равновесной структуры капли (при изменении радиуса от $R = 3$ мкм до $R = 30$ мкм), рассчитанная при $n = 10$, ${{\varepsilon }_{{{\text{ex}}}}} = 1$, $Q = 2 \times {{10}^{{ - 5}}}$ СГСЭ, ${{\rho }_{1}} = 1$ г/м3, ${{\rho }_{2}} = 1.3 \times {{10}^{{ - 3}}}$ г/м3, ${{\sigma }_{0}} = 73$ дин/см, ${{\sigma }_{\infty }} = 91$ дин/см, ${{\sigma }_{*}} = 18$ дин/см, ${{\tau }_{{\text{r}}}} = 1 \times {{10}^{{ - 4}}}$ с. Кривая 1 соответствует $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 1 \right)}}$, кривая 2 – $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}$, кривая 3 – $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 3 \right)}}$.
На рис. 2 и 3 приведены зависимости положительной вещественной компоненты комплексной частоты $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}$ от размеров $R$ и зарядов $Q$ (вплоть до критических значений ${{Q}_{{{\text{кр}}}}}$ для указанного $R$) внутриоблачных и дождевых капель.
Рис. 2.
Зависимость положительной вещественной компоненты $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}$ комплексной частоты осцилляций заряженной капли от ее радиуса $R$, построенная при тех же значениях физических величин, что на рис. 1: а – внутриоблачная капля, имеющая заряд $Q = 2 \times {{10}^{{ - 5}}}$ СГСЭ ($\sim {\kern 1pt} 0.02{{Q}_{{{\text{кр}}}}}$ при $R = 5$ мкм и $\sim {\kern 1pt} 0.001{{Q}_{{{\text{кр}}}}}$ при $R = 30$ мкм), б – дождевая капля, имеющая заряд $Q = 7 \times {{10}^{{ - 4}}}$ СГСЭ ($\sim {\kern 1pt} 2 \times {{10}^{{ - 3}}}{{Q}_{{{\text{кр}}}}}$ при $R = 0.025$ см и $\sim {\kern 1pt} 5 \times {{10}^{{ - 5}}}{{Q}_{{{\text{кр}}}}}$ при $R = 0.25$ см).
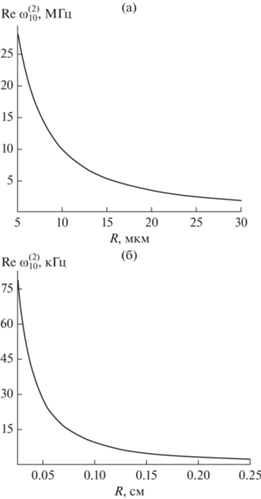
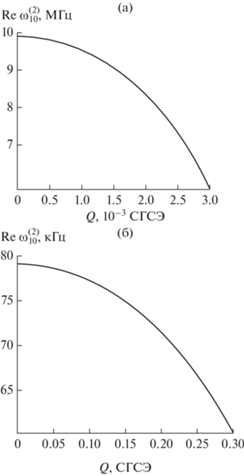
Рис. 3.
Зависимость положительной вещественной компоненты $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}$ комплексной частоты осцилляций заряженной капли от величины ее собственного заряда $Q$, построенная при тех же значениях физических величин, что на рис. 1: а – внутриоблачная капля радиусом $R = 10$ мкм, б – дождевая капля радиусом $R = 250$ см.
Из рис. 2а, 2б несложно видеть, что с ростом размера исследуемых капель собственная частота осцилляций снижается по примерно гиперболическому закону: при увеличении радиуса $R$ в три раза, частота $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}$ возрастает в пять раз.
Согласно рис. 3а и 3б возрастание величины собственного заряда капли $Q$ приводит к уменьшению частоты $\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}$. Такая зависимость наиболее заметно сказывается при приближении $Q$ к критическому значению ${{Q}_{{{\text{кр}}}}}$.
Следует отметить, что затухающие капиллярные осцилляции капли, вызванные эффектом релаксации поверхностного натяжения, приводят к тому, что периодически изменяющаяся амплитуда возмущения $\xi (\theta ,t)$ сферической формы поверхности капли экспоненциально убывает со временем:
(48)
$\begin{gathered} {{M}_{{10}}}\left( t \right) = \varepsilon R{\kern 1pt} \cos \left( {\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}t + \varphi } \right)\exp \left( { - \left| {\eta _{{10}}^{{\left( 2 \right)}}} \right|t} \right), \\ \varepsilon = {{\varepsilon }_{0}}\sqrt {1 + {{{\left( {\frac{{\left| {\eta _{{10}}^{{\left( 2 \right)}}} \right|}}{{\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}}}} \right)}}^{2}}} ;\,\,\,\,\varphi = {\text{arctg}}\left( { - \frac{{\left| {\eta _{{10}}^{{\left( 2 \right)}}} \right|}}{{\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}}}} \right), \\ \end{gathered} $На рис. 4 изображены рассчитанные по (48) графики зависимости от времени $t$ амплитуды ${{M}_{{10}}}\left( t \right)$ возмущения равновесной формы капли. Рис. 4а, 4б иллюстрируют весьма медленно затухающие капиллярные осцилляции облачных капель, периоды которых $T = 0.1$ мкс при $R = 3$ мкм и $T = 3.3$ мкс при $R = 30$ мкм приблизительно совпадают с периодами собственных осцилляций. В этом случае в силу малости величины $\left| {\eta _{{10}}^{{\left( 2 \right)}}} \right|{\text{/}}\operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}} \ll 1$ амплитуда ${{M}_{{10}}}\left( t \right)$ будет иметь экспоненциально затухающий характер только при рассмотрении весьма больших времен. Из рис. 4 в можно видеть, что период затухающих осцилляций наименьшей дождевой капли $R = 250$ мкм составляет $T = 79.6$ мкс. На рис. 4г показаны затухающие капиллярные осцилляции дождевой капли размером $R = 0.05$ см с периодом $T = 0.23$ мс. Выясняется, что с увеличением размера капли возрастает период затухающих осцилляций, так как увеличивается величина отношения $\left| {\eta _{{10}}^{{\left( 2 \right)}}} \right|{\text{/}}{\kern 1pt} \operatorname{Re} {\kern 1pt} \omega _{{10}}^{{\left( 2 \right)}}$ и, как следствие, снижается частота затухающих осцилляций.
Рис. 4.
Зависимость от времени $t$ амплитуды ${{M}_{{10}}}\left( t \right)$ возмущения равновесной формы заряженной капли, совершающей затухающие капиллярные осцилляции. Расчеты проведены при тех же физических величин, что на рис. 1: а – внутриоблачная капля радиуса $R = 30$ мкм с зарядом $Q = 2 \times {{10}^{{ - 5}}}$ СГСЭ ($\sim {\kern 1pt} 0.001{{Q}_{{{\text{кр}}}}}$), б – дождевая капля радиуса $R = 0.025$ см с зарядом $Q = 7\,\,{{ \times }}\,\,{{10}^{{ - 4}}}$ СГСЭ ($\sim {\kern 1pt} 2 \times {{10}^{{ - 3}}}{{Q}_{{{\text{кр}}}}}$), в – дождевая капля радиуса $R = 0.05$ см с зарядом $Q = 7 \times {{10}^{{ - 4}}}$ СГСЭ ($\sim {\kern 1pt} 6 \times {{10}^{{ - 4}}}{{Q}_{{{\text{кр}}}}}$); г − дождевая капля радиуса $R = 0.11$ см с зарядом $Q = 7 \times {{10}^{{ - 4}}}$ СГСЭ ($\sim {\kern 1pt} 2 \times {{10}^{{ - 4}}}{{Q}_{{{\text{кр}}}}}$).
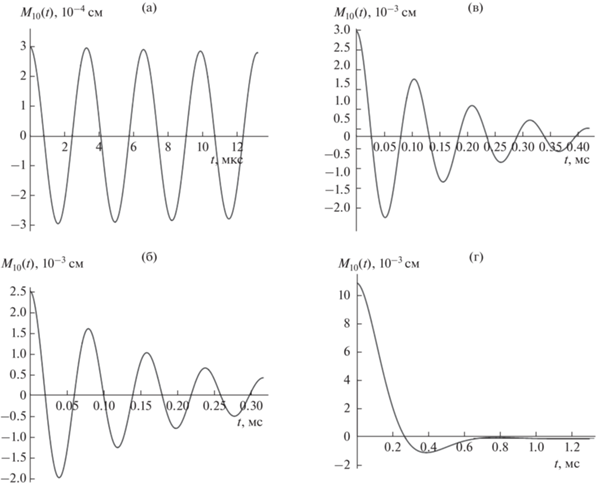
Из рис. 4г видно, что быстрое затухание осцилляций имеет место, когда период осцилляций сравним с характерным временем релаксации поверхностного натяжения.
Интересно сравнить между собой графики затухающих волн на поверхности капель, различающиxся лишь номерами мод возбужденных волн на одном и том же временном интервале, при прочих равных условиях. На рис. 5а, 5б приведены графики, аналогичные изображенному на рис. 4а, но рассчитанные для разных мод на большем временном интервале: для основной моды при $n = 2$ и для $n = 10$. Несложно видеть, что, несмотря на внешние различия, качественно графики выглядят одинаково, различаясь лишь периодами осцилляций. Удивление вызывает то обстоятельство, что к концу использованного при расчетах к рис. 5а и 5б периода времени амплитуды и второй, и десятой мод визуально одинаковы. В этой связи рассчитаны по (46) графики зависимости декремента затухания от номера моды. Они приведены на рис. 6а, 6б. Оказалось, что искомая зависимость весьма слаба.
Рис. 5.
Зависимость от времени $t$ амплитуд различных мод возмущения равновесной формы заряженной капли радиуса $R = 30$ мкм и зарядом $Q = 2 \times {{10}^{{ - 5}}}$ СГСЭ ($\sim {\kern 1pt} 2 \times {{10}^{{ - 3}}}{{Q}_{{{\text{кр}}}}}$). Расчеты проведены при: $\varepsilon = 0.1$, ${{\varepsilon }_{{{\text{ex}}}}} = 1$, ${{\rho }_{1}} = 1$ г/м3, ${{\rho }_{2}} = 1.3 \times {{10}^{{ - 3}}}$ г/м3, ${{\sigma }_{0}} = 73$ дин/см, ${{\sigma }_{\infty }} = 91$ дин/см, σ* = 18 дин/см, ${{\tau }_{r}} = 1 \times {{10}^{{ - 4}}}$ с: (а) $n = 2$; (б) $n = 10$.
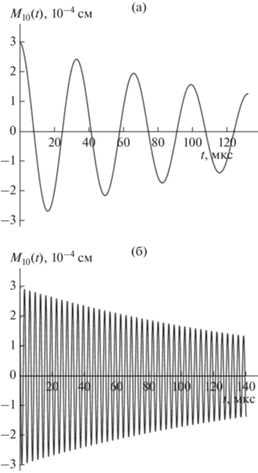
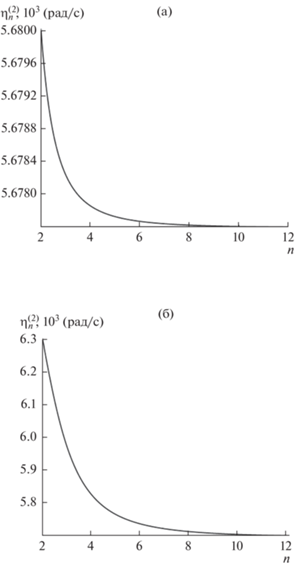
Рис. 6.
Зависимость от номера моды $n$ декремента затухания $\eta _{{10}}^{{\left( 2 \right)}}$ капиллярных осцилляций капли. Расчеты проведены при ${{\varepsilon }_{{{\text{ex}}}}} = 1$, ${{\rho }_{1}} = 1$ г/м3, ${{\rho }_{2}} = 1.3 \times {{10}^{{ - 3}}}$ г/м3, ${{\sigma }_{0}} = 73$ дин/см, ${{\sigma }_{\infty }} = 91$ дин/см, σ* = 18 дин/см, ${{\tau }_{{\text{r}}}} = 1 \times {{10}^{{ - 4}}}$ с: (а) внутриоблачной капли радиуса $R = 30$ мкм и зарядом $Q = 2 \times {{10}^{{ - 5}}}$ СГСЭ; (б) дождевой капли с радиусом $R = 0.025$ см и зарядом $Q = 7 \times {{10}^{{ - 4}}}$ СГСЭ.
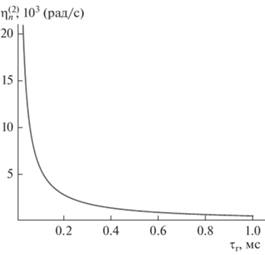
На рис. 7 приведена зависимость инкремента затухания от характерного времени релаксации поверхностного натяжения τr, рассчитанная по (46). Видно, что декремент затухания тем больше, чем меньше величина τr по примерно гиперболическому закону.
Рис. 7.
Зависимость декремента затухания $\eta _{{10}}^{{\left( 2 \right)}}$ капиллярных осцилляций капли радиуса $R = 10$ мкм с зарядом $Q = 2 \times {{10}^{{ - 5}}}$ СГСЭ ($\sim {\kern 1pt} 6 \times {{10}^{{ - 3}}}{{Q}_{{{\text{кр}}}}}$) от характерного времени релаксации τr, построенная при тех же значениях физических величин, что и на рис. 1.
5. ОБСУЖДЕНИЕ ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ
Естественно задаться вопросом, к каким последствиям приведет описанная выше картина быстрого затухания осцилляций (рис. 4г) при $\left| {\eta _{{10}}^{{\left( 2 \right)}}} \right|{\kern 1pt} {\text{/}}{\kern 1pt} \operatorname{Re} \omega _{{10}}^{{\left( 2 \right)}} \sim 1$.
Очевидно, что картина затухания волны в течение одного периода объясняется ростом декремента затухания. Согласно (45) декремент затухания $\eta \equiv \omega _{n}^{'}$ увеличивается с ростом номера моды осцилляций $n$ примерно пропорционально $n$ и убывает с увеличением радиуса капли $R$ пропорционально ${{R}^{{{3 \mathord{\left/ {\vphantom {3 2}} \right. \kern-0em} 2}}}}$.
Примем, что на поверхности капли существует высокочастотная капиллярная волна большой (нетепловой) амплитуды, возникшая из-за столкновения с другой каплей, которая может разрушить упорядоченность приповерхностных диполей. За характерное время релаксации поверхностного натяжения упорядоченность восстановится. Пройдет время, много большеe, чем время релаксации, когда амплитуда новой капиллярной волны вырастет до необходимой величины, чтобы разрушить упорядоченность диполей (или произойдет новое столкновение с другой каплей). При этом поверхностная энергия жидкости возрастет, а потом снова упорядоченность восстановится и т.д. Таким образом, образуется серия в общем случае нерегулярных снижений и повышений величины коэффициента поверхностного натяжения, иными словами, включается эффективный источник затухания амплитуд капиллярных осцилляций, связанный с разрушением упорядоченности полярных молекул жидкости в приповерхностном слое.
Как отмечалось во введении, упорядочение диполей приповерхностных молекул происходит из-за взаимодействий молекулярных квадруполей с диполями молекул. При разупорядочивании диполей за время порядка характерного времени межмолекулярных взаимодействий исчезает энергия электрического взаимодействия квадруполей с диполями, фактически в результате перемешивания молекул исчезает квадрупольный момент капли. Значит, электромагнитное излучение, связанное с разрушением упорядоченности, будет квадрупольным, которое существенно ниже дипольного [23, 24].
Интересно, что любое столкновение выделенной капли с другой или появление высокочастотной волны значительной амплитуды сразу же вызовет разрушение упорядоченности диполей на поверхности капли и появление электромагнитного импульса. Для появления еще одного подобного события нужно следующее столкновение или появление высокочастотной волны значительной амплитуды, причем эта волна должна иметь период T, удовлетворяющий условию $T \leqslant {{\tau }_{{\text{r}}}}$, тогда упорядоченность будет гарантированно разрушена (рис. 4г).
А теперь можно ответить на вопрос, сформулированный в заголовке этой работы: как происходит превращение энергии при наличии динамического поверхностного натяжения. Начнем с соударения капель, в котором механическая энергия соударения переходит в механическую энергию капиллярной волны на поверхности капли, разрушающую, в свою очередь, упорядоченное расположение молекулярных диполей на поверхности капли. При этом механическая энергия волны и энергия вандерваальсова взаимодействия соседних молекул воды идут на создание электромагнитного импульса (за счет электрической энергии взаимодействия квадруполей с диполями, высвобождающейся при разрушении электрического квадруполя капли) и на выработку тепла (за счет вязкости жидкости, не учитываемой в проведенном рассмотрении). Затем за малое время, порядка характерного времени межмолекулярного взаимодействия, упорядоченность молекулярных диполей самопроизвольно восстанавливается, поскольку этот процесс сопровождается переходом системы в положение с меньшей потенциальной энергией, в котором капля остается до следующего столкновения с другой каплей или частицей.
Встает простой, но закономерный вопрос: а почему капиллярное движение на поверхности капли идеальной жидкости вообще затухает? Если взять коэффициент поверхностного натяжения не динамическим, а обычным, то затухания (в использованной модели идеальной жидкости) не будет. Напрашивается вывод, что проблема в том, что мы выбрали коэффициент поверхностного натяжения в виде (42), где выражение (42) учитывает возможность перестройки приповерхностного слоя жидкости, которая сопровождается преобразованием энергии.
Возникает еще один вопрос: будет ли выполняться постоянство электрического потенциала при осцилляциях капли?
Сравним между собой характерное время электрической релаксации и характерное время гидродинамической релаксации.
Характерное время электрической релаксации ${{\tau }_{\chi }}$ – время, за которое амплитудное значение флуктуации электрического потенциала или заряда уменьшится за счет электропроводности в $e$ раз, имеет вид [25, с. 27]:
(49)
${{\tau }_{\chi }} \equiv {\varepsilon \mathord{\left/ {\vphantom {\varepsilon \chi }} \right. \kern-0em} \chi },$Оценим ${{\tau }_{\chi }}$ для дождевой воды количественно. Для оценки диэлектрическую проницаемость воды примем $\varepsilon = 81$, а удельную электропроводность согласно данным Интернета χ ~ 100–1300 мкСм/см. Впрочем, верхний предел электропроводности воды в зависимости от ее минерализации может быть еще на порядок больше. Это согласуется с [25, с. 531]. В связи со сказанным, примем для оценки χ ~ 103 мкСм/см или $\chi = 9 \times {{10}^{9}}\,\,{{{\text{с}}}^{{ - 1}}}$ и получим по (49) τχ ~ 10–8 c.
Характерное время выравнивания давления в капле τg (характерное время гидродинамической релаксации) оценим как отношение радиуса капли $R$ к скорости звука в воде. Принимая R ~ 1 мм, а скорость звука в воде c ~ 1000 м/c получим τg ~ 10–7 c.
Таким образом, потенциал поверхности капли будет успевать выравниваться при ее осцилляциях и его можно принимать постоянным.
Если взять удельную электропроводность на порядок больше: χ ~ 104 мкСм/см, то получим τg ~ 10–9 c.
Следовательно, можно снизить радиус капли, у которой электрический потенциал выравнивается быстрее гидродинамического давления, до R ~ 30 мкм.
Из проведенных оценок вытекает, что предлагаемый в работе механизм разрушения и восстановления упорядоченности диполей в приповерхностном слое работает тем лучше, чем больше размер капли. Для дождевых капель он будет работать.
Следует отметить, что особенности релаксационного затухания осцилляций мелких капель с R ≤ 1 мкм требуют отдельного рассмотрения, поскольку для капель столь малых размеров включается “масштабный” эффект [22]. Безразмерная вязкость (если уйти от идеальной жидкости) капли зависит не только от величины коэффициента кинематической вязкости, но и от ее размера, величины коэффициента поверхностного натяжения и массовой плотности в безразмерных переменных, в которых ρ = σ = R = 1. Осцилляции имеют место, когда безразмерная комбинация: $\mu \equiv \nu \sqrt {\frac{\rho }{{\sigma R}}} $ (безразмерный коэффициент кинематической вязкости) удовлетворяет неравенству $\mu \ll 1$, а сами осцилляции подавляются вязкостью уже при μ ~ 1 [22].
В заключение скажем несколько слов о принятой при расчетах модели идеальной жидкости. Такую модель мы приняли, чтобы выделить вклад в затухание капиллярных волн именно перестройки приповерхностного двойного электрического слоя, чтобы он не затушевался затуханием из-за вязкости в объеме вязкой жидкости. Идея такого подхода была высказана в [26], где впервые была оценена интенсивность электромагнитного излучения от осциллирующей заряженной капли: декремент затухания осцилляций капли идеальной жидкости целиком определялся ее энергопотерями на излучение.
ЗАКЛЮЧЕНИЕ
Для заряженной проводящей капли учет механизма релаксации поверхностного натяжения приводит к появлению затухающих капиллярных осцилляций так, что с увеличением размера капли возрастает декремент затухания. Затухание связано с непериодическим изменением упорядоченности полярных молекул в приповерхностном слое жидкости, причем характерное время затухания по порядку величины совпадает с экспериментально измеряемым [9]. Эффект динамического поверхностного натяжения оказывает заметное влияние на спектр капиллярных осцилляций облачных капель. Высокочастотные высокоэнергичные капиллярные волны большой амплитуды гасятся динамическим поверхностным натяжением, точнее их энергия превращается в другие виды энергии: тепловую, энергию электромагнитного излучения и т.п. Таким образом, динамическое поверхностное натяжение обеспечивает превращение механической энергии капиллярных волн в другие ее формы.
Список литературы
Rayleigh Lord. On the equilibrium of liquid conducting masses charged with electricity // Phil. Mag. 1882. V. 14. № 87. P. 184–186. https://doi.org/10.1080/14786448208628425
Kim O.V., Dunn P.F. Controlled production of droplets by in-flight electrospraying // Langmuir. 2010. V. 26. P. 15807–15813. https://doi.org/10.1021/la102793j
Karyappa R.B., Deshmukh S.D., Thaokar R.M. Breakup of a conducting drop in a uniform electric field // J. Fluid Mech. 2014. V. 754. P. 550–589. https://doi.org/10.1017/jfm.2014.402
Кистович А.В., Чашечкин Ю.Д. Поверхностные колебания свободно падающей капли идеальной жидкости // Известия РАН. ФАО. 2018. Т. 54. № 2. С. 1–7. https://doi.org/10.7868/S0003351518020095
Григорьев А.И., Колбнева Н.Ю., Ширяева С.О. Нелинейные монопольное и дипольное акустические излучения слабо заряженной капли, осциллирующей в однородном электростатическом поле // ПММ. 2022. № 6. С. 936–955. https://doi.org/10.31857/S003282352260066
Owens D.K. The dynamic surface tension of sodium dodecyl sulfate solutions // J. Colloid Interface Sci. 1969. V. 29. № 3. P. 496–501.
Kochurova N.N., Rusanov A.I. Dynamic surface properties of water: Surface tension and surface potential // J. Colloid Interface Sci. 1981. V. 81. № 2. P. 297–303.
Кочурова Н.Н., Русанов А.И. Релаксация поверхностных свойств водных растворов поверхностно-активных веществ и механизм адсорбции // Успехи химии. 1993. Т. 62. № 12. С. 1150–1163.
Hauner I.M., Deblais A., Beattie J.K, Kellay H., Bonn D. The dynamic surface tension of water // Phys. Chem. Lett. 2017. V. 8. P. 1599–1603.
Гирс С.П. Влияние границы раздела вода-воздух на заряжение облачных капель // Сб. Поверхностные явления в жидкостях и жидких растворах. Л.: Изд. ЛГУ, 1972. С. 181–183.
Френкель Я.И. Теория явлений атмосферного электричества. Л.-М.: ГОСТЕХТЕОРИЗДАТ, 1949.
Френкель Я.И. Кинетическая теория жидкостей. Л.: Наука, 1975.
Тверской П.Н. Курс метеорологии. Физика атмосферы. Л.: Гидрометеоиздат, 1962.
Мазин И.П., Шметер С.М. Облака. Строение и физика образования. Л.: Гидрометеоиздат, 1983.
Мазин И.П., Хргиан А.Х., Имянитов И.М. Облака и облачная атмосфера. Справочник. Л.: Гидрометеоиздат, 1989.
Стерлядкин В.В. Натурные измерения колебаний капель осадков // Изв. АН СССР. Сер. ФАО. 1988. Т. 24. № 6. С. 613–621.
Ландау Л.Д., Лифшиц Е.М. Гидродинамика. М.: Наука, 1986.
Найфе А.Х. Методы возмущений. М.: Мир, 1976.
Абрамовиц М., Стиган И. Справочник по специальным функциям. М.: Наука, 1979.
Быковский Ю.А., Маныкин Э.А., Нахутин И.Е., Полуэктов П.П., Рубежный Ю.Г. Спектр поверхностных колебаний жидкости с учетом релаксационных эффектов // ЖТФ. 1976. Т. 46. № 10. С. 2211–2216.
Кристенсен Р. Введение в теорию вязкоупругости. М.: Мир, 1974.
Григорьев А.И. О некоторых закономерностях реализации неустойчивости сильно заряженной вязкой капли // ЖТФ. 2001. Т. 71. № 10. С. 1–7.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 2. Теория поля. М.: Наука, 1973.
Григорьев А.И., Колбнева Н.Ю., Ширяева С.О. Квадрупольное электромагнитное излучение заряженной капли, осциллирующей в суперпозиции коллинеарных гравитационного и электростатического полей // Изв. РАН. МЖГ. 2019. № 5. С. 70–82.
Стреттон Дж. А. Теория электромагнетизма. ОГИЗ-Гостехиздат, 1948.
Калечиц В.И., Нахутин И.Е., Полуэктов П.П. О возможном механизме радиоизлучения конвективных облаков // ДАН СССР. 1982. Т. 262. № 6. С. 1344–1347.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал


