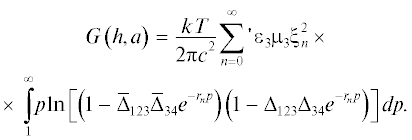Коллоидный журнал, 2023, T. 85, № 3, стр. 277-286
Исследование устойчивости пленок некоторых силиконовых лубрикантов в составе “скользких покрытий”
К. А. Емельяненко 1, *, Л. С. Феоктистова 1, И. В. Лунев 2, А. А. Галиуллин 2, И. А. Малышкина 3, В. Г. Красовский 4
1 Институт физической химии и электрохимии им. А.Н. Фрумкина
Российской академии наук
119991 Москва, Ленинский просп., 31 корп. 4, Россия
2 Казанский федеральный университет, Институт физики
420008 Казань, ул. Кремлевская, 18, Россия
3 Факультет фундаментальной физико-химической инженерии, Московский
государственный университет им. М.В. Ломоносова
119991 Москва, Ленинские горы, 1, Россия
4 Институт органической химии им. Н.Д. Зелинского Российской академии наук
119991 Москва, Ленинский просп., 47, Россия
* E-mail: emelyanenko.kirill@gmail.com
Поступила в редакцию 02.05.2023
После доработки 04.05.2023
Принята к публикации 04.05.2023
- EDN: ZQTACY
- DOI: 10.31857/S0023291223600335
Аннотация
Создание скользких покрытий на основе пористых гидрофобных или гидрофильных материалов, заполненных низколетучими вязкими жидкостями (лубрикантами) является одним из наиболее активно развиваемых направлений материаловедения полифункциональных покрытий. В этой работе мы исследовали возможность использования двух кремнийорганических жидкостей различной полярности, бис(трифторметилсульфонил)имидной дикатионной ионной жидкости и силиконового масла, в качестве лубрикантов для создания скользких покрытий, снижающих адгезию твердых и жидких водных осадков на подложках из оксида алюминия. Для проведения расчетов устойчивости пленок таких лубрикантов на основе теории вандерваальсовых сил нами были исследованы дисперсии показателей преломления и диэлектрические свойства жидкостей в области микроволновой релаксации. На основе полученных экспериментальных данных были рассчитаны спектры диэлектрических проницаемостей лубрикантов в функции мнимой частоты для всего спектрального интервала и вклад вандерваальсовых сил в устойчивость изотерм расклинивающего давления пленок лубрикантов на гидрофобных и гидрофильных подложках оксида алюминия. Полученные в данной работе изотермы расклинивающего давления позволяют рассматривать при создании скользких покрытий использование исследованной ионной жидкости в качестве более долговечного лубриканта, чем силиконовое масло, поскольку пленки ионных жидкостей при замене паровой фазы на водную среду не теряют устойчивость для более широкого интервала толщин.
1. ВВЕДЕНИЕ
В последние годы одним из наиболее активно развиваемых направлений материаловедения полифункциональных покрытий является создание скользких покрытий (SLIPS/LIS) на основе пористых гидрофобных или гидрофильных материалов, заполненных низколетучими вязкими жидкостями [1–3]. Такие жидкости (лубриканты), заполняя поры подложки, обеспечивают эффект гидродинамической или граничной смазки при контакте поверхности покрытия с различными телами, существенно упрощая разрушение такого контакта. Применение скользких покрытий показало высокую перспективность в таких областях технологии, как способность материалов уменьшать количество снега и льда, накапливаемых на поверхности в холодное время года при выпадении атмосферных осадков, снижение биообрастания поверхностей, понижение бактериальной загрязненности при контакте с бактериальными средами [1]. В то же время, более детальные исследования самого последнего времени указывают на тот факт, что скользкость такого покрытия зависит от его толщины и устойчивости пленки лубриканта на шероховатой поверхности [4–6]. Поэтому требуется тщательный подбор компонентов системы, включающий выбор материала пористой подложки и химических свойств лубриканта, обеспечивающий долговременную устойчивость пленок лубриканта на поверхности подложки при контакте как с воздушной фазой, так и с водой. Отметим, что устойчивость пленок лубрикантов при контакте с воздухом играет основную роль при хранении таких материалов, тогда как в процессе эксплуатации в открытых атмосферных условиях такие покрытия, заполненные лубрикантом, будут контактировать либо с водой, либо с твердыми водными средами (иней, лед, снег). Универсальный вклад в устойчивость пленок лубрикантов различной химической природы вносят вандерваальсовы силы. Поэтому подбор компонентов скользких покрытий по принципу устойчивости пленок лубрикантов следует начинать с расчетов знака и величины именно сил Ван-дер-Ваальса для пленок лубрикантов, ограниченных с одной стороны материалом пористой подложки, а с другой стороны воздушной средой, водой или льдом. К сожалению, на сегодняшний день в литературе отсутствуют данные, необходимые для расчета вандерваальсовых сил для большинства жидкостей, которые можно рассматривать как потенциально привлекательные лубриканты. Кроме того, даже если такие данные в литературе и представлены для отдельных температур, например, для силиконового масла ПМС-100, отсутствуют систематические исследования изменения диэлектрических проницаемостей с понижением температуры для всего спектрального интервала. Поэтому целью данной работы было получение первичных экспериментальных данных, необходимых для расчета вандерваальсовых сил. А именно, были получены данные, позволяющие рассчитать спектры диэлектрических проницаемостей для двух типов жидкостей, рассматриваемых в настоящее время в качестве перспективных кандидатов для создания противообледенительных скользких покрытий. Мы исследовали силиконовое масло ПМС-100 и бис(трифторметилсульфонил)имидную дикатионную ионную жидкость на основе 1,2-диметилимидазола с полидиметилсилоксановым линкером, синтезированную в ИОХ РАН [7]. Полученные спектры диэлектрических проницаемостей использованы в дальнейшем для расчета изотерм расклинивающего давления пленок исследуемых жидкостей на поверхности чистого алюминия или алюминия с тонким слоем гидрофобизатора. Сравнение вида изотерм и величины поверхностных сил в каждой из изученных систем позволило нам выбрать компоненты скользкого покрытия, обеспечивающие наибольшую устойчивость пленок лубрикантов, как на воздухе, так и при контакте с водными средами.
2. РАСЧЕТ ВАНДЕРВААЛЬСОВЫХ СИЛ
Классическим методом расчета вандерваальсовых сил в тонких жидких прослойках является подход Дзялошинского–Лифшица–Питаевского.
Для расчета вандерваальсовой энергии многослойных систем, к каковым относятся и исследуемые в данной работе скользкие покрытия, получаемые с применением гидрофобизованной подложки, мы использовали метод, основанный на применении подхода Дзялошинского–Лифшица–Питаевского и разработанный в [5]:
Здесь
В соотношении (1) тот факт, что первый член суммы (с n = 0) берется с половинным весом, отражается символом штрих при знаке суммирования.
Для анализа устойчивости жидкой прослойки рассчитывают изотерму расклинивающего давления П(h) для исследуемой системы в широком интервале толщин прослоек, как производную вандерваальсовой энергии взаимодействующих тел по толщине жидкой пленки лубриканта [8, 9]. Как следует из представленных уравнений, в качестве входных данных используются динамические диэлектрические проницаемости веществ всех контактирующих сред, включая жидкую прослойку и ограничивающие ее фазы.
Существует ряд методов для расчета динамической диэлектрической проницаемости $\varepsilon = \varepsilon \left( \omega \right)$, являющейся функцией мнимой частоты электромагнитного поля ($\omega = i\xi $, где $\xi $ – действительное число) [10]. Один из подходов опирается на пересчет частотной зависимости диэлектрической проницаемости из спектров поглощения или отражательной способности с помощью соотношений Крамерса–Кронига. Однако, точность таких данных, как правило, невысока и сильно зависит от полноты экспериментальных спектральных данных. Поскольку экспериментальное получение спектра поглощения во всем интервале от герцовых до эксагерцовых частот является нетривиальной задачей, на практике для расчета $\varepsilon = \varepsilon \left( \omega \right)$, как правило, используется подход, предложенный Нинхэмом и Парседжианом [11], заключающийся в аппроксимации всего диэлектрического спектра рядом осцилляторов, соответствующим основным частотам поглощения [8]. Количество осцилляторов в используемой модели, как правило, определяется количеством основных полос поглощения вещества и варьируется от 1 до 11 [11]. Для неполярных веществ (${{\varepsilon }_{{{\text{non - polar}}}}}$), как правило, используется двухосцилляторная модель, учитывающая поглощение в ИК и УФ спектре, связанное с возбуждением внутримолекулярных колебаний и электронных уровней в атомах соответственно. Для полярных жидкостей (${{\varepsilon }_{{{\text{polar}}}}}$) используют трехосцилляторную модель, которая учитывает также значительный вклад поглощения электромагнитного излучения веществом в микроволновой области:
(2)
$\begin{gathered} {{\varepsilon }_{{{\text{non - polar}}}}}\left( {i\xi } \right) = 1 + \frac{{{{C}_{{{\text{IR}}}}}}}{{1 + {{{\left( {\xi {\text{/}}{{\omega }_{{{\text{IR}}}}}} \right)}}^{2}}}} + \frac{{{{C}_{{{\text{UV}}}}}}}{{1 + {{{\left( {\xi {\text{/}}{{\omega }_{{{\text{UV}}}}}} \right)}}^{2}}}}, \\ {{\varepsilon }_{{{\text{polar}}}}}\left( {i\xi } \right) = 1 + \frac{{{{C}_{{{\text{MW}}}}}}}{{1 + \xi {\text{/}}{{\omega }_{{{\text{MW}}}}}}} + \\ + \,\,\frac{{{{C}_{{{\text{IR}}}}}}}{{1 + {{{\left( {\xi {\text{/}}{{\omega }_{{{\text{IR}}}}}} \right)}}^{2}}}} + \frac{{{{C}_{{{\text{UV}}}}}}}{{1 + {{{\left( {\xi {\text{/}}{{\omega }_{{{\text{UV}}}}}} \right)}}^{2}}}}, \\ \end{gathered} $2.1. Определение параметров ультрафиолетового осциллятора
Для определения параметров ультрафиолетового осциллятора экспериментально определялась дисперсия видимого света в исследуемом веществе.
Так как для видимой области $\xi \gg {{\omega }_{{{\text{IR}}}}} \gg {{\omega }_{{{\text{MW}}}}}$, соотношение (2) сводится к
(3)
$\varepsilon \left( {i\xi } \right) = 1 + \frac{{{{C}_{{{\text{UV}}}}}}}{{1 + {{{\left( {\xi {\text{/}}{{\omega }_{{{\text{UV}}}}}} \right)}}^{2}}}}.$Для веществ, прозрачных в видимой области, в этом диапазоне спектра диэлектрическая проницаемость ${{\varepsilon }_{{{\text{vis}}}}}$ равна квадрату коэффициента преломления: ${{\varepsilon }_{{{\text{vis}}}}}\left( {i\xi } \right) = {{n}^{2}}\left( \omega \right)$, таким образом, учитывая, что $\left( {i\xi } \right) \equiv \left( \omega \right)$, соотношение (2) можно записать в виде:
2.2. Определение параметров микроволнового осциллятора
Для определения параметров микроволнового осцилляторов использовались графики зависимости диэлектрической проницаемости от частоты в интервале частот от 103 до 109. Так, из соотношения (2) следует, что для частот, много меньшей и много большей, чем частота микроволнового осциллятора, ${{\xi }_{{{\text{low}}}}} \ll {{\omega }_{{{\text{MW}}}}}$ и ${{\omega }_{{{\text{MW}}}}} \ll {{\xi }_{{{\text{high}}}}} \ll {{\omega }_{{{\text{IR}}}}}$, верны следующие соотношения:
(4)
$\varepsilon \left( {i{{\xi }_{{{\text{low}}}}}} \right) = 1 + {{C}_{{{\text{MW}}}}} + {{C}_{{{\text{IR}}}}} + {{C}_{{{\text{UV}}}}},$(5)
$\varepsilon \left( {i{{\xi }_{{{\text{high}}}}}} \right) = 1 + {{C}_{{{\text{IR}}}}} + {{C}_{{{\text{UV}}}}}.$Из сравнения соотношений (4) и (5) следует, что параметр, пропорциональный силе микроволнового осциллятора, может быть определен из значений статической диэлектрической проницаемости ${{\varepsilon }_{0}}$ и соответствующей диэлектрической проницаемости в области прозрачности ${{\varepsilon }_{\infty }}$ для частот, превышающих частоты микроволнового поглощения:
(6)
${{C}_{{{\text{MW}}}}} = \varepsilon \left( {i{{\xi }_{{{\text{low}}}}}} \right) - \varepsilon \left( {i{{\xi }_{{{\text{high}}}}}} \right) = {{\varepsilon }_{0}} - {{\varepsilon }_{\infty }}.$При этом характерную частоту осциллятора в микроволновой области ${{\omega }_{{{\text{MW}}}}}$определяют, как частоту максимального поглощения в микроволновой области.
2.3. Параметры инфракрасного осциллятора
Для определения параметров инфракрасного осциллятора используют полученные ранее параметры ультрафиолетового и микроволнового осцилляторов (сила последнего считается равной нулю для неполярных жидкостей, для которых отсутствуют полосы поглощения в микроволновой области), а также значение статической диэлектрической проницаемости ${{\varepsilon }_{0}}$. Так, для соотношения (2) при нулевой частоте получаем:
(7)
${{\varepsilon }_{0}} = \varepsilon \left( 0 \right) = 1 + {{C}_{{{\text{MW}}}}} + {{C}_{{{\text{IR}}}}} + {{C}_{{{\text{UV}}}}},$3. ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
3.1. Материалы
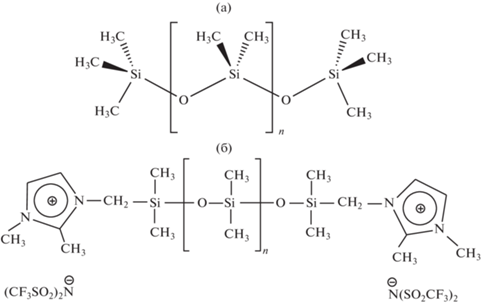
Исследования проводили на силиконовом масле ПМС100 (ООО “Силан”, Россия) и дикатионной ионной жидкости (ИЖ), синтезированной в ИОХ РАН по методике, описанной в [7]. Структура исследованных жидкостей представлена на рис. 1а, 1б. В ИЖ бис(трифторметилсульфонил)имид выполняет роль аниона, а диметилимидазольные фрагменты, соединенные полимерной силоксановой цепью, выступают в роли катиона. Представленные жидкости термостойки, низколетучи и имеют температуру стеклования значительно ниже нуля [7].
3.2. Приборы и методы
В данной работе для определения поведения диэлектрической проницаемости ионной жидкости при температурах 25 и 1°С в микроволновой области (103–109 Гц) использовали диэлектрический широкополосный спектрометр Novocontrol BDS Concept 80 (Novocontrol Technologies GmbH & Co., Германия). Для измерений использовали измерительную ячейку объемом 40 мкл с плоскопараллельными электродами из нержавеющей стали. Ячейка помещалась в измерительную головку, которая в свою очередь помещалась в криостат Quatro Cryosystem (Novocontrol Technologies GmbH & Co., Германия). Точность поддержания температуры ±0.1°С. Диэлектрические спектры для силиконового масла ПМС-100 при температурах 25 и 1°С получали в частотном диапазоне 106–108 Гц на приборе Agilent E4991A (Agilent Technologies, США) и в диапазоне 2 × 108–6 × 1010 Гц на приборе Agilent N5247A (Agilent Technologies, США). В случае использования установки Agilent N5247A использовался термостат LOIP LT900 (АО “ЛОиП”, Россия), точность поддержания температуры ±0.1°С. Точность определения значений комплексной диэлектрической проницаемости составляет 3%.
Измерения показателей преломления исследуемых жидкостей проводили с помощью термостатируемого цифрового рефрактометра Аббе Atago DR-M2 (Atago, Япония) с использованием спектральных интерференционных фильтров с узкой полосой пропускания (±1 нм). Использовались фильтры с длиной пропускаемой волны 450, 480, 486, 546, 589, 644, 656 нм. Точность измерения показателя преломления составляла 10–4. Для поддержания заданной температуры при измерении показателя преломления применяли термостат Ministat 230 (Huber, Германия), точность поддержания температуры составляла ±0.1°С.
4. РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
4.1. Определение параметров УФ осциллятора
Экспериментальные данные по показателям преломления, полученные для температур 25 и 1°С и построенные в виде Коши-плотов для семи значений длин волн, представлены на рис. 2а для силиконового масла и рис. 2б для ионной жидкости.
Рис. 2.
Показатели преломления жидкостей при 25°С и 1°С, отложенные в координатах ${{n}^{2}}\left( \omega \right) - 1$ от $\left[ {{{n}^{2}}\left( \omega \right) - 1} \right]{{\omega }^{2}}$ для ПМС-100 (а) и ионной жидкости (б).
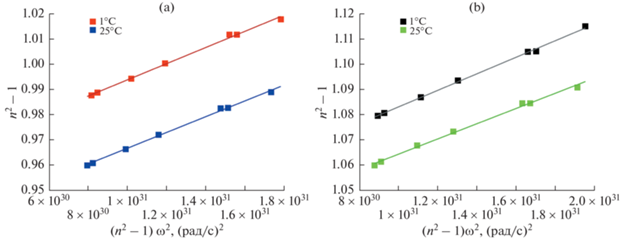
Полученные данные в указанных координатах хорошо описываются линейными зависимостями. Из отсекаемых на оси ординат отрезков и наклона прямых были определены параметры УФ осцилляторов для исследованных жидкостей, значения которых представлены в табл. 1.
Таблица 1.
Значения параметров осцилляторов, определенные на основе экспериментальных данных по частотным зависимостям показателей преломления
| Жидкость | Температура, °С | ${{C}_{{{\text{UV}}}}}$ | ωUV, рад/с |
|---|---|---|---|
| ПМС-100 | 25 | 0.94 | 1.799 × 1016 |
| ПМС-100 | 1 | 0.96 | 1.771 × 1016 |
| ИЖ | 25 | 1.03 | 1.823 × 1016 |
| ИЖ | 1 | 1.05 | 1.749 × 1016 |
4.2. Определение параметров микроволнового осциллятора
Исследование спектров ПМС-100 в области частот (106–5 × 1011) указывает на нормальную дисперсию диэлектрической проницаемости и отсутствие поглощения в микроволновой области. Значения экспериментально определенных статических диэлектрических проницаемостей для обеих исследованных температур представлены в табл. 2. Для бис(трифториметилсульфонил)имидной дикатионной ионной жидкости в микроволновой области наблюдается значительное поглощение. Спектры для мнимой и действительной частей диэлектрической проницаемости, хорошо описываемые уравнением Гаврильяка–Негами [18], представлены на рис. 3. По представленным спектрам были определены и представлены в табл. 2 частоты максимума полосы диэлектрических потерь, а также статические значения ε0 и значения ε∞ в области прозрачности при частотах, превышающих область поглощения, для диэлектрических проницаемостей ИЖ при температурах 25 и 1°С.
Таблица 2.
Значения параметров микроволновых осцилляторов
| Жидкость | Температура, °С | ε0 | ε∞ | СMW | ωMW, рад/с |
|---|---|---|---|---|---|
| ПМС-100 | 25 | 2.6 ± 0.1 | 2.6 ± 0.1 | 0 | – |
| ПМС-100 | 1 | 2.8 ± 0.1 | 2.8 ± 0.1 | 0 | – |
| ИЖ | 25 | 20.2 ± 0.6 | 3.2 ± 0.1 | 16.95 | 5.20 × 106 |
| ИЖ | 1 | 22.3 ± 0.7 | 3.1 ± 0.1 | 19.23 | 6.45 × 105 |
Рис. 3.
Спектры действительной (красные квадраты) и мнимой (синие квадраты) частей диэлектрической проницаемости ИЖ в микроволновой области при температурах 25°С (закрашенные квадраты) и 1°С (пустые квадраты).
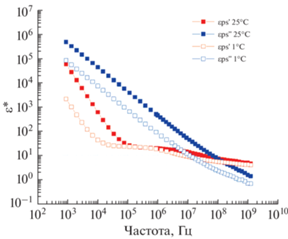
По полученным данным для микроволновой области с использованием соотношения (6) были определены параметры микроволнового осциллятора, которые также представлены в табл. 2.
4.3. Определение параметров инфракрасного осциллятора и расчет спектров диэлектрической проницаемости
Обе исследуемые нами жидкости – кремнийорганической природы. Для таких жидкостей, согласно многочисленным литературным данным, наиболее сильное интегральное поглощение полосы в ИК области связано с валентными колебаниями силоксановой связи. В качестве частоты инфракрасного осциллятора для соединений с сильной силоксановой связью, как правило, выбирают частоту 2.06 × 1014 [19], принимая, что ее положение очень слабо зависит от температуры.
Используя определенные выше константы для осцилляторов в УФ и микроволновой областях, а также значения статических диэлектрических проницаемостей, были рассчитаны константы CIR для обеих жидкостей при двух исследованных температурах (табл. 3).
Таблица 3.
Значения параметров инфракрасных осцилляторов
| Жидкость | Температура, °С | СIR | ωIR, рад/с |
|---|---|---|---|
| ПМС-100 | 25 | 0.66 | 2.06 × 1014 |
| ПМС-100 | 1 | 0.83 | 2.06 × 1014 |
| ИЖ | 25 | 1.17 | 2.06 × 1014 |
| ИЖ | 1 | 1.05 | 2.06 × 1014 |
Рассчитанные по определенным выше параметрам характеристических осцилляторов спектры диэлектрических проницаемостей в функции мнимой частоты для обеих жидкостей и обеих температур представлены на рис. 4.
Рис. 4.
Спектры диэлектрических проницаемостей в функции мнимой частоты для ПМС-100 и бис(трифториметилсульфонил)имидной дикатионной ионной жидкости на основе 1,2-диметилимидазола с полидиметилсилоксановым линкером.
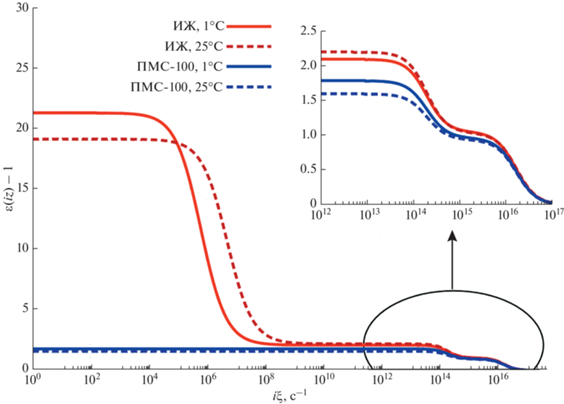
Представленные данные указывают на очень слабую температурную зависимость частотной зависимости диэлектрической проницаемости силиконового масла от температуры. Напротив, для ионной жидкости, наблюдается значительное различие при температурах 25°С и 1°С, что хорошо согласуется с тем фактом, что энергии микроволновых молекулярных движений значительно ниже энергии теплового движения. Значительное различие в величине и в спектральном поведении диэлектрической проницаемостей ИЖ и ПМС позволяет ожидать разную устойчивость пленок этих двух лубрикантов при контакте с водными средами. Для оценки влияния спектральных особенностей исследованных жидкостей на долговечность смазывающих свойств далее нами будут представлены и проанализированы вандерваальсовы вклады в изотерму расклинивающего давления прослоек лубрикантов.
5. ИЗОТЕРМЫ РАСКЛИНИВАЮЩЕГО ДАВЛЕНИЯ ПЛЕНОК ЛУБРИКАНТОВ
В литературе применение лубрикантов в виде скользких покрытий, в значительной степени, нацелено на улучшение свойств металлических материалов, контактирующих с атмосферными осадками [2, 3]. Поэтому, для сравнения устойчивости пленок двух исследованных здесь жидкостей и для подбора оптимального состава скользкого покрытия на металлах, обеспечивающего долговечность смазывающих свойств, мы рассчитали изотермы расклинивающего давления по описанному выше методу в системах Al2O3/ИЖ/паровая фаза; Al2O3/тефлон/ИЖ/паровая фаза; Al2O3/ИЖ/H2O; Al2O3/тефлон/ИЖ/H2O; Al2O3/ПМС/паровая фаза; Al2O3/тефлон/ПМС/паровая фаза; Al2O3/ПМС/H2O; Al2O3/тефлон/ПМС/H2O. Обсуждение, представленное ранее в работе [5], указывает на то, что для текстурированных поверхностей алюминия, имеющих толстый поверхностный слой оксида [20], материал металлической подложки можно моделировать полубесконечным слоем оксида, а нанометровый слой тефлона может быть использован для учета слоя фторированного гидрофобизатора, наносимого на поверхность текстуры из оксида для создания супергидрофобных покрытий.
Общий вид изотерм расклинивающего давления пленок лубрикантов на Al2O3 (гидрофильная подложка) и на Al2O3 с пленкой тефлона толщиной 10 Å (гидрофобная подложка), ограниченных как паровой, так и водной фазами, представлен на рис. 5. Врезками на каждом из рисунков показано поведение изотерм при малых расклинивающих давлениях. Поскольку общий вид изотерм для разных температур отличается слабо, здесь представлены изотермы для одной температуры Т = 25°С.
Рис. 5.
Изотермы расклинивающего давления пленок (а) ПМС-100 (SO) и (б) ИЖ (IL) на Al2O3 и на Al2O3 с пленкой тефлона (PTFE) толщиной 10 Å, ограниченных либо паровой (Air) либо водной (Water) фазами. Врезками на каждом из рисунков показано поведение соответствующих изотерм при малых расклинивающих давлениях.
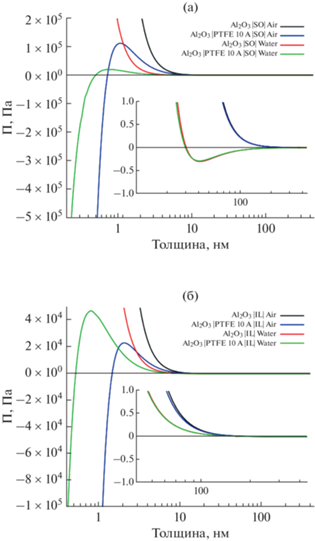
Как было показано Дерягиным [8], участки изотермы расклинивающего давления П(h) с толщинами пленок, для которых dΠ/dh < 0, соответствуют термодинамически устойчивым жидким прослойкам. Анализ рассчитанных изотерм для каждого из рассмотренных случаев позволяет сделать вывод, что на гидрофильном оксиде алюминия пленки обоих лубрикантов, ограниченные паровой фазой, устойчивы на подложке во всем интервале толщин (см. табл. 4). Т.е., при частичном удалении лубриканта с поверхности, например, за счет сдувания воздушным потоком, пленки будут оставаться устойчивыми при одновременном снижении их толщины. Такая же ситуация имеет место и для пленки ионной жидкости, нанесенной на оксид алюминия при ее контакте с водной фазой. Напротив, пленка ПМС-100, осажденная на оксид алюминия, при ее контакте с водой будет устойчива лишь для относительно тонких пленок (см. табл. 4). Например, при Т = 25°С устойчивыми будут лишь пленки с толщиной менее 410 Å. Более толстые пленки, проявляя неустойчивость, будут разрываться на более тонкие устойчивые пленки и расположенные на их поверхности микрокапли силиконового масла. На гидрофобизованном оксиде алюминия ситуация более сложная. Так, пленки ионной жидкости оказываются устойчивыми при контакте с водой в более широком интервале толщин, чем при контакте с паровой фазой. И в первом, и в последнем случае, очень тонкие пленки оказываются неустойчивыми. Т.е., если при утончении пленки, вызванном уносом лубриканта льдом, водой или воздушным потоком, ее толщина окажется ниже критической, произойдет разрыв пленки с оголением участков гидрофобного оксида алюминия. Наконец, пленки силиконового масла, ограниченные водной фазой и гидрофобным оксидом алюминия, будут сохранять устойчивость лишь в ограниченном интервале толщин пленок лубриканта. При 25°С это будет интервал пленок силиконового масла с толщинами 8 Å < h < 410 Å.
Таблица 4.
Расчетные области устойчивости толщин пленок лубрикантов в исследованных системах
| Система | Температура, °С | Область толщин устойчивых пленок лубрикантов |
|---|---|---|
| Al2O3/ПМС-100/пар | 25 | h > 0 |
| Al2O3/ПМС-100/H2O | 25 | h < 410 Å |
| Al2O3/тефлон/ПМС-100/пар | 25 | h > 11 Å |
| Al2O3/тефлон/ПМС-100/H2O | 25 | 8 Å < h < 410 Å |
| Al2O3/ПМС-100/пар | 1 | h > 0 |
| Al2O3/ПМС-100/H2O | 1 | h < 475 Å |
| Al2O3/тефлон/ПМС-100/пар | 1 | h > 13 Å |
| Al2O3/тефлон/ПМС-100/H2O | 1 | 9 Å < h < 475 Å |
| Al2O3/ИЖ/H2O | 25 | h > 0 |
| Al2O3/тефлон/ИЖ/H2O | 25 | h > 8 Å |
| Al2O3/ИЖ/пар | 25 | h > 0 |
| Al2O3/тефлон/ИЖ/пар | 25 | h > 21 Å |
| Al2O3/ИЖ/H2O | 1 | h > 0 |
| Al2O3/тефлон/ИЖ/H2O | 1 | h > 5.6 Å |
| Al2O3/ИЖ/пар | 1 | h > 0 |
| Al2O3/тефлон/ИЖ/пар | 1 | h > 20 Å |
6. ЗАКЛЮЧЕНИЕ
В этой работе мы исследовали возможность использования двух кремнийорганических жидкостей различной полярности в качестве лубрикантов для создания скользких покрытий, снижающих адгезию твердых и жидких водных осадков на металлических подложках. Для проведения расчетов устойчивости пленок таких лубрикантов нами были исследованы дисперсии показателей преломления и диэлектрические свойства жидкостей в области микроволновой релаксации, которые позволили рассчитать спектры диэлектрических проницаемостей жидкостей в функции мнимой частоты для всего спектрального интервала.
Полученные нами результаты показали, что область устойчивости пленок лубрикантов при контакте с паровой фазой и с водными средами слабо зависит от температуры в исследованном интервале толщин, однако сильно меняется при переходе от гидрофильной подложки к гидрофобной. Полученные здесь изотермы расклинивающего давления, определяемые вкладом вандерваальсовых сил, позволяют рассматривать использование ионных жидкостей в качестве более долговечных лубрикантов при создании SLIPS/LIS, поскольку пленки ионных жидкостей не теряют устойчивость при замене паровой фазы на водную среду для более широкого интервала толщин. Здесь следует подчеркнуть, что существуют и другие факторы (помимо устойчивости), также влияющие на преимущества применения того или иного лубриканта. В частности, здесь также важна величина адгезии твердых и жидких осадков к пленке лубриканта, которая, в свою очередь, определяется его поверхностным натяжением и подвижностью полимерных цепей. Однако такой анализ не связан непосредственно с представленными здесь результатами и будет выполнен в отдельной работе.
Список литературы
Kreder M.J., Alvarenga J., Kim P., Aizenberg J. Design of anti-icing surfaces: Smooth, textured or slippery? // Nature Reviews Materials. 2016. V. 1. № 1. P. 15003. https://doi.org/10.1038/natrevmats.2015.3
Emelyanenko K.A., Emelyanenko A.M., Boinovich L.B. Review of the state of the art in studying adhesion phenomena at interfaces of solids with solid and liquid aqueous media // Colloid Journal. 2022. V. 84. № 3. P. 265–286. https://doi.org/10.1134/S1061933X22030036
Peppou-Chapman S., Hong J.K., Waterhouse A., Neto C. Life and death of liquid-infused surfaces: A review on the choice, analysis and fate of the infused liquid layer // Chemical Society Reviews. 2020. V. 49. № 11. P. 3688–3715. https://doi.org/10.1039/D0CS00036A
Scarratt L.R.J., Zhu L., Neto C. How slippery are slips? Measuring effective slip on lubricated surfaces with colloidal probe atmoc force microscopy // Langmuir. 2019. V. 35. № 8. P. 2976–2982. https://doi.org/10.1021/acs.langmuir.8b03767
Emelyanenko K.A., Emelyanenko A.M., Boinovich L.B. Disjoining pressure analysis of the lubricant nanofilm stability of liquid-infused surface upon lubricant depletion // Journal of Colloid and Interface Science. 2022. V. 618. P. 121–128. https://doi.org/10.1016/j.jcis.2022.03.047
Ganne A.A. On the issue of the stability of water-repellent infusion liquids on hydrophilic and hydrophobic silica substrates // Colloid Journal. 2022. V. 84. № 4. P. 411–415. https://doi.org/10.1134/S1061933X22040068
Krasovskiy V.G., Glukhov L.M., Chernikova E.A., Kapustin G.I., Gorbatsevich O.B., Koroteev A.A., Kustov L.M. Dicationic polysiloxane ionic liquids // Russian Chemical Bulletin. 2017. V. 66. № 7. P. 1269–1277. https://doi.org/10.1007/s11172-017-1884-7
Дерягин Б.В., Чураев Н.В., Муллер В.М. Поверхностные силы. М.: Наука, 1985.
Boinovich L.B. Long-range surface forces and their role in the progress of nanotechnologies // Russian Chemical Reviews. 2007. V. 76. № 5. P. 471–488. https://doi.org/10.1070/RC2007v076n05ABEH003692
Ландау Л.Д., Лифшиц Е.М. Электродинамика сплошных сред: Теоретическая физика: в 10 томах. Т. 8. М.: Наука, 1982.
Parsegian V.A. Van der Waals Forces: A Handbook for Biologists, Chemists, Engineers, and Physicists. Cambridge University Press, 2005. https://doi.org/10.1017/CBO9780511614606
Hough D.B., White L.R. The calculation of Hamaker constants from Liftshitz theory with applications to wetting phenomena // Advances in Colloid and Interface Science. 1980. V. 14. № 1. P. 3–41. https://doi.org/10.1016/0001-8686(80)80006-6
Boinovich L.B., Emel’yanenko A.M. Alkane films on water: Stability and wetting transitions // Russian Chemical Bulletin. 2008. V. 57. № 2. P. 263–273. https://doi.org/10.1007/s11172-008-0041-8
Fernández-Varea J.M., Garcia-Molina R. Hamaker constants of systems involving water obtained from a dielectric function that fulfills the f sum rule // Journal of Colloid and Interface Science. 2000. V. 231. № 2. P. 394–397. https://doi.org/10.1006/jcis.2000.7140
Bergström L. Hamaker constants of inorganic materials // Advances in Colloid and Interface Science. 1997. V. 70. P. 125–169. https://doi.org/10.1016/S0001-8686(97)00003-1
Faure B., Salazar-Alvarez G., Bergström L. Hamaker constants of iron oxide nanoparticles // Langmuir. 2011. V. 27. № 14. P. 8659–8664. https://doi.org/10.1021/la201387d
Boinovich L., Emelyanenko A. Wetting behaviour and wetting transitions of alkanes on aqueous surfaces // Advances in Colloid and Interface Science. 2009. V. 147–148. P. 44–55. https://doi.org/10.1016/j.cis.2008.10.007
Havriliak S., Negami S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers // Polymer. 1967. V. 8. P. 161–210. https://doi.org/10.1016/0032-3861(67)90021-3
Masuda T., Matsuki Y., Shimoda T. Spectral parameters and Hamaker constants of silicon hydride compounds and organic solvents // Journal of Colloid and Interface Science. 2009. V. 340. № 2. P. 298–305. https://doi.org/10.1016/j.jcis.2009.08.028
Boinovich L.B., Modin E.B., Sayfutdinova A.R., Emelyanenko K.A., Vasiliev A.L., Emelyanenko A.M. Combination of functional nanoengineering and nanosecond laser texturing for design of superhydrophobic aluminum alloy with exceptional mechanical and chemical properties // ACS Nano. 2017. V. 11. № 10. P. 10113–10123. https://doi.org/10.1021/acsnano.7b04634
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал