1. На главную
  2. Электронные версии
  3. Коллоидный журнал
  4. T. 85, № 3, 2023

Коллоидный журнал, 2023, T. 85, № 3, стр. 307-318

Инерционное осаждение субмикронных аэрозолей в модельных волокнистых фильтрах из ультратонких волокон

В. А. Кирш *

Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
119071 Москва, Ленинский просп. 31, корп. 4, Россия

* E-mail: va_kirsch@mail.ru

Поступила в редакцию 15.03.2023
После доработки 25.04.2023
Принята к публикации 28.04.2023

Полный текст (PDF)

Аннотация

Рассмотрено влияние инерции субмикронных частиц на их осаждение в модельных тонковолокнистых фильтрах из стоксова потока. Методом граничной траектории рассчитаны коэффициенты захвата частиц волокном за счет эффектов инерции и зацепления в ячеечной модели фильтра и в ряду параллельных волокон, перпендикулярных направлению потока газа, в интервалах параметров зацепления R = 0.01–1, чисел Стокса Stk = 0–20 и Кнудсена Kn = 0–1. Расчеты согласуются с экспериментальными данными.

1. ВВЕДЕНИЕ

Необходимость учета инерционного осаждения субмикронных частиц при расчете фильтров для тонкой фильтрации воздуха возникла в связи с созданием аварийных фильтрующих систем для улавливания частиц тяжелых металлов, совершенствованием фильтрующих материалов из субмикронных волокон, и для расчета пылеемких предфильтров, устанавливаемых перед высокоэффективными фильтрами в многоступенчатых системах сверхтонкого обеспыливания воздуха. Основной задачей теории фильтрации всегда был расчет эффективности при наихудших условиях фильтрации (для наиболее проникающих частиц), которые осаждаются за счет двух механизмов – диффузии и зацепления. Инерцию частиц в теории тонкой фильтрации субмикронных аэрозолей обычно не учитывали, поскольку для испытаний фильтров использовали частицы масляного тумана, для которых число Стокса, характеризующее инерционное осаждение, мало, ${\text{Stk}}$ < 0.1, и влияния инерции нет (средний диаметр волокон 0.5 мкм, скорость потока перед фильтром $U$= 3–5 см/с). Число Стокса определяется как [1]

(1)
${\text{Stk}} = \frac{{{{\tau }_{{\text{p}}}}}}{{\left( {{a \mathord{\left/ {\vphantom {a U}} \right. \kern-0em} U}} \right)}} = \frac{{BUm}}{a} = \frac{{2{{С}_{С}}\rho r_{{\text{p}}}^{2}U}}{{9\mu a}},$
где $B = {{{{C}_{c}}} \mathord{\left/ {\vphantom {{{{C}_{c}}} {6\pi \mu {{r}_{{\text{p}}}}}}} \right. \kern-0em} {6\pi \mu {{r}_{{\text{p}}}}}}$ − подвижность частицы радиуса ${{r}_{{\text{p}}}}$, ${{\tau }_{{\text{p}}}} = Bm$ − время релаксации частицы, $m$ – масса частицы с плотностью $\rho $, ${{C}_{с}} = 1 + \left( {{\lambda \mathord{\left/ {\vphantom {\lambda {{{r}_{{\text{p}}}}}}} \right. \kern-0em} {{{r}_{{\text{p}}}}}}} \right) \times $ $ \times \left[ {1.257 + 0.4\exp \left( { - 1.1{{{{r}_{{\text{p}}}}} \mathord{\left/ {\vphantom {{{{r}_{{\text{p}}}}} \lambda }} \right. \kern-0em} \lambda }} \right)} \right]$ − эмпирическая поправка Каннингема на скольжение газа на частице, $a$ – радиус волокон фильтра, $U$– скорость потока перед фильтром, $\mu $ – динамическая вязкость воздуха, $\lambda $ – средняя длина свободного пробега молекул воздуха. В качестве характерных масштабов длины, скорости и времени здесь и далее выбраны $a$, $U$ и $a{{U}^{{ - 1}}}$.

Исследованию осаждения частиц в фильтрах под действием инерции посвящено много работ, в основном для микронных частиц и при большой скорости потока $U$ > 1 м/с. Для условий тонкой фильтрации, когда течение газа и осаждение субмикронных частиц не зависят от числа Рейнольдса ($\operatorname{Re} $ < 1), инерционное осаждение обсуждается в [2–4]. Его учет особенно важен для частиц тяжелых металлов и их оксидов из-за возможности их отскока от тонких волокон при относительно небольших числах Стокса. Этот вопрос был впервые рассмотрен в [5]. Важно уметь рассчитывать инерционное осаждение и для предфильтров, в том числе при малых Stk, поскольку форма осадка частиц на волокне при улавливании инерционных и броуновских частиц разная, из-за чего различается время эксплуатации фильтра, которое определяется как время достижения предельного перепада давления при забивке фильтра частицами [6]. К настоящему времени наиболее подробно разработаны методы расчета эффективности улавливания субмикронных частиц при одновременном действии основных механизмов осаждения (диффузии и зацепления) для фильтров из субмикронных волокон [4, 7]. Однако влияние инерции на осаждение частиц на субмикронные волокна осталось неизученным. Инерционное осаждение частиц с учетом эффекта скольжения газа на волокнах будет рассмотрено в данной статье.

2. МЕТОД РАСЧЕТА КОЭФФИЦИЕНТА ЗАХВАТА ИНЕРЦИОННЫХ ЧАСТИЦ

Будем рассматривать движение невзаимодействующих аэрозольных частиц в потоке газа в модельном фильтре при малых числах Рейнольдса (${{\operatorname{Re} }_{{\text{p}}}}$ < $\operatorname{Re} $ $ \ll $ 1) с учетом взаимного влияния соседних волокон. Здесь $\operatorname{Re} $ – число Рейнольдса, определенное по диаметру волокна, ${{\operatorname{Re} }_{{\text{p}}}}$ – по диаметру частицы. Символ * относится к размерным величинам. Частицы и волокна в фильтре считаем монодисперсными. Принимаем, что частицы имеют сферическую форму, что внешние силы, действующие на частицу, пренебрежимо малы или отсутствуют, т.е. частицы не несут электростатических зарядов, а их скорость седиментации, обусловленная действием гравитации, пренебрежимо мала (в отличие от случая тяжелых инерционных частиц [8]).

Коэффициент захвата частиц волокном – долю частиц, осевших на волокно из набегающего потока, рассчитываем методом граничной траектории. Уравнение движения частицы имеет вид:

(2)
$\frac{{d{\mathbf{v}}{\kern 1pt} *}}{{dt{\kern 1pt} *}} + \beta \left( {{\mathbf{v}}{\kern 1pt} * - \,\,{\mathbf{u}}{\kern 1pt} *} \right) = 0,$
с начальным условием
${\mathbf{v}}{\kern 1pt} * = {\mathbf{u}}_{0}^{*}{\text{ при }}t = 0,\,\,\,\,x{\kern 1pt} * = - X{\kern 1pt} *,$
где ${\mathbf{v}}{\kern 1pt} *$ – вектор средней скорости частиц, ${\mathbf{u}}{\kern 1pt} *$ – вектор скорости среды, $t{\kern 1pt} *$ – время, $\beta = {{{1 \mathord{\left/ {\vphantom {1 \tau }} \right. \kern-0em} \tau }}_{{\text{p}}}}$ – коэффициент трения. Здесь принято, что скорость частицы на входе в расчетную ячейку равна входной скорости потока ${\mathbf{u}}_{0}^{ * }$, что поток направлен по оси ${\text{O}}x$ и начало координат расположено в центре волокна кругового сечения. Также принято, что коснувшиеся волокна частицы удерживаются вандерваальсовыми силами, и что сдува частиц не происходит. Для режима тонкой фильтрации при малых скоростях потока эти условия реализуются на практике. В безразмерных переменных уравнение (2) и начальное условие принимают вид [9]
(3)
${\text{Stk}}\frac{{d{\mathbf{v}}}}{{dt}} + {\mathbf{v}} - {\mathbf{u}} = 0,$
${\mathbf{v}} = 1$ при $t = 0,\quad x = - X$.

Обыкновенное дифференциальное уравнение (3) решалось численно с помощью схемы Рунге–Кутты–Фельберга [10] для модельных фильтров с известным полем течения с учетом эффекта скольжения газа на волокнах. В модели фильтра – ряду параллельных волокон – уравнения Стокса [11] решались в терминах функции тока $\Psi $, следуя алгоритму, предложенному в работе [12]. Бигармоническое уравнение для функции тока

(4)
$\Delta \Delta \Psi = 0$
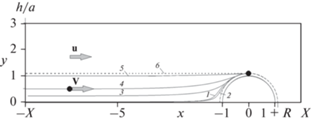
решалось в протяженной расчетной ячейке (рис. 1). Здесь функция тока связана с компонентами скоростей потока следующими формулами:
${{u}_{r}} = - \frac{1}{r}\frac{{\partial \Psi }}{{\partial \theta }},\,\,\,\,{{u}_{\theta }} = \frac{{\partial \Psi }}{{\partial r}},$
где $r,\;\theta $ – безразмерные полярные координаты (угол $\theta $ отсчитывается от передней осевой линии и направлен по часовой стрелке). Решение бигармонического уравнения находилось в виде конечного ряда, полученного из общего решения этого уравнения. Часть коэффициентов определялась аналитически из граничного условия прилипания ${\mathbf{u}} = 0$ при ${\text{Kn}} = 0$ или условия скольжения на поверхности волокна (12) при ${\text{Kn}} > 0$, где ${\text{Kn}} = {\lambda \mathord{\left/ {\vphantom {\lambda a}} \right. \kern-0em} a}$ – число Кнудсена. Оставшиеся коэффициенты определялись численно из условий на границе внешней области с помощью метода граничной коллокации [13], который применим к задачам со сложной геометрией и с произвольными граничными условиями и, что существенно, не требует дискретизации всей расчетной области. Метод решения подробно изложен в [12].

Рис. 1.

Граничные траектории инерционных частиц при осаждении из стоксова поперечного потока на волокно в ряду волокон: ${\text{Stk}}$ = 0.01 (1), 0.1 (2), 5 (3), 10 (4), 100 (5), ${\text{Stk}} \to \infty $, безинерционная частица (6); ${{b = a} \mathord{\left/ {\vphantom {{b = a} h}} \right. \kern-0em} h}$ = 1/3, $R$ = 0.1; расчет по (2), (3).

Для поля скоростей в ячеечной модели были использованы аналитические и численно-аналитические решения работ [14, 15].

В методе граничной траектории расчет каждой траектории заканчивался в момент осаждения частицы на поверхности волокна $r = 1 + R$ или ее пролета за волокно. Здесь $R = {{{{r}_{{\text{p}}}}} \mathord{\left/ {\vphantom {{{{r}_{{\text{p}}}}} a}} \right. \kern-0em} a}$ – параметр зацепления. Выбирая последовательно точки входа в ячейку {–$X$, ${{y}_{k}}$}, определяли ординату ${{y}_{0}}$, которая соответствовала траектории, ограничивающей область, в пределах которой происходит осаждение частиц (траектории с начальными ординатами $y$ > ${{y}_{0}}$ проходят мимо волокна). Безразмерный коэффициент захвата инерционной частицы определялся по формуле [4]

(5)
$\eta = {{y}_{0}},$
где ${{y}_{0}}$ – ордината граничной траектории на входе в расчетную ячейку при $x = - X$. Граничная траектория отделяет область потока, в которой все входящие частицы осаждаются на волокно. На рис. 1 показан пример граничных траекторий инерционных частиц, осаждающихся из поперечного потока на волокно.

Коэффициент проскока частиц через отдельный ряд параллельных волокон, оси которых отстоят друг от друга на расстоянии 2$h$, связан с коэффициентом захвата как [7]

(6)
$\frac{n}{{{{n}_{0}}}} = 1 - \frac{a}{h}\eta ,$
где ${{n}_{0}}$ и $n$ – концентрации частиц до и за рядом волокон. Коэффициент проскока частиц через модельный фильтр с толщиной $H$ и плотностью упаковки $\alpha $ связан с коэффициентом захвата и эффективностью улавливания частиц $E$ следующей формулой [4]

(7)
$\frac{n}{{{{n}_{0}}}} = 1 - E = \exp \left( { - 2\frac{{\alpha H}}{{\pi a}}\eta } \right).$

3. ИНЕРЦИОННОЕ ОСАЖДЕНИЕ ЧАСТИЦ В РЯДУ ПАРАЛЛЕЛЬНЫХВОЛОКОН

Модель изолированного ряда параллельных волокон (рис. 1) является наиболее удачной для расчета осаждения инерционных частиц во всем диапазоне чисел Стокса. Раcчет инерционного осаждения частиц в стоксовом потоке при обтекании ряда волокон был впервые выполнен в [16]. Были рассчитаны коэффициенты захвата для поля скоростей потока, аналитически выведенного Мияги [17]. В последующих работах (например, в [18]) использовались численные методы для нахождения полей течения и моделирования траекторий частиц в них. Использовав численно-аналитическое решение для поля скоростей, предложенное в [12], нами были проведены расчеты коэффициентов захвата для нескольких значений $b = a{{h}^{{ - 1}}}$ и параметров зацепления $R$ и проведено сравнение с экспериментальными данными для модельных фильтров, составленных из рядов параллельных волокон.

Сравнение теории с экспериментом

Экспериментальная проверка теоретических расчетов осаждения частиц на цилиндрическое волокно в результате инерционного смещения частиц с линий тока в условиях стесненного течения в модельных фильтрах при малых числах Рейнольдса возможна только в случае тонких волокон. Изготовление таких моделей даже в современных условиях довольно сложно. Первая попытка экспериментально исследовать осаждение частиц благодаря инерции на изолированных рядах параллельных волокон, обтекаемых поперечным стоксовым потоком, была предпринята в [19]. В этой работе параллельно натянутые проволочки в модельном фильтре имели слишком большой диаметр 2$a$ = 25 мкм, в результате чего максимальное значение числа Рейнольдса для сохранения автомодельного режима течения составляло $\operatorname{Re} $ = 0.54 (т.е. нельзя было увеличивать скорость, чтобы не нарушить симметричное стоксово течение). Параметр Стокса в этих опытах с частицами с ${{r}_{{\text{p}}}}$ = 0.6 мкм изменялся в узком диапазоне ${\text{Stk}}$ = 0.018–0.043, в котором инерция частиц не проявляется.

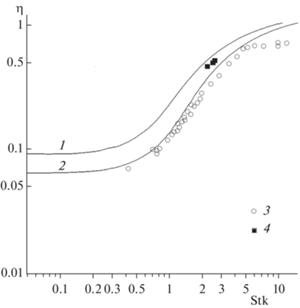
Вторая попытка экспериментальной оценки инерционного влияния на осаждение частиц была осуществлена в лаборатории Н.А. Фукса в Карповском институте с модельным фильтром, состоящем из рядов более тонких проволочек и с более крупными монодисперсным частицами [16]. Отличительной особенностью модели было строгое равенство расстояний между осями соседних волокон во всех рядах 2$h$. На рис. 2–4 приводится сравнение рассчитанных коэффициентов захвата с данными экспериментов, выполненных при $\operatorname{Re} $ < 1 на модельном фильтре, составленном из эквидистантных рядов параллельных волокон с 2$a$ = 8.9 мкм [16]. Небольшое отклонение от расчетных данных связано с тем, что для систем из параллельных волокон невозможно полностью избежать гидродинамического следа после каждого ряда. И, тем не менее, совпадение очень хорошее. Надо отметить, что точность экспериментов в сильной степени зависит от измеряемой величины общей эффективности, которая тем меньше, чем меньше коэффициент захвата, т.е. чем меньше ${\text{Stk}}$. Поэтому экспериментально не удалось установить величину минимального значения ${\text{Stk}}$, при котором начинает проявляться инерция. Это будет рассмотрено ниже.

Рис. 2.

Зависимости коэффициента захвата частиц волокном в ряду волокон от числа Стокса ${\text{Stk}}$ для $R$ = = 0.38 (1), 0.3 (2), $t$ = 0.233. Сравнение с экспериментом (рис. 2 в [16]): ${{r}_{{\text{p}}}}$ = 1.37 (3), 1.7 (4), 2$a$ = 8.9, 2$h$ = 62.7 мкм.

Рис. 3.

Зависимости коэффициента захвата частиц за счет инерции и зацепления волокном в ряду от ${\text{Stk}}$ для $R$ = 0.34, ${{r}_{{\text{p}}}}$ = 1.5 мкм (1) и ${{r}_{{\text{p}}}}$= 1.1 мкм, $R$ = 0.26 (2), $t$ = $\pi \,b$/2 = 0.233, 2$a$ = 8.9 мкм, 2$h$ = 62.7 мкм. Сравнение с экспериментом (рис. 3 в [16]): ${{r}_{{\text{p}}}}$ = 1.5 (3), 1.18 (4), 1.1 мкм (5).

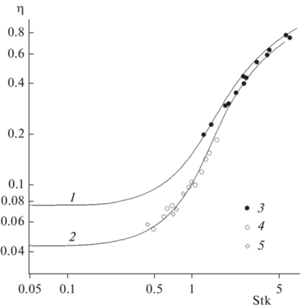
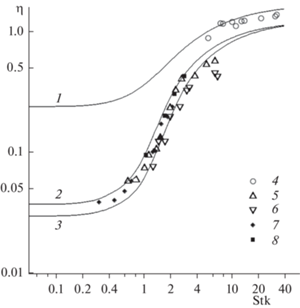
Рис. 4.

Зависимости коэффициента захвата частиц за счет инерции и зацепления волокном в ряду от ${\text{Stk}}$ для $R$ = 0.65, 0.2; ($t = {{\pi b} \mathord{\left/ {\vphantom {{\pi b} 2}} \right. \kern-0em} 2}$ = 0.233, 2$a$ = 8.9 мкм, 2$h$ = = 62.7 мкм, 4 слоя волокон, $R$ = 0.2, 0.65; $t$ = 0.157, 44 слоя волокон, $R$ = 0.2); кривая (1) rp = 2.9 мкм, $t$ = 0.223, (2) ${{r}_{{\text{p}}}}$ = 1 мкм, $t$ = 0.223; (3) rp= 2.9 мкм, $t$ = 0.157. Сравнение с экспериментом (рис. 4 в [16]): rp = 0.92 мкм (7), 1 мкм, $t$ = 0.223 (5), 0.94 (8), rp =  2.9 мкм, $t$ = 0.223 (4), rp = 2.9 мкм, $t$ = 0.157 (6).

Сравнение инерционных коэффициентов захвата в ряду волокон и в ячеечной модели

В теории фильтрации наиболее популярна ячеечная модель Кувабары [20]. Отметим, что Кувабара полагал, что предложенная им ячеечная модель описывает поле течения в слое параллельных волокон со случайным расположением. Но он не учел, что в этом случае должны появиться боковые силы. В работах [21, 22] было показано экспериментально, что его формула для силы сопротивления описывает сопротивление волокна только в системе волокон с регулярной гексагональной упаковкой. К такому же выводу позже пришли авторы теоретических работ [23, 24]. Ячеечную модель Кувабары часто использовали для оценок коэффициентов захвата частиц, например, в [8, 25–28].

На рис. 5 дано сравнение коэффициентов захвата частиц в ряду с относительным расстоянием между осями волокон ${{2{h \mathord{\left/ {\vphantom {h a}} \right. \kern-0em} a} = 2} \mathord{\left/ {\vphantom {{2{h \mathord{\left/ {\vphantom {h a}} \right. \kern-0em} a} = 2} b}} \right. \kern-0em} b}$ и в ячейке Кувабары с плотностью упаковки $\alpha = {{\pi {{b}^{2}}} \mathord{\left/ {\vphantom {{\pi {{b}^{2}}} 4}} \right. \kern-0em} 4}$. Коэффициенты захвата частиц были рассчитаны по методу граничной траектории на основе численного решения уравнения движения частицы (3), записанного в полярных координатах

(8)
$\left\{ \begin{gathered} {\text{Stk}}\left( {\frac{{d{{v}_{r}}}}{{dt}} - \frac{{v_{\theta }^{2}}}{r}} \right) + {{v}_{r}} - {{u}_{r}} = 0, \hfill \\ {\text{Stk}}\left( {\frac{{d{{v}_{\theta }}}}{{dt}} + \frac{{{{v}_{\theta }}{{v}_{r}}}}{r}} \right) + {{v}_{\theta }} - {{u}_{\theta }} = 0, \hfill \\ \end{gathered} \right.$
c начальным условием
(9)
${\mathbf{v}}\left( {{{b}_{c}},{{\theta }_{0}}} \right) = {\mathbf{u}}\left( {{{b}_{c}},{{\theta }_{0}}} \right){\text{ при }}t = 0,$
где ${{v}_{r}} = {{dr} \mathord{\left/ {\vphantom {{dr} {dt}}} \right. \kern-0em} {dt}}$, ${{v}_{\theta }} = r{{d\theta } \mathord{\left/ {\vphantom {{d\theta } {dt}}} \right. \kern-0em} {dt}}$, ${{b}_{c}} = {{\alpha }^{{ - 1/2}}}$ – радиус ячейки, ${{\theta }_{0}}$ – угол входа частицы в ячейку. На рис. 5 наглядно продемонстрировано, что совпадение имеет место только при небольших значениях ${\text{Stk}}$. Очевидно, что использование поля течения в ячеечной модели возможно только для рыхлых модельных фильтров с малой плотностью упаковки $\alpha $ и при небольших ${\text{Stk}}$. Из рис. 5 видно, что для очень пористых моделей совпадение расчетов для ячейки и ряда сохраняется до более высоких значений ${\text{Stk}}$. Обратим внимание, что вклад инерционного осаждения для частиц, соизмеримых с толщиной волокна (при $R$ = 1) невелик. Более подробно влияние плотности упаковки фильтра на инерционное осаждение частиц проиллюстрировано на рис. 6а, 6б. Здесь представлены зависимости коэффициентов захвата от числа Стокса для ячеечной модели, рассчитанные для α = 1/36 (${{b}_{c}}$ = 6) и α = 1/9 (${{b}_{c}}$ = 3) для разных параметров зацепления $R$ с интервалом 0.1 до $R$ = 1. На рисунках видно, что в пределе малых и больших чисел Стокса коэффициент захвата не зависит от ${\text{Stk}}$. При малых ${\text{Stk}}$ инерция не смещает частицу с линии тока, и она движется как бы “вмороженной” в поток, ${\mathbf{v}} = {\mathbf{u}}$. Граничная траектория совпадает с линией тока, проходящей на минимальном расстоянии от волокна в точке $r = 1 + R$, $\theta = {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}$. Осаждение происходит за счет эффекта зацепления (касания), и коэффициент захвата определяется расходом газа в пределах граничной траектории [4]
(10)
$\begin{gathered} {{\eta }_{R}} = \int\limits_1^{1 + R} {{{u}_{\theta }}} \left( {r,{\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0em} 2}} \right)dr = {{\left( {2{{k}_{0}}} \right)}^{{ - 1}}} \times \\ \times \left[ {{{{\left( {1 + R} \right)}}^{{ - 1}}} - \left( {1 + R} \right) + 2\left( {1 + R} \right)\ln \left( {1 + R} \right)} \right], \\ \end{gathered} $
где гидродинамический фактор равен

${{k}_{0}} = - \frac{1}{2}{\kern 1pt} \ln {\kern 1pt} \alpha + \alpha - \frac{3}{4} - \frac{1}{4}{{\alpha }^{2}}.$
Рис. 5.

Зависимости коэффициента захвата частиц с $R$ = 0.2 за счет инерции от ${\text{Stk}}$ в ряду параллельных волокон (1‒2) и в ячеечной модели с той же плотностью упаковки $\alpha = {{\pi {{b}^{2}}} \mathord{\left/ {\vphantom {{\pi {{b}^{2}}} 4}} \right. \kern-0em} 4}$ (1'‒2'): параметр ряда $b$ = = 0.05 (1, 1'), 0.1 (2, 2').

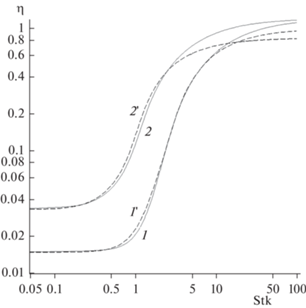
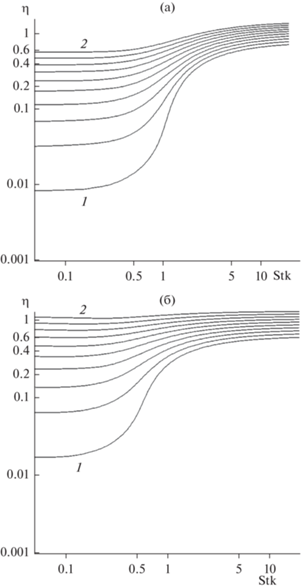
Рис. 6.

Зависимости коэффициента захвата частиц за счет инерции и зацепления от ${\text{Stk}}$для волокна в ячейке Кувабары с плотностью упаковки α = 1/36 (а), 1/9 (б) для параметров зацепления в диапазоне от $R$ = 0.1 (1) до 1 (2) с интервалом 0.1; ${\text{Kn}}$ = 0.

В пределе больших чисел Стокса инерция доминирует, и вклад гидродинамического поля течения мал. При “баллистическом” осаждении частицы движутся по прямым траекториям (рис. 1), а коэффициент захвата в этом случае не зависит от ${\text{Stk}}$ и плотности упаковки и равен $\eta = 1 + R$. По результатам расчетов для фильтров с α = 1/36, 1/16, 1/9 построена кусочно-непрерывная аппроксимационная формула, применимая при ${\text{Stk}}$ = 0.1–20 и $R$ = 0.1–1 (дана в Приложении). Отметим, что при больших числах Стокса расчетные кривые имеют лишь теоретическое значение, т.к. на практике возможен отскок инерционных частиц от поверхности волокна с возвращением их обратно в поток. Также возможны множественные отскоки частиц от волокон с $a \gg {{r}_{{\text{p}}}}$ с последующим притяжением всех или части отскочивших частиц к волокну в поле вандерваальсовых сил [5]. Эти вопросы в данной статье не рассматриваются. Отметим также, что часто используемая формула для расчета инерционного осаждения, предложенная в [29], по признанию авторов этой работы оказалась неверной, о чем они сразу же сообщили в [30], и в дальнейшем это было отмечено в [4]. Авторы [29] сообщили об ошибке из-за того, что их формула (линейная по ${\text{Stk}}$) не воспроизводит слабый минимум расчетной зависимости $\eta $ от числа Стокса при малых ${\text{Stk}}$ (см. рис. 6, 9, 10), и что уже при малых ${\text{Stk}}$ начинается резкий рост $\eta $. Это связано с тем, что в [29] при выводе формулы был использован приближенный аналитический метод решения, справедливый в пределе малых параметров зацепления $R$ $ \ll $ 1 и чисел Стокса ${\text{Stk}}$ $ \ll $ 1: скорость частицы раскладывалась по малому числу Стокса, после чего авторы ограничивались лишь первым членом разложения, при этом поле скоростей потока также было упрощено для случая предельно малой плотности упаковки $\alpha $ $ \ll $ 1. Следует подчеркнуть, что указанный минимум $\eta \left( {{\text{Stk}}} \right)$ является артефактом, характерным для приближенной ячеечной модели, в которой точность поля течения (если сравнивать профили скоростей в этой модели со строго рассчитанными в решетках параллельных волокон) уменьшается при приближении к внешней границе ячейки. Отметим, что здесь минимум $\eta \left( {{\text{Stk}}} \right)$ становится практически незаметным при увеличении радиуса ячейки и в модели ряда волокон не воспроизводится вовсе. Существование минимума $\eta \left( {{\text{Stk}}} \right)$ представляет чисто теоретический интерес, т.к. он находится в области, где инерция не проявляется. Поэтому экспериментальная проверка указанного минимума невозможна.

Рис. 7.

Зависимости ${{{{u}_{\theta }}} \mathord{\left/ {\vphantom {{{{u}_{\theta }}} {\sin {\kern 1pt} \theta }}} \right. \kern-0em} {\sin {\kern 1pt} \theta }}$ и ${{ - {{u}_{r}}} \mathord{\left/ {\vphantom {{ - {{u}_{r}}} {\cos {\kern 1pt} \theta }}} \right. \kern-0em} {\cos {\kern 1pt} \theta }}$от радиальной координаты в ячейке с ультратонким волокном для разных ${\text{Kn}}$: 1 – по (16) (кинетическая теория [15]), 2 – по (11) (течение со скольжением [14]), $\alpha $ = 1/16.

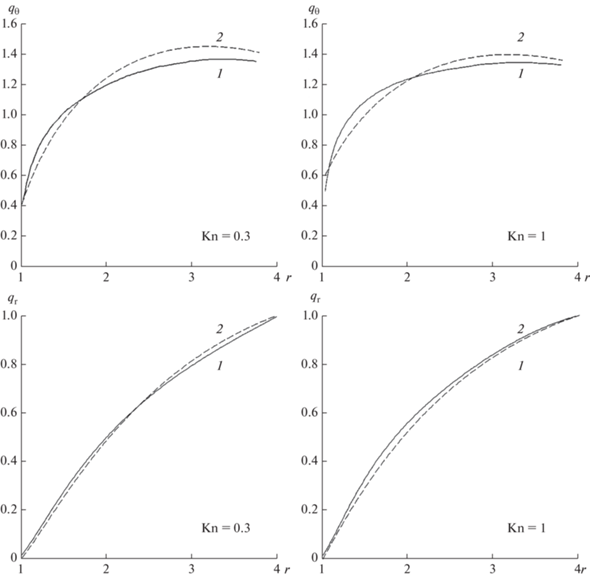
Рис. 8.

Сравнение тангенциальных скоростей потока (скоростей скольжения на поверхности волокна) при $\theta = $ π/2 и $r$ = 1 от ${\text{Kn}}$, 1 – по (11) (течение со скольжением, ${\text{Kn}}$ $ \ll $ 1) [14], точки 2 – по (16) (численно-аналитическое решение [15], промежуточные и большие ${\text{Kn}}$), $\alpha $ = 1/16.

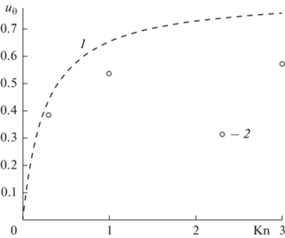
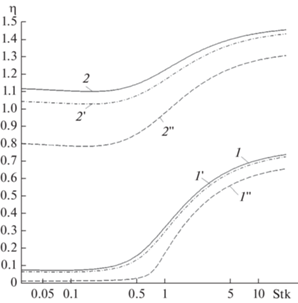
Рис. 9.

Зависимости коэффициентов захвата за счет инерции и зацепления от ${\text{Stk}}$: сплошные линии – с учетом поля скоростей (15), (16) [15], пунктирные – (11), (13) [14], для параметров зацепления в диапазоне $R$ = 0.1 (1) до $R$ = 1 (2) с интервалом 0.1; ячеечная модель, $\alpha $ = 1/16, ${\text{Kn}}$ = 0.3.

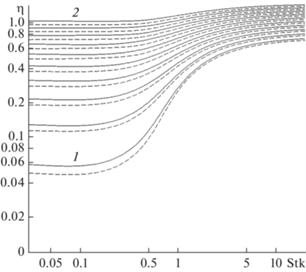
Рис. 10.

Зависимости коэффициентов захвата частиц волокном за счет инерции и зацепления для частиц конечного размера при $R$ = 0.1 (1, 1', 1'') и $R$ = 1 (2, 2', 2'') от ${\text{Stk}}$с учетом эффекта скольжения газа при ${\text{Kn}}$ = = 1 (1, 1', 2, 2') и ${\text{Kn}}$ = 0 (1'', 2''): 1, 2 – расчет для поля скоростей (16) (кинетическая теория, [15]), 1', 2' – (15) (течение со скольжением, [14]), 1'', 2'' – поля скоростей [20]; ячеечная модель Кувабары, $\alpha $ = 1/16.

В области малых ${\text{Stk}}$ следующий вопрос связан с “критическим” числом Стокса ${\text{St}}{{{\text{k}}}_{{{\text{crit}}}}}$, начиная с которого инерция частиц влияет на осаждение. Этот вопрос подробно рассматривался в [31], где было показано, что инерция не проявляется при ${\text{Stk}}$ < 0.1. Это следовало и из многочисленных экспериментов с реальными фильтрами [32]. Действительно, из рис. 2–6 видно, что инерция заметно проявляется только при числах Стокса ${\text{Stk}}$ > 0.1. Отсюда следует, что появляющиеся иногда утверждения о влиянии инерции при меньших значениях ${\text{Stk}}$ не верны. В связи с этим отметим работу [33], в которой в рамках приближенного численно-аналитического метода расчета для ячеечной модели было получено, что увеличение эффективности за счет инерции начинается при ${\text{Stk}}$ ∼ 0.01.

4. ОСАЖДЕНИЕ ЧАСТИЦ В СИСТЕМЕ УЛЬТРАТОНКИХ ВОЛОКОН

При расчете осаждения частиц на ультратонкие волокна необходимо учесть эффект скольжения газа на волокнах. На это впервые указал Г.Л. Натансон на примере захвата частиц изолированным волокном [34]. Для моделирования осаждения частиц на субмикронные волокна при небольших числах Стокса мы можем использовать поле течения в ячеечной модели, поскольку, как было показано выше, коэффициент захвата в инерционном режиме осаждения частиц в изолированном ряду и в ячеечной модели при числах Стокса ${\text{Stk}}$ < 5 совпадают. В ячеечной модели поле течения с учетом эффекта скольжения газа при малых числах Кнудсена (${\text{Kn}}$ $ \ll $ 1) имеет вид [14]:

(11)
$\Psi = f\left( r \right)\sin {\kern 1pt} \theta = \frac{{g\left( r \right)}}{{4{{k}_{1}}}}\sin {\kern 1pt} \theta ,$
где

$\begin{gathered} g\left( r \right) = \left( {2 - \alpha + 2\alpha \tau {\text{Kn}}} \right)\frac{1}{r} - 2\left( {1 - \alpha } \right)r + \\ + \,\,4\left( {1 + 2\tau {\text{Kn}}} \right)r{\kern 1pt} \ln {\kern 1pt} r - \left( {1 + 2\tau {\text{Kn}}} \right)\alpha {{r}^{3}}, \\ k = {{k}_{0}} + \frac{1}{2}\tau {\text{Kn}}\left( {1 - {{\alpha }^{2}} + 2{\kern 1pt} ln{\kern 1pt} \alpha } \right). \\ \end{gathered} $

При выводе (11) было использовано граничное условие скольжения (условие Максвелла)

(12)
${{u}_{r}} = 0,\,\,\,\,{{u}_{\theta }} = \tau {\kern 1pt} {\text{Kn}}{\kern 1pt} {{\sigma }_{{r\theta }}},$
где ${{\sigma }_{{r\theta }}}$ – касательное напряжение, $\tau $ = 1.147 – коэффициент изотермического скольжения, учитывающий взаимодействие газовых молекул с поверхностью волокна [35], а компоненты скоростей выражаются через функцию тока как:

(13)
$\begin{gathered} {{u}_{r}} = - \frac{1}{r}\frac{{\partial \Psi }}{{\partial \theta }} = - {{q}_{r}}\left( r \right)\cos \left( \theta \right), \\ {{u}_{\theta }} = \frac{{\partial \Psi }}{{\partial r}} = {{q}_{\theta }}\left( r \right)\sin {\kern 1pt} \theta . \\ \end{gathered} $

В этих формулах скорости выражены через радиальные функции, графики которых приведены на рис. 7. Из (11), (13) нетрудно найти скорость скольжения на поверхности волокна при $r = 1$. Она равна

(14)
${{u}_{{{\text{slip}}}}} = \frac{{2\tau {\kern 1pt} {\text{Kn}}}}{k}\left( {1 - \alpha } \right)\sin {\kern 1pt} \theta .$

Из (14) следует, что скорость скольжения газа на волокне увеличивается с ростом числа Кнудсена и c ростом плотности упаковки волокон в фильтре.

Решение для поля течения в ячеечной модели, применимое в широком диапазоне чисел Кнудсена, было впервые получено в [15] численно-аналитическим методом в рамках кинетической теории разреженных газов в приближении Бхатнагара–Гросса–Крукса для плотностей упаковки фильтров, равных $\alpha = {1 \mathord{\left/ {\vphantom {1 {36,\,\,{1 \mathord{\left/ {\vphantom {1 {16,\;{1 \mathord{\left/ {\vphantom {1 9}} \right. \kern-0em} 9}}}} \right. \kern-0em} {16,\;{1 \mathord{\left/ {\vphantom {1 9}} \right. \kern-0em} 9}}}}}} \right. \kern-0em} {36,\,\,{1 \mathord{\left/ {\vphantom {1 {16,\;{1 \mathord{\left/ {\vphantom {1 9}} \right. \kern-0em} 9}}}} \right. \kern-0em} {16,\;{1 \mathord{\left/ {\vphantom {1 9}} \right. \kern-0em} 9}}}}}$. Сравнение зависимостей для компонент скорости потока (13) с найденными в [15] приведено на рис. 7 и 8 для плотности упаковки $\alpha = {1 \mathord{\left/ {\vphantom {1 {16}}} \right. \kern-0em} {16}}$. Здесь и далее рассматриваем пример фильтра с этим значением α, поскольку большинство реальных высокоэффективных фильтров имеет близкую плотность упаковки. Будем использовать уточненные аппроксимации для компонент скоростей потока при обтекании ультратонкого волокна в ячейке Кувабары, построенные нами по расчетным данным [15] для $\alpha = {1 \mathord{\left/ {\vphantom {1 {16}}} \right. \kern-0em} {16}}$:

(15)
${{q}_{r}} = A + Br + C{{r}^{{ - 1}}} + D{{r}^{{ - 2}}} + E{{r}^{2}} + F{\kern 1pt} \ln {\kern 1pt} r,$
(16)
${{q}_{\theta }} = a + b{{r}^{{ - 11}}} + c{{r}^{{ - 2}}} + d{{r}^{2}} + e{\kern 1pt} \ln {\kern 1pt} r,$
где коэффициенты приведены в табл. 1 (средняя относительная погрешность аппроксимации не превышает 0.1%). Эти же формулы описывают течение разреженного газа вблизи волокна любого радиуса.

Таблица 1.  

Коэффициенты в аппроксимационных формулах (15), (16) для ячеечной модели с $\alpha = {1 \mathord{\left/ {\vphantom {1 {16}}} \right. \kern-0em} {16}}$

${\text{Kn}}$ $A$ $B$ $C$ $D$ $E$ $F$
0.3 1.362954 ‒0.285438 ‒2.082320 0.988784 0.0287823 0.557373
1 12.282844 4.939722 ‒22.377315 5.451608 ‒0.280035 ‒ 15.371139
3 5.469471 0.802511 ‒8.656095 2.419047 ‒0.029152 ‒ 3.751793
${\text{Kn}}$ $a$ $b$ $c$ $d$ $e$
0.3 1.0148095 ‒0.283836 ‒0.320505 ‒0.0264392 0.648570
1 1.321618 ‒0.272466 ‒0.499161 ‒0.0144089 0.283646
3 1.177181 ‒0.685839 0.099157 ‒0.019197 0.351284

Отметим, что для расчета сопротивления фильтра решение (11), полученное с граничным условием скольжения (12), применимо только при ${\text{Kn}} < {\text{0}}{\text{.01}}$. Важно подчеркнуть, что полученная зависимость силы сопротивления ${{F}_{{{\text{slip}}}}}$ [14] качественно и количественно отличается от экспериментальных данных практически во всем диапазоне чисел Кнудсена при ${\text{Kn}} > {\text{0}}{\text{.01}}$, совпадая с ними лишь в пределе бесконечно малых значений ${\text{Kn}}$. Поэтому для расчета силы сопротивления волокна следует либо использовать метод линейной экстраполяции величины ${1 \mathord{\left/ {\vphantom {1 {{{F}_{{{\text{slip}}}}}}}} \right. \kern-0em} {{{F}_{{{\text{slip}}}}}}}$ в область больших чисел Кнудсена [4], либо пользоваться более строгим решением, полученным в [15].

В то же время расчетные профили скоростей разреженного газа в модели со скольжением при ${\text{Kn}} > {\text{0}}{\text{.01}}$ качественно согласуются (в отличие от ${{F}_{{{\text{slip}}}}}$) с данными экспериментов и расчетов в рамках кинетической теории. Различие между ними появляется и увеличивается с ростом ${\text{Kn}}$ (при малых ${\text{Kn}}$ скорости почти совпадают). При этом на самой обтекаемой поверхности решение для течения со скольжением дает верхнюю оценку тангенциальной скорости (рис. 7, 8). Это согласуется с результатами работ по расчету обтекания разных тел [36] и течения в каналах в рамках кинетической теории. Таким образом, простое решение (11) для поля скоростей может быть использовано для приближенных оценок осаждения частиц на ультратонкие волокна или на волокна любого радиуса в условиях течения разреженного газа при 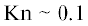во всем интервале $\alpha $. При увеличении числа Кнудсена расхождение расчетов по (11) и (15), (16) становится более заметным.

После уточнения поля течения в окрестности нановолокон в модельном фильтре было рассчитано инерционное осаждение частиц с учетом скольжения газа на волокне. Расчеты коэффициентов инерционного осаждения для полей течения (11) [14] и (15) [15] даны на рис. 9 и 10. Из представленных данных видно, что, чем больше параметр зацепления, тем больше влияние скольжения. В пределе малых чисел Стокса расчетные кривые выходят на плато, соответствующее коэффициенту захватa за счет эффекта зацепления ${{\eta }_{R}}$. Величина ${{\eta }_{R}}$ при Kn > 0 дается следующей формулой, полученной из (9) и (16):

(17)
$\begin{gathered} \eta {}_{R} = aR + \frac{b}{{10}}\left[ {1 - \frac{1}{{{{{\left( {1 + R} \right)}}^{{10}}}}}} \right] + c\left( {\frac{R}{{1 + R}}} \right) - \\ - \,\,\frac{d}{3}\left[ {1 - {{{\left( {1 + R} \right)}}^{3}}} \right] + e\left[ {\left( {1 + R} \right)\ln \left( {1 + R} \right) - R} \right]. \\ \end{gathered} $

Отличие расчетов для полей течения работ [14] (течение со скольжением) и [15] (кинетическая теория) заметно лишь при ${\text{Kn}}$ > 1. При меньших числах Кнудсена поле скоростей (11), (13) вполне применимо для оценок $\eta $. Для расчетных зависимостей коэффициента захвата от ${\text{Stk}}$ и $R$ для ${\text{Kn}}$ = 0.3 и ${\text{Kn}}$ = 1 при $\alpha $ = 1/16 были построены соответствующие аналитические аппроксимации (см. Приложение), позволяющие оценивать влияние эффекта скольжения газа на инерционное осаждение частиц. Например, для фильтра с толщиной $H$ = 0.5 мм, плотностью упаковки волокон $\alpha $ = 1/16 = 0.0625 и радиусом волокон $a$ = 0.22 мкм эффективность улавливания частиц без учета эффекта скольжения (${\text{Kn}}$ = 0) при $R$ = 0.1 и ${\text{Stk}}$ = 0.2 составит $E$ = 0.977 (соответственно, проскок ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ = 0.023), а с учетом (${\text{Kn}}$ = 0.3) увеличится до $E$ = 0.997 (проскок понизится на порядок ${n \mathord{\left/ {\vphantom {n {{{n}_{0}}}}} \right. \kern-0em} {{{n}_{0}}}}$ = = 0.003). Таким образом, учет эффекта скольжения газа совершенно необходим при вычислении инерционного осаждения аэрозольных частиц на тонкие волокна.

ЗАКЛЮЧЕНИЕ

Рассмотрено влияние инерции субмикронных частиц на их осаждение в тонковолокнистых фильтрах при малых числах Рейнольдса в широком диапазоне чисел Стокса ${\text{Stk}}$ при разных значениях чисел Кнудсена ${\text{Kn}}$ и параметров зацепления $R$. Методом граничной траектории рассчитаны коэффициенты захвата частиц волокном в модельных фильтрах, в качестве которых выбраны ячеечная модель Кувабары и ряд параллельных монодисперсных волокон, перпендикулярных направлению потока газа. Показано, что инерционное осаждение частиц в ячеечной модели фильтра с пористостью, характерной для реальных фильтров, заметно ниже, чем в отдельном ряду волокон, при числах Стокса ${\text{Stk}}$> 3. Показано также сильное влияние эффекта скольжения газа на cубмикронных волокнах на осаждение частиц при малых и промежуточных числах Стокса.

Список литературы

  1. Fuchs N.A. The Mechanics of Aerosols. N.Y.: Dover, 1989.

  2. Davies C.N. Air Filtration. N.Y.: Academic Press, 1973.

  3. Brown R.C. Air Filtration. Oxford: Pergamon Press, 1993.

  4. Kirsch A.A., Stechkina I.B. The theory of aerosol filtration with fibrous filters, Ch. 4, in Fundamentals of Aerosol Science / Ed. by Shaw D.T. N.Y.: Wiley-Interscience. 1978. P. 165‒256.

  5. Chernyakov A.L., Kirsch A.A., Kirsch V.A. Elastic vibrations of a fiber due to impact of an aerosol particle and their influence on the efficiency of fibrous filters // Phys. Rev. E. 2011. V. 83. № 5. P. 056303. https://doi.org/10.1103/PhysRevE.83.056303

  6. Стечкина И.Б., Кирш В.А. Оптимизация параметров аэрозольных волокнистых фильтров // Коллоид. журн. 2001. Т. 63. № 4. С. 517–522. https://doi.org/10.1023/A:1016762107083

  7. Кирш В.А., Кирш А.А. Улавливание субмикронных аэрозольных частиц фильтрами из нановолокон // Коллоид. журн. 2023. Т. 85. № 1. С. 38‒46. https://doi.org/10.1134/S1061933X22600476

  8. Кирш В.А. Инерционное осаждение тяжелых аэрозольных частиц в волокнистых фильтрах // Теор. основы хим. технологии. 2005. Т. 39. № 1. С. 50–55. https://doi.org/10.1007/s11236-005-0028-1

  9. Волощук В.М. Введение в гидродинамику грубодисперсных аэрозолей. Л.: Гидрометеоиздат, 1971.

  10. Hairer E., Norsett S., Wanner G. Solving Ordinary Differential Equations I: Nonstiff Problems, 2-nd ed. Berlin: Springer-Verlag, 1993.

  11. Слезкин Н.А. Динамика вязкой несжимаемой жидкости. М.: ГИТТЛ, 1955.

  12. Wang C.Y. Stokes slip flow through a grid of circular cylinders // Phys. Fluids. 2002. V. 14. № 9. P. 3358‒3360. https://doi.org/10.1063/1.1499127

  13. Kolodziej J.A. Review of application of boundary collocation methods in mechanics of continuous media // Solid Mechanics Archives. 1987. V. 12. № 4. P. 187–231.

  14. Pich J. Pressure drop of fibrous filters at small Knudsen numbers // Ann. Occup. Hyg. 1966. V. 9. № 1. P. 23‒27. https://doi.org/10.1093/annhyg/9.1.23

  15. Ролдугин В.И., Кирш А.А., Емельяненко А.М. Моделирование аэрозольных фильтров при промежуточных числах Кнудсена // Коллоид. журн. 1999. Т. 61. № 4. С. 530‒542.

  16. Кирш А.А., Стечкина И.Б. Инерционное осаждение аэрозолей в модельных фильтрах при малых числах Рейнольдса // Коллоид. журн. 1977. Т. 39. № 1. С. 36‒43.

  17. Miyagi T. Viscous flow at low Reynolds numbers past an infinite row of equal circular cylinders // J. Phys. Soc. Japan. 1958. V. 13. № 5. P. 493−496. https://doi.org/10.1143/JPSJ.13.493

  18. Muller T.K., Meyer J., Kasper G. Low Reynolds number drag and particle collision efficiency of a cylindrical fiber within a parallel array // J. Aerosol Sci. 2014. V. 77. № 11. P. 50–66. https://doi.org/10.1016/j.jaerosci.2014.07.007

  19. Gallily I. On the filtration of aerosols by filter models of various porosities // J. Colloid Sci. 1957. V. 12. № 2. P. 161–172.

  20. Kuwabara S. The forces experienced by randomly distributed parallel circular cylinders or spheres in viscous flow at small Reynolds numbers // J. Phys. Soc. Japan. 1959. V. 14. № 4. P. 527–532. https://doi.org/10.1143/JPSJ.14.527

  21. Kirsch A.A., Fuchs N.A. The fluid flow in a system of parallel cylinders perpendicular to the flow direction at small Reynolds numbers // J. Phys. Soc. Japan. 1967. V. 22. P. 1251–1255. https://doi.org/10.1143/JPSJ.22.1251

  22. Kirsch A.A., Fuchs N.A. Studies of fibrous aerosol filters – II. Pressure drops in systems of parallel cylinders // Ann. Occup. Hyg. 1967. V. 10. № 1. P. 23–30. https://doi.org/10.1093/annhyg/10.1.23

  23. Головин А.М., Лопатин В.А. Течение вязкой жидкости в двоякопериодических рядах цилиндров // ПМТФ. 1969. Т. 9. № 2. С. 99–105. https://doi.org/10.1007/BF00913184

  24. Sangani A.S., Acrivos A. Slow flow past periodic arrays of cylinders with application to heat transfer // Int. J. Multiphase Flow. 1982. V. 8. № 3. P. 193–206. https://doi.org/10.1016/0301-9322(82)90029-5

  25. Yeh H.-C., Liu B.Y.H. Aerosol filtration by fibrous filters – I. Theoretical // J. Aerosol Sci. 1974. V. 5. № 2. P. 191–204. https://doi.org/10.1016/0021-8502(74)90049-4

  26. Yeh H.-C. A fundamental study of aerosol filtration by fibrous filters. Ph.D. Thesis. Minneapolis: University of Minnesota, 1972.

  27. Ramarao B.V., Tien C., Mohan S. Calculation of single fiber efficiencies for interception and impaction with superposed Brownian motion // J. Aerosol Sci. 1994. V. 25. № 2. P. 295–313. https://doi.org/10.1016/0021-8502(94)90081-7

  28. Кирш В.А. Инерционное осаждение аэрозольных частиц в волокнистых фильтрах // Коллоид. журн. 2004. Т. 66. № 5. С. 613–618. https://doi.org/10.1023/B:COLL.0000043835.00525.83

  29. Стечкина И.Б., Кирш А.А., Фукс Н.А. Исследования в области волокнистых аэрозольных фильтров // Коллоид. журн. 1969. Т. 31. № 1. С. 121–126.

  30. Стечкина И.Б., Кирш А.А., Фукс Н.А. Влияние инерции на коэффициент захвата аэрозольных частиц на цилиндрах при малых числах Стокса // Коллоид. журн. 1970. Т. 32. № 3. С. 467.

  31. Левин Л.М. Исследования по физике грубодисперсных аэрозолей, М.: Изд. АН СССР, 1961.

  32. Wong J.B., Ranz W.E., Johnstone H.F. Collection efficiency of aerosol particles and resistance to flow through fiber mats // J. Appl. Phys. 1956. V. 27. № 2. P. 161–170. https://doi.org/10.1063/1.1722328

  33. Flagan R.C., Seinfeld J.H. Fundamentals of Air Pollution Engineering, Ch. 7. P. 441. Englewood Cliffs, New Jersey: Prentice-Hall, Inc., 1988.

  34. Натансон Г.Л. Влияние скольжения на эффект касания при захвате амикроскопических частиц цилиндром из потока // Коллоид. журн. 1960. Т. 24. № 1. С. 52−54.

  35. Albertoni S., Cereignani C., Gutusso L. Numerical evaluation of the slip coefficient // Phys. Fluids. 1963. V. 6. № 7. P. 993–996. https://doi.org/10.1063/1.1706857

  36. Zhao S., Povitsky A. A hybrid molecular and continuum method for low-Reynolds-number flows // Nonlinear Analysis. 2009. V. 71. № 12. P. e2551–e2564. https://doi.org/10.1016/j.na.2009.05.069

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Коллоидный журнал

Архивы выпусков Информация о журнале Отправить рукопись в журнал