Коллоидный журнал, 2023, T. 85, № 3, стр. 350-354

ВВЕДЕНИЕ

Анализ нанодисперсных пузырьковых сред актуален в связи с их востребованностью в современных технологиях [1–4]. Понимание свойств нанопузырей важно для широкого применения нанодисперсных газожидкостных сред, полученных только в начале 21-го века, в современных технологиях (медицина, химия и др.). Как известно, нанопузыри в воде имеют заряд, и, подобно коллоидным частицам, на их границе образуется двойной электрический слой (ДЭС) [5, 6]. Несомненно, практически важна глобальная проблема стабильности нанопузырей, которая рассматривалась во многих работах, в том числе [7, 8]. Однако решение глобальных проблем, как показывает практика, невозможно без изучения более узких вопросов. В нашем случае это анализ детальных свойств ДЭС, в том числе его структуры и ее зависимости от размеров, заряда пузырей, а также от характеристик внешней среды. Какое влияние эти свойства окажут на решение глобальной проблемы, покажет будущее. В данной работе решено сосредоточиться на решении частных вопросов, которые могут оказаться полезными в дальнейшем.

Взгляды на структуру ДЭС постепенно уточнялись, что широко нашло свое отражение в литературе. В простой модели [9, 10] заряженный нанопузырь окружен диффузным слоем, в более сложной модели [11–17] заряженная поверхность пузыря окружена слоем неподвижных противоионов – слоем Штерна и только лишь затем – диффузным слоем взвешенных противоионов. Следующее уточнение модели ДЭС на основе экспериментальных данных состоит в наличии гидратной прослойки между слоем Штерна и поверхностью пузыря [18–20]. Это теоретически поясняется в [21] большей удельной потенциальной энергией водородных связей, формирующих касательную гидратную оболочку, по сравнению с удельной потенциальной энергией радиально ориентированных моментов поляризации диполей молекул воды.

Из приведенного обзора видно, что структура ДЭС объемных нанопузырей неоднократно рассматривалась и уточнялась, однако детального теоретического анализа зависимости структуры ДЭС пузырей от их характеристик и внешней среды не было сделано.

Поэтому уточнение структуры ДЭС, в том числе условий существования слоя Штерна пузырей с учетом его заряда ${{q}_{{{\text{St}}}}}$, размеров пузырей и концентрации раствора солей углубит понимание их свойств и создаст предпосылки для технологического прогресса в данной области, что полезно и актуально.

1. ПОСТАНОВКА ЗАДАЧИ

В [21] определен заряд нанопузырей, при котором кулоновское притяжение достаточно для удержания противоионов в слое Штерна, не позволяя тепловой энергии вырывать их, переводя в диффузный слой. Однако не только тепловая энергия противоионов является определяющим фактором стабильности ДЭС, но и другие его термодинамические характеристики, в частности энтропия. Заряд слоя Штерна ${{q}_{{{\text{St}}}}}$ формируется противоионами диффузного слоя, которые в ходе броуновского движения закрепляются поверх заряда пузыря и удерживаются кулоновским притяжением в слое Штерна. В данной работе проведен анализ как термического, так и термодинамического равновесия структуры ДЭС. Определены условия формирования слоя Штерна в ДЭС: оценена величина заряда и размеров слоя Штерна, при которых энергия Гиббса ДЭС минимальна. Также учтена тепловая устойчивость слоя Штерна, которая реализуется, если энергия кулоновской связи противоионов слоя Штерна с зарядом пузыря на порядок больше их тепловой энергии. Определено влияние концентрации растворенных солей на критический радиус устойчивого слоя Штерна.

2. АНАЛИЗ ТЕРМОДИНАМИЧЕСКОГО РАВНОВЕСИЯ ДВОЙНОГО ЭЛЕКТРИЧЕСКОГО СЛОЯ

В [18] экспериментально обнаружено слоистое структурирование воды вблизи поверхности раздела фаз. Соответственно, структуру ДЭС можно представить в виде сферичных концентрических слоев, вложенных друг в друга:

1. Поверхность нанопузыря радиусом ${{r}_{0}}$ и с зарядом ${{q}_{0}}$.

2. Гидратная оболочка нанопузыря толщиной Δ ≈ 1 нм – слой т.н. межфазной воды с относительной диэлектрической проницаемостью ε(Δ) = ε_St ≈ 3, уменьшенной за счет взаимодействия диполей воды с поверхностью нанопузыря.

3. Слой Штерна радиусом ${{r}_{{{\text{St}}}}} = {{r}_{0}} + \Delta $ и зарядом q_St – плотный слой противоионов, удерживаемых кулоновским взаимодействием с зарядом нанопузыря ${{q}_{0}}$;

4. Водная среда диффузного слоя вне слоя Штерна – полярный электролит, где относительная диэлектрическая проницаемость ε = 80.

Стабильность противоионов определяется, очевидно, у внешней границы слоя Штерна при $r = {{r}_{{{\text{St}}}}}$, где имеет смысл проводить анализ. Заряд нанопузыря q₀ частично экранирован зарядом противоионов слоя Штерна q_St. Поэтому за пределами внешней границы слоя Штерна действует эффективный заряд q:

Оценим заряд слоя Штерна q_St, образованного притяжением противоионов диффузного слоя, к заряду ${{q}_{0}}$ нанопузыря, но отделенного от него, как отмечалось выше, слоем гидратной оболочки – Δ. Модель ДЭС можно представить в виде сферического конденсатора с радиусом обкладок ${{r}_{{{\text{St}}}}}$ и ${{r}_{{{\text{St}}}}} + L(c)$, зарядом q и емкостью $C({{r}_{{{\text{St}}}}})$, где

где с – концентрация растворенной одновалентной соли, длина Дебая: N_A – число Авогадро, ${{q}_{e}}$ – элементарный заряд, ${{\varepsilon }_{0}}$ – диэлектрическая проницаемость вакуума, Т – температура, k_B – постоянная Больцмана.

Энергия такого сферического конденсатора с учетом (1) равна:

Рассмотрим процесс установления термодинамического равновесия ДЭС при формировании заряда слоя Штерна. Пусть в начальный момент пузырь с зарядом ${{q}_{0}}$ и гидратной оболочкой окружен противоионами диффузного слоя, общий заряд которых равен заряду ${{q}_{0}}$ пузыря (по условию нейтральности среды), а заряд слоя Штерна $q_{{{\text{St}}}}^{0} = 0$. Постепенно кулоновские силы втягивают часть противоионов диффузного слоя в слой Штерна, и система приходит к некоторому термодинамическому равновесию, при котором установится искомое значение заряда слоя Штерна ${{q}_{{{\text{St}}}}}$. Этот процесс описывается уравнением Гиббса [22] $dG = dU - TdS$, где $dU$ – изменение внутренней энергии U. В нашем случае электростатической формой $dU$ является $dW$, а $TdS$ – изменение энтропийной (тепловой) энергии. Таким образом, изменение энергии Гиббса ДЭС dG равно:

Дифференциал энергии (4) имеет вид: $dW = \frac{{ - 2({{q}_{0}} - {{q}_{{{\text{St}}}}})d{{q}_{{{\text{St}}}}}}}{{2C({{r}_{{{\text{St}}}}})}}$, а $ТdS = T\frac{{{{S}^{0}}}}{{{{N}_{{\text{A}}}}}}\left( { - \frac{{d{{q}_{{{\text{St}}}}}}}{{{{q}_{e}}}}} \right)$, где S⁰ = 58.45 Дж/К моль – энтропия ионов Na⁺ в водном растворе при стандартных условиях и концентрации раствора солей с₀ = 1 моль/кг (моль соли в 1 кг воды) [23], что соответствует концентрации 10^–3 моль/м³. При пересчете справочного значения S⁰ к значению S(с) при используемой концентрации с получим: $S(c) = c{{S}^{0}} \times \,\,{{10}^{{ - 3}}}$. Поясним также, что $\left( { - \frac{{d{{q}_{{{\text{St}}}}}}}{{{{q}_{e}}}}} \right)$ – число противоионов диффузного слоя, перешедших в слой Штерна при переносе заряда (–$d{{q}_{{{\text{St}}}}}$). Знак минус здесь отображает уменьшение числа противоионов диффузного слоя, когда их часть переходит в слой Штерна. Из (5) при условии равновесия системы $dG = 0$ получим:

Убыль энергии (4) конденсатора с ростом радиуса ${{r}_{{{\text{St}}}}}$ постепенно снижает количество противоионов диффузного слоя, захваченных слоем Штерна. Наконец, при некотором значении $r_{{{\text{St}}}}^{*}$ радиуса слоя Штерна (назовем его критическим) противоионы диффузного слоя перестают закрепляться на пузыре и ${{q}_{{{\text{St}}}}} = 0$, когда сниженный электростатический фактор перестает уравновешивать энтропийный. Слой Штерна не образуется. С учетом этого из (6) найдем нижнюю границу зависимости заряда пузыря с критическим радиусом слоя Штерна ${{q}_{0}}(r_{{{\text{St}}}}^{*})$ от этого радиуса при термодинамическом равновесии ДЭС:

Однако стабильность слоя Штерна может нарушаться, если тепловая энергия kT вырывает противоионы из него. Условие термической стабильности слоя Штерна имеет вид [21]:

с учетом критерия термической стабильности [24]: ${{W}_{q}} > 10{{k}_{{\text{B}}}}T$, где энергия электростатической связи заряда ${{q}_{e}}$ противоионов диффузного слоя с зарядом ${{q}_{0}}$ пузыря ${{W}_{q}} = \frac{{{{q}_{0}}{{q}_{e}}}}{{4\pi {{\varepsilon }_{0}}\varepsilon (\Delta ){{r}_{{{\text{St}}}}}}}$.

На рис. 1 показана нижняя граница зависимости (7) заряда пузыря ${{q}_{0}}(r_{{{\text{St}}}}^{*})$ от критического радиуса его слоя Штерна при различных концентрациях с растворенной соли, а также (пунктиром) – линейная зависимость (8) заряда пузыря ${{q}_{{0T}}}({{r}_{{{\text{St}}}}})$ от радиуса термически стабильного слоя Штерна, причем значения заряда нанопузыря должны одновременно удовлетворять условиям (7) и (8).

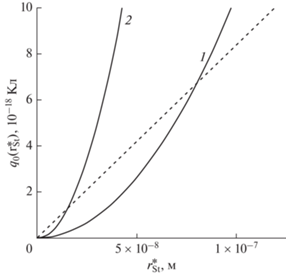
Обсудим смысл полученного графика на рис. 1. Согласно (7), ${{q}_{0}}(r_{{{\text{St}}}}^{*})$ – заряд пузыря со слоем Штерна с зарядом ${{q}_{{{\text{St}}}}} = 0$ и такого радиуса, при котором этот слой термодинамически равновесен для соответствующей концентрации с. Одновременно при анализе (8) получим, что ${{q}_{{0T}}}({{r}_{{{\text{St}}}}})$ – нижняя граница заряда пузыря с термически стабильным слоем Штерна. Поэтому в общем случае ${{q}_{{{\text{St}}}}} > 0$ стабильному слою Штерна соответствуют только значения левее и выше параболических кривых заряда пузыря над штриховой прямой, поскольку ниже нее происходит отрыв противоионов из слоя Штерна за счет их термической энергии.

Остановимся на применимости (7) и (8). Равенство (7) изначально получено при условии ${{q}_{{{\text{St}}}}}({{r}_{{{\text{St}}}}}) = 0$. С неравенством (8) ситуация сложнее. Заряд ${{q}_{{{\text{St}}}}}({{r}_{{{\text{St}}}}})$ слоя Штерна экранирует заряд пузыря q₀, согласно (1). Для определенности в [21] был принят заряд ${{q}_{{{\text{St}}}}} = 0$ из-за неизвестности его реального значения. Однако там же было показано, что величина ${{q}_{{St}}}$ на стабильность слоя Штерна не влияет. Поэтому неравенство (8) остается справедливым и при условии ${{q}_{{{\text{St}}}}}({{r}_{{{\text{St}}}}}) = 0$. Это делает возможным совместное применение (7) и (8).

Из приведенных на рис. 1 графиков видно, что крутизна зависимости заряда пузыря с термодинамически стабильным слоем Штерна от радиуса этого слоя возрастает с повышением концентрации раствора. При этом минимальные размеры критического радиуса слоя Штерна пузыря с повышением концентрации уменьшаются.

3. АНАЛИЗ ВЛИЯНИЯ КОНЦЕНТРАЦИИ СОЛЕЙ НА РАЗМЕР СЛОЯ ШТЕРНА

Понятно, что зона заряда пузыря с устойчивым слоем Штерна (термодинамически и термически) зависит от концентрации солей и лежит выше графиков, соответствующих уравнениям (7) и (8), одновременно. Приравняем эти функции и из полученного уравнения ${{q}_{0}}(r_{{{\text{St}}}}^{*}) = {{q}_{{0T}}}({{r}_{{{\text{St}}}}})$ определим с учетом (2) и (3) зависимость критического радиуса $r_{{{\text{St}}}}^{*}$ слоя Штерна от концентрации с растворенной соли:

График зависимости (9) приведен на рис. 2.

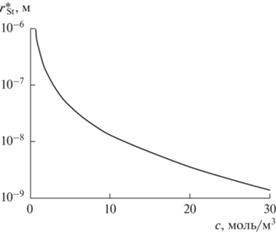
Поскольку при критическом радиусе $r_{{{\text{St}}}}^{*}$ слоя Штерна пузыря его заряд ${{q}_{{{\text{St}}}}} = 0$, то для общего случая ${{q}_{{{\text{St}}}}} > 0$ зона реальных значений $r_{{{\text{St}}}}^{*}$ ограничена сверху графиком на рис. 2.

В качестве примера укажем, что в пресной воде (с = 0.01 М) стабильны пузыри с радиусом слоя Штерна $r_{{{\text{St}}}}^{*}(c)$ < 13 нм, что близко к результату авторов [10].

ЗАКЛЮЧЕНИЕ

Проведенный анализ показал, что общего ответа о наличии или отсутствии слоя Штерна у объемных нанопузырей в воде нет. Этот слой формируется при определенных условиях: заряде и размере нанопузырей, а также концентрации раствора соли. Физическая основа этого следующая:

– стабильность слоя Штерна нанопузырей обеспечивается, когда энтропийная составляющая энергии Гиббса противоионов диффузного слоя уравновешивается кулоновской энергией противоионов, достаточной для термической устойчивости слоя Штерна;

– с ростом концентрации раствора граница стабильности смещается в сторону меньших размеров и зарядов пузыря.