Коллоидный журнал, 2023, T. 85, № 3, стр. 287-295
Оценка фактора формы агрегатов в самоассоциирующихся системах на основе металлопав
Е. П. Жильцова 1, *, Д. Р. Исламов 2, Л. Я. Захарова 1
1 Институт органической и физической химии им. А.Е. Арбузова
ФИЦ Казанский научный центр РАН
420088 Казань, ул. Акад. Арбузова 8, Россия
2 Лаборатория структурного анализа биомакромолекул, Казанский
научный центр РАН
420008 Казань, ул. Кремлевская 31, Россия
* E-mail: Zhiltsova@iopc.ru
Поступила в редакцию 20.03.2023
После доработки 07.04.2023
Принята к публикации 10.04.2023
- EDN: ZPTVOO
- DOI: 10.31857/S0023291223600177
Аннотация
На основании данных метода динамического светорассеяния для самоассоциирующихся систем на основе металлокомплексов алкилированных производных 1,4-диазабицикло[2.2.2]октана с нитратами Ag(I) и Gd(III), лиганда и смеси лиганд–неорганическая соль проведена математическая оценка фактора формы агрегатов, сформированных амфифильными соединениями в водной среде. Использованы мицеллярное и везикулярное приближения. Для везикулярных систем показана взаимосвязь фактора формы с параметрами водного пула агрегата.
ВВЕДЕНИЕ
Способность поверхностно–активных веществ (ПАВ) адсорбироваться на поверхности раздела фаз, а также образовывать в растворе надмолекулярные структуры различного типа (мицеллы, везикулы, бислои, жидкие кристаллы и т.д. [1–3]) является важным свойством амфифильных соединений и придает им и системам на их основе многочисленные практически полезные свойства. Морфологические особенности агрегатов в растворах при этом могут существенным образом отражаться на физико-химических характеристиках, а также функциональном отклике самоассоциирующихся систем. Так, формирование червеобразных мицелл влияет на вязкоупругие свойства растворов [4], а переход одной морфологической формы в другую изменяет солюбилизирующую способность агрегатов ПАВ [5, 6].
Каждой из форм характерна определенная последовательность образования при изменении концентрации ПАВ в растворе. Для мицеллярных систем наиболее распространенным считается случай, когда при достижении критической концентрации мицеллообразования (ККМ) формируются сферические мицеллы, превращающиеся из-за возрастания чисел агрегации в эллипсоидные (дискообразные, то есть сплюснутые с противоположных сторон сферы), затем в цилиндрические, и далее в пластинчатые структуры [7]. При склонности ПАВ к образованию везикул (как правило, это ПАВ с числом длинноцепных алкильных радикалов равным 2, 3 и выше) возможен также переход мицелла–везикула или сосуществование этих форм [8]. Можно отметить, что и для одноцепочечных ПАВ известны случаи переходов этих двух форм друг в друга. Так, авторы [6, 9] описали пример формирования крупных везикулярных структур в низкоконцентрированных растворах (в области критической концентрации везикулообразования, фиксируемой до ККМ), переходящих в более концентрированных растворах (при ККМ) в сферические мицеллы малого размера. Такие переходы наблюдаются для моноалкилированных анионных ПАВ и объясняются авторами образованием псевдобинарной смешанной системы из молекул амфифила, находящихся в различном состоянии из-за реализации кислотно-основных равновесий и водородного связывания. Концентрационный переход крупных везикулярных структур и нанотрубок, образуемых ПАВ с карбоксилатными головными группами, в мицеллярные (вследствие реализации межмолекулярных водородных связей) приводится также в работах [10, 11]. Помимо концентрационного фактора, на морфологические переходы в растворах ПАВ существенным образом влияет присутствие добавок (как неорганической, так и органической природы [4, 12–14]), среда (в том числе ее рН) [15, 16] и внешние условия (температура, осмотическое давление, сдвиговые поля) [17–19]. Все эти факторы, как и концентрационный, могут служить средством управления морфологией надмолекулярных образований. Примером могут выступать везикулярные системы с возможными формами в виде сфер, сплюснутых и вытянутых эллипсоидов, гантелей и т.д. [19, 20]. Поскольку везикулы являются упрощенными моделями биомембран, то проводимые в этой области исследования позволяют лучше понять связь изменения формы последних с проявляемыми биологическими функциями [19].
Можно отметить также и другой биомиметический аспект вопроса морфологических переходов. От реализации той или иной формы агрегатов в растворах ПАВ существенным образом зависит направленность и эффективность каталитического действия супрамолекулярных систем. Так, переход сферических мицелл в несферические сопровождается увеличением плотности упаковки молекул ПАВ, уменьшением диэлектрической проницаемости и более высокой степенью ионизации молекул ПАВ в агрегате, что приводит к повышению селективности реакции рециклизации четвертичных солей пиридина [21]. Помимо влияния на каталитическую активность в химических процессах (в том числе в реакции гидролитического разложения эфиров фосфорных и карбоновых кислот [22–24]), морфологические перестройки организованных систем позволяют регулировать их солюбилизационное действие по отношению к практически важным субстратам (красителям, лекарственным препаратам) [6, 25, 26].
Таким образом, вопрос установления структуры агрегатов, образующихся в растворах ПАВ, ее видоизменения в пределах одной формы (мицеллярной, везикулярной и т.д.) под действием различных факторов, и переход одной морфологической формы в другую (по типу везикула–мицелла, и т.п.) имеет не только теоретическое, но и важное практическое значение.
Экспериментальное исследование агрегации амфифильных соединений и формы надмолекулярных структур может осуществляться целым рядом физических методов, в том числе микроскопических, а также методами малоуглового рассеяния нейтронов (МУРН) и рентгеновского рассеяния (МУРР) [27]. При всей наглядности микроскопических методов для их применения, как правило, требуется твердое или замороженное жидкое состояние образца, что вносит некоторую неоднозначность в интерпретации исходной 3D-формы исследуемых объектов. К достоинствам МУРН можно отнести высокую степень проникновения в вещество, а также “мягкость” по отношению к исследуемым объектам (в том числе к биологическим). Для МУРР характерна высокая скорость накопления данных, доступность и относительная дешевизна метода. Однако к недостаткам методов малоуглового рассеяния относятся их сложность, низкая чувствительность и низкое разрешение [27].
Нами для изучения агрегатов, формирующихся в растворах ПАВ, использован доступный, не требующий сложной предварительной пробоподготовки, неразрушающий, чувствительный и быстрый метод динамического рассеяния света (ДРС). В качестве объектов исследования использованы растворы комплексов алкилированных (гексадецильных) производных 1,4-диазабицикло[2.2.2]октана (DA-BCO) – 1-гексадецил-4-аза-1-азониабицикло[2.2.2]октан нитрат (D-16(NO3)) и 1-гексадецил-4-аза-1-азониабицикло[2.2.2]октан бромид (D‑16(Br)), с нитратом Ag(I) (с соотношением металл-лиганд 1 : 1 ([D-16(NO3) ⋅ AgNO3]) и 1 : 2 ([2D-16(NO3) ⋅ AgNO3]) и нитратом Gd(III) состава металл-лиганд 1 : 1 ([D-16(Br) ⋅ Gd(NO3)3]).
Ранее спектрофотометрическим методом (солюбилизация гидрофобных красителей и лекарственных препаратов) установлено, что для исследованных ПАВ формирование агрегатов происходит в низкоконцентрационной области (0.5–0.75 мМ) [20]. О размере и предполагаемой морфологии агрегатов металлокомплексов ПАВ (металлоПАВ) в присутствии гидрофобного субстрата судили по данным метода ДРС. В растворах диалкилированного комплекса Ag(I) ([2D-16(NO3) ⋅ AgNO3]) происходит образование крупных, предположительно везикулярных структур. Для комплекса Gd(III) наблюдается концентрационный переход везикула–мицелла. Возможной причиной различий в концентрационном изменении морфологии комплексов Ag(I) и Gd(III), по-видимому, может быть более значительный вклад неблагоприятного электростатического взаимодействия головных групп последнего в процесс агрегации в системе и в формирование крупных надмолекулярных структур.
В настоящей работе на основании данных метода ДРС проведена математическая оценка фактора формы агрегатов металлоПАВ. Разработанный подход применен также для растворов лиганда и смеси лиганд–неорганическая соль.
ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
Реагенты и материалы
Лиганд D-16(Br) получен кватернизацией 1,4-диазабицикло[2.2.2]октана гексадецилбромидом по методике [28]. Лиганд D-16(NO3) синтезирован взаимодействием лиганда D-16(Br) с нитратом серебра по реакции ионного обмена путем перемешивания в метаноле при комнатной температуре исходных реагентов и удаления выпавшего в осадок бромида серебра. Комплексы [D-16(NO3) ⋅ AgNO3] и [2D-16(NO3) ⋅ AgNO3] получены в метаноле при 25°С в отсутствие света путем взаимодействия лиганда D-16(NO3) с нитратом серебра при мольном соотношении, соответственно, 1 : 1 и 2 : 1 и последующем фильтровании выпавшего в осадок комплекса. Синтез комплекса [D-16(Br) ⋅ Gd(NO3)3] с участием D-16(Br) и нитрата гадолиния проведен путем перемешивания эквимольного количества лиганда и неорганической соли при нагревании реакционной смеси в метаноле (50°С) с последующей промывкой целевого продукта этилацетатом. Состав продуктов подтвержден данными элементного анализа, ИК-спектроскопии и спектроскопии ЯМР 1Н.
Неорганические соли AgNO3 (99.9%, ACS) и Gd(NO3)3 ⋅ 6H2O (99.9%, Alfa Aesar) применяли без предварительной очистки. Для приготовления растворов использовали воду, очищенную с помощью системы Direct-Q 5 UV (Millipore S.A.S., Франция).
Методы исследования
Размеры агрегатов определяли с использованием системы для характеристики наночастиц “Malvern Zetasizer Nano” (Великобритания). Угол рассеяния света составлял 173°. Источником лазерного излучения служил газовый He-Nе–лазер c длиной волны 633 нм. Исследуемые растворы ПАВ перед измерениями пропускали через фильтры Millipore Millex (0.45 мкм).
РЕЗУЛЬТЫ И ОБСУЖДЕНИЕ
Метод ДРС с использованием системы для характеристики наночастиц “Malvern Zetasizer Nano” (Великобритания) позволяет путем измерения автокорреляционной функции (с помощью программного обеспечения Malvern DTS) находить экспериментальный коэффициент трансляционной диффузии (Dt,эфф) частиц. Для сферических частиц экспериментальный (эффективный) гидродинамический диаметр (dH,эксп) агрегатов рассчитывается по уравнению Стокса–Эйнштейна (1):
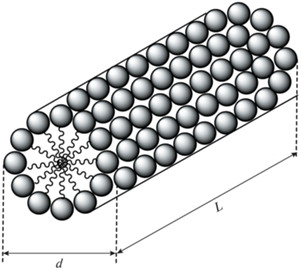
где kB – постоянная Больцмана, T – абсолютная температура, η – вязкость растворителя.Для цилиндрических мицеллярных агрегатов (рис. 1), согласно [29–31], выполняются уравнения (2)–(4):
(2)
${{D}_{{{\text{t,эфф}}}}} = {\text{ }}{{k}_{B}}T({\text{ln}}{\kern 1pt} 2p--{{\gamma }_{t}}){\text{/}}3\pi \eta L,$Из уравнений (1)–(4) следует математическая связь определяемого экспериментально в сферическом приближении значения dH,эксп (уравнение (1)) с фактором формы цилиндрической мицеллы p (уравнение (5)).
(5)
$1{\text{/}}{{d}_{{{\text{H,эксп}}}}} = {\text{ }}({\text{ln}}{\kern 1pt} 2p--0.373 + 0.57{\text{/}}p){\text{/}}2p{{R}_{{{\text{ПАВ}}}}}.$Исходя из уравнения (5), значение фактора формы p математически может быть найдено путем нахождения минимального (стремящегося к нулевому) значения величины Δмиц, описываемой уравнением (6).
(6)
$\begin{gathered} {{\Delta }_{{{\text{миц}}}}} = {\text{ }}({\text{ln}}2p--0.373 + \\ + \,\,0.57{\text{/}}p){\text{/}}2p{{R}_{{{\text{ПАВ}}}}}--1{\text{/}}{{d}_{{{\text{H,эксп}}}}}. \\ \end{gathered} $На рис. 2 приведен пример распределения частиц по размерам, а в табл. 1 и 2 значения dH,эксп, индекс полидисперсности (PdI), а также значения р, рассчитанные по уравнению (6), отвечающему цилиндрической форме агрегатов, формирующихся в водных растворах комплексов гексадецильных производных DABCO с нитратами Ag(I) и Gd(III). Использованные в расчетах значения RПАВ составляли для комплексов Ag(I) 2.594 нм, (с учетом длины алкильной цепи (C16H33) 2.1 нм [32], расстояния между атомами азота в бициклическом фрагменте 0.264 нм [33] и определенной по данным РСА длины связи N…Ag 0.23 нм), для лигандов 2.364 нм, для комплекса Gd(III) 2.629 нм (с учетом размера лиганда и среднего для известных из литературы комплексов гадолиния значения длины связи Gd(III)…N 0.265 нм [34, 35]). Расчет фактора формы проводили при достижении значений Δмиц порядка 10–6–10–5, и ошибка определения р составляла не более 0.15%. Из представленных в табл. 2 значений р видно, что для системы на основе комплекса гадолиния и смешанной системы D-16(Br)–Gd(NO3)3 ⋅ 6H2O (1 : 1) небольшие агрегаты с размером порядка 4–8 нм, отвечающие мицеллярным структурам, характеризуются фактором формы в диапазоне 0.68–2.2 и могут иметь форму, близкую к сферической (р = = 0.68–0.99) или к цилиндрической (р = 2.2). Более крупные образования комплекса Gd(III) с эффективным гидродинамическим диаметром 75 нм, а также системы на основе комплексов Ag(I), лиганда D-16(NO3) и его смеси с неорганической солью Ag(NO3)3 с диаметром порядка 50–143 нм имеют рассчитанный фактор формы в пределах 43–149 (табл. 1, 2), то есть гипотетически могут иметь форму червеобразных мицелл. Если для алкилированного D-16 образование последних возможно [36], то, согласно данным методов просвечивающей электронной микроскопии (ПЭМ) и атомной силовой микроскопии (АСМ), крупные агрегаты металломицеллярных систем на основе амфифильных комплексов DABCO с солями переходных металлов (Cu(II), Ni(II), Co(II), La(III)) лишь в редких случаях имеют вид нитевидных разветвленных структур различной длины (комплексы D-16(Br) c нитратами никеля и кобальта) [37]. Наиболее характерной формой агрегатов для этих металлоПАВ может быть названа существенно менее асимметричная везикулярная сфероподобная (комплексы [D-16(Br) ⋅ CuBr2], [D-14(Br) ⋅ ⋅ La(NO3)3], [2D-18(Br) ⋅ La(NO3)3] [2, 36, 38]) или овальная форма с соотношением осей, как правило, в пределах 2–5 (комплексы [2D-16(Br) ⋅ ⋅ La(NO3)3] и [2D-18(Br) ⋅ La(NO3)3] [2, 38]). В связи с этим для крупных агрегатов металлоПАВ серебра и гадолиния был проведен дополнительный расчет фактора формы систем, исходя из везикулярного приближения. В рамках последнего значение d агрегата (то есть dвезик) будет равно не удвоенному размеру молекулы ПАВ (как в случае мицеллы, рис. 1), а выражаться через уравнение (7), учитывающеe бислойный характер агрегата, а также размер водного пула (dпул).
Рис. 2.
Кривая распределения частиц по размерам для металлокомплекса [2D-16(NO3) ⋅ AgNO3], СПАВ = = 1.0 мМ, 37°С.
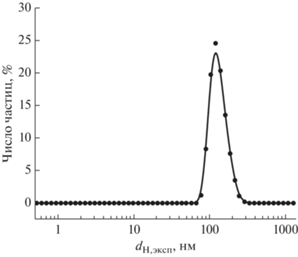
Таблица 1.
Фактор формы агрегатов комплексов [2D-16(NO3) ⋅ AgNO3] и [D-16(NO3) ⋅ AgNO3], лиганда D-16(NO3) и смеси D-16(NO3)–AgNO3 (1 : 1) в воде при 37°С, рассчитанный по формуле (6), отвечающей мицеллярному приближению для предполагаемой цилиндрической формы мицелл, и значение параметра dпул,max для расчетов фактора формы в везикулярном приближении
| Соединение | C, мM | dH,эксп (по числу ч-ц), нм | PdI | р | dпул,max, нм |
|---|---|---|---|---|---|
| [2D-16(NO3) ⋅ AgNO3] | 1.0 | 136 | 0.151 | 137.8 | 125.6 |
| 10 | 143 | 0.124 | 146.6 | 132.6 | |
| [D-16(NO3) ⋅ AgNO3] | 1.0 | 63 | 0.220 | 52.1 | 52.6 |
| 10 | 56 | 0.361 | 44.6 | 45.6 | |
| D-16(NO3) | 1.0 | 84; (390)а | 0.448 | 84.6б | 74.5б |
| 10 | 132 | 0.199 | 148.6 | 122.5 | |
| D-16(NO3)–AgNO3 (1 : 1) | 1.0 | 80 | 0.253 | 79.5 | 70.5 |
| 10 | 50 | 0.243 | 43.3 | 40.5 |
Таблица 2.
Фактор формы агрегатов комплекса [D-16(Br) ⋅ Gd(NO3)3] и смеси D-16(Br)–Gd(NO3)3 ⋅ 6H2O (1 : 1) в воде при 25°С, рассчитанный по формуле (6), отвечающей мицеллярному приближению для предполагаемой цилиндрической формы мицелл
| Соединение | C, мM | dH,эксп (по числу ч-ц), нм |
PdI | р |
|---|---|---|---|---|
| [D-16(Br) ⋅ Gd(NO3)3] | 0.6 | 75; (281)а | 0.387 | 64.0б |
| 30 | 5.9 | 0.354 | 0.99 | |
| D-16(Br)–Gd(NO3)3 ⋅ 6H2O (1 : 1) | 1.0 | 4.2 | 0.393 | 0.69 |
| 10 | 4.9 | 0.310 | 0.86 | |
| 30 | 7.7 | 0.175 | 2.2 |
В этом случае уравнение (6) принимает вид уравнения (8):
(8)
$\begin{gathered} {{\Delta }_{{{\text{везик}}}}} = ({\text{ln}}2p--0.373 + \\ + \,\,0.57{\text{/}}p){\text{/}}p(4{{R}_{{{\text{ПАВ}}}}} + {{d}_{{{\text{пул}}}}})--1{\text{/}}{{d}_{{{\text{H,эксп}}}}}, \\ \end{gathered} $В предельном варианте можно считать, что в уравнении (8)
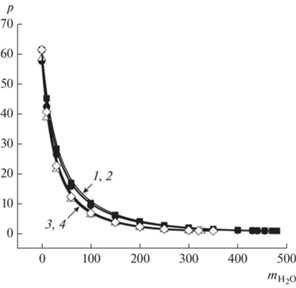
где m – число молекул воды между противоположно расположенными частями бислоя везикулы, ${{d}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{О}}}}}$ – эффективный диаметр молекулы воды.В литературе встречаются разные трактовки ${{d}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{О}}}}}$, то есть эффективного диаметра воды. В случае если это минимальное расстояние, на которое сближаются центры двух молекул при столкновении [39], его значение равно 0.276 нм [40]. Если в качестве эффективного радиуса молекулы воды принимается радиус шара, объем которого равен абсолютному мольному объему воды при 25°С, приходящемуся на одну молекулу, то он равен 0.193 нм, а диаметр, соответственно, 0.386 нм [41]. На рис. 3 приведен пример рассчитанной по уравнениям (8) и (9) зависимости р = f(m) как для ${{d}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{О}}}}}$, равного 0.276 нм, так и для 0.386 нм. При этом сделано допущение незначительного различия ${{d}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{О}}}}}$ при 25°С и при использованной нами для комплексов серебра температуре 37°С. Полученные в обоих случаях значения фактора формы отличаются незначительно. Кроме того, прослеживается существенная зависимость параметра р от числа m.
Рис. 3.
Зависимость фактора формы р от параметра m (уравнения (8) и (9)) для металлокомплекса [2D-16(NO3) ⋅ AgNO3] для значений ${{d}_{{{{{\text{Н}}}_{{\text{2}}}}{\text{О}}}}}$ = 0.276 (1, 2) и 0.386 нм (3, 4), СПАВ (мМ): 1.0 (1, 3), 10 (2, 4), 37°C.
Однако уравнение (9) отражает лишь частную, причем трудно реализуемую ситуацию в системах. В связи с этим для основных расчетов использовано исходное уравнение (8). На рис. 4–6 представлены определенные по нему значения фактора формы агрегатов (везикул) р комплексов при dпул в диапазоне от нуля до dпул,max, а также гипотетических везикулярных образований лиганда и его смеси с нитратом серебра. За максимальное (dпул,max) принимается значение, при котором dвезик = dH,эксп, и выполняется равенство (10):
из которого следует, чтоРис. 4.
Зависимость фактора формы р от параметра dпул в уравнении (8) для металлокомплекса [2D-16(NO3) ⋅ AgNO3], СПАВ (мМ): 1.0 (1), 10 (2), 37°C. На вставке приведен участок зависимостей для значений dпул, близких к dпул,max.
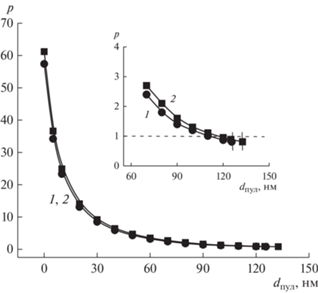
Рис. 5.
Зависимость фактора формы р от параметра dпул в уравнении (8) для металлокомплексов [D-16(NO3) ⋅ Ag-NO3] (1, 2) и [D-16(Br) ⋅ Gd(NO3)3] (3), СПАВ (мМ): 1.0 (1), 10 (2), 0.6 (3), 37°C (1, 2), 25°C (3). На вставке приведен участок зависимостей для значений dпул, близких к dпул,max.
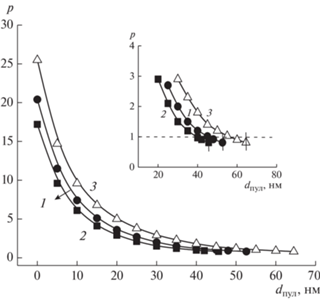
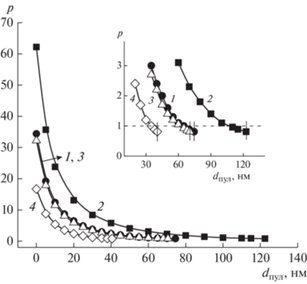
Рис. 6.
Зависимость фактора формы р от параметра dпул в уравнении (8) для лиганда D-16(NO3) (1, 2) и смеси D-16(NO3)–AgNO3 (1 : 1) (3, 4), СПАВ (мМ): 1.0 (1, 3), 10 (2, 4), 37°C. На вставке приведен участок зависимостей для значений dпул, близких к dпул,max.
Значения dпул,max для агрегатов комплексов Ag(I) и лиганда приведены в табл. 1. Для комплекса Gd(III) (при СПАВ = 0.6 мМ) dпул,max равно 64.5 нм.
Согласно приведенным на рис. 4 и 6 данным, для рассматриваемых систем нулевым значениям dпул отвечают р в пределах 17–62. Можно отметить также, что для всех зависимостей р = f(dпул) на начальном участке (для dпул со значениями от 0 до 20–60 нм) характерно резкое снижение параметра р, тогда как для диапазона с более высокими значениями dпул и вплоть до dпул,max (последние на вставках рис. 4, 6 обозначены вертикальными реперными линиями), падение р существенно замедляется, и при приближении к dпул,max фактор формы становится близким к единице. Поскольку степень заполняемости водного пула должна стремиться к максимальной, то для крупных агрегатов рассматриваемых металлоПАВ наиболее вероятными значениями фактора формы можно считать те значения, которые отвечают dпул, близким к dпул,max, то есть с р в пределах порядка 0.8–3 (рис. 4, 5). Это соответствует везикулярным образованиям с низкой степенью асимметрии и согласуется с ранее полученными результатами для систем на основе металлокомплексов алкилированных DABCO [2, 36, 38]. Аналогичный результат получен также и для систем на основе лиганда и его смеси с нитратом серебра (рис. 6).
ЗАКЛЮЧЕНИЕ
Таким образом, использованный подход, предусматривающий знание диаметра агрегатов, определенного методом динамического светорассеяния, и размера молекул амфифильного соединения, позволяет проводить количественный анализ фактора формы мицелл и везикул. Для рассмотренных систем на основе комплекса гадолиния и смеси D-16(Br)–Gd(NO3)3 (1 : 1) мицеллярные структуры небольшого размера (до 8 нм) могут иметь как близкую к сферической (с р в диапазоне 0.7–0.99), так и несколько асимметричную овальную форму (при р 2.2). Для крупных агрегатов комплекса гадолиния(III), а также моно- и диалкилированного металлоПАВ Ag(I) анализ значений фактора формы надмолекулярных структур проведен, исходя из их везикулярной природы. Установлена зависимость степени асимметрии везикул как от значения определенного методом ДРС эффективного диаметра агрегата, так и размера водного пула.
Список литературы
Русанов А.И., Щёкин А.К. Мицеллообразование в растворах поверхностно-активных веществ. 2-ое изд. СПб.: Лань, 2016.
Zakharova L.Ya., Voloshina A.D., Ibatullina M.R., Zhiltsova E.P., Lukashenko S.S., Kuznetsova D.A., Kutyreva M.P., Sapunova A.S., Kufelkina A.A., Kulik N.V., Kataeva O., Ivshin K.A., Gubaidullin A.T., Salnikov V.V., Nizameev I.R., Kadirov M.K., Sinyashin O.G. Self-assembling metallocomplexes of the amphiphilic 1,4-diazabicyclo[2.2.2]octane derivative as a platform for the development of nonplatinum anticancer drugs // ACS Omega. 2022. V. 7. № 3. P. 3073–3082. https://doi.org/10.1021/acsomega.1c06465
Карпичев Е.А., Захарова Л.Я., Гайсин Н.К., Гнездилов О.И., Жильцова Е.П., Паширова Т.Н., Лукашенко С.С., Аникеев А.В., Горбань О.А., Коновалов А.И., Попов А.Ф. Самоорганизация симметричных и диссимметричных дикатионных ПАВ в твердой фазе и в растворе // Изв. АН. Сер. хим. 2014. № 1. С. 68–75.
Квятковский А.Л., Молчанов В.С., Филиппова О.Е. Полимероподобные червеобразные мицеллы ионогенных поверхностно-активных веществ: структура и реологические свойства // Высокомолек. соед. Сер. А. 2019. Т. 61. № 2. С. 180–192. https://doi.org/10.1134/S0965545X19020081
Walter A., Kuehl G., Barnes K., VanderWaerdt G. The vesicle-to-micelle transition of phosphatidylcholine vesicles induced by nonionic detergents: Effects of sodium chloride, sucrose and urea // Biochimica et Biophysica Acta, Biomembranes. 2000. V. 1508. № 1–2. P. 20–33. https://doi.org/10.1016/S0304-4157(00)00005-8
Sakai T., Ikoshi R., Toshida N., Kagaya M. Thermodynamically stable vesicle formation and vesicle-to-micelle transition of single-tailed anionic surfactant in water // J. Phys. Chem. B. 2013. V. 117. № 17. P. 5081–5089. https://doi.org/10.1021/jp402314f
Захарченко В.Н. Коллоидная химия. 2-ое изд. М.: Высшая школа, 1989.
Koutsantonis G.A., Nealon G.L., Buckley C.E., Paskevicius M., Douce L., Harrowfield J.M., McDowall A.W. Wormlike micelles from a cage amine metallosurfactant // Langmuir. 2007. V. 23. № 24. P. 11986–11990. https://doi.org/10.1021/la701283b
Sakai T., Miyaki M., Tajima H., Shimizu M. Precipitate deposition around CMC and vesicle-to-micelle transition of monopotassium monododecyl phosphate in water // J. Phys. Chem. B. 2012. V. 116. № 36. P. 11225–11233. https://doi.org/10.1021/jp307070e
Roy S., Dey J. Self-organization and microstructures of sodium 11-acrylamidoundecanoate in water // Langmuir. 2003. V. 19. № 23. P. 9625–9629. https://doi.org/10.1021/la0348113
Ohta A., Danev R., Nagayama K., Mita T., Asakawa T., Miyagishi S. Transition from nanotubes to micelles with increasing concentration in dilute aqueous solution of potassium N-acyl phenylalaninate // Langmuir. 2006. V. 22. № 20. P. 8472–8477. https://doi.org/10.1021/la0611110
Kwiatkowski A.L., Molchanov V.S., Orekhov A.S., Vasiliev A.L., Philippova O.E. Impact of salt co- and counterions on rheological properties and structure of wormlike micellar solutions // J. Phys. Chem. B. 2016. V. 120. № 49. P. 12547–12556. https://doi.org/10.1021/acs.jpcb.6b09817
Valeeva F.G., Vasilieva E.A., Gaynanova G.A., Kashapov R.R., Zakharov S.V., Kuryashov D.A., Lukashenko S.S., Bashkirtseva N.Y., Zakharova L.Y. Supramolecular systems based on hydrotropes, their analogues and mixtures with typical surfactants. Structural behavior, enhanced solubilization and viscosity properties // J. Mol. Liq. 2015. V. 203. P. 104–110. https://doi.org/10.1016/j.molliq.2014.12.027
Vaid Z.S., Kumar A., El Seoud O.A., Malek N.I. Drug induced micelle-to-vesicle transition in aqueous solutions of cationic surfactants // RSC Advances. 2017. № 7. P. 3861–3869. https://doi.org/10.1039/c6ra25577a
Zhou Q., Gao D., Liu J., Sun X., Zhang L., Qi B., Zhang H., Xia C., Zhou X. Transformation of micelles into supramolecular vesicles triggered by the formation of [4]pseudorotaxanes // J. Colloid Interface Sci. 2013. V. 410. P. 131–139. https://doi.org/10.1016/j.jcis.2013.08.019
Yan Z., Dai C., Zhao M., Zhao G., Li Yu., Wu X., Du M., Liu Y. pH-switchable wormlike micelle formation by N-alkyl-N-methylpyrrolidinium bromide-based cationic surfactant // Colloids Surf. A. 2015. V. 482. P. 283–289. https://doi.org/10.1016/j.colsurfa.2015.06.019
Мицеллообразование, солюбилизация и микроэмульсии / Под ред. Миттела К.Л. М.: Мир, 1980.
Кузнецов В.С., Жердев В.П., Баделин В.Г., Жердева В.В. Термодинамика и структура мицелл в водных растворах додецилсульфата натрия в области третьей критической концентрации мицеллообразования // Журн. физ. химии. 2019. Т. 93. № 8. С. 1175–1181. https://doi.org/10.1134/S0044453719080156
Wang C., Guo Y.-K., Tian W.-D., Chen K. Shape transformation and manipulation of a vesicle by active particles // J. Chem. Phys. 2019. V. 150. P. 044907. https://doi.org/10.1063/1.5078694
Жильцова Е.П., Ибатуллина М.Р., Сафина Н.Х., Захарова Л.Я. Самоассоциирующиеся системы комплексов алкилированных 1,4-диазабицикло[2.2.2]октанов с Ag(I) и Gd(III) для увеличения растворимости гризеофульвина и Оранж ОТ // Журн. общей химии. 2022. Т. 92. № 4. С. 640–651.
Спутникова Т.В., Сердюк А.И., Калафат В.Н., Сагитуллин P.C., Марштупа В.П. Влияние мицеллообразования четвертичных солей пиридина на их рециклизацию в анилины // Химия гетероциклических соединений. 1981. № 4. С. 508–510.
Zhiltsova E.P., Ibatullina M.R., Kashapov R.R., Kashapova N.E., Ziganshina A.Yu., Zakharova L.Ya., Sinyashin O.G. Supramolecular metal-modified nanocontainers based on amphiphilic and hybrid matrix: Self-assembling behavior and practical applications // Metallosurfactants: From Fundamentals to Catalytic and Biomedical Applications. Chapter 12. Ed. by Mehta S.K., Kaur R. Weinheim: Wiley-VCH GmbH, 2022. P. 223–248. https://doi.org/10.1002/9783527831289.ch12
Onel L., Buurma N.J. Reactivity in organised assemblies // Annual Reports Progress Chem., Sect. B: Org. Chem. 2009. V. 105. P. 363–379. https://doi.org/10.1039/b905116n
Миргородская А.Б., Кушназарова Р.А., Кузнецов Д.М., Тырышкина А.А., Захарова Л.Я. Агрегационное поведение и каталитическое действие карбаматсодержащих ПАВ в водных средах // Кинетика и катализ. 2022. Т. 63. № 3. С. 309–319. https://doi.org/10.31857/S0453881122030108
Ибатуллина М.Р., Жильцова Е.П., Лукашенко С.С., Захарова Л.Я. Супрамолекулярные системы металлокомплексов 1-цетил-4-аза-1-азониабицикло[2.2.2]октан бромида для увеличения растворимости гризеофульвина // Коллоид. журн. 2020. Т. 82. № 1. С. 18–25. https://doi.org/10.1134/S0023291220010061
Яцкевич Е.И., Миргородская А.Б., Захарова Л.Я., Синяшин О.Г. Растворимость и гидролитическая устойчивость индометацина в водных мицеллярных растворах // Изв. АН. Сер. хим. 2015. № 9. С. 2232–2237.
Куклин А.И., Иваньков О.И., Рогачев А.В., Соловьев Д.В., Исламов А.Х., Ской В.В., Ковалев Ю.С., Власов А.В., Рижиков Ю.Л., Соловьев А.Г., Кучерка Н., Горделий В.И. Малоугловое рассеяние на импульсном источнике нейтронов ИБР-2: настоящее и будущее // Кристаллография. 2021. Т. 66. № 2. С. 230–241. https://doi.org/10.31857/S0023476121020089
Паширова Т.Н., Жильцова Е.П., Кашапов Р.Р., Лукашенко С.С., Литвинов А.И., Кадиров М.К., Захарова Л.Я., Коновалов А.И. Супрамолекулярные системы на основе 1-алкил-4-аза-1-азониабицикло[2.2.2]октанбромидов // Изв. АН. Сер. хим. 2010. № 9. С. 1699–1706.
Nicoli D.F., Ellas J.G., Eden D. Transient electric birefringence study of CTAB micelles. Implications for rodlike growth // J. Phys. Chem. 1981. V. 85. № 20. P. 2866–2869. https://doi.org/10.1021/j150620a002
Tirado M.M., De la Torre J.G. Translational friction coefficients of rigid, symmetric top macromolecules. Application to circular cylinders // J. Chem. Phys. 1979. V. 71. № 6. P. 2581–2587. https://doi.org/10.1063/1.438613
Мовчан Т.Г., Соболева И.В., Плотникова Е.В., Щекин А.К., Русанов А.И. Исследование методом динамического рассеяния света водных растворов бромида цетилтриметиламмония // Коллоид. журн. 2012. Т. 74. № 2. С. 257–265.
Спиридонов А.М., Апросимова Е.В., Заболоцкий В.И., Федосеева В.И., Соколова М.Д., Охлопкова А.А. Адсорбция цетилтриметиламмоний бромида на поверхности цеолита // Журн. физ. химии. 2019. Т. 93. № 5. С. 722–729. https://doi.org/10.1134/S0044453719050285
Wada T., Kishida E., Tomiie Y., Suga H., Seki S., Nitta I. Crystal structure and thermodynamical investigations of triethylenediamine, C6H12N2 // Bull. Chem. Soc. Jpn. 1960. V. 33. № 9. P. 1317–1318. https://doi.org/10.1246/bcsj.33.1317
Wang R.-Y., Zhang H.-J., Jin T.-Z., Zhou Z.-Y., Zhou X.-G. Synthesis and crystal structure of gadolinium mononuclear complex with triethylenetetraaminehexaacetic acid // Chem. J. Chin. Univ. 1999. V. 20. № 2. P. 176–180.
Конник О.В., Бекирова З.З., Шульгин В.Ф., Минин В.В., Александров Г.Г., Еременко И.Л. Координационные соединения гадолиния с диацилдигидразонами 3-метил-1-фенил-4-формилпиразол-5-она // Изв. высших учебных заведений. Химия и химическая технология. 2014. Т. 57. № 2. С. 10–14.
Жильцова Е.П., Ибатуллина М.Р., Лукашенко С.С., Паширова Т.Н., Волошина А.Д., Зобов В.В., Зиганшина С.А., Кутырева М.П., Захарова Л.Я. Комплекс 1-гексадецил-4-аза-1-азониабицикло[2.2.2]октанбромида с дибромидом меди. Структура, агрегация и биологическая активность // Изв. АН. Сер. хим. 2016. № 5. С. 1365–1371.
Ибатуллина М.Р., Жильцова Е.П., Лукашенко С.С., Волошина А.Д., Сапунова А.С., Ленина О.А., Низаме-ев И.Р., Кутырева М.П., Захарова Л.Я. Металломицеллярные системы на основе комплексов 1-гексадецил-4-аза-1-азониабицикло[2.2.2]октанбромида с нитратами переходных металлов // Журн. общей химии. 2018. Т. 88. № 11. С. 1883–1892. https://doi.org/10.1134/S0044460X18110185
Жильцова Е.П., Ибатуллина М.Р., Лукашенко С.С., Низамеев И.Р., Кадиров М.К., Захарова Л.Я. Каталитические системы на основе металлокомплексов 1-алкил-4-аза-1-азониабицикло[2.2.2]октан бромидов // Кинетика и катализ. 2020. Т. 61. № 2. С. 247–253. https://doi.org/10.31857/S0453881120010165
Леденев А.Н. Физика. Книга 2. Молекулярная физика и термодинамика. М.: Физматлит, 2005.
Багоцкий В.С. Основы электрохимии. М.: Химия, 1988.
Мищенко К.П., Полторацкий Г.М. Термодинамика и строение водных и неводных растворов электролитов. 2-ое изд. Л.: Химия, 1976.
Дополнительные материалы отсутствуют.
Инструменты
Коллоидный журнал