1. На главную
  2. Электронные версии
  3. Координационная химия
  4. T. 45, № 2, 2019

Координационная химия, 2019, T. 45, № 2, стр. 92-98

Компьютерное моделирование спин-кроссовера в смешанолигандных биядерных комплексах железа и кобальта с 5,6-бис(салицилиденимино)-1,10-фенантролином

А. Г. Стариков 1, А. А. Старикова 1, *, М. Г. Чегерев 1, В. И. Минкин 1

1 Научно-исследовательский институт физической и органической химии Южного федерального университета
Ростов-на-Дону, Россия

* E-mail: alstar@ipoc.sfedu.ru

Поступила в редакцию 19.06.2018
После доработки 24.08.2018
Принята к публикации 17.08.2018

Полный текст (PDF)

Аннотация

Проведено квантово-химическое моделирование (DFT UTPSSh/6-311++G(d,p)) биядерных гомо- и гетерометаллических комплексов Fe и Co, сконструированных на основе 5,6-бис(салицилиден-имино)-1,10-фенантролинового лиганда и двух молекул дипиридила. Показано, что магнитные свойства таких соединений могут переключаться в результате протекания термически наведенного спин-кроссовера на ионах кобальта. Предсказанные энергетические и магнитные характеристики изомеров изученных систем позволяют рассматривать их в качестве перспективных молекулярных переключателей.

Ключевые слова: комплексы железа, комплексы кобальта, спин-кроссовер, магнитные свойства, квантово-химическое моделирование

Спин-кроссовер (СКО) – детально изученный эффект, приводящий к проявлению координационными соединениями переходных металлов магнитно-активных свойств [1]. На молекулярном уровне он заключается в изменении спинового состояния металлоцентра, вызванном воздействием температуры, давления, облучения или магнитного поля. Использование механизма СКО в качестве движущей силы, приводящей к переключению спиновых состояний комплексов переходных металлов – одно из активно развиваемых направлений в координационной химии [2–5]. Комплексы, демонстрирующие такое поведение, могут найти применение при разработке молекулярных переключателей и памяти с магнитной функцией отклика, сенсоров и устройств отображения информации, квантовых битов [6–8].

Наиболее широкий класс соединений, восприимчивых к СКО перегруппировкам, представлен псевдооктаэдрическими комплексами двухвалентного железа с N-донорными лигандами [9–11]. Менее изучены кобальтовые системы, в которых подходящая для реализации СКО сила поля лигандов достигается в молекулах с пентакоординированным центральным атомом, типичным примером которых являются моноаддукты бис-салицилидениминатов Сo(II) с азотсодержащими основаниями [12–15], а также в комплексах с шестью донорными атомами азота [16–20].

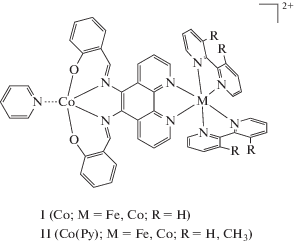
Выполненные ранее теоретические исследования биядерных координационных соединений, претерпевающих СКО переходы, показали перспективность таких систем при разработке элементной базы устройств молекулярной электроники и спинтроники [21, 22]. В настоящей работе посредством квантово-химического моделирования исследованы смешанолигандные биядерные комплексы I (Co; M = Fe, Co; R = H) и II (Co(Py); M = Fe, Co; R = H, CH3) c 5,6-бис(салицилиден-имино)-1,10-фенантролином [23], в которых координационные узлы металлов M достроены молекулами дипиридила.

МЕТОДИКА РАСЧЕТОВ

Расчеты проводили с помощью программы Gaussian 09 [24] методом теории функционала плотности (DFT) с использованием функционала UTPSSh [25, 26] и расширенного базиса 6‑311++G(d,p), корректно воспроизводящих энергетические характеристики СКО в катионных комплексах [27–31]. Согласно полученным в данном приближении результатам, спиновые переходы ожидаются на ионе Fe2+ при ΔEHS–LS < < 11 ккал/моль [27, 28] и на Сo2+ при ΔEHS–LS < < 5 ккал/моль [29, 30]. Локализацию стационарных точек на поверхности потенциальной энергии (ППЭ) осуществляли путем полной оптимизации геометрии молекулярных структур с проверкой стабильности DFT волновой функции. Вычисление параметров обменного взаимодействия (J, см–1) проводили в рамках формализма “нарушенной симметрии” (broken symmetry – BS) [32] с использованием формулы Ямагучи [33] посредством расчета всех возможных спиновых состояний. Графические изображения молекулярных структур получали при помощи программы ChemCraft [34].

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

С целью оценки характера и силы обменных взаимодействий между парамагнитными центрами и принципиальной возможности протекания СКО на ионах железа и кобальта, связанных дипиридильными лигандами, изучены модельные системы I (Co; M = Fe, Co; R = H), не содержащие координированной молекулы пиридина (рис. 1). Как следует из результатов расчетов, разность энергий между изомерами LSCoII–LSFeII и LSCoII–HSFeII, различающимися спиновыми состояниями иона железа, превышает 11 ккал/моль (табл. 1), что не позволяет ожидать СКО перегруппировки. В гомометаллическом комплексе I (Co; M = Co; R = H) электронно-возбужденная структура LSCoII–HSСоII и основное состояние LSCoII–LSСоII практически изоэнергетичны (ΔEHS–LS = 0.5 ккал/моль). Следовательно, оба изомера обсуждаемого соединения могут сосуществовать в равновесии. Предсказанное слабое антиферромагнитное связывание в высокоспиновом электромере и отсутствие обменных взаимодействий между металлоцентрами в структуре LSCoII–LSСоII свидетельствуют о парамагнетизме комплекса в широком диапазоне температур. Таким образом, соединение I (Co; M = Co; R = H) может представлять интерес как основа молекулярного переключателя с магнитной функцией отклика.

Рис. 1.

Оптимизированные геометрии изомеров комплексов I (Co; M = Fe, Co; R = H), рассчитанные методом DFT UTPSSh/6-311++G(d,p). Здесь и далее атомы водорода опущены для ясности, длины связей даны в ангстремах, стрелками показан возможный СКО переход, все структуры имеют заряд +2.

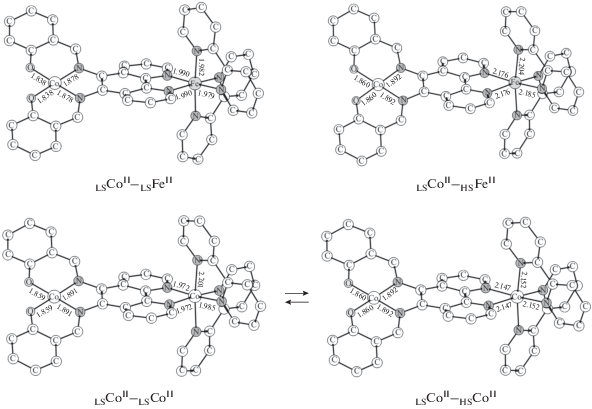
Таблица 1.

Спин (S), полная энергия (Еполн), относительная энергия (ΔE), значения оператора квадрата спина (S2), спиновая плотность на ионе кобальта в бис-салицилиденовом фрагменте $(q_{{\text{s}}}^{{{\text{Co}}}})$ и ионе металла M в октаэдрическом окружении $\left( {q_{{\text{s}}}^{{\text{M}}}} \right)$, величина параметра обменных взаимодействий (J) в изомерах комплексов I (Co; M = = Fe, Co; R = H) и II (Co(Py); M = Fe, Co; R = H, CH3), рассчитанные методом DFT UTPSSh/6-311++G(d,p)

Структура S Еполн, ат. ед. ΔЕ*, ккал/моль S2 $q_{{\text{s}}}^{{{\text{Co}}}}$ qsM J, см–1
I (Co; M = Fe; R = H)
LSCoII–LSFeII 1/2 –5007.64903 0.0 0.773 1.07 0.00  
LSCoII–HSFeII 5/2 –5007.62467 17.8 8.800 1.07 3.75 –6
LSCoII–HSFeII BS 3/2 –5007.62478   4.789      
I (Co; M = Co; R = H)
LSCoII–LSСоII 2/2 –5126.67374 0.0 2.020 1.00 0.89 0
LSCoII–LSСоII BS 0 –5126.67374   1.021      
LSCoII–HSСоII 4/2 –5126.67293 0.5 6.021 1.00 2.25 1
LSCoII–HSСоII BS 2/2 –5126.67293   3.021      
II (Co(Py); M = Fe; R = CH3)
LSCoII(Py)–LSFeII 1/2 –5413.34042 0.0 0.764 0.84 0.00  
LSCoII(Py)–HSFeII 5/2 –5413.32035 12.6 8.789 0.83 3.41 2
LSCoII(Py)–HSFeII BS 3/2 –5413.32032   4.787      
HSCoII(Py)–LSFeII 3/2 –5413.33253 3.3 3.768 2.55 0.00  
HSCoII(Py)–HSFeII 7/2 –5413.31252 17.5 15.793 2.55 3.43 0
HSCoII(Py)–HSFeII BS 1/2 –5413.31251   3.791      
II (Co(Py); M = Co; R = H)
LSCoII(Py)–LSСoII 2/2 –5375.06589 0.0 2.025 0.85 0.89 1
LSCoII(Py)–LSСoII BS 0 –5375.06589   1.024      
LSCoII(Py)–HSСoII 4/2 –5375.06469 0.8 6.025 0.83 2.41 2
LSCoII(Py)–HSСoII BS 2/2 –5375.06466   3.028      
HSCoII(Py)–LSСoII 4/2 –5375.05819 4.8 6.029 2.55 0.90 3
HSCoII(Py)–LSСoII BS 2/2 –5375.05815   3.028      
HSCoII(Py)–HSСoII 6/2 –5375.05687 5.7 12.029 2.55 2.45 3
HSCoII(Py)–HSСoII BS 0 –5375.05676   3.028      
II (Co(Py); M = Co; R = CH3)
LSCoII(Py)–LSСoII 2/2 –5532.36833 0.0 2.024 0.86 0.88 15
LSCoII(Py)–LSСoII BS 0 –5532.36827   1.024      
LSCoII(Py)–HSСoII 4/2 –5532.36564 1.7 6.025 0.85 2.33 2
LSCoII(Py)–HSСoII BS 2/2 –5532.36562   3.023      
HSCoII(Py)–LSСoII 4/2 –5532.36058 4.9 6.029 2.55 0.89 8
HSCoII(Py)–LSСoII BS 2/2 –5532.36048   3.028      
HSCoII(Py)–HSСoII 6/2 –5532.35590 7.8 12.026 2.55 2.39 15
HSCoII(Py)–HSСoII BS 0 –5532.35530   3.028      

* ΔЕ рассчитаны относительно наиболее устойчивого изомера комплекса.

Существенная дестабилизация структуры LS-CoII–HSFeII с высокоспиновым ионом железа относительно низкоспинового изомера LSCoII–LSFeII побудила изучить комплексы, включающие в качестве вспомогательных лигандов производные дипиридила с метильными заместителями в положениях 3, 3'. Ожидалось, что создаваемые СH3-группами стерические препятствия при формировании комплекса приведут к понижению силы поля лигандов и реализации СКО на ионе Fe2+. Другим направлением модификации модельных соединений I стала координация молекул пиридина, способная обеспечить протекание СКО в бис-салицилиденовом фрагменте [12–15, 35].

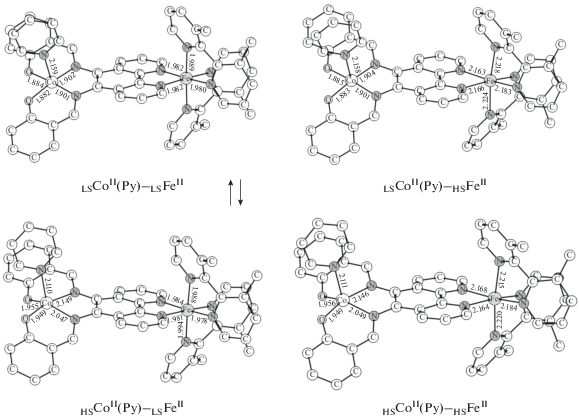
Анализ вычисленных длин связей в аддукте II (Co(Py); M = Fe; R = CH3) показал увеличение расстояний Fe–N в структурах LSCoII(Py)–LSFeII и HSCoII(Py)–LSFeII, приводящее к понижению относительной устойчивости изомеров (рис. 2, табл. 1). Эти изменения способствуют сокращению (по сравнению с комплексом I (Co; M = Fe; R = H)) разностей энергий между электромерами, содержащими ионы железа в различных спиновых состояниях, однако полученные величины (12.6 и 17.5 ккал/моль) по-прежнему не достигают значений, характерных для термически инициированных спиновых переходов на ионах Fe2+. В то же время разность энергий между структурами LSCoII(Py)–LSFeII и HSCoII(Py)–LSFeII (3.3 ккал/моль) позволяет ожидать протекание СКО на ионе кобальта (рис. 2). Высокоспиновая форма комплекса HSCoII(Py)–HSFeII располагается на 4.9 ккал/моль выше по энергии изомера LSCoII(Py)–HSFeII, что указывает на возможность второго спинового перехода в бис-салицилиденовом фрагменте аддукта II (Co(Py); M = Fe; R = = CH3). Однако дестабилизация обсуждаемых электромеров относительно основного состояния ставит под сомнение их формирование.

Рис. 2.

Оптимизированные геометрии изомеров комплексов II (Co(Py); M = Fe; R = CH3), рассчитанные методом DFT UTPSSh/6-311++G(d,p).

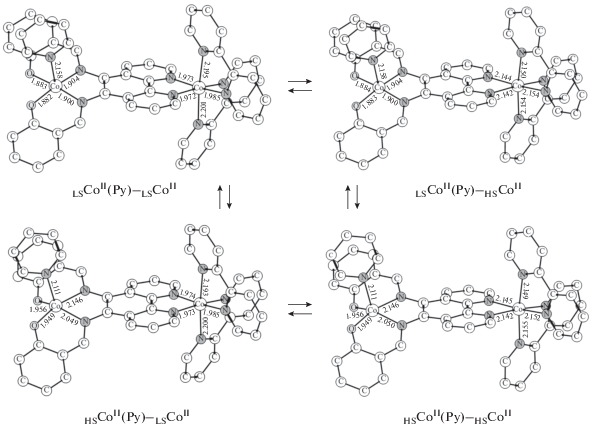
С целью поиска соединения, способного демонстрировать СКО на двух металлоцентрах, исследован комплекс II (Co(Py); M = Co; R = H). Согласно результатам квантово-химических расчетов, разницы энергии изомеров, содержащих ионы металлов в различных спиновых состояниях, лежат в интервале 0.8–5.7 ккал/моль (табл. 1). Это дает основание ожидать протекания СКО перегруппировок на всех кобальтовых центрах (рис. 3). Расчеты состояний BS и последующий анализ обменных взаимодействий указывают на слабый ферромагнитный обмен (J = 1–3 cм–1) между неспаренными электронами металлов (табл. 1). Ожидаемые синхронизированные спиновые переходы в бис-салицилиденовом фрагменте (LSCoII(Py)–LSСoII ⇄ HSCoII(Py)–LSСoII и LSCoII(Py)–HSСoII ⇄ ⇄ HSCoII(Py)–HSСoII) и в противоположной части молекулы (LSCoII(Py)–LSСoII ⇄ LSCoII(Py)–HSСoII и HSCoII(Py)–LSСoII ⇄ HSCoII(Py)–HSСoII), сопровождающиеся изменением спина системы с S =  2/2 до S = 6/2, а также парамагнетизм всех электромерных форм в широком диапазоне температур позволяют рассматривать аддукт II (Co(Py); M = Co; R = H) в качестве перспективного молекулярного переключателя.

Рис. 3.

Оптимизированные геометрии изомеров комплексов II (Co(Py); M = Co; R = H), рассчитанные методом DFT UTPSSh/6-311++G(d,p).

Теоретическое рассмотрение биядерного комплекса кобальта II (Co(Py); M = Co; R = CH3), включающего молекулы 3,3'-диметил-2,2'-дипридила, показало, что, как и в соединении II (Co(Py); M = Co; R = H), оба металлоцентра способны претерпевать спиновые переходы в результате спин-кроссовера (рис. 4). Согласно вычисленным геометрическим характеристикам, алкильные заместители в пиридиновых кольцах способствуют удлинению связей Co–донорный атом вспомогательных лигандов, в то время как расстояния между металлоцентром и атомом азота фенантролинового фрагмента сокращаются. Предсказываемое увеличение разностей энергий между электромерами, а также незначительное усиление ферромагнитных взаимодействий (табл. 1) по сравнению с описанным выше аддуктом, не содержащим метильные группы, не будут препятствовать вовлечению всех форм комплекса в синхронизированные спиновые переходы и проявлению им свойств молекулярного переключателя.

Рис. 4.

Оптимизированные геометрии изомеров комплексов II (Co(Py); M = Co; R = CH3), рассчитанные методом DFT UTPSSh/6-311++G(d,p).

Таким образом, на основе данных квантово-химических расчетов (DFT UTPSSh/6-311++G(d,p)) биядерных гомо- и гетерометаллических комплексов железа и кобальта с 5,6-бис(салицилиденимино)-1,10-фенантролином показана возможность управления энергетическими и магнитными характеристиками электромеров изученных координационных соединений посредством модификации природы металла и координации дополнительного азотсодержащего основания. В соединениях I (Co; M = Fe, Co; R = H) переключение спиновых состояний ожидается только на ионах кобальта в октаэдрическом окружении, формируемом атомами азота фенантролинового фрагмента и дипиридилов. Координация пиридина к иону кобальта в бис-салицилиденовой части комплекса способствует реализации СКО. Независимо от присутствия в бидентатных лигандах метильных групп (аддукт II (Co(Py); M = Fe; R = CH3)), разность энергий изомеров с высоко- и низкоспиновыми ионами Fe2+ превышает значения, позволяющие ожидать спиновые переходы на этом ионе металла. Парамагнетизм всех изомеров гомометаллических комплексов кобальта II (Co(Py); M = Co; R = H) и II (Co(Py); M = Co; R = CH3), а также возможные синхронизированные спиновые переходы и варьируемые в широком диапазоне спиновые состояния системы дают основания рассматривать эти соединения в качестве эффективных молекулярных переключателей с магнитной функцией отклика.

Работа выполнена при финансовой поддержке Российского научного фонда (грант № 14-13-00573).

Список литературы

  1. Spin crossover in transition metal compounds I: Topics in current chemistry. V. 233 / Eds Gutlich P., Goodwin H.A. Berlin: Springer, 2004. 341 p.

  2. Functional Metallosupramolecular Materials / Eds Hardy J., Schacher F. Cambridge: The Royal Society of Chemistry, 2015. P. 290.

  3. Spin States in Biochemistry and Inorganic Chemistry: Influence on Structure and Reactivity / Eds Swart M., Costas M. Chichester: John Wiley & Sons, 2016. 448 p.

  4. Senthil Kumar K., Ruben M. // Coord. Chem. Rev. 2017. V. 346. P. 176.

  5. Ferrando-Soria J., Vallejo J., Castellano M. et al. // Coord. Chem. Rev. 2017. V. 339. P. 17.

  6. Magnetism: molecules to materials II: molecule-based materials / Eds Miller J.S., Drillon M. N.Y.: Wiley-VCH, 2001. 489 p.

  7. Leuenberger M.N., Loss D. // Nature. 2001. V. 410. P. 789.

  8. Halcrow M.A. Spin-Crossover Materials: Properties and Applications. Chichester: John Wiley & Sons, 2013. 564 p.

  9. Hauser A., Enachescu C., Daku M.L. et al. // Coord. Chem. Rev. 2006. V. 250. № 13–14. P. 1642.

  10. Bousseksou A., Molnár G., Real J.A., Tanaka K. Spin crossover and photomagnetism in dinuclear iron(II) compounds // Coord. Chem. Rev. 2007. V. 251. № 13–14. P. 1822.

  11. Halcrow M.A. // Polyhedron. 2007. V. 26. № 14. P. 3523.

  12. Murray K.S., Sheahan R.M. // Dalton. Trans. 1976. V. 11. P. 999.

  13. Kennedy B.J., Fallon G.D., Gatehouse B.M.K.C., Murray K.S. // Inorg. Chem. 1984. V. 23. № 5. P. 580.

  14. Koenig E., Ritter G., Dengler J. et al. // Inorg. Chem. 1989. V. 28. № 9. P. 1757.

  15. Min K.S., Arthur J., Shum W.W. et al. // Inorg. Chem. 2009. V. 48. № 11. P. 4593.

  16. Sieber R., Decurtins S., Stoeckli-Evans H. et al. // Chem. Eur. J. 2000. V. 6. № 2. P. 361.

  17. Zerara M., Hauser A. // Chem. Phys. Chem. 2004. V. 5. № 3. P. 395.

  18. Krivokapic I., Zerara M., Daku M.L. et al. // Coord. Chem. Rev. 2007. V. 251. № 3–4. P. 364.

  19. Voloshin Ya.Z., Varzatskii O.A., Novikov V.V. et al. // Eur. J. Inorg. Chem. 2010. № 34. P. 5401.

  20. Vologzhanina A.V., Belov A.S., Novikov V.V. et al. // Inorg. Chem. 2015. V. 54. № 12. P. 5827.

  21. Minkin V.I., Starikova A.A., Starikov A.G. // Dalton Trans. 2016. V. 45. № 30. P. 12103.

  22. Старикова А.А., Стариков А.Г., Минкин В.И. // Коорд. химия. 2017. Т. 43. № 11. С. 650. (Starikova A.A., Starikov A.G., Minkin V.I. // Russ. J. Coord. Chem. 2017. V. 43. P. 718. doi 10.1134/S1070328417110094).

  23. Komatsuzaki N., Himeda Y., Goto M. et al. // Chem. Lett. 1999. V. 28. № 4. P. 327.

  24. Frisch M.J., Trucks G.W., Schlegel H.B. et al. Gaussian-09. Revision E. 01. Wallingford: Gaussian, 2013.

  25. Tao J.M., Perdew J.P., Staroverov V.N., Scuseria G.E. // Phys. Rev. Lett. 2003. V. 91. № 14. P. 146401.

  26. Staroverov V.N., Scuseria G.E., Tao J., Perdew J.P. // J. Chem. Phys. 2003. V. 119. № 23. P. 12129.

  27. Bannwarth A., Schmidt S.O., Peters G. et al. // Eur. J. Inorg. Chem. 2012. № 16. P. 2776.

  28. Cirera J., Paesani F. // Inorg. Chem. 2012. V. 51. № 15. P. 8194.

  29. Стариков А.Г., Старикова А.А., Минкин В.И. // До-кл. РАН. 2016. Т. 467. № 3. С. 300.

  30. Starikova A.A., Chegerev M.G., Starikov A.G., Minkin V.I. // Comp. Theor. Chem. 2018. V. 1124. P. 15.

  31. Старикова А.А., Минкин В.И. // Коорд. химия. 2018. Т. 44. № 4. С. 229. (Starikova A.A., Minkin V.I. // Russ. J. Coord. Chem. 2018. V. 44. № 8. P. 483. doi 10.1134/S1070328418080079).

  32. Noodleman L. // J. Chem. Phys. 1981. V. 74. № 10. P. 5737.

  33. Shoji M., Koizumi K., Kitagawa Y. et al. // Chem. Phys. Lett. 2006. V. 432. № 1. P. 343.

  34. Chemcraft, version 1.7, 2013: http://www.chemcraftprog.com.

  35. Starikov A.G., Minkin V.I., Starikova A.A. // Struct. Chem. 2014. V. 25. № 6. P. 1865.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Координационная химия

Архивы выпусков Информация о журнале Отправить рукопись в журнал