Космические исследования, 2020, T. 58, № 1, стр. 73-84

ВВЕДЕНИЕ

В космической навигации часто встречаются задачи, в которых задаются краевые условия, которым должны удовлетворять начальные и конечные состояния космического аппарата. Это, например, запуск КА на орбиту, межорбитальный перелет, стыковка, пространственный разворот, спуск на поверхность планеты и др. При этом возникает необходимость решения задач оптимального управления (ЗОУ), в которых требуется перевести КА из заданного начального состояния в желаемое конечное состояние с минимальными затратами топлива или за кратчайшее время. Эти ЗОУ рассматриваются на конечном отрезке времени и при условии ограниченности управляющего воздействия.

Для решения краевых задач оптимального управления могут быть использованы принцип максимума Понтрягина [1], метод динамического программирования Беллмана [2], достаточные условия оптимальности Кротова [3], а также численные методы (например, метод последовательных приближений Крылова–Черноусько [4] и его модификации [5]). Среди новых подходов, появившихся в последние годы, можно отметить псевдоспектральные методы [6], основанные на использовании полиномов Лежандра и Чебышева. Имеется также прикладной пакет DIDO в среле MATLAB, предназначенный для решения задач динамической оптимизации [7]. Эти алгоритмы и программы в настоящее время успешно используются NASA для оптимального управления маневрами МКС [8].

Различным аспектам задачи оптимального управления угловым движением КА при закрепленных концах траекторий системы и методам ее решения посвящены, в частности, работы [9–12]. В [9] найдено оптимальное программное управление, реализующее разворот КА вдоль так называемой траектории “свободного движения”. Предлагаемый здесь аналитический подход к решению задачи дает значительный выигрыш в быстродействии при формировании законов управления, однако требование принадлежности траектории КА к определенному классу сужает исходную постановку задачи.

В [10–12] исследована задача управления вращательным движением космического аппарата в случаях, когда КА рассматривается как твердое тело со сферически симметричной, осесимметричной или произвольной динамической конфигурацией. Для задачи оптимального разворота КА получены точное аналитическое решение в классе конических движений и приближенное аналитическое решение в классе обобщенных конических движений при произвольных начальных и конечных условиях на угловые скорости и угловые координаты, без учета ограничений на управление. Отметим, что произвольное движение твердого тела вокруг неподвижной точки может быть представлено как обобщенное коническое движение. Минимизируемый целевой функционал выбран в виде линейной комбинации затраты времени и расхода энергии на разворот КА [13]. В разделе 5 приводится сравнение результатов, полученных при использовании методов, предлагаемых в [12] и в данной работе.

Несмотря на наличие большого количества работ, посвященных различным постановкам задач и методам решения ЗОУ угловым движением КА, является актуальной проблема разработки новых подходов для их решения с учетом специфики рассматриваемых конкретных систем управления. Это связано отсутствием в общем случае аналитических методов решения ЗОУ для нелинейных систем и с трудностями численного решения краевых задач дифференциальных уравнений, возникающих при решении этих ЗОУ.

Для описания ориентации твердого тела в пространстве могут быть использованы различные кинематические параметры, такие как углы Эйлера и Крылова, направляющие косинусы, параметры Родрига–Гамильтона (кватернион) и параметры Кейли–Клейна [14–16]. В данной работе для описания вращательного движения КА использована кватернионная модель [17], в которой правые части дифференциальных уравнений билинейны относительно фазовых координат и линейны относительно управлений. Это позволяет достичь большой степени точности приближений при применении в дальнейшем процедуры квазилинеаризации. При использовании кватернионной модели, в отличие от уравнений в углах Эйлера [18], удается избежать таких недостатков как “вырождение” кинематических уравнений [19] и наличие тригонометрических функций в правых частях дифференциальных уравнений. Мы используем здесь аналитический метод для решения двухточечной краевой задачи (ДТКЗ), возникающей на каждом шаге процесса квазилинеаризации. Таким образом, учет особенностей математической модели рассматриваемого объекта управления позволяет сконструировать алгоритм решения задачи, обладающий достаточной степенью точности, и значительно сократить затраты компьютерного времени.

Приведенный в данной работе метод полного разделения уравнений для фазовых и сопряженных переменных является дальнейшим обобщением предложенного ранее метода [20, 21], в котором был использован алгоритм, позволяющий осуществить частичное разделение переменных (при этом удается получить отдельное дифференциальное уравнение только для вектора сопряженных переменных).

1. ПОСТАНОВКА ЗАДАЧИ

Пусть положение связанного с КА базиса ${\mathbf{E}}$ относительно опорного базиса ${\mathbf{I}}$ задается с помощью кватерниона. Предполагается, что базис ${\mathbf{I}}$ является инерциальным. Тогда уравнения вращательного движения КА, рассматриваемого как твердое тело, будут иметь следующий вид [9]:

где ${\mathbf{x}} = ({{{\omega }}_{1}},{{{\omega }}_{2}},{{{\omega }}_{3}},{{{\lambda }}_{0}},{{{\lambda }}_{1}},{{{\lambda }}_{2}},{{{\lambda }}_{3}}){\kern 1pt} '$ – вектор состояния КА, ${\mathbf{M}} = ({{M}_{1}},{{M}_{2}},{{M}_{3}}){\kern 1pt} '$ – вектор управления. Символ “штрих” означает операцию транспонирования. Изменения компонент вектора угловой скорости ${\mathbf{\omega }}(t) = ({{{\omega }}_{1}}(t),\;{{{\omega }}_{2}}(t),\;{{{\omega }}_{3}}(t)){\kern 1pt} '$ описываются динамическими уравнениями Эйлера (1), а изменения компонент кватерниона ${\mathbf{\Lambda }} = ({{{\lambda }}_{0}},{{{\lambda }}_{{\text{1}}}},{{{\lambda }}_{2}},{{{\lambda }}_{3}}){\kern 1pt} '$ – уравнениями (2). Здесь использованы такие же обозначения, как в [9]: ${{J}_{i}}$ – главные центральные моменты инерции КА, ${{M}_{i}}$ – проекции главного момента сил ${\mathbf{M}}$ на главные центральные оси инерции КА, ${{{\omega }}_{i}}$ – проекции вектора абсолютной угловой скорости ${\mathbf{\omega }}$ на оси связанного базиса ${\mathbf{E}}$, образованного центральными осями эллипсоида инерции КА $(i = \overline {1,\,3} ).$

Мы рассматриваем задачу на фиксированном отрезке времени $[{{t}_{0}},T]$ и с закрепленными концами траекторий: в системе (1), (2) для вектора угловой скорости ${\mathbf{\omega }}$ и кватерниона ${\mathbf{\Lambda }}$ заданы начальные условия

и конечные условия

Для описания пространственной ориентации КА мы используем нормированный кватернион, поэтому в (3), (4) предполагается выполнение условия $\left\| {{\mathbf{\Lambda }}\;({{t}_{0}})} \right\| = \left\| {{\mathbf{\Lambda }}(T)} \right\| = 1.$ Отметим, что если начальное условие для кватерниона выбрано таким образом, что $\left\| {{\mathbf{\Lambda }}\;({{t}_{0}})} \right\| = 1,$ то в конечный момент времени $T$ условие нормировки $\left\| {{\mathbf{\Lambda }}(T)} \right\| = 1$ будет выполнено автоматически, поскольку система (1), (2) имеет первый интеграл $\left\| {{\mathbf{\Lambda }}(t)} \right\| = 1,$ $\forall \,t \in [{{t}_{0}},T]$ (см. [14]).

Пусть для вектора управления ${\mathbf{M}}$ задано ограничение вида

где $U$ – выпуклое замкнутое множество. В данной статье будут рассмотрены задачи, в которых множество допустимых управлений $U$ представляет собой параллелепипед или эллипсоид, т.е. компоненты вектора управления должны удовлетворять условиям или где ${{D}_{0}}$ – положительно определенная $(3 \times 3)$-матрица. Эти условия связаны с ограниченностью управляющего воздействия, создаваемого микрореактивными двигателями или гиродинами, с помощью которых осуществляются маневры КА.

Целевой функционал имеет вид

где ${{f}_{0}}({\mathbf{M}}(t))$ – неотрицательная функция времени. Мы будем рассматривать следующие целевые функционалы:

а) минимизация расхода топлива [9, 14]:

где ${{l}_{i}} > 0,$ $(i = \overline {1,\,3} )$ – плечи установки двигателей ориентации КА;

б) минимизация затрат на управление [9]:

Требуется найти управление ${\mathbf{M}}(t),$ удовлетворяющее ограничению (5), которое переводит систему (1), (2) из заданного начального состояния (3) в желаемое конечное состояние (4) за интервал времени $[{{t}_{0}},T],$ минимизируя при этом целевой функционал (8). Здесь ограничение на управление может быть задано в виде (6) или (7), а целевой функционал может иметь вид (9) или (10). Для того, чтобы ЗОУ (1)–(5), (8) имела решение, необходимо выполнение неравенства $T > T*,$ где $T{\text{*}}$ – момент окончания процесса управления в задаче оптимального быстродействия при условиях (1)–(5).

Сложность решения рассматриваемой ЗОУ оптимальным разворотом КА заключается в том, система (1), (2) имеет континуум стационарных состояний

т.е. любая пространственная ориентация КА, в которой угловая скорость равна нулю, является положением равновесия. В правые части дифференциальных уравнений (2) управления не входят. Влияние на динамику кватерниона фактически осуществляется здесь через вектор угловой скорости ${\mathbf{\omega }}(t).$ Однако, если учесть, что во многих случаях в конечном условии (4) задается ${\mathbf{\omega }}(T) = {\mathbf{0}},$ то понятно, что ближе к концу интервала $[{{t}_{0}},T]$ КА становится плохо управляемым. Отметим также, что система (1), (2) является нелинейной, подинтегральные функции в целевых функционалах (9) и (10) не являются квадратичными формами. Все это приводит к необходимости разработки специальных методов решения, учитывающих особенности рассматриваемой ЗОУ. Применяемая в данной работе процедура квазилинеаризации позволяет использовать для целевых функционалов (9) и (10) приближенные представления, в которых подинтегральные функции аппроксимируются с помощью квадратичных форм.

2. РЕШЕНИЕ ЗАДАЧИ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Для решения поставленной выше задачи оптимального разворота КА рассмотрим систему, описываемую в интервале времени $[{{t}_{0}},T]$ векторным дифференциальным уравнением вида

где ${\mathbf{x}} = ({{x}_{1}},\;...\;,\;{{x}_{n}}){\kern 1pt} '$ – вектор состояния объекта, ${\mathbf{u}} = ({{u}_{1}},\;...\;,\;{{u}_{m}}){\kern 1pt} '$ – вектор управления, $B(t)$ – $(n \times m)$-матрица. Управление ${\mathbf{u}}$ удовлетворяет ограничению где допустимое множество управлений $U$ является выпуклым и замкнутым.

Требуется перевести систему (11) из заданного начального положения

в желаемое конечное состояние выбирая управление ${\mathbf{u}}(t),$ $t \in [{{t}_{0}},T],$ удовлетворяющее ограничению (12), и минимизируя при этом квадратичный функционал где $(n \times n)$-матрица $Q(t)$ является положительно полуопределенной, $(m \times m)$-матрица $R(t)$ – положительно определенной для всех $t \in {\text{[}}{{t}_{0}},T].$

Рассматриваемая задача (11)–(15) относится к классу задач оптимального управления (ЗОУ) на конечном отрезке времени, с закрепленными концами траекторий и с ограниченным управлением. Отметим, что правая часть дифференциальных уравнений (11) может быть нелинейной относительно фазовых координат ${\mathbf{x}}.$ Предполагается, что задача (11)–(14) (без учета требования минимизации целевого функционала (15)) имеет решение, т.е. существует хотя бы одно управление ${\mathbf{u}}(t) \in U,$ $t \in [{{t}_{0}},T],$ которое за заданный интервал времени $[{{t}_{0}},T]$ переводит систему (11) из (13) в (14).

Используя принцип максимума, для решения ЗОУ (11)–(15) составим функцию Гамильтона–Понтрягина

где $p* = {\text{const}} \leqslant 0;$ ${\mathbf{p}} = ({{p}_{1}},\;...\;,\;{{p}_{n}}){\kern 1pt} '$ – сопряженный вектор. В дальнейшем будем рассматривать невырожденный случай, когда $p* < 0.$ При этом в силу линейности и однородности (16) по $p{\text{*}}$ и ${\mathbf{p}}$ можно считать, что $p* = - 1$ (см. [22]). Функция (16) является сильно вогнутой относительно ${\mathbf{u}}$, поскольку матрица $R(t)$ положительно определена для всех $t \in [{{t}_{0}},T].$

Пусть ${\mathbf{x}}(t)$ – решение системы (11), соответствующее начальному условию (13) и некоторому управлению ${\mathbf{u}}(t).$ Паре $({\mathbf{x}}(t),{\mathbf{u}}(t))$ поставим в соответствие сопряженный вектор ${\mathbf{p}}(t),$ удовлетворяющий дифференциальному уравнению

В каждый момент времени $t \in [{{t}_{0}},T]$ определим стационарную точку функции $H({\mathbf{x}}(t),{\mathbf{u}},t,p*,{\mathbf{p}}(t))$ по ${\mathbf{u}}$ из условия ${{\partial H} \mathord{\left/ {\vphantom {{\partial H} {\partial {\mathbf{u}}}}} \right. \kern-0em} {\partial {\mathbf{u}}}} = 0{\text{:}}$Если ${\mathbf{\hat {u}}}(t) \in U,$ т.е. стационарная точка принадлежит множеству допустимых управлений $U,$ то значение искомого управления в момент времени $t$ принимаем равным ${\mathbf{u}}(t) = {\mathbf{\hat {u}}}(t).$ Если ${\mathbf{\hat {u}}}(t) \notin U,$ то решаем задачу максимизации функции $H({\mathbf{x}}(t),{\mathbf{u}},t,p*,{\mathbf{p}}(t))$ по ${\mathbf{u}}$ на множестве $U$ и находим точку ${\mathbf{u}}(t) = {\mathbf{\bar {u}}}(t),$ лежащую на границе множества $U,$ в которой достигается максимум. Данная задача имеет единственное решение в каждый фиксированный момент времени $t \in [{{t}_{0}},T],$ поскольку функция (16) является сильно вогнутой относительно ${\mathbf{u}},$ а множество допустимых управлений $U$ выпукло и замкнуто.

Таким образом, ${\mathbf{u}}(t)$ будет зависеть от сопряженного вектора ${\mathbf{p}}(t),$ который необходимо выбрать таким образом, чтобы найденное управление обеспечивало прохождение траектории ${\mathbf{x}}(t)$ через заданную конечную точку: ${\mathbf{x}}(T) = {{{\mathbf{x}}}_{T}}.$ Из принципа максимума Понтрягина следует, что вектор ${\mathbf{p}}(t),$ обладающий данным свойством, является решением двухточечной краевой задачи (ДТКЗ) для системы из $2n$ дифференциальных уравнений в интервале времени $[{{t}_{0}},T]{\text{:}}$

с $2n$ краевыми условиями

заданными для траектории ${\mathbf{x}}(t)$ в двух разных точках временного интервала: при $t = {{t}_{0}}$ и $t = T.$ В формуле (17) использованы следующие обозначения: $(n \times n)$-матрица $S(t) = B(t){{R}^{{ - 1}}}(t)B{\kern 1pt} '(t);$ $n$‑вектор-функция

Таким образом, приходим к необходимости решения ДТКЗ для нелинейной системы (17) с краевыми условиями (18). Фактически мы должны ДТКЗ (17), (18) привести к задаче Коши, где начальное условие^{${\mathbf{p}}({{t}_{0}}) = {{{\mathbf{p}}}_{0}}$ для сопряженного вектора ${\mathbf{p}}(t)$ следует выбрать таким образом, чтобы траектория системы ${\mathbf{x}}(t),$ исходящая в начальный момент времени ${{t}_{0}}$ из точки ${{{\mathbf{x}}}_{0}},$ пришла бы к точке ${{{\mathbf{x}}}_{T}}$ в конечный момент времени $T.$}

3. РАЗДЕЛЕНИЕ ПЕРЕМЕННЫХ

Для решения ДТКЗ (17), (18) предлагается метод разделения переменных, суть которого заключается в том, что производится преобразование $({\mathbf{x}},{\mathbf{p}}) \to ({\mathbf{y}},{\mathbf{q}}),$ при котором происходит полное разделение уравнений для новых векторов фазовых и сопряженных переменных (правая часть дифференциального уравнения для ${\mathbf{y}}$ не будет зависеть от ${\mathbf{q}}$ и, наоборот, правая часть дифференциального уравнения для ${\mathbf{q}}$ не будет зависеть от ${\mathbf{y}}$).

Используя процедуру квазилинеаризации Беллмана [23], на $k$-й итерации разложим правые части (17) в ряды Тейлора относительно решения $({{{\mathbf{x}}}^{{(k - 1)}}}(t),\,\,{{{\mathbf{p}}}^{{(k - 1)}}}(t)),$ полученного на предыдущей $(k - 1)$-й итерации. Ограничиваясь линейными членами разложения, составим систему дифференциальных уравнений для нахождения следующего приближения $({{{\mathbf{x}}}^{{(k)}}}(t),\,\,{{{\mathbf{p}}}^{{(k)}}}(t)){\text{:}}$

где $(n \times n)$-матрица ${{A}^{{(k)}}}(t)$ = ${{\partial {\mathbf{f}}({\mathbf{x}},t)} \mathord{\left/ {\vphantom {{\partial {\mathbf{f}}({\mathbf{x}},t)} {{{{\left. {\partial {\mathbf{x}}} \right|}}_{{{\mathbf{x}} = {{{\mathbf{x}}}^{{(k - 1)}}}(t)}}}}}} \right. \kern-0em} {{{{\left. {\partial {\mathbf{x}}} \right|}}_{{{\mathbf{x}} = {{{\mathbf{x}}}^{{(k - 1)}}}(t)}}}}}{\text{;}}$ $n$‑вектор

В (22) значения вектор-функции ${{{\mathbf{s}}}^{{(k)}}}(t)$ на $k$-й итерации вычисляются с использованием формулы (19), где ${{{\mathbf{\hat {u}}}}^{{(k)}}}(t)$ и ${{{\mathbf{\bar {u}}}}^{{(k)}}}(t)$ определяются на основании известных значений ${{{\mathbf{p}}}^{{(k - 1)}}}(t)$ из предыдущей $(k - 1)$-й итерации. Управление ${{{\mathbf{u}}}^{{(k)}}}(t),$ удовлетворяющее ограничению (12), будет равно

В дальнейшем для упрощения записи не будем указывать индексы $(k),$ означающие принадлежность к $k$-й итерации, и не будем явно указывать зависимость векторов и матриц от времени $t.$ Например, будем использовать обозначения ${\mathbf{x}} = {{{\mathbf{x}}}^{{(k)}}}(t),$ $A = {{A}^{{(k)}}}(t),$ $S = S(t)$ и т.п. Тогда (20), (21) можно переписать в виде

Для решения ДТКЗ (23), (24) на каждой $k$-й итерации процесса квазилинеаризации предлагается использовать преобразование $({\mathbf{x}},{\mathbf{p}}) \to ({\mathbf{y}},{\mathbf{q}}),$ т.е. осуществить переход к новым векторам фазовых и сопряженных переменных ${\mathbf{y}}$ и ${\mathbf{q}}.$

Введем в рассмотрение симметрические $(n \times n)$-матрицы $K = K(t)$ и $L = L(t),$ определяемые в интервале $[{{t}_{0}},T]$ как решения системы матричных дифференциальных уравнений

где $\tilde {A} = A - SK.$ Здесь (25) представляет собой матричное дифференциальное уравнение Риккати, (26) – матричное дифференциальное уравнение Ляпунова. Интегрируя систему (25), (26) в обратном направлении изменения времени, можно найти ${{K}_{0}} = K({{t}_{0}})$ и ${{L}_{0}} = L({{t}_{0}}).$

Далее произведем преобразование координат $({\mathbf{x}},{\mathbf{p}}) \to ({\mathbf{y}},{\mathbf{q}}),$ используя следующие соотношения:

где $I$ – единичная $(n \times n)$-матрица. Можно показать, что преобразование (27) является невырожденным в интервале $[{{t}_{0}},T].$ Действительно, используя формулу Шура [24] для вычисления определителя блочных матриц, получим т.е. определитель матрицы преобразования (27) тождественно равен 1 для любого $t \in [{{t}_{0}},T],$ следовательно предлагаемое преобразование невырождено. Из соотношений (27) следует, что

Подставляя (27) в систему дифференциальных уравнений (23) и учитывая, что матрицы $K$ и $L$ удовлетворяют соотношениям (25), (26), получим следующие уравнения для ${\mathbf{y}}$ и ${\mathbf{q}}{\text{:}}$

Таким образом, дифференциальные уравнения (29) для новых фазовых и сопряженных векторов оказываются полностью разделенными. Вектор-функции ${\mathbf{y}}$ и ${\mathbf{q}}$ будут связаны между собой только через краевые условия (24):

Уравнения (29) можно проинтегрировать в интервале $[{{t}_{0}},T]$ в обратном направлении изменения времени, задав некоторые конечные условия ${\mathbf{y}}(T) = {{{\mathbf{y}}}_{T}}$ и ${\mathbf{q}}(T) = {{{\mathbf{q}}}_{T}}.$ При этом значения ${\mathbf{y}}$ и ${\mathbf{q}}$ в начальный момент времени ${{t}_{0}}$ будут равны

где $\Phi (t,{\tau })$ и $\Psi (t,{\tau })$ – матрицы Коши (переходные матрицы) для однородных векторных дифференциальных уравнений вида ${\mathbf{\dot {y}}} = \tilde {A}{\mathbf{y}}$ и ${\mathbf{\dot {q}}} = - \tilde {A}{\kern 1pt} '{\mathbf{q}}$ соответственно. Отметим, что матрицы $\Phi (t,{\tau })$ и $\Psi (t,{\tau })$ связаны соотношением [25] поскольку уравнения ${\mathbf{\dot {y}}} = \tilde {A}{\mathbf{y}}$ и ${\mathbf{\dot {q}}} = - \tilde {A}{\kern 1pt} '{\mathbf{q}}$ являются взаимно сопряженными. Матрицу $\Phi ({{t}_{0}},T),$ векторы ${{{\mathbf{a}}}_{0}} = {\mathbf{a}}({{t}_{0}})$ и ${{{\mathbf{b}}}_{0}} = {\mathbf{b}}({{t}_{0}}),$ входящие в формулу (31), можно вычислить, интегрируя в интервале $[{{t}_{0}},T]$ дифференциальные уравнения

С учетом (30) и (31) можно составить систему алгебраических уравнений

из которой определяются конечные значения

Далее из (28) с учетом формул (31), (32), (34) можно получить

Таким образом, для системы дифференциальных уравнений (23) приходим к задаче Коши с начальными условиями

Из (35) следует, что начальное значение сопряженного вектора можно представить в виде

Здесь постоянные $(n \times n)$-матрицы $C,$ $D$ и $n$-вектор ${\mathbf{e}}$ вычисляются следующим образом:

где матрица $G = {{[{{L}_{0}} - \Phi ({{t}_{0}},T){{L}_{T}}\Phi {\kern 1pt} '({{t}_{0}},T)]}^{{ - 1}}}.$

Замечания. 1. Отметим некоторые возможности для сокращения вычислений.

а) Можно выбрать конечное условие для матрицы $L$ в виде $L(T) = {{L}_{T}} = O,$ где $O$ – нулевая $(n \times n)$-матрица. При этом формула (38) преобразуется к виду:

б) В частном случае, когда в целевом функционале (15) отсутствует квадратичная форма от ${\mathbf{x}},$ т.е. $Q \equiv O,$ выбирая в (25) конечное условие для матрицы $K$ в виде $K(T) = {{K}_{T}} = O,$ получим $K \equiv O.$ При этом в силу дифференциального уравнения для ${\mathbf{b}}$ (см. (33)) имеем ${\mathbf{b}} \equiv {\mathbf{0}}.$ Тогда формула (38) примет вид:

2. Использование метода квазилинеаризации позволяет представить рассматриваемые в постановке задачи (см. раздел 1) целевые функционалы в виде квадратичных функционалов на каждом $k$-м шаге итерации:

а) минимизация расхода топлива (9):

б) минимизация затрат на управление (10):

Таким образом, для рассматриваемой задачи оптимального разворота КА с функционалами вида (9) или (10) получаем возможность применения предлагаемого метода разделения переменных, где предполагается, что целевой функционал имеет квадратичный вид (15).

4. ЕДИНСТВЕННОСТЬ РЕШЕНИЯ ДВУХТОЧЕЧНОЙ КРАЕВОЙ ЗАДАЧИ

Покажем единственность решения ДТКЗ (23), (24), получаемого на каждом шаге процесса квазилинеаризации. При применении предлагаемого метода разделения переменных она сводится к задаче Коши (23), (36), где начальное условие для вектора сопряженных переменных вычисляется по формулам (37), (38). Задавая различные конечные условия $K(T) = {{K}_{T}},$ $L(T) = {{L}_{T}}$ для матричных дифференциальных уравнений (25), (26), получим различные матрицы $K(t),$ $L(t),$ $t \in [{{t}_{0}},T]$ и соответственно различные начальные значения $K({{t}_{0}}) = {{K}_{0}},$ $L({{t}_{0}}) = {{L}_{0}}.$ Однако оказывается, что в соотношении (37) матрицы $C,$ $D$ и вектор ${\mathbf{e}}$ определяются однозначно, т.е. их значения не зависят от выбора $K(T) = {{K}_{T}}$ и $L(T) = {{L}_{T}}.$

Решение системы (23) при начальных условиях (36) имеет вид

Здесь $\Omega (t,{\tau })$ – матрица Коши размерности $(2n \times 2n)$ для однородного векторного дифференциального уравнения вида ${\mathbf{\dot {w}}}(t) = W(t)\;{\mathbf{w}}(t),$ где $W(t) = \left( {\begin{array}{*{20}{c}} {A(t)}&{S(t)} \\ {Q(t)}&{ - A{\kern 1pt} '(t)} \end{array}} \right).$ Представим $\Omega (t,{\tau })$ в виде блочной матрицы $\Omega (t,{\tau })$ = $\left( {\begin{array}{*{20}{c}} {{{\Omega }_{{11}}}(t,{\tau })}&{{{\Omega }_{{12}}}(t,{\tau })} \\ {{{\Omega }_{{21}}}(t,{\tau })}&{{{\Omega }_{{22}}}(t,{\tau })} \end{array}} \right),$ где ${{\Omega }_{{ij}}}(t,{\tau }),$ $(i,j = 1,\,2)$ – матрицы размерности $(n \times n).$ Подставляя (37) в (39), при $t = T$ получим где векторы ${{{\mathbf{g}}}_{T}},$ ${{{\mathbf{h}}}_{T}}$ вычисляются следующим образом: Здесь для определения матриц ${{\Omega }_{{ij}}}(T,{{t}_{0}}),$ $(i,j = 1,\,2)$ необходимо проинтегрировать уравнение в интервале $[{{t}_{0}},T]$ при начальных условиях

А значения векторов ${\mathbf{g}}(T) = {{{\mathbf{g}}}_{T}}$ и ${\mathbf{h}}(T) = {{{\mathbf{h}}}_{T}}$ могут быть найдены путем интегрирования уравнения

в интервале $[{{t}_{0}},T]$ при начальных условиях

Из (40) имеем

Поскольку ${{{\mathbf{x}}}_{0}}$ и ${{{\mathbf{x}}}_{T}}$ могут принимать произвольные значения, то выполнение равенства (43) возможно только при

При условии невырожденности ${{\Omega }_{{12}}}(T,{{t}_{0}})$ отсюда следует, что в ДТКЗ (23), (24) постоянные матрицы $C,$ $D$ и вектор ${\mathbf{e}}$ можно однозначно вычислить по формуле (44), их значения не зависят от выбора конечных условий $K(T) = {{K}_{T}}$ и $L(T) = {{L}_{T}}$ в системе матричных дифференциальных уравнений (25), (26).

5. ПРИМЕРЫ

Для реализации предлагаемого алгоритма решения рассматриваемой ЗОУ была разработана программа с использованием Digital Visual Fortran 6.0 в среде Microsoft Visual Studio. Для численного интегрирования систем дифференциальных уравнений производится обращение к стандартной подпрограмме DOPRI8, в которой реализован алгоритм Дормана–Принса 8-го порядка точности [26]. Численные расчеты на компьютере проведены с удвоенной точностью (до 16 значащих цифр в десятичном представлении вещественных чисел).

Пример 1. Рассмотрим задачу оптимального управления с совмещением режимов торможения вращательного движения КА и его переориентации в пространстве. При этом имеется возможность начальную кинетическую энергию вращательного движения частично направить на разворот КА в желаемом направлении, тем самым сэкономив затраты топлива.

Пусть целевой функционал имеет вид (9), а управление принимает значения из параллелепипеда (6), где

Управление КА осуществляется в интервале времени $[{{t}_{0}},\;T] = [0,\;500\,\,{\text{c}}].$ Главные центральные моменты инерции КА взяты равными

плечи установки двигателей ориентации КА Начальные условия:

Конечные условия:

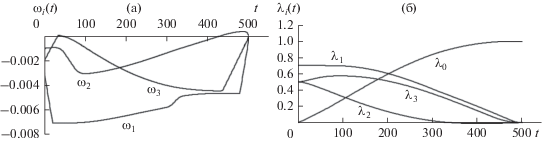
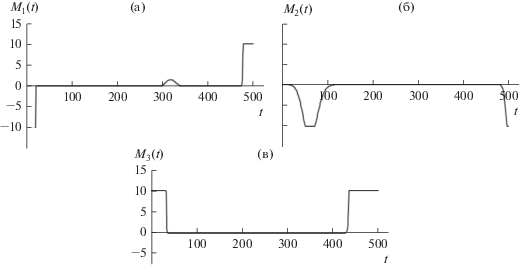
Результаты численных расчетов представлены на рис. 1 и 2. Графики оптимальных траекторий (угловых скоростей ${{{\omega }}_{i}}(t),$ $(i = \overline {1,\;3} )$ и компонент кватерниона ${{{\lambda }}_{i}}(t),$ $(i = \overline {0,\;3} )$) для исходной нелинейной системы (1), (2) приведены на рис. 1а и 1б. На рис. 2а, 2б, 2в показаны графики для компонент оптимального момента внешних сил ${{M}_{i}}(t),$ $(i = \overline {1,\;3} ).$ Компоненты найденного управления удовлетворяют заданным двусторонним ограничениям (6), принимая значения от $ - 10$ до $ + 10.$ Система (1), (2) с достаточно высокой степенью точности приводится в желаемое конечное состояние (47):

Пример 2. Рассмотрим задачу оптимального разворота КА в случае, когда задан целевой функционал (10), а допустимое множество управлений имеет вид эллипсоида (7), где

Управление КА осуществляется в интервале времени $[{{t}_{0}},T] = [0,250\,\,{\text{c}}].$ Значения главных центральных моментов инерции КА ${{J}_{i}},$ $(i = \overline {1,\;3} )$ взяты такими же как в предыдущем примере (см. (45)). Начальные условия:

Здесь в отличие от (46) рассматривается случай, когда КА в начальный момент времени находится в состоянии покоя; конечные условия совпадают с (47).

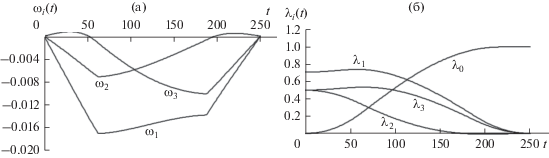
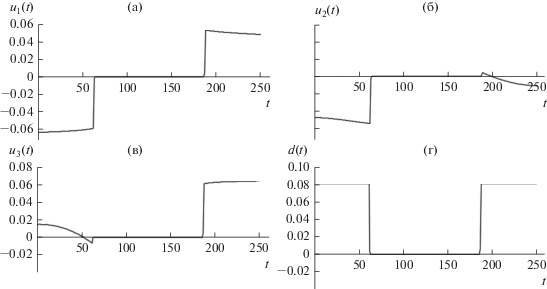
Результаты расчетов на компьютере представлены на рис. 3 и 4. Графики оптимальных траекторий (угловых скоростей ${{{\omega }}_{i}}(t),$ $(i = \overline {1,\;3} )$ и компонент кватерниона ${{{\lambda }}_{i}}(t),$ $(i = \overline {0,\;3} )$) для исходной нелинейной системы (1), (2) приведены на рис. 3а и 3б. На рис. 4а, 4б и 4в показаны графики для компонент вектора оптимального управления ${{u}_{i}}(t) = {{{{M}_{i}}(t)} \mathord{\left/ {\vphantom {{{{M}_{i}}(t)} {\sqrt {{{J}_{i}}} }}} \right. \kern-0em} {\sqrt {{{J}_{i}}} }},$ $(i = \overline {1,\;3} ),$ а из рис. 3г видно, как изменяется его норма $d(t) = \;\left\| {{\mathbf{u}}(t)} \right\|$ = = $\sqrt {{{M_{1}^{2}(t)} \mathord{\left/ {\vphantom {{M_{1}^{2}(t)} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}} + {{M_{2}^{2}(t)} \mathord{\left/ {\vphantom {{M_{2}^{2}(t)} {{{J}_{2}}}}} \right. \kern-0em} {{{J}_{2}}}} + {{M_{3}^{2}(t)} \mathord{\left/ {\vphantom {{M_{3}^{2}(t)} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}} ,$ $t \in [{{t}_{0}},T].$ Компоненты найденного управления удовлетворяют заданному ограничению (7), которое может быть записано в виде $d(t) \leqslant {{d}_{0}} = 0.08,$ $t \in [{{t}_{0}},T].$ В численных расчетах получены следующие значения для состояния системы (1), (2) в конечный момент времени $T{\text{:}}$

Рассмотренные выше примеры показывают эффективность применения предлагаемого в работе численно-аналитического метода решения задачи оптимальной пространственной переориентации КА. Найденные управления удовлетворяют заданным ограничениям и с достаточно высокой степенью точности обеспечивают приведение системы в желаемое конечное состояние. Отметим, что имеются интервалы, где двигатели полностью отключаются и КА продолжает вращательное движение по инерции, что вполне соответствует цели минимизации затрат на управление.

Пример 3. Рассмотрим далее задачу оптимальной переориентации реального КА (МКС), для которого моменты инерции имеют следующие значения [27]:

В статье [12] исследована задача оптимального разворота КА в традиционной и модифицированной постановках. Для обеспечения сравнимости результатов, получаемых при различных значениях исходных параметров, численные расчеты произведены в безразмерных единицах измерений.

Краевые условия для рассматриваемого примера возьмем такими же, как в [12] (в безразмерных единицах):

Целевой функционал

является линейной комбинацией затрат времени и энергии на разворот КА. Конечный момент времени $T$ заранее не задан и подлежит определению из ЗОУ (1), (2), (48)–(50). Ниже для сравнения приведены результаты, полученные с использованием различных подходов:

1) в традиционной постановке ЗОУ [12]: $T = 0.991,$ $J = 1.3547;$

2) в модифицированной постановке ЗОУ [12]: $T = 0.966,$ $J = 1.3674{\text{;}}$

3) в предлагаемом методе: $T = 0.9934,$ $J = 1.354469.$

Здесь через $J$ обозначено оптимальное значение целевого функционала (50) в соответствующем методе решения задачи.

При применении изложенного в данной работе алгоритма отклонения угловых скоростей и компонент кватерниона от желаемых значений в конечный момент $T$ оказались по модулю порядка ${{10}^{{ - 5}}}.$ Таким образом, траектория системы (1), (2), исходящая из начальной точки (48), с достаточно высокой степенью точности приводится в заданное конечное состояние (49), минимизируя при этом комбинированный целевой функционал (50).

Рассмотренный пример показывает возможность применения предлагаемого метода решения ЗОУ для случая с нефиксированным конечным моментом времени $T.$ Здесь на каждом $k$-м шаге итерационного процесса квазилинеаризации производится постепенное уменьшение значения $T = {{T}^{{(k)}}}$ с некоторым постоянным шагом $\Delta T$ до тех пор, пока не будет достигнуто минимальное значение функционала (50).

ЗАКЛЮЧЕНИЕ

Работа посвящена решению задачи оптимального управления пространственной переориентацией КА, который описывается системой дифференциальных уравнений, нелинейных по фазовым координатам и линейных по управлению; подинтегральная функция в целевом функционале не является квадратичной формой. Рассматриваемая задача относится к классу ЗОУ на конечном отрезке времени, с закрепленными концами траекторий и с ограниченным управлением. Для ее решения в работе предложен численно-аналитический алгоритм с использованием принципа максимума, процедуры квазилинеаризации и метода разделения фазовых и сопряженных переменных. На каждом шаге квазилинеаризации возникает ДТКЗ для некоторой нелинейной системы дифференциальных уравнений, которая далее сводится к задаче Коши, где начальное условие ${\mathbf{p}}({{t}_{0}}) = {{{\mathbf{p}}}_{0}}$ для вектора сопряженных переменных имеет вид (37). Для решения ДТКЗ мы не используем итеративные алгоритмы типа методов стрельбы [28], многократной стрельбы [29] и др. На каждом шаге процедуры квазилинеаризации осуществляется аналитическое решение ДТКЗ, что позволяет существенно сократить затраты компьютерного времени и повысить точность вычислений.

В статье показана единственность представления ${{{\mathbf{p}}}_{0}}$ в виде (37) при условии невырожденности матрицы ${{\Omega }_{{12}}}(T,{{t}_{0}}).$ В принципе матрицы $C,$ $D$ и вектор ${\mathbf{e}}$ могут быть вычислены по формуле (44). При этом потребуется численное интегрирование $4{{n}^{2}} + 2n$ дифференциальных уравнений (41), (42). А при использовании предлагаемого метода разделения переменных число дифференциальных уравнений в (25), (26), (33) с учетом симметричности матриц $K$ и $L$ будет равно $2{{n}^{2}} + 3n,$ что дает значительный выигрыш в затратах компьютерного времени. А в некоторых частных случаях (см. замечание 1) вычисление матриц $C,$ $D$ и вектора ${\mathbf{e}}$ еще больше упрощается.

В ЗОУ с закрепленными концами требуется, чтобы траектория системы в конечный момент времени проходила через заданную точку, т.е. необходимо обеспечить выполнение условия ${\mathbf{x}}(T) = {{{\mathbf{x}}}_{T}}$ (14). Существуют методы, в которых исходная задача с закрепленными концами сводится к задаче со свободными правыми концами, в которой условие (14) отсутствует. К целевому функционалу $J({\mathbf{u}})$ добавляется терминальное слагаемое, например, в виде “штрафа” $0.5\,[{\mathbf{x}}(T) - {{{\mathbf{x}}}_{T}}]{\kern 1pt} '(T)F[{\mathbf{x}}(T) - {{{\mathbf{x}}}_{T}}]$ за отклонение траектории системы в конечный момент времени от желаемого состояния. При этом для обеспечения достаточно точного выполнения условия ${\mathbf{x}}(T) \approx {{{\mathbf{x}}}_{T}}$ приходится увеличивать “штраф”, задавая большие значения для диагональных элементов матрицы $F.$ Это приводит к тому, что терминальное слагаемое начинает превалировать над исходным целевым функционалом, т.е. фактически получаем задачу минимизации “штрафа” вместо минимизации $J({\mathbf{u}}).$ В связи с этим в данной статье исходная ЗОУ с закрепленными концами решается без использования методов сведения к задаче со свободными правыми концами.

Следует также отметить, что мы не заменяем исходное нелинейное дифференциальное уравнение, описывающее динамику объекта управления, на линеаризованное уравнение. Процедура квазилинеаризации здесь применяется для решения ДТКЗ (17), (18). Используя найденное на $k$-м шаге квазилинеаризации значение ${{{\mathbf{p}}}_{0}} = {\mathbf{p}}_{0}^{{(k)}}$ в качестве начального условия ${\mathbf{p}}({{t}_{0}}) = {{{\mathbf{p}}}_{0}},$ решаем задачу Коши для нелинейной системы (17). Далее вычисленную вектор-функцию ${\mathbf{p}}(t)$ используем для определения управления ${\mathbf{u}}(t),$ удовлетворяющего ограничению (12). Полученное управление ${\mathbf{u}}(t)$ подставляем в исходное нелинейное уравнение (11) с начальным условием ${\mathbf{x}}({{t}_{0}}) = {{{\mathbf{x}}}_{0}}$ и проверяем выполнение конечного условия ${\mathbf{x}}(T) = {{{\mathbf{x}}}_{T}}.$ Процедура квазилинеаризации для ДТКЗ (17), (18) продолжается до тех пор, пока на некоторой $k$-й итерации не будет достигнуто выполнение конечного условия для уравнения (11) с некоторой заданной точностью: $\left| {{\mathbf{x}}(T) - {{{\mathbf{x}}}_{T}}} \right| < {\varepsilon },$ где ${\varepsilon } > 0$ – достаточно малое число.

Задача оптимального управления пространственным разворотом КА решается здесь для общего случая ${{J}_{1}} \ne {{J}_{2}} \ne {{J}_{3}},$ без предположения сферически симметричности или осесимметричности КА. Не требуется, чтобы КА находился в состоянии покоя в начальный и конечный моменты времени. Предполагается, что разворот КА происходит не вокруг некоторой неподвижной оси, мгновенная ось вращения КА может динамически менять свое направление в пространстве в течение интервала времени $[{{t}_{0}},T].$ Возможно рассмотрение задачи совмещения режимов торможения и переориентации КА, когда требуется остановить вращение КА, т.е. добиться выполнения условия ${\mathbf{\omega }}(T) = {\mathbf{0}},$ и одновременно обеспечить желаемую ориентацию КА в конечный момент времени: ${\mathbf{\Lambda }}(T) = {{{\mathbf{\Lambda }}}_{T}}.$

Показана возможность применения предлагаемого метода решения ЗОУ в случаях, когда целевой функционал не является квадратичным, а допустимая область управлений имеет вид параллелепипеда или эллипсоида (см. примеры 1 и 2). В примере 3 для реального КА (МКС) показана возможность решения ЗОУ с заранее не заданным конечным моментом времени $T$. Найденные управления обеспечивают выполнение конечного условия (14) с достаточно высокой степенью точности для исходной нелинейной системы (11).

Функция ${\mathbf{f}}({\mathbf{x}},t)$ в правой части дифференциального уравнения (11) является нелинейной относительно фазовых координат ${\mathbf{x}}$ и зависит от времени t. Такая модель объекта управления позволяет учесть в будущем влияние гравитационного поля Земли и аэродинамических сил на низкоорбитальные КА. Функционал (15) является квадратичным относительно ${\mathbf{x}}$ и ${\mathbf{u}},$ т.е. можно рассмотреть задачу разворота КА с целевым функционалом, предусматривающим не только минимизацию затрат на управление, но и улучшение качества переходных процессов.