Космические исследования, 2020, T. 58, № 3, стр. 235-248

1. ВВЕДЕНИЕ

Рассматривается актуальная проблема оптимизации траекторий космического аппарата, оснащенного электроракетным двигателем (ЭРД) [1]. Такой двигатель обеспечивает высокие скорости истечения реактивной струи (десятки километров в секунду) и, поэтому, в целом более эффективен, чем химический. Ставится задача отыскания управления движением КА, совершающего перелет за фиксированное время при помощи ЭРД с идеально регулируемой тягой в центральном гравитационном поле из одного заданного положения, характеризующегося координатами и скоростями КА, в другое заданное положение. При этом требуется максимизировать величину конечной массы КА. Следует отметить, что для практических расчетов часто применяются математические модели КА, в которых тяга ЭРД ограничена по модулю и изменяется ступенчато. Однако результаты, полученные в рамках модели идеально регулируемой тяги, также весьма важны, поскольку зависят от траекторных, но не от массовых параметров КА и, поэтому, могут быть использованы на ранних этапах проектирования, когда технические характеристики КА еще находятся в стадии уточнения.

Анализ многочисленных работ посвященных проблеме оптимизации перелетов с идеально регулируемой тягой [1–10] позволяет заключить, что задача носит многоэкстремальный характер. При этом отыскание оптимальных решений математическими методами [11–14], не учитывающими специфики конкретной задачи, хотя и возможно [7], но сопряжено со значительными вычислительными затратами и требует проведения дополнительных исследований. Другой подход к проблеме основан на построении серии экстремальных траекторий, отличающихся друг от друга целым количеством витков вокруг гравитационного центра и последующем анализе полученных результатов [8].

В данной работе отыскание оптимального управления осуществляется в рамках второго подхода. При этом для построения экстремальных траекторий с заданной угловой дальностью предлагается следующий способ. На первом этапе расчетов определяется нулевое приближение (составная транспортирующая траектория) являющееся решением вспомогательной задачи оптимизации в импульсной постановке. Для его построения используется метод, основанный на принципе оптимальности Беллмана [15]. Затем делается “правдоподобное” предположение о том, что решение исходной непрерывной задачи при заданной угловой дальности находится в окрестности составной транспортирующей траектории. Для его отыскания на последующих этапах расчетов используется метод локальных вариаций (задача решается в линейной постановке) [16] и метод локального спуска (решается нелинейная краевая задача принципа максимума Понтрягина в точной постановке) [17].

Указанная схема была предложена Н.Н. Моисеевым [18] для поиска экстремума невыпуклой аддитивной функции. В работах [4–6], на ее основе, для широкого диапазона краевых условий было получено множество оптимальных траекторий перелета КА от Земли к астероиду Апофис. При этом в процессе проведения расчетов были выявлены некоторые недостатки, присущие описанным в [4–6] вычислительным процедурам (низкая точность определения базовой траектории, большие вычислительные затраты), а также ограничения самой схемы поиска (невозможность отыскания нескольких различных решений для одних и тех же краевых условий). Предложенный в данной работе метод свободен от указанных выше недостатков.

Некоторые особенности практического применения указанного метода проиллюстрированы на примере решения одной частной задачи оптимизации перелета КА к сближающемуся с Землей астероиду Апофис.

2. ПОСТАНОВКА И ОБСУЖДЕНИЕ ЗАДАЧИ

Рассмотрим движение КА с идеально регулируемым ЭРД в центральном гравитационном поле. Пусть задана некоторая прямоугольная инерциальная система координат OXYZ и математическая модель движения КА:

где ${\mathbf{r}} = {{\left[ {x,y,z} \right]}^{{\text{T}}}}$ и ${\mathbf{v}} = {{\left[ {{{v}_{x}},{{v}_{y}},{{v}_{z}}} \right]}^{{\text{T}}}}$ – радиус-вектор и вектор скорости КА в OXYZ; ${\mathbf{f}}\left( {\mathbf{r}} \right) = - {\mu }\frac{{\mathbf{r}}}{{{{r}^{3}}}}$ – ускорение силы тяготения; $r = \left| {\mathbf{r}} \right|$; ${\mu }$ – гравитационный параметр; ${\mathbf{\alpha }}$ – вектор управляющего ускорения КА; $t$ – текущее время. Полагается, что момент начала перелета ${\tau }$, момент конца перелета $\vartheta $, начальные условия: и конечные условия траектории КА: известны, а ограничения на вектор ${\mathbf{\alpha }}$ отсутствуют. В соответствии с [3] масса КА с ЭРД в момент $\vartheta $ определяется по формуле: где ${{m}_{{SC}}}\left( {\tau } \right)$ – начальная масса КА; ${{N}_{{SC}}}$ – постоянная во времени мощность ЭРД; $J$ – функционал вида:

Очевидно, что при прочих равных условиях величина ${{m}_{{SC}}}\left( \vartheta \right)$ тем больше, чем меньше значение функционала (4).

Минимум (4), по-видимому, можно найти только численно. При этом наиболее точные численные результаты в этой области были получены при помощи принципа максимума Понтрягина [19]. Применяя принцип максимума к (1)–(4) запишем сопряженную систему дифференциальных уравнений:

где ${{\psi }_{r}}$ и ${{\psi }_{v}}$ – векторы сопряженных переменных, а также формулу для определения ${\mathbf{\alpha }}\left( t \right)$

Введем в рассмотрение: $\psi \left( t \right) = {{\left[ {{{\psi }_{v}}{{{\left( t \right)}}^{{\text{T}}}},{{\psi }_{r}}{{{\left( t \right)}}^{{\text{T}}}}} \right]}^{{\text{T}}}}.$ Тогда минимизация функционала (4) сводится к подбору некоторого вектора начальных условий ${{\psi }^{e}} = \psi \left( {\tau } \right)$, который и является решением двухточечной краевой задачи, т.е. переводит (1), (5) из (2) в (3).

К сожалению, для моделей, описываемых нелинейными системами дифференциальных уравнений типа (1, 5), принцип максимума Понтрягина является необходимым, но не достаточным условием оптимальности [19]. На практике это означает, что из целого ряда возможных решений ${{\psi }^{e}}$ краевой задачи (1)–(3), (5), (6) лишь некоторые на самом деле доставляют минимум функционалу (4) [7]. Кроме того, следует иметь в виду, что оптимум (4) может одновременно достигаться на нескольких различных траекториях системы (1)–(3), (5), (6) [3, 7]. Таким образом, в общем случае задача определения глобального минимума (4) для (1)–(3) на сегодняшний день неразрешима. Тем не менее, существуют различные подходы, позволяющие получать некоторые частные результаты, имеющие важное практическое значение. Один из таких подходов основывается на использовании методов многоэкстремальной оптимизации [11–14]. К их числу относятся методы мультистарта, детерминированные или стохастические; метаэвристические методы, а именно генетические алгоритмы, алгоритмы частиц в стае и т.д.; методы перехода из одного локального минимума в другой, например алгоритм тяжелого шарика, метод Бранина и т.д. Для (1)–(3), (5), (6) все они сведутся к генерации серии начальных (нулевых) приближений ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$ сопряженных переменных $\psi \left( {\tau } \right)$ и их последующему уточнению теми или иными способами. Следует, однако, отметить, что обосновано задать допустимые диапазоны изменения $\psi \left( {\tau } \right)$ весьма затруднительно. Кроме того, нелинейная краевая задача принципа максимума для (1)–(3), (5), (6) чрезвычайно чувствительна к выбору ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$, особенно когда результирующая траектория проходит в относительной близости гравитационного центра. Таким образом, непосредственное применение известных алгоритмов многоэкстремальной оптимизации к изучаемой задаче может быть сопряжено со значительными вычислительными затратами.

Поэтому был принят другой подход к решению проблемы [8]. Этот подход базируются на том, что при заданных граничных условиях и времени перелета оптимум (4) часто достигается на траекториях (1)–(3), (5), (6), отличающихся друг от друга целым числом $\Omega $ витков вокруг притягивающего центра. Следовательно, для различных значений угловой дальности перелета $\delta \varphi \left( {\omega } \right)$, где ${\omega } = {\text{0,}}...{\text{,}}\Omega $, можно построить соответствующие экстремали (1)–(3), (5), (6) и сравнить между собой полученные величины функционала (4), или, иначе говоря, решить следующую оптимизационную задачу.

Задача 1. Необходимо найти векторы ${{\psi }^{e}}\left( {\omega } \right)$, обеспечивающие заданное значение угловой дальности $\delta \varphi \left( {\omega } \right)$ при перемещении (1), (5), (6) из (2) в (3), а также сформировать множество

элементы которого суть различные ${{\psi }^{e}}\left( {\omega } \right)$, на которых функционал (4) достигает своего минимума – величины ${{J}_{{opt}}}$, также подлежащей определению.

В данной работе для решения задачи 1 предложен алгоритм построения экстремальных траекторий с заданной угловой дальностью. Этот алгоритм реализует стратегию поиска, сформулированную Н.Н. Моисеевым в [18], и состоит из трех основных этапов. На первом этапе нулевое приближение (составная транспортирующая траектория) составляется из участков кеплеровских орбит, соединяющих опорные точки ${{P}_{i}}$ $\left( {i = 0,..,N} \right)$, положение которых определяется в процессе решения вспомогательной задачи в импульсной постановке методом динамического программирования (МДП). Следует отметить, что МДП подвержен “проклятию размерности” и на практике широко применяется его модификация – метод дифференциального динамического программирования (МДДП), который основан на разложении реккурентного соотношения Беллмана в ряд Тейлора относительно некоторой опорной траектории [20–22]. Однако в нашем случае решение вспомогательной задачи (точнее, ее конечномерной аппроксимации) строится при помощи классического МДП, который позволяет отыскивать глобальный экстремум аддитивной функции на соответствующей вычислительной сетке, даже при условии, что эта функция не является унимодальной в расчетной области [18]. Получить такое решение без существенных затрат вычислительных ресурсов возможно, приняв некоторые допущения, позволяющие смягчить “проклятие размерности”. В нашем случае полагается, что оптимальные траектории перелета КА близки к плоскости OXY (например, к плоскости эклиптики) и $\delta \varphi \left( {{\omega ,}t} \right)$ монотонно возрастает (т.е. смена направления движения невозможна). Обычно на практике трансверсальная составляющая вектора скорости КА, как правило, очень велика и маневр, в процессе которого эта составляющая меняла бы знак, редко может оказаться оптимальным. Однако такое возможно (особенно при необходимости значительного изменении плоскости движения) [23]. Поэтому указанные допущения, безусловно, ограничивают область применения данной методики.

На втором этапе расчетов, делается “правдоподобное” предположение о том, что решение исходной непрерывной задачи при заданной угловой дальности находится вблизи составной транспортирующей траектории. Поэтому в ее окрестности при помощи метода локальных вариаций и МТТ строятся траектории первого приближения, описывающие движение линеаризованной системы уравнений КА. Наконец на третьем этапе траектории начального приближения используются методом локального спуска для точного решения нелинейной краевой задачи принципа максимума (1)–(3), (5), (6). Иными словами, точное пространственное решение (1)–(3), (5), (6) отыскивается на основе использования плоского начального приближения. Затем полученные для различных значений $\delta \varphi \left( {\omega } \right)$ величины (4) сравниваются между собой на предмет выявления ${{J}_{{opt}}}$.

3. ФОРМИРОВАНИЕ СОСТАВНЫХ ТРАНСПОРТИРУЮЩИХ ТРАЕКТОРИЙ

Пусть движение КА в основном совершается в плоскости OXY системы координат OXYZ (т.е. составляющими $z$, ${{v}_{z}}$ на данном этапе расчетов можно пренебречь). Будем полагать, что положение некоторой опорной точки ${{P}_{i}}$ полностью определяется параметром:

и вектором ${\mathbf{x}}\left( {{{\varphi }_{i}}} \right) = {{\left[ {r\left( {{{\varphi }_{i}}} \right),t\left( {{{\varphi }_{i}}} \right)} \right]}^{{\text{T}}}}$, где $N$ – количество опорных точек, $r\left( {{{\varphi }_{i}}} \right)$ и $t\left( {{{\varphi }_{i}}} \right)$ – величины $r$ и $t$ для ${{\varphi }_{i}}$, символ ${{\left( {...} \right)}_{{0 - 2{\pi }}}}$ означает, что величина искомого угла должна вычисляться с учетом знаков числителя и знаменателя аргумента арктангенса и лежать в диапазоне от 0 до $2{\pi }$ радиан.

Пусть также:

У. 1. При $i = 0,...,N - 1$ верно неравенство $t\left( {{{\varphi }_{{i + 1}}}} \right) > t\left( {{{\varphi }_{i}}} \right).$

У. 2. Точка ${{P}_{0}}$ характеризуется параметром ${{\varphi }_{0}} = {{\varphi }_{{\tau }}}$ и вектором ${\mathbf{x}}\left( {{{\varphi }_{0}}} \right) = {{\left[ {\sqrt {x_{{\tau }}^{2} + y_{{\tau }}^{2}} ,{\tau }} \right]}^{{\text{T}}}}.$

У. 3. Точка ${{P}_{N}}$ характеризуется параметром ${{\varphi }_{N}} = {{\varphi }_{\vartheta }}\left( {\omega } \right)$ и вектором ${\mathbf{x}}\left[ {{{\varphi }_{N}}} \right] = {{\left[ {\sqrt {x_{\vartheta }^{2} + y_{\vartheta }^{2}} ,\vartheta } \right]}^{{\text{T}}}}.$

Соотношение (8) задает траектории, у которых угол ${{\varphi }_{i}}$ монотонно увеличивается от ${{P}_{i}}$ к ${{P}_{{i + 1}}}$. Следуя [18], введем в рассмотрение элементарную операцию ${{{\mathbf{E}}}_{x}}\left( {{{\varphi }_{i}},{\mathbf{x}}\left( {{{\varphi }_{i}}} \right),{{\varphi }_{{i + 1}}},{\mathbf{x}}\left( {{{\varphi }_{{i + 1}}}} \right)} \right)$, которая каждой паре $\left\{ {{{P}_{i}},{{P}_{{i + 1}}}} \right\}$ ставит в соответствие векторы ${\mathbf{u}}\left( {{{\varphi }_{i}}} \right)$, ${\mathbf{w}}\left( {{{\varphi }_{{i + 1}}}} \right)$ скоростей КА в точках ${{P}_{i}}$ и ${{P}_{{i + 1}}}$, рассчитанные при условии, что перелет КА из ${{P}_{i}}$ в ${{P}_{{i + 1}}}$ совершается по кеплеровской орбите. В данной работе искомые ${\mathbf{u}}\left( {{{\varphi }_{i}}} \right)$ и ${\mathbf{w}}\left( {{{\varphi }_{{i + 1}}}} \right)$ определяются на основе использования весьма эффективного и надежного алгоритма, описанного в [24]. В узловых точках ${{P}_{0}}$,${{P}_{1}}$,..,${{P}_{N}}$ составной транспортирующей траектории КА должен получать соответствующие управляющие импульсы:

Предлагается задавать ${\mathbf{x}}\left( {{{\varphi }_{i}}} \right)$ таким образом, чтобы сумма модулей импульсов (9)

была минимальна. Таким образом, построение составной транспортирующей траектории можно свести к решению следующей задачи.

Задача 2. Найти векторы ${\mathbf{x}}\left( {{{\varphi }_{i}}} \right)$, удовлетворяющие условиям У. 1–У. 3 и доставляющие минимум функционалу (10), при заданном значении ${\omega }$.

Для отыскания ${\mathbf{x}}\left( {{{\varphi }_{i}}} \right)$ будем использовать МДП [15, 18]. Проведем двухэтапную конечномерную аппроксимацию задачи 2. На первом этапе каждому углу ${{\varphi }_{i}}$, $i = 1, \ldots ,N - 1$ поставим в соответствие множество ${{{\mathbf{X}}}_{i}}$, состоящее из $L \cdot M$ векторов (иначе, узлов) ${{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right),$ таких что: ${{{\mathbf{X}}}_{i}} = \left\{ {{{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right) = {{{\left[ {{{r}^{{\left( l \right)}}},{{t}^{{\left( m \right)}}}} \right]}}^{{\text{T}}}}:} \right.$ $l = 1,..,L,$ $m = 1, \ldots ,M,$ $\left. {_{{^{{}}}}^{{^{{}}}}j = M\left( {l - 1} \right) + m} \right\}$, где ${{r}^{{\left( l \right)}}}\left( {{{\varphi }_{i}}} \right)$ и ${{t}^{{\left( m \right)}}}\left( {{{\varphi }_{i}}} \right)$ известные дискретные значения величин $r\left( {{{\varphi }_{i}}} \right)$ и $t\left( {{{\varphi }_{i}}} \right)$. Кроме того зададим ${{{\mathbf{X}}}_{0}} = \left\{ {{{{\mathbf{x}}}^{{\left( 1 \right)}}}\left( {{{\varphi }_{0}}} \right)} \right\}$ и ${{{\mathbf{X}}}_{N}} = \left\{ {{{{\mathbf{x}}}^{{\left( 1 \right)}}}\left( {{{\varphi }_{N}}} \right)} \right\}$, где ${{{\mathbf{x}}}^{{\left( 1 \right)}}}\left( {{{\varphi }_{0}}} \right)$ совпадает с ${\mathbf{x}}$ из У. 2, а ${{{\mathbf{x}}}^{{\left( 1 \right)}}}\left( {{{\varphi }_{N}}} \right)$ совпадает с ${\mathbf{x}}$ из У. 3. На втором этапе для всех допустимых пар ${{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right) \in {{{\mathbf{X}}}_{i}}$ и ${{{\mathbf{x}}}^{{\left( k \right)}}}\left( {{{\varphi }_{{i + 1}}}} \right) \in {{{\mathbf{X}}}_{{i + 1}}}$, где $i = 1, \ldots ,N - 2$; $j = 1, \ldots ,L \cdot M$; $k = 1,..,L \cdot M$, при помощи элементарной операции ${{{\mathbf{E}}}_{x}}\left( {{{\varphi }_{i}},{{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right)} \right.,$ $\left. {{{\varphi }_{{i + 1}}},{{{\mathbf{x}}}^{{\left( k \right)}}}\left( {{{\varphi }_{{i + 1}}}} \right)} \right)$ определим скорости ${{{\mathbf{u}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{i}}} \right)$ отлета КА от ${{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right)$, а также скорости ${{{\mathbf{w}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{{i + 1}}}} \right)$ подлета КА к ${{{\mathbf{x}}}^{{\left( k \right)}}}\left( {{{\varphi }_{{i + 1}}}} \right)$ и сформируем множества ${{{\mathbf{U}}}_{i}} = \left\{ {{{{\mathbf{u}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{i}}} \right)} \right\},$ ${{{\mathbf{W}}}_{{i + 1}}} = \left\{ {{{{\mathbf{w}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{{i + 1}}}} \right)} \right\},$ состоящие из ${{\left( {L \cdot M} \right)}^{2}}$ элементов. Здесь и далее первый верхний индекс обозначает начальный, а второй верхний индекс – конечный узел перелета. Аналогичным образом построим ${{{\mathbf{U}}}_{0}}$, ${{{\mathbf{W}}}_{1}}$ для $i = 0$, и ${{{\mathbf{U}}}_{{N - 1}}}$, ${{{\mathbf{W}}}_{N}}$ для $i = N - 1$, включающие в себя $L \cdot M$ элементов.

Процедура пошагового построения решения задачи 2 на основе ${{{\mathbf{X}}}_{i}}$, ${{{\mathbf{U}}}_{i}}$, ${{{\mathbf{W}}}_{i}}$ имеет следующий вид. Первоначально полагаем $i = 1$ и для всех индексов $j = 1,..,L \cdot M$ и $k = 1,..,L \cdot M$ вычисляем:

где ${{{\mathbf{u}}}^{{\left( {1,j} \right)}}}\left( {{{\varphi }_{0}}} \right) \in {{{\mathbf{U}}}_{0}}$, ${{{\mathbf{u}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{1}}} \right) \in {{{\mathbf{U}}}_{1}}$, ${{{\mathbf{w}}}^{{\left( {1,j} \right)}}}\left( {{{\varphi }_{1}}} \right) \in {{{\mathbf{W}}}_{1}}$. Затем задаемся начальными значениями $i = 2,$ $j = k = 1$, перебираем все допустимые узлы из множества ${{{\mathbf{X}}}_{{i - 1}}}$, и, для каждого ${{{\mathbf{x}}}^{{\left( n \right)}}}\left( {{{\varphi }_{{i - 1}}}} \right)$, где $n = 1,..,L \cdot M$, по заданным индексам $n$ и $j$ находим вектор ${{{\mathbf{w}}}^{{\left( {n,j} \right)}}}\left( {{{\varphi }_{i}}} \right) \in {{{\mathbf{W}}}_{i}}.$ Тогда, в соответствии с МДП, оптимальное значение функционала $\Delta {{v}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{0}},{{\varphi }_{i}}} \right)$ и искомый узел ${{{\mathbf{x}}}^{{\left( n \right)}}}\left( {{{\varphi }_{{i - 1}}}} \right)$, на котором это значение достигается, можно найти при помощи следующих реккурентных соотношений:

Перебирая допустимые $j$, $k$ и, двигаясь последовательно от $i = 2$ к $i = N,$ определим искомую траекторию ${{P}_{0}}$,${{P}_{1}}$,..,${{P}_{N}}$. В рамках конечномерной аппроксимации задачи 2, такая траектория доставляет глобальный минимум функционалу (10) на расчетной сетке $\left\{ {{{\varphi }_{i}},{{{\mathbf{X}}}_{i}}:i = 0,...,N} \right\}$, даже если (10) не является унимодальным в расчетной области.

Покажем, что указанный способ отыскания ${{P}_{0}}$, ${{P}_{1}}$, …,${{P}_{N}}$ требует меньших вычислительных затрат нежели методика, изложенная в [4–6]. Следуя [18], введем в рассмотрение координатную сетку ${{\left\{ {t,{{v}_{x}},{{v}_{y}},x,y} \right\}}^{{}}}$ такую, что количество точек на каждой из шкал ${{v}_{x}}$, ${{v}_{y}}$, $x$, $y$ равно $K$. Тогда на интервале $\left[ {{\tau } = {{t}_{i}},\vartheta = {{t}_{{i + 1}}}} \right],$ где ${{t}_{i}},{{t}_{{i + 1}}}$ – соседние точки на шкале времени, величина функционала (4) определяется восемью параметрами варьирования: ${{v}_{x}}\left( {{{t}_{i}}} \right),$ ${{v}_{y}}\left( {{{t}_{i}}} \right),$ $x\left( {{{t}_{i}}} \right),$ $y\left( {{{t}_{i}}} \right),$ ${{v}_{x}}\left( {{{t}_{{i + 1}}}} \right),$ ${{v}_{y}}\left( {{{t}_{{i + 1}}}} \right)$, $x\left( {{{t}_{{i + 1}}}} \right)$, $y\left( {{{t}_{{i + 1}}}} \right)$, и должна быть вычислена ${{K}^{8}}$ раз. При этом в рамках задачи 2, функционал (10) зависит от шести параметров варьирования: $r\left( {{{\varphi }_{i}}} \right),$ $t\left( {{{\varphi }_{i}}} \right),$ $r\left( {{{\varphi }_{{i + 1}}}} \right),$ $t\left( {{{\varphi }_{{i + 1}}}} \right),$ ${{{\mathbf{u}}}_{1}}\left( {{{\varphi }_{{i + 1}}}} \right),$ ${{{\mathbf{u}}}_{2}}\left( {{{\varphi }_{{i + 1}}}} \right).$ Если предположить, что число расчетных точек на каждой из шкал $r$, $t$, ${{{\mathbf{u}}}_{1}}$, ${{{\mathbf{u}}}_{2}}$ также равно K, то на интервале $\left[ {{{\varphi }_{i}},{{\varphi }_{{i + 1}}}} \right]$ величину $\Delta v$ необходимо вычислить ${{K}^{6}}$ раз.

Подробный алгоритм решения задачи 2 описан ниже.

Алгоритм решения задачи 2.

Этап 1. Инициализация.

1.1. Задаем ${\omega }$ (число дополнительных витков вокруг гравитационного центра), сохраняем ${{{\mathbf{x}}}^{{\left( 1 \right)}}}\left( {{{\varphi }_{0}}} \right)$ = ${{\left[ {\sqrt {x_{\tau }^{2} + y_{\tau }^{2}} ,{\tau }} \right]}^{{\text{T}}}}$ и ${{{\mathbf{x}}}^{{\left( 1 \right)}}}\left( {{{\varphi }_{N}}} \right)$ = ${{\left[ {\sqrt {x_{\vartheta }^{2} + y_{\vartheta }^{2}} ,\vartheta } \right]}^{{\text{T}}}}.$

1.2. Полагаем индексы $i = 1$, $l = m = 1$.

1.3. Вычисляем $j = M\left( {l - 1} \right) + m$ и сохраняем ${{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right) = {{\left[ {{{r}^{{\left( l \right)}}},{{t}^{{\left( m \right)}}}} \right]}^{{\text{T}}}}.$

1.4. Если $m = M$ переходим к шагу 1.5, иначе, полагаем $m = m + 1$, и переходим к шагу 1.3.

1.5. Если $l = L$ переходим к шагу 1.6, иначе, полагаем $l = l + 1$, $m = 1$, и переходим к шагу 1.3.

1.6. Если $i = N - 1$ переходим к шагу 1.7, иначе, полагаем $i = i + 1$, $l = m = 1$, и переходим к шагу 1.3.

1.7. Полагаем индексы $i = j = k = 1$.

1.8. Извлекаем ${\mathbf{x}}_{2}^{{\left( j \right)}}\left( {{{\varphi }_{i}}} \right)$ и ${\mathbf{x}}_{2}^{{\left( k \right)}}\left( {{{\varphi }_{{i + 1}}}} \right)$. Проверяем, что ${\mathbf{x}}_{2}^{{\left( k \right)}}\left( {{{\varphi }_{{i + 1}}}} \right) > {\mathbf{x}}_{2}^{{\left( j \right)}}\left( {{{\varphi }_{i}}} \right)$ (см. У. 1). Если это условие выполнено, переходим к шагу 1.9, иначе к шагу 1.11.

1.9. При помощи элементарной операции ${{{\mathbf{E}}}_{x}}\left( {{{\varphi }_{i}},{{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right),} \right.$ $\left. {{{\varphi }_{{i + 1}}},{{{\mathbf{x}}}^{{\left( k \right)}}}\left( {{{\varphi }_{{i + 1}}}} \right)} \right)$ вычисляем и сохраняем векторы ${{{\mathbf{u}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{i}}} \right)$ и ${{{\mathbf{w}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{{i + 1}}}} \right).$

1.10. Значение $\Delta {{v}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{0}},{{\varphi }_{i}}} \right)$ инициализируем большим положительным числом.

1.11. Если $k = L \cdot M$, или $i = N - 1$, переходим к шагу 1.12, иначе, полагаем $k = k + 1$, и переходим к шагу 1.8.

1.12. Если $j = L \cdot M$, то переходим к шагу 1.13, иначе, полагаем $j = j + 1$, $k = 1$, и переходим к шагу 1.8.

1.13. Если $i = N - 1$, то выходим из цикла, иначе, полагаем $i = i + 1$,$j = 1$, $k = 1$, и переходим к шагу 1.8.

Этап 2. Первый шаг.

2.1. Полагаем индексы $j = k = 1$.

2.2. Извлекаем ${\mathbf{x}}_{2}^{{\left( j \right)}}\left( {{{\varphi }_{0}}} \right)$ и ${\mathbf{x}}_{2}^{{\left( k \right)}}\left( {{{\varphi }_{1}}} \right).$ Проверяем, что ${\mathbf{x}}_{2}^{{\left( k \right)}}\left( {{{\varphi }_{1}}} \right) > {\mathbf{x}}_{2}^{{\left( j \right)}}\left( {{{\varphi }_{0}}} \right)$ (см. У. 1). Если это условие выполнено, переходим к шагу 2.3, иначе к шагу 2.4.

2.3. При помощи ${{{\mathbf{E}}}_{x}}\left( {{{\varphi }_{0}},{{{\mathbf{x}}}^{{\left( 1 \right)}}}\left( {{{\varphi }_{0}}} \right),{{\varphi }_{1}},{{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{1}}} \right)} \right)$ находим ${{{\mathbf{u}}}^{{\left( {1,j} \right)}}}\left( {{{\varphi }_{0}}} \right),$ ${{{\mathbf{w}}}^{{\left( {1,j} \right)}}}\left( {{{\varphi }_{1}}} \right)$ и сохраняем $\Delta {{v}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{0}},{{\varphi }_{1}}} \right) = $ $ = \left| {{{{\mathbf{u}}}^{{\left( {1,j} \right)}}}\left( {{{\varphi }_{0}}} \right) - {{{\left[ {{{v}_{x}}\left( \tau \right),{{v}_{y}}\left( \tau \right)} \right]}}^{{\text{T}}}}} \right|$ + $\left| {{{{\mathbf{u}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{1}}} \right) - {{{\mathbf{w}}}^{{\left( {1,j} \right)}}}\left( {{{\varphi }_{1}}} \right)} \right|.$

2.4. Если $k = L \cdot M$, то переходим к шагу 2.5, иначе, полагаем $k = k + 1$, и переходим к шагу 2.2.

2.5. Если $j = L \cdot M$, то выходим из цикла, иначе, полагаем $j = j + 1$, $k = 1$, и переходим к шагу 2.2.

Этап 3. Последующие шаги.

3.1. Полагаем индексы $i = 2$, $j = k = n = 1$.

3.2. Извлекаем ${\mathbf{x}}_{2}^{{\left( n \right)}}\left( {{{\varphi }_{{i - 1}}}} \right)$ и ${\mathbf{x}}_{2}^{{\left( j \right)}}\left( {{{\varphi }_{i}}} \right).$ Проверяем, что ${\mathbf{x}}_{2}^{{\left( j \right)}}\left( {{{\varphi }_{i}}} \right) > {\mathbf{x}}_{2}^{{\left( n \right)}}\left( {{{\varphi }_{{i - 1}}}} \right)$ (см. У. 1). Если это условие выполнено, переходим к шагу 3.3, иначе к шагу 3.5.

3.3. Извлекаем $\Delta {{v}^{{\left( {n,j} \right)}}}\left( {{{\varphi }_{0}},{{\varphi }_{{i - 1}}}} \right),$ ${{{\mathbf{u}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{i}}} \right),$ ${{{\mathbf{w}}}^{{\left( {n,j} \right)}}}\left( {{{\varphi }_{i}}} \right).$ Вычисляем $\Delta v = \Delta {{v}^{{\left( {n,j} \right)}}}$ $\left( {{{\varphi }_{0}},{{\varphi }_{{i - 1}}}} \right)$ + $ + \,\,\left| {{{{\mathbf{u}}}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{i}}} \right) - {{{\mathbf{w}}}^{{\left( {n,j} \right)}}}\left( {{{\varphi }_{i}}} \right)} \right|.$

3.4. Если окажется что $\Delta v < \Delta {{v}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{0}},{{\varphi }_{i}}} \right),$ то сохраняем $\Delta {{v}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{0}},{{\varphi }_{i}}} \right) = \Delta v$ и ${{{\eta }}^{{\left( {j,k} \right)}}}\left( {{{\varphi }_{i}}} \right) = n.$

3.5. Если $k = L \cdot M$, или $i = N - 1$, переходим к шагу 3.6, иначе, полагаем $k = k + 1$, и переходим к шагу 3.2.

3.6. Если $n = L \cdot M$, то переходим к шагу 3.7, иначе, полагаем $n = n + 1$, $k = 1$, и переходим к шагу 3.2.

3.7. Если $j = L \cdot M,$ то переходим к шагу 3.8, иначе, полагаем $j = j + 1$, $n = 1$, $k = 1$, и переходим к шагу 3.2.

3.8. Если $i = N - 1$, то выходим из цикла, иначе, полагаем $i = i + 1$,$j = 1$, $n = 1$, $k = 1$, и переходим к шагу 3.2.

Этап 4. Заключительный шаг.

4.1. Полагаем индекс $j = 1$.

4.2. Извлекаем ${\mathbf{x}}_{2}^{{\left( j \right)}}\left( {{{\varphi }_{{N - 1}}}} \right).$ Проверяем, что $\vartheta > {\mathbf{x}}_{2}^{{\left( j \right)}}\left( {{{\varphi }_{{N - 1}}}} \right)$ (см. У. 1). Если это условие выполнено, переходим к шагу 4.2, иначе к шагу 4.4

4.2. Извлекаем $\Delta {{v}^{{\left( {j,1} \right)}}}\left( {{{\varphi }_{0}},{{\varphi }_{{N - 1}}}} \right)$ и ${{{\mathbf{w}}}^{{\left( {j,1} \right)}}}\left( {{{\varphi }_{N}}} \right),$ после чего вычисляем $\Delta v = \Delta {{v}^{{\left( {j,1} \right)}}}$ $\left( {{{\varphi }_{0}},{{\varphi }_{{N - 1}}}} \right)$ + $ + \,\,\left| {{{{\left[ {{{v}_{x}}\left( \vartheta \right),{{v}_{y}}\left( \vartheta \right)} \right]}}^{{\text{T}}}} - {{{\mathbf{w}}}^{{\left( {j,1} \right)}}}\left( {{{\varphi }_{N}}} \right)} \right|.$

4.3. Если окажется, что $\Delta v < \Delta v\left( {{{\varphi }_{0}},{{\varphi }_{N}}} \right),$ то сохраняем $\Delta v\left( {{{\varphi }_{0}},{{\varphi }_{N}}} \right) = \Delta v$ и ${{{\eta }}_{1}} = j.$

4.4. Если $j = L \cdot M$, то выходим из цикла, иначе, полагаем $j = j + 1$, и переходим к шагу 4.2.

Этап 5. Построение траектории.

5.1. Извлекаем ${{{\eta }}_{1}}$. В соответствии с У. 3 формируем точку ${{P}_{N}}$.

5.2. Полагаем $i = N - 1$, ${{{\eta }}_{2}} = 1.$

5.3. Извлекаем ${{{\mathbf{x}}}^{{\left( {{{{\eta }}_{1}}} \right)}}}\left( {{{\varphi }_{i}}} \right).$ Формируем точку ${{P}_{i}}$, характеризующуюся параметром ${{\varphi }_{i}}$, а также вектором ${\mathbf{x}}\left( {{{\varphi }_{i}}} \right) = {{{\mathbf{x}}}^{{\left( {{{{\eta }}_{1}}} \right)}}}\left( {{{\varphi }_{i}}} \right).$

5.4. Извлекаем ${{{\eta }}^{{\left( {{{{\eta }}_{1}},{{{\eta }}_{2}}} \right)}}}\left( {{{\varphi }_{i}}} \right).$ Вычисляем ${{{\eta }}_{3}}$ = ${\text{ = }}\,\,{{{\eta }}^{{\left( {{{{\eta }}_{1}},{{{\eta }}_{2}}} \right)}}}\left( {{{\varphi }_{i}}} \right),$ ${{{\eta }}_{2}} = {{{\eta }}_{1}},$ ${{{\eta }}_{1}} = {{{\eta }}_{3}}.$

5.5. Если $i = 1$, то переходим к шагу 5.6, иначе, полагаем $i = i - 1$, и переходим к шагу 5.3.

5.6. В соответствии с У. 2 формируем точку ${{P}_{0}}$ и выходим из алгоритма.

Проходящая через точки ${{P}_{0}}$, ${{P}_{1}}$, …,${{P}_{N}}$, составная транспортирующая траектория характеризуется угловой дальностью $\delta \varphi \left( {\omega } \right) = {{\varphi }_{\vartheta }}\left( {\omega } \right) - {{\varphi }_{{\tau }}}$ и используется в дальнейшем для отыскания траектории первого приближения с управлением, непрерывным на интервале $\left[ {{\tau ,}\vartheta } \right]$.

4. ФОРМИРОВАНИЕ ТРАЕКТОРИИ ПЕРВОГО ПРИБЛИЖЕНИЯ С НЕПРЕРЫВНЫМ УПРАВЛЕНИЕМ

Построим в окрестности составной транспортирующей траектории приближенную траекторию перелета КА с непрерывным управлением на всем интервале времени $\left[ {{\tau ,}\vartheta } \right]$. Для этого сгенерируем еще одну систему опорных точек ${{Q}_{0}}$, ${{Q}_{1}}$, …, ${{Q}_{N}}$, целиком лежащих в плоскости OXY, такую, что ${{Q}_{i}}$ полностью определяются углом (8), а также вектором ${\mathbf{y}}\left( {{{\varphi }_{i}}} \right)$ = ${{\left[ {r\left( {{{\varphi }_{i}}} \right),t\left( {{{\varphi }_{i}}} \right),{{v}_{x}}\left( {{{\varphi }_{i}}} \right),{{v}_{y}}\left( {{{\varphi }_{i}}} \right)} \right]}^{{\text{T}}}}.$ Первоначально будем полагать, что ${{Q}_{i}}$ близки к ${{P}_{0}}$, ${{P}_{1}}$, …,${{P}_{N}}$ и задаются формулами:

Здесь ${\mathbf{x}}\left( {{{\varphi }_{i}}} \right)$ известен (см. п. 5.3 алгоритма решения задачи 2), а скорости ${\mathbf{u}}\left( {{{\varphi }_{i}}} \right)$, ${\mathbf{w}}\left( {{{\varphi }_{i}}} \right)$ легко получить при помощи ${{{\mathbf{E}}}_{x}}\left( {{{\varphi }_{i}},{\mathbf{x}}\left( {{{\varphi }_{i}}} \right),} \right.$ $\left. {{{\varphi }_{{i + 1}}},{\mathbf{x}}\left( {{{\varphi }_{{i + 1}}}} \right)} \right)$, ${\lambda } = 1,2.$

Соединим ${{Q}_{i}}$ и ${{Q}_{{i + 1}}}$ при помощи элементарной операции E_x(φ_i, [y₁(φ_i), y₂(φ_i)]^T, ${{\varphi }_{{i + 1}}},$ $\left. {{{{\left[ {{{{\mathbf{y}}}_{1}}\left( {{{\varphi }_{{i + 1}}}} \right),{{{\mathbf{y}}}_{2}}\left( {{{\varphi }_{{i + 1}}}} \right)} \right]}}^{{\text{T}}}}} \right)$ кеплеровской орбитой и вычислим соответствующие ${\mathbf{u}}\left( {{{\varphi }_{i}}} \right)$ и ${\mathbf{w}}\left( {{{\varphi }_{{i + 1}}}} \right).$ На i-ом отрезке времени $t \in \left[ {{{{\tau }}_{i}},{{\vartheta }_{i}}} \right],$ где ${{{\tau }}_{i}} = {{{\mathbf{y}}}_{2}}\left( {{{\varphi }_{i}}} \right)$ и ${{\vartheta }_{i}} = {{{\mathbf{y}}}_{2}}\left( {{{\varphi }_{{i + 1}}}} \right),$ линеаризуем уравнения (1) относительно указанной орбиты с учетом того, что функция изменения ее радиус-вектора ${{\rho }^{{\left( i \right)}}}\left( t \right)$ от времени $t \in \left[ {{{{\tau }}_{i}},{{\vartheta }_{i}}} \right]$ известна. Пренебрегая составляющими $z$, ${{v}_{z}}$, получим

где $\delta {\mathbf{v}}_{{\lambda }}^{{\left( i \right)}} = {\mathbf{v}}_{{\lambda }}^{{\left( i \right)}} - \frac{{d(\rho _{{\lambda }}^{{\left( i \right)}})}}{{dt}},$ $\delta {\mathbf{r}}_{{\lambda }}^{{\left( i \right)}} = {\mathbf{r}}_{{\lambda }}^{{\left( i \right)}} - {\mathbf{\rho }}_{{\lambda }}^{{\left( i \right)}},$ ${\mathbf{A}}({{\rho }^{{\left( i \right)}}})$ = $ = \frac{{\mu }}{{{{{\left| {{{\rho }^{{\left( i \right)}}}} \right|}}^{3}}}}\left( {\frac{{3{{\rho }^{{\left( i \right)}}}{{{({{\rho }^{{\left( i \right)}}})}}^{{\text{T}}}}}}{{{{{\left| {{{\rho }^{{\left( i \right)}}}} \right|}}^{2}}}} - {\mathbf{E}}} \right),$ ${\mathbf{E}}$ – единичная матрица, ${\lambda } = 1,2$. Начальные и конечные условия для (12) вычислим по формулам:

а также

Найдем функцию ${{\alpha }^{{\left( i \right)}}} = {{\alpha }^{{\left( i \right)}}}\left( t \right),$ доставляющую минимум функционалу:

при условии соблюдения (13), (14). Применяя принцип максимума Понтрягина, получим систему сопряженных уравнений: где $\delta \psi _{r}^{{\left( i \right)}}$ и $\delta \psi _{v}^{{\left( i \right)}}$ – векторы сопряженных переменных, а также соотношение:

Минимизация (15) сводится к подбору вектора начальных условий

который переводит (12), (16)–(17) из (13) в (14). Поскольку системы (12) и (16) линейны, ${{J}_{i}}$ и $\delta {{\psi }^{{\left( i \right)}}}$ вычисляются аналитически на основе МТТ [9]. Таким образом, нами была введена в рассмотрение элементарная операция ${{{\mathbf{E}}}_{y}}\left( {\varphi ,{\mathbf{y}}\left( {{{\varphi }_{i}}} \right),{{\varphi }_{{i + 1}}},{\mathbf{y}}\left( {{{\varphi }_{{i + 1}}}} \right)} \right),$ которая каждой паре точек $\left\{ {{{Q}_{i}},{{Q}_{{i + 1}}}} \right\},$ где $i = 0,..,N - 1$, ставит в соответствие величину функционала (15). Сформулируем следующую задачу.

Задача 3. Найти векторы ${\mathbf{y}}\left( {{{\varphi }_{i}}} \right),$ $i = 1, \ldots ,N - 1$, доставляющие минимум:

при условии, что ${{J}_{i}}$ определяются при помощи ${{{\mathbf{E}}}_{y}}\left( {{{\varphi }_{i}},{\mathbf{y}}\left( {{{\varphi }_{i}}} \right),{{\varphi }_{{i + 1}}},{\mathbf{y}}\left( {{{\varphi }_{{i + 1}}}} \right)} \right).$

Решение задачи 3 будем отыскивать численно, на основе использования метода локальных вариаций [16]. В соответствии с [16], сформируем вектор ${\mathbf{h}}$, содержащий шаги варьирования ${\mathbf{y}}$ и обозначим символами $s$ и ${\lambda }$ текущий номер итерации алгоритма, а также текущий индекс компоненты ${\mathbf{y}}$. Затем, для $s = 0$, $i = 1$, ${\lambda } = {\text{1}}$, а также вектора ${\mathbf{\delta }}$, у которого компонента с индексом ${\lambda }$ равняется единице, а все остальные нулю, вычислим:

Тогда:

Последовательно увеличивая $i$ вплоть до $N - 1$, выполняем варьирование (19) сначала для первой компоненты ${\mathbf{y}}$, затем для второй и т.д. Если проварьированы все компоненты ${\mathbf{y}}$ и функционал (18) уменьшился, то полагаем $i = 1$, ${\lambda } = {\text{1}}$, после чего повторяем процедуру. В противном случае проверяем условие останова: $s \geqslant S$, где $S$ – предельно допустимое число итераций $s$. Если условие останова выполнено, процесс определения искомой траектории первого приближения можно считать оконченным. Иначе следует уменьшить компоненты вектора ${\mathbf{h}}$ в два раза, положить $s = s + 1$, $i = 1$, ${\lambda } = {\text{1}}$ и повторить итерацию. Соответствующий алгоритм решения задачи 3 описан ниже.

Алгоритм решения задачи 3.

Этап 1. Инициализация.

1.1. Полагаем индекс $i = 0$.

1.2. Инициализируем ${\mathbf{y}}\left( {{{\varphi }_{i}}} \right)$ по формулам (11).

1.3. Если $i = N$, то переходим к шагу 1.4, иначе, полагаем $i = i + 1$, и переходим к шагу 1.2.

1.4. Вычисляем ${{J}_{\Sigma }}\left( {{{\varphi }_{0}},{{\varphi }_{{N - 1}}}} \right)$ по формуле (18). Сохраняем ${{J}_{\Sigma }}\left( {{{\varphi }_{0}},{{\varphi }_{{N - 1}}}} \right)$ и ${{J}_{\Sigma }} = {{J}_{\Sigma }}\left( {{{\varphi }_{0}},{{\varphi }_{{N - 1}}}} \right).$

Этап 2. Варьирование.

2.1. Задаем $S$, а также вектор ${\mathbf{h}}$ и полагаем индексы $s = 0$, $i = 1$, ${\lambda } = 1$.

2.2. Выполняем варьирование по формуле (19). Если новое значение $\sum\nolimits_{i = 0}^{N - 1} {{{J}_{i}}} < {{J}_{\Sigma }}$, то сохраняем ${\mathbf{y}}\left( {{{\varphi }_{i}}} \right)$, ${{J}_{\Sigma }} = \sum\nolimits_{i = 0}^{N - 1} {{{J}_{i}}} $, а также векторы $\delta {{\psi }^{{\left( i \right)}}}$.

2.3. Если $i = N - 1$, то переходим к шагу 2.4, иначе, полагаем $i = i + 1$, и переходим к шагу 2.2.

2.4. Если ${\lambda } = 4$, то переходим к шагу 2.5, иначе, полагаем $i = 1$, ${\lambda } = {\lambda } + 1$, и переходим к шагу 2.2.

2.5. Если ${{J}_{\Sigma }} < {{J}_{\Sigma }}\left( {{{\varphi }_{0}},{{\varphi }_{{N - 1}}}} \right)$, то сохраняем ${{J}_{\Sigma }}\left( {{{\varphi }_{0}},{{\varphi }_{{N - 1}}}} \right) = {{J}_{\Sigma }}$, полагаем $i = 1$, ${\lambda } = 1$ и переходим к шагу 2.2, иначе, переходим к шагу 2.6.

2.6. Проверяем условие $s \geqslant S$. Если оно выполняется, то выходим из алгоритма, иначе, полагаем $s = s + 1$, $i = 1$, ${\lambda } = 1$, и переходим к шагу 2.7.

2.7. Полагаем $k = 1$.

2.8. Вычисляем ${{{\mathbf{h}}}_{k}} = {{{{{\mathbf{h}}}_{k}}} \mathord{\left/ {\vphantom {{{{{\mathbf{h}}}_{k}}} 2}} \right. \kern-0em} 2}.$

2.9. Если $k = 4$, то переходим к шагу 2.2, иначе, полагаем $k = k + 1$, и переходим к шагу 2.7.

Построенная таким образом траектория первого приближения проходит через точки ${{Q}_{0}}$, ${{Q}_{1}}$, …, ${{Q}_{N}}$ и может быть использована для отыскания точного пространственного решения нелинейной краевой задачи принципа максимума (1)–(3), (5), (6).

5. ОПИСАНИЕ ПРОЦЕДУРЫ РЕШЕНИЯ КРАЕВОЙ ЗАДАЧИ МЕТОДОМ ЛОКАЛЬНОГО СПУСКА

Пусть каким-либо образом (например, при помощи информации, полученной в предшествующем разделе) удалось определить вектор ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$, величину $\vartheta - {\tau }$, а также начальные (2) и конечные (3) условия перелета КА. Сформулируем следующую вспомогательную задачу.

Задача 4. Найти вектор ${{\psi }^{e}}$, переводящий (1), (5) из (2) в (3) за время $\vartheta - {\tau }$, при условии, что начальное приближение ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$ задано.

Решение задачи 4 будем отыскивать численно, на основе использования метода локального спуска. В соответствии с [17], зададим $\psi \left( {\tau } \right) = {{{\mathbf{p}}}^{{\left( 0 \right)}}}$ и, проинтегрировав уравнения (1), (5), (6) от ${\tau }$ до $\vartheta $, получим ${\mathbf{r}}\left( \vartheta \right)$, ${\mathbf{v}}\left( \vartheta \right)$, вообще говоря, отличающиеся от (3). Введем в рассмотрение функцию невязки:

где ${{q}_{v}}$ и ${{q}_{r}}$ – масштабные коэффициенты, $s$ – индекс текущей итерации. Выполнив квадратичную аппроксимацию (20), имеем: где ${\mathbf{g}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right) = \nabla \sigma \left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)$ – вектора градиента, ${\mathbf{G}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)$ = $ = {{\nabla }^{2}}\sigma \left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)$ – матрица Гессе, $\nabla $ – набла-оператор, ${{{\mathbf{l}}}^{{\left( s \right)}}}$ – ненулевой вектор, называемый направлением спуска. Минимум (21) достигается при условии, что ${{{\mathbf{l}}}^{{\left( s \right)}}}$ удовлетворяет равенству: а матрица Гессе положительно определена. Однако на практике ${\mathbf{G}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)$ не всегда обладает этим свойством. Поэтому направление спуска целесообразно вычислять по формуле: где вместо ${\mathbf{G}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)$ используется связанная с ней, положительно определенная матрица ${\mathbf{H}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)$ вида: ${\mathbf{H}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)$ = ${\mathbf{G}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right) + {{{\mathbf{D}}}^{{\left( s \right)}}},$ а ${{{\mathbf{D}}}^{{\left( s \right)}}}$ – неотрицательная диагональная матрица, алгоритм построения которой основан на модифицированном разложении Холесского и подробно изложен в [17].

Введем, также, в рассмотрение единичный вектор ${{{\mathbf{e}}}^{{\left( s \right)}}} = \frac{{{{{\mathbf{l}}}^{{\left( s \right)}}}}}{{\delta }},$ $\delta = \left| {{{{\mathbf{l}}}^{{\left( s \right)}}}} \right|$ и скалярную величину ${{\delta }^{{\left( s \right)}}} \in \left[ {0,\delta } \right],$ которая должна обеспечить монотонное уменьшение функции (20):

где

В данной работе искомое значение ${{\delta }^{{\left( s \right)}}}$ получается из решения вспомогательной задачи одномерной минимизации:

при помощи хорошо известного метода золотого сечения. Если же в процессе вычислений вдруг оказывается, что функция $\sigma \left( {{{\delta }^{{\left( s \right)}}}} \right)$ не унимодальна, то ${{{\delta }}^{{\left( s \right)}}}$ отыскивается на основе простого и надежного, но не столь быстрого метода сканирования.

Итерационный процесс локального спуска следует прервать, в случае если: достигнута требуемая точность решения; приемлемое решение еще не найдено, но скорость продвижения к оптимуму сильно упала; выполнено максимальное число итераций. При этом условия останова имеют вид:

где ${{\varepsilon }_{\sigma }}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right) = \left| {1 + \sigma \left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)} \right|\max \left( {{{\varepsilon }_{M}},\frac{{{{\varepsilon }_{\sigma }}\left( {{{{\mathbf{p}}}^{{\left( 0 \right)}}}} \right)}}{{\left| {1 + \sigma \left( {{{{\mathbf{p}}}^{{\left( 0 \right)}}}} \right)} \right|}}} \right)$ – абсолютная погрешность вычислений функции (20), ${{\varepsilon }_{M}}$ = 2.2204460492503131 ⋅ 10^–16 – машинная точность. Таким путем определяется вектор ${{\psi }^{e}} = {{{\mathbf{p}}}^{{\left( s \right)}}},$ который обеспечивает соблюдение (3). Соответствующий алгоритм локального спуска, при условии, что ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$ известен, описан ниже.

Алгоритм решения задачи 4.

1. Задаем величины ${{\varepsilon }_{\sigma }}$, $S$, $\sigma \left( {{{{\mathbf{p}}}^{{\left( { - 1} \right)}}}} \right) = 0.$ Полагаем $s = 0,$ $\psi \left( {\tau } \right) = {{{\mathbf{p}}}^{{\left( s \right)}}}$.

2. Интегрируем уравнения (1), (5), (6) от ${\tau }$ до $\vartheta $ и вычисляем функцию (20).

3. Проверяем условия (26). Если хотя бы одно из них выполнено, то полагаем ${{\psi }^{e}} = {{{\mathbf{p}}}^{{\left( s \right)}}}$ и выходим из алгоритма, иначе переходим к шагу 4.

4. Если $s = 0$, то переходим к шагу 6, иначе переходим к шагу 5.

5. Проверяем условие (23). Если оно не выполнено, то выходим из алгоритма с признаком аварийного срабатывания.

6. Вычисляем ${\mathbf{g}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right),$ ${\mathbf{H}}\left( {{{{\mathbf{p}}}^{{\left( s \right)}}}} \right)$ и по формуле (22) определяем ${{{\mathbf{l}}}^{{\left( s \right)}}}$.

7. Методом золотого сечения, либо методом сканирования решаем вспомогательную подзадачу (25) и определяем ${{{\delta }}^{{\left( s \right)}}}$.

8. Вычисляем вектор (24), полагаем $s = s + 1$ и переходим к шагу 2.

Следует отметить, что метод локального спуска из [17] обладает высокой скоростью сходимости, не требует существенных вычислительных ресурсов и удобен в реализации.

6. РЕШЕНИЕ МНОГОЭКСТРЕМАЛЬНОЙ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ

Перейдем теперь непосредственно к решению задачи 1. Пусть задано максимальное число витков КА вокруг гравитационного центра $\Omega $ (см. раздел 3). Тогда для каждого значения угловой дальности $\delta \varphi \left( {\omega } \right)$ построим при помощи алгоритмов решения задач 2, 3 составную транспортирующую траекторию, траекторию первого приближения, а также последовательность $\left\{ {\delta {{\psi }^{{\left( i \right)}}}:i = 0, \ldots ,N - 1} \right\}$ (см. алгоритм решения задач 3, пункт 2.2). Затем, на основе $\left\{ {\delta {{\psi }^{{\left( i \right)}}}} \right\}$ сформируем вектор ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$. Может показаться, что наиболее очевидным кандидатом на эту роль является:

Однако практика показывает, что траектория (1), (2), (5), (6) чрезвычайно чувствительна к выбору ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$, особенно, если она включает в себя дополнительные витки вокруг гравитационного центра. Поэтому в данной работе принят следующий подход к решению задачи.

Первоначально движение системы (1), (2), (5), (6) рассматривается лишь на сравнительно коротком интервале времени $\left[ {{\tau },{{{\mathbf{y}}}_{2}}\left( {{{\varphi }_{1}}} \right)} \right]$, где ${{\varphi }_{1}}$ и ${\mathbf{y}}\left( {{{\varphi }_{1}}} \right)$ характеризуют положение точки ${{Q}_{1}}$. При этом ${{{\mathbf{r}}}_{\vartheta }} = [{{{\mathbf{y}}}_{1}}\left( {{{\varphi }_{1}}} \right)\cos \left( {{{\varphi }_{1}}} \right),$ ${{{\mathbf{y}}}_{1}}\left( {{{\varphi }_{1}}} \right)\sin \left( {{{\varphi }_{1}}} \right),0{{]}^{{\text{T}}}}$, ${{{\mathbf{v}}}_{\vartheta }} = [{{{\mathbf{y}}}_{3}}\left( {{{\varphi }_{1}}} \right),$ ${{{\mathbf{y}}}_{4}}\left( {{{\varphi }_{1}}} \right),0{{]}^{{\text{T}}}}$. Задав ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$ по формуле (27), решаем соответствующую нелинейную краевую задачу методом локального спуска (алгоритм решения задачи 4) и получаем вектор ${{\psi }^{e}}$. Затем движение системы (1), (2), (5), (6) рассматривается на более продолжительном интервале времени $\left[ {{\tau },{{{\mathbf{y}}}_{2}}\left( {{{\varphi }_{2}}} \right)} \right]$. При этом ${{{\mathbf{r}}}_{\vartheta }} = {{\left[ {{{{\mathbf{y}}}_{1}}\left( {{{\varphi }_{2}}} \right)\cos \left( {{{\varphi }_{2}}} \right),{{{\mathbf{y}}}_{1}}\left( {{{\varphi }_{2}}} \right)\sin \left( {{{\varphi }_{2}}} \right),0} \right]}^{{\text{T}}}}$, ${{{\mathbf{v}}}_{\vartheta }} = {{\left[ {{{{\mathbf{y}}}_{3}}\left( {{{\varphi }_{2}}} \right),{{{\mathbf{y}}}_{4}}\left( {{{\varphi }_{2}}} \right),0} \right]}^{{\text{T}}}}$. Положив ${{{\mathbf{p}}}^{{\left( 0 \right)}}} = {{\psi }^{e}}$, применим метод локального спуска к указанной задаче и получим новый вектор ${{\psi }^{e}}$. Действуя таким образом, последовательно увеличиваем временной интервал $\left[ {{\tau },{{{\mathbf{y}}}_{2}}\left( {{{\varphi }_{i}}} \right)} \right]$ и, доведя его до $\left[ {\tau ,\vartheta } \right]$, находим ${{\psi }^{e}}\left( {\omega } \right)$ – решение исходной краевой задачи (1)–(3),(5), (6).

Наконец сравнивая между собой величины $J\left( {\omega } \right)$ функционала (4), полученные для ${\omega } = {\text{0,}}...{\text{,}}\Omega $, определяем ${{J}_{{opt}}}$, а также формируем множество (7), на элементах которого ${{J}_{{opt}}}$ реализуется. При этом полагаем, что $J\left( {\omega } \right) = {{J}_{1}}$ и $J\left( {\omega } \right) = {{J}_{2}}$ различаются, если выполнено условие: $\left| {{{J}_{{\text{1}}}} - {{J}_{{\text{2}}}}} \right| > {{{\varepsilon }}_{J}}$, где ${{{\varepsilon }}_{J}}$ – некоторое фиксированное пороговое значение. Таким образом, полный алгоритм решения задачи 1 имеет следующий вид.

Алгоритм решения задачи 1.

1. Задаемся величинами $\Omega $ и ${{\varepsilon }_{J}}$. Инициализируем величину ${{J}_{{opt}}}$ большим положительным числом.

2. Полагаем ${\omega } = {\text{0}}$.

3. При помощи алгоритма решения задачи 2 получаем точки ${{P}_{0}}$,${{P}_{1}}$, ..., ${{P}_{N}}$.

4. Для точек ${{P}_{0}}$,${{P}_{1}}$, ..., ${{P}_{N}}$, при помощи алгоритм решения задачи 3, получаем ${{Q}_{0}}$,${{Q}_{1}}$, ..., ${{Q}_{N}}$, а также $\delta {{\psi }^{{\left( 0 \right)}}}$,$\delta {{\psi }^{{\left( 1 \right)}}}$, …, $\delta {{\psi }^{{\left( {N - 1} \right)}}}$.

5. Задаем $i = 1$ и определяем вектор ${{{\mathbf{p}}}^{{\left( 0 \right)}}}$ по формуле (27).

6. Вычисляем ${{{\mathbf{r}}}_{\vartheta }}$ = [y₁(φ_i)cos(φ_i), y₁(φ_i)sin(φ_i),0]^T и ${{{\mathbf{v}}}_{\vartheta }} = {{\left[ {{{{\mathbf{y}}}_{3}}\left( {{{\varphi }_{i}}} \right),{{{\mathbf{y}}}_{4}}\left( {{{\varphi }_{i}}} \right),0} \right]}^{{\text{T}}}}.$

7. Для начальных условий (2) и конечных условий из пункта 6 выполняем алгоритм решения задачи 4 на временном интервале $\left[ {{\tau },{{{\mathbf{y}}}_{2}}\left( {{{\varphi }_{i}}} \right)} \right]$ и получаем ${{\psi }^{e}}$.

8. Если $i < N - 1$, то полагаем $i = i + 1,$ ${{{\mathbf{p}}}^{{\left( 0 \right)}}} = {{\psi }^{e}}$ и переходим к шагу 6. Иначе, полагаем ${{{\mathbf{p}}}^{{\left( 0 \right)}}} = {{\psi }^{e}}$ и переходим к шагу 9.

9. Для начальных условий (2) и конечных условий (3) выполняем алгоритм решения задачи 4 на временном интервале $\left[ {{\tau },\vartheta } \right]$, получаем вектор ${{\psi }^{e}}\left( {\omega } \right)$, и, по формуле (4), вычисляем функционал $J$.

10. Если $\left| {{{J}_{{opt}}} - J} \right| < {{{\varepsilon }}_{J}},$ то включаем ${{\psi }^{e}}\left( {\omega } \right)$ в ${{{\mathbf{\Psi }}}_{{opt}}}$ иначе, если ${{J}_{{opt}}} < J,$ то удаляем все элементы множества ${{{\mathbf{\Psi }}}_{{opt}}}$, полагаем $J = {{J}_{{opt}}}$ и включаем ${{\psi }^{e}}\left( {\omega } \right)$ в ${{{\mathbf{\Psi }}}_{{opt}}}$. Переходим к шагу 11.

11. Если ${\omega } < \Omega $, то полагаем ${\omega } = {\omega } + {\text{1}}$ и переходим к шагу 3, иначе выходим из алгоритма.

В заключение отметим, что задача 1 также может быть решена методом продолжения по гравитационному параметру [8]. Указанный метод позволяет отыскивать экстремаль нелинейной краевой задачи принципа максимума при помощи гомотопии. При этом качестве параметра продолжения выступает гравитационная постоянная ${\mu }$, а траекторией начального приближения оказывается некоторая фиктивная орбита, удовлетворяющая условию (2) и построенная для константы ${\mu } = {{{\mu }}_{{\text{0}}}}$, значение которой подбирается так, чтобы обеспечить заданную угловую дальность перелета.

В нашем случае, нулевое приближение, удовлетворяющее не только начальным (2), но и конечным (3) краевым условиям, строится наиболее простым и естественным образом и представляет собой составную транспортирующую траекторию, на которой сумма управляющих импульсов (10) минимальна. Поэтому, есть основания полагать, что искомая траектория непрерывного управлением, доставляющая локальный минимум функционалу (4), будет находиться в близкой окрестности импульсного нулевого приближения и ее отыскание не потребует привлечения значительных вычислительных ресурсов.

Кроме того, составная транспортирующая траектория позволяет получить важную информацию о характере и параметрах искомой экстремали и с успехом может быть использована в рамках различных методов оптимизации, (квазилинеаризация, метод множественной стрельбы и т.д.), отличных от изложенных в разделах 4 и 5. Таким образом, у разработчика сохраняется относительная свобода выбора способа окончательной оптимизации (4), что позволяет ему наилучшим образом учесть специфику конкретной задачи.

Наконец, побочным продуктом работы алгоритма решения задачи 2, при условии, что он был выполнен от конца к началу, являются полученные в результате процедуры синтеза оптимальные траектории, соединяющие каждый узел расчетной сетки $\left\{ {{{\varphi }_{i}},{{{\mathbf{X}}}_{i}}:i = 0,...,N - 1} \right\}$ и конечный узел. Они также могут найти себе применение на последующих этапах исследования, например, в процессе изучения возмущенного движения КА.

7. ЧИСЛЕННЫЙ ПРИМЕР

Для иллюстрации работы описанного выше метода рассмотрим задачу оптимизации траекторий перелета КА от Земли к астероиду Апофис. Выберем в качестве OXYZ гелиоцентрическую эклиптическую прямоугольную систему координат, ось OX которой направлена в точку весеннего равноденствия, ось OZ указывает на северный полюс эклиптики, ось OY дополняет систему до правой. Следуя схеме полета из [7], будем полагать, что КА массой ${{m}_{{\text{0}}}}$, находящийся на круговой околоземной орбите радиусом ${{R}_{{\text{0}}}}$ разгоняется двигателем большой тяги до параболической скорости, в результате чего покидает сферу действия Земли. Таким образом, в заданный момент начала гелиоцентрического движения ${\tau }$ = 2.IX.2018 (JD = = 2 458 364.34) массу КА ${{m}_{{SC}}}\left( {\tau } \right)$ можно оценить по формуле:

а условия (2) примут вид: ${{{\mathbf{r}}}_{{\tau }}} = {{{\mathbf{r}}}_{{\text{E}}}},$ ${{{\mathbf{v}}}_{{\tau }}} = {{{\mathbf{v}}}_{{\text{E}}}},$ где $\Delta V = \sqrt {\frac{{2{{{\mu }}_{{\text{E}}}}}}{{{{R}_{{\text{0}}}}}}} - \sqrt {\frac{{{{{\mu }}_{{\text{E}}}}}}{{{{R}_{{\text{0}}}}}}} $, ${{{\mu }}_{{\text{E}}}}$ – гравитационный параметр Земли, $W$ – скорость истечения частиц в реактивной струе для химического двигателя большой тяги, ${{m}_{B}}$ – масса отбрасываемого разгонного блока, ${{{\mathbf{r}}}_{{\text{E}}}}$ и ${{{\mathbf{v}}}_{{\text{E}}}}$ – радиус-вектор и вектор скорости Земли. В проекциях на оси OXYZ соответственно получим: $x\left( {\tau } \right)$ = 141 837 938.1 км, $y\left( {\tau } \right)$ = –51 586 562.08 км, $z\left( {\tau } \right)$ = 0.0 км, ${{v}_{x}}\left( {\tau } \right)$ = 9.696559723 км/с, ${{v}_{y}}\left( {\tau } \right)$ = = 27.88321627 км/с, ${{v}_{z}}\left( {\tau } \right)$ = 0.0 км/с. Требуется, чтобы спустя 185 суток, КА, совершив при помощи ЭРД гелиоцентрический перелет, оказался в точке с координатами ${{{\mathbf{r}}}_{\vartheta }} = {{{\mathbf{r}}}_{A}}$, имея при этом скорость ${{{\mathbf{v}}}_{\vartheta }} = {{{\mathbf{v}}}_{A}}$, где ${{{\mathbf{r}}}_{A}}$ и ${{{\mathbf{v}}}_{A}}$ – радиус-вектор и вектор скорости Апофиса. При этом отметим, что дата старта и продолжительность перелета КА не являются оптимальными; они заимствованы из [7] и призваны продемонстрировать наличие в задаче двух экстремалей с одинаковым значением (4).

В проекциях на оси OXYZ соответственно получим: $x\left( \vartheta \right)$ = –16 866 036.34 км, $y\left( \vartheta \right)$ = 148 415 503.4 км, $z\left( \vartheta \right)$ = –8 273 116.384 км, ${{v}_{x}}\left( \vartheta \right)$ = –28.44266644 км/с, ${{v}_{y}}\left( \vartheta \right)$ = 1.669202204 км/с, ${{v}_{z}}\left( \vartheta \right)$ = –0.7733438831 км/с. Встретившись там с астероидом, КА, также при помощи ЭРД, выполнит торможение и перейдет на орбиту его искусственного спутника. Поскольку энергетические затраты, необходимые для перехода КА на астероидоцентрическую орбиту, в этом случае, невелики [6], то:

где ${{m}_{A}}$ – конечная масса КА на орбите Апофиса. Необходимо найти траектории перелета КА и соответствующее им значение ${{J}_{{opt}}}$, для которых величина ${{m}_{A}}$, или, как следует из (28), величина ${{m}_{{SC}}}\left( \vartheta \right)$, достигала бы максимума.

Анализ параметров $z\left( {\tau } \right),$ ${{v}_{z}}\left( {\tau } \right),$ $z\left( \vartheta \right)$, ${{v}_{z}}\left( \vartheta \right)$ позволяет заключить, что перелет КА от Земли к астероиду будет осуществляться вблизи плоскости эклиптики. Поэтому для решения поставленной задачи будем использовать алгоритм решения задачи 1. Зададимся параметрами ${{\varepsilon }_{J}} = 2.0 \cdot {{10}^{{ - 3}}}$ м²/с³ и $\Omega = 1$ (шаг 1). Таким образом, оптимум (4) будет отыскиваться на траекториях прямого перелета, а также траекториях с одним дополнительным витком. Рассмотрим случай ${\omega } = {\text{0}}$ (шаг 2, траектории прямого перелета). По формулам (8) получим ${{\varphi }_{{\tau }}}$ = = 340.0136362 град, ${{\varphi }_{\vartheta }}\left( 0 \right) - {{\varphi }_{{\tau }}}$ = 116.4696808 градусов. Примем $N = 2$, в результате чего угол перелета КА на одном участке составной транспортирующей траектории не превысит 60 град. Зададим узлы ${{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right)$, такие что:

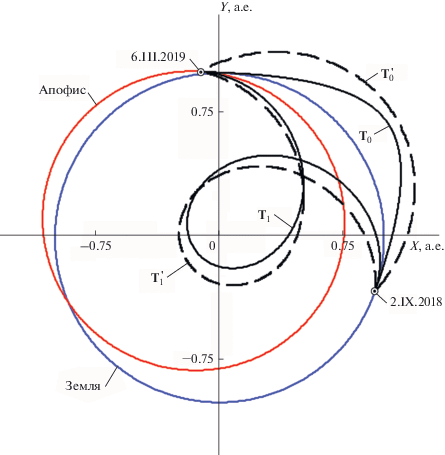
где ${{t}_{{\min }}}\left( {{{\varphi }_{i}}} \right) = t\left( {{{\varphi }_{i}}} \right) - {{{\delta }}_{t}},$ ${{t}_{{\max }}}\left( {{{\varphi }_{i}}} \right) = t\left( {{{\varphi }_{i}}} \right) + {{{\delta }}_{t}},$ $t\left( {{{\varphi }_{i}}} \right) = \frac{{\vartheta - {\tau }}}{N}i + {\tau ,}$ r_min = 140.0 · 10⁶ км, r_max = 240.0 · · 10⁶ км, ${{{\delta }}_{t}}$ = 50 суток, $L$ = 31, $M$ = 61. Выполнив шаг 3 алгоритма решения задачи 1, получим величину (10) равную 27.18911743 км/с. При этом единственная промежуточная точка ${{P}_{1}}$ характеризуется следующими параметрами: ${{\varphi }_{1}}$ – ${{\varphi }_{\tau }}$ = 58.23484039 град, $r\left( {{{\varphi }_{1}}} \right)$ = 193.(3) ⋅ 10⁶ км, $t\left( {{{\varphi }_{1}}} \right)$ – ${\tau }$ = 92.5 суток. Составная транспортирующая траектория перелета КА из (2) в (3) обозначена на рисунке символом ${\mathbf{T}}_{0}^{'}$. Следует отметить, что в данном случае ${\mathbf{T}}_{0}^{'}$ фактически совпадает с кеплеровской орбитой, соединяющей (2) и (3). Построим далее траекторию первого приближения (шаг 4). Для этого по формулам (11) сформируем ${\mathbf{y}}\left( {{{\varphi }_{i}}} \right)$, зададим $S = 20$ и вектор ${\mathbf{h}}$, такой что ${{{\mathbf{h}}}_{1}} = 2.5 \cdot {{10}^{6}}$ км, ${{{\mathbf{h}}}_{2}} = 1.0$ суток, ${{{\mathbf{h}}}_{3}} = {{{\mathbf{h}}}_{4}} = 2.0$ км/с. Применив алгоритм решения задачи 3, получим величину (18) равную 168.5265666 м²/с³. Единственная промежуточная точка ${{Q}_{1}}$ характеризуется следующими параметрами: ${{\varphi }_{1}}$ – ${{\varphi }_{\tau }}$ = 58.23484039 град, $r\left( {{{\varphi }_{1}}} \right)$ = = 183014710.7 км, $t\left( {{{\varphi }_{1}}} \right)$ – ${\tau }$ = 99.42506027 сут, ${{v}_{x}}\left( {{{\varphi }_{1}}} \right)$ = –10.99439222 км/с, ${{v}_{y}}\left( {{{\varphi }_{1}}} \right)$ = 9.775907364 км/с. По формуле (27) имеем: ${\mathbf{p}}_{1}^{{\left( 0 \right)}}$ = 93.8106916025 ⋅ 10^–7, ${\mathbf{p}}_{2}^{{\left( 0 \right)}}$ = –54.6452421284 ⋅ 10^–7, ${\mathbf{p}}_{4}^{{\left( 0 \right)}}$ = 239.664827357 ⋅ 10^–14, ${\mathbf{p}}_{5}^{{\left( 0 \right)}}$ = –64.2359106942 · 10^–14, ${\mathbf{p}}_{3}^{{\left( 0 \right)}}$ = ${\mathbf{p}}_{6}^{{\left( 0 \right)}}$ = 0. Соответствующая траектория первого приближения обозначена на рисунке символом T₀. Затем, задавшись ${{\varepsilon }_{\sigma }}({{{\mathbf{p}}}^{{(0)}}})$ = 1.0 ⋅ 10^–12, $S$ = 100, ${{q}_{v}}$ = ${{10}^{{ - 7}}}$ км/с, ${{q}_{r}}$ = ${{10}^{{ - 14}}}$ км, выполним шаги с 5 по 9 алгоритма решения задачи 1 и вычислим вектор ${{\psi }^{e}}$, являющийся первым элементом множества ${{{\mathbf{\Psi }}}_{{opt}}}$ (шаг 10): $\psi _{1}^{e}$ = 94.66532165 ⋅ 10^–7, $\psi _{2}^{e}$ = –51.42365888 ⋅ 10^–7, $\psi _{3}^{e}$ = 0.3813270949 ⋅ 10^–7, $\psi _{4}^{e}$ = 251.0494271 ⋅ 10^–14, $\psi _{5}^{e}$ = –48.40369378 ⋅ 10^–14, $\psi _{6}^{e}$ = 5.344841215 ⋅ 10^–14. При этом величина (4) равна 168.5541035 м²/с³, а соответствующая траектория перелета КА из (2) в (3) на рисунке визуально совпадает с траекторией первого приближения T₀.

Поскольку ${\omega } = {\text{ 0}} < \Omega $, положим ${\omega } = {\text{1}}$ и перейдем к рассмотрению траекторий с одним дополнительным витком вокруг Солнца (шаг 3). По формулам (8) получим ${{\varphi }_{\vartheta }}\left( 1 \right) - {{\varphi }_{{\tau }}}$ = 476.4696808 град. Примем $N = 8$, в результате чего угол перелета КА на одном участке составной транспортирующей траектории будет близок к 60 град. Будем полагать, что при расчете ${{{\mathbf{x}}}^{{\left( j \right)}}}\left( {{{\varphi }_{i}}} \right)$ по формулам (29) ${{r}_{{\min }}} = {\text{20}}{\text{.0}} \cdot {\text{1}}{{{\text{0}}}^{{\text{6}}}}$ км, ${{r}_{{\max }}} = {\text{150}}{\text{.0}} \cdot {\text{1}}{{{\text{0}}}^{{\text{6}}}}$ км, ${{{\delta }}_{t}}$ = 50 сут, $L$ = 31, $M$ = 61. Выполнив шаг 3 алгоритма решения задачи 1, получим величину (10) равную 43.80742264 км/с. При этом параметры, характеризующие промежуточные точки ${{P}_{i}}$, приводятся в табл. 1. Составная транспортирующая траектория перелета КА из (2) в (3) обозначена на рис. 1 символом ${\mathbf{T}}_{1}^{'}$. Построим далее траекторию первого приближения (шаг 4). Для этого сформируем ${\mathbf{y}}\left( {{{\varphi }_{i}}} \right)$ по формулам (11), зададим $S = 20$ и вектор ${\mathbf{h}}$, такой что ${{{\mathbf{h}}}_{1}} = 2.5 \cdot {{10}^{6}}$ км, ${{{\mathbf{h}}}_{2}} = 1.0$ сут, ${{{\mathbf{h}}}_{3}} = {{{\mathbf{h}}}_{4}} = 2.0$ км/с. Применив алгоритм решения задачи 3, получим величину (18) равную 167.6679442 м²/с³. Информация, характеризующая промежуточные точки ${{Q}_{i}}$, приводятся в табл. 2. В соответствии с (27) имеем ${\mathbf{p}}_{1}^{{\left( 0 \right)}}$ = = –102.281590402 ⋅ 10^–7, ${\mathbf{p}}_{2}^{{\left( 0 \right)}}$ = = ‒30.7907152907 ⋅ 10^–7, ${\mathbf{p}}_{4}^{{\left( 0 \right)}}$ = –387.113857394 ⋅ 10^–14, ${\mathbf{p}}_{5}^{{\left( 0 \right)}}$ = 64.2118702125 ⋅ 10^–14, ${\mathbf{p}}_{3}^{{\left( 0 \right)}}$ = ${\mathbf{p}}_{6}^{{\left( 0 \right)}}$ = 0. Соответствующая траектория первого приближения обозначена на рис. 1 символом T₁. Выполнив шаги с 5 по 9 алгоритма решения задачи 1, вычислим искомый вектор ${{\psi }^{e}}$ с компонентами: $\psi _{1}^{e}$ = –101.890974187 × 10^–7, $\psi _{2}^{e}$ =  –31.2262700771 ⋅ 10^–7, $\psi _{3}^{e}$ = –4.03357164751 ⋅ 10^–7, $\psi _{4}^{e}$ = –386.554657820 ⋅ 10^–14, $\psi _{5}^{e}$ = –58.0257795804 ⋅ 10^–14, $\psi _{6}^{e}$ = –0.17249478303 ⋅ 10^–14 и величину (4), равную 168.5525918 м²/с³. Соответствующая траектория перелета КА из (2) в (3) на рис. 1 визуально совпадает с траекторией первого приближения T₁. Так как |168.5541035 – 168.5525918| < $ < 2.0 \cdot {{10}^{{ - 3}}}$, указанный ${{\psi }^{e}}$ выступает в качестве второго элемента множества ${{{\mathbf{\Psi }}}_{{opt}}}$ (шаг 10). Таким образом, для ${\tau }$ = 2.IX.2018 (JD = 2458364.34) и $\vartheta - {\tau }$ = 185 сут ${{J}_{{opt}}} = $ 168.55 м²/с³ с заданной точностью ${{{\varepsilon }}_{J}}$ достигается на двух различных траекториях перелета КА к астероиду Апофис, обозначенных на рис. 1 как T₀ и T₁.

Следует отметить, что полученные результаты также можно использовать в качестве хорошего начального приближения при решении задач с ненулевым гиперболическим избытком скорости КА у Земли, когда импульс скорости двигателя большой тяги на круговой околоземной орбите оценивается по формуле:

где ${{{\mathbf{v}}}_{\infty }}$ – вектор гиперболического избытка скорости, оптимальная величина и направление которого подлежат определению.

Общее время решения поставленной задачи ${{T}_{{calc}}}$ на одном ядре процессора с частотой 2.4 ГГц составило 478 с. При этом на построение составной транспортирующей траектории было затрачено $0.6 \cdot {{T}_{{calc}}}$, формирование траектории первого приближения потребовало $0.35 \cdot {{T}_{{calc}}}$, а точное решение краевой задачи методом локального спуска было выполнено за $0.05 \cdot {{T}_{{calc}}}$. Очевидно, что приведенные выше оценки вычислительных затрат носят исключительно ориентировочный характер, а величину ${{T}_{{calc}}}$ можно существенно снизить, оптимизировав соответствующий программный код по быстродействию. Целесообразно также воспользоваться возможностями метода динамического программирования и распараллелить вычисления алгоритма решения задачи 2 между несколькими процессорными ядрами.

ЗАКЛЮЧЕНИЕ

В работе предложен регулярный метод численной оптимизации траекторий перелета КА с идеально регулируемой тягой ЭРД, основные особенности которого заключаются в следующем:

1. Метод позволяет отыскивать экстремальные траектории с заданной угловой дальностью, отличающиеся друг от друга числом витков вокруг притягивающего центра.

2. Процедура решения поставленной задачи регулярна и выполняется в три этапа: генерация серии составных транспортирующих траекторий в импульсной постановке, построение траекторий первого приближения в линейной постановке, точное решение нелинейных краевых задач с последующим анализом полученных результатов.

3. Алгоритм построения импульсных составных транспортирующих траекторий основан на методе оптимизации, позволяющем отыскивать оптимум аддитивной функции на соответствующей вычислительной сетке, даже при условии, что эта функция не является унимодальной в расчетной области.

4. Процедура поиска точных решений нелинейной краевой задачи в окрестности нулевого приближения достаточно надежна, поскольку разработана с учетом высокой чувствительности этих решений к качеству начального приближения.

5. Вся привлекаемая в процессе работы метода априорная информация имеет очевидную физическую интерпретацию (так, например, пользователю нет необходимости задавать начальные диапазоны изменения сопряженных переменных).

6. Все использованные алгоритмы не требуют значительных затрат вычислительных ресурсов.

К числу недостатков данной методики следует отнести ограничения, которые она накладывает на характер оптимальных траекторий перелета КА; полагается, что такие траектории хотя и носят пространственный характер, но не могут далеко отклоняться от некоторой плоскости (например, плоскости эклиптики).

Автор выражает искреннюю признательность В.В. Ивашкину за неоценимую помощь при подготовке данной статьи.