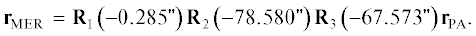Космические исследования, 2020, T. 58, № 3, стр. 223-234
Перелеты с малой тягой на окололунные орбиты с гало-орбит вокруг лунных точек либрации L1 и L2
М. Г. Широбоков 1, *, С. П. Трофимов 1
1 Институт прикладной математики им. М.В. Келдыша РАН
г. Москва, Россия
* E-mail: shirobokov@keldysh.ru
Поступила в редакцию 11.10.2018
После доработки 21.12.2018
Принята к публикации 25.04.2019
Аннотация
Работа посвящена поиску окололунных орбит, доступных при сходе вдоль неустойчивого инвариантного многообразия гало-орбит вокруг лунных точек либрации L1 и L2. Предполагается, что космический аппарат оснащен двигателем малой тяги. Рассматриваются два уровня реактивного ускорения из типичного диапазона реактивных ускорений малых космических аппаратов с двигателями малой тяги. Работа состоит из двух частей: 1) поиск оскулирующих окололунных орбит, получающихся при пассивном движении от гало-орбит, 2) стабилизация орбит силой тяги, направленной против скорости аппарата. Найдены множества гало-орбит, сход с которых вдоль неустойчивого многообразия позволяет достичь полярных и околополярных орбит. Задача решается в рамках модели круговой ограниченной задачи трех тел.
1. ВВЕДЕНИЕ
К настоящему моменту осуществлено почти два десятка научных миссий к точкам либрации систем Солнце–Земля и Земля–Луна. За последние 30 лет орбиты вокруг них зарекомендовали себя как надежное местоположение для проведения широкого спектра наблюдений за космической погодой (миссии Deep Space Climate Observatory, Advanced Composition Explorer, Solar and Heliospheric Observatory, Wind spacecraft), решения астрометрических задач (Gaia spacecraft), измерения фонового излучения (Wilkinson Microwave Anisotropy Probe), наблюдения за космосом (Herschel Space Observatory, Planck Space Observatory). К точкам либрации прорабатываются и две отечественные миссии: Спектр-РГ [1] и Миллиметрон [2]. Все перечисленные миссии нацелены на окрестность коллинеарных точек либрации системы Солнце–Земля, однако несколько аппаратов были направлены в точки либрации ${{L}_{1}}$ и ${{L}_{2}}$ системы Земля–Луна: Acceleration, Reconnection, Turbulence, and Electrodynamics of the Moons Interaction with the Sun (ARTEMIS), Chang’e 5-T1 и аппарат Queqiao.
Точки либрации ${{L}_{1}}$ и ${{L}_{2}}$ привлекают разработчиков миссий прежде всего богатой динамикой в их окрестности. Эта динамика включает несколько типов периодических орбит (плоские и вертикальные орбиты Ляпунова, гало-орбиты, аксиальные орбиты), квазипериодических орбит (орбиты Лиссажу, квазигало-орбиты), а также асимптотические траектории, связанные с перечисленными орбитами, которые формируют устойчивые и неустойчивые инвариантные многообразия. Все это помогает делать научные миссии осуществимыми, так как траектории и орбиты, получаемые классическими инструментами астродинамики в рамках задачи двух тел, в реальной возмущенной динамике требуют непрерывного управления и коррекции движения космического аппарата; вместе с тем, динамика задачи трех тел ближе к реальной динамике и потому менее требовательна с точки зрения затрат топлива на детерминистские маневры.
Глубокое изучение динамики трех тел за последние 30 лет позволило получить удобные инструменты для проектирования межпланетных траекторий и траекторий между различными системами трех тел. Понятие об устойчивых и неустойчивых инвариантных многообразиях, связанных с орбитами вокруг точек либрации, позволяет построить регулярные процедуры поиска траекторий между различными системами трех тел: например, между системой Земля–Луна и Солнце–Земля. В начале 2000-х годов таким образом появилась концепция межпланетного суперхайвея (Interplanetary Superhighway) или межпланетной транспортной сети (Interplanetary Transport Network) [3]. Потенциальная доступность дальнего космоса из окрестности точек либрации системы Земля–Луна, а также актуальность освоения и изучения Луны дали старт новому международному проекту Lunar Orbital Platform-Gateway (бывш. название – Deep Space Gateway) по построению и вводу в эксплуатацию обитаемой окололунной станции. В проекте участвуют все лидирующие космические агентства: Роскосмос, Национальное управление по аэронавтике и исследованию космического пространства (NASA), Европейское космическое агентство, Японское агентство аэрокосмических исследований, а также Канадское космическое агентство.
В последние годы также наблюдается тенденция на создание и запуск малых межпланетных аппаратов. И хотя аппараты Deep Space 1 и Small Missions for Advanced Research in Technology-1 (SMART-1) формально относятся к малым космическим аппаратам, важно заметить, что за последние несколько лет появились технологии, которые сделают возможным межпланетные перелеты для аппаратов в классе микро и нано. Среди этих технологий создание высокоскоростного лазерного канала связи посредством остронаправленной развертываемой антенны, появление более стойкой к высоким дозам радиации и низким температурам элементной базы, усовершенствование двигателей малой тяги и отработка технологии солнечного паруса, появление новых решений в области абсолютной и относительной автономной навигации и, наконец, развитие прецизионной навигации в условиях хаотической динамики. В ближайшие годы ожидается крупная волна демонстрационных и научных миссий с микро- и наноаппаратами. Так, в рамках миссии Exploration Mission 1 в дальний космос будут выпущены 13 кубсатов: Lunar IceCube, Lunar Flashlight, Near Earth Asteroid Scout mission, BioSentinel, Lunar Polar Hydrogen Mapper и др. Кроме того, новые технологии будут отрабатываться также в рамках миссий Interplanetary NanoSpacecraft Pathfinder In Relevant Environment (INSPIRE) и Demonstration and Experiment of Space Technology for Interplanetary Voyage (DESTINY). Два кубсата Mars Cube One уже запущены к Марсу с целью поддерживать связь между спускаемым аппаратом InSight и Землей [4].
Все это говорит о том, что в ближайшее время вопросы об исследовании окололунного пространства и поиске подходящих для целей миссии орбит в рамках сложных динамических моделей стоят актуально.
Цель данной работы – поиск окололунных орбит, доступных при сходе с гало-орбит вокруг точек либрации ${{L}_{1}}$ и ${{L}_{2}}$ системы Земля–Луна. Рассматривается малый космический аппарат, снабженный двигателем малой тяги. Насколько известно авторам, до сих пор подобная задача ставилась лишь в работах Дж.С. Паркера (см. монографию [5] для информации). Однако там рассматривалась лишь точка L2 и, самое важное, не ставился вопрос дальнейшей стабилизации окололунных орбит. В данной работе мы рассматриваем семейства гало-орбит вокруг точек L1 и L2 и ставим задачу стабилизации окололунных орбит, получаемых при сходе с гало-орбит, с помощью двигателя малой тяги. Рассматриваются два класса малых аппаратов – мини и нано – и соответствующие двигатели. Особое внимание уделено поиску полярных и околополярных орбит в связи с интересом различных научных программ к поиску и исследованию залежей водяного льда вблизи лунных полюсов. В этих же приполярных областях находятся предполагаемые места будущих окололунных баз.
2. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ О ДИНАМИКЕ КРУГОВОЙ ОГРАНИЧЕННОЙ ЗАДАЧИ ТРЕХ ТЕЛ
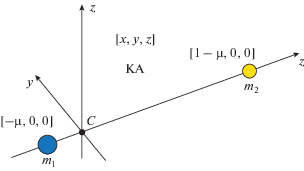
Всюду в данной работе используется модель круговой ограниченной задачи трех тел (circular restricted three-body problem, CR3BP). Согласно модели CR3BP, две массы ${{m}_{1}}$ и ${{m}_{2}} \leqslant {{m}_{1}}$ движутся по круговым орбитам вокруг их общего центра масс $C$, а космический аппарат пренебрежимо малой массы движется в гравитационном поле масс ${{m}_{1}}$ и ${{m}_{2}}$. В нашем случае ${{m}_{1}}$ обозначает массу Земли, а ${{m}_{2}}$ – массу Луны, поэтому система трех тел ${{m}_{1}}$–${{m}_{2}}$–КА называется системой Земля–Луна.
Уравнения движения обычно записываются в стандартной вращающейся системе координат (см. рис. 1) с началом в точке $C$; при этом ось $x$ соединяет массы ${{m}_{1}}$ и ${{m}_{2}}$ в направлении ${{m}_{2}}$, ось $z$ направлена вдоль вектора угловой скорости орбитального движения ${{m}_{2}}$ вокруг ${{m}_{1}}$, а ось $y$ дополняет систему $Cxyz$ до правой тройки.
Кроме того, будем пользоваться безразмерной системой единиц, в которой 1) ${{m}_{1}} = 1 - \mu $ и ${{m}_{2}} = \mu $, где $\mu = {{{{m}_{2}}} \mathord{\left/ {\vphantom {{{{m}_{2}}} {\left( {{{m}_{1}} + {{m}_{2}}} \right)}}} \right. \kern-0em} {\left( {{{m}_{1}} + {{m}_{2}}} \right)}}$ – массовый параметр системы, 2) угловая скорость вращающейся системы координат равна единице и 3) расстояние между ${{m}_{1}}$ и ${{m}_{2}}$ равно единице. В этом случае массы ${{m}_{1}}$ и ${{m}_{2}}$ находятся на фиксированных позициях на оси $x$ в точках $\left[ { - \mu ,0,0} \right]$ и $\left[ {1 - \mu ,0,0} \right]$, соответственно. В системе Земля–Луна массовый параметр $\mu = 1.2150668 \cdot {{10}^{{ - 2}}}$.
Уравнения движения можно записать в следующем виде:
(1)
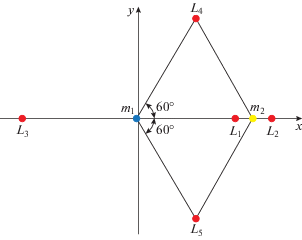
$\ddot {x} - 2\dot {y} = {{U}_{x}},\,\,\,\,{\text{ }}\ddot {y} + 2\dot {x} = {{U}_{y}},\,\,\,\,{\text{ }}\ddot {z} = {{U}_{z}},$Система уравнений (1) обладает пятью положениями равновесия (см. рис. 2); три из них лежат на оси $x$ и называются коллинеарными точками либрации. Они обозначаются символами ${{L}_{1}}$, ${{L}_{2}}$ и ${{L}_{3}}$. Эти точки являются неустойчивыми по Ляпунову. В системе Земля–Луна их координаты равны, соответственно, ${{x}_{{{{L}_{1}}}}} = {\text{0}}{\text{.8369147,}}$ ${{x}_{{{{L}_{2}}}}} = {\text{1}}{\text{.1556825}}$ и ${{x}_{{{{L}_{3}}}}} = {\text{1}}{\text{.0050627}}{\text{.}}$ В оставшейся части работы внимание будет уделено лишь точкам ${{L}_{1}}$ и ${{L}_{2}}$.
В окрестности точек либрации ${{L}_{1}}$ и ${{L}_{2}}$ существуют семейства периодических орбит, наиболее известные среди которых – плоские орбиты Ляпунова и гало-орбиты (см. рис. 3–4). Формально гало-орбиты можно определить как пространственные периодические орбиты, ответвляющиеся от плоских орбит Ляпунова при некотором значении интеграла энергии. Эти орбиты симметричны относительно плоскости $yz$ и пересекают ее ортогонально в двух точках. Часть гало-орбиты находится над плоскостью $xy$, а другая часть – под плоскостью $xy$. Различают так называемые северные и южные гало-орбиты. У северных гало-орбит часть над плоскостью $xy$ удаляется от этой плоскости на большую величину, чем часть под плоскостью $xy$. Южные гало-орбиты – это зеркальное отражение северных гало-орбит относительно плоскости$xy.$ В данной работе рассматриваются лишь северные гало-орбиты вокруг точек ${{L}_{1}}$ и ${{L}_{2}}$.
Рис. 4.
Семейство северных гало-орбит вокруг точки ${{L}_{1}}$ системы Земля–Луна с проекциями на плоскости $xy$, $xz$ и $yz$.

Геометрически гало-орбиты характеризуются следующими параметрами: максимальной ${{x}_{{\max }}}$ и минимальной ${{x}_{{\min }}}$ координатами $x$, максимальной ${{y}_{{\max }}}$ и минимальной ${{y}_{{\min }}}$ координатами $y$ (причем ${{y}_{{\min }}} = - {{y}_{{\max }}}$), а также максимальной ${{z}_{{\max }}}$ и минимальной ${{z}_{{\min }}}$ координатами $z$.
Гало-орбиты – это однопараметрическое семейство орбит. Можно показать (см. рис. 5), что вплоть до ${{z}_{{\max }}} = 70$ тыс. км параметром, однозначно определяющим орбиту в семействе, может служить величина ${{z}_{{\max }}}$. В данной работе рассматриваются только гало-орбиты с ${{z}_{{\max }}} \leqslant 70$ тыс. км.
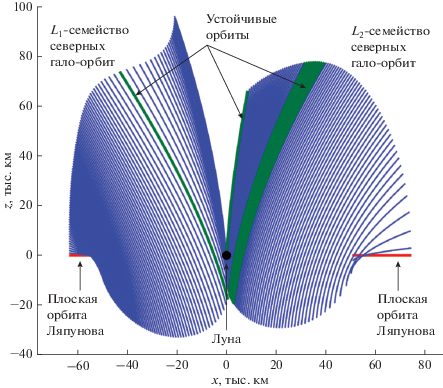
Рис. 5.
Семейства гало-орбит вокруг точек ${{L}_{1}}$ и ${{L}_{2}}$ в проекции на плоскость $xz$. Показаны также две плоские орбиты Ляпунова, от которых ответвляются соответствующие семейства гало-орбит, а также устойчивые гало-орбиты, для которых все мультипликаторы Флоке по модулю равны единице.
Существует множество способов построения орбит вокруг точек либрации, они включают в себя как численные, так и полуаналитические методы. Для построения орбит Ляпунова можно применять стандартные процедуры дифференциальной коррекции и методов продолжения [6]. Гало-орбиты можно аппроксимировать рядами Линдштедта-Пуанкаре [6, 7], а затем уточнять их в модели CR3BP с помощью техники дифференциальной коррекции; этот подход и используется в данной работе.
Помимо периодического движения, в модели CR3BP существует два множества асимптотических траекторий, связанных с орбитами вокруг коллинеарных точек либрации. Они формируют устойчивые и неустойчивые инвариантные многообразия. Траектории устойчивого многообразия стремятся к орбите при $t \to + \infty $, а траектории неустойчивого многообразия стремятся к орбите при $t \to - \infty .$ Каждая асимптотическая траектория связана с некоторой точкой на орбите. Для того, чтобы рассчитать асимптотическую траекторию связанную с точкой ${{{\mathbf{x}}}_{0}} = \left[ {{{x}_{0}},{{y}_{0}},{{z}_{0}},{{{\dot {x}}}_{0}},{{{\dot {y}}}_{0}},{{{\dot {z}}}_{0}}} \right]$ на периодической орбите, необходимо совместно с уравнениями движения проинтегрировать уравнения в вариациях:
(2)
${\mathbf{\dot {\Phi }}}\left( {t;{{t}_{0}}} \right) = {\mathbf{A}}\left( t \right){\mathbf{\Phi }}\left( {t;{{t}_{0}}} \right),$Для определенности будем считать первую компоненту вектора ${{{\mathbf{u}}}_{u}}$ положительной. Тогда при положительном $\varepsilon $ соответствующая асимптотическая траектория удаляется от гало-орбиты в сторону возрастания координаты $x$, а при отрицательном – в сторону убывания этой координаты.
3. ПОСТАНОВКА ЗАДАЧИ
Задача состоит в поиске окололунных орбит, доступных при сходе вдоль неустойчивого многообразия гало-орбит вокруг точек ${{L}_{1}}$ и ${{L}_{2}}$ системы Земля–Луна. При этом необходимо определить множество наклонений и перицентральных расстояний искомых окололунных орбит, доступность полярных и околополярных орбит, зависимость диапазона доступных наклонений от величины ${{z}_{{\max }}}$ гало-орбиты.
Рассматриваются только гало-орбиты с ${{z}_{{\max }}} \leqslant 70$ тыс. км.
Все расчеты производятся в рамках круговой ограниченной задачи трех тел. Влияние других тел Солнечной системы, давления солнечного света, гармоник высокого порядка модели гравитационного поля Луны в данной работе не изучается.
Орбитальные элементы рассчитываются по отношению к инерциальной системе координат, главная плоскость которой совпадает с плоскостью орбиты Луны, т.е. плоскостью $xy$. Получаемые таким образом данные не зависят от времени, в отличие от данных, получаемых по отношению к селенографическим координатам. Трансляция в селенографические координаты описана в разделе 6.
Рассматриваются два космических аппарата: в классе мини (250 кг) и нано (9 кг). Космические аппараты снабжены двигателями малой тяги, их характеристики перечислены в таблице. Прототипом двигателя для миниаппарата служит двигатель СПД-100В компании ОКБ Факел, а для наноаппарата – BIT-3 компании Busek.
4. ОСКУЛИРУЮЩИЕ ОКОЛОЛУННЫЕ ОРБИТЫ ИЗ НЕУСТОЙЧИВОГО МНОГООБРАЗИЯ ГАЛО-ОРБИТ
Рассмотрим гало-орбиту вокруг точки ${{L}_{1}}$ или ${{L}_{2}}$. Точки на гало-орбите будем обозначать параметром $\varphi \in \left[ {0,1} \right]$. Пусть выбрана точка $\varphi $, тогда ей соответствует некоторый фазовый вектор ${{{\mathbf{x}}}_{0}}$. Пусть ${{{\mathbf{u}}}_{u}}$ – единичный вектор вдоль неустойчивого многообразия в точке ${{{\mathbf{x}}}_{0}}$ и точка ${{{\mathbf{x}}}_{1}} = {{{\mathbf{x}}}_{0}} + \varepsilon {{{\mathbf{u}}}_{u}}$ принадлежит асимптотической траектории неустойчивого многообразия. Если рассматривается орбита вокруг точки ${{L}_{1}}$, то выберем $\varepsilon = {{10}^{{ - 6}}} > 0$, чтобы движение было направлено к Луне. Если же гало-орбита находится в окрестности точки ${{L}_{2}}$, то выберем $\varepsilon = - {{10}^{{ - 6}}} < 0$. В этом случае движение также направлено к Луне.
Под точкой периселения будем понимать такую точку на траектории космического аппарата, в которой достигается локальный минимум расстояния до Луны. Дополнительно потребуем также, чтобы эта точка была достаточно близка к Луне: в данной работе это 10 радиусов Луны, т.е. 17374 км.
Сначала будем распространять пассивные траектории (без включения тяги) и регистрировать оскулирующие орбитальные элементы в точке периселения. Если распространить траекторию вперед во времени от точки ${{{\mathbf{x}}}_{1}}$, то первым произойдет одно из следующих событий:
1. аппарат достиг точки периселения,
2. аппарат столкнулся с Луной,
3. аппарат удалился от Луны через окрестность точки ${{L}_{1}}$ ($x$ – координата стала меньше 0.7 безразмерных единиц),
4. аппарат удалился от Луны через окрестность точки ${{L}_{2}}$ ($x$ – координата стала больше 1.3 безразмерных единиц).
Если произошло одно из событий 2–4, то траектория далее не распространяется, никакие результаты для данной траектории не сохраняются. Если же произошло событие 1, то в точке периселения рассчитываются параметры оскулирующей окололунной орбиты, которые записываются в общую базу данных. Эти параметры соответствуют первому пролету Луны. Далее траектория снова распространяется вперед во времени до тех пор, пока не будет выполнено одно из вышеперечисленных условий. Если произошло одно из событий 2–4, то распространение траектории на этом заканчивается, и в базе данных сохраняется лишь сведения о первом пролете Луны. Если же произошло событие 1, то рассчитываются новые параметры оскулирующей окололунной орбиты. Эти параметры соответствуют второму пролету Луны. Далее траектория снова распространяется вперед во времени, и процедура расчетов и записи результатов повторяются вновь. Практика показывает, что такая процедура рано или поздно останавливается, т.к. будет выполнено одно из условий 2–4.
Так как в процессе расчета расстояние до Луны варьируется в больших пределах и возможны траектории столкновения с Луной, решено было регуляризировать уравнения движения модели CR3BP, воспользовавшись преобразованием Сундмана [8]. А именно, в качестве независимой переменной выбирается переменная $s$, связанная со временем $t$ выражением $dt = {{r}_{2}}{\kern 1pt} ds,$ где ${{r}_{2}}$ – расстояние до центра Луны. Уравнения движения в этом случае станут
Регуляризация уравнений позволяет воспользоваться классическим методом интегрирования Рунге–Кутты четвертого порядка с постоянным шагом, который был выбран равным $\Delta s = {1 \mathord{\left/ {\vphantom {1 {16}}} \right. \kern-0em} {16}},$ что приблизительно соответствует 1 часу в окрестности точки либрации ${{L}_{1}}$ или ${{L}_{2}}$.
Расчеты были проведены для набора северных гало-орбит вокруг ${{L}_{1}}$ или ${{L}_{2}}$. Набор состоял из 70 гало-орбит с ${{z}_{{\max }}}$, равными 1000, 2000 км, и так далее вплоть до 70 000 км. На каждой гало-орбите было выбрано 1000 точек, из которых вдоль неустойчивого многообразия распространялись траектории. Окололунные орбиты, которые получаются при сходе с южного семейства гало-орбит, имеют те же самые параметры, что орбиты при сходе с северных гало-орбит, за исключением долготы восходящего узла и аргумента перицентра, которые отличаются от соответствующих значений на 180°.
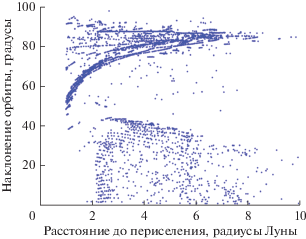
На рис. 6 показаны расстояние до периселения и наклонение оскулирующих орбит, получающихся при первом пролете Луны в точке периселения при сходе с гало-орбит вокруг ${{L}_{1}}$. Цветами выделены точки, соответствующие гало-орбите с ${{z}_{{\max }}}$, равными 15 000, 25 000 и 35 000 км. Эти результаты показывают, что достижимы окололунные орбиты с произвольным наклонением от 0° до 126° при рассмотрении схода вдоль неустойчивого многообразия с гало-орбит размеров от 1000 до 70 000 км, причем чем крупнее гало-орбита, тем более высокое наклонение можно получить. Отметим, что наклонения вблизи 90° удается получить лишь для гало-орбит размера не ниже 30 000 км. Аналогичная картина получена для гало-орбит вокруг ${{L}_{2}}$, см. рис. 7. Здесь достижимы орбиты с наклонениями до 120°, а выход на полярные орбиты возможен лишь с гало-орбит размера не меньше 45 000 км.
Рис. 6.
Расстояние до периселения и наклонение оскулирующих орбит, получающихся при первом пролете Луны в точке периселения при движении вдоль неустойчивого многообразия гало-орбит вокруг ${{L}_{1}}$.
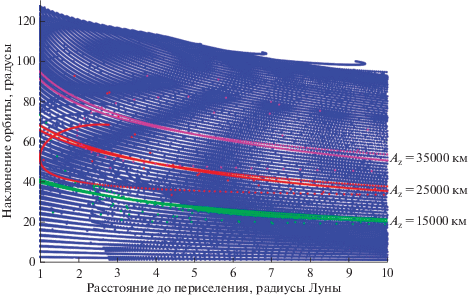
Рис. 7.
Расстояние до периселения и наклонение оскулирующих орбит, получающихся при первом пролете Луны в точке периселения при движении вдоль неустойчивого многообразия гало-орбит вокруг ${{L}_{2}}$.
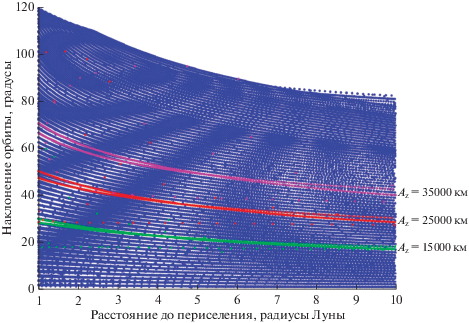
Рис. 8, 9, 10 и 11 показывают, сколько витков вокруг Луны совершает аппарат прежде чем он столкнется с ее поверхностью или удалится от Луны через окрестность точки ${{L}_{1}}$ или ${{L}_{2}}$. Эти данные относятся к сходу с гало-орбит вокруг ${{L}_{1}}$. Аналогичные результаты для гало-орбит вокруг ${{L}_{2}}$ собраны вместе на рис. 12.
Рис. 8.
Количество витков вокруг Луны, которое совершает аппарат после первого пролета Луны до столкновения с ее поверхностью. Данные получены для случая гало-орбит вокруг ${{L}_{1}}$.
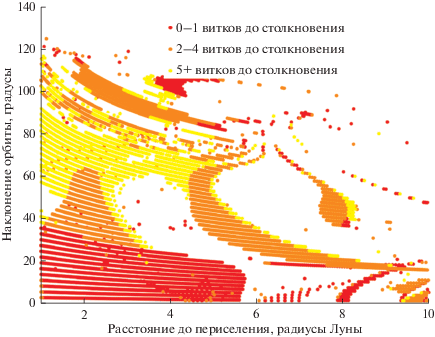
Рис. 9.
Количество витков вокруг Луны, которое совершает аппарат после первого пролета Луны до вылета через окрестность точки ${{L}_{1}}$.
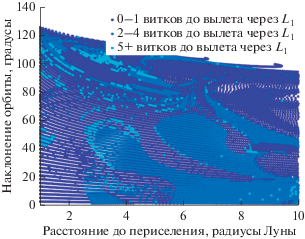
Рис. 10.
Количество витков вокруг Луны, которое совершает аппарат после первого пролета Луны до вылета через окрестность точки ${{L}_{2}}$.
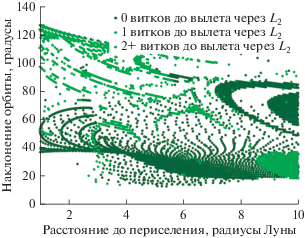
Рис. 11.
Объединенные рис. 8, 9 и 10. Более яркие области отвечают более устойчивым траекториям, которые совершают несколько витков вокруг Луны, прежде чем столкнуться с ее поверхностью либо удалиться от Луны через окрестность точки ${{L}_{1}}$ или ${{L}_{2}}$.
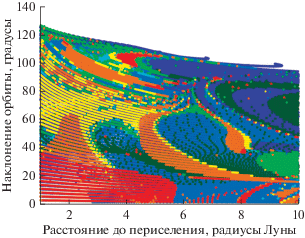
Рис. 12.
Объединенные рис. для гало-орбит вокруг ${{L}_{2}}$. Более яркие области отвечают более устойчивым траекториям, которые совершают несколько витков вокруг Луны, прежде чем столкнуться с ее поверхностью либо удалиться от Луны через окрестность точки ${{L}_{1}}$ или ${{L}_{2}}$.

Из полученных результатов следует одно важное наблюдение: околополярные орбиты с низким перигеем более устойчивы (совершают больше витков). Сравнивая рис. 11 и 12, можно обратить внимание, что сталкивающихся с Луной траекторий намного больше при сходе с гало-орбит вокруг ${{L}_{1}}$, а не ${{L}_{2}}$.
Орбитальные параметры всех полученных здесь орбит являются в значительной степени изменяются: вариации расстояния до периселения за виток могут составить от 10 000 до 15 000 км, а наклонение может измениться на десятки и даже сотню градусов. В связи с этим обстоятельством встает вопрос о возможности стабилизации таких орбит малой тягой.
5. СТАБИЛИЗАЦИЯ ОКОЛОЛУННЫХ ОРБИТ МАЛОЙ ТЯГОЙ
Стабилизация орбиты малой тягой выполняется следующим образом: всякий раз, когда аппарат подлетает к Луне на достаточно близкое расстояние ${{r}_{{\max }}}$ (10 радиусов Луны в данной работе), двигатель создает тягу против скорости КА в инерциальной системе отсчета. В некоторый момент времени расстояние до точки апоселения опустится ниже значения ${{r}_{{\max }}}$, и тогда тяга будет включена постоянно. Распространение траектории заканчивается в момент, когда максимальная вариация наклонения и расстояния до периселения около своих средних значений за последовательные два витка не будет меньше заранее заданной величины: ${{1}^{ \circ }}$ для наклонения и 1000 км для расстояния до периселения. В какой-то момент, впрочем, может оказаться, что тяги недостаточно для стабилизации траектории, и аппарат соударяется с Луной либо удаляется от Луны через окрестность точки ${{L}_{1}}$ или ${{L}_{2}}$. Такие траектории не сохраняются, так как нас интересуют лишь стабилизированные траектории. Более того, устанавливается ограничение и на время стабилизации: оно не должно превышать 10 оборотов Луны вокруг Земли (т.е. 10 месяцев).
Результаты были получены для миниаппарата массой 250 кг, оснащенного двигателем малой тяги СПД-100В, а также для наноаппарата массой 9 кг с двигателем из серии BIT-3. Для миниаппарата на гало-орбите вокруг точки ${{L}_{1}}$ удается стабилизировать 25.16% траекторий, для наноаппарата – 15.49% траекторий. Что касается гало-орбит вокруг точки ${{L}_{2}}$, то для миниаппарата стабилизируются 31.52% траекторий, а для наноаппарата – 6.07% траекторий.
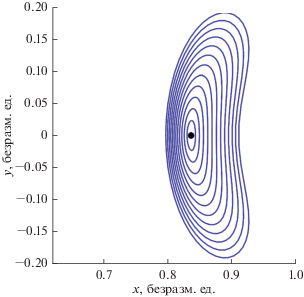
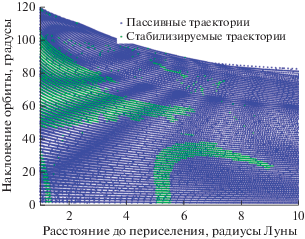
На рис. 13 показаны орбиты, найденные при пассивном распространении траекторий, и те из них, которые удается стабилизировать для миниаппарата. Похожая картина распределения стабилизируемых орбит была найдена и для наноаппарата. Отметим, что пока орбита не стабилизирована, ее орбитальные параметры претерпевают значительные изменения. Финальные, стабилизированные, параметры для случая миниаппарата при сходе с гало-орбит вокруг ${{L}_{1}}$ изображены на рис. 14. Из рисунка видно, что в большом количестве существуют околополярные траектории, актуальные для современных практических задач. Аналогичные результаты были получены для миниаппарата при сходе с гало-орбит вокруг ${{L}_{2}}$, см. рис. 15 и 16.
Рис. 13.
Орбиты, найденные при пассивном распространении траекторий с гало-орбит вокруг ${{L}_{1}}$, и те из них, которые удается стабилизировать для миниаппарата.
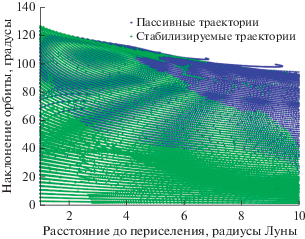
Рис. 14.
Стабилизированные окололунные орбиты при сходе с гало-орбит вокруг ${{L}_{1}}$ для миниаппарата.
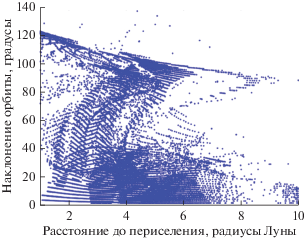
Рис. 15.
Орбиты, найденные при пассивном распространении траекторий с гало-орбит вокруг ${{L}_{2}}$, и те из них, которые удается стабилизировать для миниаппарата.
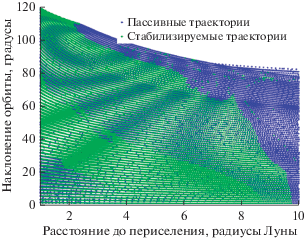
Рис. 16.
Стабилизированные окололунные орбиты при сходе с гало-орбит вокруг ${{L}_{2}}$ для миниаппарата.
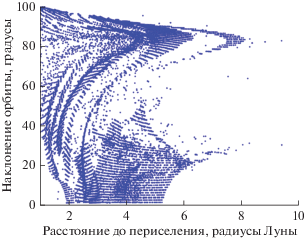
Приведем также результаты для наноаппарата при сходе с гало-орбит вокруг ${{L}_{1}}$ (рис. 17 и 18) и ${{L}_{2}}$ (рис. 19 и 20). Отметим, что в последнем случае, несмотря на малое относительное число стабилизируемых орбит, существует крупное множество достижимых околополярных орбит.
Рис. 17.
Орбиты, найденные при пассивном распространении траекторий с гало-орбит вокруг ${{L}_{1}}$, и те из них, которые удается стабилизировать для наноаппарата.
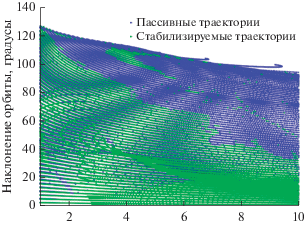
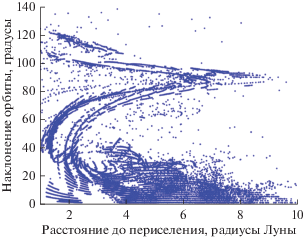
Рис. 18.
Стабилизированные окололунные орбиты при сходе с гало-орбит вокруг ${{L}_{1}}$ для наноаппарата.
6. ПЕРЕВОД В СЕЛЕНОГРАФИЧЕСКИЕ КООРДИНАТЫ
В данной работе наклонения окололунных орбит рассчитываются по отношению к системе координат, в которой главная плоскость совпадает с плоскостью $xy$ вращающейся системы координат. Чтобы перевести фазовый вектор из этой системы координат в селенографические координаты, можно поступить следующим образом. Сначала траектория адаптируется к эфемеридной модели движения тел Солнечной системы, например, с помощью техники параллельной пристрелки (см., например, [9]). При этом, движение описывается в селеноцентрической небесной системе координат (Selenocentric Celestial Reference System, SCRS). Ориентация фигуры Луны относительно осей SCRS задается углами Эйлера $\left( {\varphi ,\theta ,\psi } \right)$, входящими в состав эфемеридной информации [10, 11]. Далее, радиус-вектор ${{{\mathbf{r}}}_{{{\text{SCRS}}}}}$ в осях SCRS переводится в радиус-вектор ${{{\mathbf{r}}}_{{{\text{PA}}}}}$ в связанной с Луной селеноцентрической системе координат Principal Axis (PA) Reference System, оси которой совпадают с главными осями инерции Луны:
Положения объектов на поверхности Луны традиционно задаются селенографическими координатами – широтой и долготой – в системе координат с главной плоскостью, ортогональной усредненному направлению лунной оси вращения, и нулевым меридианом, в среднем ориентированным на центр Земли. Такая селеноцентрическая система координат называется Mean-Earth/Mean-Rotation (MER) Reference System. Ее оси близки к PA-осям. Малые углы, которые связывают эти две системы координат, специфичны для каждого набора эфемерид. Например, для эфемерид DE430 Лаборатории реактивного движения NASA преобразование осуществляется по формуле [10]
ЗАКЛЮЧЕНИЕ
При сходе вдоль неустойчивого многообразия гало-орбит параметры окололунных орбит оказываются сильно изменяются со временем. Исследование показало, что без стабилизации каждая такая орбита рано или поздно столкнется с Луной или вылетит через окрестности точек либрации L1 и L2. Малая тяга позволяет стабилизировать только часть этих траекторий – не более трети, причем так как двигатель малой тяги на миниаппарате дает большее реактивное ускорение, то для него стабилизированных траекторий больше, чем для наноаппарата, двигатель которого дает меньшее реактивное ускорение.
Главный результат данной работы – найденные полярные и околополярные окололунные орбиты, доступные в результате схода вдоль неустойчивого многообразия гало-орбит и последующей их стабилизации малой тягой на малых аппаратах. Показано, что эти орбиты доступны как для миниаппарата, так и для наноаппарата, оснащенных существующими на сегодняшний день двигателями малой тяги. Найдены орбиты в широком диапазоне наклонений (от 0 до 120 градусов) и высоты перицентра (от 0 до 10 лунных радиусов).
Работа полностью поддержана грантом Российского научного фонда (проект 14-11-00621).
Список литературы
Cпeктp-Peнтгeн-Гaммa. http://srg.iki.rssi.ru/.
Астрофизическая обсерватория “Спектр-М” // Научно-производственное объединение им. С.А. Лавочкина: https://www.laspace.ru/projects/astrophysics/ spectrum-m/
Lo M.W. The interplanetary superhighway and the origins program // Aerospace Conference Proceedings. 2002. V. 7. P. 7-3543–7-3562.
Mission Overview // Mars Cube One (MarCO): https:// www.jpl.nasa.gov/cubesat/missions/marco.php
Parker J.S., Anderson R.L. Low-energy lunar trajectory design. 2013.
Koon W.S., Lo M.W., Marsden J.E., Ross S.D. Dynamical Systems, the Three-Body Problem and Space Mission Design. New York City: Springer, 2011.
Gomez G., Llibre J., Matinez R., Simo C. Dynamics and Mission Design Near Libration Point Orbits. V. I: Fundamentals: The Case of Collinear Libration Points. V II. World Scientific. 2001.
Авдюшев В.А. Численное моделирование орбит. Томск: НТЛ, 2010. 31–37 с.
Pavlak T.A. Mission Design Applications in the Earth-Moon System. MS Thesis, Purdue University, West Lafayette, Indiana, USA. 2010.
Folkner W.M., Williams J.G., Boggs D.H. et al. The Planetary and Lunar Ephemerides DE430 and DE431. IPN Progress Report 42-196. 2014.
Seidelmann P.K., Archinal B.A., A’Hearn M.F. et al. Report of the IAU/IAG Working Group on cartographic coordinates and rotational elements: 2006 // Celestial Mechanics and Dynamical Astronomy. V. 98. № 3. 2007. P. 155–180.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования