Космические исследования, 2020, T. 58, № 4, стр. 305-311

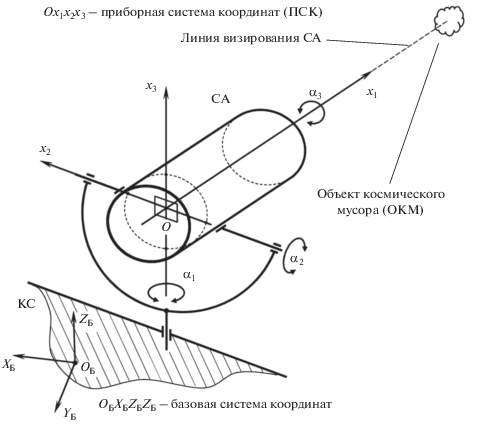
Рассматриваемая космическая станция является частью некоторой системы, предназначенной для “уборки” околоземного пространства от объектов космического мусора. С конструкцией КС связана базовая система координат, далее – БСК. На борту КС, на поворотной платформе установлена съемочная аппаратура (СА) для наблюдения за ОКМ, которая схематично представлена на рис. 1. С указанной аппаратурой связана приборная система координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ (ПСК). Ось ${{x}_{1}}$ совпадает с направлением линии визирования СА, оси ${{x}_{2}}$ и ${{x}_{3}}$ перпендикулярны линии визирования и лежат в экранной плоскости СА. Поворотная платформа представляет собой трехстепенной карданов подвес с углами поворота ${{\alpha }_{1}}$, ${{\alpha }_{2}}$ и ${{\alpha }_{3}}$. Внешняя ось подвеса (угол поворота ${{\alpha }_{1}}$) жестко соединена с корпусом КС, а внутренняя ось (угол поворота ${{\alpha }_{3}}$) совпадает с осью ${{x}_{1}}$. Точка пересечения осей вращения подвеса совпадает с точкой $O$.

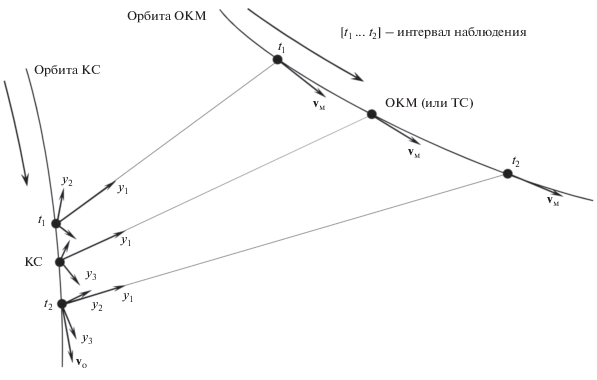
Предположим, что орбита КС и параметры ее вращательного движения хорошо известны, а также хорошо известна и орбита ОКМ. В этом случае, очевидно, задача съемки ОКМ заключается в совмещении линии визирования СА с направлением из точки КС в точку ОКМ в течение заданного времени. На рис. 2 схематично представлен этот процесс. Границы интервала съемки на рисунке обозначены точками ${{t}_{1}}$ и ${{t}_{2}}$. Вращательное движение СА будет включать в себя вращение вместе с ортом относительного положения ОКМ и, в общем случае – одновременный поворот вокруг направления указанного орта таким образом, чтобы изображение ОКМ было заданным образом ориентировано на экранной плоскости СА.

Далее будет использоваться определение “точка съемки” (ТС) – некоторая точка на орбите ОКМ, в которую в данный момент направлена линия визирования СА. ТС может совпадать или не совпадать с текущим положением ОКМ. С направлением из точки КС в ТС связана некоторая технологическая система координат (ТСК) $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$. Начало ТСК совпадает с текущим положением КС, ось ${{y}_{1}}$ направлена из точки КС в ТС, ось ${{y}_{2}}$ перпендикулярна оси ${{y}_{1}}$ и одновременно перпендикулярна еще одному вектору, далее – ориентирующему вектору. Ориентирующим вектором может быть, например, вектор относительной или собственной линейной скорости ОКМ. Ось ${{y}_{3}}$ дополняет систему до правой. Будем считать, что в режиме съемки ПСК будет заданным образом ориентирована относительно ТСК, в частности, ПСК может быть совмещенной с ТСК.

Приведем кинематические соотношения для ТСК, отслеживающей относительное положение ОКМ. Для определенности, выражения будем записывать в системе координат J2000. Матрица перехода от ТСК к J2000 определяется выражением: $A = [{{{\mathbf{n}}}_{1}},\;{{{\mathbf{n}}}_{2}},\;{{{\mathbf{n}}}_{3}}]$, где ${{{\mathbf{n}}}_{1}}$ ${{{\mathbf{n}}}_{2}}$ ${{{\mathbf{n}}}_{3}}$ – орты, направленные по соответствующим осям ТСК. В соответствии с определением ТСК: ${{{\mathbf{n}}}_{1}} = {{\mathbf{r}} \mathord{\left/ {\vphantom {{\mathbf{r}} r}} \right. \kern-0em} r},$ ${{{\mathbf{n}}}_{2}} = {{({\mathbf{v}}{\text{*}} \times {\mathbf{r}})} \mathord{\left/ {\vphantom {{({\mathbf{v}}{\text{*}} \times {\mathbf{r}})} {\left| {{\mathbf{v}}{\text{*}} \times {\mathbf{r}}} \right|}}} \right. \kern-0em} {\left| {{\mathbf{v}}{\text{*}} \times {\mathbf{r}}} \right|}}$, ${{{\mathbf{n}}}_{3}} = {{{\mathbf{n}}}_{1}} \times {{{\mathbf{n}}}_{2}}$. Здесь ${\mathbf{r}} = {{{\mathbf{r}}}_{{\text{м}}}} - {{{\mathbf{r}}}_{{\text{о}}}}$ – радиус-вектор относительного положения ОКМ, ${{{\mathbf{r}}}_{{\text{o}}}}$– геоцентрический радиус-вектор КС, ${{{\mathbf{r}}}_{{\text{м}}}}$ – геоцентрический радиус-вектор ОКМ, ${\mathbf{v}}{\text{*}}$ – вектор собственной или относительной линейной скорости ОКМ, $r = \left| {\mathbf{r}} \right|$. Далее в тексте нижний индекс “о” означает принадлежность вектора к КС, а индекс “м” – принадлежность к ОКМ (ТС).

Выражения для компонент вектора абсолютной угловой скорости ТСК можно найти из уравнения ${{{\mathbf{\omega }}}_{{{\text{ТСК}}}}} = \sum {({{{\mathbf{n}}}_{3}} \cdot {{{{\mathbf{\dot {n}}}}}_{2}}){{{\mathbf{n}}}_{1}}} $ с циклической перестановкой индексов $1 \to 2 \to 3 \to 1$, где

В приведенных соотношениях ${\mathbf{v}} = {{{\mathbf{v}}}_{{\text{м}}}} - {{{\mathbf{v}}}_{{\text{о}}}}$ – вектор относительной линейной скорости ОКМ. Если в качестве ориентирующего вектора была выбрана собственная скорость ОКМ, то ${\mathbf{v}}{\text{*}} = {{{\mathbf{v}}}_{{\text{м}}}}$, ${\mathbf{a}}{\text{*}} = {{{\mathbf{a}}}_{{\text{м}}}}$. Если в качестве ориентирующего вектора была выбрана относительная скорость ОКМ, то ${\mathbf{v}}* = {\mathbf{v}}$, ${\mathbf{a}}{\text{*}} = {{{\mathbf{a}}}_{{\text{м}}}} - {{{\mathbf{a}}}_{{\text{o}}}}$, при этом приведенное выше соотношение для ${{{\mathbf{\dot {n}}}}_{2}}$ несколько упрощается. Если начальные условия орбитального движения КС и ОКМ известны, текущие значения параметров ${{{\mathbf{r}}}_{{\text{o}}}}$, ${{{\mathbf{v}}}_{{\text{o}}}}$, ${{{\mathbf{a}}}_{{\text{o}}}}$, ${{{\mathbf{r}}}_{{\text{м}}}}$, ${{{\mathbf{v}}}_{{\text{м}}}}$, ${{{\mathbf{a}}}_{{\text{м}}}}$ можно найти, интегрируя уравнения модели орбитального движения КС и ОКМ [1]. Если ПСК совмещается с ТСК, то выписанные соотношения для матрицы $A$ и вектора абсолютной угловой скорости ${{{\mathbf{\omega }}}_{{{\text{ТСК}}}}}$ можно сразу использовать для расчета кинематических параметров ПСК, которые затем по известным соотношениям могут быть приведены к заданной БСК и преобразованы в углы поворота соответствующих осей карданова подвеса. В данной работе этот этап расчетов подробно не рассматривается.

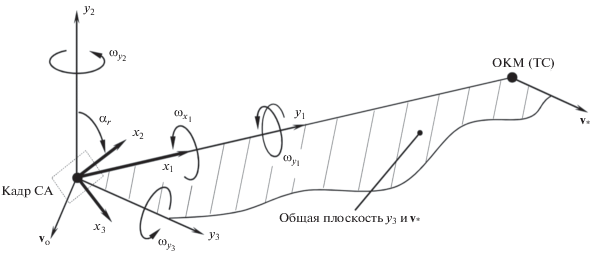
Иногда для организации съемки ОКМ нет необходимости в полном совмещении ПСК с ТСК. При отслеживании ОКМ, чтобы не потерять его из кадра, достаточно совместить только оси ${{x}_{1}}$ и ${{y}_{1}}$. При этом ПСК может вращаться относительно ТСК вокруг совмещенных осей (см. рис. 3). Соответственно, изображение ОКМ на экранной плоскости СА также получит некоторое дополнительное вращение. Угловая скорость ПСК в этом случае будет вычисляться как сумма угловой скорости ТСК и скорости ${{\omega }_{{x1}}}$ относительного вращения ПСК вокруг совмещенных осей ${{x}_{1}}$ и ${{y}_{1}}$: ${{{\mathbf{\omega }}}_{{{\text{ПСК}}}}} = {{{\mathbf{\omega }}}_{{{\text{ТСК}}}}} + {{\omega }_{{x1}}}{{{\mathbf{n}}}_{1}}$. Матрицу перехода от ПСК к J2000 можно найти из соотношения $B = AR_{x}^{T}$, где ${{R}_{x}} = f({{\alpha }_{r}})$ – матрица поворота вокруг оси ${{x}_{1}}$ на угол относительного поворота ${{\alpha }_{r}}$,

где ${{t}_{1}}$ и ${{t}_{2}}$ – моменты времени, ограничивающие интервал наблюдения. Такой режим съемки можно использовать, например, для ограничения динамических нагрузок на СА, или для упрощения конструкции аппаратуры – применении двухстепенного подвеса СА вместо трехстепенного.

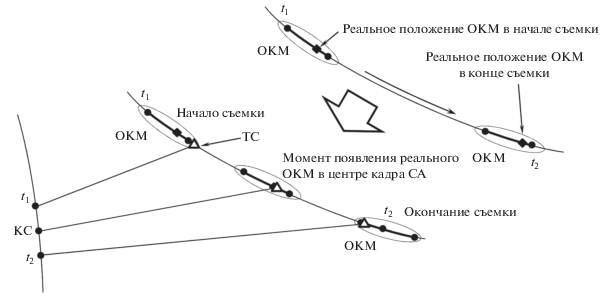
Предположим теперь, что параметры орбитального движения ОКМ известны с ограниченной точностью. Будем считать известными форму орбиты ОКМ и ее пространственную ориентацию, при этом положение ОКМ на орбите известно с некоторой ошибкой. Тогда орбитальное положение ОКМ можно рассматривать не как точку, а как некоторую область – отрезок орбиты, внутри которого находится ОКМ. Указанный отрезок схематично изображен на рис. 4 в виде вытянутого вдоль траектории ОКМ эллипса. За время съемки этот отрезок смещается вдоль орбиты ОКМ, переходя из некоторого начального положения – в конечное. Далее будем считать, что на интервале наблюдения длина отрезка меняется несущественно и истинное положение ОКМ не выходит за пределы этого отрезка.

Очевидно, что размеры отрезка орбиты, внутри которого находится ОКМ (далее – отрезка), могут быть шире, чем угловой размер поля зрения СА. При этом если в течение всего интервала наблюдения ТС будет, например, совпадать с номинальным положением ОКМ, то ОКМ в своем истинном положении внутри рассматриваемого отрезка может никогда не попасть в поле зрения СА. Вместе с тем можно утверждать, что если за время съемки ТС переместится от одного края отрезка – к противоположному его краю, то любое возможное положение ОКМ внутри этого отрезка в какой-то момент времени окажется в поле зрения СА.

Другими словами, точка съемки, оставаясь на траектории орбитального движения ОКМ, должна иметь скорость, отличную от скорости ОКМ, чтобы перемещаясь по орбите вместе с отрезком, отставать или опережать его заданным образом. При этом разность скорости ОКМ и ТС в данной точке орбиты ОКМ будет определять относительную скорость движения ОКМ в кадре СА. Кинематика вращательного движения ТСК, как и прежде, будет в этом случае определяться относительным движением КС и ТС. Матрица ориентации и угловая скорость ТСК вычисляются по приведенным выше соотношениям, в которых вместо кинематических параметров ${{{\mathbf{r}}}_{{\text{м}}}}$, ${{{\mathbf{v}}}_{{\text{м}}}}$, ${{{\mathbf{a}}}_{{\text{м}}}}$ используются соответствующие параметры ${{{\mathbf{r}}}_{s}}$, ${{{\mathbf{v}}}_{s}}$, ${{{\mathbf{a}}}_{s}}$ движения точки съемки, движущейся независимо от ОКМ.

Расчет указанных параметров движения ТС представляет отдельную задачу, для решения которой в вектор состояния модели орбитального движения КС и ОКМ вводится дополнительный параметр – путь $s(t)$, пройденный ОКМ вдоль своей орбиты в функции времени. Для этого совместно с уравнениями модели орбитального движения КС и ОКМ интегрируется абсолютное значение линейной скорости ОКМ. На границах интервала интегрирования параметр $s(t)$ принимает значения:

Интервал интегрирования ${{t}_{1}} \leqslant t \leqslant {{t}_{2}}$ выбирается таким образом, чтобы параметр $s(t)$ охватывал весь участок съемки. При этом учитывается длина отрезка, внутри которого находится ОКМ, и положение этого отрезка на орбите в начальный и конечный момент интервала наблюдения. Результаты интегрирования сохраняются на некоторой плотной сетке, после чего строятся зависимости ${{{\mathbf{r}}}_{{\text{м}}}}(s)$ и ${{{\mathbf{v}}}_{{\text{м}}}}(s)$ в виде “векторных” степенных полиномов ${{{\mathbf{P}}}_{s}}$ и ${{{\mathbf{Q}}}_{s}}$. Расчет данных полиномов не вызывает затруднений, т.к. на сравнительно коротком интервале наблюдения компоненты векторов ${{{\mathbf{r}}}_{{\text{м}}}}$ и ${{{\mathbf{v}}}_{{\text{м}}}}$ представляют собой гладкие кривые. Пример таких кривых приведен на рис. 5.

“Векторные” в данном случае означает, что полиномы вычисляются для каждой из компонент векторов ${{{\mathbf{r}}}_{{\text{м}}}}$ и ${{{\mathbf{v}}}_{{\text{м}}}}$. Полином ${{{\mathbf{P}}}_{s}}$ определяет опорную траекторию ТС в функции $s$ в виде пространственной кривой, с заданной точностью совпадающей с орбитальной траекторией ОКМ на участке съемки. Полином ${{{\mathbf{Q}}}_{s}}$ служит для нахождения вектора скорости ОКМ в заданной точке опорной траектории ТС.

Далее выбирается характер движения ТС по найденной опорной траектории – выбирается зависимость пути ${{S}_{{{\text{TC}}}}}(t)$, проходимого ТС на участке съемки вдоль опорной траектории в функции времени. Выбранное движение ТС затем рассчитывается на плотной сетке и аппроксимируется полиномами Эрмита 5-го порядка, допускающими получение гладких зависимостей для ${{\dot {S}}_{{{\text{ТС}}}}}(t)$ и ${{\ddot {S}}_{{{\text{ТС}}}}}(t)$. Искомые кинематические параметры ТС вычисляются по соотношениям (штрихами обозначены производные по S):

Приведенные соотношения позволяют рассчитать кинематические параметры вращательного движения ТСК при наблюдении с ТС, движущейся относительно отрезка возможного нахождения ОКМ.

При построении зависимости ${{S}_{{{\text{ТС}}}}}(t)$, могут использоваться разные соображения, например – можно обеспечить равномерное движение ТС вдоль траектории ОКМ. В этом случае ТС, двигаясь равномерно, за время съемки должна пройти расстояние вдоль траектории ОКМ из точки ${{s}_{1}}$, соответствующей одному из крайних положений ОКМ на отрезке в начале съемки, в точку ${{s}_{2}}$, соответствующую противоположному положению ОКМ на отрезке, но уже в конце съемки. При этом постоянная скорость ТС будет определяться соотношением: ${{\dot {S}}_{{{\text{TC}}}}}(t) = ({{s}_{2}} - {{s}_{1}}){{({{t}_{2}} - {{t}_{1}})}^{{ - 1}}} = {\text{const}}$. На рис. 6 приведены два варианта организации такого движения. Рисунок состоит из двух частей − верхней и нижней, каждая из которых есть одномерное представление относительного движения кадра СА и ОКМ. Траектория ОКМ на рисунке представляет собой прямую, вдоль которой отложен параметр $s(t)$. За время съемки ТС проходит путь $d{{S}_{{{\text{ТС}}}}}$ из положения ${{s}_{1}}$ в положение ${{s}_{2}}$. Для определенности ось ${{x}_{3}}$ ПСК направлена вдоль траектории ОКМ и совпадает с осью ${{y}_{3}}$. В нижней части рисунка показано движение ТС со скоростью, превышающей собственную скорость ОКМ, в верхней части рисунка скорость ТС меньше скорости ОКМ. На каждой из частей рисунка также изображена ось $\dot {s}$ и схематично отрезками показаны абсолютные величины скоростей ${{\dot {S}}_{{{\text{ТС}}}}}$ и ${{\dot {S}}_{{{\text{ОКМ}}}}}$ движения, соответственно, ТС и ОКМ вдоль орбитальной траектории ОКМ.

Часто со стороны СА предъявляются требования равномерности скорости движения изображения ОКМ в кадре [2]. В этом случае, при построении зависимости ${{\dot {S}}_{{{\text{ТС}}}}}(t)$ учитывается текущий угол между направлением линии визирования и вектором собственной скорости ОКМ в точке съемки, а также отношение текущей дальности до ОКМ к некоторой базовой дальности ${{r}_{0}}$. Для этого на участке съемки итерационно, с уточнением параметра $\mu $, интегрируется уравнение:

где ${\mathbf{r}} = {{{\mathbf{P}}}_{s}}({{S}_{{{\text{TC}}}}}(t)) - {{{\mathbf{r}}}_{{\text{o}}}}(t)$, ${\mathbf{v}} = {{{\mathbf{Q}}}_{s}}({{S}_{{{\text{TC}}}}}(t))$, $r = \left| {\mathbf{r}} \right|$ – текущее расстояние до ТС, $v = \left| {\mathbf{v}} \right|$ – модуль скорости ОКМ в точке съемки. Указанное уравнение интегрируется на интервале съемки, с начальным значением ${{S}_{{{\text{TC}}}}}(0) = {{s}_{1}}$. Итерации завершаются по выполнению условия $\left| {{{S}_{{{\text{TC}}}}}(\Delta T) - {{s}_{2}}} \right| < \varepsilon $, где $\varepsilon $ – необходимая точность попадания в заданную точку в конце интервала съемки, $\Delta T = {{t}_{2}} - {{t}_{1}}$. После завершения итераций полученная зависимость ${{\dot {S}}_{{{\text{ТС}}}}}(t)$ используется для расчета искомой функции ${{S}_{{{\text{ТС}}}}}(t)$.

Далее приведен пример расчета программной угловой скорости СА при съемке ОКМ с борта КС с учетом неопределенности его положения вдоль собственной орбиты в описанных выше режимах движения ТС, как с постоянной скоростью, так и при условии обеспечения равномерного движения ОКМ на экранной плоскости СА. Дата проведения съемки – 25.I.2019 г. Параметры орбиты КС на 02:12:22.3 UTC в системе координат эпохи даты: высота апогея 413 км, высота перигея 406 км, аргумент перигея 356.5°, наклонение 51.6°, долгота восходящего узла 38.6°, аргумент широты КС 101.2°. Орбитальные параметры ОКМ на эпоху 2019 01 24 23 01 58.0 UTC: высота апогея 472 км, высота перигея 463 км, аргумент перигея 327.1°, наклонение 57.63°, долгота восходящего узла 39.1°, аргумент широты ОКМ 102°. Максимальное сближение с КС происходит 25.I.2019 в 05:37:56.2, при этом дистанция до ОКМ составляет порядка 70 км.

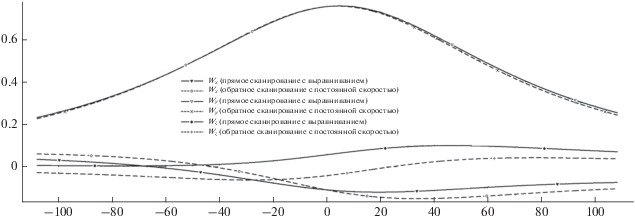
На рис. 7 приведены графики абсолютных угловых скоростей ТСК, град/с. По оси абсцисс отложено относительное время в секундах. Началу координат соответствует момент середины участка съемки. Этот момент может, например, совпадать с точкой максимального сближения с ОКМ. Рассмотрено два варианта съемки: “прямое” сканирование – ТС движется по области возможного нахождения ОКМ, в каждый момент времени обгоняя ОКМ (на рис. 6 этот вариант приведен в нижней части), и “обратное” сканирование – ТС в каждый момент времени отстает от ОКМ (на рис. 6 этот вариант приведен в верхней части). Прямое сканирование организовано с выравниванием скорости ОКМ в кадре СА, обратное сканирование – с равномерным движением ТС по траектории ОКМ. Различия этих режимов проиллюстрированы на рис. 8, на котором изображены графики модулей скорости движения ТС относительно ОКМ в проекции на экранную плоскость СА, м/с. По оси абсцисс отложена та же величина, что и на рис. 7. Интерпретировать кривые на рис. 8 надо следующим образом: если ОКМ оказался в кадре СА в момент времени, соответствующий некоторому значению на оси абсцисс, соответствующее значение на графике при этом будет характеризовать скорость перемещения ОКМ на экранной плоскости СА в этот момент времени. Крайние значения на оси абсцисс соответствуют крайним положениям ОКМ в области его возможного нахождения. Можно видеть, что в режиме выравнивания относительной скорости ОКМ, вне зависимости от фактического положения ОКМ внутри области, скорость прохождения его по кадру СА будет одинаковой. В противном случае при равномерном движении ТС по траектории ОКМ скорость прохождения ОКМ по кадру СА будет зависеть от того, в каком месте на собственной орбите фактически оказался ОКМ в момент съемки, что и показывает пунктирная кривая на рис. 8.

Работа выполнена при поддержке гранта РФФИ № 17-01-00143.