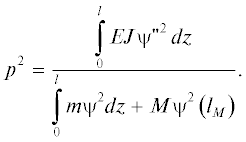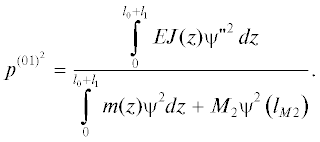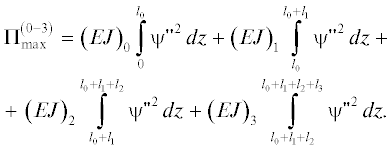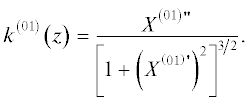Космические исследования, 2021, T. 59, № 1, стр. 71-77

Собственные колебания крыла солнечной батареи космического аппарата

А. К. Томилин^1, *, Г. Р. Зиякаев¹

¹ Национальный исследовательский томский политехнический университет
г. Томск, Россия

Поступила в редакцию 19.10.2019
После доработки 27.02.2020
Принята к публикации 29.05.2020

DOI: 10.31857/S002342062101009X

Аннотация

В процессе раскрытия крыльев солнечных батарей космического аппарата в них возникают собственные поперечные колебания. Исследование этих вибраций является актуальной проблемой, поскольку в некоторых случаях они способны нарушить коммутацию фотоэлектрических преобразователей. Поперечные колебания крыла создаются в результате соединения его секций при зачековке (сцепке) шарнирных устройств. Кинетическая энергия секций при этом преобразуется в потенциальную энергию собственных колебаний крыла солнечной батареи. Эта задача традиционно решается путем применения конечно-элементной модели с последующими расчетами в программе ANSYS. Цель исследования заключается в разработке приближенно-аналитического метода математического моделирования собственных упругих колебаний элементов КСБ, возникающих в процессе его раскрытия.

ВВЕДЕНИЕ

Крылья солнечных батарей (КСБ) космических аппаратов (КА) представляют собой сложную многослойную конструкцию, в состав которой входят фотоэлектрические преобразователи (ФЭП) размером $25 \times 50$ мм. Все ФЭП интегрированы в единую электрическую систему при помощи соединительных клемм. Нарушения соединений в клеммах могут возникать в результате вибраций КСБ. Поэтому к КСБ предъявляются определенные требования по вибропрочности, в частности по ограничению уровня, возникающих в них вибраций, с целью исключения коммутационных дефектов. Увеличение габаритов панелей, использование облегченных сплавов и полимерных соединений при производстве солнечных батарей для КА привели к тому, что анализ влияния упругих деформаций элементов КСБ стал актуальной конструкционной проблемой. Наиболее значительные вибрации КСБ испытывают в процессе их раскрытия. В связи с этим при проектировании КСБ необходимо адекватно моделировать процесс собственных колебаний, возникающих при раскрытии, с последующими виброиспытаниями на специальном стенде [1–4]. Обычно достаточно определить основную частоту колебаний и основную амплитудную форму, а также исследовать кривизну линии изгиба каждой панели.

Для ракетно-космических конструкций эта задача традиционно решается путем применения конечно-элементной модели (КЭМ) с последующими расчетами в программе ANSYS [5–9]. Однако в некоторых случаях, результаты расчетов существенно расходятся с данными экспериментов. Основная причина объясняется сложностью КЭМ, которая обычно включает сотни тысяч элементов. При этом необходимо определить оптимальный размер элементов разбиения, чтобы обеспечить достаточную степень точности расчетов при допустимых временных затратах. Поэтому, прежде чем производить дорогостоящие стендовые испытания, полученные расчетные результаты желательно верифицировать, используя альтернативный путь. При исследовании собственных колебаний КСБ можно составить достаточно простую модель и получить приближенное аналитическое решение.

Цель исследования заключается в разработке приближенно-аналитического метода математического моделирования собственных упругих колебаний элементов КСБ, возникающих в процессе его раскрытия. Метод предлагается использовать в качестве альтернативного при проектировании КСБ и определении их конструкционных особенностей, а также при выборе типа клемм коммутации ФЭП.

В качестве объекта исследования рассматривается модель крыла (рис. 1), описанная в [10]. Крыло состоит из штанги и трех секций. Штанга и секции последовательно соединены шарнирами вращения с одной степенью свободы. В процессе раскрытия их центры масс перемещаются в направлении оси OX. Массы и жесткости секций различаются. Секции 1 и 3 – одиночные панели. Секция 2 объединяет три сложенных панели, поэтому имеет самую большую массу и жесткость. Процесс раскрытия секции 2 в поперечном к рисунку направлении в данной работе не рассматривается.

Рис. 1.

Схематическое представление КСБ: 0 – штанга, 1 – первая секция-панель, 2 – вторая (трехпанельная) секция, 3 – третья секция-панель.

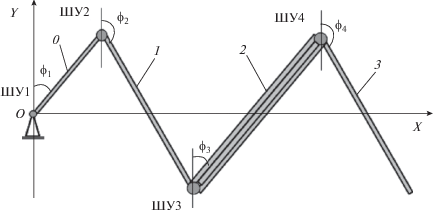
В результате моделирования процесса раскрытия такого КСБ установлена [10] следующая последовательность зачековки шарнирных устройств (ШУ):

$\begin{gathered} {\text{ШУ}}1\left( {51.51\,с} \right) \to {\text{ШУ}}2\left( {51.51\,с} \right) \to \\ \to {\text{ШУ}}4\left( {67.26\,с} \right) \to {\text{ШУ}}3\left( {109.82\,с} \right). \\ \end{gathered} $

В скобках указано время зачековки соответствующего ШУ с начала процесса раскрытия крыла. Заметим, что ШУ1 и ШУ2 зачековываются практически одновременно.

Каркасы всех элементов КСБ представляют собой трубчатые конструкции и выполнены из одного материала. После зачековки ШУ1 и ШУ2 штангу и первую панель, соединенные между собой, можно моделировать единым стержнем. Левый конец этого стержня закреплен консольно, а с правым концом шарнирно связаны секции 2 и 3. Затем происходит зачековка ШУ4. При этом между собой соединяются секции 2 и 3. На последнем этапе зачековывается ШУ3 и все крыло моделируется составным стержнем с четырьмя разнородными участками.

ОПРЕДЕЛЕНИЕ СОБСТВЕННЫХ ЧАСТОТ И ВОЛНОВЫХ ЧИСЕЛ

Причиной возникновения начальных деформаций элементов КСБ в процессе раскрытия является зачековка смежных элементов крыла. Соединенные между собой секции моделируются одним упругим линейным стержнем. Механические свойства сочлененных секций могут различаться [11], поэтому составной стержень не является однородным. Вибрационные процессы следует рассматривать отдельно в пределах каждого временного этапа для каждой секции с учетом стыковки решений на границах.

На некоторых временных этапах, когда еще не все секции соединены между собой, используется модель консольного стержня с присоединенной на свободном конце массой М, которая отражает инерционные свойства незачекованных секций. Рассмотрим задачу о поперечных вибрациях консольного стержня длиной l с точечной массой М на конце. Амплитудные функции удобно выражать в функциях А.Н. Крылова [12]:

(1)

$\begin{gathered} {{X}_{i}}(z) = {{C}_{1}}{{K}_{1}}({{\alpha }_{i}}z) + {{C}_{2}}{{K}_{2}}({{\alpha }_{i}}z) + \\ + \,\,{{C}_{3}}{{K}_{3}}({{\alpha }_{i}}z) + {{C}_{4}}{{K}_{4}}({{\alpha }_{i}}z),\,\,\,\,\left( {i = 1,\infty } \right), \\ \end{gathered} $

где K₁–K₄– функции Крылова, C₁–C₄– произвольные константы, ${{\alpha }_{i}}$ – волновые числа.

Краевые условия в рассматриваемом случае записываются в виде:

(2)

$\begin{gathered} {{X}_{i}}\left( 0 \right) = 0,\,\,\,{{\left( {\frac{{d{{X}_{i}}}}{{dz}}} \right)}_{{z = 0}}} = 0, \\ EJ{{\left( {\frac{{{{d}^{3}}{{X}_{i}}}}{{d{{z}^{3}}}}} \right)}_{{z = l}}} = - Mp_{i}^{2}{{X}_{i}}\left( l \right),\,\,\,\,{{\left( {\frac{{{{d}^{2}}{{X}_{i}}}}{{d{{z}^{2}}}}} \right)}_{{z = l}}} = 0, \\ \end{gathered} $

где ${{p}_{i}}$ – круговые частоты собственных колебаний, EJ – изгибная жесткость стержня. Волновые числа и круговые частоты для однородного участка связаны соотношением

(3)

${{\alpha }_{i}} = \sqrt[4]{{\frac{{p_{i}^{2}m}}{{EJ}}}}.$

Первые два условия (2) называются геометрическими и соответствуют консольной заделке стержня: отсутствует смещение и угол поворота. Последние два условия являются динамическими: на правом конце сила упругости уравновешивается силой инерции присоединенной массы М, изгибающий момент отсутствует.

Ограничимся определением основной частоты $\left( {i = 1} \right)$, применив метод Рэлея [13]. Индекс “1” в дальнейшем опускаем. В процессе зачековки шарнирных устройств кинетическая энергия соединенных звеньев преобразуется в потенциальную энергию упругих деформаций, это приводит к возникновению собственных колебаний системы. В методе Рэлея используется максимальные значения кинетической и потенциальной энергий:

(4)

${{p}^{2}} = \frac{{{{{\text{П}}}_{{\max }}}}}{{{{Т}_{{\max }}}}},$

где

(5)

${{{\text{П}}}_{{\max }}} = \int\limits_0^l {EJ\psi {\kern 1pt} '{{'}^{2}}(z)dz,} \,\,\,\,{{Т}_{{\max }}} = \int\limits_0^l {m{{\psi }^{2}}(z)dz.} $

Здесь ψ(z) – базисная (координатная) функция, которая выражает статическую деформацию стержня от заданной нагрузки, или от нагрузки, близко воспроизводящей общий вид деформации стержня в первом его главном колебании. Масса и жесткость стержня могут быть неоднородными по длине стержня. В этом случае они задаются в виде функций z. Размерность базисной функции ψ(z) – метры. Заметим, что ${{T}_{{max}}}$ лишь условно называется кинетической энергией. Чтобы получить реальную кинетическую энергию ее нужно умножить на квадрат частоты: ${{p}^{2}}{{Т}_{{\max }}}$.

Определим основную частоту колебаний упругого стержня постоянного сечения длиной l с погонной массой m. Форму колебаний примем в виде упругой линии от произвольной сосредоточенной силы F, приложенной на свободном конце [13]:

(6)

$\psi (z) = \frac{F}{{6EJ}}(3l{{z}^{2}} - {{z}^{3}}),$

тогда

(7)

$\psi {\kern 1pt} ''(z) = \frac{F}{{EJ}}(l - z).$

Заметим, что функция (6) соответствует геометрическим граничным условиям (2). В случае неоднородного стержня с присоединенной точечной массой в соответствие с (4) имеем:

(8)

Под ${{l}_{M}}$ в (8) следует понимать расстояние от закрепленного конца стержня до точечной массы М. Сила F в (8) сокращается, поэтому искомая частота $p$ от нее не зависит.

Определение частот упругих колебаний КСБ в процессе раскрытия следует выполнять поэтапно. Числовые расчеты выполнялись в программе Mathcad.

Первый этап (от зачековки ШУ1 и ШУ2 до зачековки ШУ4, от 51.51 до 67.26 с). Произведем расчет основной частоты вибраций штанги, сочлененной с секцией 1 (идентификационный индекс “01”), с точечной массой, отражающей инерционные свойства незачекованных секций 2 и 3.

Обоснуем способ вычисления приведенной точечной массы применительно к рассматриваемой задаче. Секция 2 имеет массу в три раза больше, чем секция 3, к тому же ШУ3 между ними не зачековано. Поэтому приближенно достаточно учесть только инерционные свойства панели 2. Приведенную массу М₂ можно определить из сравнения моментов инерции стержня и двухмассовой гантели такой же длины:

(9)

$\frac{{{{m}_{2}}l_{2}^{3}}}{{12}} = 2{{M}_{2}}{{\left( {\frac{{{{l}_{2}}}}{2}} \right)}^{2}},\,\,\,\,{\text{тогда}}\,\,\,\,{{M}_{2}} = \frac{{{{m}_{2}}l_{2}^{{}}}}{6}.$

Учитывая, что приведенная масса М₂ от ШУ1 находится на расстоянии ${{l}_{{M2}}} = {{l}_{0}} + {{l}_{1}},$ условную кинетическую энергию запишем в виде:

(10)

$T_{{\max }}^{{\left( {01} \right)}} = \int\limits_0^{{{l}_{0}}} {{{m}_{0}}{{\psi }^{2}}(z)dz + \int\limits_{{{l}_{0}}}^{{{l}_{0}} + {{l}_{1}}} {{{m}_{1}}{{\psi }^{2}}(z)dz + } {{M}_{2}}{{\psi }^{2}}\left( {{{l}_{{M2}}}} \right)} .$

Используем формулу (8) с учетом (10), получим выражение для основной частоты собственных колебаний:

(11)

Здесь

$\begin{gathered} m(z) = \left\{ \begin{gathered} {{m}_{0}},\,\,\,0 < z \leqslant {{l}_{0}}, \hfill \\ {{m}_{1}},\,\,\,{{l}_{0}} < z \leqslant {{l}_{0}} + {{l}_{1}}, \hfill \\ \end{gathered} \right. \\ EJ(z) = \left\{ \begin{gathered} {{\left( {EJ} \right)}_{0}}{\kern 1pt} ,\,\,\,0 < z \leqslant {{l}_{0}}, \hfill \\ {{\left( {EJ} \right)}_{1}}{\kern 1pt} ,\,\,\,{{l}_{0}} < z \leqslant {{l}_{0}} + {{l}_{1}}, \hfill \\ \end{gathered} \right. \\ \end{gathered} $

а базисная функция (6) и ее вторая производная (7) имеют соответственно вид

$\begin{gathered} \psi (z) = \frac{F}{{6EJ\left( z \right)}}(3{{l}_{{01}}}{{z}^{2}} - {{z}^{3}}), \\ \psi {\kern 1pt} ''(z) = \frac{F}{{EJ\left( z \right)}}({{l}_{{01}}} - z), \\ \end{gathered} $

где ${{l}_{{01}}} = {{l}_{0}} + {{l}_{1}}$.

Волновые числа для каждой секции определяются из соотношений

(12)

$\begin{gathered} \alpha _{{}}^{{\left( 0 \right)}} = \sqrt[4]{{\frac{{p_{{}}^{{{{{\left( {01} \right)}}^{2}}}}{{m}_{0}}}}{{E{{J}_{0}}}}}},\,\,\,\,\alpha _{{}}^{{\left( 1 \right)}} = \sqrt[4]{{\frac{{p_{{}}^{{{{{\left( {01} \right)}}^{2}}}}{{m}_{1}}}}{{E{{J}_{1}}}}}}, \\ \alpha _{{}}^{{\left( {01} \right)}} = \left\{ \begin{gathered} \alpha _{{}}^{{\left( 0 \right)}},\,\,\,0 < z \leqslant {{l}_{0}}, \hfill \\ \alpha _{{}}^{{\left( 1 \right)}},\,\,\,\,{{l}_{0}} < z \leqslant {{l}_{0}} + {{l}_{1}}. \hfill \\ \end{gathered} \right. \\ \end{gathered} $

Используем следующие числовые значения механических характеристик элементов крыла, записанные в порядке их расположения на рис. 1:

$\begin{gathered} {{l}_{0}} = 3.349\,\,{\text{м}},\,\,\,\,{{l}_{1}} = 4.118\,\,{\text{м}}, \\ {{l}_{2}} = 4.035\,\,{\text{м}},\,\,\,\,{{l}_{3}} = 3.935\,\,{\text{м}}, \\ {{m}_{0}} = 3.9{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {\text{м}}}} \right. \kern-0em} {\text{м}}},\,\,\,\,{{m}_{1}} = 8.0\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}, \\ {{m}_{2}} = 18.1\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {\text{м}}}} \right. \kern-0em} {\text{м}}},\,\,\,\,{{m}_{3}} = 6.1\,\,{{{\text{кг}}} \mathord{\left/ {\vphantom {{{\text{кг}}} {\text{м}}}} \right. \kern-0em} {\text{м}}}, \\ {{\left( {EJ} \right)}_{0}} = 1200\,\,{\text{H}}{{{\text{м}}}^{2}},\,\,\,{{\left( {EJ} \right)}_{1}} = 400\,\,\,\,{\text{H}}{{{\text{м}}}^{2}}, \\ {{\left( {EJ} \right)}_{2}} = 1600\,\,{\text{H}}{{{\text{м}}}^{2}},\,\,\,\,{{\left( {EJ} \right)}_{3}} = 400\,\,{\text{H}}{{{\text{м}}}^{2}}. \\ \end{gathered} $

Используя (12), получим:

${{p}^{{(01)}}} = 0.224\,\,{{{\text{с}}}^{{ - 1}}},\,\,{{\alpha }^{{(0)}}} = 0.113\,\,{{{\text{м}}}^{{ - 1}}},\,\,{{\alpha }^{{(1)}}} = 0.178\,\,{{{\text{м}}}^{{ - 1}}}.$

Второй этап (от зачековки ШУ4 до зачековки ШУ3, от 67.26 до 109.82 с). Расчет основной частоты колебаний секции 3 производится в системе отсчета, связанной с ШУ3. Применяются формулы:

${\text{П}}_{{\max }}^{{\left( 3 \right)}} = \int\limits_0^{{{l}_{3}}} {{{{\left( {EJ} \right)}}_{3}}\psi {\kern 1pt} '{{'}^{2}}(z)dz,} \,\,\,\,Т_{{\max }}^{{\left( 3 \right)}} = \int\limits_0^{{{l}_{3}}} {{{m}_{3}}{{\psi }^{2}}(z)dz.} $

Основная частота собственных колебаний и соответствующее волновое число определяются по формулам:

(13)

${{p}^{{(3)}}} = \frac{{3.57}}{{{{l}_{3}}^{2}}}\sqrt {\frac{{E{{J}_{3}}}}{{{{m}_{3}}}}} ,\,\,\,\,{{\alpha }^{{(3)}}} = \sqrt[4]{{\frac{{{{p}^{{{{{(3)}}^{2}}}}}{{m}_{3}}}}{{E{{J}_{3}}}}}}.$

Получаем числовые значения: ${{p}^{{(3)}}} = 1.86\,\,{{{\text{с}}}^{{ - 1}}},$ ${{\alpha }^{{(3)}}} = 0.48\,\,{{{\text{м}}}^{{ - 1}}}.$

Третий этап (от зачековки ШУ3 в момент времени 109.82 с и до затухания колебаний). Произведем расчет основной частоты колебаний неоднородного стержня, состоящего из всех четырех зачекованных секций (идентификационный индекс “0–3”) методом Рэлея. В этом случае при расчете максимальных значений кинетической и потенциальной энергий, следует воспользоваться формулами:

(14)

$\begin{gathered} T_{{\max }}^{{\left( {0 - 3} \right)}} = {{m}_{0}}\int\limits_0^{{{l}_{0}}} {{{\psi }^{2}}\left( z \right)dz} + {{m}_{1}}\int\limits_{{{l}_{0}}}^{{{l}_{0}} + {{l}_{1}}} {{{\psi }^{2}}\left( z \right)dz} + \\ + \,\,{{m}_{2}}\int\limits_{{{l}_{0}} + {{l}_{1}}}^{{{l}_{0}} + {{l}_{1}} + {{l}_{2}}} {{{\psi }^{2}}\left( z \right)dz} + {{m}_{3}}\int\limits_{{{l}_{0}} + {{l}_{1}} + {{l}_{2}}}^{{{l}_{0}} + {{l}_{1}} + {{l}_{2}} + {{l}_{3}}} {{{\psi }^{2}}dz} , \\ \end{gathered} $

(15)

Здесь $\psi (z) = \frac{F}{{6EJ\left( z \right)}}(3{{l}_{{0 - 3}}}{{z}^{2}} - {{z}^{3}}),$ $\psi {\kern 1pt} ''(z) = $ $ = \frac{F}{{EJ\left( z \right)}}({{l}_{{0 - 3}}} - z),$ и используются значения

$EJ(z) = \left\{ \begin{gathered} {{\left( {EJ} \right)}_{0}},\,\,\,\,0 < z \leqslant {{l}_{0}}, \hfill \\ {{\left( {EJ} \right)}_{1}},\,\,\,\,{{l}_{0}} < z \leqslant {{l}_{0}} + {{l}_{1}}, \hfill \\ {{\left( {EJ} \right)}_{2}},\,\,\,\,{{l}_{0}} + {{l}_{1}} < z \leqslant {{l}_{0}} + {{l}_{1}} + {{l}_{2}}, \hfill \\ {{\left( {EJ} \right)}_{3}},\,\,\,{{l}_{0}} + {{l}_{1}} + {{l}_{2}} < z \leqslant {{l}_{0}} + {{l}_{1}} + {{l}_{2}} + {{l}_{3}}. \hfill \\ \end{gathered} \right.$

В итоге имеем:

$\begin{gathered} p_{{}}^{{\left( {0 - 3} \right)}} = 0.179\,\,{{{\text{c}}}^{{ - 1}}},\alpha _{{}}^{{\left( 0 \right)}} = 0.101\,\,{{{\text{м}}}^{{ - 1}}},\alpha _{{}}^{{\left( 1 \right)}} = 0.159\,\,{{{\text{м}}}^{{ - 1}}}, \\ {{\alpha }^{{\left( 2 \right)}}} = 0.138\,\,{{{\text{м}}}^{{ - 1}}},\,\,\,\,\,{{\alpha }^{{\left( 3 \right)}}} = 0.149\,\,{{{\text{м}}}^{{ - 1}}}. \\ \end{gathered} $

ИССЛЕДОВАНИЕ ФОРМ ОСНОВНЫХ КОЛЕБАНИЙ

Определим основные амплитудные функции на каждом этапе раскрытия КСБ и исследуем кривизну изгиба панелей.

Первый этап (от 51.51 до 67.26 с). Вначале определим амплитудную функцию в пределах штанги: $0 \leqslant z \leqslant {{l}_{0}}$. Используем идентификационный индекс “0”.

Из геометрических условий (2) применительно к (1) следует:

${{С}_{1}} = 0,\,\,\,\,{{С}_{2}} = 0.$

Приняв масштабный коэффициент С₄ = 1, используя граничное условие:

${{\left( {\frac{{{{d}^{2}}{{X}^{{\left( 0 \right)}}}}}{{d{{z}^{2}}}}} \right)}_{{z = {{l}_{0}}}}} = 0,$

получим: $C_{3}^{{\left( 0 \right)}} = - \frac{{{{K}_{2}}\left( {{{\alpha }^{{\left( 0 \right)}}}{{l}_{0}}} \right)}}{{{{K}_{1}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{l}_{0}}} \right)}}.$

Запишем амплитудную функцию для штанги с использованием аргумента ${{z}_{0}}$ в пределах $0 \leqslant {{z}_{0}} \leqslant {{l}_{0}}$:

(16)

$X_{{}}^{{\left( 0 \right)}}\left( {{{z}_{0}}} \right) = - \frac{{{{K}_{2}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{l}_{0}}} \right)}}{{{{K}_{1}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{l}_{0}}} \right)}}{{K}_{3}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{z}_{0}}} \right) + {{K}_{4}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{z}_{0}}} \right).$

Амплитудную функцию в пределах секции 1 запишем с использованием новой шкалы отсчета от конца штанги, который в новой системе отсчета считается неподвижным. Используя координату z₁ в пределах $0 \leqslant {{z}_{1}} \leqslant {{l}_{1}}$, запишем

(17)

$\begin{gathered} X_{{}}^{{\left( 1 \right)}}\left( {{{z}_{1}}} \right) = - \frac{{{{K}_{2}}\left( {\alpha _{{}}^{{\left( 1 \right)}}{{l}_{1}}} \right)}}{{{{K}_{1}}\left( {\alpha _{{}}^{{\left( 1 \right)}}{{l}_{1}}} \right)}}{{K}_{3}}\left( {\alpha _{{}}^{{\left( 1 \right)}}{{z}_{1}}} \right) + \\ + \,\,{{K}_{4}}\left( {\alpha _{{}}^{{\left( 1 \right)}}{{z}_{1}}} \right) + X_{{}}^{{\left( 0 \right)}}\left( {{{l}_{0}}} \right). \\ \end{gathered} $

Условие стыковки функций (16) и (17): $X_{1}^{{\left( 0 \right)}}\left( {{{l}_{0}}} \right) = X_{1}^{{\left( 1 \right)}}\left( 0 \right).$

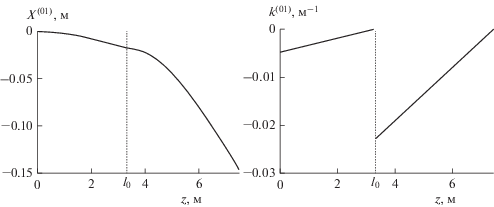
График сопряженных функций (16) и (17) представлен на рис. 2а.

Рис. 2.

(а) Амплитудная функция X⁽⁰¹⁾. (б) Амплитудная функция k⁽⁰¹⁾.

Функцию смещений основного колебания для состыкованных между собой штанги и секции 1 запишем в виде:

(18)

$U_{{}}^{{\left( {01} \right)}}\left( {z,t} \right) = X_{{}}^{{\left( {01} \right)}}\sin p_{{}}^{{\left( {01} \right)}}t.$

Здесь амплитудная функция разбивается на два участка:

$X_{{}}^{{\left( {01} \right)}} = \left\{ \begin{gathered} X_{{}}^{{\left( 0 \right)}}\left( {{{z}_{0}}} \right);\,\,\,0 \leqslant {{z}_{0}} \leqslant {{l}_{0}}; \hfill \\ X_{{}}^{{\left( 1 \right)}}\left( {{{z}_{1}}} \right);\,\,\,\,0 \leqslant {{z}_{1}} \leqslant {{l}_{1}}. \hfill \\ \end{gathered} \right.$

Изгиб стержневой системы характеризуется кривизной, которая определяется по формуле:

(19)

Именно эту характеристику следует в первую очередь учитывать при определении вероятности возникновения коммутационных дефектов ФЭП. Функция кривизны имеет разрыв в точке сочленения секций, поскольку их изгибные жесткости различаются (рис. 2б). Наибольшая по модулю кривизна изгиба панели 1 возникает вблизи ШУ2, следовательно, на данном этапе раскрытия КСБ, в этом сечении нарушение коммутации ФЭП наиболее вероятно.

Второй этап (от 67.26 до 109.82 с). Функция смещений секции 3 в системе отсчета, связанной с ШУ3, записывается в виде

$\begin{gathered} U_{{}}^{{\left( 3 \right)}}\left( {{{z}_{3}},t} \right) = \\ = \left[ { - \frac{{{{K}_{2}}\left( {\alpha _{{}}^{{\left( 3 \right)}}{{l}_{3}}} \right)}}{{{{K}_{1}}\left( {\alpha _{{}}^{{\left( 3 \right)}}{{l}_{3}}} \right)}}{{K}_{3}}\left( {\alpha _{{}}^{{\left( 3 \right)}}{{z}_{3}}} \right) + {{K}_{4}}\left( {\alpha _{{}}^{{\left( 3 \right)}}{{z}_{3}}} \right)} \right]\sin p_{{}}^{{\left( 3 \right)}}t. \\ \end{gathered} $

Здесь аргумент изменяется в пределах $0 \leqslant {{z}_{3}} \leqslant {{l}_{3}}$.

Третий этап (от 109.82 с до затухания колебаний). На третьем этапе упругие вибрации КСБ возникают за счет зачековки ШУ3. Функция смещений запишется в виде

(21)

$U_{{}}^{{\left( {0 - 3} \right)}}\left( {z,t} \right) = X_{{}}^{{\left( {0 - 3} \right)}}\sin p_{{}}^{{\left( {0 - 3} \right)}}t,$

где

$X_{{}}^{{\left( {0 - 3} \right)}} = \left\{ \begin{gathered} X_{{}}^{{\left( 0 \right)}}\left( {{{z}_{0}}} \right) = - \frac{{{{K}_{2}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{l}_{0}}} \right)}}{{{{K}_{1}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{l}_{0}}} \right)}}{{K}_{3}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{z}_{0}}} \right) + \hfill \\ + \,\,{{K}_{4}}\left( {\alpha _{{}}^{{\left( 0 \right)}}{{z}_{0}}} \right),\,\,\,\,0 \leqslant {{z}_{0}} \leqslant {{l}_{0}}; \hfill \\ X_{{}}^{{\left( 1 \right)}}\left( {{{z}_{1}}} \right) = - \frac{{{{K}_{2}}\left( {\alpha _{{}}^{{\left( 1 \right)}}{{l}_{1}}} \right)}}{{{{K}_{1}}\left( {\alpha _{{}}^{{\left( 1 \right)}}{{l}_{1}}} \right)}}{{K}_{3}}\left( {\alpha _{{}}^{{\left( 1 \right)}}{{z}_{1}}} \right) + \hfill \\ + \,\,{{K}_{4}}\left( {\alpha _{{}}^{{\left( 1 \right)}}{{z}_{1}}} \right) + X_{{}}^{{\left( 0 \right)}}\left( {{{l}_{0}}} \right),\,\,\,\,0 \leqslant {{z}_{1}} \leqslant {{l}_{1}}; \hfill \\ X_{{}}^{{\left( 2 \right)}}\left( {{{z}_{2}}} \right) = - \frac{{{{K}_{2}}\left( {\alpha _{{}}^{{\left( 2 \right)}}{{l}_{2}}} \right)}}{{{{K}_{1}}\left( {\alpha _{{}}^{{\left( 2 \right)}}{{l}_{2}}} \right)}}{{K}_{3}}\left( {\alpha _{{}}^{{\left( 2 \right)}}{{z}_{2}}} \right) + \hfill \\ + \,\,{{K}_{4}}\left( {\alpha _{{}}^{{\left( 2 \right)}}{{z}_{2}}} \right) + X_{{}}^{{\left( 1 \right)}}\left( {{{l}_{1}}} \right),\,\,\,0 \leqslant {{z}_{2}} \leqslant {{l}_{2}}; \hfill \\ X_{{}}^{{\left( 3 \right)}}\left( {{{z}_{3}}} \right) = - \frac{{{{K}_{2}}\left( {\alpha _{{}}^{{\left( 3 \right)}}{{l}_{3}}} \right)}}{{{{K}_{1}}\left( {\alpha _{{}}^{{\left( 3 \right)}}{{l}_{3}}} \right)}}{{K}_{3}}\left( {\alpha _{{}}^{{\left( 3 \right)}}{{z}_{3}}} \right) + \hfill \\ + \,\,{{K}_{4}}\left( {\alpha _{{}}^{{\left( 3 \right)}}{{z}_{3}}} \right) + X_{{}}^{{\left( 2 \right)}}\left( {{{l}_{2}}} \right),\,\,0 \leqslant {{z}_{3}} \leqslant {{l}_{3}}. \hfill \\ \end{gathered} \right.$

Функция кривизны на каждом участке определяется по формуле, аналогичной (19).

На рис. 3 представлена основная форма колебаний всего КСБ и график функции кривизны для каждой секции. Из них следует, что самым опасным является сечение секции 1 вблизи ШУ2, а для секции 3 – вблизи ШУ4. В секции 2, сложенной из трех панелей, на этом этапе раскрытия КСБ повреждения коммутации ФЭП маловероятны.

Рис. 3.

(а) Основная форма колебаний КСБ; (б) График функции кривизны $k_{{}}^{{\left( {0 - 3} \right)}}$.

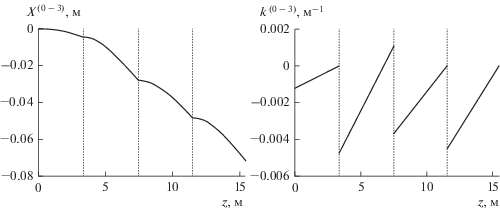
Если сравнить первый и третий временные этапы и возникающие максимальные значения кривизны, то первый этап представляется на порядок более опасным.

Предложенный метод позволяет приближенно определить характеристики основной моды вибрационного процесса колебаний КСБ. При этом не учитываются диссипативные силы внешнего и внутреннего трения. За счет этого полученные значения собственных частот несколько больше реальных демпфированных частот. В космосе, где внешнее сопротивление практически отсутствует, эту разность можно оценить не более, чем в 10%. Однако этот недостаток не является критическим, поскольку завышенное значение частоты не снижает критерий вибропрочности.

Использованная модель не учитывает упругие свойства корпуса КА, к которому крепится штанга КСБ. С учетом линейных размеров КСБ и изгибной жесткости его элементов этим несоответствием можно пренебречь.

ЗАКЛЮЧЕНИЕ

В статье предлагается приближенно-аналитический метод математического моделирования колебаний КСБ, возникающих в процессе его раскрытия. Предложенный метод опирается на стержневую модель КСБ и позволяет с достаточной степенью точности определять основные частоты, волновые числа и амплитудные функции колебаний всех звеньев КСБ на каждом временном этапе его раскрытия. Особое внимание при этом обращается на кривизну изгиба секций с целью определения сечений, в которых наиболее вероятны нарушения коммутации ФЭП.

Подобный расчет можно использовать в качестве проверочного при проектировании КСБ и определении их конструкционных особенностей, в частности при выборе типа клемм коммутации ФЭП. При разработке испытательных стендов следует обратить внимание на возможность фиксации определенных выше характеристик собственных колебаний КСБ, возникающих в процессе раскрытия.

Список литературы

Spacecraft Systems Engineering / Eds. Peter Fortescue, Graham Swinerd, John Stark. Wiley, 2011.
Бакулин Д.В., Борзых С.В., Ососов Н.С. и др. Моделирование процесса раскрытия солнечных батарей// Изв. РАН. Математическое моделирование. 2004. Т. 16. № 6. С. 88–92.
Борзых С.В., Ильясова И.Р. Моделирование и экспериментальная отработка процесса раскрытия крупногабаритных многозвенных солнечных батарей космических аппаратов // Вестник МГТУ им. Н.Э. Баумана, Сер. Машиностроение. 2012. № 8. С. 60–68.
Shpyakin I., Malyshenko A. Comparative analysis of gravity compensation systems for ground tests of deployable solar arrays. 2015 International Siberian Conference on Control and Communications, SIBCON 2015 – Proceedings. Institute of Electrical and Electronics Engineers Inc. 2015. https://doi.org/10.1109/SIBCON.2015.7147290
Соустин Б.П., Тестоедов Н.А., Рудомёткин А.Г. и др. Виброиспытания космических аппаратов. М.: Наука, 2000.
Кармишин А.В., Лиходед А.И., Паничкин Н.Г., Сухинин С.Н. Основы отработки прочности ракетно-космических конструкций. М.: Машиностроение, 2007.
Хейлен В., Ламменс С. Модальный анализ: теория и испытания. М.: Новатест, 2010.
Софинский А.Н. Система отработки вибропрочности: опыт применения и перспективы развития // Космическая техника и технологии. 2016. № 1(12). С. 12–21.
Безмозгий И.М., Софинский А.Н., Чернягин А.Г. Отработка вибропрочности узлового модуля российского сегмента международной космической станции // Космическая техника и технологии. 2015. № 3(10). С. 15–25.
Tomilin A., Shpyakin I. Mathematical modeling of a solar arrays deploying process at ground tests. IOP Conference Series: Materials Science and Engineering, 124(1), [012103]. 2016.https://doi.org/10.1088/1757-899X/124/1/012103
Шатров А.К., Назарова Л.П., Машуков А.В. Механические устройства космических аппаратов. Конструктивные решения и динамические характеристики: Учеб. пособие. Красноярск: Сиб. гос. аэрокосмич. ун-т, 2006.
Крылов А.Н. О расчете балок, лежащих на упругом основании. Л.: АН СССР, 1931.
Волков А.С., Плотников Ю.Г. Динамические расчеты упругих систем: Учебное пособие. Хабаровск: ДВГУПС, 2007.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал