Космические исследования, 2021, T. 59, № 2, стр. 149-164
Реконструкция вращательного движения кораблей Прогресс в режиме одноосной солнечной ориентации по данным измерений тока солнечных батарей
М. Ю. Беляев 1, Т. В. Матвеева 1, М. И. Монахов 1, Д. Н. Рулев 1, В. В. Сазонов 2, *
1 Ракетно-космическая корпорация “Энергия” им. С.П. Королева
Королев, Россия
2 Институт прикладной математики им. М.В. Келдыша РАН
Москва, Россия
* E-mail: sazonov@keldysh.ru
Поступила в редакцию 04.07.2019
После доработки 24.11.2019
Принята к публикации 19.12.2019
Аннотация
Реконструировано неуправляемое вращательное движение транспортных грузовых кораблей Прогресс М-24М и М-25М в режиме одноосной солнечной ориентации (так называемая закрутка на Солнце). Начальные условия движения в этом режиме – закрутка корабля с угловой скоростью 2.2–2.4 град/с вокруг нормали к плоскости солнечных батарей, направленной на Солнце. Продолжительность режима – несколько орбитальных витков. Реконструкция выполнена с помощью интегральной статистической методики по телеметрическим значениям тока, снимаемого с его солнечных батарей. В результате определяется вращательное движение корабля относительно направления Земля–Солнце. Проведено исследование спектра колебаний тока во время закрутки, поясняющее возможность реконструкции на основании таких, на первый взгляд, малоинформативных данных.
ОДНООСНАЯ СОЛНЕЧНАЯ ОРИЕНТАЦИЯ ТГК ПРОГРЕСС
Одноосная солнечная ориентация (закрутка на Солнце) – один из штатных режимов автономного полета транспортный грузовых кораблей (ТГК) Прогресс. Начальные условия дви-жения в этом режиме – закрутка корабля с угловой скоростью 2.2–2.4 град/с вокруг направленной на Солнце нормали к плоскости солнечных батарей (СБ). Нормаль образует малый угол с главной центральной осью максимального момента инерции ТГК, поэтому ориентированное движение близко стационарному вращению корабля вокруг этой оси. По своим амплитудно-частотным характеристикам микроускорения на борту ТГК в этом режиме очень удачно подходят для экспериментов с датчиком конвекции ДАКО-Н [1, 2]. С одной стороны, они достаточно велики в области низких частот, а с другой стороны, имеют чисто дискретный спектр с небольшим числом гармоник. Это упростит анализ показаний датчика.
Для такого анализа необходимо знать реальные квазистатические микроускорения, имевшие место во время проведения экспериментов. Микроускорения можно найти расчетным путем, реконструировав вращательное движение ТГК. Реконструкция движения, происходившего во время закруток, выполняется по телеметрическим значениям компонент угловой скорости корабля в его строительной системе координат и тока, вырабатываемого солнечными батареями [3–5]. Данные измерений, собранные на некотором интервале времени, обрабатываются совместно методом наименьших квадратов с помощью интегрирования уравнений движения ТГК относительно центра масс. В результате обработки оцениваются начальные условия движения корабля относительно направления Земля–Солнце и параметры используемых математических моделей.
Если измерения угловой скорости отсутствуют, то движение корабля в режиме солнечной закрутки можно реконструировать только по измерениям тока СБ. Точность при этом будет ниже, чем при использовании двух видов измерений, но микроускорения найти удается. Ниже проведено исследование, поясняющее возможность реконструкции по таким малоинформативным, на первый взгляд, данным. Приведены примеры реконструкции неуправляемого вращательного движения ТГК Прогресс М-24М (№ 423) и М-25М (№ 424).
МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТГК И ДАННЫЕ ИЗМЕРЕНИЙ ТОКА СОЛНЕЧНЫХ БАТАРЕЙ
ТГК считается твердым телом. Для записи уравнений движения корабля относительно центра масс и соотношений, используемых при обработке данных измерений введем две правые декартовые системы координат. Строительная система $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ жестко связана с корпусом ТГК. Точка $O$ – центр масс корабля, ось $O{{y}_{1}}$ параллельна его продольной оси и направлена от стыковочного узла к агрегатному отсеку, ось $O{{y}_{2}}$ перпендикулярна плоскости солнечных батарей (СБ). Светочувствительная сторона СБ обращена к полупространству ${{y}_{2}} > 0$. Система $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ образована главными центральными осями инерции ТГК. Оси $O{{x}_{i}}$ составляют малые углы с осями $O{{y}_{i}}$ $(i = 1,\;2,\;3)$.
Положение системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ относительно системы $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ будем задавать углами $\gamma $, $\alpha $ и $\beta $, которые введем посредством следующего условия. Система $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ может быть переведена в систему $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ тремя последовательными поворотами. Первый поворот совершается вокруг оси $O{{y}_{2}}$ на угол $\alpha $. Второй поворот совершается на угол $\beta $ вокруг оси $O{{y}_{3}}$, полученной после первого поворота. Третий поворот совершается на угол $\gamma $ вокруг оси $O{{y}_{1}}$, полученной после первых двух поворотов. Такая ось $O{{y}_{1}}$ совпадает с осью $O{{x}_{1}}$. Матрицу перехода от системы $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$ к системе $O{{y}_{1}}{{y}_{2}}{{y}_{3}}$ обозначим $\left\| {{{a}_{{ij}}}} \right\|_{{{\kern 1pt} i,j = 1}}^{3}$, ${{a}_{{ij}}}$ – косинус угла между осями $O{{y}_{i}}$ и $O{{x}_{j}}$. Элементы этой матрицы выражаются через введенные углы по известным формулам (см., например, [5]). Ниже используются только направляющие косинусы оси $O{{y}_{2}}$ в системе $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$: ${{a}_{{21}}} = \sin \beta $, ${{a}_{{22}}} = \cos \beta \cos \gamma $, ${{a}_{{23}}} = - \cos \beta \sin \gamma $.
Введем обозначения: ${{s}_{i}}$ – компоненты орта ${\mathbf{S}}$ направления Земля–Солнце, ${{\omega }_{i}}$ – компоненты абсолютной угловой скорости ТГК $(i = 1,\;2,\;3)$. Оба набора компонент относятся к системе координат $O{{x}_{1}}{{x}_{2}}{{x}_{3}}$. Уравнения движения ТГК относительно центра масс образованы динамическими уравнениями Эйлера
(1)
$\begin{gathered} {{{\dot {\omega }}}_{1}} = \mu {{\omega }_{2}}{{\omega }_{3}},\,\,\,\,{{{\dot {\omega }}}_{2}} = \frac{{\mu {\kern 1pt} '\,\, - \mu }}{{1 - \mu \mu {\kern 1pt} '}}{{\omega }_{1}}{{\omega }_{3}}, \\ {{{\dot {\omega }}}_{3}} = - \mu {\kern 1pt} '{{\omega }_{1}}{{\omega }_{2}} \\ \end{gathered} $(2)
$\begin{gathered} {{{\dot {s}}}_{1}} = {{s}_{2}}{{\omega }_{3}} - {{s}_{3}}{{\omega }_{2}},\,\,\,\,{{{\dot {s}}}_{2}} = {{s}_{3}}{{\omega }_{1}} - {{s}_{1}}{{\omega }_{3}}, \\ {{{\dot {s}}}_{3}} = {{s}_{1}}{{\omega }_{2}} - {{s}_{2}}{{\omega }_{1}}. \\ \end{gathered} $Здесь точка над символом означает дифференцирование по времени $t$,
Если считать, что на СБ вырабатывает ток только под действием солнечных лучей, падающих на их светочувствительную поверхность, то расчетный аналог тока СБ выражается формулой
Здесь ${{I}_{0}}$ – ток СБ при нулевом угле падения на них солнечных лучей. Соотношения (1)–(3) не содержат угла $\alpha $. Этот параметр по измерениям тока оценить нельзя.Углы $\gamma $, $\alpha $, $\beta $ и параметры $\mu $, $\mu {\kern 1pt} '$ оцениваются по измерениям угловой скорости, выполненным в режиме закрутки на Солнце. В табл. 1, взятой из [4], приведены оценки этих величин для ТГК № 423 вместе с их стандартными отклонениями. Как будет показано ниже, при обработке измерений тока СБ в принципе можно уточнить $\mu $, $\mu {\kern 1pt} '$, $\gamma $, и $\beta $.
Таблица 1.
Оценки параметров тензора инерции ТГК № 423 (ноябрь 2014)
| $\mu $ | ${{\sigma }_{\mu }}$$ \cdot \,{{10}^{4}}$ | μ' | ${{\sigma }_{{\mu {\kern 1pt} '}}}$$ \cdot \,{{10}^{3}}$ | $\gamma $ | ${{\sigma }_{\gamma }}$$ \cdot \,{{10}^{5}}$ | $\alpha $ | ${{\sigma }_{\alpha }}$$ \cdot \,{{10}^{3}}$ | $\beta $ | ${{\sigma }_{\beta }}$$ \cdot \,{{10}^{4}}$ |
|---|---|---|---|---|---|---|---|---|---|
| 0.193 | 7.7 | 0.867 | 3.5 | –0.0711 | 8.5 | 0.0059 | 2.4 | –0.0033 | 1.8 |
| 0.182 | 51 | 0.899 | 25 | –0.0716 | 56 | 0.0137 | 15 | –0.0033 | 13 |
| 0.196 | 28 | 0.859 | 12 | –0.0718 | 24 | –0.0046 | 8.8 | –0.0019 | 6.7 |
| 0.196 | 22 | 0.867 | 11 | –0.0705 | 21 | 0.0072 | 6.9 | –0.0034 | 5.9 |
| 0.197 | 27 | 0.863 | 12 | –0.0727 | 20 | 0.0072 | 8.3 | –0.0031 | 6.4 |
| 0.194 | 15 | 0.877 | 6.6 | –0.0698 | 10 | 0.0100 | 4.6 | –0.0026 | 3.3 |
| 0.196 | 46 | 0.863 | 20 | –0.0729 | 26 | –0.0026 | 14 | –0.0026 | 11 |
| 0.196 | 54 | 0.834 | 23 | –0.0725 | 28 | 0.0149 | 17 | –0.0035 | 13 |
Данные измерений тока СБ представляют собой три ряда значений, получаемые от трех датчиков:
Здесь $I_{j}^{{(n)}}$ – приближенное значение тока, фиксируемое в момент времени ${{t}_{n}}$ датчиком с номером $j$ $(j = 1,\;2,\;3)$, ${{t}_{1}} < {{t}_{2}} < \ldots < {{t}_{N}}$. Показания датчиков почти одинаковы, поэтому измерением тока в момент ${{t}_{n}}$ считается величина ${{I}_{n}} = [I_{1}^{{(n)}} + I_{2}^{{(n)}} + {{I_{3}^{{(n)}}]} \mathord{\left/ {\vphantom {{I_{3}^{{(n)}}]} 3}} \right. \kern-0em} 3}$. На отрезках времени более 15 мин величины ${{I}_{n}}$ не удается аппроксимировать выражением (3), рассчитываемым вдоль решений системы (1), (2). На таких отрезках в данных ${{I}_{n}}$ проявляется низкочастотная составляющая, не связанная с вращательным движением ТГК [4, 5]. Перед реконструкцией движения она исключается (см. ниже).ИССЛЕДОВАНИЕ ВОЗМОЖНОСТИ РЕКОНСТРУКЦИИ ДВИЖЕНИЯ ТГК ПО ИЗМЕРЕНИЯМ ТОКА СОЛНЕЧНЫХ БАТАРЕЙ
Движение ТГК в режиме солнечной закрутки происходит с большой угловой скоростью в окрестности стационарного решения уравнений (1), принадлежащего семейству
Здесь $\Omega $ – произвольная постоянная, которую считаем положительной (таковы рассматриваемые ниже закрутки). Решения этого семейства описывают стационарные вращения ТГК вокруг его главной центральной оси максимального момента инерции. Общее решение уравнений (1), лежащих в окрестности стационарного решения (4) можно описать приближенными формулами(5)
$\begin{gathered} {{{\hat {\omega }}}_{1}} = \lambda (A\sin \nu t + B\cos \nu t),\,\,\,\,{{{\hat {\omega }}}_{2}} = \Omega + \Delta {{{\hat {\omega }}}_{2}}, \\ \Delta {{{\hat {\omega }}}_{2}} = \frac{{\mu {\kern 1pt} '\,\, - \mu }}{{4\Omega \mu {\kern 1pt} '(1 - \mu \mu {\kern 1pt} ')}}\,\, \cdot \\ \cdot \,\,[2AB\sin 2\nu t - ({{A}^{2}} - {{B}^{2}})\cos 2\nu t], \\ {{{\hat {\omega }}}_{3}} = A\cos \nu t - B\sin \nu t,\,\,\,\,\lambda = \sqrt {\frac{\mu }{{\mu {\kern 1pt} '}}} ,\,\,\,\nu = \Omega \sqrt {\mu \mu {\kern 1pt} '} . \\ \end{gathered} $Уравнения (2) системы (1), (2) имеют точное решение
(6)
$\begin{gathered} {{s}_{1}} = \frac{{1 - \mu {\kern 1pt} '}}{G}{{\omega }_{1}},\,\,\,\,{{s}_{2}} = \frac{{1 - \mu \mu {\kern 1pt} '}}{G}{{\omega }_{2}},\,\,\,{{s}_{3}} = \frac{{1 - \mu }}{G}{{\omega }_{3}}, \\ {{G}^{2}} = {{(1 - \mu {\kern 1pt} ')}^{2}}\omega _{1}^{2} + {{(1 - \mu \mu {\kern 1pt} ')}^{2}}\omega _{2}^{2} + {{(1 - \mu )}^{2}}\omega _{3}^{2}, \\ \end{gathered} $(8)
$\begin{gathered} {{{\dot {s}}}_{1}} + \Omega {{s}_{3}} = {{{\hat {\omega }}}_{3}},\,\,\,\,{{{\dot {s}}}_{3}} - \Omega {{s}_{1}} = - {{{\hat {\omega }}}_{1}}, \\ \Delta {\kern 1pt} {\kern 1pt} {{{\dot {s}}}_{2}} + {{s}_{3}}{{{\hat {\omega }}}_{1}} - {{s}_{1}}{{{\hat {\omega }}}_{3}} = 0, \\ \end{gathered} $Соотношения (6) позволяют выписать частное решение неоднородной системы (8) и найти согласованное с условием (7) постоянное слагаемое в $\Delta {\kern 1pt} {\kern 1pt} {{s}_{2}}$:
(9)
$\begin{gathered} s_{1}^{ * } = \frac{{(1 - \mu {\kern 1pt} '){{{\hat {\omega }}}_{1}}}}{{(1 - \mu \mu {\kern 1pt} ')\Omega }},\,\,\,\,s_{3}^{ * } = \frac{{(1 - \mu ){{{\hat {\omega }}}_{3}}}}{{(1 - \mu \mu {\kern 1pt} ')\Omega }}, \\ \Delta {\kern 1pt} s_{2}^{ * } = \frac{{\Delta {{{\hat {\omega }}}_{2}}}}{\Omega } - \frac{{\lambda {{{(1 - \mu {\kern 1pt} ')}}^{2}} + {{{(1 - \mu )}}^{2}}}}{{4{{\Omega }^{2}}{{{(1 - \mu \mu {\kern 1pt} ')}}^{2}}}}({{A}^{2}} + {{B}^{2}}). \\ \end{gathered} $Общее ненормированное решение однородной системы (8) имеет вид
(10)
$\begin{gathered} s_{1}^{^\circ } = {{c}_{1}}\cos \Omega t - {{c}_{2}}\sin \Omega t, \\ s_{3}^{^\circ } = {{c}_{1}}\sin \Omega t + {{c}_{2}}\cos \Omega t, \\ \Delta {\kern 1pt} s_{2}^{^\circ } = \frac{{\lambda - 1}}{{2(\Omega - \nu )}}[(A{{c}_{1}} + B{{c}_{2}})\sin (\Omega - \nu )t + \\ + \,\,(A{{c}_{2}} - B{{c}_{1}})\cos (\Omega - \nu )t] - \\ - \,\,\frac{{\lambda + 1}}{{2(\Omega + \nu )}}[(A{{c}_{1}} - B{{c}_{2}})\sin (\Omega + \nu )t + \\ + \,\,(A{{c}_{2}} + B{{c}_{1}})\cos (\Omega + \nu )t] + {{c}_{3}}. \\ \end{gathered} $Согласно формуле (3) телеметрические значения тока СБ содержат гармоники с частотами $\Omega $, $\Omega \pm \nu $, $\nu $ и $2\nu $. Частоты $\Omega $ и $\nu $ входят в (3) через ${{s}_{1}}$ и ${{s}_{3}}$. Им отвечают амплитуды:
Частота $2\nu $ также входит через ${{s}_{2}}$, но ей отвечает малая амплитуда. Из сказанного следует, что, выполнив спектральный анализ телеметрических значений тока СБ, можно найти частоты $\Omega $, $\nu $ и величину $\sqrt {\mu \mu {\kern 1pt} '} = {\nu \mathord{\left/ {\vphantom {\nu \Omega }} \right. \kern-0em} \Omega }$. Отношение $R$ амплитуд с частотами $\Omega - \nu $ и $\Omega + \nu $ имеет вид
Найдя это отношение из периодограмм, можно оценить
Приведем основные соотношения используемого спектрального анализа [6]. Пусть ${{I}_{n}}$ $(n = 1,\;2,\; \ldots ,\;N)$ – исследуемые данные измерений. Значение ${{I}_{n}}$ отвечает моменту времени (точке) ${{t}_{n}}$, причем $0 = {{t}_{1}} < {{t}_{2}} < \ldots < {{t}_{N}}$. Для большинства соседних точек ${{t}_{{n + 1}}} - {{t}_{n}} \approx 1$ с, но иногда в данных встречаются пропуски. Сначала из исследуемых данных выделяются отдельные гармонические составляющие (гармоники). С этой целью данные аппроксимируются функцией
где ${{a}_{0}}$, $a$, $b$ и $f$ – параметры. Значения параметров разыскиваются методом наименьших квадратов. Составим выражениеСогласно методу наименьших квадратов определение параметров ${{a}_{0}}$, $a$, $b$ и $f$ сводится к минимизации по ним выражения (12).
Функция $\Psi = \Psi ({{a}_{0}},\,a,\,b,\,f)$ имеет, как правило, много локальных минимумов, поэтому ее минимизация проводится поэтапно. Сначала в результате решения ряда одинаковых линейных задач наименьших квадратов вычисляются значения функции
в узлах достаточно мелкой равномерной сетки на отрезке $0 \leqslant f \leqslant F$, строится график этой функции, и находятся приближенные значения точек минимума. Значения $f$ для достаточно значимых (по величине ${{\Psi }_{1}}$) минимумов являются частотами искомых гармоник. В случае ${{t}_{{n + 1}}} - {{t}_{n}} = 1$ с для полного анализа данных надо взять $F = 0.5$ Гц, но в данной задаче оказалось возможным принять $F = 0.025$ Гц. Пусть описанным способом найдены частоты ${{f}_{k}}$ $(k = 1,2, \ldots ,M;\,\,M \ll N)$. Отвечающий этим частотам тренд ищем в виде(13)
$I(t) = {{a}_{0}} + \sum\limits_{k = 1}^M {({{a}_{k}}\cos 2\pi {{\lambda }_{k}}t + {{b}_{k}}\sin 2\pi {{\lambda }_{k}}t} ),$Чтобы проверить результат первого этапа, наряду с функцией ${{\Psi }_{1}}(f)$ рассматривалась функция
Ниже для наглядности вместо графиков функций ${{\Psi }_{1}}(f)\,$ и $I(f)$ приводятся графики функций
Минимумы функции $E(f)$ дают оценки среднеквадратичной ошибки аппроксимации функции $x(t)$ выражением (11), максимумы функции $A(f)$ – оценки амплитуды $\sqrt {{{a}^{2}} + {{b}^{2}}} $.Результаты спектрального анализа данных измерений тока СБ, а также результаты предваряющего этот анализ исключения из данных измерений низкочастотной составляющей приведены на рис. 1, 3, 5 и 7. Все рисунки в данной работе сгруппированы по отрезкам измерений, поэтому нумерация рисунков, относящихся к спектральному анализу, не является сплошной. Преобразованию и анализу были подвергнуты отрезки данных, основные характеристики которых приведены в табл. 2. Для каждого отрезка в таблице указаны его номер, начальная точка ${{t}_{1}}$ (дата и время), продолжительность ${{t}_{N}} - {{t}_{1}}$, число $N$ включенных в обработку моментов времени с измерениями и некоторые результаты обработки. Началом отсчета времени $t$ на всех рисунках данной работы служит точка ${{t}_{1}}$.
Подготовка данных для спектрального анализа и реконструкции движения состояла в их предварительной коррекции. Из измерений тока исключалась составляющая, которая, по-видимому, обусловлена светом, отраженным от земной поверхности. Эту составляющую трудно выделить точно. Приближенное выделение основано на частотных соображениях. Составляющая, обусловленная отраженным от Земли светом, – низкочастотная. Она довольно сложно зависит от времени, и в ее представлении рядом Фурье необходимо учесть несколько гармоник с частотами, кратными ${{\omega }_{{{\text{осв}}}}} = {\pi \mathord{\left/ {\vphantom {\pi {({{t}_{N}} - {{t}_{1}})}}} \right. \kern-0em} {({{t}_{N}} - {{t}_{1}})}}$. Здесь $[{{t}_{1}},\;{{t}_{N}}]$ – обрабатываемый интервал времени с измерениями, его длина не превышает времени полета ТГК по освещенному участку орбиты. Составляющая тока, обусловленная прямым солнечным светом, – высокочастотная. Ее основные частоты $\Omega $, $\nu $ и $\Omega \pm \nu $ существенно больше ${{\omega }_{{{\text{осв}}}}}$. В такой ситуации составляющую, обусловленную отраженным от Земли светом, можно выделить с помощью низкочастотной фильтрации.
Использованный способ фильтрации состоял в следующем. Сначала строилась аппроксимация низкочастотной составляющей с помощью выражения (конечного ряда Фурье)
(15)
$\begin{gathered} \chi (t) = {{a}_{{M + 1}}} + {{a}_{{M + 2}}}(t - {{t}_{1}}) + \\ + \,\,\sum\limits_{m = 1}^M {{{a}_{m}}\sin \frac{{\pi m(t - {{t}_{1}})}}{{{{t}_{N}} - {{t}_{1}}}}} , \\ \end{gathered} $Рис. 1.
Коррекция и спектральный анализ измерений на интервале 1; (а) удаление низкочастотной составляющей ($M = 12$), (б) спектры скорректированных измерений, (в) аппроксимация измерений суммой гармоник с частотами 0.00277, 0.00391, 0.00668, 0.00945 Гц и амплитудами 0.13, 0.33, 0.85, 0.42 A, СКО = 0.18 А. Оценки параметров модели: $\Omega = 2.40\,\,{{{\text{град}}} \mathord{\left/ {\vphantom {{{\text{град}}} {\text{c}}}} \right. \kern-0em} {\text{c}}}$, $\mu = 0.210$, $\mu {\kern 1pt} ' = 0.822$.
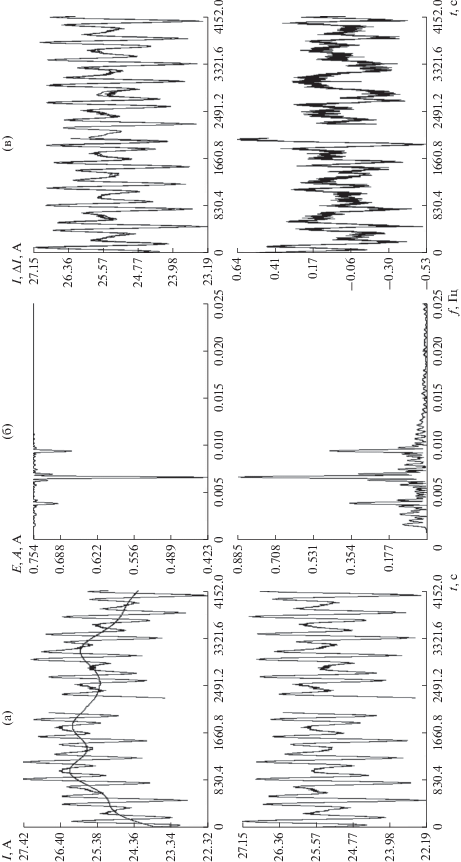
Рис. 2.
Результаты обработки скорректированных измерений тока на интервале 1; (а), (б) решение системы (1), (2), (в) аппроксимация измерений, $\sigma = 0.18$ А. Оценки параметров модели: $\mu = 0.199$, $\mu {\kern 1pt} ' = 0.868$, ${{I}_{0}} = 27.9$ А, $\gamma = - 0.075$.
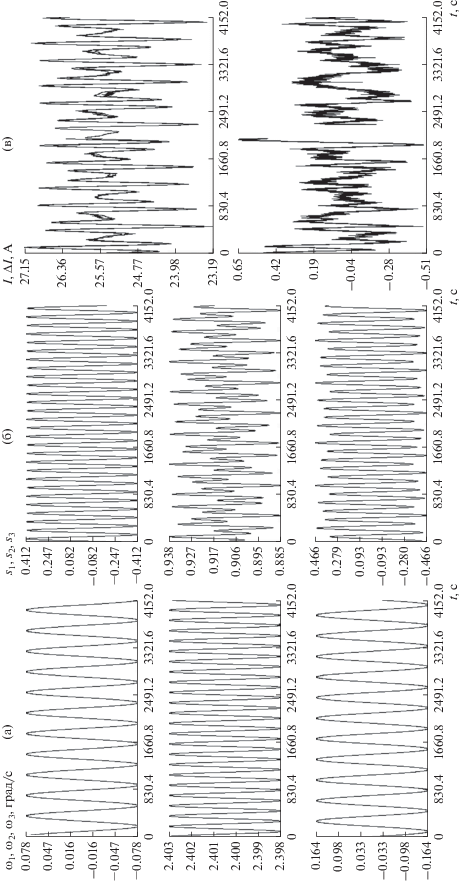
Рис. 3.
Коррекция и спектральный анализ измерений на интервале 2; (а) удаление низкочастотной составляющей ($M = 10$), (б) спектры скорректированных измерений, (в) аппроксимация измерений суммой гармоник с частотами 0.00271, 0.00403, 0.00678, 0.00958 Гц амплитудами 0.078, 0.62, 0.54, 0.19 A, СКО = 0.077 А. Оценки параметров модели: $\Omega = {{2.44\,\,{\text{град}}} \mathord{\left/ {\vphantom {{2.44\,\,{\text{град}}} {\text{c}}}} \right. \kern-0em} {\text{c}}}$, $\mu = 0.189$, $\mu {\kern 1pt} ' = 0.884$.
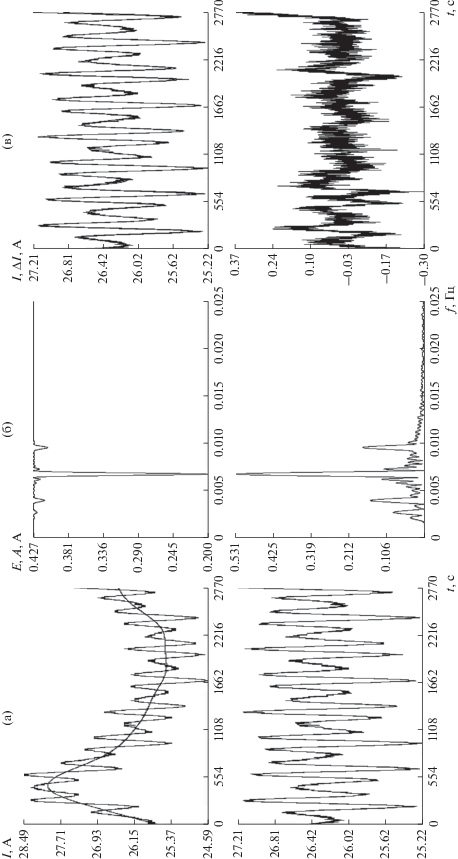
Рис. 4.
Результаты обработки скорректированных измерений тока на интервале 2; (а), (б) решение системы (1), (2), (в) аппроксимация измерений, $\sigma = 0.083$ А. Оценки параметров модели: $\mu = 0.188$, $\mu {\kern 1pt} ' = 0.886$, ${{I}_{0}} = 27.7$ А, $\gamma = - 0.065$.
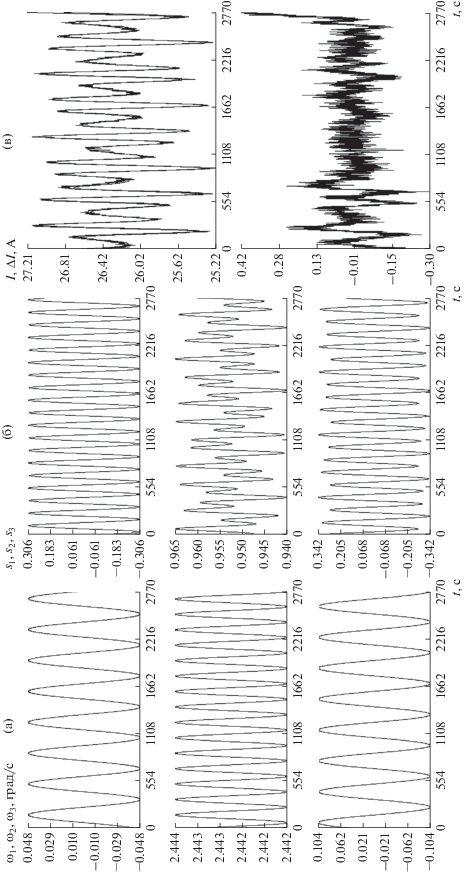
Рис. 5.
Коррекция и спектральный анализ измерений на интервале 3; (а) удаление низкочастотной составляющей ($M = 8$), (б) спектры скорректированных измерений, (в) аппроксимация измерений суммой гармоник с частотами 0.00255, 0.00370, 0.00616, 0.00860 Гц амплитудами 0.017, 0.45, 0.87, 0.49 A, СКО = 0.15 А. Оценки параметров модели: $\Omega = 2.22\,\,{{{\text{град}}} \mathord{\left/ {\vphantom {{{\text{град}}} {\text{c}}}} \right. \kern-0em} {\text{c}}}$, $\mu = 0.174$, $\mu {\kern 1pt} ' = 0.908$.
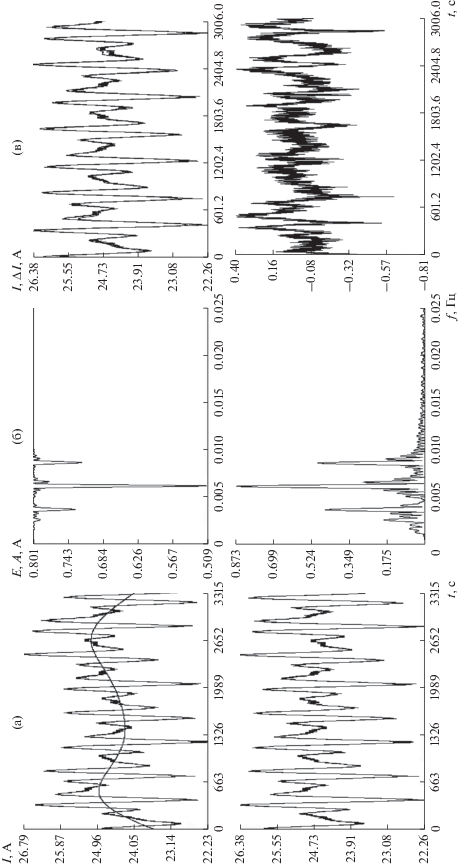
Таблица 2.
Результаты обработки измерений тока на ТГК № 423 (ноябрь 2014) и № 424 (апрель 2015)
| № инт. | Дата | ${{t}_{1}}$ (ДМВ) | ${{t}_{N}} - {{t}_{1}}$, с | $N$ | $M$ | $\sigma $, A | ${{\omega }_{{10}}}$ | ${{\omega }_{{20}}}$ | ${{\omega }_{{30}}}$ | ${{\sigma }_{{\omega 1}}}$ | ${{\sigma }_{{\omega 2}}}$ | ${{\sigma }_{{\omega 3}}}$ |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (${{10}^{{ - 3}}}\,{{{\text{c}}}^{{ - 1}}}$) | (10–6 c–1) | |||||||||||
| 1 | 1.XI.2014 | 09:40:28 | 4152 | 3893 | 12 | 0.177 | 1.336 | 41.942 | 0.582 | 22 | 21 | 39 |
| 2 | 17.XI.2014 | 21:34:17 | 2770 | 2725 | 10 | 0.083 | –0.759 | 42.644 | 0.741 | 14 | 36 | 32 |
| 3 | 26.IV.2015 | 00:40:46 | 3315 | 3309 | 8 | 0.188 | –0.412 | 38.575 | –3.285 | 22 | 51 | 47 |
| 4 | 26.IV.2015 | 02:10:47 | 3321 | 3322 | 9 | 0.157 | –0.929 | 38.692 | 0.804 | 20 | 26 | 33 |
| 5 | 26.IV.2015 | 00:40:46 | 8722 | 6631 | – | 0.183 | –0.466 | 38.657 | –3.061 | 14 | 17 | 33 |
| № инт. | $\mu $ | ${{\sigma }_{\mu }}$$ \cdot \,{{10}^{4}}$ | $\mu {\kern 1pt} '$ | ${{\sigma }_{{\mu {\kern 1pt} '{\kern 1pt} }}}$$ \cdot \,{{10}^{3}}$ | ${{z}_{1}}$$ \cdot \,{{10}^{4}}$ | ${{\sigma }_{{z1}}}$$ \cdot \,{{10}^{4}}$ | ${{z}_{2}}$$ \cdot \,{{10}^{4}}$ | ${{\sigma }_{{z2}}}$$ \cdot \,{{10}^{4}}$ | ${{A}_{2}}$, А | ${{\sigma }_{{A2}}}$, А | ${{A}_{3}}$, А | ${{\sigma }_{{A{\kern 1pt} 3}}}$, А |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.199 | 1.3 | 0.869 | 28 | –1707 | 28 | –1165 | 25 | 27.84 | 0.073 | 2.09 | 0.029 |
| 2 | 0.188 | 2.5 | 0.886 | 47 | – 662 | 16 | 1497 | 24 | 27.60 | 0.044 | 1.79 | 0.028 |
| 3 | 0.186 | 1.8 | 0.861 | 15 | 1031 | 20 | 1406 | 31 | 26.94 | 0.060 | 2.13 | 0.026 |
| 4 | 0.171 | 1.4 | 0.927 | 28 | –2711 | 50 | –7 | 24 | 28.48 | 0.15 | 1.73 | 0.028 |
| 5 | 0.185 | 0.46 | 0.858 | 51 | 1185 | 15 | 1324 | 21 | 26.69 | 0.044 | 2.13 | 0.019 |
Выбор $M$ контролировался спектральным анализом. Для пробного выражения (13) вычислялось его среднее значение $\langle \chi \rangle $ на сетке $\{ \,{{t}_{n}}\} $. Функция $\chi (t) - \langle \chi \rangle $ считалась той посторонней составляющей, которую следует удалить из данных измерений. Удаление состояло в замене величин ${{I}_{n}}$ величинами ${{I}_{n}} - \chi ({{t}_{n}}) + \langle \chi \rangle $ с сохранением прежних обозначений. Примеры ломаных, проходящих через новые точки $({{t}_{n}},\;{{I}_{n}})$, приведены в нижней части рисунков с индексом (а). Для модифицированных таким образом значений тока вычислялись периодограммы (14). Примеры графиков этих периодограмм приведены на рисунках с индексом (б). На графиках видны несколько значимых пиков (минимумов функции $E(f)$ и максимумов функции $A(f)$), отвечающих гармоническим составляющим в данных измерений. Выделялись 4 наиболее значимых пика. Частоты пиков обозначим ${{f}_{k}}$ $(k = 1,\;2,\;3,\;4)$. Нумерация частот определяется соотношениями $2\pi {{f}_{1}} \approx \nu $, $2\pi {{f}_{2}} \approx \Omega - \nu $, $2\pi {{f}_{3}} \approx \Omega $, $2\pi {{f}_{4}} \approx \Omega + \nu $. Для определяемых движений ${{f}_{1}} < {{f}_{2}} < {{f}_{3}} < {{f}_{4}}$. Число $M$ в (15) выбиралось максимальным среди тех чисел, что оставляли на периодограммах не менее четырех значимых пиков. Пикам приписывались частоты ${{f}_{1}}$, ${{f}_{2}}$… При этом учитывались следующие обстоятельства. Во-первых, описанное преобразование измерений с помощью выражения (15) практически исключает из измерений составляющие с частотами меньше $M{{[2({{t}_{N}} - {{t}_{1}})]}^{{ - 1}}}$. Во-вторых, наиболее значимый пик отвечает частоте ${{f}_{3}} \approx {\Omega \mathord{\left/ {\vphantom {\Omega {2\pi }}} \right. \kern-0em} {2\pi }}$. В-третьих, должны выполняться указанные выше приближенные соотношения для частот ${{f}_{1}}$, ${{f}_{2}}$ и ${{f}_{4}}$, рассчитываемые по найденному из периодограмм значению ${{f}_{3}}$ и проектному значению $\sqrt {\mu \mu {\kern 1pt} '} $.
Значения частот ${{f}_{k}}$, найденные по периодограммам, уточнялись при построении аппроксимации измерений выражением (13). Графики этих выражений приведены плавными линиями в верхней части рассматриваемых рисунков, имеющих индекс (в). В одних системах координат с ними изображены графики аппроксимируемых данных – ломаные, звенья которых соединяют соседние по времени точки $({{t}_{n}},\;{{I}_{n}})$. В нижней части рисунков (в) приведены графики ошибок аппроксимации – ломаные с вершинами в точках $({{t}_{n}},\;{{I}_{n}} - I({{t}_{n}}))$. По уточненным частотам ${{\lambda }_{1}}$, … ${{\lambda }_{4}}$ найдены оценки величин $\Omega $, $\mu $ и $\mu {\kern 1pt} '$. Эти оценки, а также частоты ${{\lambda }_{k}}$ и амплитуды $\sqrt {a_{k}^{2} + b_{k}^{2}} $ приведены в подписях к рисункам. Частоты выражены в герцах, амплитуды – в амперах.
РЕКОНСТРУКЦИЯ ДВИЖЕНИЯ ТГК ПО ИЗМЕРЕНИЯМ ТОКА СБ
Значения угла $\beta $ малы (см. табл. 1) и оцениваются с большой ошибкой. В такой ситуации целесообразно положить в (3) $\beta = 0$. Тогда
(16)
$\begin{gathered} I = {{A}_{2}}{{s}_{2}} + {{A}_{3}}{{s}_{3}},\,\,\,\,{{A}_{2}} = {{I}_{0}}\cos \gamma , \\ {{A}_{3}} = - {{I}_{0}}\sin \gamma , \\ \end{gathered} $(17)
$\Phi = \sum\limits_{n = 1}^N {{{{[{{I}_{n}} - {{A}_{2}}{{s}_{2}}({{t}_{n}}) - {{A}_{3}}{{s}_{3}}({{t}_{n}})]}}^{2}}} .$Минимизация выполняется по начальным условиям решения и параметрам $\mu $, $\mu {\kern 1pt} '$, ${{A}_{2}}$, ${{A}_{3}}$. Начальные условия для уравнений (1) обозначим ${{\omega }_{{i0}}} = {{\omega }_{i}}({{t}_{1}})$ $(i = 1,\;2,\;3)$. Решения уравнений (2) должны удовлетворять условию (7). Это условие выполняется при всех $t$, если оно выполнено в начальной точке ${{t}_{1}}$. По этой причине начальные условия переменных ${{s}_{i}}$ выражались через независимые параметры ${{z}_{1}}$ и ${{z}_{2}}$ по формулам
В большинстве случаев использования режима закрутки на Солнце $\left| {{{z}_{1}}} \right| \ll 1$, $\left| {{{z}_{2}}} \right| \ll 1$, и такую параметризацию можно приближенно представить в виде ${{s}_{1}} \approx 2{{z}_{1}}$, ${{s}_{2}} \approx 1$, ${{s}_{3}} \approx 2{{z}_{2}}$. Последние соотношения поясняют смысл параметров ${{z}_{1}}$ и ${{z}_{2}}$.
Функционал (17) зависит от 9 величин: ${{\omega }_{{10}}}$, ${{\omega }_{{20}}}$, ${{\omega }_{{30}}}$, $\mu $, $\mu {\kern 1pt} '$, ${{z}_{1}}$, ${{z}_{2}}$, ${{A}_{2}}$, ${{A}_{3}}$. Так система (1), (2) выдерживает замену переменных
Функционал (17) можно упростить. В уравнения (2) вместо решения уравнений (1) подставим формулы (5) и будем рассматривать $\Phi $ как функцию величин $A$, $B$, $\Omega $, $\lambda $, $\nu $, ${{z}_{1}}$, ${{z}_{2}}$, ${{A}_{2}}$, ${{A}_{3}}$. Такое упрощение использовалось для поиска начального приближения точки минимума $\Phi $.
Минимизация функционала (17) выполнялась методом Левенберга–Марквардта [7]. В некоторых случаях на начальном этапе минимизировался функционал $\Phi + \varepsilon [{{(\mu - {{\mu }_{0}})}^{2}} + {{(\mu {\kern 1pt} '\,\, - \mu _{0}^{'})}^{2}}]$ с априорными оценками ${{\mu }_{0}}$, $\mu _{0}^{'}$ параметров $\mu $, $\mu {\kern 1pt} '$ и $\varepsilon > 0$. На последнем этапе регуляризирующее слагаемое отбрасывалось. Метод Гаусса–Ньютона на последнем этапе в большинстве случаев расходился, и за оценку точки минимума принимался результат, полученный методом Левенберга–Марквардта.
Точность аппроксимации скорректированных измерений тока и оценок уточняемых параметров характеризовались в рамках метода наименьших квадратов соответствующими стандартными отклонениями. Пусть ${{\Phi }_{{\min }}}$ – значения функционала (17) в точке минимума, $C$ – вычисленная в этой точке матрица системы нормальных уравнений, используемых в методе Гаусса–Ньютона (матрица $2C$ приближенно равна матрице квадратичной формы ${{d}^{2}}\Phi $). Тогда формулы стандартного отклонения $\sigma $ ошибок в измерениях и ковариационной матрицы $K$ уточняемых параметров можно записать в виде
Стандартные отклонения уточняемых параметров – квадратные корни из соответствующих диагональных элементов матрицы $K$ – обозначим ${{\sigma }_{{\omega 1}}}$, ${{\sigma }_{{\omega 2}}}$,${{\sigma }_{{\omega 3}}}$, ${{\sigma }_{\mu }}$, ${{\sigma }_{{\mu '}}}$, ${{\sigma }_{{z1}}}$, ${{\sigma }_{{z2}}}$, ${{\sigma }_{{A2}}}$, ${{\sigma }_{{A3}}}$.
Результаты обработки скорректированных измерений тока приведены в табл. 2 и на рис. 2, 4, 6 и 8. Таблица 2 содержит оценки параметров ${{\omega }_{{10}}}$, ${{\omega }_{{20}}}$, ${{\omega }_{{30}}}$, $\mu $, $\mu {\kern 1pt} '$, ${{z}_{1}}$, ${{z}_{2}}$, ${{A}_{2}}$, ${{A}_{3}}$ и их стандартные отклонения для каждого обработанного отрезка данных, рисунки иллюстрируют найденные реконструкции движения ТГК на интервалах времени ${{t}_{1}} \leqslant t \leqslant {{t}_{N}}$. Измерения тока на интервале 5 получены объединением скорректированных измерений на интервалах 3 и 4. Рисунки для него не представлены – они выглядят как объединение соответствующих рисунков для интервалов 3 и 4.
Рис. 6.
Результаты обработки скорректированных измерений тока на интервале 3; (а), (б) решение системы (1), (2), (в) аппроксимация измерений, $\sigma = 0.19$ А. Оценки параметров модели: $\mu = 0.186$, $\mu {\kern 1pt} ' = 0.861$, ${{I}_{0}} = 27.0$ А, $\gamma = - 0.079$.
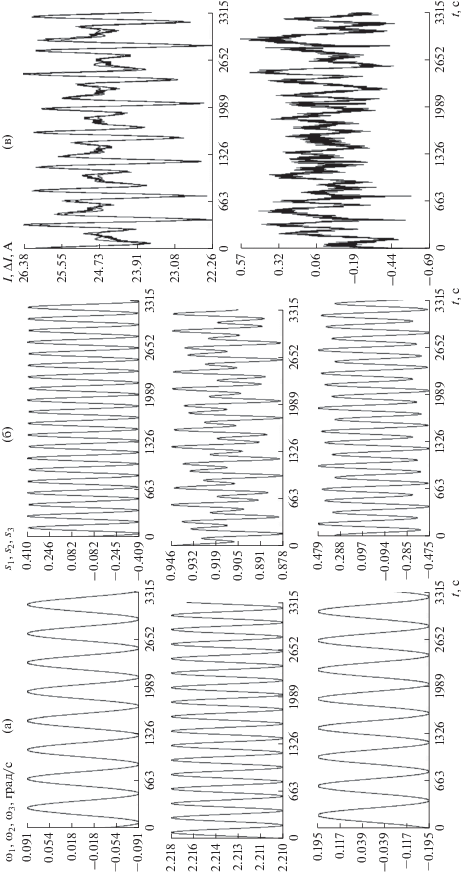
Рис. 7.
Коррекция и спектральный анализ измерений на интервале 4; (а) удаление низкочастотной составляющей ($M = 9$), (б) спектры скорректированных измерений, (в) аппроксимация измерений суммой гармоник с частотами 0.00249, 0.00371, 0.00615, 0.00860 Гц амплитудами 0.012, 0.39, 0.86, 0.44 A, СКО = 0.12 А. Оценки параметров модели: $\Omega = 2.21\,\,{{{\text{град}}} \mathord{\left/ {\vphantom {{{\text{град}}} {\text{c}}}} \right. \kern-0em} {\text{c}}}$, $\mu = 0.178$, $\mu {\kern 1pt} ' = 0.887$.
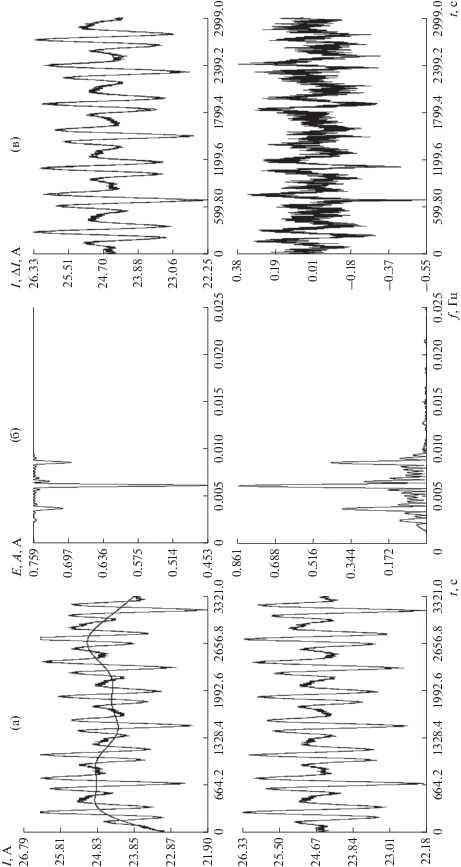
Рис. 8.
Результаты обработки скорректированных измерений тока на интервале 4; (а), (б) решение системы (1), (2), (в) аппроксимация измерений, $\sigma = 0.15$ А. Оценки параметров модели: $\mu = 0.171$, $\mu {\kern 1pt} ' = 0.927$, ${{I}_{0}} = 28.5$ А, $\gamma = - 0.061$.
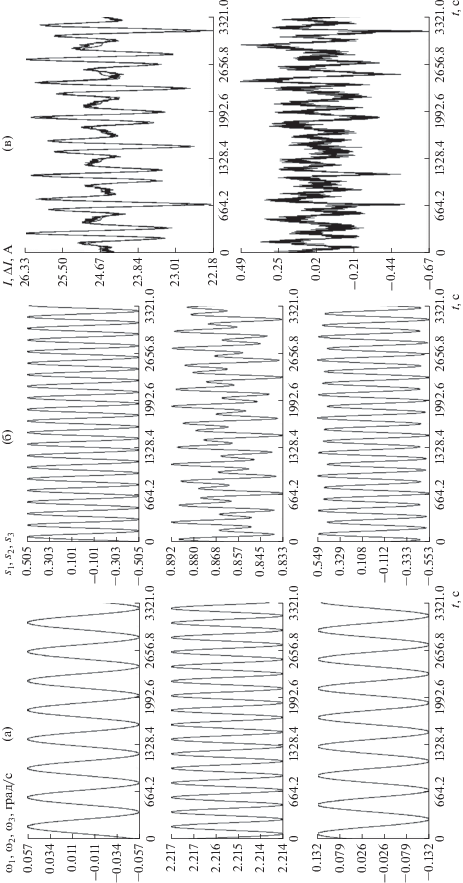
На перечисленных рисунках с индексом (а) приведены графики решений системы (1), на рисунках с индексом (б) – графики решений системы (2). На рисунках с индексом (в) приведены найденные аппроксимации измерений тока. В верхней части этих рисунков плавными линиями изображены графики функции $\hat {I}(t) = {{A}_{2}}{{s}_{2}}(t) + {{A}_{3}}{{s}_{3}}(t)$, ${{t}_{1}} \leqslant t \leqslant {{t}_{N}}$. В тех же системах координат изображены графики скорректированных измерений. Они представляют собой ломаные, звенья которых соединяют соседние по времени точки $({{t}_{n}},\;{{I}_{n}})$, $n = 1,\;2,\; \ldots ,\;N$. Графики почти сливаются, поэтому в нижней части рисунков (в) изображены графики ошибок аппроксимации – ломаные с вершинами в точках $({{t}_{n}},\;{{I}_{n}} - \hat {I}({{t}_{n}}))$. В подписях к рисункам повторены некоторые данные из табл. 2.
По поводу рисунков (в) необходимо отметить, что описанная в п. 3 коррекция измерений тока сохраняет их среднее значение по обрабатываемому интервалу. Но если из данных измерений удаляется низкочастотная составляющая, обусловленная отраженным от Земли светом, то при коррекции следовало бы уменьшить это среднее. Например, принять в качестве удаляемой составляющей функцию $\chi (t) - \langle \chi \rangle + {\text{const}}$, const > 0. Однако значение const неизвестно, поэтому было принято нулем. В определенной степени этот недостаток компенсируется тем, что параметры ${{A}_{2}}$ и ${{A}_{3}}$ уточняются.
Как видим, аппроксимация измерений получилась правдоподобной, оценки параметров $\mu $ и $\mu {\kern 1pt} '$ близки значениям в табл. 1. Оценки параметров ${{A}_{2}}$, ${{A}_{3}}$ позволяют найти ${{I}_{0}} = \sqrt {A_{2}^{2} + A_{3}^{2}} $ и $\gamma = - {\text{arctg}}({{{{A}_{3}}} \mathord{\left/ {\vphantom {{{{A}_{3}}} {{{A}_{2}}}}} \right. \kern-0em} {{{A}_{2}}}})$. Оценки ${{I}_{0}}$ получаются достаточно близкими к априорному значению ${{I}_{0}} = 28$ А, оценки $\gamma $ близки к значениям в табл. 1 (см. подписи к рис. 2, 4, 6 и 8).
Точность построенных реконструкций движения корабля по описанной методике характеризуется стандартными отклонениями уточняемых параметров. Анализ этих стандартных отклонений вместе с анализом собственных векторов матрицы $C$, отвечающих ее нескольким минимальным собственным числам, позволяет понять характер неопределенности, которая возникает при реконструкции движения. Анализ основан на формуле
В качестве примера такого анализа исследуем точность реконструкции движения на интервале 2. Собственные числа матрицы $C$ имеют значения:
Тот факт, что минимальное собственное число положительно, означает принципиальную возможность реконструкции движения описанным способом. Компоненты используемых ниже векторов упорядочены в соответствии с записью: ${{\omega }_{{10}}}$, ${{\omega }_{{20}}}$, ${{\omega }_{{30}}}$, $\mu $, $\mu {\kern 1pt} '$, ${{z}_{1}}$, ${{z}_{2}}$, ${{A}_{2}}$, ${{A}_{3}}$. Наиболее значимые векторы чувствительности в рассматриваемом примере
Компоненты, обозначенные здесь нулями, и компоненты остальных векторов чувствительности не превосходят по абсолютной величине 0.004. Как видим, наименее точно определяются параметры $\mu {\kern 1pt} '$, ${{A}_{2}}$, ${{A}_{3}}$ (ср. табл. 2).
Отметим, что минимальное собственное число матрицы $C$ было значимо больше нуля во всех вариантах реконструкции движения ТГК.
ЗАКЛЮЧЕНИЕ
Реконструировано неуправляемое вращательное движение ТГК Прогресс М-24М и М-25М в режиме закрутки на Солнце. Реконструкция выполнена с помощью интегральной статистической методики по телеметрическим значениям тока, снимаемого с его солнечных батарей. Данные телеметрии, собранные на освещенном участке орбиты, обрабатывались совместно с помощью интегрирования уравнений вращательного движения ТГК. В результате обработки оценивались начальные условия движения корабля относительно направления Земля–Солнце и параметры используемых математических моделей. Проведено исследование, поясняющее возможность реконструкции на основания таких, на первый взгляд, малоинформативных данных.
Во-первых, с помощью спектрального анализа выделены гармонические составляющие в исходных данных, несущие информацию о движении ТГК и некоторых его параметрах. Предложена методика удаления из этих данных посторонней низкочастотной составляющей, обусловленной, по-видимому, отраженным от Земли солнечным светом.
Во-вторых, исследована обусловленность задачи метода наименьших квадратов, лежащей в основе используемой интегральной статистической методики. Показано, что в принципе задача является невырожденной, хотя для некоторых отрезков обрабатываемых данных ее обусловленность может быть плохой. В таких случаях реконструкция движения может оказаться не достаточно точной.
Список литературы
Путин Г.Ф., Глухов А.Ф., Бабушкин И.А. и др. Исследование микроускорений на борту Международной космической станции с помощью датчика конвекции // Космич. исслед. 2012. Т. 50. № 5. С. 373–379.
Путин Г.Ф., Глухов А.Ф., Бабушкин И.А. и др. Эксперименты с датчиком конвекции ДАКОН-М // Космич. исслед. 2017. Т. 55. № 4. С. 278–284.
Беляев М.Ю., Легостаев В.П., Матвеева Т.В. и др. Отработка методов проведения экспериментов в области микрогравитации в автономном полете грузового корабля Прогресс М-20М // Космическая техника и технологии. 2014. Т. 3. № 6. С. 19–32.
Беляев М.Ю. и др. Эксперименты с вращательным движением космических кораблей Прогресс. Препринты ИПМ им. М.В. Келдыша. 2014. № 4.
Беляев М.Ю., Матвеева Т.В., Монахов М.И. и др. Режимы неуправляемого вращательного движения корабля Прогресс М-29М // Космич. исслед. 2018. Т. 56. № 1. С. 54–67.
Теребиж В.Ю. Анализ временных рядов в астрофизике. М.: Наука, 1992.
Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. М.: Мир, 1985.
Дополнительные материалы отсутствуют.
Инструменты
Космические исследования


