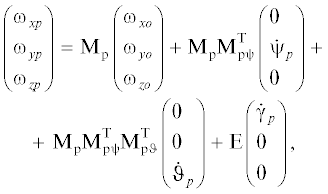Космические исследования, 2021, T. 59, № 3, стр. 247-254

ВВЕДЕНИЕ

В современных системах управления КА гирокомпас остается востребованным устройством, которое удобно для организации режимов восстановления орбитальной ориентации и автономного ориентирования КА на неограниченном отрезке времени без использования данных от глобальной навигационной системы. Длительное время орбитальный гирокомпас считался недостаточно точным и нефункциональным прибором, позволяющим ориентировать КА строго в орбитальной системе координат (ОСК). Появление прецизионных приборов ориентации по Земле с суммарной погрешностью определения вертикали места менее 5′ и гироскопических измерителей угловых скоростей с величинами собственных дрейфов не хуже 1 ⋅ 10^‒3 ″/с, изменили отношения к гирокомпасу и позволили рассматривать его как полноценный резерв основной (прецизионной) системы ориентации. В этой связи повышение функциональности и точности гирокомпаса для орбитальных КА становится актуальной задачей.

1. СИСТЕМЫ КООРДИНАТ

Гирокомпас в приложении к ориентации космических аппаратов относительно ОСК впервые был применен в 60-х годах прошлого века [1]. В состав такой системы трехосной ориентации входят построитель местной вертикали (ПМВ) – датчик горизонта инфракрасного типа и гироорбитант – другое название гироорбита (ГО), выполненный в виде 3-х степенного астатического гироскопа, охваченного обратными связями. КА стабилизируется относительно местной вертикали по сигналам ПМВ, а вектор кинетического момента $H$ гироорбитанта под влиянием гироскопического момента $H\,\, \times \,\,\dot {u}$ автоматически совмещается с вектором $\dot {u}$ орбитальной угловой скорости (аналогично корабельному гирокомпасу). Система стабилизации по сигналу датчика угла, установленному на вертикальной (курсовой) оси ГО, отслеживает положение $H$, вследствие чего корпус КА приводится в плоскость орбиты, завершая построение ОСК.

Введем направление осей.

${{X}_{{ro}}}{{Y}_{{ro}}}{{Z}_{{ro}}}$ – инерциальная система координат (ИСК): ${{X}_{{ro}}}$ лежит в плоскости экватора Земли и направлена в точку весеннего равноденствия, ${{Z}_{{ro}}}$ – совпадает с осью мира и направлена на север Земли, ${{Y}_{{ro}}}$ – дополняет систему до правой. ${{X}_{o}}{{Y}_{o}}{{Z}_{o}}$ – орбитальная система координат (ОСК): ${{X}_{o}}$ проходит через центр масс КА, лежит в плоскости орбиты, перпендикулярна оси ${{Y}_{o}}$ и направлена в сторону движения КА, ось ${{Y}_{o}}$ проходит через центр масс Земли и центр масс КА и направлена от Земли в сторону КА, ось ${{Z}_{o}}$ дополняет систему координат до правой. $X{\kern 1pt} Y{\kern 1pt} Z$ – связанные оси КА (ССК) в номинальном положении совпадают с осями ОСК: ось $X{\kern 1pt} $ – крен, ось $Y{\kern 1pt} $ – курс, ось $Z$ – тангаж.

Положение ОСК относительно ИСК определяется тремя поворотами: поворотом вокруг оси ${{{\text{Z}}}_{{ro}}}$ со скоростью $\dot {\Omega }$ на угол $\Omega $ – определяется положение линии узлов, поворотом вокруг нового положения оси $X_{{ro}}^{'}$ со скоростью $\dot {i}$ на угол $i$ – определяется угол наклона плоскости орбиты к плоскости экватора Земли и поворотом вокруг нового положения оси $Z_{{ro}}^{'}$ со скоростью $\dot {u}$ на угол $u$ – определяется аргумент широты (угловое положение КА в плоскости орбиты относительно линии узлов). После переименования полученной системы координат ($X_{o}^{*} \to {{Y}_{o}},$ $Y_{o}^{*} \to {{X}_{o}},$ ${\text{Z}}_{o}^{*} \to - {{Z}_{o}}$), получим положение принятой ОСК относительно ИСК. При этом скорости вращения ОСК относительно ИСК по соответствующим осям будут равны: ${{\omega }_{{xo}}} = \dot {\Omega }\sin i\cos u - \dot {i}\sin u$, ${{\omega }_{{yo}}} = \dot {\Omega }\sin i\sin u + \dot {i}\cos u$, ${{\omega }_{{zo}}} = - \dot {\Omega }\cos i - \dot {u}$.

2. БЕСПЛАТФОРМЕННЫЙ ГИРОКОМПАС

Гирокомпасы карданного типа обладают большой массой и значительным энергопотреблением. Альтернативой ГО является бесплатформенный орбитальный гирокомпас (БОГК) на базе дифференцирующих или интегрирующих гироскопов. Практическая реализация БОГК стала возможной после появления качественных гироскопических приборов с собственными дрейфами 1 ⋅ 10^‒1–1 ⋅ 10^‒3 ″/с. Преимущество таких гирокомпасов заключается в их компактности, меньшем весе, меньшем электропотреблении, высокой функциональности.

Уравнения движения БОГК в форме наблюдателя имеют известный вид [2]:

где $\psi ,\vartheta ,\gamma ,\dot {\psi },\dot {\vartheta },\dot {\gamma }$ – углы и угловые скорости стабилизации КА относительно приборных осей БОГК по курсу, тангажу и крену; ${{\gamma }_{{hs}}},{{\vartheta }_{{hs}}}$ – сигналы ПМВ в каналах крена и тангажа; ${{k}_{1}},{{k}_{2}},{{k}_{3}}$ – коэффициенты коррекции; ${{\omega }_{{xo}}},{{\omega }_{{yo}}},{{\omega }_{{zo}}}$ – угловые скорости ОСК относительно ИСК; ${{p}_{g}},{{q}_{g}},{{r}_{g}}$ – показания гироскопических датчиков угловых скоростей в ССК по каналам крена, курса и тангажа.

Эти уравнения называют так же обращенными, так как они отображают изменение углов и угловых скоростей стабилизации КА – $\gamma ,\dot {\gamma },\vartheta ,\dot {\vartheta },\psi ,\dot {\psi }$ относительно приборных осей гирокомпаса, а не движение самих приборных осей гирокомпаса относительно ОСК, движение которых, в этих уравнениях “скрыто”.

Очень большим недостатком БОГК является наложение ограничений на повороты КА относительно ОСК. Это связано с тем, что приведенные выше уравнения отражают движения приборных осей гирокомпаса и связанных осей КА в малых угловых отклонениях относительно ОСК. Такая “неповоротливость” классического БОГК существенно ограничивает его эксплуатационные свойства, по существу запрещает программные повороты и тем самым обесценивает применение БОГК в современных системах ориентации орбитальных КА.

3. ПРОГРАММНЫЕ ПОВОРОТЫ. ПРОСТРАНСТВЕННЫЙ 3D-ГИРОКОМПАС. КОРРЕКТИРУЕМЫЙ СЛУЧАЙ

Рассмотрим задачу выполнения космическим аппаратом программных поворотов относительно ОСК на произвольные программные углы курса, тангажа и крена ${{\psi }_{p}},{{\vartheta }_{p}},{{\gamma }_{p}}$ в режиме непрерывной коррекции гирокомпаса показаниями ПМВ.

Введем программную систему координат (ПСК) ${{X}_{p}}{{Y}_{p}}{{Z}_{p}}$ и рассмотрим переходы ИСК → → ОСК → ПСК → ССК с матрицами $А(\Omega ,i,u) \to {{М}_{p}}({{\psi }_{p}},{{\vartheta }_{p}},{{\gamma }_{p}}) \to С(\psi ,\vartheta ,\gamma )$ соответственно. При вычислениях учтем, что угловые отклонения и угловые скорости $\psi ,\dot {\psi },\vartheta ,\dot {\vartheta },\gamma ,\dot {\gamma }$ космического аппарата (ССК относительно ПСК) отрабатываются исполнительными органами КА и в течение всего времени ориентации не превышают величин первого порядка малости.

Программное движение ПСК складывается из переносного движения ОСК относительно ИСК и относительного движения ПСК относительно ОСК. Выражения для угловых скоростей ПСК относительно ИСК в проекциях на оси ПСК имеют вид:

где ${{\omega }_{{x{\kern 1pt} o}}},{{\omega }_{{y{\kern 1pt} o}}},{{\omega }_{{z{\kern 1pt} o}}}$ – скорости ОСК относительно ИСК, ${{\dot {\psi }}_{p}},{{\dot {\vartheta }}_{p}},{{\dot {\gamma }}_{p}}$ – программные скорости ПСК относительно ОСК, E – единичная матрица, T – знак транспонирования.

Положение связанных осей КА относительно ПСК определяется матрицей: ${\text{С}} = {{{\text{С}}}_{\gamma }}{{{\text{С}}}_{\vartheta }}{{{\text{С}}}_{\psi }}$, где ${{{\text{С}}}_{\gamma }},{{{\text{С}}}_{\vartheta }},{{{\text{С}}}_{\psi }}$ – матрицы элементарных поворотов ССК относительно ПСК в каналах – курса, тангажа и крена на малые углы $\psi ,\vartheta ,\gamma $ соответственно.

Угловые скорости КА относительно ИСК в проекциях на оси ССК будут равны:

С учетом сказанного, подставляя (4) в (5), с точностью до величин второго порядка малости получим соотношение, которое запишем в следующем виде:

где ${{L}_{x}},{{L}_{y}},{{L}_{z}}$ – сигналы коррекции БОГК, которые подлежит определить.

Рассмотрим рассогласование ОСК и ПСК (рис. 1) и найдем проекции показаний ПМВ на оси ОСК.

Матрица перехода из ОСК в ПСК с учетом принятой последовательности поворотов:

где ${{M}_{{i{\kern 1pt} j}}}$ – функции программных углов КА ${{\psi }_{p}},{{\vartheta }_{p}},{{\gamma }_{p}}$.

Из (7) и рис. 1 получим:

Построим контур коррекции гирокомпаса. Заметим, что для этого есть несколько возможностей, однако главной идеей является контроль положения ОСК при любом программном положении КА. Исходя из этого принципа, зададим корректирующие сигналы по “образу” классического БОГК в виде:

Подчиним ориентацию КА в каналах крена и тангажа сигналам ПМВ, при этом программная ориентация КА будет достигнута равенством сигналов ПМВ по крену и тангажу соответствующим программным положениям КА с допустимыми ошибками стабилизации:

Задачей контура коррекции в канале курса, как было отмечено выше, является контроль за положением ОСК в любом программном положении КА. Очевидно, что для этого достаточно контролировать одну их осей ОСК ${{X}_{o}}$ или ${{Z}_{o}}$.

Примем (см. рис. 1):

(допускается ${{М}_{{31}}} \simeq \cos {{\vartheta }_{p}}sin{{\psi }_{p}}$).

Подставляя (10)–(15) в (6), получим алгоритм функционирования орбитального гирокомпаса, позволяющий космическому аппарату совершать программные повороты одновременно на углы курса, тангажа и крена с сохранением непрерывной коррекции от ПМВ:

Интегрируя систему уравнений (16) найдем углы и угловые скорости космического аппарата $\psi ,\dot {\psi },\vartheta ,\dot {\vartheta },\gamma ,\dot {\gamma }$, необходимые для стабилизации КА (ССК) относительно ПСК.

В процессе вычислений на вход алгоритма (16) подаются сигналы гироскопических датчиков угловых скоростей ${{p}_{g}},{{q}_{g}},{{r}_{g}}$, которые отождествляют абсолютные угловые скорости КА – $p,q,r$; сигналы ПМВ – ${{\gamma }_{{hs}}},{{\vartheta }_{{hs}}}$, программные углы – ${{\psi }_{p}},{{\vartheta }_{p}},{{\gamma }_{p}}$ и соответствующие им программные угловые скорости ${{\dot {\psi }}_{p}},{{\dot {\vartheta }}_{p}},{{\dot {\gamma }}_{p}}$ КА относительно ОСК, а также скорости ОСК относительно ИСК: ${{\omega }_{{xo}}} = \dot {\Omega }\sin i\cos u - i{\kern 1pt} '\sin u$, ${{\omega }_{{yo}}} = \dot {\Omega }\sin i\sin u$ + $ + \,\,i{\kern 1pt} '\cos u$, ${{\omega }_{{zo}}} = - \dot {\Omega }\cos i - \dot {u}$, полученные из данных баллистического расчета.

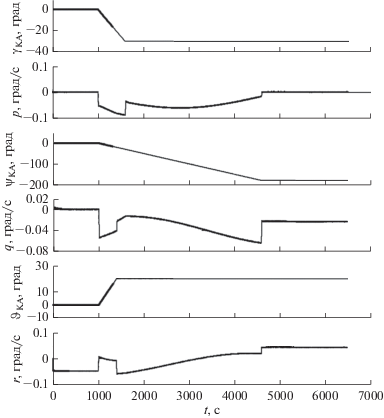
Результаты численного решения показаны на рис. 2 для случая программных поворотов КА (ССК) относительно ОСК одновременно на три угла: ${{\gamma }_{p}} = - 30^\circ $, ${{\psi }_{p}} = - 180^\circ ,$ ${{\vartheta }_{p}} = + 20^\circ $ (принимались ${{k}_{1}} = 0.01\,\,{{{\text{c}}}^{{ - 1}}},$ ${\text{ }}{{k}_{2}} = 0.02\,\,{{{\text{c}}}^{{ - 1}}},$ ${\text{ }}{{k}_{3}} = 0.03\,\,{{{\text{c}}}^{{ - 1}}}$, орбита круговая, линейный диапазон характеристики ПОЗ в каналах крена и тангажа $ \pm 30^\circ $).

КА совершает качественный (с погрешностью метода интегрирования) и асимптотически устойчивый на неограниченном интервале времени программный поворот. В устойчивости процесса программной ориентации КА можно убедиться так же из анализа характеристического уравнения системы (16) для некоторого произвольного программного положения. Например, для ${{\psi }_{p}} \ne 0^\circ ,$ ${\text{ }}{{\vartheta }_{p}} = {{\gamma }_{p}} = 0^\circ $, условие устойчивости выглядит так: $\dot {u}(\dot {u} + {{k}_{2}})({{k}_{1}}{{\cos }^{2}}{{\psi }_{p}} + {{k}_{3}}{{\sin }^{2}}{{\psi }_{p}})$ > 0, т.е. процесс устойчив при любом программном положении КА.

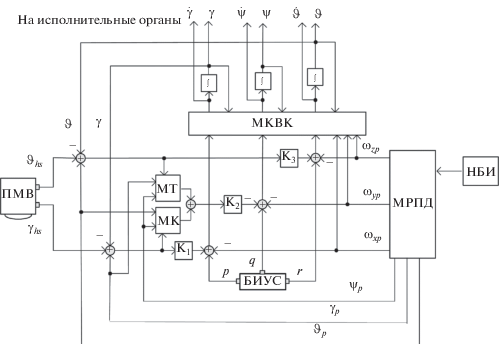
Схема нового гирокомпаса, назовем его “Пространственный 3D-гирокомпас” или коротко “3D-гирокомпас”, показана на рис. 3.

На рис. 3 показано: МКВК – модуль компенсации взаимовлияния каналов ориентации соотвествует второму члену в уравнении (16); МТ, МК – модули контроля курса в каналах крена и тангажа соответствуют (15); МРПД – модуль расчета программных движений; БИУС – блок гироскопических измерителей угловых скоростей; НБИ – устройство навигационно-баллистической информации (${{\omega }_{{xo}}},{{\omega }_{{yo}}},{{\omega }_{{zo}}},u$).

Для оптимизации программных поворотов по времени и по качеству переходных процессов можно воспользоваться заданием программных движений, в форме полиномов третьей степени и выше, например, вида $\varphi = \sum\nolimits_{n = 0}^{n = m} {{{C}_{n}}{{t}^{n}}} , m \geqslant 3$ в каждом канале ориентации и наложения ограничений на сами координаты и их производные на начальных и конечных участках программной траектории.

Таким образом, 3D-гирокомпас позволяет совершать точные пространственные программные повороты КА непосредственно в режиме гирокомпасирования, т.е. в режиме коррекции от ПМВ, при этом ориентациия КА в процессе всего движения носит устойчивый характер.

Отметим, что устойчивые по времени программные повороты КА возможны по курсу неограниченно, а по крену и тангажу только в пределах линейной зоны выходной характеристики ПМВ. Такими характеристиками обладают некоторые отечественные приборы, линейные зоны точных измерений у которых ограничены углами $\left| {{{\gamma }_{{hs}}}} \right| \leqslant 25^\circ ,\,\left| {{{\vartheta }_{{hs}}}} \right| \leqslant 25^\circ $. Применяя эти приборы можно добиться точности угловой ориентации КА на уровне 1–2′ по каждому из каналов (см. ниже) и устойчивой программной ориентации КА в диапазонах углов: $\left| {{{\psi }_{p}}} \right| \leqslant 360^\circ ,$ $\left| {{{\gamma }_{p}}} \right| \leqslant 25^\circ ,\left| {{{\vartheta }_{p}}} \right| \leqslant 25^\circ $.

АВТОНОМНЫЙ СЛУЧАЙ

Программные повороты на углы превышающие зону линейности ПМВ возможны либо путем применения других датчиков, например, астродатчика, включенного в режим построения вертикали места, либо путем перевода гирокомпаса в автономный режим ориентации (режим гиропамяти), т.е. с полным отключением контура коррекции от ПМВ (${{k}_{1}} = {{k}_{2}} = {{k}_{3}} = 0$). В этом режиме у 3D-гирокомпаса появляется возможность выполнять программные повороты корпусом КА на любые произвольные углы, т.е. на ±$~\infty $^о по каждому каналу ориентации или одновременно. На рис. 4 приведен пример программного поворота КА на углы крена, курса и тангажа: ${{\gamma }_{p}} = {{\psi }_{p}} = {{\vartheta }_{p}} = 720^\circ $. Результирующий угол поворота КА выражен в форме косинуса угла ($\cos \phi $) для вектора конечного поворота Эйлера.

3D-гирокомпас в автономном режиме неустойчив. Это связано с тем, что, при отсутствии коррекции от ПМВ, собственный дрейф датчиков угловых скоростей приводит к нарастанию ошибок в программном положении КА. Однако с достаточно точными гироскопическими датчиками программная ориентация КА может продолжаться длительное время. Например, при дрейфе гироскопов 1 · 10^‒1 град/час накопление ошибок ориентации КА в одну угловую минуту произойдет через 600 с, а при дрейфе 1 · 10^‒3 град/час – уже через 60 000 с. Для выполнения каких-либо работ на орбите этого времени вполне достаточно.

Следует отметить, что лучший результат организации автономного режима достигается путем запоминания полного вектора математических ожиданий сигналов коррекции на момент перехода в автономный режим [3].

4. ПЛОСКИЙ ПРОГРАММНЫЙ ПОВОРОТ

Рассмотрим полезный для практических применений частный случай выполнения программного поворота КА только по каналу курса, при котором: ${{\vartheta }_{p}} = {{\dot {\vartheta }}_{p}} = {{\gamma }_{p}} = {{\dot {\gamma }}_{p}} = 0$.

Из уравнений (16) для поворота КА на заданный угол курса в пределах ±360°, в которых, для простоты, положим ${{\omega }_{{xo}}} = {{\omega }_{{yo}}} = 0,$ ${\text{ }}{{\omega }_{{zo}}} = - \dot {u}$, получим:

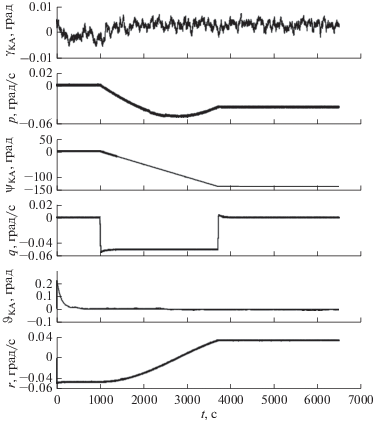
Результаты численного решения показаны на рис. 5 для программного поворота КА относительно ОСК на угол курса: ${{\psi }_{p}} = - 135^\circ $.

Результат может быть полезен для различных практических приложений, например, для решения вопросов курсовой ориентации КА в процессе коррекции наклона плоскости орбиты или маневрирования, ускоренного восстановления курсовой ориентации относительно ОСК.

5. АВТОКОМПЕНСАЦИЯ ОШИБОК

Свойства 3D-гирокомпаса позволяют выполнить автокомпенсацию детерминированных (инструментальных) ошибок ориентации, вызванных соответствующими ошибками ПМВ и гироскопических датчиков. Это связано с тем, что при поворотах КА на программные углы происходит полное взаимное замещение каналов ориентации. Например, при повороте КА на угол ${{\psi }_{p}} = \pm 90^\circ $ канал крена замещается на канал тангажа и, наоборот, канал тангажа замещается каналом крена, что позволяет “наблюдать” и компенсировать ошибки ПМВ в канале тангажа и что ранее сделать было нельзя. Покажем это на частном примере плоского программного поворота.

Для упрощения расчетов перейдем к приборным осям гирокомпаса (приводятся без доказательства):

где $\alpha ,\beta ,\theta $ – ошибки ориентации 3D-гирокомпаса относительно ПСК в каналах курса, крена и тангажа; $\Delta {{\gamma }_{{hs}}},\Delta {{\vartheta }_{{hs}}}$ – ошибки построителя вертикали в каналах крена и тангажа.

Положим, что оси чувствительности гироскопических датчиков угловых скоростей и ПМВ точно совмещены с осями ССК и найдем для программных положений КА ${{\psi }_{p}} = 0^\circ ,{\text{ }}90^\circ ,{\text{ }}180^\circ ,{\text{ }}270^\circ $ математические ожидания сигналов коррекции ОГК. При этом в каждом программном положении необходимо дождаться завершения переходных процессов, измерить (снять показания) сигналов коррекции ${{\gamma }_{{hs}}} - \gamma = \beta + \Delta {{\gamma }_{{hs}}}$, ${{\vartheta }_{{hs}}} - \vartheta = \theta + \Delta {{\vartheta }_{{hs}}}$ и рассчитать их математические ожидания.

Выполним программные повороты КА по курсу: первый на ${{\psi }_{p}} = 0{\kern 1pt} ^\circ $, второй на ${{\psi }_{p}} = 180^\circ $ и найдем сигналы коррекции в канале курса:

Из (17), (18) найдем оценки погрешности ПМВ по крену $\hat {\Delta }{{\gamma }_{{hs}}}$ и постоянной составляющей дрейфа гироскопа курса ${{\hat {\dot {D}}}_{y}}$:

Выполним программные повороты КА: третий на ${{\psi }_{p}} = + 90^\circ $, четвертый на ${{\psi }_{p}} = - 90^\circ {\text{ }}( + 270^\circ )$ и найдем сигналы коррекции так же в канале курса:

Из (21), (22) найдем оценки погрешностей ПОЗ по тангажу и постоянной составляющей дрейфа гироскопа курса:

Найденные оценки (19), (20), (23), (24) вводятся в выходные сигналы приборов для компенсации их погрешностей, например, в форме:

после ввода указанных поправок доопределяются ${{\hat {\dot {D}}}_{x}}$ и ${{\hat {\dot {D}}}_{z}}$.

ВЫВОДЫ

Получен алгоритм и схемное решение орбитального гирокомпаса нового типа – пространственный 3D-гирокомпас. В отличие от классического орбитального гирокомпаса, функция которого ограничена индикацией направления угловой скорости орбитального движения и построением плоскости орбиты, 3D-гирокомпас решает задачу точного программного управления ориентацией КА относительно орбитальной системы координат одновременно по трем каналам курса, тангажа и крена.

Следствием полученных свойств 3D-гирокомпаса стала возможность применения принципа автокомпенсации детерминированных ошибок, обусловленных инструментальными ошибками построителя вертикали и гироскопических датчиков в каждом канале ориентации, включая канал тангажа (группа ненаблюдаемых в классическом гирокомпасе ошибок), что позволяет с применением современных датчиков повысить точность угловой ориентации КА в режиме орбитального гирокомпасирования до уровня $ \leqslant $1–2′.

Возможность выполнения космическим аппаратом пространственных программных поворотов и повышенная точность 3D-гирокомпаса позволяют с его помощью решать достаточно большой круг задач, включая задачи дистанционного зондирования Земли, ускоренное восстановление курсовой ориентации КА, ориентирование КА в процессе коррекции орбиты по углу наклона и эксцентриситету, выдаче тормозного импульса и многие другие.