Космические исследования, 2021, T. 59, № 3, стр. 240-246

Об оценке среднего времени пребывания ИСЗ в земной тени при движении в плоскости эклиптики

А. В. Доброславский^*

Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

Поступила в редакцию 30.01.2020
После доработки 17.04.2020
Принята к публикации 29.05.2020

DOI: 10.31857/S0023420621030031

Аннотация

Рассмотрена процедура определения конуса земной тени при движении спутника в плоскости эклиптики. Оценивается среднее время пребывания спутника в зоне земной тени в зависимости от параметров его орбиты во внешней сфере гравитационного влияния Земли. Полученная оценка относительного времени пребывания спутника в тени позволяет не учитывать тень при качественном анализе движения спутника. Результаты, полученные для конической формы тени, сравниваются с результатами, полученными для цилиндрической формы, и делается выбор в пользу конической.

ВВЕДЕНИЕ

Возмущения от светового давления Солнца являются важной составляющей при исследовании движения спутников, находящихся на геостационарных и высокоэллиптических орбитах [1]. Впервые с этой проблемой столкнулись при исследовании движения спутника Vanguard 1 [2, 3]. Но особенное значение световое давление приобретает при исследовании движения объектов, имеющих большое отношение площади миделева сечения к его массе: спутников-баллонов, спутников с большой площадью солнечных батарей, а также элементов космического мусора. Пересечение такими объектами зоны земной тени вносит дополнительное возмущение в их движение [4–7]. При этом исследователи полагали тень Земли цилиндрической: Ф. Мелло [5], Лидов [6, 7], Вашковьяк [8], хотя в работе Лидова [7] оговаривалось, что используемый расчетно-аналитический метод годится и для других форм земной тени.

При рассмотрении светового давления на спутник, находящийся в значительном удалении от Земли, в задачах трех [9] и четырех тел [10], эффектом земной тени зачастую пренебрегают. Но, поскольку отсутствует оценка влияния земной тени в вышеупомянутых случаях, требуется обоснование таким математическим моделям.

Целью статьи является уточнение формы земной тени на высоких орбитах, находящихся во внешней сфере гравитационного влияния Земли, расположенной за лунной орбитой. Вследствие того, что Солнце не является точечным источником, земная тень представляет собой конус. В работе исследуется такая форма тени (без учета полутеней) и сравнивается с более грубой, цилиндрической на асимптотически больших временных промежутках. Также делается оценка влияния параметров орбиты спутника на среднее время пребывания объекта в земной тени в случае внешней сферы гравитационного влияния Хилла. Рассматриваемые орбиты находятся в плоскости эклиптики, так как в этом случае земная тень оказывает наибольшее воздействие.

ОПРЕДЕЛЕНИЕ ЗОНЫ ЗЕМНОЙ ТЕНИ

Рассмотрим движение спутника в плоскости эклиптики (см. рис. 1). Пусть $E$ – центр Земли, свяжем с ним полярную систему координат $\left( {r,\theta } \right)$, ось которой направим в центр Солнца $S$. Введем обозначения: пусть ${{R}_{E}}$ – радиус Земли, ${{R}_{S}}$ – радиус Солнца, а ${{r}_{S}} = ES$ – расстояние от Земли до Солнца. Пусть также $F$ – вершина конуса земной тени, а ${{r}_{f}} = EF$ – расстояние от нее до Земли, которое подлежит определению.

Рис. 1.

Зона земной тени.

Тогда, из подобия треугольников $\Delta FE{{E}_{1}}$ и $\Delta FS{{S}_{1}}$, а также представления кеплеровской орбиты Солнца, как функции истинной аномалии, следует выражение:

${{r}_{f}}\left( {{{\nu }_{S}}} \right) = \frac{{{{a}_{S}}\left( {1 - e_{S}^{2}} \right){{R}_{E}}}}{{\left( {1 + {{e}_{S}}\cos {{\nu }_{S}}} \right)\left( {{{R}_{S}} - {{R}_{E}}} \right)}},$

где ${{a}_{S}}$, ${{e}_{S}}$, ${{\nu }_{S}}$ – соответственно, большая полуось, эксцентриситет и истинная аномалия орбиты Солнца.

Запишем уравнение прямой $F{{S}_{1}}$ в полярных координатах:

(1)

$r = \frac{{{{R}_{E}}}}{{\cos \left( {\theta - {{\phi }_{1}}} \right)}},$

где ${{R}_{E}}$ – кратчайшее расстояние от центра координат до прямой $F{{S}_{1}}$, ${{\phi }_{1}} = \angle SE{{E}_{1}}$ – полярный угол отрезка $E{{E}_{1}}$, $r = r\left( \theta \right)$ – радиус-вектор прямой $F{{S}_{1}}$, а $\theta $ – свободная переменная. Учитывая, что угол ${{\phi }_{1}} = \frac{\pi }{2} + \alpha $ (см. рис. 1), преобразуем (1) следующим образом:

(2)

$r = \frac{{{{R}_{E}}}}{{\cos \left( {\theta - \left( {\frac{\pi }{2} + \alpha } \right)} \right)}} = \frac{{{{R}_{E}}}}{{\sin \theta \cos \alpha - \cos \theta \sin \alpha }},$

где угол $\alpha $ определяется по формуле:

$\alpha = \arcsin \left( {\frac{{{{R}_{E}}}}{{{{r}_{f}}\left( {{{\nu }_{S}}} \right)}}} \right).$

Аналогичным образом записывается уравнение прямой $F{{S}_{2}}$: пусть ${{\phi }_{2}}$ – полярный угол отрезка $E{{E}_{2}}$, тогда его выражение через угол $\alpha $ будет ${{\phi }_{2}} = \frac{{3\pi }}{2} - \alpha $ и

(3)

$\begin{gathered} r = \frac{{{{R}_{E}}}}{{\cos \left( {\theta - \left( {\frac{{3\pi }}{2} - \alpha } \right)} \right)}} = \\ = - \frac{{{{R}_{E}}}}{{\sin \theta \cos \alpha + \cos \theta \sin \alpha }}. \\ \end{gathered} $

ТОЧКА ЗАХОДА СПУТНИКА В ТЕНЬ

Введем геоцентрическую полярную систему координат с центром в точке $E$ (см. рис. 2), полярную ось $Ex$ направим в перицентр орбиты Солнца. Пусть эллиптическая орбита спутника расположена в плоскости эклиптики. Здесь, так же, как и на рис. 1, $S$ означает центр Солнца, а $F$ – вершину конуса земной тени.

Рис. 2.

Транзит спутника через земную тень.

Поскольку средняя линия тени $EF$ составляет угол $\pi $ с направлением на Солнце $ES$, уравнение границы тени (2) в выбранной системе координат примет вид:

(4)

$\begin{gathered} r = \frac{{{{R}_{E}}}}{{\cos \left( {\theta - \left( {\frac{\pi }{2} + \alpha + {{\nu }_{S}}} \right)} \right)}} = \\ = \frac{{{{R}_{E}}}}{{\sin \theta \cos \left( {\alpha + {{\nu }_{S}}} \right) - \cos \theta \sin \left( {\alpha + {{\nu }_{S}}} \right)}}, \\ \end{gathered} $

где ${{\nu }_{S}}$ – истинная аномалия орбиты Солнца.

Найдем теперь полярный угол ${{\theta }_{1}}$ точки входа спутника в земную тень ${{P}_{1}}$:

(5)

$\begin{gathered} \frac{{{{R}_{E}}}}{{\sin {{\theta }_{1}}\cos \left( {\alpha + {{\nu }_{S}}} \right) - \cos {{\theta }_{1}}\sin \left( {\alpha + {{\nu }_{S}}} \right)}} = \\ = \frac{{a\left( {1 - {{e}^{2}}} \right)}}{{1 + e\cos \left( {{{\theta }_{1}} - \omega } \right)}}, \\ \end{gathered} $

где $a$ и $e$, соответственно, большая полуось и эксцентриситет орбиты спутника, а $\omega $ – аргумент перицентра орбиты, отсчитываемый от полярной оси. Введем обозначение $\xi $: $\xi = \frac{{a\left( {1 - {{e}^{2}}} \right)}}{{{{R}_{E}}}}.$

С учетом введенного обозначения, уравнение (5) можно записать в виде:

(6)

$\begin{gathered} \xi \left( {\sin {{\theta }_{1}}\cos \left( {\alpha + {{\nu }_{S}}} \right) - \cos {{\theta }_{1}}\sin \left( {\alpha + {{\nu }_{S}}} \right)} \right) = \\ = 1 + e\left( {\cos {{\theta }_{1}}\cos \omega + \sin {{\theta }_{1}}\sin \omega } \right). \\ \end{gathered} $

Возведя выражение (6) в квадрат, и сгруппировав слагаемые, получим квадратное уравнение относительно $\cos {{\theta }_{1}}$:

$\begin{gathered} \left( {{{e}^{2}} + {{\xi }^{2}} - 2e\xi \sin \left( {\alpha + {{\nu }_{S}} - \omega } \right)} \right){{\cos }^{2}}{{\theta }_{1}} + \\ + \,\,2\left( {e\cos \omega + \xi \sin \left( {\alpha + {{\nu }_{S}}} \right)} \right)\cos {{\theta }_{1}} + \\ + \,\,1 - {{\left( {\xi \cos \left( {\alpha + {{\nu }_{S}}} \right) - e\sin \omega } \right)}^{2}} = 0. \\ \end{gathered} $

Разрешив которое получим:

(7)

$\cos {{\theta }_{1}} = \frac{{ - {{\psi }_{1}} \pm {{\varphi }_{1}}\sqrt {\psi _{1}^{2} + \varphi _{1}^{2} - 1} }}{{\psi _{1}^{2} + \varphi _{1}^{2}}}.$

И, соответственно,

(8)

$\sin {{\theta }_{1}} = \sqrt {1 - {{{\cos }}^{2}}{{\theta }_{1}}} = \frac{{{{\varphi }_{1}} \pm {{\psi }_{1}}\sqrt {\psi _{1}^{2} + \varphi _{1}^{2} - 1} }}{{\psi _{1}^{2} + \varphi _{1}^{2}}}.$

Где функции ${{\psi }_{1}}$, ${{\varphi }_{1}}$ имеют выражения:

$\begin{gathered} {{\psi }_{1}} = e\cos \omega + \xi \sin \left( {\alpha + {{\nu }_{S}}} \right), \\ {{\varphi }_{1}} = e\sin \omega - \xi \cos \left( {\alpha + {{\nu }_{S}}} \right). \\ \end{gathered} $

Знак в (7) и (8) берется согласованно, из условия попадания спутника в зону тени: ${{\theta }_{1}} - {{\nu }_{S}} \in \left[ {\frac{\pi }{2},\frac{{3\pi }}{2}} \right].$

ТОЧКА ВЫХОДА СПУТНИКА ИЗ ЗОНЫ ТЕНИ

Запишем уравнение границы тени (3) в полярной системе координат, введенной на рис. 2:

$\begin{gathered} r = \frac{{{{R}_{E}}}}{{\cos \left( {\theta - \left( {\frac{{3\pi }}{2} + {{\nu }_{S}} - \alpha } \right)} \right)}} = \\ = - \frac{{{{R}_{E}}}}{{\sin \theta \cos \left( {\alpha - {{\nu }_{S}}} \right) + \cos \theta \sin \left( {\alpha - {{\nu }_{S}}} \right)}}. \\ \end{gathered} $

Найдем теперь полярный угол ${{\theta }_{2}}$ точки выхода спутника из земной тени ${{P}_{2}}$ (см. рис. 2):

(9)

$\begin{gathered} - \frac{{{{R}_{E}}}}{{\sin {{\theta }_{2}}\cos \left( {\alpha - {{\nu }_{S}}} \right) + \cos {{\theta }_{2}}\sin \left( {\alpha - {{\nu }_{S}}} \right)}} = \\ = \frac{{a\left( {1 - {{e}^{2}}} \right)}}{{1 + e\cos \left( {{{\theta }_{2}} - \omega } \right)}}. \\ \end{gathered} $

Используя то же обозначение, что и в (6), перепишем (9) в виде:

$\begin{gathered} - \xi \left( {\sin {{\theta }_{2}}\cos \left( {\alpha - {{\nu }_{S}}} \right) + \cos {{\theta }_{2}}\sin \left( {\alpha - {{\nu }_{S}}} \right)} \right) = \\ = 1 + e\left( {\cos {{\theta }_{2}}\cos \omega + \sin {{\theta }_{2}}\sin \omega } \right). \\ \end{gathered} $

И, проводя аналогичные (6) преобразования, запишем относительно $\cos {{\theta }_{2}}$ квадратное уравнение:

$\begin{gathered} \left( {{{e}^{2}} + {{\xi }^{2}} + 2e\xi \sin \left( {\alpha - {{\nu }_{S}} + \omega } \right)} \right){{\cos }^{2}}{{\theta }_{2}} + \\ + \,\,2\left( {e\cos \omega + \xi \sin \left( {\alpha - {{\nu }_{S}}} \right)} \right)\cos {{\theta }_{2}} + \\ + \,\,1 - {{\left( {\xi \cos \left( {\alpha - {{\nu }_{S}}} \right) + e\sin \omega } \right)}^{2}} = 0. \\ \end{gathered} $

Разрешив которое, получим:

(10)

$\cos {{\theta }_{2}} = \frac{{ - {{\psi }_{2}} \pm {{\varphi }_{2}}\sqrt {\psi _{2}^{2} + \varphi _{2}^{2} - 1} }}{{\psi _{2}^{2} + \varphi _{2}^{2}}},$

и, соответственно:

(11)

$\sin {{\theta }_{2}} = \sqrt {1 - {{{\cos }}^{2}}{{\theta }_{2}}} = \frac{{{{\varphi }_{2}} \pm {{\psi }_{2}}\sqrt {\psi _{2}^{2} + \varphi _{2}^{2} - 1} }}{{\psi _{2}^{2} + \varphi _{2}^{2}}},$

где ${{\psi }_{2}} = e\cos \omega + \xi \sin \left( {\alpha - {{\nu }_{S}}} \right),$ ${{\varphi }_{2}} = e\sin \omega - $ ‒ ξcos(α – ν_S).

Знак в (10) и (11) берется согласованно, из условия попадания спутника в зону тени: ${{\theta }_{2}} - {{\nu }_{S}} \in \left[ {\frac{\pi }{2},\frac{{3\pi }}{2}} \right]$.

Обратим внимание, что при выполнении какого-либо из условий: $\psi _{1}^{2} + \varphi _{1}^{2} < 1$ или $\psi _{2}^{2} + \varphi _{2}^{2} < 1$ спутник в земную тень не заходит.

Заметим, что цилиндрическая земная тень является частным случаем конической тени, если в выражениях (7), (8) и (10), (11) положить $\alpha \to 0$.

ВРЕМЯ НАХОЖДЕНИЯ В ТЕНИ

Как известно, интеграл площадей в полярной системе координат имеет вид:

(12)

${{r}^{2}}\frac{{d\theta }}{{dt}} = \sigma ,$

где $\sigma $ – константа площади, имеющая следующее выражение через период вращения спутника $T$, а также большую $a$ и малую $b$ полуоси эллиптической орбиты спутника:

(13)

$\sigma = \frac{{2\pi }}{T}ab.$

Разделив переменные в (12) и проинтегрировав по интервалу прохождения полярного угла в тени, будем иметь:

$\begin{gathered} \int\limits_{{{t}_{1}}}^{{{t}_{2}}} {dt} = \int\limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} {\frac{{{{r}^{2}}}}{\sigma }d\theta } = \frac{{{{{\left( {a\left( {1 - {{e}^{2}}} \right)} \right)}}^{2}}}}{\sigma }\,\, \cdot \\ \cdot \,\,\,\int\limits_{{{\theta }_{1}}}^{{{\theta }_{2}}} {\frac{{d\theta }}{{{{{\left( {1 + e\cos \left( {\theta - \omega } \right)} \right)}}^{2}}}}} . \\ \end{gathered} $

Используя (13), получаем:

(14)

$\begin{gathered} \tau \left( {{{\theta }_{1}},{{\theta }_{2}},\omega } \right) = {{t}_{2}} - {{t}_{1}} = \sqrt {\frac{{{{a}^{3}}}}{{f{{m}_{E}}}}} \,\, \cdot \\ \cdot \,\,\left( {2{\text{arctg}}\left( {\sqrt {\frac{{1 - e}}{{1 + e}}} \left( {\frac{{\sin \left( {\theta - \omega } \right)}}{{1 + \cos \left( {\theta - \omega } \right)}}} \right)} \right)} \right. - \\ \left. { - \,\,\frac{{e\sqrt {1 - {{e}^{2}}} \sin \left( {\theta - \omega } \right)}}{{1 + e\cos \left( {\theta - \omega } \right)}}} \right)_{{{{\theta }_{1}}}}^{{{{\theta }_{2}}}}, \\ \end{gathered} $

где $f$ – гравитационная постоянная, ${{m}_{E}}$ – масса Земли, $\tau = \tau \left( {{{\theta }_{1}},{{\theta }_{2}},\omega } \right)$ – время пребывания спутника в земной тени за один виток, а ${{\theta }_{1}}$ и ${{\theta }_{2}}$ определяются из (7), (8), (10), (11).

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ

Для оценки влияния земной тени на спутник определим среднее относительное время пребывания спутника в зоне земной тени на временном промежутке, равном солнечному году ${{T}_{S}}$, принимая, что за время транзита спутника по зоне тени, истинная аномалия Солнца ${{\nu }_{S}}$ изменяется на малую величину. Выпишем выражение для центра зоны тени:

(15)

$\nu \left( t \right) = {{\nu }_{S}}\left( t \right) + \pi ,$

где $\nu $ – истинная аномалия орбиты спутника.

Будем искать моменты времени $t$, удовлетворяющие соотношению (15). Для численного решения возьмем шаг в 1 секунду. На каждом шаге, положив ${{t}_{0}} = 0$, будем вычислять средние аномалии спутника $M$ и Солнца ${{M}_{S}}$:

$M = {{M}_{0}} + n\left( {t - {{t}_{0}}} \right),\,\,\,\,{{M}_{S}} = {{M}_{{S0}}} + {{n}_{S}}\left( {t - {{t}_{0}}} \right),$

здесь $n$, ${{n}_{S}}$ – среднее движение спутника и Солнца соответственно. Для простоты ${{M}_{0}}$ и ${{M}_{{S0}}}$ (соответственно, средние аномалии на эпоху ${{t}_{0}}$ для спутника и для Солнца) положены равными нулю. Далее, решив уравнения Кеплера, определим эксцентрические аномалии спутника $E$ и Солнца ${{E}_{S}}$: $E - e\sin E = M,$ ${{E}_{S}} - {{e}_{S}}\sin {{E}_{S}} = {{M}_{S}}$.

Для решения используем известное соотношение [11], где ${{J}_{k}}\left( x \right)$ – функция Бесселя:

$E = M + 2\sum\limits_{k = 1}^\infty {\frac{{{{J}_{k}}\left( {ke} \right)}}{k}} \sin \left( {kM} \right).$

Подставим эксцентрические аномалии в выражения:

${\text{tg}}\frac{\nu }{2} = \sqrt {\frac{{1 + e}}{{1 - e}}} {\text{tg}}\frac{E}{2},\,\,\,\,{\text{tg}}\frac{{{{\nu }_{S}}}}{2} = \sqrt {\frac{{1 + {{e}_{S}}}}{{1 - {{e}_{S}}}}} {\text{tg}}\frac{{{{E}_{S}}}}{2},$

и получим истинные аномалии $\nu $, ${{\nu }_{S}}$. Подставив их в (15), определим искомые моменты времени ${{t}^{{\left( 1 \right)}}}, \ldots ,{{t}^{{\left( N \right)}}}$. Тогда относительное время пребывания спутника в земной тени $\hat {t}$:

$\hat {t}\left( {e,a,\omega } \right) = \frac{1}{{{{T}_{S}}}}\sum\limits_{i = 1}^N {\tau \left( {{{\theta }_{1}}\left( {\nu _{S}^{{\left( i \right)}}} \right),{{\theta }_{2}}\left( {\nu _{S}^{{\left( i \right)}}} \right),\omega } \right)} ,$

где $\nu _{S}^{{\left( i \right)}} = {{\nu }_{S}}\left( {{{t}^{{\left( i \right)}}}} \right)$. Однако, как показали расчеты, среднее время пребывания в земной тени существенно зависит от аргумента перицентра спутника $\omega $. Для компенсации этой зависимости следует вычислять среднее значение и по $\omega $:

(16)

$\bar {t}\left( {e,a} \right) = \frac{1}{{{{T}_{S}}}}\sum\limits_{i = 1}^N {\frac{1}{L}\sum\limits_{j = 1}^L {\tau \left( {{{\theta }_{1}}\left( {\nu _{S}^{{\left( i \right)}}} \right),{{\theta }_{2}}\left( {\nu _{S}^{{\left( i \right)}}} \right),{{\omega }_{j}}} \right)} } ,$

где $L$ – количество рассматриваемых значений аргумента перицентра спутника $\omega $.

Ввиду того, что выражение (14) содержит разрывы второго рода, при попадании ${{\theta }_{1}}$ и ${{\theta }_{2}}$ на разные ветви, всякий раз в вычислительной процедуре были сделаны переходы к следующей ветви.

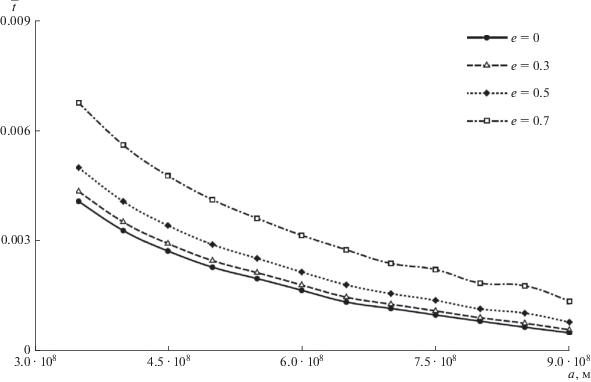
Используя (16), было проведено численное моделирование со следующими параметрами: $a \in \left\{ {3.5 \cdot {{{10}}^{8}},4 \cdot {{{10}}^{8}}, \ldots ,9 \cdot {{{10}}^{8}}} \right\}$ м, $e \in \left\{ {0,0.3,0.5,0.7} \right\}$, $\omega \in \left\{ {0,{\pi \mathord{\left/ {\vphantom {\pi 6}} \right. \kern-0em} 6}, \ldots ,{{11\pi } \mathord{\left/ {\vphantom {{11\pi } 6}} \right. \kern-0em} 6}} \right\}$. Результаты представлены на рис. 3, рис. 4 и рис. 5.

Рис. 3.

Случай конической тени.

Рис. 4.

Случай цилиндрической тени.

Рис. 5.

Относительная погрешность.

Как можно видеть на рис. 3, увеличение большой полуоси орбиты спутника $a$ приводит к уменьшению среднего времени нахождения в земной тени. Так, если на внутренней границе внешней сферы гравитационного влияния, при $a = 3.5 \cdot {{10}^{8}}$ м, спутник находится в тени от 0.4% (при $e = 0$) до 0.62% (при $e = 0.7$) за виток, то на внешней границе сферы, при $a = 9 \cdot {{10}^{8}}$ м, всего от 0.05% ($e = 0$) до 0.14% ($e = 0.7$). Также заметно воздействие эксцентриситета $e$: его увеличение приводит к увеличению среднего времени нахождения спутника в тени $\bar {t}$, хотя, с приближением к внешней границе сферы гравитационного влияния Земли, это воздействие уменьшается.

Таким образом, максимальное значение относительного времени пребывания спутника в области земной тени в случае внешней сферы гравитационного влияния Земли составляет 0.62% (при $e = 0.7$, $a = 3.5 \cdot {{10}^{8}}$ м), что позволяет не учитывать земную тень при проведении качественных исследований в ограниченной задаче трех [9] и четырех [10] тел.

При расчете тем же методом цилиндрической модели тени (при $\alpha = 0$) рис. 4, сохраняется характер зависимости $\bar {t}$ от большой полуоси $a$: на внутренней границе сферы, при $a = 3.5 \cdot {{10}^{8}}$ м, спутник находится в тени от 0.55% (при $e = 0$) до 0.82% (при $e = 0.7$) за виток, на внешней границе, при $a = 9 \cdot {{10}^{8}}$ м, от 0.15% ($e = 0$) до 0.23% ($e = 0.7$). Характер зависимости от эксцентриситета также сохраняется.

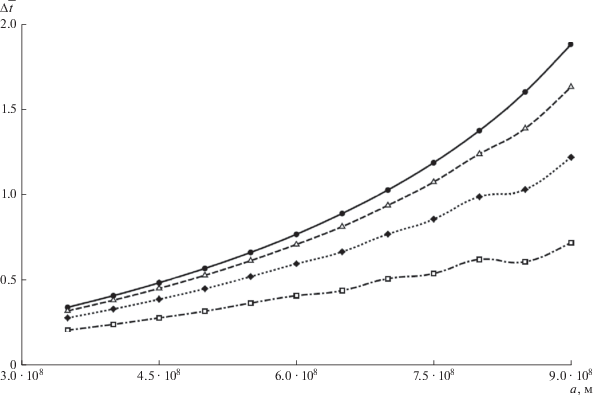
При сравнении конической и цилиндрической моделей тени (рис. 5) можно заметить, что если вблизи с внутренней границей внешней сферы гравитационного влияния Земли относительная погрешность не превышает 50%, то с ростом большой полуоси орбиты погрешность возрастает от 71% при $e = 0.7$, до 187% при $e = 0$. Таким образом, погрешность цилиндрической модели невелика во внутренней сфере гравитационного влияния Земли, но при переходе во внешнюю сферу коническая модель на наш взгляд предпочтительней.

ЗАКЛЮЧЕНИЕ

Исследовано влияние зоны земной тени орбиты спутников, находящиеся в плоскости эклиптики во внешней сфере гравитационного влияния Земли. Были найдены границы конусной тени и точки ее пересечения с эллиптической орбитой спутника. В частности установлено, что точки пересечения в случае цилиндрической тени являются частным случаем конусной. Было выведено выражение для относительного времени пребывания спутника в зоне земной тени.

В результате численного моделирования было установлено, что увеличение большой полуоси орбиты спутника $a$, ведет к уменьшению среднего времени нахождения в земной тени. Также установлено влияние эксцентриситета $e$: его увеличение приводит к увеличению среднего времени нахождения спутника в тени, хотя с приближением к внешней границе сферы гравитационного влияния Земли влияние уменьшается.

Максимальное значение относительного времени пребывания спутника в области земной тени в случае внешней сферы гравитационного влияния Земли составляет 0.62% (при $e = 0.7$), что позволяет не учитывать земную тень при проведении качественных исследований.

Сравнение с цилиндрической моделью тени показало, что во внутренней сфере гравитационного влияния Земли разница между конусной и цилиндрической моделью тени невелика, однако, с увеличением большой полуоси орбиты $a$, цилиндрическая модель тени приводит к большей погрешности, и в этом случае должна использоваться уже коническая модель.

В настоящий момент, в космонавтике актуальны также случаи анализа тени от сильно несферических тел: тень от ядер комет и астероидов, тень от элементов космического мусора и т.д. Все эти случаи – тема наших дальнейших исследований.

Автор признателен П.С. Красильникову за ценные замечания и обсуждения.

Исследования выполнены в Московском авиационном институте при поддержке гранта РФФИ № 18-01-00820 А.

Список литературы

Аксенов Е.П. Теория движения искусственных спутников Земли. М.: Наука, 1977.
Musen P. The Influence of the Solar Radiation Pressure on the Motion of an Artifical Satellite // J. Geophys. Res. 1960. V. 65. № 5. P. 1391–1396.
Parkinson R.W., Jones H.M., Shapiro I.I. Effects of Solar Radiation Pressure on Earth Satellite Orbits // Science. 1960. V. 131. P. 920–921.
Kozai Y. Effect of solar radiation pressure on the motion of an artificial satellite // Smithsonian Astrophys. Obs. Special Rept. 1961. V. 56. P. 25–34.
Ferraz Mello S. Analytical study of the Earth’s shadowing effects on satellite orbits // Celestial Mechanics. 1972. V. 5. P. 80–101.
Лидов М.Л. Вековые эффекты эволюции орбит под влиянием светового давления // Космич. исслед. 1969. Т. 7. № 4. С. 467–484.
Лидов М.Л., Иванова Е.Я. Метод учета сил светового давления при полу аналитическом расчете движения спутников / Математическое обеспечение космических экспериментов. М.: Наука, 1978. С. 149–193.
Вашковьяк С.Н. Изменение орбит спутников-баллонов под действием светового излучения // Астрономический журн. 1976. Т. 53. С. 1085–1094.
Доброславский А.В., Красильников П.С. Об эволюции движений спутника-баллона в плоской ограниченной задаче трех тел с учетом светового давления // Письма в астрономический журнал. 2018. Т. 44. № 8–9. С. 618–630.
Доброславский А.В., Красильников П.С. Об эволюции движений спутника-баллона в плоской ограниченной планетной задаче четырех тел с учетом светового давления // Прикладная математика и механика. 2020. Т. 84. № 1. С. 26–43.
Мюррей К., Дермотт С. Динамика солнечной системы. М.: Физматлит, 2010.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал