Космические исследования, 2021, T. 59, № 3, стр. 255-264

Использование функций Ляпунова для вычисления локально-оптимального управления вектором тяги при межорбитальном перелете с малой тягой

Р. В. Ельников^*

Научно-исследовательский институт прикладной механики и электродинамики Московского авиационного института (национального исследовательского университета)
Москва, Россия

^* E-mail: elnikov_rv@mail.ru

Поступила в редакцию 23.06.2020
После доработки 19.10.2020
Принята к публикации 10.12.2020

DOI: 10.31857/S0023420621030043

Полный текст (PDF)

Аннотация

В статье представлена методика локально-оптимального управления вектором тяги электроракетной двигательной установки (ЭРДУ) КА, осуществляющего многовитковый межорбитальный переход с начальной эллиптической орбиты на геостационарную орбиту (ГСО). Управлением являются временные зависимости углов, характеризующих ориентацию вектора тяги ЭРДУ в пространстве. При этом предполагается, что ЭРДУ постоянно включена. Предлагаемый алгоритм управления относится к классу алгоритмов управления с обратной связью и базируется на использовании функций Ляпунова. Приведены численные примеры, характеризующие работоспособность предлагаемой методики управления. Значительное внимание в статье уделено сравнению данных решений с оптимальными решениями, полученными в рамках формализма принципа максимума.

ВВЕДЕНИЕ

Электроракетные двигательные установки (ЭРДУ) в настоящее время достаточно широко используются на борту КА различного назначения: от аппаратов, работающих на низких околоземных орбитах, до автоматических межпланетных станций. Такие двигательные установки используются как для коррекции траектории, так и в качестве маршевых двигательных установок.

Благодаря высоким значениям удельного импульса тяги, которым обладают ЭРДУ, они позволяют обеспечить существенную экономию рабочего тела (топлива) на борту КА. В силу этого, интерес к использованию таких двигательных установок возник практически в самом начале космической эры. Исследованиям в области анализа траекторий движения КА с ЭРДУ посвящено большое число работ, начало которым положено в середине прошлого века [1–12].

Большая часть этих работ посвящена задачам нахождения оптимального (или квазиоптимального) управления по разомкнутому контуру. Такой подход к нахождению управления вполне правомерен для задач проектирования траекторий движения КА.

Вместе с тем, для реализации управления на борту КА должны быть разработаны алгоритмы управления, которые, в соответствии с терминологией теории автоматического регулирования, должны быть отнесены к классу алгоритмов управления с обратной связью. Впрочем, такие подходы также могут применяться и для задач проектирования траекторий. По-видимому, один из наиболее эффективных подходов к синтезу управления с обратной связью представлен в работах [13, 14].

Идея использования функций Ляпунова для нахождения законов управления вектором тяги КА с ЭРДУ также является достаточно плодотворной и была использована большим числом авторов [15–20].

Основным достоинством рассматриваемого в данной работе алгоритма управления является его простота. Для работы предлагаемого алгоритма не требуется больших вычислительных ресурсов и при необходимости он может быть реализован на борту КА.

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ КА

Движение КА рассматривается в невращающейся геоцентрической экваториальной системе координат (ГЭСК), начало которой расположено в центре масс Земли, а оси коллинеарны осям Международной системы астрономических координат ICRS (International Celestial Reference System). Для расчета возмущений от нецентральности гравитационного поля Земли используется Международная земная система координат ITRS (International Terrestrial Reference System).

Система уравнений движения КА в ГЭСК может быть представлена в виде:

(1)

$\begin{gathered} \frac{{{{d}^{2}}r}}{{d{{t}^{2}}}} = - \frac{\mu }{{{{r}^{3}}}}r + {\mathbf{Q}}\frac{{\partial R}}{{\partial {{r}_{g}}}} + {\mathbf{a}} + \frac{{\delta P}}{m}{{{\mathbf{e}}}_{p}}; \hfill \\ \frac{{dm}}{{dt}} = - \frac{{\delta P}}{w}; \hfill \\ \end{gathered} $

где $r$ – вектор положения КА, t – время; μ – гравитационный параметр Земли, P – величина реактивной тяги ЭРДУ, $\delta $ – функция тяги ($\delta = 1$ при включенной ЭРДУ и $\delta = 0$ – при выключенной), m – масса КА, ${{{\mathbf{e}}}_{p}}$ – орт вектора тяги ЭРДУ, w – эффективная скорость истечения ЭРДУ, ${\mathbf{Q}}$ – матрица перехода из системы координат ITRS в ICRS, ${{r}_{g}} = {{{\mathbf{Q}}}^{T}}r$ – вектор положения КА в системе координат ITRS, R – возмущающая функция, обусловленная нецентральностью гравитационного поля Земли, a – возмущающие ускорения от притяжения Луны и Солнца.

Возмущающая функция, обусловленная нецентральностью гравитационного поля Земли, рассматривается в следующем виде:

$\begin{gathered} R = \frac{\mu }{r} \cdot \left[ {\sum\limits_{n = 2}^N {{{c}_{{n0}}}{{{\left( {\frac{{{{r}_{{\text{E}}}}}}{r}} \right)}}^{n}}P_{n}^{0}} } \right. + \\ \left. { + \,\,\sum\limits_{n = 2}^M {{{{\left( {\frac{{{{r}_{{\text{E}}}}}}{r}} \right)}}^{n}}\sum\limits_{m = 1}^n {\left( {{{c}_{{nm}}}{{C}_{m}} + {{d}_{{nm}}}{{S}_{m}}} \right)P_{n}^{m}} } } \right], \\ \end{gathered} $

где r_E – экваториальный радиус Земли, c_n0 – коэффициенты при зональных гармониках, c_nm и d_nm – ненормированные коэффициенты при тессеральных и секториальных гармониках, $P_{n}^{m} = {{d}^{m}}{{P}_{n}}{{\left( {\sin \varphi } \right)} \mathord{\left/ {\vphantom {{\left( {\sin \varphi } \right)} {d{{{\left( {\sin \varphi } \right)}}^{m}}}}} \right. \kern-0em} {d{{{\left( {\sin \varphi } \right)}}^{m}}}}$ – m-я производная полинома Лежандра ${{P}_{n}}\left( {\sin \varphi } \right)$, ${{C}_{m}} = {{\cos }^{m}}\varphi \cdot \cos m\lambda $, ${{S}_{m}} = {{\cos }^{m}}\varphi \cdot \sin m\lambda $, φ – геодезическая широта подспутниковой точки, λ – долгота подспутниковой точки, N, M – порядок и степень используемой модели гравитационного поля (в работе используется модель EGM96, N = M = 70).

Возмущающие ускорения от притяжения Луны и Солнца:

${\mathbf{a}} = \sum\limits_{j = 1}^2 {{{\mu }_{j}} \cdot \left( {\frac{{{{{\mathbf{r}}}_{j}} - {\mathbf{r}}}}{{{{{\left| {{{{\mathbf{r}}}_{j}} - {\mathbf{r}}} \right|}}^{3}}}} - \frac{{{{{\mathbf{r}}}_{j}}}}{{r_{j}^{{\mathbf{3}}}}}} \right)} {\kern 1pt} {\kern 1pt} ,$

где ${{\mu }_{j}}$− гравитационный параметр j-го небесного тела (индексом 1 обозначена Луна, индексом 2 − Солнце), ${{{\mathbf{r}}}_{j}}$ – радиус-вектор j-го небесного тела в ГЭСК.

Для вычисления положения небесных тел ${{{\mathbf{r}}}_{j}}$ используется эфемеридное программно-математическое обеспечение DE405 [21].

СИНТЕЗ УПРАВЛЕНИЯ С ОБРАТНОЙ СВЯЗЬЮ

Известна система уравнений возмущенного движения КА в оскулирующих классических кеплеровых элементах [22]. При этом уравнения для фокального параметра орбиты, эксцентриситета и наклонения можно представить следующим образом:

(2)

$\begin{gathered} \frac{{dp}}{{dt}} = 2p\sqrt {\frac{p}{\mu }} \frac{1}{{1 + e\cos \upsilon }}\left( {T + {{f}_{T}}} \right); \\ \frac{{de}}{{dt}} = \sqrt {\frac{p}{\mu }} \left( {\sin \upsilon \cdot \left( {S + {{f}_{S}}} \right) + \frac{{^{{}}}}{{}}} \right. \\ \left. { + \,\,\frac{{e{{{\cos }}^{2}}\upsilon + 2\cos \upsilon + e}}{{1 + e\cos \upsilon }}\left( {T + {{f}_{T}}} \right)} \right); \\ \frac{{di}}{{dt}} = \sqrt {\frac{p}{\mu }} \frac{{\cos u}}{{1 + e\cos \upsilon }}\left( {W + {{f}_{W}}} \right); \\ \end{gathered} $

где $p$ − фокальный параметр, $e$ − эксцентриситет, $i$ − наклонение, $\upsilon $ − истинная аномалия, $u$ − аргумент широты, ${{f}_{S}}$,${{f}_{T}}$,${{f}_{W}}$ − соответственно радиальная, трансверсальная и бинормальная проекция реактивного ускорения, действующего на КА, S, T, W − соответственно радиальная, трансверсальная и бинормальная проекция суммарного возмущающего ускорения от иных возмущающих траекторию факторов (нецентральности гравитационного поля Земли, лунно-солнечных возмущений и т.д.).

Предполагая, что вектор тяги ЭРДУ направлен по продольной оси КА, можно записать: ${{f}_{S}} = f\sin \theta ;$ ${{f}_{T}} = f\cos \theta \cos \psi ;$ ${{f}_{W}} = f\cos \theta \sin \psi ,$ где $f = {{\delta P} \mathord{\left/ {\vphantom {{\delta P} m}} \right. \kern-0em} m}$ − модуль реактивного ускорения, $\theta $ − угол тангажа, $\psi $ − угол рыскания.

Движение будем рассматривать без выключения ЭРДУ, т.е. примем, что $\delta \equiv 1$.

Задача межорбитального перелета формулируется следующим образом: требуется найти такие функции $\theta = \theta \left( t \right);\,\;\;\psi = \psi \left( t \right)$, чтобы перевести КА из начального состояния: ${{p}_{0}} = p\left( {{{t}_{0}}} \right);$ ${{e}_{0}} = e\left( {{{t}_{0}}} \right);$ ${{i}_{0}} = i\left( {{{t}_{0}}} \right);$ в конечное: ${{p}_{f}} = p\left( {{{t}_{f}}} \right);$ ${{e}_{f}} = e\left( {{{t}_{f}}} \right);$ ${{i}_{f}} = i\left( {{{t}_{f}}} \right).$

В рассматриваемом нами случае перехода на ГСО: ${{p}_{f}}$ = 42164 км; ${{e}_{f}}$= 0; ${{i}_{f}}$ = 0.

Далее введем в рассмотрение функцию Ляпунова в следующем виде:

(3)

$L\left( t \right) = {{k}_{1}}\Delta {{p}^{2}} + {{k}_{2}}\Delta {{e}^{2}} + {{k}_{3}}\Delta {{i}^{2}};$

где ${{k}_{1}};\;{{k}_{2}};\;{{k}_{2}}$ − некоторые постоянные коэффициенты, $\Delta p;\;\;\Delta e;\;\;\Delta i$ − текущие обезразмеренные значения невязок по фокальному параметру, эксцентриситету и наклонению (в данной точке оскулирующей перелетной траектории): $\Delta p\left( t \right) = p\left( t \right) - {{p}_{f}};$ $\Delta e\left( t \right) = e\left( t \right) - {{e}_{f}};$ $\Delta i\left( t \right) = i\left( t \right) - {{i}_{f}}.$

Рассмотрим производную от функции Ляпунова (3) по времени:

(4)

$\begin{gathered} g\left( {\theta ,\psi } \right) = \frac{{dL}}{{dt}} = \\ = 2\left( {{{k}_{1}}\Delta p\frac{{d\Delta p}}{{dt}} + {{k}_{2}}\Delta e\frac{{d\Delta e}}{{dt}} + {{k}_{3}}\Delta i\frac{{d\Delta i}}{{dt}}} \right). \\ \end{gathered} $

Из необходимых и достаточных условий минимума дважды дифференцируемой по $\theta $ и $\psi $ функции (4), можно получить закон управления вектором реактивного ускорения, обеспечивающий в каждый момент времени минимум производной функции Ляпунова:

(5)

$\begin{gathered} {{f}_{S}} = f\frac{{ - {{\lambda }_{S}}}}{{\sqrt {\lambda _{T}^{2} + \lambda _{S}^{2} + \lambda _{W}^{2}} }};\;\,\,\,\,{{f}_{T}} = f\frac{{ - {{\lambda }_{T}}}}{{\sqrt {\lambda _{T}^{2} + \lambda _{S}^{2} + \lambda _{W}^{2}} }}; \\ {{f}_{W}} = f\frac{{ - {{\lambda }_{W}}}}{{\sqrt {\lambda _{T}^{2} + \lambda _{S}^{2} + \lambda _{W}^{2}} }}; \\ \end{gathered} $

где

$\begin{gathered} {{\lambda }_{S}} = {{k}_{2}}\Delta e \cdot \sin \upsilon \cdot \left( {1 + \tilde {e}\cos \upsilon } \right); \\ {{\lambda }_{T}} = 2{{k}_{1}}\Delta p \cdot \tilde {p} + {{k}_{2}}\Delta e\left[ {\tilde {e}\left( {{{{\cos }}^{2}}\upsilon + 1} \right) + 2\cos \upsilon } \right]; \\ {{\lambda }_{W}} = {{k}_{3}}\Delta i \cdot \cos u;\,\,\,\tilde {p} = \Delta p + {{p}_{f}};\,\,\,\tilde {e} = \Delta e + {{e}_{f}}. \\ \end{gathered} $

Предполагая, что значение фокального параметра начальной орбиты отлично от требуемого конечного значения, а сама начальная орбита является эллиптической и имеющей ненулевое наклонение, коэффициенты, входящие в (3), могут быть введены следующим образом: ${{k}_{1}} = {1 \mathord{\left/ {\vphantom {1 {{{{\left( {{{p}_{f}} - {{p}_{0}}} \right)}}^{2}}}}} \right. \kern-0em} {{{{\left( {{{p}_{f}} - {{p}_{0}}} \right)}}^{2}}}};$ ${{k}_{2}} = {{{{k}_{e}}} \mathord{\left/ {\vphantom {{{{k}_{e}}} {e_{0}^{2}}}} \right. \kern-0em} {e_{0}^{2}}};$ ${{k}_{3}} = {{{{k}_{i}}} \mathord{\left/ {\vphantom {{{{k}_{i}}} {i_{0}^{2}}}} \right. \kern-0em} {i_{0}^{2}}}$ где ${{k}_{e}},\;{{k}_{i}}$ − постоянные коэффициенты, характеризующие вес невязки по эксцентриситету и наклонению соответственно.

Не трудно найти компоненты орта тяги в ГЭСК:

${{{\mathbf{e}}}_{p}} = \left( {\begin{array}{*{20}{c}} {{{r}_{х}}}&{{{n}_{x}}}&{{{b}_{x}}} \\ {{{r}_{y}}}&{{{n}_{y}}}&{{{b}_{y}}} \\ {{{r}_{z}}}&{{{n}_{z}}}&{{{b}_{z}}} \end{array}} \right) \times \left( {\begin{array}{*{20}{c}} {{{f}_{S}}} \\ {{{f}_{T}}} \\ {{{f}_{W}}} \end{array}} \right);$

где ${{\left( {\begin{array}{*{20}{c}} {{{r}_{x}}}&{{{r}_{y}}}&{{{r}_{z}}} \end{array}} \right)}^{T}} = {{r}_{0}};$ ${{\left( {\begin{array}{*{20}{c}} {{{n}_{x}}}&{{{n}_{y}}}&{{{n}_{z}}} \end{array}} \right)}^{T}} = {{n}_{0}};$ ${{\left( {\begin{array}{*{20}{c}} {{{b}_{x}}}&{{{b}_{y}}}&{{{b}_{z}}} \end{array}} \right)}^{T}} = $ $ = {{b}_{0}}$ – компоненты ортов радиали, трансверсали и бинормали в ГЭСК: ${{r}_{0}} = \frac{r}{r};$ ${{n}_{0}} = {{b}_{0}} \times {{r}_{0}};$ ${{b}_{0}} = \frac{{r \times \dot {r}}}{{\left| {r \times \dot {r}} \right|}}.$

Длительность межорбитального перехода (${{t}_{f}}$) определяется интервалом времени, в течение которого все параметры оскулирующей перелетной траектории принимают требуемые значения на правом конце. При этом необходимо отметить, что элементы орбиты могут приходить к своим требуемым значениям не одновременно.

Путем варьирования весовых коэффициентов ${{k}_{e}},\;{{k}_{i}}$ возможно получать различные решения задачи межорбитального перехода. Все они будут отличаться длительностью перелета, которое, таким образом, может рассматриваться как некая функция от выбираемых весовых коэффициентов:

(6)

${{t}_{f}} = {{t}_{f}}\left( {{{k}_{e}},{{k}_{i}}} \right).$

Выполняя численную минимизацию (6) в пространстве весовых коэффициентов, можно добиться уменьшения длительности транспортной операции перехода и обеспечить одновременное удовлетворение всех краевых условий.

При этом необходимо отметить, что точность удовлетворения краевых условий на правом конце траектории, к сожалению, зависит от самих значений выбираемых весовых коэффициентов. Это приводит к тому, что в процессе численного поиска минимума функции (6) появляются решения, не удовлетворяющие необходимой точности. Эти решения необходимо отсеивать. В результате этого, функция (6) имеет области, где она, фактически, не определена. Поэтому для нахождения ее минимума весьма желательно использовать какие-либо неградиентные методы поиска, например представленные в работах [23, 24].

ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ

Работоспособность представленного подхода будет проиллюстрирована на нескольких численных примерах. Но при этом возникает закономерный вопрос: на сколько полученные решения близки к оптимальным, например, по критерию длительности перелета?

Для ответа этот вопрос и нахождения оптимальных по быстродействию траекторий перехода на ГСО использовался непрямой метод оптимизации траекторий движения КА с ЭРДУ, основанный на применении формализма принципа максимума Понтрягина [25], позволяющий свести задачу нахождения оптимального управления к краевой задаче для системы обыкновенных дифференциальных уравнений.

На первом этапе, движение КА с ЭРДУ будем анализировать в центральном ньютоновском поле тяготения Земли. В данном случае удобно использовать запись уравнений движения в равноденственных элементах, не имеющих особенностей в окрестности нулевого эксцентриситета и наклонения:

(7)

$\begin{gathered} \frac{{dA}}{{dt}} = \frac{{2\sqrt {{{A}^{3}}} }}{{\sqrt {\gamma \cdot \mu } }}\left[ {\xi {{f}_{T}} + \left( {{{g}_{1}}\sin F - {{g}_{2}}\cos F} \right){{f}_{S}}} \right]; \\ \frac{{d{{g}_{1}}}}{{dt}} = \frac{1}{\xi }\sqrt {\frac{{A \cdot \gamma }}{\mu }} \times \\ \times \,\,\left\{ {\left[ {\left( {1 + \xi } \right)\cos F + {{g}_{1}}} \right]{{f}_{T}} + \xi \sin F \cdot {{f}_{S}} + {{g}_{2}}\eta {{f}_{W}}} \right\}; \\ \frac{{d{{g}_{2}}}}{{dt}} = \frac{1}{\xi }\sqrt {\frac{{A \cdot \gamma }}{\mu }} \times \\ \times \,\,\left\{ {\left[ {\left( {1 + \xi } \right)\sin F + {{g}_{2}}} \right]{{f}_{T}} - \xi \cos F \cdot {{f}_{S}} - {{g}_{1}}\eta {{f}_{W}}} \right\}; \\ \frac{{d{{g}_{3}}}}{{dt}} = - \sqrt {\frac{{A \cdot \gamma }}{\mu }} \frac{{\phi \cos F}}{{2\xi }}{{f}_{W}}; \\ \frac{{d{{g}_{4}}}}{{dt}} = - \sqrt {\frac{{A \cdot \gamma }}{\mu }} \frac{{\phi \sin F}}{{2\xi }}{{f}_{W}}; \\ \frac{{dF}}{{dt}} = \sqrt {\frac{\mu }{{{{{\left( {A \cdot \gamma } \right)}}^{3}}}}} {{\xi }^{2}} - \\ - \,\,\frac{1}{\xi }\sqrt {\frac{{A \cdot \gamma }}{\mu }} \left( {{{g}_{3}}\sin F - {{g}_{4}}\cos F} \right){{f}_{W}}; \\ \frac{{dm}}{{dt}} = - \frac{{\delta P}}{w}; \\ \end{gathered} $

где $A$ − большая полуось оскулирующей перелетной траектории, $F$− истинная долгота КА.

В системе (7) введены следующие обозначения:

$\begin{gathered} \xi = 1 + {{g}_{1}}\cos F + {{g}_{2}}\sin F;\,\,\,\,\eta = {{g}_{3}}\sin F - {{g}_{4}}\cos F; \\ \phi = 1 + g_{3}^{2} + g_{4}^{2};\,\,\,\gamma = 1 - g_{1}^{2} - g_{2}^{2}. \\ \end{gathered} $

Упомянем, что равноденственные переменные связаны с классическими элементами следующим образом:

$\begin{gathered} {{g}_{1}} = e\cos \left( {\omega + \Omega } \right);\,\,\,\,{{g}_{2}} = e\sin \left( {\omega + \Omega } \right); \\ {{g}_{3}} = {\text{tg}}\frac{i}{2} \cdot \cos \Omega ;\,\,\,{{g}_{4}} = {\text{tg}}\frac{i}{2} \cdot \sin \Omega ; \\ F = \Omega + \omega + \upsilon ; \\ \end{gathered} $

где $\omega $ − аргумент перицентра, $\Omega $ − долгота восходящего узла оскулирующей траектории.

КА с начальной массой m₀ требуется перевести из перицентра некоторой начальной эллиптической орбиты, долгота восходящего узла и аргумент перицентра которой нулевые:

$\begin{gathered} A\left( {{{t}_{0}}} \right) = {{A}_{0}};\,\,\,\,{{g}_{1}}\left( {{{t}_{0}}} \right) = {{g}_{{10}}};\,\,\,\,{{g}_{2}}\left( {{{t}_{0}}} \right) = {{g}_{{20}}}; \\ {{g}_{3}}\left( {{{t}_{0}}} \right) = {{g}_{{30}}};\,\,\,{{g}_{4}}\left( {{{t}_{0}}} \right) = {{g}_{{40}}};\,\,\,F\left( {{{t}_{0}}} \right) = 0; \\ \end{gathered} $

на ГСО за минимальное время.

Конечные условия примут вид:

$\begin{gathered} A\left( {{{t}_{f}}} \right) = 42\,164\,\,{\text{км}};\,\,\,\,{{g}_{1}}\left( {{{t}_{f}}} \right) = 0; \\ {{g}_{2}}\left( {{{t}_{f}}} \right) = 0;\,\,\,\,{{g}_{3}}\left( {{{t}_{f}}} \right) = 0;\,\,\,{{g}_{4}}\left( {{{t}_{f}}} \right) = 0. \\ \end{gathered} $

Управление вектором тяги должно обеспечивать минимум времени межорбитального перехода. Таким образом, рассматривается задача минимизации функционала: $J = \int_{{{t}_{0}}}^{{{t}_{f}}} {dt \to \min .} $

В этом случае гамильтониан задачи оптимального управления может быть записан следующим образом:

(8)

$H = - 1 + {{\lambda }_{A}}\frac{{dA}}{{dt}} + {{\lambda }_{F}}\frac{{dF}}{{dt}} + \sum\limits_{j = 1}^4 {{{\lambda }_{j}}} \frac{{d{{g}_{j}}}}{{dt}};$

где ${{\lambda }_{A}}$ − переменная, сопряженная к большой полуоси, ${{\lambda }_{F}}$ − переменная, сопряженная к истинной долготе; ${{\lambda }_{j}}$ (j = 1 … 4) − переменные, сопряженные к равноденственным элементам g₁, …, g₄.

Ориентация вектора реактивного ускорения находится из условия максимума гамильтониана (8):

(9)

$\begin{gathered} {{f}_{T}} = f\frac{{{{b}_{1}}}}{{\sqrt {b_{1}^{2} + b_{2}^{2} + b_{3}^{2}} }};\,\,\,{{f}_{S}} = f\frac{{{{b}_{2}}}}{{\sqrt {b_{1}^{2} + b_{2}^{2} + b_{3}^{2}} }}; \\ {{f}_{W}} = f\frac{{{{b}_{3}}}}{{\sqrt {b_{1}^{2} + b_{2}^{2} + b_{3}^{2}} }}; \\ \end{gathered} $

где:

(10)

$\begin{gathered} {{b}_{1}} = \frac{{2{{\lambda }_{A}}A\xi }}{\gamma } + {{\lambda }_{1}}\left( {\cos F + \frac{{{{g}_{1}} + \cos F}}{\xi }} \right) + \\ + \,\,{{\lambda }_{2}}\left( {\sin F + \frac{{{{g}_{2}} + \sin F}}{\xi }} \right); \\ {{b}_{2}} = \frac{{2{{\lambda }_{A}}A}}{\gamma }\left( {{{g}_{1}}\sin F + {{g}_{2}}\cos F} \right) + \\ + \,\,{{\lambda }_{1}}\sin F - {{\lambda }_{2}}\cos F; \\ {{b}_{3}} = \frac{1}{\gamma }\left[ {\eta \left( {{{\lambda }_{1}}{{g}_{2}} - {{\lambda }_{2}}{{g}_{1}}} \right) - \frac{\phi }{2}\left( {{{\lambda }_{3}}\cos F + {{\lambda }_{4}}\sin F} \right)} \right]. \\ \end{gathered} $

Сопряженные переменные, входящие в закон оптимального управления (9)–(10), могут быть найдены из системы следующего вида:

(11)

$\frac{{d\lambda }}{{dt}} = - \frac{{\partial H}}{{\partial x}};$

где $x = {{\left( {A\;{{g}_{1}}\;{{g}_{2}}\;{{g}_{3}}\;{{g}_{4}}\;F} \right)}^{T}}$ − вектор фазовых переменных, $\lambda = {{\left( {{{\lambda }_{A}}\;{{\lambda }_{1}}\;{{\lambda }_{2}}\;{{\lambda }_{3}}\;{{\lambda }_{4}}\;{{\lambda }_{F}}} \right)}^{T}}$− вектор сопряженных переменных.

Можно показать, что для задачи быстродействия на всей траектории $\delta = 1$, т.е. движение КА осуществляется с постоянно включенной ЭРДУ.

Совместно системы (7) и (11) при подстановке в (7) закона управления (9) образуют систему уравнений оптимального движения КА. Для ее интегрирования необходимо найти вектор сопряженных переменных в начальный момент времени ${{\lambda }_{0}} = \lambda \left( {{{t}_{0}}} \right)$ и время межорбитального перелета ${{t}_{f}}$.

Точка выхода на конечную орбиту не фиксируется, поэтому из условия трансверсальности ${{\lambda }_{F}}\left( {{{t}_{f}}} \right) = 0$. Время межорбитального перехода может быть найдено из условия $H\left( {{{t}_{f}}} \right) = 0$. Таким образом, вектор невязок на правом конце траектории перелета может быть представлен следующим образом:

$\begin{gathered} g(x) = \left[ {A\left( {{{t}_{f}}} \right)} \right. - \\ {{\left. { - A*{{g}_{1}}\left( {{{t}_{f}}} \right){{g}_{2}}\left( {{{t}_{f}}} \right){{g}_{3}}\left( {{{t}_{f}}} \right){{g}_{4}}\left( {{{t}_{f}}} \right){{\lambda }_{F}}\left( {{{t}_{f}}} \right)H\left( {{{t}_{f}}} \right)} \right]}^{T}}; \\ \end{gathered} $

где $A{\text{*}}$ − большая полуось конечной орбиты (ГСО), x − вектор неизвестных параметров: $x = \left( \begin{gathered} \lambda \left( {{{t}_{0}}} \right) \hfill \\ \,\,\,{{t}_{f}} \hfill \\ \end{gathered} \right).$

Таким образом, задача поиска оптимального управления сводится к численному решению системы уравнений следующего вида: $g(x) = 0.$

Для ее решения может быть использован гибридный метод Пауэла (алгоритм HYBRD [26]).

ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ

Работоспособность предлагаемой методики управления на основе применения функций Ляпунова проанализируем на нескольких численных примерах перелета КА с малой тягой на ГСО. Сравним полученные результаты с результатами, найденными в рамках решения задачи оптимального быстродействия. Для обоих вариантов управления движение КА анализировалось в рамках модели центрального ньютоновского поля тяготения Земли.

Для примера рассматривается транспортная система на базе ракеты-носителя (РН) Союз-2-1Б и разгонного блока (РБ) Фрегат. Схема выведения полезной нагрузки на ГСО следующая. РН обеспечивает выведение головного блока на опорную круговую орбиту. Головной блок включает в свой состав РБ, адаптер полезной нагрузки и саму полезную нагрузку − КА, предназначенный для выведения на ГСО. С помощью РБ головной блок переводится на некоторую промежуточную эллиптическую орбиту, аргумент перицентра которой принят равным нулю. На данной орбите происходит отделение РБ вместе с адаптером полезной нагрузки от КА. Дальнейшее выведение КА осуществляется под действием силы тяги ЭРДУ.

Масса головного блока, выводимого на опорную круговую орбиту высотой 200 км и наклонением 51.7°, составляет при запуске с космодрома Восточный 8320 кг (https://www.samspace.ru/ products/launch_vehicles/rn_soyuz_2/ [Дата обращения: 08.06.2020]). Конечная масса РБ составляет 1050 кг, а удельный импульс тяги его маршевой двигательной установки − 333.2 с [27]. Масса адаптера полезной нагрузки принята равной 50 кг. Э-РДУ КА включает в свой состав два холловских стационарных плазменных двигателя СПД-100Д, работающих одновременно. Тяга одного двигателя составляет 90 мН, удельный импульс тяги − 1740 с (https://fakel-russia.com/index.php/ru/produktsiya [Дата обращения: 08.06.2020]).

Варианты промежуточных эллиптических орбит, обеспечивающих различные времена перелета на ГСО, представлены в табл. 1. Оценка массы КА, доставляемого на промежуточную орбиту с помощью РБ, осуществлялась в предположении, что межорбитальный переход является двухимпульсным апсидальным. Величина гравитационных потерь и потерь на управление при реализации первого импульса составляет 2.5%. Второй импульс реализуется идеально.

Таблица 1.

Варианты промежуточных эллиптических орбит

№ п.п.	Высота перицентра, км	Высота апоцентра, км	Наклонение, град	Масса КА на промеж. орбите, кг
1	17 793	62 800	7	1326.414
2	13 543	70 800	8.5	1460.163
3	10 043	73 800	12	1581.836
4	7293	78 800	15.5	1696.044
5	5293	84 800	20	1802.960

Нахождение управления вектором тяги ЭРДУ для межорбитального перехода с указанных промежуточных орбит на ГСО осуществлялось с помощью двух вышеизложенных подходов: управления с обратной связью на основе функций Ляпунова и оптимального управления в рамках принципа максимума Понтрягина.

В табл. 2 представлены результаты решения задач межорбитального перелета в рамках первого подхода. Номера решений в данной таблице соответствуют номерам промежуточных орбит из табл. 1. Выход из интегрирования уравнений движения КА осуществлялся при достижении требуемого значения большой полуоси. Невязки по эксцентриситету и наклонению, реализованные в конечный момент времени, также представлены в табл. 2.

Таблица 2.

Результаты решения задач межорбитального перелета на ГСО при использовании управления с обратной связью на основе функций Ляпунова

№ п.п.	Время перелета на ГСО, сут	Реализованные невязки на правом конце траектории		Весовые коэффициенты функции Ляпунова
№ п.п.	Время перелета на ГСО, сут	по эксцентриситету	по наклонению, град	${{k}_{e}}$	${{k}_{i}}$
1	97.73	0.00327	0.005	1.5173	0.3632
2	125.12	0.00034	0.003	2.6314	0.5424
3	155.11	0.00191	0.000	2.9277	1.8451
4	185.43	0.00177	0.000	2.1535	1.3734
5	213.25	0.00019	0.024	3.0913	1.5251

Оценим на сколько полученные решения близки к оптимальным. В табл. 3 представлены основные результаты расчета участка перехода с промежуточной орбиты на ГСО для двух рассматриваемых подходов. Номера решений в таблице соответствуют номерам промежуточных орбит из табл. 1.

Таблица 3.

Основные результаты расчета участка перехода с промежуточной орбиты на ГСО для двух рассматриваемых подходов

№ п.п.	Управление с использованием функций Ляпунова		Оптимальное управление в рамках принципа максимума Понтрягина
№ п.п.	масса КА на ГСО, кг	длительность перелета, сут	масса КА на ГСО, кг	длительность перелета, сут
1	1237.34	97.73	1239.09	95.81
2	1346.13	125.12	1350.64	120.17
3	1440.47	155.11	1443.00	152.33
4	1527.04	185.43	1530.00	182.18
5	1608.60	213.25	1610.31	211.37

Из анализа табл. 3 можно видеть, что решения, полученные в рамках предложенного подхода, оказываются весьма близкими к оптимальным по длительности перелета и, соответственно, по конечной массе КА. Действительно, длительность перелета на оптимальных решениях всего на 2−4% меньше по сравнению с решениями, полученными с использованием обсуждаемой методики управления на основе функций Ляпунова. Конечная масса КА, доставленного на ГСО, для обоих вариантов управления практически одинакова: различие не превышает 4.51 кг.

Также проанализируем эволюцию основных орбитальных элементов перелетной траектории для случая использования управления с обратной связью на основе функций Ляпунова и для случая оптимального управления. В качестве примера рассмотрим 4-е решение (в табл. 1, 2 и 3 оно выделено курсивом). Длительность перелета на ГСО в этом случае составляет около полугода.

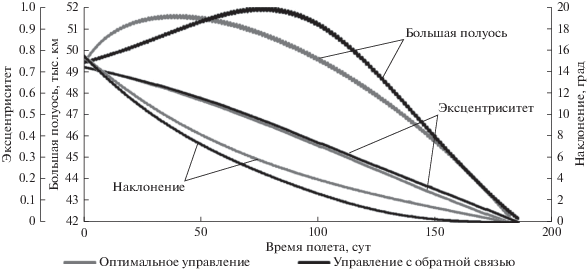
На рис. 1 показаны временные зависимости большой полуоси, эксцентриситета и наклонения оскулирующей перелетной траектории для оптимального управления и случая использования управления с обратной связью на основе функций Ляпунова.

Рис. 1.

Временные зависимости элементов перелетной траектории.

Как видим, характер изменения эксцентриситета и наклонения в целом схож на обоих решениях, наиболее сильно отличается характер изменения большой полуоси орбиты.

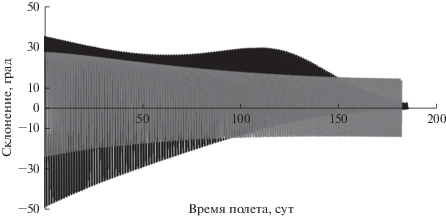
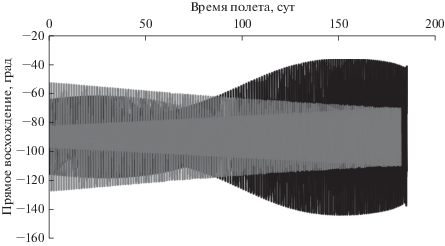
Проанализируем полученное управление для обоих вариантов решений. На рис. 2 и 3 представлены зависимости углов склонения и прямого восхождения вектора тяги ЭРДУ от времени полета в ГЭСК.

Рис. 2.

Зависимости угла склонения вектора тяги ЭРДУ от времени полета.

Рис. 3.

Зависимости углов прямого восхождения вектора тяги ЭРДУ от времени полета.

Изменения углов склонения и прямого восхождения носят колебательный характер на обоих типах решения. Можно заметить, что характер управления на оптимальном решении и в рамках предлагаемого подхода управления различен. Несмотря на это, длительности перелета, как на оптимальных решениях, так и на решениях, соответствующих управлению с обратной связью на основе применения функции Ляпунова, достаточно близки по величине.

ВОЗМУЩЕННОЕ ДВИЖЕНИЕ КА

Одним из достоинств предлагаемого подхода к управлению вектором тяги ЭРДУ является его простота адаптации к случаю возмущенного движения. В заключительной части статьи приведем пример реализации рассматриваемой методики управления в рамках уточненной модели движения (1) с учетом гравитационного воздействия на траекторию перелета от Луны и Солнца, а также нецентральности гравитационного поля Земли.

Сравним решения, полученные в рамках модели центрального поля тяготения Земли и в рамках уточненной модели. Для примера рассмотрим уже анализировавшийся выше вариант межорбитального перелета на ГСО (вариант № 4 из табл. 1, 2 и 3 ).

В случае возмущенного движения необходимо задаться начальным моментом времени для вычисления возмущающих ускорений. В качестве такого момента, т.е. момента времени прохождения перицентра промежуточной орбиты № 4 (см. табл. 1), рассматривается 1.I.2025; 00.00.00 UTC. Весовые коэффициенты ${{k}_{e}},\;{{k}_{i}}$, входящие в закон управления, такие же, как и для случая невозмущенного движения (они представлены в табл. 2).

Анализ возмущенного движения КА показал, что временные зависимости изменения большой полуоси, эксцентриситета и наклонения в процессе перелета практически не отличаются от аналогичных зависимостей для случая движения в центральном поле.

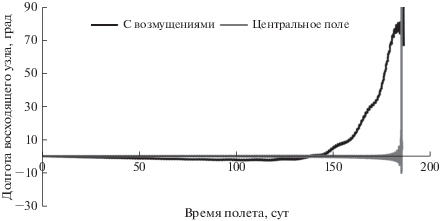
Наиболее значительные отличия наблюдаются в эволюциях долготы восходящего узла и аргумента перицентра (см. рис. 4).

Рис. 4.

Эволюция долготы восходящего узла.

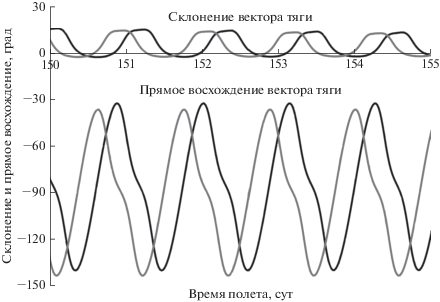
Характер управления на возмущенном и невозмущенном решении также оказывается близким, однако в случае возмущенного движения наблюдается сдвиг по фазе колебаний углов склонения и прямого восхождения вектора тяги ЭРДУ. Этот фазовый сдвиг постепенно увеличивается к концу полета. Для примера, на рис. 5 показан интервал 150–155 сут полета.

Рис. 5.

Зависимости углов склонения и прямого восхождения вектора тяги ЭРДУ от времени полета для случая возмущенного и невозмущенного движения.

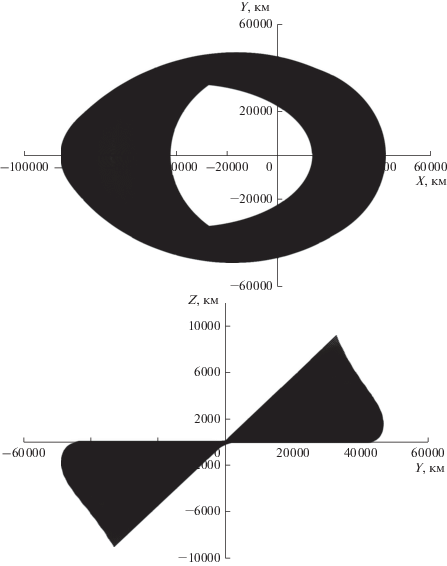
Включение в модель возмущений привело к некоторому увеличению длительности перелета (до 186.82 сут против 185.43 сут перелета в центральном поле). Это привело к некоторому уменьшению конечной массы КА, которое, впрочем, оказывается незначительным. На рис. 6 представлены проекции полученной перелетной траектории в ГЭСК.

Рис. 6.

Проекции перелетной траектории в ГЭСК.

ЗАКЛЮЧЕНИЕ

Итак, в рамках данной работы предложена методика управления вектором тяги КА, осуществляющего межорбитальный переход на ГСО с помощью ЭРДУ. Данная методика управления отличается простотой и базируется на использовании функций Ляпунова. В рамках рассмотренного класса задач межорбитального перехода, она позволяет находить решения, весьма близкие к оптимальным по длительности перелета.

Еще одним достоинством предлагаемого подхода является то, что он с легкостью может быть использован для точных моделей движения КА с различным набором возмущающих факторов.

В связи с тем, что предлагаемый закон управления задается как функция текущего фазового состояния КА, данное управление относится к классу алгоритмов управления с обратной связью, а сам алгоритм не требует больших вычислительных ресурсов и может быть применен на борту КА.

Исследование выполнено за счет гранта Российского научного фонда (проект № 16-19-10429).

Список литературы

Иванов Ю.Н., Шалаев Ю.В. Метод скорейшего спуска в применении к расчету межорбитальных траекторий с двигателями ограниченной мощности // Космич. исслед. 1964. Т. 2. № 3.
Edelbaum T.N. Optimum Power-Limited Orbit Transfer in Strong Gravity Fields // AIAA J. 1965. V. 3. № 5. P. 921–925.
Гродзовский Г.Л., Иванов Ю.Н., Токарев В.В. Механика космического полета. Проблемы оптимизации. М.: Наука, 1975.
Eneev T.M., Egorov V.A., Efimov G.B. et al. Some Methodical Problems of Low Thrust Trajectory Optimization // Keldysh Institute of Applied Mathematics, Russia Academy of Sciences. 1996. Preprint Keld, 1946. № 110. P. 124.
Kechichian J.A. Optimal Low-Earth-Orbit-Geostationary-Earth-Orbit Intermediate Acceleration Orbit Transfer // J. Guidance, Control, and Dynamics. 1997. V. 20. № 4. P. 803–811.
Geffroy S., Epenoy R. Optimal Low-Thrust Transfers with Constraints – Generalization of Averaging Techniques // Astronautica Acta. 1997. V. 41. № 3. P. 133–149.
Kluever C.A., Oleson S.R. A Direct Approach for Computing Near-Optimal Low-Thrust Transfers // AAS/AIAA Astrodynamics Specialist Conference. Sun Valley, Idaho. 1997. AAS P. 97–717.
Whiffen G.J., Sims J.A. Application of a Novel Optimal Control Algorithm to Low-Thrust Trajectory Optimization // AAS/AIAA Space Flight Mechanics Meeting. Santa Barbara, California. 2001. AAS. P. 01–209.
Whiting J.K. Three-dimensional low-thrust trajectory optimization, with applications // 39th AIAA/ASME/ SAE/ASEE Joint Propulsion Conference and Exhibit. Huntsville, Alabama. 2003. AIAA. P. 2003–5260.
Chilan C.M., Conway B.A. Optimal Low-Thrust Supersynchronous-to-Geosynchronous Orbit Transfer // AAS/AIAA Astrodynamics Specialist Conference. Big Sky, Montana. 2003. Paper AAS 03-632.
Петухов В.Г. Оптимизация многовитковых перелетов между некомпланарными эллиптическими орбитами // Космич. исслед. 2004. Т. 42. № 3. С. 260–279. (Cosmic Research. P. 250–268).
Петухов В.Г. Оптимальные многовитковые траектории выведения космического аппарата с малой тягой на высокую эллиптическую орбиту // Космич. исслед. 2009. Т. 47. № 3. С. 271–279. (Cosmic Research. P. 243–250).
Петухов В.Г. Робастное квазиоптимальное управление с обратной связью для перелета с мапой тягой между некомпланарными эллиптической и круговой орбитами // Вестник МАИ. 2010. Т. 17. № 3. С. 50–58.
Петухов В.Г. Квазиоптимальное управление с обратной связью для многовиткового перелета с малой тягой между некомпланарным и эллиптической и круговой орбитами // Космич. исслед. 2011. Т. 49. № 2. С 128–137. (Cosmic Research. P. 121–130).
Petropoulos A.E. Low-Thrust Orbit Transfers Using Candidate Lyapunov Functions with a Mechanism for Coasting // AIAA/AAS Astrodynamics Specialist Conference. Providence, Rhode Island. 2004. AIAA Paper 2004–5089.
Ilgen M.R. Low thrust OTV guidance using Liapunov optimal feedback control techniques // AAS/AIAA Astrodynamics Specialist Conference. Victoria, Canada. 1993. AAS Paper 93–680.
Chang D.E., Chichka D.F., Marsden J.E. Lyapunov functions for elliptic orbit transfer, AAS/AIAA Astrodynamics Specialist Conference. Qu’ebec City, Canada, 2001. AAS Paper 01-441.
Chang D.E., Chichka D.F., Marsden J.E. Lyapunov-based transfer between Keplerian orbits // Discrete Cont. Dyn. Syst. Series B. 2002. V. 2. P. 57–67.
Bonnard B., Caillau J.-B., Trélat E. Geometric optimal control of elliptic Keplerian orbits // Discrete Contin. Dyn. Syst. Ser. B 5. 2005. V. 4. P. 929–956.
Боннар Б., Фобур Л., Треля Э. Небесная механика и управление космическими летательными аппаратами. Ижевск: НИЦ “Регулярная и хаотическая динамика”, Институт компьютерных исследований, 2014.
Standish E.M. JPL planetary and lunar ephemerides, DE405/LE405. Interoffice Memorandum, 1998, 312.F-98-048, 1–18.
Константинов М.С., Каменков Е.Ф., Перелыгин Б.П. и др. Механика космического полета. М.: Машиностроение, 1989.
Hansen N., Ostermeier A. Completely derandomized self-adaptation in evolution strategies // Evolutionary Computation. 2001. V. 9. № 2. P. 159–195.
Hansen N., Kern S. Evaluating the CMA evolution strategy on multimodal test functions. Parallel Problem Solving from Nature. Springer, 2004. PPSN VIII. P. 282–291.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В. и др. Математическая теория оптимальных процессов. М.: Наука, 1976.
Moré J.J., Sorensen D.C., Hillstrom K.E., Garbow B.S. The MINPACK project. Sources and Development of Mathematical Software. Prentice-Hall, 1984. P. 88–111.
Аксюшкин В.А., Викуленков В.П., Ишин С.В. Итоги создания и начальных этапов эксплуатации межорбитальных космических буксиров типа “Фрегат” // Вестник НПО имени С.А. Лавочкина. 2014. Т. 22. № 1. С. 3–9.

Дополнительные материалы отсутствуют.

Инструменты

предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал