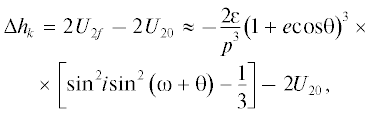Космические исследования, 2021, T. 59, № 5, стр. 373-376

ПОСТАНОВКА ЗАДАЧИ

При полете КА или, вообще, материальной точки в центральном ньютоновском гравитационном поле Земли, движение КА в невращающейся геоцентрической геоэкваториальной системе координат удовлетворяет уравнению:

где r (x, y, z) – радиус-вектор точки КА; r = |r|; * – знак транспонирования; μ – гравитационный параметр Земли; – потенциал притяжения Земли без учета возмущений. Системе (1) соответствуют кеплеровские движения в поле притяжения сферической, однородной Земли. Одним из важнейших первых интегралов в этом случае является интеграл энергии [1–6]: где V = |V|; V – геоцентрическая скорость точки; h_k – кеплеровская константа энергии; элемент a в случае эллиптического движения, когда h_k < 0, является большой полуосью орбиты. При гиперболическом движении, когда h_k > 0, будет a < 0, геометрический смысл имеет модуль |а| = α [3]. Рассмотрим, как изменяется интеграл (3) при учете возмущения от сжатия Земли, как тела вращения, и его использование при анализе орбитального движения материальной точки.

ОБОБЩЕННЫЙ ИНТЕГРАЛ ЭНЕРГИИ ПРИ УЧЕТЕ СЖАТИЯ ЗЕМЛИ

В простейшем случае анализа движения у Земли для учета ее сжатия в потенциале Земли U к основному члену U₀ добавляется вторая зональная гармоника U₂ [2, 3, 5, 6]:

где φ – геоцентрическая широта КА; J₂ = –С₂₀ – коэффициент зональной гармоники 2-го порядка, R_E – средний экваториальный радиус Земли: R_E ≈ 6378.137 км; J₂ ≈ 1082.63 ⋅ 10^–6 [6]; ε ≈ ≈ 2.63328 ⋅ 10¹⁰ км⁵/c². Уравнение движения (1) меняется: где U(r) есть потенциал (4), (2), (5). К основному ускорению (1) добавится возмущающее a_P, которое есть градиент функции U₂ и в прямоугольных координатах запишется в форме [2]:

Удвоенная полная механическая энергия движения точки единичной массы h(r, V) имеет вид:

Теорема. Полная механическая энергия движения материальной точки в модели (6), где потенциал U(r) соответствует (4), (2), (5), постоянна на траектории точки.

Действительно, в данном случае ускорение в (6) определяется однозначной скалярной силовой функцией U = U(r), движение происходит в потенциальном поле, силовая функция U = U(r) есть потенциал, не зависящий от времени. Тогда из общей теоремы механики [1, 4] следует, что на траектории точки dh/dt = 0 в силу уравнения движения (6), h = const. Можно и непосредственно показать это, используя (6), (1), (7). Следовательно, на любой траектории точки энергия (8) постоянна, имеем первый интеграл:

Будем называть этот интеграл обобщенным интегралом энергии, имея в виду, что он обобщает интеграл (3) на случай учета сжатия Земли при расчете траектории материальной точки КА.

Замечание 1. Из (8), (9) следует, что в данной модели потенциала для заданной константы энергии h движение точки происходит в области пространства $h + 2U = h + 2{{U}_{0}} + 2{{U}_{2}}$ = $h + \frac{{2{{\mu }}}}{r} - \frac{{2{{\varepsilon }}}}{{{{r}^{3}}}}\left( {\frac{{{{z}^{2}}}}{{{{r}^{2}}}} - \frac{1}{3}} \right) = {{V}^{2}} \geqslant $ ≥ 0. Видно отличие от кеплеровского случая.

Замечание 2. Данный подход может быть применен и для более полной модели зональных гармоник. Используя модель Земли, как тела вращения, симметричного относительно плоскости экватора, добавляют, например, в потенциал U, кроме второй, еще зональную гармонику 4-го порядка. Тогда обобщенный интеграл энергии принимает вид:

Можно использовать и все разложение потенциала по зональным гармоникам, что позволяет повысить точность и учесть несимметричность относительно экватора:

Здесь – полином Лежандра n-го порядка. Для Земли следующие после 2-го порядка коэффициенты: J₃ = –2.53 ∙ 10^–6; J₄ = –1.61 ∙ 10^–6 [6], т.е. ~ на три порядка меньше, чем J₂.

Замечание 3. В данном случае потенциального осесимметричного силового поля есть еще интеграл осевого момента количества движения точки [4]: M_z = (e_z, [r, V]) = m = const, где e_z – орт по оси вращения Земли.

ИЗМЕНЕНИЕ КЕПЛЕРОВСКОЙ КОНСТАНТЫ ЭНЕРГИИ НА ОРБИТАХ ОТЛЕТА К ЛУНЕ И ПЛАНЕТАМ

Выписав интеграл (9) для начальной точки траектории x₀ (r₀, V₀, t₀) и для некоторой другой ее точки x_f (r_f, V_f, t_f), получим соотношение:

Применим его к анализу траекторий отлета КА от Земли к Луне и планетам.

Из (10) следует, что изменение кеплеровской константы энергии в точном анализе удовлетворяет соотношению:

здесь i, ω – наклонение и аргумент перигея орбиты; u, θ – аргумент широты и истинная аномалия точки.

Замечание 4. Интеграл энергии (9) и точное соотношение (11) для изменения Δh_k справедливы для любой орбиты, в частности, для любых значений наклонения и эксцентриситета.

Если перейти от кеплеровской константы h_k к полуоси a (3) и линеаризовать по a, то из (11) получим вариацию Δa в первом приближении:

При полете КА к планете отлет от Земли будет происходить по гиперболической орбите (в оскулирующем приближении). Для оценок возьмем для этой орбиты скорость “на бесконечности” V_∞ = 3–4 км/c. В этом случае расстояние r_f возрастает неограниченно, и предпоследний член в (11) 2U_2f стремится к нулю, поэтому изменение кеплеровской константы энергии Δh_K стремится к предельному значению Δh_Kl:

Если ${\text{si}}{{{\text{n}}}^{2}}{{{{\varphi }}}_{0}} < \frac{1}{3}$ (|φ₀| < ${{\varphi }}_{0}^{*}$ = 35.2644°), то Δh_Kl < 0. Если ${\text{si}}{{{\text{n}}}^{2}}{{{{\varphi }}}_{0}} > \frac{1}{3},$ то Δh_Kl > 0. Для полета к Луне полагаем, что используется сильно вытянутая околопараболическая эллиптическая орбита, ее перигей – в начальной точке, r_π = r₀ ≈ 6578 км, начальное расстояние в апогее r_α соответствует расстоянию до Луны r_M при подлете КА к Луне, r_α ≥ (r_M – Δr_α), r_M ≈ (360–405) тыс. км; Δr_α (<0) – поправка на уменьшение r_α за счет сжатия Земли, Δr_α ≈ 2Δa. В (11) расстояние r_f возрастает в процессе движения КА от r₀ до r_M < ∞, при этом предпоследний член в (11) убывает до некоторой малой величины (~10^–6 км²/c²), и предельное изменение кеплеровской константы h_Kl:

Для численных оценок, для начальной точки отлета к Луне и планетам с околоземной опорной орбиты возьмем, для определенности, u₀ = 0, что близко к характеристикам межпланетных и лунных полетов. Тогда в формулах (13), (14) будет φ₀ = 0 и z₀ = 0, получим:

В этом случае для отлета от Земли как к планете по гиперболической орбите, так и к Луне по вытянутой эллиптической орбите, Δh_Kl ≈ –0.0617 км²/c². Численные расчеты подтверждают эти оценки [7, 8]. При h_K < 0 это изменение кеплеровской константы энергии (14) соответствует изменению большой полуоси орбиты, в соответствии с (12): Δa ≈ –6200 км при a₀ = 200 тыс. км, Δa ≈ –8900 км при a₀ = 220 тыс. км, Δa ≈ –56000 км при a₀ = = 600 тыс. км. Практически это изменение происходит быстро, в течение ~ первых трех часов начального полета КА от Земли, при возрастании расстояния r_f до ~70 тыс. км.

СКОРОСТЬ ОТЛЕТА КА С ОКОЛОЗЕМНОЙ ОПОРНОЙ ОРБИТЫ

Изменение кеплеровской константы энергии, вызванное сжатием Земли, приводит в рамках модели (4), (5) к изменению начальной скорости КА отлета от Земли по сравнению с кеплеровской моделью движения. Для корректности анализа зададим для орбиты отлета некоторое значение кеплеровской константы энергии h_Kg (или V_∞, a). Тогда в кеплеровской модели движения КА (1)–(2), в силу интеграла (3), начальная скорость:

При учете сжатия Земли, в модели (4)–(5), при условии h_Kf = h_Kg, в силу интеграла (10), начальная скорость определится из соотношения:

где

Дадим численные оценки для случая z₀ = 0. При отлете от Земли к планете по геоцентрической орбите с V_∞ = 3–4 км/с учет сжатия Земли в (16) увеличивает по сравнению с кеплеровским случаем (15) начальную скорость V₀ от ~11.410–11.713 до ~11.413–11.716 км/с, т.е. на ~3 м/с. При полете к Луне, при r_α = r_M + |Δr_α|, r_M = = 400 тыс. км, учет сжатия увеличивает начальную скорость V₀ от ~10.919 до ~10.922 км/с, т.е. тоже на ~3 м/с. Это приводит к заданию начальной оскулирующей большой полуоси орбиты, увеличенной (по сравнению с кеплеровским случаем) на ~6.5 тыс. км, и увеличенного на ~13 тыс. км [7, 8] начального апогейного расстояния r_α, как отмечено выше.

ОЦЕНКА ИЗМЕНЕНИЯ КЕПЛЕРОВСКОЙ КОНСТАНТЫ ЭНЕРГИИ В ПЕРВОМ ПРИБЛИЖЕНИИ

При анализе движения КА по гиперболической и сильно вытянутой эллиптической орбите мы использовали расстояние до центра Земли в качестве параметра на траектории. В общем случае удобнее взять за параметр на орбите истинную аномалию θ [9] или время t, или среднюю аномалию M [10, 11]. Преобразуем соотношения (11), (12) для использования угла θ при определении изменения кеплеровской константы Δh_K (или полуоси Δa), в первом приближении. Тогда, согласно (11), (11a), учитывая также уравнение орбиты, получим:

где элементы орбиты: фокальный параметр p, эксцентриситет e, i, ω равны их начальным значениям p₀, e₀, i₀, ω₀. Изменение Δa определится по (12). Если орбита эллиптическая, a > 0, и рассматривается многооборотное движение точки, то можно провести осреднение движения. Для упрощения этой процедуры, используя элементарные тождественные тригонометрические преобразования, приводим 2U_2f к сумме константы с_0θ и нескольких слагаемых вида: (2ε/p³) ${{c}_{j}}\left( {i,{\text{\;}}e} \right){\text{cos}}({{n}_{j}}{{\omega }} + {{m}_{j}}\theta ),$ где ${{n}_{j}},~{{m}_{j}}~$ – целые числа:

Эта константа дает “среднее” смещение кеплеровской константы энергии h_K за счет сжатия Земли, согласно (17). В данной задаче этот параметр θ удобен, но принято делать осреднение по средней аномалии M. Тогда, после некоторых преобразований, получим “среднее” по M значение функции 2U_2f:

Замечание 5. Пусть небесное тело не отлетает от Земли, а приближается к ней, входя в ее атмосферу. Тогда изменение кеплеровской константы энергии со временем осуществляется в обратном направлении. При этом расстояние от Земли r уменьшается со временем, и величина потенциала U₂ возрастает до конечного значения, соответствующего входу в атмосферу, r ~ 6478 км.

Замечание 6. Если небесное тело (КА, астероид, комета) приближается к Земле, двигаясь на большом расстоянии (r ~ 300–400 тыс. км) от Земли по эллиптической околопараболической орбите, для которой – Δh_K < h_K < 0, то из-за сжатия Земли кеплеровская константа энергии может увеличиться до положительного значения, и это тело сблизится с Землей по гиперболической орбите. Возможен и другой случай, когда под влиянием сжатия Земли орбита меняет свою структуру с гиперболической на эллиптическую.

ВЫВОДЫ

Упрощенный анализ влияния сжатия Земли как тела вращения – на основе зональных гармоник гравитационного потенциала – позволяет использовать интеграл энергии, обобщающий интеграл энергии в кеплеровском случае. Это дает возможность рассмотреть некоторые качественные особенности движения КА при полете к Луне и планетам и при возврате к Земле, а также небесных тел, астероидов и комет, тесно сближающихся с Землей. Сжатие Земли может вызвать изменение структуры орбит этих тел – с эллиптической на гиперболическую и обратно.

В заключение автор выражает искреннюю признательность В.В. Сазонову и А.А. Суханову за интересное обсуждение работы.