Космические исследования, 2022, T. 60, № 1, стр. 73-79

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДВИЖЕНИЯ ВС

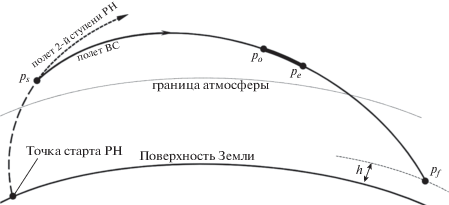
Рассматриваемый интервал полета ВС включает три этапа (см. рис. 1). Первый этап – участок ${{p}_{s}}{{p}_{o}}$ пассивного полета ВС от момента отделения ВС от РН до момента начала тормозного импульса. Второй этап – участок ${{p}_{o}}{{p}_{e}}$ выдачи тормозного импульса. Третий этап – участок ${{p}_{e}}{{p}_{f}}$ пассивного полета ВС до момента достижения заданной точки на поверхности Земли, или на некоторой высоте h для обеспечения необходимых условий для посадки. Максимальная высота полета ВС на всем интервале не превышает 150 км.

Движение центра масс ВС рассматривается в гринвичской системе координат (ГСК) $O{{X}_{1}}{{X}_{2}}{{X}_{3}},$ начало которой находится в центре Земли. ГСК равномерно вращается вокруг неподвижной в инерциальном пространстве оси ${{X}_{3}}$ c постоянной угловой скоростью ${{\omega }_{{\text{E}}}}.$ В ГСК задается положение начальной точки ${{p}_{s}}$ движения ВС и некоторой заданной точки ${{p}_{f}}$ – конечной точки движения ВС, далее – точки приведения (ТП). Положение точек ${{p}_{s}}$ и ${{p}_{f}}$ задается соответствующими геоцентрическими радиус-векторами ${{{\mathbf{r}}}_{s}}$ и ${{{\mathbf{r}}}_{f}}.$ В точке ${{p}_{s}}$ также задается вектор ${{{\mathbf{v}}}_{s}}$ линейной скорости ВС.

Уравнения движения центра масс ВС (1) учитывают гравитационное притяжение Земли как точечной массы с учетом второй зональной гармоники геопотенциала, влияние аэродинамического сопротивления атмосферы и ускорение под действием тяги ДУ на участке торможения [1]. В ГСК уравнения модели записываются в виде:

Здесь ${\mathbf{r}}$ и ${\mathbf{v}}$ – текущие радиус-вектор и вектор скорости центра масс ВС, ${v}$ – модуль вектора скорости, $\mu $ – гравитационный параметр Земли, ${{{\mathbf{\omega }}}_{{\text{E}}}} = [0,0,{{\omega }_{{\text{E}}}}]$ – вектор угловой скорости Земли, ${{S}_{m}}$ – площадь миделя, ${{C}_{x}}$ – аэродинамический коэффициент, $m$ – текущая масса, ${{P}_{{du}}}$ – величина тяги ДУ, ${\mathbf{e}}$ – орт, задающий направление вектора тяги ДУ, ${{\delta }_{u}}$ – функция, принимающая значение 1 на участке выдачи тормозного импульса и 0 – на участке пассивного полета, ${{\xi }_{{du}}}$ – массовый расход ДУ, $\rho $ – плотность атмосферы, ${\mathbf{b}} = {{[1,1,3]}^{T}},$ ${\mathbf{c}} = {{[1,1,1]}^{T}}$ – вектора констант, символом $ * $ здесь и далее обозначена операция покомпонентного умножения векторов. Плотность атмосферы в диапазоне высот 0–150 км аппроксимируется в соответствии с ГОСТ 25645.116-2004. Атмосфера считается неподвижной относительно Земли. Длительность участка торможения составляет несколько секунд, поэтому ориентацию вектора тяги ДУ в ГСК на участке торможения можно считать неизменной, т.е. ${\mathbf{e}} = {\text{const}}{\text{.}}$ Будем также полагать, что после выдачи тормозного импульса ВС движется на атмосферном участке с нулевыми углами атаки и скольжения, то есть коэффициент ${{C}_{x}}$ является функцией только числа Маха.

РАСЧЕТ ОРИЕНТАЦИИ ТОРМОЗНОГО ИМПУЛЬСА

Рассмотрим движение ВС на отрезке ${{p}_{o}}{{p}_{f}}.$ Задачу расчета ориентации тормозного импульса можно сформулировать в следующем виде: для известных начальных условий ${\mathbf{r}}({{t}_{o}}) = {{{\mathbf{r}}}_{o}},$ ${\mathbf{v}}({{t}_{o}}) = {{{\mathbf{v}}}_{o}}$ в точке ${{p}_{o}}$ необходимо найти орт ${\mathbf{e}},$ такой, чтобы траектория пассивного полета ВС после приложения тормозного импульса проходила через точку ${{p}_{f}}{\text{:}}$ ${\mathbf{r}}({{t}_{f}}) = {{{\mathbf{r}}}_{f}},$ ${{t}_{f}}$ – произвольное. Начальные условия ${{{\mathbf{r}}}_{o}}$ и ${{{\mathbf{v}}}_{o}}$ находятся интегрированием системы (1) на участке ${{p}_{s}}{{p}_{o}}.$

Траектория пассивного движения ВС по окончании участка выдачи тормозного импульса определяется начальными условиями на момент ${{t}_{e}}$ окончания торможения: ${\mathbf{r}}({{t}_{e}}) = {{{\mathbf{r}}}_{e}},$ ${\mathbf{v}}({{t}_{e}}) = {{{\mathbf{v}}}_{e}}.$ Так как тормозной импульс короткий, приближенно можно записать ${{{\mathbf{v}}}_{e}} = {{{\mathbf{v}}}_{o}} + {\mathbf{q}}$, где ${\mathbf{q}} = {{[{{q}_{1}},{{q}_{2}},{{q}_{3}}]}^{T}}$ – вектор приращения скорости ВС вследствие тормозного импульса, ${\mathbf{e}} = {{\mathbf{q}} \mathord{\left/ {\vphantom {{\mathbf{q}} {\left| {\mathbf{q}} \right|}}} \right. \kern-0em} {\left| {\mathbf{q}} \right|}}.$ Вектор ${\mathbf{q}}$ и соответствующий ему орт ${\mathbf{e}}$ можно найти, итерационно решая уравнение $J{{{\mathbf{q}}}_{{{\Delta }}}} = {\mathbf{\Delta }},$ где J – матрица частных производных ${{\partial {\mathbf{r}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}} {\partial {\mathbf{q}}}}} \right. \kern-0em} {\partial {\mathbf{q}}}},$ ${{{\mathbf{q}}}_{{{\Delta }}}}$ – уточняющая поправка к вектору ${\mathbf{q}}$ на текущей итерации, ${\mathbf{\Delta }} = {{{\mathbf{r}}}_{f}} - {{{\mathbf{r}}}_{*}}$ – вектор промаха ВС относительно ТП. В последнем соотношении ${{{\mathbf{r}}}_{*}}$ – радиус-вектор ВС на момент расчета промаха. Вычисления заканчиваются, когда модуль вектора промаха становится меньше заданного предельного значения.

Для расчета вектора ${\mathbf{\Delta }}$ на каждой итерации, с использованием текущего приближения ${\mathbf{e}}$ интегрируются уравнения системы (1) с начальными условиями ${\mathbf{r}}(0) = {{{\mathbf{r}}}_{o}},$ ${\mathbf{v}}(0) = {{{\mathbf{v}}}_{o}}.$ В качестве начального приближения ${\mathbf{e}}$ используется направление против вектора линейной скорости ВС. Так как время ${{t}_{f}}$ произвольно, уравнения интегрируются до момента достижения ВС некоторой сферической поверхности (далее – приводящей поверхности), радиуса ${{R}_{*}} = \left| {{{{\mathbf{r}}}_{f}}} \right|.$ На момент достижения ВС приводящей поверхности рассчитываются вектор промаха и элементы матрицы J.

Для расчета элементов матрицы J, совместно с уравнениями модели (1) интегрируются уравнения в вариациях ${{\partial {\mathbf{r}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}} {\partial {{q}_{j}}}}} \right. \kern-0em} {\partial {{q}_{j}}}}$ и ${{\partial {\mathbf{v}}} \mathord{\left/ {\vphantom {{\partial {\mathbf{v}}} {\partial {{q}_{j}}}}} \right. \kern-0em} {\partial {{q}_{j}}}},$ $j = 1,2,3.$

Уравнения в вариациях имеют вид:

В приведенных уравнениях ${{{\mathbf{a}}}_{c}}$ – вектор ускорения в центральном поле Земли, ${{{\mathbf{a}}}_{2}}$ – добавка к ускорению вследствие полярного сжатия Земли, ${{{\mathbf{a}}}_{e}}$ – переносное ускорение в ГСК, ${{{\mathbf{a}}}_{d}}$ – ускорение под действием аэродинамической силы. Соотношения для составляющих правой части второго уравнения системы (2):

В приведенных уравнениях $A = {\mathbf{r}} \cdot \frac{{\partial {\mathbf{r}}}}{{\partial q}},$ $B = \frac{{\mathbf{v}}}{{v}} \cdot \frac{{\partial {\mathbf{v}}}}{{\partial q}},$ ${\mathbf{c}} = {{\left[ {7,7,\frac{7}{2}} \right]}^{T}},$ индексы j для простоты опущены. Выписанные соотношения составлены с учетом особенностей движения ВС в плотных слоях атмосферы – зависимости коэффициента ${{C}_{x}}$ от скорости ВС и местной скорости звука, а также существенного изменения плотности атмосферы в зависимости от текущей высоты ВС. В связи с этим в соответствующие уравнения включены частные производные ${{\partial \rho } \mathord{\left/ {\vphantom {{\partial \rho } {\partial q}}} \right. \kern-0em} {\partial q}}$ и ${{\partial {{C}_{x}}} \mathord{\left/ {\vphantom {{\partial {{C}_{x}}} {\partial q}}} \right. \kern-0em} {\partial q}}.$

В соответствии с ГОСТ 25645.116-2004 изменение плотности в функции высоты описывается соотношением $\rho = {{k}_{i}}\exp (\chi ),$ где χ = (h – h_i) × $ \times \,\,({{a}_{i}}(h - {{h}_{i}}) - {{b}_{i}}),$ h – текущая высота ВС над поверхностью земного эллипсоида с параметрами ${{R}_{{\text{E}}}},{{f}_{{\text{E}}}}.$ Параметры ${{k}_{i}},$ ${{a}_{i}},$ ${{b}_{i}}$ – табличные значения модели атмосферы, являющиеся константами в пределах некоторого диапазона высоты ВС ${{h}_{i}} \leqslant h \leqslant {{h}_{{i + 1}}}.$ Соответствующая частная производная записывается в виде:

Коэффициент ${{C}_{x}}$ задается в виде кусочно-линейной функции числа Маха – отношения скорости ВС к местной скорости звука, которая в свою очередь также задается кусочно-линейной функцией высоты. Выражение для соответствующей частной производной:

где $r = \left| {\mathbf{r}} \right|,$ ${{\kappa }_{i}}$ и ${{\eta }_{i}}$ – константы соответствующих моделей, ${{M}_{i}}$ и ${{h}_{i}}$ – узлы интерполяции.

Как уже было сказано, интегрирование проводится до момента достижения ВС приводящей поверхности. При этом, так как ряд моделей представлен кусочными функциями, в процедуре интегрирования предусматривается контроль достижения соответствующих узловых значений ${{h}_{i}},$ ${{M}_{i}}.$

В рассматриваемой задаче абсолютная величина импульса фиксирована (задается длительностью включения ДУ), поэтому удобно перейти к параметризации вектора ${\mathbf{q}}$ посредством абсолютного значения $\upsilon = \left| {\mathbf{q}} \right|$ вектора приращения скорости ВС и углов ориентации $\alpha $ и $\beta $ этого вектора в осях ГСК. Угол $\alpha $ – это угол между проекцией продольной оси ВС, противоположной направлению силы тяги двигательной установки (оси $x$), на плоскость ${{X}_{1}}{{X}_{2}}.$ Этот угол отсчитывается от оси ${{X}_{1}}$ в сторону оси ${{X}_{2}}.$ Угол $\beta $ – угол между осью $x$ и ее проекцией на плоскость ${{X}_{1}}{{X}_{2}}.$ Положительное значение $\beta $ соответствует положительной проекции $x$ на ось ${{X}_{3}}.$ В соответствии с введенными определениями, связь проекций приращения скорости ВС на оси ГСК с углами $\alpha $ и $\beta $ определяется соотношениями: ${{q}_{1}} = \upsilon \cos \alpha \cos \beta ,$ ${{q}_{2}} = \upsilon sin\alpha \cos \beta ,$ ${{q}_{3}} = \upsilon sin\beta .$ Таким образом, вектор ${\mathbf{q}}$ заменяется вектором ${\mathbf{\tilde {q}}} = {{[\alpha ,\beta ]}^{T}} = {{[{{\tilde {q}}_{1}},{{\tilde {q}}_{2}}]}^{T}}.$ Соответствующие частные производные ${{\partial {{q}_{j}}} \mathord{\left/ {\vphantom {{\partial {{q}_{j}}} {\partial {{{\tilde {q}}}_{k}}}}} \right. \kern-0em} {\partial {{{\tilde {q}}}_{k}}}}$ находятся в силу выписанных соотношений. Пространственное положение ВС в момент времени ${{t}_{f}}$ удобно параметризовать сферическими координатами: долготой $\lambda $ и широтой $\varphi $ ВС на приводящей поверхности. Другими словами, пространственный вектор ${\mathbf{\Delta }}$ промаха ВС относительно ТП может быть представлен на приводящей поверхности в виде вектора ${\mathbf{\tilde {\Delta }}} = {{[\delta \lambda ,\delta \varphi ]}^{T}},$ где $\delta \lambda = {{\lambda }_{n}} - \lambda ,$ $\delta \varphi = {{\varphi }_{n}} - \varphi ,$ ${{\lambda }_{n}}$ и ${{\varphi }_{n}}$ – координаты ТП на приводящей поверхности. Таким образом, линеаризованная задача теперь записывается как $J{\text{*}}{{{\mathbf{\tilde {q}}}}_{\Delta }} = {\mathbf{\tilde {\Delta }}},$ где $J{\text{*}}$ – матрица частных производных ${{\partial \lambda } \mathord{\left/ {\vphantom {{\partial \lambda } {\partial {{{\tilde {q}}}_{k}}}}} \right. \kern-0em} {\partial {{{\tilde {q}}}_{k}}}},$ ${{\partial \varphi } \mathord{\left/ {\vphantom {{\partial \varphi } {\partial {{{\tilde {q}}}_{k}}}}} \right. \kern-0em} {\partial {{{\tilde {q}}}_{k}}}},$ имеющая размерность 2 × 2.

Уравнения для вычисления новых частных производных записываются в виде: $\frac{{\partial \lambda }}{{\partial {{{\tilde {q}}}_{k}}}} = \sum\nolimits_{j = 1}^3 {\frac{{\partial \lambda }}{{\partial {{q}_{j}}}}\frac{{\partial {{q}_{j}}}}{{\partial {{{\tilde {q}}}_{k}}}}} ,$ $\frac{{\partial \varphi }}{{\partial {{{\tilde {q}}}_{k}}}} = \sum\nolimits_{j = 1}^3 {\frac{{\partial \varphi }}{{\partial {{q}_{j}}}}\frac{{\partial {{q}_{j}}}}{{\partial {{{\tilde {q}}}_{k}}}}} ,$ $k = 1,2.$ С учетом определения $\lambda $ и $\varphi ,$ в приведенных соотношениях нужно принимать во внимание, что $r_{1}^{2} + r_{2}^{2} \ne 0.$

Численные расчеты показывают, что итерационная задача размерности 2 × 2 сходится, если заданное значение модуля тормозного импульса позволяет привести ВС в заданную ТП. В случаях, когда при фиксированной длительности тормозного импульса достижение ТП оказывается невозможным, можно решить задачу в пространственной постановке, с использованием ранее выписанного уравнения $J{{{\mathbf{q}}}_{\Delta }} = {\mathbf{\Delta }}.$ При этом можно определить как направление, так и абсолютную величину тормозного импульса, потребного для приведения ВС в заданную ТП.

Рассмотрим численный пример – расчет направления тормозного импульса фиксированной длительности для приведения ВС в заданную ТП с компенсацией погрешностей траекторного движения ВС, полученных на момент отделения ВС от РН.

Иллюстрировать пространственное движение ВС удобно в системе координат (см. рис. 2), образованной поверхностью сферической земли (подстилающей поверхностью) и некоторой плоскостью (далее – проекционной плоскостью), задаваемой векторами ${{{\mathbf{r}}}_{s}}$ и ${{{\mathbf{v}}}_{s}}.$ Ось H совпадает с вектором ${{{\mathbf{r}}}_{s}}.$ Ось D является линией пересечения подстилающей поверхности и проекционной плоскости. Ось B дополняет тройку HDB до правой. Проекция точки ВС на ось D – характеризует текущую дальность ВС на подстилающей поверхности от некоторой начальной точки, проекция на ось H – текущую высоту ВС над поверхностью Земли, проекция на ось B характеризует боковое удаление ВС от проекционной плоскости. Координата D является криволинейной, но на рисунках она для упрощения условно спрямляется.

На рис. 2 жирные черные кривые – проекции траектории ВС, соответственно, на подстилающую поверхность и на проекционную плоскость; ${{d}_{o}},{{h}_{o}},{{b}_{o}}$ – координаты ВС в точке ${{p}_{o}}.$

В расчетах использовались следующие исходные данные. Начальные условия движения ВС заданы в ГСК, в точке ${{p}_{s}}{\text{:}}$ ${{{\mathbf{r}}}_{s}} = [1.89,4.04,4.64]$ км ∙ 10³, ${{{\mathbf{v}}}_{s}} = [ - 1.93,0.84,1.34]$ км/с. Основные параметры ВС: $m = 60\,\,{\text{т,}}$ ${{S}_{m}} = 12$ м², ${{P}_{{du}}} = 360$ тс, удельный импульс ДУ ${{I}_{{du}}} = 300$ с. Коэффициент ${{C}_{x}}$ задавался как табличная функция в диапазоне чисел Маха от 0.5 до 12. При этом численные значения ${{C}_{x}}$ лежат в диапазоне от 1.4 до 2.0. Начало торможения ${{t}_{o}}$ – через 210 с после начала пассивного полета в точке ${{p}_{s}}.$ Длительность торможения – 10 с. Координаты ТП: ${{\lambda }_{n}} = 72.5^\circ ,$ ${{\varphi }_{n}} = 48.2^\circ .$ Параметры гравитационного поля Земли и земного эллипсоида принимались в соответствии с моделью EGM96. Местная скорость звука вычислялись в соответствии с ГОСТ 4401-81.

На рис. 3 приведены проекции траектории движения центра масс возвращаемой ступени на плоскости DH и DB (напомним, что ось D условно выпрямлена). Траектория вычислена для номинальных начальных условий в точке ${{p}_{s}}.$ Рисунок состоит из трех графиков. На каждом графике изображены по 2 кривые: свободное движение ступени без выдачи тормозного импульса (пунктирная кривая), движение с расчетным тормозным импульсом для приведения в заданную ТП (сплошная кривая). На третьем графике укрупненно показаны траектории движения ВС на поверхности Земли в окрестности ТП в сферических координатах. Черным кружком отмечена точка падения ВС при свободном движении. Можно видеть, что расчетный тормозной импульс приводит возвращаемую ступень в точку с заданными координатами.

Используя приведенные выше начальные условия в качестве номинальных значений, были проведены статистические расчеты по определению потребной области вариации направления вектора тормозного импульса заданной длительности для приведения ВС в заданную ТП при известных параметрах отклонений начальных условий траекторного движения ВС в точке ${{p}_{s}}.$ На каждом шаге расчета к начальным условиям прибавлялись некоторые ошибки. Отклонения начального положения ВС задавались вдоль осей D, B, H, отклонения начального вектора скорости ВС задавались углами в плоскостях DB (отклонение в горизонтальной плоскости) и DH (отклонение в вертикальной плоскости), а также отклонением по модулю скорости. Амплитудные значения отклонений по координатам ±5 км, по угловым параметрам ±0.5°, по модулю скорости ±40 м/с.

Рис. 4 построен аналогично рис. 3, за исключением третьего графика. Можно видеть, что во всех случаях тормозной импульс длительностью 10 с позволяет направить баллистическое движение возвращаемой ступени в заданную ТП. На рисунке черные сплошная и пунктирная кривые – номинальные траектории ступени при отсутствии возмущений. Серые кривые – траектории ВС с выдачей расчетных тормозных импульсов при наличии возмущений начальных условий. Для всех вариантов время начала выдачи тормозного импульса – 210 с от момента разделения 1 и 2 ступеней. На нижнем графике дополнительно изображены точки падения ВС в свободном движении при наличии возмущений начальных условий. Совокупность данных точек характеризует район падения ВС в случае отсутствия тормозного импульса. Тонкими пунктирными кривыми на графиках обозначены проекции границ “трубки траекторий” на плоскости DB и DH при свободном движении ВС.

Направление вектора тормозного импульса удобно задавать углами ориентации ${{\alpha }_{s}}$ и ${{\beta }_{s}}$ вектора тяги ДУ в системе координат ${{p}_{o}}{{Y}_{1}}{{Y}_{2}}{{Y}_{3}}$ (см. рис. 5). Ось ${{Y}_{1}}$ совпадает с вектором ${{{\mathbf{v}}}_{o}},$ ось ${{Y}_{3}}$ перпендикулярна оси ${{Y}_{1}},$ лежит в плоскости, образованной векторами ${{{\mathbf{v}}}_{o}}$ и ${{{\mathbf{r}}}_{o}},$ и составляет острый угол с вектором ${{{\mathbf{r}}}_{o}}.$ Ось ${{Y}_{2}}$ дополняет систему до правой. На рис. 5 обозначены: ${\mathbf{p}}$ – вектор тяги двигательной установки ВС, ось $x$ – продольная ось ВС, направленная из центра масс в сторону сопла ДУ. Угол ${{\alpha }_{s}}$ – это угол между проекцией оси $x$ на плоскость осью ${{Y}_{1}}{{Y}_{2}},$ отсчитываемый от оси ${{Y}_{1}}$ в сторону оси ${{Y}_{3}}.$ Угол ${{\beta }_{s}}$ – угол между осью $x$ и ее проекцией на плоскость ${{Y}_{1}}{{Y}_{2}}.$ Положительное значение ${{\beta }_{s}}$ соответствует положительной проекции $x$ на ось ${{Y}_{3}}.$ Нулевые значения ${{\alpha }_{s}}$ и ${{\beta }_{s}}$ соответствуют тормозному импульсу, выдаваемому против скорости движения ВС.

На рис. 6 приведены углы ${{\alpha }_{s}}$ и ${{\beta }_{s}}$ для всех расчетных случаев. Плоскость рисунка представляет собой развертку сферической поверхности, каждая точка на которой представляет собой след оси х в конкретной реализации расчета. На рисунке можно видеть, что угол ${{\alpha }_{s}}$ достигал в отдельных случаях значений ~42°, угол ${{\beta }_{s}}$ не превышал по модулю 35°. Совокупность точек на плоскости рисунка дает представление об области вариации направления тормозного импульса. Полученная информация может быть использована при дальнейшем проектировании ВС.