Космические исследования, 2022, T. 60, № 3, стр. 246-253

Стабилизация относительного равновесия спутника при помощи магнитных моментов с учетом аэродинамических сил

В. М. Морозов¹, В. И. Каленова^1, *

¹ Научно-исследовательский институт механики МГУ им. М.В. Ломоносова
Москва, Россия

Поступила в редакцию 10.09.2021
После доработки 18.11.2021
Принята к публикации 24.11.2021

EDN: YNWHPR
DOI: 10.31857/S0023420622030074

Аннотация

Рассматривается стабилизация относительного равновесия спутника на круговой орбите, снабженного магнитной системой ориентации, при учете аэродинамических моментов. Линеаризованная система уравнений движения относится к специальному классу линейных нестационарных систем, приводимых к стационарным. Исследована управляемость как стационарной, так и нестационарной системы. Построен работоспособный алгоритм стабилизации на основе приведенной стационарной системы. Проведено моделирование, демонстрирующее эффект влияния аэродинамических моментов.

1. ВВЕДЕНИЕ

Эта работа является продолжением серии работ по стабилизации стационарных движений спутника, центр масс которого движется по круговой орбите, при помощи моментов различной природы, возникающих при взаимодействии с геомагнитным полем [1–6]. Исследования проводились на основании факта принадлежности линеаризованных уравнений движения к специальному классу приводимых линейных нестационарных систем (ЛНС). Свойство приводимости ЛНС к стационарным системам позволило разработать строгий аналитический подход к исследованию указанных задач. Были получены необходимые и достаточные условия управляемости систем и предложены работоспособные оптимальные алгоритмы стабилизации.

В предлагаемой работе указанный подход применяется для решения задачи стабилизации относительного равновесия спутника при учете аэродинамических моментов.

Рассматривается движение спутника по круговой орбите в гравитационном поле. Аэродинамические моменты оказывают существенное влияние на движение спутника около центра масс на низких орбитах (до 700 км). Выражения для аэродинамических моментов в большинстве работ используются в традиционном виде, удобном для аналитических исследований [7–11]. Влияние гравитационных, аэродинамических и магнитных моментов на устойчивость положений равновесия спутника на круговой орбите рассмотрено в [7, 11–13]. При этом характер устойчивости в общем случае не является асимптотическим, и вопрос о стабилизации тем или иным способом представляет практический интерес. Как известно, одним из таких способов является стабилизация при помощи магнитных систем, который основан на взаимодействии собственного магнитного момента спутника с внешним магнитным полем. Различным аспектам проблем управления и определения ориентации спутников с помощью магнитных катушек и магнитометров посвящено много работ (см., например, [3, 14–16]). Обзор работ по управлению ориентацией космических аппаратов при помощи магнитных моментов содержится в [17, 18].

Задача стабилизации относительного равновесия при помощи магнитных моментов с учетом аэродинамических сил рассматривалась в [19, 20]. В этой работе желаемая ориентация соответствует гравитационно-неустойчивому положению равновесия, и магнитное управление необходимо для обеспечения устойчивости. Исследованы также вопросы управляемости и предложены алгоритмы управления, основанные на LQR-методе для дискретного времени.

Линеаризованные модели рассматриваемых задач представляются линейными нестационарными системами (ЛНС), так как управляющий момент является функцией геомагнитного поля, которое изменяется во время движения спутника по орбите. В большинстве работ предполагается, что изменение носит периодический характер, если орбита спутника – круговая. Как отмечено в [18], это предположение вполне оправдано. Поэтому математические модели рассматриваемых задач представляют собой системы дифференциальных уравнений с периодическими коэффициентами. Это обстоятельство вносит существенные трудности как в изучение управляемости системы, так и в разработку эффективных алгоритмов управления.

Выбор коэффициентов усиления в алгоритме управления с обратной связью, обеспечивающий асимптотическую устойчивость равновесия спутника – центральный вопрос в этой задаче. При построении алгоритмов управления с обратной связью используются, в основном, следующие подходы. Один подход приводит к численному анализу линейной периодической системы на основании теории Флоке (см. работы [16, 17, 21]). Другой подход основан на применении метода функций Ляпунова (см. [22, 23]). Следует подчеркнуть, что при обоих подходах способ выбора коэффициентов обратной связи не указывается.

Как уже указывалось, предлагаемый в работе подход основан на приводимости исходной нестационарной системы к стационарной системе большей размерности [24, 25]. Для приведенной стационарной системы строится оптимальный алгоритм стабилизации, основанный на LQR-методе.

Использование алгоритмов стабилизации для стационарных систем имеет ряд достоинств.

1) Управление строится с помощью линейно-квадратичного регулятора на бесконечном интервале времени, что приводит к управлению в виде обратной связи с постоянными коэффициентами. Это управление обеспечивает асимптотическую устойчивость приведенной стационарной системы;

2) Процесс построения управления хорошо алгоритмизирован. Для получения результата достаточно задать лишь параметры оптимизируемого функционала.

Полученное на основании стационарной системы стабилизирующее управление вводится в исходную нестационарную систему при помощи вспомогательных переменных, которые выбираются таким образом, чтобы преобразование от исходных переменных к переменным стационарной системы было невырожденным.

Работоспособность и эффективность предлагаемых алгоритмов подтверждается математическим моделированием.

2. ПОСТАНОВКА ЗАДАЧИ

Рассматривается движение спутника вокруг центра масс в гравитационном поле Земли. Предполагается, что центр масс спутника движется по круговой орбите. На спутник действует также восстанавливающий аэродинамический момент, выражение для которого принимается в соответствии с [20]. Управляющий момент создается за счет взаимодействия собственного магнитного момента спутника с магнитным полем Земли.

2.1. Системы координат и уравнения движения

Используются две системы координат: $OXYZ$ – орбитальная система координат с началом в точке $O$ – центре масс спутника: ось $OZ$ направлена по радиус-вектору центра масс; $OY$ – по нормали к плоскости орбиты, $OX$ дополняет систему до правой тройки; $Oxyz$ – связанная система координат, оси которой направлены по главным центральным осям инерции спутника.

Ориентация системы $Oxyz$ относительно орбитальной задается с помощью углов Эйлера ${{\theta }_{1}},{{\theta }_{2}},{{\theta }_{3}}.$ Матрица $\Theta $ направляющих косинусов осей системы $OXYZ$ в системе $Oxyz$ имеет вид [26]

$\begin{gathered} \Theta = \left\| {{{\Theta }_{{ij}}}} \right\|; \\ {{\Theta }_{{11}}} = \cos {{\theta }_{1}}\cos {{\theta }_{3}} - \sin {{\theta }_{1}}\sin {{\theta }_{2}}\sin {{\theta }_{3}}, \\ {{\Theta }_{{12}}} = - \sin {{\theta }_{1}}\cos {{\theta }_{2}}, \\ {{\Theta }_{{13}}} = \cos {{\theta }_{1}}\sin {{\theta }_{3}} + \sin {{\theta }_{1}}\sin {{\theta }_{2}}\cos {{\theta }_{3}}, \\ {{\Theta }_{{21}}} = \sin {{\theta }_{1}}\cos {{\theta }_{3}} + \cos {{\theta }_{1}}\sin {{\theta }_{2}}\sin {{\theta }_{3}}, \\ {{\Theta }_{{22}}} = \cos {{\theta }_{1}}\cos {{\theta }_{2}}, \\ {{\Theta }_{{23}}} = \sin {{\theta }_{1}}\sin {{\theta }_{3}} - \cos {{\theta }_{1}}\sin {{\theta }_{2}}\cos {{\theta }_{3}}, \\ {{\Theta }_{{31}}} = - \cos {{\theta }_{2}}\sin {{\theta }_{3}},\quad {{\Theta }_{{32}}} = \sin {{\theta }_{2}}, \\ {{\Theta }_{{33}}} = \cos {{\theta }_{2}}\cos {{\theta }_{3}}. \\ \end{gathered} $

Компоненты абсолютной угловой скорости спутника ${\mathbf{\omega }}$ в проекциях на оси системы координат $Oxyz$ имеют вид

(2.1)

$\begin{gathered} {{\omega }_{1}} = - {{{\dot {\theta }}}_{1}}\cos {{\theta }_{2}}\sin {{\theta }_{3}} + {{{\dot {\theta }}}_{2}}\cos {{\theta }_{3}} + {{\omega }_{0}}{{\Theta }_{{21}}}, \\ {{\omega }_{2}} = {{{\dot {\theta }}}_{3}} + {{{\dot {\theta }}}_{1}}\sin {{\theta }_{2}} + {{\omega }_{0}}{{\Theta }_{{22}}}, \\ {{\omega }_{3}} = {{{\dot {\theta }}}_{1}}\cos {{\theta }_{2}}\cos {{\theta }_{3}} + {{{\dot {\theta }}}_{2}}\sin {{\theta }_{3}} + {{\omega }_{0}}{{\Theta }_{{23}}}, \\ \end{gathered} $

где ${{\omega }_{0}}$ – величина орбитальной угловой скорости.

Динамические уравнения движения спутника около центра масс имеют вид

(2.2)

${\mathbf{J}}\frac{{d{\mathbf{\omega }}}}{{dt}} + {\mathbf{\omega }} \times {\mathbf{J\omega }} = {{{\mathbf{M}}}_{g}} + {{{\mathbf{M}}}_{a}} + {{{\mathbf{M}}}_{m}}.$

Здесь ${\mathbf{J}} = {\text{diag(}}{{J}_{1}}{{J}_{2}}{{J}_{3}}{\text{);}}$ ${{J}_{1}},{{J}_{2}},{{J}_{3}}$ – главные центральные моменты инерции спутника; ${{{\mathbf{e}}}_{r}}$ – единичный вектор оси $OZ;$ ${{{\mathbf{M}}}_{g}} = 3\omega _{0}^{2}({{{\mathbf{e}}}_{r}} \times {\mathbf{J}}{{{\mathbf{e}}}_{r}})$ – гравитационный момент; ${{{\mathbf{M}}}_{a}}$ – аэродинамический момент [20]; ${{{\mathbf{M}}}_{m}}$ – управляющий момент, который можно представить в виде [27]

${{{\mathbf{M}}}_{m}} = {\mathbf{m}} \times {\mathbf{b}},$

где ${\mathbf{m}} = {{[{{m}_{1}}\;{{m}_{2}}\;{{m}_{3}}]}^{T}}$ – собственный магнитный момент спутника; ${\mathbf{b}}(t) = \Theta {{{\mathbf{b}}}_{0}}(t),$ ${{{\mathbf{b}}}_{0}}(t)$ – индукция геомагнитного поля, которое аппроксимируется прямым магнитным диполем в орбитальной системе координат [27]

${{{\mathbf{b}}}_{0}}(t) = \frac{{{{\mu }_{e}}}}{{{{a}^{3}}}}\left[ {\begin{array}{*{20}{c}} {\cos {{\omega }_{0}}t\sin I} \\ { - \cos I} \\ {2sin{{\omega }_{0}}t\sin I} \end{array}} \right].$

Здесь $I$ – угол наклона плоскости орбиты спутника к плоскости экватора; ${{\mu }_{e}}$ – постоянная магнитного поля Земли, $a$ – радиус орбиты. Величины ${{m}_{1}},{{m}_{2}},{{m}_{3}}$ далее считаются управляющими воздействиями.

2.2. Линеаризованные уравнения движения

Уравнения движения (2.1), (2.2) при ${{{\mathbf{M}}}_{m}} = 0$ допускают стационарное решение, отвечающее положению относительного равновесия спутника, в котором оси связанной системы координат $Oxyz$ совпадают с осями орбитальной системы координат $OXYZ$ [26]. Углы поворота ${{\theta }_{i}}(i = 1,2,3)$ выбраны таким образом, что в положении относительного равновесия все углы и относительные угловые скорости равны нулю

(2.3)

${{\theta }_{i}} = 0,\,\,\,\,\frac{{d{{\theta }_{i}}}}{{dt}} = 0,\,\,\,\,(i = 1,2,3).$

При линеаризации уравнений движения (2.1), (2.2) в окрестности относительного равновесия (2.3), очевидно, линеаризуются и выражения для моментов ${{{\mathbf{M}}}_{g}},$ ${{{\mathbf{M}}}_{a}},$ ${{{\mathbf{M}}}_{m}}.$ В проекциях на оси связанной системы координат $Oxyz$ эти выражения имеют вид ${{{\mathbf{M}}}_{g}} = - 3{{\omega }^{2}}[{{J}_{2}} - {{J}_{3}}){{\theta }_{1}}\,({{J}_{3}} - {{J}_{1}}){{\theta }_{2}}\,({{J}_{2}} - {{J}_{1}}){{\theta }_{3}}{{]}^{T}};$ ${{{\mathbf{M}}}_{a}}$ в соответствии с [20] ${{{\mathbf{M}}}_{a}} = \omega _{0}^{2}\Gamma {{[0\,{{\theta }_{2}}\,{{\theta }_{3}}]}^{T}},$ коэффициент $\Gamma $ зависит от аэродинамических характеристик спутника и радиуса орбиты. В выражении для управляющего момента ${{{\mathbf{M}}}_{m}} = {\mathbf{m}} \times \Theta {{{\mathbf{b}}}_{0}}(t)$ управление ${\mathbf{m}}$ формируется в виде линейной обратной связи по компонентам вектора состояния ${{\theta }_{i}},$ $\frac{{d{{\theta }_{i}}}}{{dt}},$ $(i = 1,2,3).$ Поэтому можно считать (как и в [3, 5]), что $\Theta = {{E}_{3}}$ (${{E}_{k}}$ – единичная матрица ($k \times k$)) и ${\mathbf{M}} = {\mathbf{m}} \times {{{\mathbf{b}}}_{0}}(t).$

Тогда линеаризованные уравнения управляемого движения при введении безразмерного времени $\tau = {{\omega }_{0}}t$ имеют вид

(2.4)

$\begin{gathered} {{{\ddot {x}}}_{1}} - {{d}_{1}}{{{\dot {x}}}_{3}} - {{\kappa }_{1}}{{x}_{1}} = {{\mu }_{0}}[2{{\beta }_{1}}{\text{s}}\tau {{u}_{2}} + {{\beta }_{4}}{{u}_{3}}], \\ {{{\ddot {x}}}_{3}} + {{d}_{3}}{{{\dot {x}}}_{1}} - {{{\bar {\kappa }}}_{3}}{{x}_{3}} = - {{\mu }_{0}}[{{\beta }_{5}}{{u}_{1}} + {{\beta }_{3}}{\text{c}}\tau {{u}_{2}}], \\ {{{\ddot {x}}}_{2}} - {{{\bar {\kappa }}}_{2}}{{x}_{2}} = {{\mu }_{0}}[ - 2{{\beta }_{2}}{\text{s}}\tau {{u}_{1}} + {{\beta }_{2}}{\text{c}}\tau {{u}_{3}}]. \\ \end{gathered} $

Здесь $x = {{\left[ {{{x}_{1}}{{x}_{2}}{{x}_{3}}} \right]}^{T}}$ = ${{\left[ {{{\theta }_{1}}\,{{\theta }_{2}}\,{{\theta }_{3}}} \right]}^{T}}$ – малые углы рассогласования между осями орбитальной и связанной системами координат; ${\text{c}}\tau = \cos \tau ,$ ${\text{s}}\tau = \sin \tau ;$ m = u = $ = {{\left[ {{{u}_{1}}{{u}_{2}}{{u}_{3}}} \right]}^{T}};$ ${{\mu }_{0}} = \frac{{{{\mu }_{e}}}}{{{{a}^{3}}\omega _{0}^{2}}};$ $d = {{J}_{2}} - {{J}_{1}} - {{J}_{3}};$

$\begin{gathered} {{\kappa }_{1}} = {{4({{J}_{3}} - {{J}_{2}})} \mathord{\left/ {\vphantom {{4({{J}_{3}} - {{J}_{2}})} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}},\,\,\,\,{{{\bar {\kappa }}}_{2}} = {{3({{J}_{3}} - {{J}_{1}})} \mathord{\left/ {\vphantom {{3({{J}_{3}} - {{J}_{1}})} {{{J}_{2}}}}} \right. \kern-0em} {{{J}_{2}}}} + {\Gamma \mathord{\left/ {\vphantom {\Gamma {{{J}_{2}}}}} \right. \kern-0em} {{{J}_{2}}}}, \\ {{{\bar {\kappa }}}_{3}} = {{({{J}_{1}} - {{J}_{2}})} \mathord{\left/ {\vphantom {{({{J}_{1}} - {{J}_{2}})} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}} + {\Gamma \mathord{\left/ {\vphantom {\Gamma {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}};\,\,\,{{d}_{i}} = {d \mathord{\left/ {\vphantom {d {{{J}_{i}}}}} \right. \kern-0em} {{{J}_{i}}}},\,\,\,(i = 1,3); \\ {{\beta }_{j}} = {{{\text{sin}}I} \mathord{\left/ {\vphantom {{{\text{sin}}I} {{{J}_{j}}}}} \right. \kern-0em} {{{J}_{j}}}},\,\,\,\,(j = 1,2,3);\,\,\,\,{{\beta }_{4}} = {{\cos I} \mathord{\left/ {\vphantom {{\cos I} {{{J}_{1}}}}} \right. \kern-0em} {{{J}_{1}}}}, \\ {{\beta }_{5}} = {{\cos I} \mathord{\left/ {\vphantom {{\cos I} {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}. \\ \end{gathered} $

Для круговой орбиты $\omega _{0}^{2} = \frac{{{{\mu }_{g}}}}{{{{a}^{3}}}},$ где ${{\mu }_{g}}$ – гравитационный параметр Земли. Тогда параметр ${{\mu }_{0}} = \frac{{{{\mu }_{e}}}}{{{{\mu }_{g}}}}$ не зависит от радиуса орбиты.

Требуется построить управление, обеспечивающее асимптотическую устойчивость рассматриваемого положения относительного равновесия, основываясь на системе уравнений (2.4).

Отметим, что ранг матрицы коэффициентов при управлениях в системе (2.4) равен двум, поэтому среди управлений только два независимых.

3. ПРЕОБРАЗОВАНИЕ К СТАЦИОНАРНОЙ СИСТЕМЕ

Система (2.4) относится к классу линейных нестационарных систем, которые допускают приведение к стационарным системам большей размерности [24, 25]. Этот класс систем характеризуется тем, что функции, входящие в коэффициенты при управлении, являются решениями линейной однородной системы с постоянными коэффициентами.

Преобразование системы (2.4) к стационарной системе. Согласно [24, 25], введем новые переменные ${{y}_{j}}(j = 1,...8)$ по формулам

(3.1)

$\begin{gathered} {{x}_{1}} = {{y}_{1}}{\text{c}}\tau + {{y}_{3}}{\text{s}}\tau + {{y}_{5}},\,\,\,\,{{x}_{3}} = {{y}_{2}}{\text{c}}\tau + {{y}_{4}}{\text{s}}\tau + {{y}_{6}}, \\ {{x}_{2}} = {{y}_{7}}{\text{c}}\tau + {{y}_{8}}{\text{s}}\tau . \\ \end{gathered} $

Дважды дифференцируя эти соотношения, подставляя их в систему (2.4) и приравнивая коэффициенты при функциях $\operatorname{c} \tau ,\operatorname{s} \tau ,1,$ получим

(3.2)

$\begin{gathered} {{{\ddot {y}}}_{1}} - \kappa _{1}^{*}{{y}_{1}} - {{d}_{1}}{{{\dot {y}}}_{2}} + 2{{{\dot {y}}}_{3}} - {{d}_{1}}{{y}_{4}} = 0, \\ {{{\ddot {y}}}_{2}} - \kappa _{3}^{*}{{y}_{2}} + {{d}_{3}}{{{\dot {y}}}_{1}} + 2{{{\dot {y}}}_{4}} + {{d}_{3}}{{y}_{3}} = - {{\mu }_{0}}{{\beta }_{3}}{{u}_{2}}, \\ {{{\ddot {y}}}_{3}} - \kappa _{1}^{*}{{y}_{3}} - {{d}_{1}}{{{\dot {y}}}_{4}} - 2{{{\dot {y}}}_{1}} + {{d}_{1}}{{y}_{2}} = 2{{\mu }_{0}}{{\beta }_{1}}{{u}_{2}}, \\ {{{\ddot {y}}}_{4}} - \kappa _{3}^{*}{{y}_{4}} + {{d}_{3}}{{{\dot {y}}}_{3}} - 2{{{\dot {y}}}_{2}} - {{d}_{3}}{{y}_{1}} = 0, \\ \end{gathered} $

(3.3)

$\begin{gathered} {{{\ddot {y}}}_{5}} - {{\kappa }_{1}}{{y}_{5}} - {{d}_{1}}{{{\dot {y}}}_{6}} = {{\mu }_{0}}{{\beta }_{4}}{{u}_{3}}, \\ {{{\ddot {y}}}_{6}} - {{{\bar {\kappa }}}_{3}}{{y}_{6}} + {{d}_{3}}{{{\dot {y}}}_{5}} = - {{\mu }_{0}}{{\beta }_{5}}{{u}_{1}}, \\ {{{\ddot {y}}}_{7}} - \kappa _{2}^{*}{{y}_{7}} + 2{{{\dot {y}}}_{8}} = {{\mu }_{0}}{{\beta }_{2}}{{u}_{3}}, \\ {{{\ddot {y}}}_{8}} - \kappa _{2}^{*}{{y}_{8}} - 2{{{\dot {y}}}_{7}} = - 2{{\mu }_{0}}{{\beta }_{2}}{{u}_{1}}, \\ \end{gathered} $

$\kappa _{1}^{*} = {{\kappa }_{1}} + 1,\,\,\,\,\;\kappa _{i}^{*} = {{\bar {\kappa }}_{i}} + 1,\,\,\,\,(i = 2,3).$

Стационарная система (3.2), (3.3) состоит из двух независимых систем, в которые входят управления ${{u}_{2}}$ и ${{u}_{1}},{{u}_{3}}$ соответственно.

4. УПРАВЛЯЕМОСТЬ

Если считать, что ${{u}_{2}} = 0,$ то систему (3.2) рассматривать не требуется (переменные ${{y}_{1}},...{{y}_{4}}$ вводить не нужно). Расширенная стационарная система (3.3) тогда имеет 8-й порядок (порядок исходной нестационарной системы равен 6).

Управляемость в данной задаче можно исследовать, как исходя из анализа нестационарной системы (2.4), так и анализируя стационарную систему (3.3). Стационарная система является избыточной по отношению к исходной системе. Если стационарная система управляема, то управляема исходная нестационарная система. Однако неуправляемость стационарной системы может и не повлечь неуправляемость исходной нестационарной системы.

Далее полагаем, что рассматриваемая орбита не является ни полярной, ни экваториальной, т.е. $I \ne 0,$ $I \ne \frac{\pi }{2}$ (${{\beta }_{i}} \ne 0$).

4.1. Управляемость стационарной системы (3.3)

Согласно [24], стационарная система неуправляема, если в ней существует интеграл, не зависящий от наличия управлений. Умножим второе уравнение системы (3.3) на 2${{\beta }_{2}}$, четвертое уравнение на $ - {{\beta }_{5}}$ и сложим, ${{\beta }_{5}}\kappa _{2}^{*}{{y}_{4}} - 2{{\beta }_{2}}{{\bar {\kappa }}_{3}}{{y}_{6}} = 0.$ Откуда следует, что при выполнении условий $\kappa _{2}^{*} = 0,$ ${{\bar {\kappa }}_{3}} = 0$ т.е.

(4.1)

${{J}_{1}} = \frac{1}{4}(2{{J}_{2}} + 3{{J}_{3}}),\,\,\,\,\Gamma = \frac{1}{4}(2{{J}_{2}} - 3{{J}_{3}})$

в системе (3.3) существует не зависящий от наличия управления ${{u}_{1}}$ интеграл

$2{{\beta }_{2}}({{\dot {y}}_{6}} + {{d}_{3}}{{y}_{5}}) + {{\beta }_{5}}({{\dot {y}}_{8}} - 2{{y}_{7}}) = {\text{const}}{\text{.}}$

Умножим первое уравнение системы (3.3) на $2{{\beta }_{2}},$ третье уравнение на $ - {{\beta }_{4}}$ и сложим. Тогда в системе (3.3) существует не зависящий от наличия управления ${{u}_{3}}$ интеграл

${{\beta }_{2}}({{\dot {y}}_{5}} - {{d}_{1}}{{y}_{6}}) + {{\beta }_{4}}({{\dot {y}}_{7}} + 2{{y}_{8}}) = {\text{const,}}$

если выполняется условие $2{{\beta }_{2}}{{\kappa }_{1}}{{y}_{5}} - {{\beta }_{4}}\kappa _{2}^{*}{{y}_{7}} = 0$ или

(4.2)

${{\kappa }_{1}} = 0,\,\,\,\kappa _{2}^{*} = 0,\,\,\,{\text{т}}{\text{.е}}{\text{.}}\,\,\,{{J}_{2}} = {{J}_{3}},\,\,\,\Gamma = 3{{J}_{1}} - 4{{J}_{3}}.$

Итак, если условия (4.1), (4.2) не выполняются, то стационарная система (3.3) управляема, и следовательно, управляема исходная нестационарная система (2.4).

4.2. Управляемость нестационарной системы

Для исследования управляемости системы (2.4) представим ее в виде системы первого порядка

(4.3)

$\begin{gathered} \dot {\xi } = {{A}_{\xi }}\xi + {{B}_{\xi }}(\tau )u,\,\,\,\,\xi = {{\left[ {{{{\begin{array}{*{20}{c}} {{{x}_{1}}}&{{{x}_{3}}}&{{{{\dot {x}}}_{1}}}&{{{{\dot {x}}}_{3}}}&{{{x}_{2}}}&{\dot {x}} \end{array}}}_{2}}} \right]}^{T}}, \\ {{A}_{\xi }} = {\text{diag}}({{A}_{1}},{{A}_{2}}), \\ \end{gathered} $

$\begin{gathered} {{A}_{1}} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}}&{{{E}_{2}}} \\ {{{K}_{1}}}&{ - {{D}_{1}}} \end{array}} \right],\,\,\,\,{{K}_{1}} = {\text{diag}}({{\kappa }_{1}},{{{\bar {\kappa }}}_{3}}),\,\,\,\,{{D}_{1}} = \left[ {\begin{array}{*{20}{c}} 0&{ - {{d}_{1}}} \\ {{{d}_{3}}}&0 \end{array}} \right], \\ {{A}_{2}} = \left[ {\begin{array}{*{20}{c}} 0&1 \\ {{{{\bar {\kappa }}}_{2}}}&0 \end{array}} \right],\,\,\,\,{{B}_{\xi }}(\tau ) = \left[ {\begin{array}{*{20}{c}} {{{B}^{{(1)}}}} \\ {{{B}^{{(2)}}}} \end{array}} \right],\,\,\,\,\mathop {{{B}^{{(1)}}}}\limits_{4 \times 2} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}} \\ {{{B}_{1}}(\tau )} \end{array}} \right], \\ \mathop {{{B}^{{(2)}}}}\limits_{2 \times 2} = \left[ {\begin{array}{*{20}{c}} {{{O}_{{12}}}} \\ {{{B}_{2}}(\tau )} \end{array}} \right], \\ \end{gathered} $

${{B}_{1}} = {{\mu }_{0}}\left[ {\begin{array}{*{20}{c}} 0&{{{\beta }_{4}}} \\ { - {{\beta }_{5}}}&0 \end{array}} \right],\,\,\,\,{{B}_{2}} = {{\mu }_{0}}[\begin{array}{*{20}{c}} { - 2{{\beta }_{2}}\sin \tau }&{{{\beta }_{2}}\cos \tau } \end{array}].$

Здесь ${{O}_{2}}(2 \times 2),$ ${{O}_{{12}}}(1 \times 2)$ – нулевые матрицы соответствующих размеров

Нестационарная система (4.3), согласно критерию [28], управляема, если можно указать такую точку $\tau *,$ в которой

(4.4)

${\text{rank}}U(\tau *) = 6,$

$\begin{gathered} {{U}_{1}}(\tau ) = \left[ {{{W}_{1}}(\tau )...{{W}_{6}}(\tau )} \right],\,\,\,\,{{W}_{1}}(\tau ) = B(\tau ), \\ {{W}_{k}}(\tau ) = {{A}_{\xi }}(\tau ){{W}_{{k - 1}}}(\tau ) - {{{\dot {W}}}_{{k - 1}}}(\tau ),\,\,\,\,(k = 2,...,6). \\ \end{gathered} $

Матрица $U(\tau )$ имеет вид

$U(\tau ) = \left[ {\begin{array}{*{20}{c}} 0&0&0&{{{\beta }_{4}}}&{ - {{d}_{1}}{{\beta }_{5}}}&0&0&{{{l}_{{26}}}{{\beta }_{4}}} \\ 0&0&{ - {{\beta }_{5}}}&0&0&{ - {{d}_{3}}{{\beta }_{4}}}&{{{l}_{{45}}}{{\beta }_{5}}}&0 \\ 0&{{{\beta }_{4}}}&{ - {{d}_{1}}{{\beta }_{5}}}&0&0&{{{l}_{{26}}}{{\beta }_{4}}}&{{{l}_{{27}}}{{\beta }_{5}}}&0 \\ { - {{\beta }_{5}}}&0&0&{ - {{d}_{3}}{{\beta }_{4}}}&{{{l}_{{45}}}{{\beta }_{5}}}&0&0&{{{l}_{{48}}}{{\beta }_{4}}} \\ 0&0&{ - 2{{\beta }_{2}}{\text{s}}\tau }&{{{\beta }_{2}}{\text{c}}\tau }&{4{{\beta }_{2}}{\text{c}}\tau }&{2{{\beta }_{2}}{\text{s}}\tau }&{2{{l}_{{57}}}{{\beta }_{2}}{\text{s}}\tau }&{{{l}_{{58}}}{{\beta }_{2}}{\text{c}}\tau } \\ { - 2{{\beta }_{2}}s\tau }&{{{\beta }_{2}}{\text{c}}\tau }&{2{{\beta }_{2}}{\text{c}}\tau }&{{{\beta }_{2}}{\text{s}}\tau }&{2{{l}_{{65}}}{{\beta }_{2}}{\text{s}}\tau }&{{{l}_{{66}}}{{\beta }_{2}}{\text{c}}\tau }&{2{{l}_{{67}}}{{\beta }_{2}}{\text{c}}\tau }&{{{l}_{{68}}}{{\beta }_{2}}{\text{s}}\tau } \end{array}} \right],$

$\begin{gathered} {{l}_{{26}}} = - {{d}_{1}}{{d}_{3}} + {{\kappa }_{1}},\,\,\,\,{{l}_{{45}}} = {{d}_{1}}{{d}_{3}} - {{{\bar {\kappa }}}_{3}},\,\,\,\,{{l}_{{48}}} = - {{d}_{3}}({{l}_{{26}}} + {{{\bar {\kappa }}}_{3}}), \\ {{l}_{{65}}} = - {{l}_{{66}}} = 1 - {{{\bar {\kappa }}}_{2}},\,\,\,\,{{l}_{{27}}} = {{d}_{1}}({{l}_{{45}}} - {{\kappa }_{1}}),\,\,\,\,{{l}_{{57}}} = 2 + {{l}_{{65}}}, \\ {{l}_{{67}}} = {{l}_{{68}}} = 2{{{\bar {\kappa }}}_{2}} - {{l}_{{65}}},\,\,\,\,{{l}_{{58}}} = {{l}_{{66}}} - 2. \\ \end{gathered} $

Нетрудно видеть, что первые пять столбцов матрицы управляемости $U(\tau )$ линейно независимы при любых значениях параметров. Можно показать, что шестой столбец матрицы $U(\tau )$ является линейной комбинацией первых пяти только при выполнении условия (4.2). (При условии (4.1) ${\text{rank}}U(\tau ) = 6$). Рассмотрим ранг матрицы $U(\tau ),$ составленной из первых пяти столбцов и седьмого. В этом случае седьмой столбец является линейной комбинацией первых пяти, если выполнены условия

(4.5)

${{J}_{2}} = {{J}_{3}} = 3{{J}_{1}},\,\,\,\,\Gamma = - 9{{J}_{1}}.$

Если выполнены условия (4.5), то зависимыми оказываются все последующие столбцы матрицы $U(\tau ),$ в том числе и не выписанные здесь.

Таким образом, условиями неуправляемости исходной нестационарной системы (4.3) являются условия (4.5). В частности, при отсутствии аэродинамических сил ($\Gamma = 0$) эти условия не выполняются, т.е., как уже указывалось в [12], система (4.3) управляема при любых значениях моментов инерции спутника.

Замечание (см. [3]). В работе [20] указаны лишь достаточные условия управляемости системы (4.5) для любой не экваториальной орбиты, имеющие вид

(4.6)

$\begin{gathered} {{J}_{3}} \ne {{J}_{2}},\, \\ {{J}_{3}}\left[ {6({{J}_{3}} - {{J}_{1}}) + 2\Gamma } \right] \ne {{J}_{2}}({{J}_{1}} - {{J}_{2}} + {{J}_{3}} - 2\Gamma ). \\ \end{gathered} $

В самом деле, если тензор инерции спутника, например, – шаровой (${{J}_{1}} = {{J}_{2}} = {{J}_{3}}$), то условия (4.6) нарушаются. В то время как согласно условию (4.5) управляемость имеет место.

5. АЛГОРИТМ ПОСТРОЕНИЯ СТАБИЛИЗИРУЮЩЕГО УПРАВЛЕНИЯ

Анализ управляемости, проведенный выше, показал, что система (3.3) управляема, за исключением случая (4.5).

Алгоритм стабилизации строится на основании системы (3.3), в предположении, что условия (4.5) не выполнены.

Для построения алгоритма стабилизации удобнее представить систему (3.3) в форме Коши, вводя переменные

$\begin{gathered} {{z}_{1}} = {{y}_{5}},\,\,\,\,{{z}_{2}} = {{y}_{6}},\,\,\,\,{{z}_{3}} = {{{\dot {y}}}_{5}},\,\,\,\,{{z}_{4}} = {{{\dot {y}}}_{6}},\,\,\,\,{{z}_{5}} = {{y}_{7}}, \\ {{z}_{6}} = {{y}_{8}},\,\,\,\,{{z}_{7}} = {{{\dot {y}}}_{7}},\,\,\,\,{{z}_{8}} = {{{\dot {y}}}_{8}}, \\ \end{gathered} $

которые удовлетворяют системе уравнений

(5.1)

$\dot {z} = {{A}_{z}}z + {{B}_{z}}\bar {u},\,\,\,\,\bar {u} = {{({{u}_{1}}{{u}_{3}})}^{T}},$

$\begin{gathered} {{A}_{z}} = {\text{diag}}({{A}_{{z1}}},{{A}_{{z2}}});\,\,\,\,{{A}_{{z1}}} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}}&{{{E}_{2}}} \\ {K_{{\text{1}}}^{*}}&{ - {{D}_{1}}} \end{array}} \right], \\ {{A}_{{z2}}} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}}&{ - {{E}_{2}}} \\ {K_{{\text{2}}}^{*}}&{ - {{D}_{2}}} \end{array}} \right], \\ K_{{\text{1}}}^{*} = {\text{diag}}({{\kappa }_{1}},{{{\bar {\kappa }}}_{3}}),\,\,\,\,K_{{\text{2}}}^{*} = {\text{diag}}\left( {\kappa _{{\text{2}}}^{*},\kappa _{{\text{2}}}^{*}} \right), \\ {{D}_{2}} = \left[ {\begin{array}{*{20}{c}} 0&{ - 2} \\ 2&0 \end{array}} \right], \\ \end{gathered} $

${{B}_{z}} = \left[ {\begin{array}{*{20}{c}} {{{O}_{2}}} \\ {{{B}_{1}}} \\ {{{O}_{2}}} \\ {{{B}_{2}}} \end{array}} \right],\,\,\,\,{{B}_{1}} = {{\mu }_{0}}\left[ {\begin{array}{*{20}{c}} 0&{{{\beta }_{4}}} \\ { - {{\beta }_{5}}}&0 \end{array}} \right],\,\,\,\,{{B}_{2}} = {{\mu }_{0}}\left[ {\begin{array}{*{20}{c}} 0&{{{\beta }_{2}}} \\ { - 2{{\beta }_{2}}}&0 \end{array}} \right].$

Задача стабилизации стационарной управляемой системы (5.1) состоит в том, чтобы построить управление $\bar {u},$ обеспечивающее стремление к нулю компонент вектора состояния $z(\tau )$ при $\tau \to \infty .$ Стабилизирующее управление $\bar {u}(\tau )$ строится в виде обратной связи по состоянию $\bar {u}(\tau ) = - {{K}_{z}}z(\tau ),$ а матрица коэффициентов управления ${{K}_{z}}(2 \times 8) = {\text{const}}$ выбирается из условия минимума квадратичного функционала

$J = \frac{1}{2}\int\limits_0^\infty {\left[ {{{z}^{T}}(\tau )Qz(\tau ) + {{{\bar {u}}}^{T}}(\tau )W\bar {u}(\tau )} \right]} d\tau .$

Здесь $Q\;{\text{и}}\;W$ – положительно определенные постоянные матрицы размерности $8 \times 8$ и $2 \times 2$ соответственно.

Оптимальное управление имеет вид [29]

(5.2)

$\bar {u}(\tau ) = - {{K}_{z}}z(\tau ),\,\,\,\,{{K}_{z}} = {{W}^{{ - 1}}}{{B}_{z}}P.$

Матрица $P$ размерности $8 \times 8$ является положительно определенным решением матричного алгебраического уравнения Риккати

$P{{A}_{z}} + A_{z}^{T}P - P{{B}_{z}}{{W}^{{ - 1}}}B_{z}^{T}P + Q = 0.$

Синтезированное управляющее воздействие является функцией переменных $z(\tau )$ стационарной системы (5.1) более высокого порядка, чем исходная нестационарная система (4.3). Для введения управления непосредственно в исходную систему (4.3) выразим вектор $z(\tau )(8 \times 1)$ через исходный вектор состояния $\xi (6 \times 1),$ дополненный вектором $\xi {\kern 1pt} ' = {{[{{\xi }_{7}}{{\xi }_{8}}]}^{T}}$ так, чтобы матрица $T$ преобразования

(5.3)

$\bar {\xi } = Tz,\,\,\,\,\left( {\bar {\xi } = {{{[\xi \xi {\kern 1pt} ']}}^{T}}} \right)$

была невырожденной.

Компоненты вектора $\bar {\xi }$ связаны с компонентами вектора состояния $z(\tau )$ стационарной системы (5.1) соотношениями

(5.4)

$\begin{gathered} {{x}_{1}} = {{\xi }_{1}} = {{z}_{1}},\,\,\,{{x}_{3}} = {{\xi }_{2}} = {{z}_{2}}, \\ {{{\dot {x}}}_{1}} = {{\xi }_{3}} = {{z}_{3}},\,\,\,{{{\dot {x}}}_{3}} = {{\xi }_{4}} = {{z}_{4}}, \\ {{x}_{2}} = {{\xi }_{5}} = {{z}_{5}}\operatorname{c} \tau + {{z}_{7}}\operatorname{s} \tau ,\,\,\,\,{{{\dot {x}}}_{2}} = {{\xi }_{6}} = {{z}_{6}}\operatorname{c} \tau + {{z}_{8}}\operatorname{s} \tau , \\ {{\xi }_{7}} = - {{z}_{5}}\operatorname{s} \tau + {{z}_{7}}\operatorname{c} \tau ,\,\,\,\,{{\xi }_{8}} = - {{z}_{6}}\operatorname{s} \tau + {{z}_{8}}\operatorname{c} \tau . \\ \end{gathered} $

Матрица преобразования имеет вид

$T(\tau ) = {\text{diag}}({{T}_{1}},{{T}_{2}}),\,\,\,\,{{T}_{1}} = {{E}_{4}},\,\,\,\,{{T}_{2}}(\tau ) = \left[ {\begin{array}{*{20}{c}} {\operatorname{c} \tau {{E}_{2}}}&{\operatorname{s} \tau {{E}_{2}}} \\ { - \operatorname{s} \tau {{E}_{2}}}&{\operatorname{c} \tau {{E}_{2}}} \end{array}} \right].$

Уравнения для дополнительного вектора $\xi {\kern 1pt} ' = {{[{{\xi }_{7}}{{\xi }_{8}}]}^{T}}$ имеют вид

(5.5)

$\dot {\xi }{\kern 1pt} ' = {{A}_{2}}\xi {\kern 1pt} '\, + B{\kern 1pt} '(\tau )\tilde {u},\,\,\,\,B{\kern 1pt} '(\tau ) = {{B}_{0}}\left[ {\begin{array}{*{20}{c}} { - 2{{\beta }_{2}}\operatorname{c} \tau }&{{{\beta }_{2}}\operatorname{s} \tau } \end{array}} \right].$

Тогда уравнение для вектора $\tilde {\xi }$ можно записать в виде

(5.6)

$\begin{gathered} \dot {\bar {\xi }} = {{{\bar {A}}}_{\xi }}\bar {\xi } + {{{\bar {B}}}_{\xi }}(\tau )\bar {u},\,\,\,\,{{{\bar {A}}}_{\xi }} = {\text{diag}}({{A}_{1}},{{A}_{2}},{{A}_{2}}), \\ {{{\bar {B}}}_{\xi }} = {{B}_{0}}\left[ {\begin{array}{*{20}{c}} {{{B}^{{(1)}}}(\tau )} \\ {{{B}^{{(2)}}}(\tau )} \\ {B{\kern 1pt} {\text{'}}(\tau )} \end{array}} \right]. \\ \end{gathered} $

Нестационарная система (5.6) включает в себя исходную систему (4.3), в качестве подсистемы. Управление (5.2), построенное для стационарной системы (5.1), при помощи выражения (5.3) можно ввести в систему (5.6) в виде

$\bar {u} = - {{K}_{z}}{{T}^{{ - 1}}}(\tau )\bar {\xi }.$

Замкнутая этим управлением система имеет вид

(5.7)

$\dot {\bar {\xi }} = \left( {{{{\bar {A}}}_{\xi }} - {{{\bar {B}}}_{\xi }}(\tau ){{K}_{z}}{{T}^{{ - 1}}}(\tau )} \right)\bar {\xi }.$

Решения $\bar {\xi }(\tau )$ системы (5.7), содержащие компоненты исходного вектора $\xi (\tau ),$ стремятся к нулю при $\tau \to \infty ,$ в силу выбора матрицы ${{K}_{z}},$ т. к. компоненты вектора $\bar {\xi }$ связаны с компонентами вектора $z$ ограниченным преобразованием (5.4).

6. МОДЕЛИРОВАНИЕ

Цель проведения моделирования – показать влияние величины аэродинамического момента на процесс стабилизации.

Моделирование проводилось в пакете MATLAB 7.1. Коэффициенты вычислялись и использованием стандартной программы LQR для стационарной системы восьмого порядка (5.1). Характеристики квадратичного функционала $Q = q{{E}_{8}},$ $W = w{{E}_{2}}.$

Рассматривалась стабилизация спутника с параметрами ${{J}_{1}} = 0.036\,\,{\text{кг}} \cdot {{{\text{м}}}^{2}},$ ${{J}_{2}} = 0.09\,\,{\text{кг}} \cdot {{{\text{м}}}^{2}},$ ${{J}_{3}} = 0.088\,\,{\text{кг}} \cdot {{{\text{м}}}^{2}}$ [20]. Угол наклона орбиты $I = 51.6^\circ .$ Высота орбиты $H = 415\,\,{\text{км}}{\text{.}}$ Начальные отклонения по углам 0.15, 0.15, 0.2 по скоростям 0.1, 0.1, 0.15. Величины

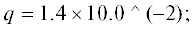
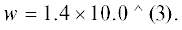
На рис. 1, 2 представлено поведение переменных ${{\theta }_{i}},$ ${{d{{\theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\theta }_{i}}} {d\tau }}} \right. \kern-0em} {d\tau }}\,\,(i = 1,2,3)$ в зависимости от величины аэродинамического момента, где использованы обозначения ${{\Gamma }_{0}} = 0,$ ${{\Gamma }_{1}} = 0.5 \times [3.0 \times \left( {{{J}_{3}} - {{J}_{1}}} \right)],$ ${{\Gamma }_{2}} = 3.0 \times \left( {{{J}_{3}} - {{J}_{1}}} \right).$

Рис. 1.

Влияние аэродинамического момента на процесс стабилизации углов ${{\theta }_{i}}(i = 1,2,3){\text{:}}$ а) ${{\theta }_{1}}(\tau );$ б) ${{\theta }_{2}}(\tau );$ в) ${{\theta }_{3}}(\tau ).$

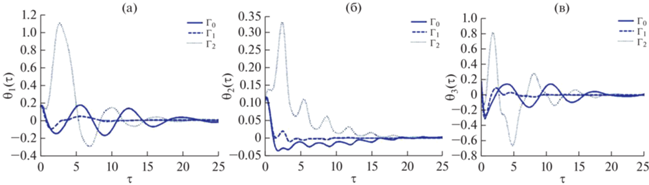
Рис. 2.

Влияние аэродинамического момента на процесс стабилизации угловых скоростей ${{d{{\theta }_{i}}} \mathord{\left/ {\vphantom {{d{{\theta }_{i}}} {d\tau }}} \right. \kern-0em} {d\tau }}\,\,(i = 1,2,3){\text{:}}$ а) ${{d{{\theta }_{1}}(\tau )} \mathord{\left/ {\vphantom {{d{{\theta }_{1}}(\tau )} {d\tau }}} \right. \kern-0em} {d\tau }};$ б) ${{d{{\theta }_{2}}(\tau )} \mathord{\left/ {\vphantom {{d{{\theta }_{2}}(\tau )} {d\tau }}} \right. \kern-0em} {d\tau }};$ в) ${{d{{\theta }_{3}}(\tau )} \mathord{\left/ {\vphantom {{d{{\theta }_{3}}(\tau )} {d\tau }}} \right. \kern-0em} {d\tau }}.$

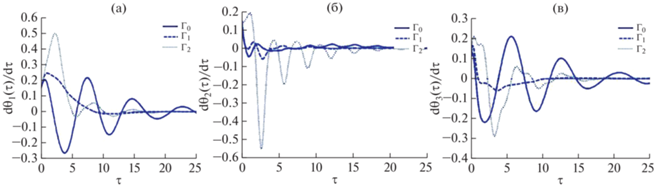
Из рисунков видно, что величина аэродинамического момента практически не сказывается на времени сходимости, но существенно влияет на амплитуду переходного процесса.

Предлагаемый алгоритм применим для спутников с различными моментами инерции и при различных углах наклона и высот орбит.

ЗАКЛЮЧЕНИЕ

Линеаризованная в окрестности положения относительного равновесия система уравнений движения спутника относится к специальному классу линейных нестационарных систем, допускающих приведение к стационарным системам большей размерности. При помощи соответствующего конструктивного преобразования получена стационарная система. Исследована управляемость системы как стационарной, так и нестационарной. Достаточные условия управляемости стационарной системы получены при помощи условий существования в системе линейных интегралов, не зависящих от наличия управлений.

Следует подчеркнуть, что в отличие от других работ преимущество предлагаемого алгоритма стабилизации положения относительного равновесия в том, что для его построения требуется лишь задание параметров квадратичного функционала, и его применение гарантирует асимптотическую устойчивость.

Проведенное математическое моделирование подтверждает эффективность предложенной методики.

Список литературы

Morozov V.M., Kalenova V.I. Linear time-varying systems and their applications to cosmic problems // AIP Conference Proceedings (The Eighth Polyakhov’s Reading: Proceedings of the International Scientific Conference on Mechanics). V. 1959. P. 020003–020003. https://doi.org/10.1063/1.5034579
Морозов В.М., Каленова В.И. Управление с помощью магнитных моментов ориентацией спутника, движущегося по полярной орбите // Инженерный журн.: наука и инновации. 2018. Т. 81. № 9. С. 8–14. https://doi.org/10.18698/2308-6033-2018-9-1798
Морозов В.М., Каленова В.И. Управление спутником при помощи магнитных моментов: управляемость и алгоритмы стабилизации // Космич. исслед. 2020. Т. 58. № 3. С. 199–207.
Kalenova V.I., Morozov V.M. Novel Approach to Attitude Stabilization of Satellite using Geomagnetic Lorentz forces // Aerosp. Sci. Technol. 2020. V. 106. https://doi.org/10.1016/j.ast.2020.106105
Каленова В.И., Морозов В.М. Стабилизация положения относительного равновесия спутника при помощи магнитных и лоренцевых моментов // Космич. исслед. 2021. Т. 59. № 5. С. 1–15.
Морозов В.М., Каленова В.И., Рак М.Г. О стабилизации регулярных прецессий спутника при помощи магнитных моментов // ПММ. 2021. Т. 85. № 4. С. 436–453.
Белецкий В.В. Движение искусственного спутника относительно центра масс. М.: Наука, 1965.
Sarychev V.A., Mirer S.A. Relative Equilibria of a Satellite // Celestial Mechanics and Dynamical Astronomy. 2000. V. 76. № 1. P. 55–68.
Rawashdeh A., Lumpp J.E., Rawashdeh J. et al. Aerodynamic Stability for CubeSats at ISS Orbit // J. Small Satellite. 2013. V. 2. № 1. P. 85–104.
Белоконов И.В., Иванов Д.С. и др. Система демпфирования углового движения наноспутника SamSat-QB50 // Препринты ИПМ им. М.В. Келдыша. 2015. Т. 59. С. 1–28.
Mostaza-Prieto D., Roberts P.C.E. Methodology to Analyze Attitude Stability of Satellites Subjected to Aerodynamic Torques // J. Guidance Control and Dynamics. 2016. V. 39. P. 437–449. https://doi.org/10.2514/1.G001481
Sarychev V.A., Mirer S.A., Degtyarev A.A., Duarte E.K. Investigation of equilibria of a satellite subjected to gravitational and aerodynamic torques // Celestial Mechanics and Dynamical Astronomy. 2007. V. 97. № 4. P. 267–287.
Морозов В.М. Об устойчивости относительного равновесия спутника при действии гравитационного, магнитного и аэродинамического моментов // Космич. исслед. 1969. Т. 7. № 3. С. 395–401.
Silani E., Lovera M. Magnetic spacecraft attitude control: a survey and some new results // Control engineering practice. 2005. V. 13. P. 357–371.
Lovera M., Astolfi A. Global Magnetic Attitude Control of Spacecraft in the Presence of Gravity Gradient // IEEE Trans. On Aerospace and Electronic Systems. 2006. V. 12. P. 796–805.
Ovchinnikov M.Yu., Roldugin D.S., Penkov V.I. Three-axis active magnetic attitude control asymptotical study // Acta Astronautica. 2015. V. 110. P. 279–286.
Ovchinnikov M.Yu., Roldugin D.S. A survey on active magnetic attitude control algorithms for small satellites // Progress in Aerospace Sciences. 2019. V. 109. P. 100 546. https://doi.org/10.1016/j.paerosci.2019.05.006
Овчинников М.Ю., Ролдугин Д.С. Современные алгоритмы активной магнитной ориентации спутников // Космические аппараты и технологии. 2019. Т. 3. № 2(28). С. 73–86. https://doi.org/10.26732/2618-7957-2019-2-73-86
Psiaki M.L. Nanosatellite Attitude Stabilization Using Passive Aerodynamics and Active Magnetic Torquing // J. Guidance, Control, and Dynamics. 2004. V. 27. P. 347–355.
Sutherland R., Kolmanovsky I.K., Girard A.R. Attitude Control of a 2U Cubesat by Magnetic and Air Drag Torques // Trans. Control Systems Technology. IEEE. 2017. arXiv:1707.04959.
Ivanov D.S., Ovchinnikov M.Y. et al. Advanced numerical study of the three-axis magnetic attitude control and determination with uncertainties // Acta Astronautica. 2017. V. 132. P. 103–110.
Aleksandrov A.Yu., Tikhonov A.A. Asymptotic stability of a satellite with electrodynamic attitude control in the orbital frame // Acta Astronautica. 2017. V. 139. P. 122–129.
Aleksandrov A.Yu., Aleksandrova E.B., Tikhonov A.A. Stabilization of a programmed rotation mode for a satellite with electrodynamic attitude control system // Advances in Space Research. 2018. V. 62. P. 142–151.
Каленова В.И., Морозов В.М. Линейные нестационарные системы и их приложения к задачам механики. М.: Физматлит, 2010.
Каленова В.И., Морозов В.М. Приводимость линейных нестационарных систем второго порядка с управлением и наблюдением // ПММ. 2012. Т. 76. № 4. С. 576–588.
Белецкий В.В. Движение спутника относительно центра масс в гравитационном поле. М.: Изд-во Моск. ун-та, 1975.
Wertz J. Spacecraft attitude determination and control. Dordrecht: D. Reidel Publishing Company, 1978.
Красовский Н.Н. Теория управления движением. Линейные системы. М.: Наука, 1968.
Ройтенберг Я.Н. Автоматическое управление. М.: Наука, 1978.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Космические исследования

Архивы выпусков Информация о журнале Отправить рукопись в журнал