Кристаллография, 2020, T. 65, № 5, стр. 715-724
Отображения четырехмерного 240-вершинного многогранника {240}. I. линейные алмазоподобные структуры и тетракоординированные цепи
А. Л. Талис 1, *, А. Л. Рабинович 2
1 Институт элементоорганических соединений им. А.Н. Несмеянова РАН
Москва, Россия
2 Институт биологии КарНЦ РАН
Петрозаводск, Россия
* E-mail: talishome@mail.ru
Поступила в редакцию 12.12.2019
После доработки 12.12.2019
Принята к публикации 20.02.2020
Аннотация
Рассмотрены отображения линейных подструктур четырехмерного 240-вершинного алмазоподобного многогранника – политопа {240} в трехмерное евклидово пространство. Выявлены варианты этих подструктур, определяющие “идеальные прототипы” линейных тетракоординированных структур, графы которых не содержат висячих вершин или циклов. Полученные варианты выявляют линейные алмазоподобные подструктуры и тетракоординированные цепи различного состава, некристаллографическая (скрытая) симметрия которых способна обеспечить их объединение в соответствии с симметриями политопа {240} или восьмимерной решетки Е8.
ВВЕДЕНИЕ
“Политоп” {240}, впервые описанный в работах [1, 2], затем в [3–5], – это конечный аналог алмазоподобной структуры в четырехмерном евклидовом пространстве E4. Он содержит 240 вершин, все они являются тетракоординированными и лежат в E4 на трехмерной сфере S3 (принадлежат пространству постоянной положительной кривизны). Политоп {240} можно представить объединением двух копий правильного четырехмерного многогранника – политопа {3, 3, 5} (четырехмерного аналога икосаэдра) [5–7], который является объединением 600 одинаковых правильных тетраэдров (“ячеек”) в S3, имеет 120 вершин, 720 ребер, 1200 граней в виде правильных треугольников. Отличительные характеристики политопа {3, 3, 5} отражены в его обозначении: любая грань тетраэдра {3, 3} содержит три вершины, в каждой вершине сходятся три треугольника, у каждого ребра политопа объединяются пять тетраэдров. Каждая вершина в политопе {3, 3, 5} соединена ребрами с 12 ближайшими, которые являются вершинами правильного икосаэдра, все 13 вершин являются вершинами 20 тетраэдров, для которых центральная вершина икосаэдра является общей [6, 7]. В политопе {240} все вершины обеих копий политопа {3, 3, 5} (условно “белой” и “черной”) лежат на одной и той же сфере S3, но один многогранник повернут относительно другого [5, 6]. При этом 120 белых вершин находятся в центрах 120 из шестисот черных тетраэдров, а 120 черных вершин – в центрах 120 из шестисот белых тетраэдров. Группой политопа {3, 3, 5} является Y' × Y '/Z2, ее порядок равен 26 ⋅ 32 ⋅ 52 = 14 400; группа политопа {240} есть O' × Y '/Z2, ее порядок равен 26 ⋅ 32 ⋅ 5 = = 2880 [5, 6]. Здесь знак × обозначает прямое произведение, O' и Y ' – “удвоенные” группы O и Y соответственно, в которых к каждому элементу g точечной группы симметрии добавляется его образ σg (преобразование группы неточечной симметрии) в специальной унитарной группе SU, образованной матрицами 2 × 2 [5]:
где σ2 = 1, m – плоскость симметрии, O – точечная группа вращений октаэдра; Oh – группа симметрии октаэдра, Y – точечная группа вращений икосаэдра, Yh – группа симметрии икосаэдра, Z2 – группа 2-го порядка; ↔ – символ изоморфизма.Политоп {3, 3, 5} (политоп{240}) является “идеальным прототипом” для тетраэдрических (тетракоординированных) структур, поэтому решение ряда задач достигается отображением этих политопов в трехмерное евклидово пространство E3 [5, 8]. Такое отображение позволяет получить линейные структуры (или фрагменты структур), которые можно объединить в E3 по закону политопа {3, 3, 5} или определяющей его восьмимерной решетки Е8. Данную некристаллографическую симметрию можно назвать подрешетчатой некристаллографической симметрией, а симметрия есть геометрический эквивалент физического требования минимума энергии трехмерной системы [9, с. 31]. Например, если реальная упаковка атомов может быть аппроксимирована только правильными тетраэдрами, то политоп {3, 3, 5} может служить ее прототипом для описания в ней ближнего порядка и закона объединения плотнейших линейных упаковок тетраэдров [5, 10, 11]. Идеальная структура “прототипа” на S3 может быть спроектирована в структуру в пространстве E3 прокатыванием (без скольжения) сферы S3 по евклидовому многообразию вдоль фиксированной траектории [10]. В частности, такой алгоритм позволяет априори определять строение упорядоченных (не только кристаллических) структур. Обоснованием такого метода служит теорема: “Существует евклидова метрика, соприкасающаяся с данной (римановой [12]) метрикой вдоль всей данной кривой” [12, р. 99], поскольку одним из ее следствий является утверждение о том, что “отображение риманова пространства на соприкасающееся евклидово сохраняет расстояния, измеренные в соседстве с заданной кривой, с точностью до бесконечно малых второго порядка” [12, p. 101].
“Идеальные прототипы” структур обладают высокой вероятностью реализации, хотя и претерпевают физически допустимые искажения. В настоящей работе с помощью расслоения Хопфа рассмотрены отображения в E3 линейных подструктур политопа {240}. Выявлены варианты, в которых эти подструктуры образуют наряду с известной алмазоподобной структурой “канала” [5] новые конструкции тетракоординированных цепей различного состава. Полученные результаты являются основой для определения некристаллографической (скрытой) симметрии подобных структур, которая способна обеспечить их объединение по закону политопа {240} или восьмимерной решетки Е8.
СТРУКТУРНЫЕ ХАРАКТЕРИСТИКИ ПОЛИТОПА {240}
Политоп {240} обладает структурными характеристиками, которые для тетракоординированных систем являются экстремальными. Одна из них – плотность окружения данной вершины другими вершинами. Критерием количественной оценки плотности может служить количество гексациклов (замкнутых шестерок последовательных связей), сходящихся на данной вершине. В [5] этот критерий был предложен для оценки степени “ближнего порядка” в тетракоординированных структурах. Такой гексацикл может принимать три конформации: “кресло”, “ванна” и “скрученная ванна” (твист-ванна) [5]. При этом в каждой из трех конформаций гексацикла длины связей и валентные углы равны своим равновесным значениям, поэтому все три конформации являются низкоэнергетическими. Из гексациклов в конформации “скрученная ванна” можно собрать кластер, содержащий 27 вершин (атомов), в котором все гексациклы замыкаются на одной вершине, – на рис. 1а это центральная белая вершина 1 [5]. Цифрами без штриха обозначены номера белых вершин, со штрихом – черных. Кластер на рис. 1а отличается тем, что в нем количество “оборванных” связей, т.е. связей, направленных наружу из этого кластера (всего их 28 [5]), меньше, чем количество оборванных связей в любом кластере сопоставимого размера с алмазоподобной структурой [5]. Дополним эти данные и другими характеристиками структуры этого 27-вершинного кластера, позволяющими выделить его среди фрагментов алмазоподобных структур.
Рис. 1.
Кластер из 27 вершин (атомов), образованный гексациклами в конформации “скрученная ванна” (адаптировано из [5]). Это “вершинная фигура” политопа {240} (объединения “белого” и “черного” политопов {3, 3, 5}), в которой все гексациклы (их 18) сходятся в центральной белой вершине 1 [5, 6] (а); структура алмаза, объединение “белой” и “черной” гранецентрированных кубических решеток. В белой вершине 1 сходятся 12 гексациклов (б). Кластеры а и б содержат цепи вершин, например 10–3'–1–4'–11.
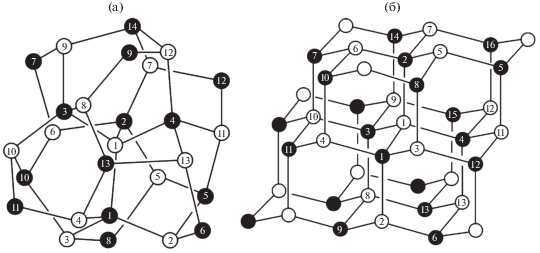
I. Этот кластер содержит меньше вершин, чем аналогичный минимальный фрагмент структуры алмаза. В этом можно убедиться при сравнении рис. 1а с рис. 1б, на котором представлена структура алмаза как объединение двух – “черной” и “белой” – гранецентрированных кубических решеток. Все вершины, образующие гексациклы (“кресло”), сходящиеся на вершине 1, пронумерованы. В этот минимальный фрагмент структуры алмаза вошло 29 вершин (13 белых и 16 черных), при этом количество “оборванных” связей равно 35, т.е. на одну вершину кластера приходится 35/29 “оборванных” связей, что больше, чем 28/27 “оборванных” связей в кластере на рис. 1а.
II. Каждая из 240 вершин политопа {240} является центром кластера (рис. 1а), обладающего точечной группой T порядка 12, поэтому порядок группы симметрии политопа 2880 = 12 ⋅ 240 [3–5]. Кластер представляет собой объединение правильных многогранников: центрированного икосаэдра (на рис. 1а его образуют вершины 2, 3, …, 13, центр – вершина 1), двух тетраэдров (вершины 1', 2', 3', 4' и 5', 10', 13', 14') и октаэдра (шесть вершин 6', 7', 8', 9', 11', 12'). В то же время этот кластер является “вершинной фигурой” политопа {240} [6, p. 298–299, Tabl. V], т.е. объединением в Е3 нескольких его параллельных трехмерных “сечений”, отличающихся “четвертой координатой” секущего пространства Е3. Эти сечения возникают в Е3 в “процессе” пересечения трехмерного пространства политопом {240}, который исходно имеет с этим пространством единственную общую точку (0, 0, 0). Последовательные сечения представляют собой точку, тетраэдр, икосаэдр, второй тетраэдр, октаэдр [6, p. 298–299, Tabl. V]. Эти “сечения” дают представление о взаимном расположении вершин политопа {240}. Оси 3-го и 2-го порядка группы T являются общими осями всех этих многогранников. Политопу {240} присуща хиральность, он может быть правым или левым (с правыми или левыми конформациями “скрученная ванна” в гексациклах).
III. В 27-вершинном кластере рис. 1а на центральной вершине 1 сходятся 18 гексациклов (в конформации “скрученная ванна”). Действительно, группа T порядка 12 может быть разложена в смежные классы по подгруппам:
(3)
$T = \bigcup\limits_{i = 1}^4 {{{g}_{i}}} {{C}_{3}} = \bigcup\limits_{k = 1}^6 {{{g}_{k}}} {{C}_{2}},$1–1'–2–6'–13–4'–1; 1–1'–2–5'–5–2'–1; 1–1'–2–5'–11–4'–1; 1–1'–3–8'–5–2'–1;
1–1'–3–10'–6–2'–1; 1–1'–3–10'–10–3'–1; 1–1'–4–11'–10–3'–1; 1–1'–4–13'–8–3'–1;
1–1'–4–13'–13–4'–1; 1–2'–5–5'–11–4'–1; 1–2'–6–7'–9–3'–1; 1–2'–6–10'–10–3'–1;
1–2'–7–12'–11–4'–1; 1–2'–7–14'–9–3'–1; 1–2'–7–14'–12–4'–1; 1–3'–8–13'–13–4'–1;
1–3'–8–9'–12–4'–1; 1–3'–9–14'–12–4'–1.
При этом количество гексациклов (в конформации “кресло”) в структуре алмаза равно 12. На рис. 1б гексациклы образуют следующие последовательности вершин:
1–1'–3–12'–11–4'–1; 1–3'–9–15'–12–4'–1; 1–1'–4–11'–10–3'–1; 1–1'–2–9'–8–3'–1;
1–4'–11–5'–5–2'–1; 1–4'–12–16'–7–2'–1; 1–1'–2–6'–13–4'–1; 1–3'–8–13'–13–4'–1;
1–2'–6–10'–4–1'–1; 1–2'–6–7'–10–3'–1; 1–1'–3–8'–5–2'–1; 1–3'–9–14'–7–2'–1.
IV. Оказалось, что 18 гексациклов – это теоретически максимально достижимое количество гексациклов для одной вершины в тетракоординированной системе. Это следует из анализа изменений расстояний в структуре алмаза, возникающих при вращении четырех “троек” вершин его второй координационной сферы [8]. Например, на рис. 1б для вершины 1 “тройки” образуют следующие вершины: 2, 3, 4 (ось вращения 1–1'); 5, 6, 7 (ось 1–2'); 8, 9, 10 (ось 1–3') и 11, 12, 13 (ось 1–4'). При вращении исходные 12 гексациклов разрушаются, но при определенном значении угла вращения возникает конфигурация с гексациклами, сходящимися в вершине 1 [8]. Оказалось, что это единственная конфигурация, отличающаяся от исходной, и она совпадает с вершинами кластера рис. 1а.
Таким образом, в политопе {240} реализуется единственный вариант расположения вершин, в котором для каждой из них имеет место самое плотное окружение из всех достижимых в тетракоординированных системах. Поэтому политоп {240} и его подструктуры могут служить “идеальными прототипами” для упорядоченных тетракоординированных структур в пространстве E3.
ОТОБРАЖЕНИЕ ПОЛИТОПОВ В ПРОСТРАНСТВО E3
Способ отображения политопа {3, 3, 5} в E3 описан в [5, 7, 8, 13]. Используется стереографическая проекция сферы S3 из E4; в E3 она покрывает все пространство, за исключением вертикальной прямой, и представляет собой семейство коаксиальных торов (один внутри другого). Согласно [5], 120 вершин политопа {3, 3, 5} можно разбить на четыре совокупности по 30 вершин в каждой, они отображаются в E3 на поверхности четырех разных торов, которые скручены друг с другом. На каждый тор отображаются три окружности – “окружности Вилларсо”, содержащие по 10 вершин политопа. Вершины трех таких окружностей образуют тетраэдры, слегка отличающиеся от правильных и объединенные по граням (30 вершин на торе образуют 30 тетраэдров). Если “разрезать” эти четыре тора (преобразовать координаты вершин с тора на цилиндр, т.е. “разомкнуть” эти окружности), то образуются четыре цилиндра. На каждом цилиндре последовательность 30 правильных тетраэдров образует спираль Бердийка–Коксетера. Она не имеет трансляционного периода (спираль БК, иррациональная тетраспираль). Все 120 вершин в политопе {3, 3, 5} содержатся в четырех идеальных замкнутых тетраспиралях (из правильных тетраэдров) [6, 13–15]. Поскольку политоп {3, 3, 5} содержит 600 тетраэдров, можно выделить несколько разных четверок идеальных тетраспиралей [5, 6]. Существуют разные конгруэнтные варианты разбиения 120 вершин на четыре набора по 30 вершин в каждом. Пять хиральных пар приведены в [5]. Способ объединения по граням 30 правильных тетраэдров, который был в политопе {3, 3, 5}, остается при этом неизменным и в E3 на цилиндре, но замкнуть в E3 объединение правильных тетраэдров в тор невозможно (для этого они должны быть слегка искажены), замкнуть 30 правильных тетраэдров можно только в политопе {3, 3, 5}. Поэтому, если спираль из объединяемых по граням правильных тетраэдров с вершинами на цилиндре в E3 содержит 30 тетраэдров, она может быть вложена в политоп {3, 3, 5}, в котором она обладает некристаллографической симметрией оси 30/11 – равномерным распределением 30 вершин по 11 виткам. Наличие симметрии 30/11 означает возможность объединения спиралей с симметрией 30/11 по закону политопа {3, 3, 5} или определяющей его восьмимерной решетки Е8, поэтому симметрия 30/11 является подрешетчатой некристаллографической симметрией. Если спираль обладает некристаллографической симметрией произвольной оси (например, 35/11), то не существует политопа (решетки), содержащего симметрию 35/11, следовательно, симметрийных законов объединения спиралей, учитывающих их симметрию, не существует. Такую некристаллографическую симметрию (аналогичную группе симметрии молекулы) можно назвать локальной некристаллографической симметрией.
Отображения в E3 белого и черного политопов {3, 3, 5} дают отображение политопа {240}. Торы от черных политопов {3, 3, 5} совпадают в E3 с торами от белых, но каждая белая окружность Вилларсо оказывается расположенной между двумя черными, и наоборот. В противном случае центрирования тетраэдров вершинами противоположного цвета не возникнет. В итоге к каждой белой 30-вершинной тетраспирали добавляется черная с вершинами на том же торе.
Как белые, так и черные тетраспирали на каждом из четырех торов обладают винтовой осью 30/11, поэтому в [5] их объединили в четыре “канала” на торах: удалили исходные ребра между вершинами одного цвета и каждую белую вершину соединили с ближайшей черной. Отметим, что стенки канала [5] образованы гексациклами в конформации “скрученная (твист) ванна”. В отличие от политопа {3, 3, 5} в политопе {240} есть также винтовая ось 40/9. Канал с симметрией 40/9 из “твист-ванн” рассмотрен в [5].
РАССЛОЕНИЕ ХОПФА
Симметрию сферы S3 в пространстве E4 удобно описать, используя расслоение Хопфа [7, 13]. Расслоениями (набором “слоев-волокон”) в S3 являются окружности одного диаметра. А именно, сферу S3 можно представить “базой” – сферой S2 в пространстве E3, каждой точке которой соответствует “слой” – окружность Вилларсо S1 [5]; это расслоение Хопфа [7, 13]:
Политоп {3, 3, 5}. Как упоминалось, группой политопа {3, 3, 5} является Y ' × Y '/Z2 [5, 6]. Согласно соотношению (1) Y ' содержит преобразования неточечной симметрии, тогда как преобразования “базы” должны принадлежать только точечной группе симметрии Yh многогранника [7]. Для описания симметрии политопа {3, 3, 5} возможен дискретный вариант расслоения Хопфа (4) в следующем виде:
где “база” – многогранник {p, q}: икосаэдр, додекаэдр или икосидодекаэдр (все обладают группой симметрии икосаэдра Yh), число вершин 12, 20 или 30 которого, соответственно, совпадает с числом слоев (p – число вершин грани, q – число граней, сходящихся в вершине). Каждый слой состоит из p* вершин, p* = 10, 6 или 4, объединяемых винтовыми осями 101, 61 или 41 соответственно. Группа симметрии базы должна быть согласована с группой симметрии политопа [16]. Тетраспираль с винтовой осью 30/11 получается только в том случае, когда слой p* = 10 и объединены три спирали 101. Варианты слоев с осями 61 или 41 для отображения тетраспирали не подходят, т.е. использование додекаэдра и икосидодекаэдра в качестве базы расслоения для объединения тетраспиралей невозможно. В соответствии с этим группа симметрии икосаэдра Yh может быть факторизована следующим образом: где D5d – группа симметрии 10-реберного многоугольника Петри (экваториального пояса) икосаэдра. Группа симметрии треугольной грани икосаэдра – ${{C}_{{3{v}}}}$, поэтому треугольнику икосаэдра (базы в (5)) соответствует тетраспираль с винтовой осью 30/11. Кроме того, только эта ось сохраняется в политопе {240}, поэтому данный вариант расслоения может быть использован для построения расслоения также для политопа {240}.Итак, в качестве “базы” расслоения для политопа {3, 3, 5} необходимо принять правильный икосаэдр (рис. 2а). Из множества точек сферы S2 выбирают 12 вершин так, чтобы они совпали с 12 вершинами правильного икосаэдра. Через каждую из этих вершин проводят окружность Вилларсо. На каждой из 12 окружностей размещают по 10 точек – они “обозначают” вершины политопа {3, 3, 5}, т.е. каждая вершина базы “нагружена” слоем из 10 вершин, всего 120 вершин. Существуют правила [7]:
Рис. 2.
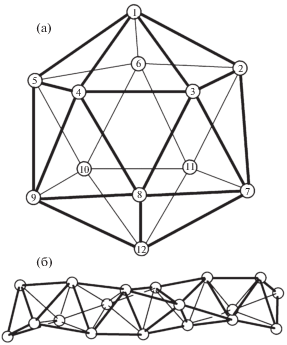
База расслоения Хопфа для политопа {3, 3, 5} – икосаэдр. Все 12 его вершин охватываются четырьмя правильными треугольниками (а); объединение в тетраспираль трех соседних 10-вершинных цепей в расслоении Хопфа для политопа {3, 3, 5}, соответствующее одному из этих четырех треугольников икосаэдра (б).
– если у вершины на S2 есть k соседних вершин, то в S3 у соответствующей “окружности” с 10 вершинами есть k соседних “окружностей”;
– ребра, соединяющие вершины на окружностях – это ребра тетраэдрических ячеек;
– грани икосаэдра как правильному треугольнику из трех соседних вершин “базы” соответствуют три соседние окружности по 10 вершин на каждой. Эти 30 вершин образуют цепь объединенных по граням тетраэдров, тетраспираль (рис. 2б).
В итоге правило расслоения таково: треугольник на “базе” – это тетраспираль при отображении [7].
Все 120 вершин политопа {3, 3, 5}, как указано в предыдущем разделе, дают при отображении четыре тетраспирали [6, 13–15], скрученные друг с другом. На “языке” расслоения Хопфа этим четырем тетраспиралям соответствуют четыре треугольника икосаэдра (базы расслоения), охватывающие все 12 вершин икосаэдра и не имеющие общих вершин. Все 20 граней икосаэдра можно раскрасить в пять цветов так, что центры четырех граней одного цвета образуют тетраэдр. Существуют два варианта четверок треугольников, которыми можно охватить все вершины базы. Пусть в качестве исходного избран, например, треугольник 3–4–8 на рис. 2а. Тогда первый вариант – это треугольники (3–4–8, 1–2–6, 7–11–12, 5–9–10), они одного цвета, второй вариант – это треугольники (3–4–8, 2–7–11, 9–10–12, 1–5–6), они разных цветов. Первая четверка треугольников переводится во вторую четверку плоскостью симметрии, проходящей через треугольник 3–4–8; аналогично для других четверок.
База (икосаэдр) не принадлежит политопу {3, 3, 5}, но формализм описания симметрии системы через расслоение Хопфа позволяет в условной форме “визуализировать” эту систему и ее отображение, упростить анализ разных вариантов. Для “базы” все четыре тетраспирали эквивалентны, поэтому формализм позволяет сразу указать условную картину взаимного расположения отображаемых структур в S3. Строгое соответствие данной вершине соседних вершин в пространстве расслоения Хопфа можно установить, если использовать понятие связности расслоения [17].
Политоп {240}. Поскольку политоп {240} – это объединение двух политопов {3, 3, 5}, то в расслоении Хопфа для политопа {240} база должна быть представлена объединением двух икосаэдров. Группа симметрии этого объединения должна быть согласована с группой симметрии политопа {240}. Далее политоп {240}, как упоминалось во Введении, обладает группой симметрии (O' × × Y ')/Z2 или (Y ' × O')/Z2 для политопа противоположной хиральности [5]. Но O' содержит преобразования группы неточечной симметрии (уравнение (2)), тогда как преобразования “базы” должны принадлежать только точечной группе симметрии Oh многогранника, ее порядок 48. Эти два условия выполняются только для объединения двух прямых икосаэдров, вершины которого совпадают с 24 вершинами равнореберного усеченного октаэдра (параллелоэдра Федорова) [18] (рис. 3а, 4а, 4в). Параллелоэдр Федорова содержит 14 граней, восемь из которых – правильные шестиугольники, а шесть – квадраты, и обозначается символом [46, 68]. Группой симметрии параллелоэдра Федорова является группа Oh:
(7)
${{O}_{h}} = {{T}_{h}} \cup {{m}_{d}} \cdot {{T}_{h}} = {{D}_{2}} \cdot {{D}_{{3d}}} = {{C}_{{3{v}}}} \cdot {{D}_{{2h}}},$(8)
$[{{4}^{6}},{{6}^{8}}] \cong {{\{ 3,5\} }_{{\text{п}}}} \cup \{ 3,5\} _{{\text{п}}}^{'} \cong {{\{ 3,5\} }_{{\text{п}}}} \cup {{m}_{d}}{{\{ 3,5\} }_{{\text{п}}}}.$Рис. 3.
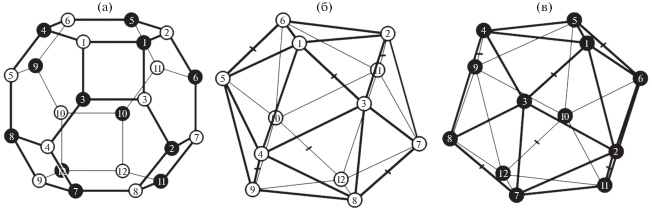
База расслоения Хопфа для политопа {240} – параллелоэдр Федорова [46, 68] (а), являющийся объединением (элементом симметрии 2-го порядка) двух прямых икосаэдров: {3,5}п с белыми вершинами (б) и $\{ 3,5\} _{{\text{п}}}^{'}$ с черными вершинами (в). Из 20 граней в прямом икосаэдре 8 – правильные треугольники и 12 – равнобедренные; основания равнобедренных треугольников маркированы штрихами, на рис. 3б и 3в они короче ребер правильных треугольников в (2/3)1/2 раза. Номера вершин обоих прямых икосаэдров б, в соответствуют номерам вершин правильного икосаэдра на рис. 2а.
Рассмотрим расслоение Хопфа для политопа {240} в следующем варианте “произведения” базы и слоя:
Для того чтобы осуществить формализм расслоения Хопфа, нужно охватить 24 вершины параллелоэдра Федорова ([46, 68]) минимальным количеством треугольников, не имеющих общих вершин (каждому треугольнику будет отвечать 30-вершинная тетраспираль). Представляется естественным решать эту задачу в два этапа: рассмотреть сначала варианты охвата треугольниками всех 12 вершин прямого икосаэдра, затем варианты построения параллелоэдра Федорова из прямых икосаэдров, вершины которых разбиты на четверки треугольников. В качестве исходного треугольника при проведении процедуры охвата 12 вершин прямого икосаэдра можно выбрать либо равносторонний, либо равнобедренный треугольник. Для охвата остальных девяти вершин должны быть избраны треугольники, вершины которых соединены друг с другом лишь одним ребром. Все номера вершин, приведенные ниже в пп. i и ii, отвечают белому прямому икосаэдру рис. 3б. Для черного икосаэдра (рис. 3в) результаты будут, очевидно, теми же.
i. Если исходный треугольник – равносторонний (например, 3–4–8), то для охвата остальных вершин могут быть избраны либо три равносторонних 1–2–6, 7–11–12, 5–9–10, либо три равнобедренных треугольника 2–7–11, 9–10–12, 1–5–6. Отметим, что через центры треугольника 3–4–8 и треугольника 6–10–11, расположенного параллельного ему на противоположной грани, проходит ось 3-го порядка, переводящая три указанных равносторонних (и три равнобедренных) треугольника друг в друга соответственно. Оси 3-го порядка проходят через центры и других пар равносторонних треугольников, поэтому выбор в качестве исходного любого из них по соображениям симметрии оставляет результат неизменным. Итак, в данном случае для охвата 12 вершин прямого икосаэдра можно использовать либо (а) четыре равносторонних треугольника, либо (б) один равносторонний треугольник и три равнобедренных.
ii. Пусть исходный треугольник – равнобедренный, например 2–7–11. К нему можно добавить либо равносторонний, либо равнобедренный треугольник. Если к 2–7–11 добавить равносторонний треугольник, то из восьми имеющихся это может быть один из следующих четырех (только они отвечают всем требованиям): 3–4–8, 8–9–12, 5–9–10 или 1–4–5. Система симметрична относительно осей 3-го порядка, проходящих через центр любого равностороннего треугольника. Поэтому для охвата оставшихся вершин придется выбрать еще те два равнобедренных треугольника, в которые исходный треугольник 2–7–11 переводится соответствующей осью. Это либо треугольники 9–10–12 и 1–5–6, либо 1–3–4 и 5–6–10, и т.п. Так или иначе, в итоге это один равносторонний и три равнобедренных треугольника, т.е. вариант б пункта i. Но к исходному равнобедренному 2–7–11 можно было добавить не равносторонний, а один или два равнобедренных треугольника, в которые исходный равнобедренный переводится осью 3-го порядка (проходящей через центр какого-либо равностороннего). Если добавлены два равнобедренных треугольника (например, 9–10–12 и 1–5–6, или 1–3–4 и 5–6–10, и т.п.), то для охвата всех вершин нужно добавить еще один треугольник, но это может быть только равносторонний (соответственно, 3–4–8 или 8–9–12 и т.п.). В итоге снова возникает вариант б. Но если к 2–7–11 добавлены не два, а только один равнобедренный треугольник (например, 9–10–12), то между этими двумя треугольниками на прямом икосаэдре образуется одна “изолированная” вершина 8, которая не может войти ни в какой треугольник охвата, кроме равностороннего 3–4–8. Тогда симметрия прямого икосаэдра относительно оси 3-го порядка через центр треугольника 3–4–8 не оставляет возможности иного выбора третьего треугольника, как только равнобедренного 1–5–6. И это снова вариант б. Ясно, что все остальные комбинации выбора треугольников охвата вследствие симметрии прямого икосаэдра эквивалентны тем, что рассмотрены выше.
Полный перебор возможных ситуаций при проведении процедуры охвата треугольниками 12 вершин прямого икосаэдра, который фактически проведен в пп. i и ii, показал, что возможны лишь варианты а и б. Рассмотрим теперь варианты объединения белого и черного прямых икосаэдров с треугольными “разбиениями” а и б.
А. Пусть вершины обоих – белого и черного – прямых икосаэдров охвачены по варианту а. Тогда при объединении икосаэдров в базе политопа {240} могут образоваться либо четыре пары “черно-белых” правильных треугольников, расположенных на одних и тех же шестиугольных гранях, либо четыре белых и четыре черных правильных треугольника, расположенных на разных шестиугольных гранях. В первом случае пары белого и черного треугольников – это (1–2–6, 1'–4'–5'), (3–4–8, 2'–3'–7'), (5–9–10, 8'–9'–12'), (7–11–12, 6'–10'–11') на рис. 4а, из них две первые пары отмечены пунктиром. Данному объединению четырех пар правильных треугольников соответствует следующее разложение группы Oh:
где gi $ \in $ D2, D3d – надгруппа группы ${{C}_{{3{v}}}}$ объединения правильных треугольников.Рис. 4.
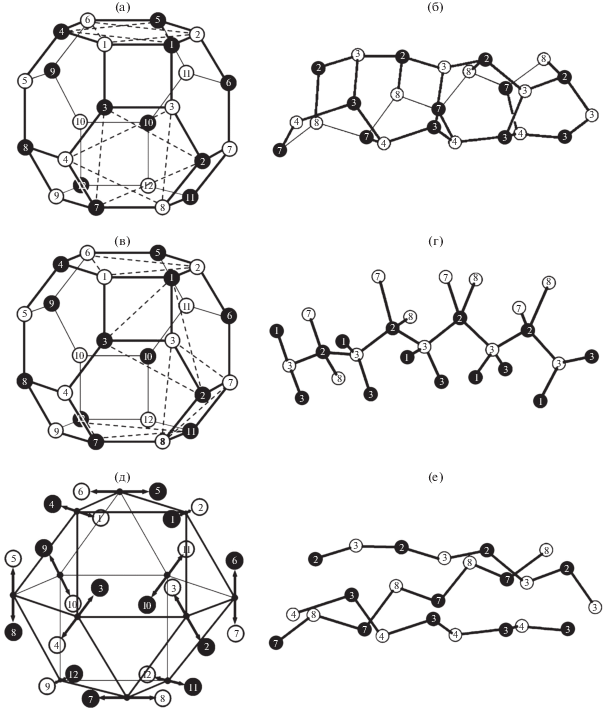
Параллелоэдр Федорова (объединение двух прямых икосаэдров) [18], (а) и (в) как база расслоения Хопфа для правого политопа {240}, соотношение (9). Все 24 вершины базы могут охватить: (а) четыре пары – “белого” и “черного” – правильных треугольников; две пары из них выделены пунктирными линиями; каждому из четырех объединений правильных треугольников в правильный шестиугольник отвечает 60-вершинный “канал” (б) в политопе {240} [5] (показан частично); (в) три пары “белых” и “черных” равнобедренных треугольников (из них одна пара выделена), один правильный треугольник на верхнем и один на нижнем основании (выделены). Каждому из трех объединений равнобедренных треугольников соответствует линейная тетракоординированная цепь в политопе {240} (цепь г отвечает выделенной паре), каждому правильному треугольнику на основании соответствует совокупность из 30 вершин, образующих тетраспирали при переходе в E3; (д) кубооктаэдр [22], образуемый серединами 12 “двойных” стрелок, как база расслоения Хопфа для правого политопа {240}, соотношение (12). Концы стрелок охватывают все 24 вершины параллелоэдра Федорова, каждая из “двойных” стрелок охватывает ближайшие белую и черную вершину шестиугольника базы а, в и соответствует 20-вершинной цепи; (е) три цепи (показанные частично) отвечают стрелкам 3–2', 4–3' и 8–7' базы (д). В структурах б, г и е указаны номера вершин-слоев баз а, в и д соответственно.
При объединении пары черного и белого треугольников, расположенных на одной и той же грани базы, у каждой вершины белого треугольника есть соседняя вершина черного. Согласно формализму расслоения Хопфа, это означает возможность объединения белой и черной 30-вершинных тетраспиралей, расположенных на одном торе, в одну 60-вершинную структуру. Это “канал” (рис. 4б), и он соответствует варианту объединения вершин, описанному в [5]. Отметим, что система ребер этого канала является замкнутой “на себя”, отсутствуют “висячие” связи. Использование для политопа {240} базы рис. 4а и формализма расслоения Хопфа позволяет сразу “визуально” представить такое отображение, хотя математическая процедура отображения вершин при этом явно не фигурирует. Она проводится методом стереографической проекции и приведена в [5, 7].
В том случае, когда четыре белых и четыре черных правильных треугольника расположены на разных шестиугольных гранях базы, объединение черного и белого треугольников в пары дает смешанный “тетраэдрически-тетракоординированный” вариант. Подробнее он будет рассмотрен в другой работе.
Б. Пусть вершины обоих – белого и черного – прямых икосаэдров охвачены по варианту б. Тогда при объединении икосаэдров в базе политопа {240} могут возникнуть разные конфигурации. Рассмотрим следующую конфигурацию: на боковых гранях базы (рис. 4в) образуются три пары “черно-белых” равнобедренных треугольников (3–7–8, 1'–2'–3' – помечены пунктиром), (4–5–9, 4'–8'–9') и (10–11–12, 5'–6'–10'), кроме того, есть правильные треугольники 1–2–6, 7'–11'–12' на верхнем и нижнем шестиугольниках базы соответственно. Иные конфигурации будут рассмотрены в другой работе.
Данному объединению трех пар равнобедренных и пары правильных треугольников соответствует следующее разложение группы Oh:
где ${{D}_{3}} \cap {{C}_{{2{v}}}}$ = С2.Вариант объединения прямых икосаэдров, приведенный на рис. 4в, означает, что вершины в отображении объединяются в единые структуры иначе, чем в случае А. Рассмотрим на рис. 4в пару треугольников: 3–7–8 и 1'–2'–3'. Окружности Вилларсо с 10 вершинами, которые соединены ребрами тетраэдрических ячеек, проходят через две разные шестиугольные грани, т.е. лежат на двух разных торах из четырех (грань – это один тор). В то же время все четыре тора скручены друг с другом, и вдоль разных окружностей Вилларсо на поверхности двух из них находятся одновременно 10 белых и 10 черных вершин (на базе рис. 4в окружности проходят через вершины 3 и 2'). Три белые вершины 3, 7 и 8 белого прямого икосаэдра означают белую тетраспираль, три черные вершины 1', 2' и 3' черного прямого икосаэдра – черную тетраспираль. Поскольку спирали состоят из тетраэдров и все углы в них тетраэдрические, подобная система может реализоваться только в случае, если спирали сдвинуты друг относительно друга вдоль больших осей торов так, что черные вершины черной окружности Вилларсо 2' попадают в центры белых тетраэдров, а белые вершины белой окружности Вилларсо 3 – в центры черных тетраэдров.
Иначе говоря, на базе рис. 4в тетраэдрические спирали вставлены друг в друга (с указанным сдвигом). Это 60-вершинная структура. Если удалить исходные ребра между вершинами одного цвета и каждую белую вершину соединить с ближайшей черной, то эта структура преобразуется в линейную тетракоординированную цепь [21].
Выше было рассмотрено расслоение Хопфа для политопа {240} в варианте “произведения” базы и слоя, отвечающем соотношению (9). Вместе с тем белый и черный политопы {3, 3, 5} объединяются в политоп {240} осью 2-го порядка. Эта же ось объединяет белый и черный 10-вершинные слои (расслоений Хопфа для этих политопов) в один 20-вершинный слой [22] расслоения Хопфа для политопа {240}. Таких слоев будет 12, и каждому из них будет соответствовать вершина кубооктаэдра $\left\{ {_{4}^{3}} \right\}$ – середина ребра, разделяющего два шестиугольника в параллелоэдре Федорова (рис. 4д, 4е). Точечная группа кубооктаэдра – та же (Oh), что и у многогранника [46, 68], поэтому расслоение Хопфа для политопа {240} можно представить также в виде следующего варианта “произведения” базы и слоя:
Таким образом, если вершине [46, 68] соответствует слой {10} (согласно (9), рис. 4а, 4в), то вершине $\left\{ {_{4}^{3}} \right\}$ – середина “двойной” стрелки, соответствующая слою {20} (согласно (12), рис. 4д).Если использовать расслоение Хопфа в варианте (12), то вариант отображения рис. 4в, 4г может быть интерпретирован формально и более просто – рис. 4д, 4е. Действительно, каждая из “двойных” стрелок на рис. 4д охватывает ближайшие белую и черную вершины шестиугольника базы (рис. 4а, 4в) и соответствует одной 20-вершинной цепи, подобной цепи 〈110〉 алмаза. Объединение двух равнобедренных треугольников (например, 3–7–8, 1'–2'–3' на рис. 4в) содержит лишь одну “двойную” стрелку 2'–3 на рис. 4д, поэтому отображение дает лишь одну 〈110〉-подобную цепочку на рис. 4г. При этом каждая из вершин 7 и 8, а также 1' и 3' базы (рис. 4в) отображаются в 10-вершинные спирали. При соединении этих 40 вершин с вершинами основной 20-вершинной 〈110〉-подобной цепи образуется тетракоординированная цепь.
Отметим, что вариант рис. 4в, 4г отображения линейной подструктуры политопа {240} является “противоположным” варианту рис. 4а, 4б, описанному в [5], так как в нем ближайшие вершины, соединенные ребрами, образуют цепные тетракоординированные последовательности, содержащие максимально большое количество “висячих” связей (от каждой вершины основной цепи – по две), и не содержат ни одного цикла.
В политопе {3, 3, 5} максимальный порядок оси есть 30 [5, 7], т.е. в соответствующей цепи может быть только 30 вершин [6], поэтому в политопе {240} в тетракоординированной цепи, соответствующей этой оси, может быть максимум 60 вершин, что ограничивает протяженность цепи. Тогда, казалось бы, 240 вершин можно разбить на четыре совокупности по 60 вершин. Однако проведенный анализ показал, что теоретически возможно выделить лишь три такие 60-вершинные цепи, при этом остаются еще две совокупности по 30 вершин, образующие при переходе в E3 тетраспирали.
Поскольку выбор подсистемы ребер, охватывающих все 240 вершин политопа {240}, очевидно, не является однозначным, факт обнаружения варианта выделения линейных подструктур политопа, отличающегося от варианта, описанного в [5], не удивителен. Более того, формализм расслоения Хопфа показал, что существуют и другие варианты. Можно указать еще один путь их выявления: при объединении в параллелоэдр Федорова двух прямых икосаэдров, вершины которых охвачены треугольниками, можно использовать смешанные варианты охвата: например в белом прямом икосаэдре – охват по варианту а, а в черном – по варианту б. Подобные варианты также обсудим в другой работе.
ЗАКЛЮЧЕНИЕ
Описаны варианты отображения в трехмерное евклидово пространство линейных тетракоординированных подструктур высокосимметричного четырехмерного многогранника (политопа) {240}. В нем все 240 вершин тетракоординированы, и для каждой из них реализуется самое плотное окружение из всех возможных в тетракоординированных системах. Использован формализм расслоения Хопфа, позволивший выявить подструктуры, в которых совокупности вершин образуют в отличие от известных ранее каналов тетракоординированные цепи, а также указать на существование смешанных вариантов. Эти результаты имеют не только теоретическую значимость (прежде всего, для симметрийной классификации структур), но и важны для приложений, в частности для установления возможных ограничений, при которых реальные линейные алмазоподобные структуры и тетракоординированные цепи могут обладать “подрешетчатой” некристаллографической (скрытой) симметрией.
Работа выполнена при поддержке Министерства науки и высшего образования РФ (гос. задание КарНЦ РАН № 0218-2019-0076, № г.р. АААА-А17-117031710039-3 – для А.Л.Р.).
Список литературы
Robinson G. de B. // Proc. Camb. Phil. Soc. 1931. V. 27. P. 37.
Coxeter H.S.M. // Philos. Trans. R. Soc. London. A. 1930. V. 229. P. 346.
Sadoc J.F., Mosseri R. // J. Phys. Collog. 1981. V. 42. P. C. 4-189.
Sadoc J.F., Mosseri R. // Philos. Mag. B. 1982. V. 45. № 5. P. 467.
Mosseri R., DiVincenzo D.P., Sadoc J.F., Brodsky M.H. // Phys. Rev. B. 1985. V. 32. № 6. P. 3974.
Coxeter H.S.M. Regular Polytopes. N.Y.: Dover Publ, 1973. 321 p.
Sadoc F.J. // Eur. Phys. J. E. 2001. V. 5. P. 575.
Ishii Y. // Acta Cryst. A. 1988. V. 44. P. 987.
Вайнштейн Б.К. Современная кристаллография. Т. 1. Симметрия кристаллов. М.: Наука, 1979. 384 с.
Kléman M., Sadoc J.F. // J. Phys. Lett. (Paris). 1979. V. 40. № 21. P. L569.
Sadoc J.F. // J. Non-Cryst. Solids. 1981. V. 44. № 1. P. 1.
Cartan E. Geometry of Riemannian spaces. Brookline: Math Sci. Press. 1983. 506 p. (Engl. transl. from Cartan É. Leçons sur la Géométrie des Espaces de Riemann. Paris: Gauthier-Villars. 1951).
Lord E.A., Ranganathan S. // Eur. Phys. J. D. 2001. V. 15. P. 335.
Lord E.A. // Struct. Chem. 2002. V. 13. № 3/4. P. 305.
Boerdijk A.H. // Philips Res. Rep. 1952. V. 7. P. 303.
Дубровин Б.A., Новиков С.П., Фоменко А.Т. Современная геометрия: Методы и приложения. Т. 1. М.: Эдиториал УРСС, 1998. 336 с.
Manton N.S. // Commun. Math. Phys. 1987. V. 113. P. 341.
Samoylovich M., Talis A. // Acta Cryst. A. 2014. V. 70. P. 186.
Галиулин Р.В. // Материаловедение. 1999. № 6. С. 2.
Талис А.Л., Беляев О.А., Реу А.А., Талис Р.А. // Кристаллография. 2008. Т. 53. № 3. С. 391.
Талис А.Л., Рабинович А.Л. // Обозр. прикл. и промышл. матем. 2019. Т. 26. Вып. 2. С. 182.
Самойлович М.И., Талис А.Л. // Кристаллография. 2013. Т. 58. № 4. С. 519.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография


