1. На главную
  2. Электронные версии
  3. Кристаллография
  4. T. 66, № 3, 2021

Кристаллография, 2021, T. 66, № 3, стр. 478-481

Влияние размера ячейки моделирования и концентрации ионов осадителя на поведение димера тетрагонального лизоцима

Ю. В. Кордонская 1, 2, *, В. И. Тимофеев 1, 2, Ю. А. Дьякова 1, 2, М. А. Марченкова 1, 2, Ю. В. Писаревский 1, 2, М. В. Ковальчук 1, 2

1 Институт кристаллографии им. А.В. Шубникова ФНИЦ “Кристаллография и фотоника” РАН
Москва, Россия

2 Национальный исследовательский центр “Курчатовский институт”
Москва, Россия

* E-mail: yukord@mail.ru

Поступила в редакцию 13.11.2020
После доработки 10.12.2020
Принята к публикации 10.12.2020

Полный текст (PDF)

Аннотация

Методом молекулярной динамики проведено 10-наносекундное моделирование димера лизоцима, являющегося фрагментом структуры тетрагонального кристалла лизоцима, при различных размерах ячейки моделирования и при разных концентрациях осадителя в растворе. Для оценки стабильности димера посчитаны значения RMSF атомов белка. Показано, что на относительно короткой траектории размер ячейки не влияет существенным образом на подвижность атомов белка, в то время как влияние концентрации ионов осадителя на этой траектории является заметным.

ВВЕДЕНИЕ

Исследование процессов кристаллизации белков, а также свойств белковых кристаллов представляет несомненный интерес как для разработки подходов к поиску условий кристаллизации белков, так и для изучения разницы в строении белковой молекулы в кристаллическом состоянии и в растворе. Для нескольких белков установлено, что в предкристаллизационном растворе присутствуют построенные из белковых молекул олигомеры, структура которых хорошо описывается структурами олигомеров, выявленных в кристаллах исследуемых белков [1–3].

Для изучения процессов кристаллизации белков, а также для изучения свойств белковых кристаллов широко применяют метод молекулярной динамики (МД). Результаты работ по моделированию свойств методом МД представлены в [4–9]. Для изучения процесса кристаллообразования также применяются различные вычислительные методы. Так, в [10] исследовалась зависимость стабильности кристалла белка от концентрации ионов в кристаллизационном растворе, а также от зарядов аминокислотных остатков на поверхности белка. В [11] была предпринята попытка промоделировать процесс образования кристалла белка. Кроме того, методом МД исследовались свойства белковых олигомеров, содержащихся в предкристаллизационном растворе [12, 13].

Отметим, что масса работ, посвященных исследованию процессов кристаллизации белков методами вычислительной биологии, опираются и на анализ подвижности атомов белковой молекулы при различных условиях [10, 12, 13]. Было показано, что на стабильность биологической тетрамерной молекулы гемоглобина человека при моделировании методом МД в растворе оказывает влияние наряду с другими параметрами размер ячейки моделирования [14]. Неизвестно, однако, в какой степени этот факт [14], свидетельствующий о влиянии выбора параметров ячейки моделирования на стабильность белкового олигомера, можно учитывать при моделировании методом МД олигомеров, образующихся в кристаллизационном растворе белков. Для ответа на этот вопрос в настоящей работе методом МД проведено исследование димера лизоцима, являющегося фрагментом структуры тетрагонального кристалла лизоцима [15], в двух разных ячейках моделирования и при трех разных концентрациях осадителя в растворе для выяснения степени влияния этих параметров на стабильность атомов белкового димера.

МАТЕРИАЛЫ И МЕТОДЫ

Подготовка модели димера. Молекулярная модель возможной единицы роста кристаллов построена на основании данных о тетрагональной кристаллической структуре лизоцима (PDB_ID: 6QWY), определенной с разрешением 1.35 Å [15]. Кристалл принадлежит пр. гр. P43212 с параметрами элементарной ячейки: a = b = 77.147, c = 37.139 Å, α = β = γ = 90.00°. Независимая часть элементарной ячейки содержит один мономер лизоцима.

В кристаллической структуре 6QWY аминокислотные остатки ASN19, ASN59 и SER85 существуют в двух конформациях с одинаковыми коэффициентами заполнения 0.5, из которых была оставлена конформация А. С помощью программы PyMOL [16], применяя операторы симметрии пр. гр. P43212 (–X, –Y, Z +1/2; –Y +1/2, X + 1/2, Z + 3/4; Y + 1/2, –X + 1/2, Z + 1/4; –X + 1/2, Y + 1/2, –Z + 3/4; X + 1/2, –Y + 1/2, –Z + 1/4; Y, X, –Z; –Y, –X, –Z + 1/2), был восстановлен фрагмент тетрагональной кристаллической структуры лизоцима, из которого выделен димер и получены координаты димера лизоцима. В структуре олигомера были оставлены ионы осадителя, связанные с лизоцимом (на одну молекулу белка приходится три иона натрия и четыре иона хлора), и удалены молекулы воды.

МД-исследование. Все расчеты выполнены с помощью программного пакета GROMACS версии 2020.3 [17]. Молекулярную динамику проводили в поле Amber ff99SB-ILDN [18], поскольку новые торсионные потенциалы, применяемые в этой версии поля, точнее по сравнению с предыдущими версиями силового поля Amber. Состояния протонирования аминокислотных остатков в составе димеров лизоцима при pH 4.5 (в соответствии с экспериментальными условиями [15]) определены с помощью сервера PROPKA [19].

Моделирование проводили с применением периодических граничных условий. Димер белка помещали в центр кубической ячейки. Размеры ячейки моделирования задавали таким образом, чтобы расстояние между любым атомом белка и краем ячейки было в одном эксперименте не менее 1 нм, в другом – не менее 2.5 нм, длина ребра ячейки составляла 8.6 и 11.6 нм соответственно. Потенциалы взаимодействия учитывали только для атомов, находящихся в радиусе 1 нм.

Для заполнения ячейки моделирования явно заданным растворителем была выбрана 4-центровая модель воды TIP4P-Ew, при которой возможно использование методов суммирования по Эвальду [20]. Чтобы точнее воспроизвести экспериментальные условия, в которых находится белок в процессе кристаллизации, димеры лизоцима моделировали в водном растворе с осадителем. Для этого часть молекул воды заменяли ионами натрия и хлора таким образом, чтобы концентрация соли в ячейке составляла 0.4 М (25 мг/мл) для кубической ячейки с ребром 11.6 нм и 0.2, 0.4, 0.6 М для ячейки с ребром 8.6 нм. Общий заряд системы нейтрализовали добавлением незначительного количества ионов хлора.

Перед началом каждого расчета методом МД проводили минимизацию энергии системы методом наискорейшего спуска (50 000 шагов) до тех пор, пока сила, действующая на любой атом, не оказывалась меньше 1000 кДж/(М·нм).

Затем проводили 100-пикосекундное термостатирование системы улучшенным методом Берендсена [21] и баростатирование методом Паринелло–Рамана [22] (100 пс), при этом на все неводородные атомы белка накладывались ограничивающие силы (kpr = 1000 кДж/(М нм2)), а на все связи накладывались ограничения с помощью алгоритмов LINCS [23].

Моделирование МД проводили в изотермическо-изобарическом ансамбле c использованием термостата Берендсена и баростата Паринелло–Рамана (при Р = 1 атм для всех систем). Интегрирование проводили с помощью стандартного интегратора leap-frog [24], временной шаг интегрирования составлял 2 фс, координаты атомов сохраняли каждые 1000 пс. Электростатические взаимодействия вычисляли методом ускоренного суммирования по Эвальду PME (Particle Mesh Ewald [25]) с интерполяцией четвертого порядка (кубической) и шагом сетки в пространстве Фурье 0.16 нм. Длительность каждой рассчитанной траектории димеров белка составила 10 нс.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

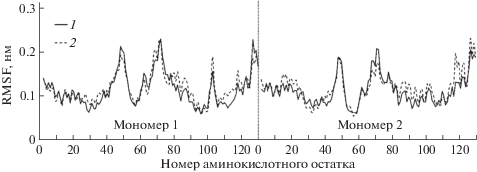
По результатам МД-моделирования после применения структурного выравнивания траекторий к исходному положению были посчитаны и построены графики RMSF (Root Mean Square Fluctuation) атомов, т.е. флуктуации координат атомов, усредненные по всему времени моделирования (10 нс), которые удобно использовать для оценки подвижности атомов белка в различных условиях. На рис. 1 показаны RMSF для Сα-атомов димера лизоцима в растворе при концентрации осадителя 0.4 М для разных размеров ячеек моделирования (ребро ячейки 2.5 и 1.0 нм). Из рисунка видно, что на относительно короткой траектории в 10 нс размер ячейки моделирования не имеет существенного влияния на подвижность атомов белка, хотя следует отметить некоторую разницу в подвижностях атомов на определенных участках белка. Отметим остатки с разницей в значениях RMSF, превышающей 0.0275 нм: SER81, ALA82, GLY102, TRP111, ARG112, ASN113, GLY117, GLY126 в мономере 1 и остатки HIP15 (HIS в протонированной форме), PRO70, GLY71, THR89, ALA90, ARG114, LYS116, GLY117, THR118, ASP119, ALA122 в мономере 2.

Рис. 1.

RMSF Сα-атомов димера лизоцима в растворе с концентрацией осадителя 0.4 М при расстоянии между краем ячейки моделирования и ближайшим к нему атомом белка 1 (1) и 2.5 нм (2).

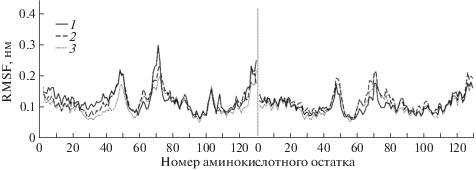
На рис. 2 показаны RMSF для Сα-атомов димера лизоцима в растворе при концентрации осадителя 0.2, 0.4 и 0.6 М. Видно, что влияние концентрации осадителя на подвижность атомов белка на такой же траектории наиболее заметно. Так, для ASN37, ALA42, ASN44, ARG45, THR47, ARG68, THR69, PRO70, ALA107, ALA122, TRP123, TRP124, GLY126, LEU129 в мономере 1 и GLY67, ARG68, THR69 в мономере 2 разница между значениями RMSF для одних и тех же остатков, но при разных концентрациях осадителя составляет более 0.05 нм. Для PRO70 в мономере 1 разница между значениями RMSF Cα-атомов составляет более 0.1 нм для систем с концентрацией NaCl 0.2 и 0.6 М.

Рис. 2.

RMSF Сα-атомов димера лизоцима в растворе при концентрациях осадителя 0.2 (1), 0.4 (2) и 0.6 М (3).

Полученные результаты показывают, что при оценке стабильности димеров лизоцима с помощью МД концентрация осадителя в растворе играет более существенную роль, чем размеры ячейки моделирования – даже на относительно короткой траектории (10 нс) подвижность Сα-атомов белка изменяется более чем на 30% в зависимости от концентрации осадителя, в то время как эффект, описанный в [14], для исследуемых систем практически не наблюдается. Отметим, что с увеличением количества ионов хлорида натрия в диапазоне от 0.2 до 0.6 М подвижность Сα-атомов мономера 1 постепенно уменьшается, при этом зависимость подвижности Сα-атомов мономера 2 от концентрации осадителя не является монотонной.

Работа выполнена с использованием оборудования центра коллективного пользования “Комплекс моделирования и обработки данных исследовательских установок мега-класса” НИЦ “Курчатовский институт”, http://ckp.nrcki.ru/.

Работа выполнена при частичной финансовой поддержке Министерства науки и высшего образования РФ в рамках выполнения работ по Государственному заданию ФНИЦ “Кристаллография и фотоника” РАН, Российского фонда фундаментальных исследований (грант № 19-29-12042 мк), НИЦ “Курчатовский институт” (приказ № 1360).

Список литературы

  1. Kovalchuk M.V., Blagov A.E., Dyakova Y.A. et al. // Cryst. Growth Des. 2016. V. 16. P. 1792.

  2. Марченкова М.А., Волков В.В., Благов А.Е. и др. // Кристаллография. 2016. Т. 61. № 1. С. 10.

  3. Бойкова А.С., Дьякова Ю.А., Ильина К.Б. и др. // Кристаллография. 2017. Т. 62. № 6. С. 876.

  4. Meinhold L., Smith J.C. // Proteins. 2007. V. 66. № 4. P. 941.

  5. Meinhold L., Merzel F., Smith J.C. // Phys. Rev. Lett. 2007. V. 99. № 13. P. 138101.

  6. Cerutti D.S., Le Trong I., Stenkamp R.E. et al. // Biochem. 2008. V. 47. № 46. P. 12065.

  7. Cerutti D.S., Le Trong I., Stenkamp R.E. et al. // J. Phys. Chem. B. 2009. V. 113. № 19. P. 6971.

  8. Schnieders M.J., Fenn T.D., Pande V.S. et al. // Acta Cryst. D. 2009. V. 65. № 9. P. 952.

  9. Cerutti D.S., Freddolino P.L., Duke Jr R.E. et al. // J. Phys. Chem. B. 2010. V. 114. № 40. P. 12811.

  10. Kuzmanic A., Zagrovic B. // Biophys. J. 2014. V. 106. № 3. P. 677.

  11. Taudt A., Arnold A., Pleiss J. // Phys. Rev. E. 2015. V. 91. № 3. P. 33311.

  12. Kordonskaya Y.V., Marchenkova M.A., Timofeev V.I. et al. // Crystallography Reports. 2018. V. 63. № 6. P. 947. https://doi.org/10.1134/S1063774518060196

  13. Kordonskaya Y.V., Marchenkova M.A., Timofeev V.I. et al. // J. Biomol. Struct. Dynamics. 2020. Published online. P. 1. https://doi.org/10.1080/07391102.2020.1803138

  14. El Hage K., Hedin F., Gupta P.K. et al. // Elife. 2018. V. 7. P. e35560.

  15. Marchenkova M.A., Kuranova I.P., Timofeev V.I. et al. // J. Biomol. Struct. Dynamics. 2020. V. 38. № 17. P. 5159.

  16. DeLano W.L. // 2002. The PyMOL molecular graphics system. http://www.pymol.org.

  17. Van Der Spoel D., Lindahl E., Hess B. et al. // J. Comp. Chem. 2005. V. 26. № 16. P. 1701.

  18. Lindorff-Larsen K., Piana S., Palmo K. et al. // Proteins: Structure, Function, and Bioinformatics. 2010. V. 78. № 8. P. 1950.

  19. Dolinsky T.J., Nielsen J.E., McCammon J.A. et al. // Nucleic Acids Res. 2004. V. 32. № 2. P. W665.

  20. Horn H.W., Swope W.C., Pitera J.W. et al. // J. Chem. Phys. 2004. V. 120. № 20. P. 9665.

  21. Berendsen H.J.C., Postma J.V., van Gunsteren W.F. et al. // J. Chem. Phys. 1984. V. 81. № 8. P. 3684.

  22. Parrinello M., Rahman A. // J. Chem. Phys. 1982. V. 76. № 5. P. 2662.

  23. Hess B., Bekker H., Berendsen H.J. et al. // J. Comp. Chem. 1997. V. 18. № 12. P. 1463.

  24. Van Gunsteren W.F., Berendsen H.J.C. // Mol. Simulation. 1988. V. 1. № 3. P. 173.

  25. Essmann U., Perera L., Berkowitz M.L. et al. // J. Chem. Phys. 1995. V. 103. № 19. P. 8577.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Кристаллография

Архивы выпусков Информация о журнале Отправить рукопись в журнал