Кристаллография, 2021, T. 66, № 3, стр. 388-398
Пересечения спиралей Бердийка–Коксетера в трехмерном евклидовом пространстве
1 Институт физической химии и электрохимии им. А.Н. Фрумкина РАН
Москва, Россия
* E-mail: lmm@phyche.ac.ru
Поступила в редакцию 26.11.2019
После доработки 21.08.2020
Принята к публикации 27.10.2020
Аннотация
Рассмотрены различные пересечения спиралей Бердийка–Коксетера (БК) одного знака хиральности из идеальных тетраэдров в трехмерном евклидовом пространстве и вычислены углы между их осями. В строгие геометрические модели пересечений спиралей БК внесены физически обоснованные искажения (слияние близкорасположенных вершин и образование дополнительных связей между вершинами, разделенными расстоянием порядка длины ребра тетраэдра). Показано, что после введения этих искажений существует семь различных видов пересечения двух спиралей БК, проходящих через один икосаэдр, которые соответствуют семи видам пересечений спиралей 30/11 в политопе {3, 3, 5}. Для разных способов расслоения Хопфа множества вершин политопа {3, 3, 5} показано, что локальную структуру политопа {3, 3, 5} в окрестности окружности Хопфа, проходящей через вершины политопа, можно описать как определенную совокупность пересекающихся спиралей 30/11.
ВВЕДЕНИЕ
В последнее время привлекают большое внимание такие состояния вещества, в которых порядок расположения атомов сложнее, чем периодический, или периодический, но с большим размером элементарной ячейки и выраженной иерархией [1]. К ним относятся, например, аморфное состояние, кластеры, квазикристаллы, интерметаллические соединения [1], синтетические пористые материалы [2] и т.д. Сюда же можно отнести структуры гидратационных оболочек молекул растворенных в воде веществ, в частности биомолекул [3]. Часто для изучения и интерпретации этих структур, а также для синтеза соответствующих материалов (например, [2]) существенную роль играет предварительное структурное моделирование. Оно бывает полезно и для интерпретации уже известных структур кристаллов неорганических веществ.
К подобным геометрическим построениям, используемым для изучения структур плотных упаковок, относятся структуры из смежных (здесь и далее имеется в виду смежных по граням) тетраэдров с атомами в их вершинах [1]. Примерами служат 13-атомный икосаэдрический кластер и стержни из таких взаимопроникающих икосаэдров (в органометаллических соединениях [4] и металлических сплавах [1]), 45-атомный икосаэдр Бергмана в металлических сплавах и 26-атомный кластер γ-латуни из четырех взаимопроникающих икосаэдров, а также спиральные структуры из смежных тетраэдров (СТ) [1]. Так, структуры некоторых спиральных биомолекул описываются как производные от линейной спиральной структуры из смежных идеальных тетраэдров (СИТ) (рис. 1), которая получила название спираль Бердийка–Коксетера (БК) [1].
Спираль БК неожиданным образом была выявлена и в структуре кристаллов простого неорганического вещества – β-марганца. Существует несколько различных интерпретаций этой структуры, однако наиболее просто она описывается как система слегка искаженных спиралей БК, идущих в трех взаимоперпендикулярных направлениях и пересекающихся во фрагменте слегка искаженного икосаэдра [1, 5].
В настоящей работе перечислены все возможные виды пересечений двух спиралей БК одного знака хиральности из идеальных тетраэдров в трехмерном евклидовом пространстве E3 для случаев, когда спирали имеют какой-либо общий элемент: хотя бы один общий тетраэдр, или общую грань, или общее ребро. В последнем случае для определенности будем считать, что обе спирали имеют по общей грани с одним и тем же им не принадлежащим идеальным тетраэдром, отчего и возникает общее ребро. Для этих строгих геометрических моделей вычислены углы между осями пересекающихся спиралей БК.
Для спиралей БК, состоящих из идеальных тетраэдров, при переходе от строгой геометрической модели к структурной часто нужно вводить искажения, состоящие в объединении каждых двух вершин, находящихся на расстоянии, много меньшем длины ребра тетраэдра, в одну. Появление таких пар близко расположенных вершин связано с тем, что в пространстве E3 пять идеальных СТ, расположенных вокруг одного общего ребра, образуют известную щель величиной в ~7.35° (так как угол между гранями идеального тетраэдра при общем ребре равен arccos(1/3) ≈ ≈ 70.53°), а двенадцать СИТ с одной общей вершиной складываются в икосаэдр с образованием многочисленных щелей.
Объединение близкорасположенных вершин в одну позволяет перейти к физически осмысленной структуре из атомов (например, атомов металлов) в вершинах тетраэдров. Другое возможное искажение строгой геометрической модели – это введение дополнительных связей между атомами разных спиралей, находящимися на расстоянии, близком к длине ребра тетраэдра. Подобные искажения в [6] удачно названы физически обоснованными искажениями. Степень “неидеальности” тетраэдров при введении указанных искажений сравнима со степенью “неидеальности” тетраэдров в идеальном икосаэдре, где отношение расстояния r от центра до вершины к длине ребра l равно r : l = (1/2)(τ2 + 1)1/2 ≈ 0.951 : 1 ≈ ≈ 1 : 1.051, τ = (1 + √5)/2 – параметр золотого сечения, а углы между направлениями из центра на соседние вершины равны arccos(τ/(τ + 2)) ≈ 63.43°.
В настоящей работе показано, что после введения физически обоснованных искажений все возможные пересечения спиралей БК, проходящих через один икосаэдр, сводятся к четырем категориям: трем выше перечисленным, когда две спирали имеют хотя бы один общий тетраэдр, или общую грань, или по общей грани с одним и тем же им не принадлежащим тетраэдром, или выполняется сразу несколько из перечисленных условий, и к четвертой, когда спирали имеют только одну общую точку.
В четырехмерном евклидовом пространстве E4 спираль БК может быть как прямолинейной, так и изогнутой различными способами с сохранением смежности тетраэдров и их идеальности. В частности, фрагмент из 30 тетраэдров прямолинейной спирали БК можно согнуть в замкнутую спираль с сохранением идеальности тетраэдров и их смежности и образованием еще одной смежной грани между крайними тетраэдрами. Такие спирали присутствуют в политопе {3, 3, 5} – правильном многограннике пространства E4, который состоит из СИТ, сложенных таким образом, что вокруг каждого ребра находится пять СТ [7, 8]. Каждая вершина политопа {3, 3, 5} является общей для окружающих ее двадцати СИТ, а все вершины лежат на одной трехмерной сфере S3 [7, 8]. Политоп {3, 3, 5} имеет 120 вершин и состоит из 600 СИТ [7, 8]. Осями замкнутых спиралей, состоящих из 30 СИТ политопа {3, 3, 5}, являются большие окружности на сфере S3, на которой лежат вершины политопа {3, 3, 5}, а симметрия этих спиралей описывается формулой 30/11 [7, 9]11. Поэтому часто их называют спиралями 30/11. Политоп {3, 3, 5} не энантиоморфен, и выделяемые в нем спирали 30/11 могут быть как левыми, так и правыми.
В настоящей рабете сначала рассмотрены способы пересечений спиралей БК одного знака хиральности в E3. Далее показано, что введенные физически обоснованные искажения соответствуют элементам структуры политопа {3, 3, 5}, а виды пересечений спиралей 30/11 в политопе {3, 3, 5} (на сфере S3) те же, что у спиралей БК (с физически обоснованными искажениями) в E3. В конце работы показана связь между некоторыми видами пересечений спиралей БК и разными способами дискретного расслоения Хопфа множества вершин политопа {3, 3, 5}.
НАПРАВЛЕНИЕ ОСИ СПИРАЛИ БК, ПРОХОДЯЩЕЙ ЧЕРЕЗ ТЕТРАЭДР С ЗАДАННЫМИ КООРДИНАТАМИ ВЕРШИН, В ПРОСТРАНСТВЕ E3
Опишем способ определения направления оси спирали БК, проходящей в E3 в заданном порядке через вершины идеального тетраэдра, координаты которых известны. В дальнейшем это понадобится для вычисления углов между осями пересекающихся спиралей БК.
Следуя [10], предположим, что ось спирали БК параллельна координатной оси z, а радиус r – единичный. Пусть α – угол поворота за один шаг, а h – длина шага вдоль оси спирали (оси z). Тогда координаты вершин первого тетраэдра записываются как xn = cos(nα), yn = sin(nα), zn = nh, где n = = 0, 1, 2, 3. Из условия равенства длин ребер правильного тетраэдра l12 = l13 = l14 получаем α = arccos(–2/3) ≈ 131.81°, h = $\sqrt {10{\text{/}}27} $ [10]. Координаты вершин 1, 2, 3 и 4 равны (1, 0, 0), (–2/3, $\sqrt 5 {\text{/}}3$, $\sqrt {10{\text{/}}27} $), (–1/9, $ - 4\sqrt 5 {\text{/}}9$, $2\sqrt {10{\text{/}}27} $) и (22/27, $7\sqrt 5 {\text{/}}27$, 3$\sqrt {10{\text{/}}27} $) соответственно. Соотношение длины ребра тетраэдра, шага спирали вдоль ее оси и радиуса спирали записывается как $l:h:r = $ $ = \frac{{10}}{{\sqrt {27} }}:\sqrt {\frac{{10}}{{27}}} :1$ [10].
Зная координаты вершин 1–4, можно вычислить координаты точек пересечения оси z с гранями 123 и 234 тетраэдра 1234. Получаем, что точка пересечения оси z с гранью 123 лежит на биссектрисе угла 1–2–3 и имеет координаты (0, 0, $\sqrt {10{\text{/}}27} $), расстояние от нее до центра грани 123 равно 1/9, до вершины 2 – радиусу спирали, т.е. единице, а до вершин 1 и 3 – $\sqrt {37{\text{/}}27} $. Точка пересечения грани 234 и оси z лежит на биссектрисе угла 2–3–4, имеет координаты (0, 0, $2\sqrt {10{\text{/}}27} $) и находится на расстоянии 1/9 от центра грани 234, на единичном расстоянии от вершины 3 и на расстоянии $\sqrt {37{\text{/}}27} $ от вершин 2 и 4. Расстояние между точками пересечения оси спирали с гранями тетраэдра равно шагу спирали. Ось спирали БК не проходит ни через центры составляющих ее тетраэдров, ни через центры их граней.
Таким образом, если вершины A, B, C и D правильного тетраэдра с ребром l образуют спираль A–B–C–D, то ее ось пересекает грань ABC тетраэдра в точке, лежащей на биссектрисе угла ABC на расстоянии $\sqrt {27} $l/10 от вершины B, и грань BCD в точке, лежащей на биссектрисе угла BCD на расстоянии $\sqrt {27} $l/10 от вершины C. При этом радиус спирали равен $r = {{\sqrt {27} }_{{}}}l{\text{/}}10$, а шаг спирали вдоль оси составляет $h = l{\text{/}}\sqrt {10} $. Используя эти результаты, можно вычислить направления осей спиралей 30/11, проходящих через различные грани тетраэдра.
ВИДЫ ПЕРЕСЕЧЕНИЙ ПРАВЫХ СПИРАЛЕЙ БК
Углы между правыми спиралями БК, проходящими по крайней мере через один общий тетраэдр. Если вершины идеального тетраэдра лежат в точках 1 (1, 0, 0), 2 (0, 1, 0), 3 (0, 0, 1) и 4 (1, 1, 1), то длина ребра тетраэдра равна $\sqrt 2 $, спираль 1–2–3–4 является правой, шаг спирали вдоль ее оси равен $1{\text{/}}\sqrt 5 $, а радиус спирали равен $3\sqrt 6 {\text{/}}10$. Проведя четные перестановки номеров вершин тетраэдра 1234, можно получить порядок следования этих вершин во всех шести различных правых спиралях, содержащих тетраэдр 1234. Все они перечислены в табл. 1, где приводятся также направления их осей и углы, образуемые ими с осью спирали 1–2–3–4.
Таблица 1.
Углы между осями двух правых спиралей БК для точных геометрических моделей с общими тетраэдрами и общей гранью
| Спираль 1 и направление ее оси | Спираль 2 и направление ее оси | Угол между осями спиралей 1 и 2 | Рисунок |
|---|---|---|---|
| Спирали БК с двумя общими тетраэдрами | |||
| 1–2–3–4, [0 1 2] | 1–4–2–3, [–2 0 1] | arccos(2/5) ≈ 66.42° | 2а |
| 1–3–4–2, [–1 2 0] | |||
| 2–3–1–4, [2 0 1] | |||
| 3–1–2–4, [1 2 0] | |||
| Спирали БК с одним общим тетраэдром | |||
| 1–2–3–4, [0 1 2] | 2–1–4–3, [0 –1 2] | arccos(3/5) ≈ 53.13° | 2е |
| Спирали БК с общей треугольной гранью | |||
| 1–4–2–3, [–2 0 1] | 1–8–3–2, [–4 5 2] | arccos(2/3) ≈ 48.18° | 2л |
| 2–8–1–3, [2 –4 5] | arccos(1/15) ≈ 86.17° | 2р | |
| 3–8–2–1, [5 2 –4 ] | arccos(–14/15) ≈ 158.96° | 2м | |
| 1–3–4–2, [–1 2 0] | 1–8–3–2, [–4 5 2] | arccos(14/15) ≈ 21.03° | 2м |
| 2–8–1–3, [2 –4 5] | arccos(–2/3) ≈ 131.81° | 2л | |
| 3–8–2–1, [5 2 –4 ] | arccos(–1/15) ≈ 93.82° | 2р | |
| 2–1–4–3, [0 –1 2] | 1–8–3–2, [–4 5 2] | arccos(–1/15) ≈ 93.82° | 2р |
| 2–8–1–3, [2 –4 5] | arccos(14/15) ≈ 21.03° | 2м | |
| 3–8–2–1, [5 2 –4 ] | arccos(–2/3) ≈ 131.81° | 2л | |
Спирали 1–4–2–3, 1–3–4–2, 2–3–1–4 и 3–1–2–4 имеют два общих СТ со спиралью 1–2–3–4 (рис. 2а), а спираль 2–1–4–3 – только один (рис. 2е), поэтому угол между ее осью и осью спирали 1–2–3–4 (~53°) не такой, как у остальных спиралей (~66°).
Рис. 2.
Спирали БК, проходящие через общие два (а–д) или один (е–к) тетраэдр и спирали, имеющие одну или много общих треугольных граней (л–с). Строгие геометрические модели (а, б, е, л, м), модели с физически обоснованными искажениями (д, ж, з, н, п, р) и соответствующие некоторые возможные взаимные расположения спиралей внутри одного икосаэдра (в, г, и, к, о, с). Серым цветом закрашены грани, к которым должны быть приставлены следующие тетраэдры спиралей. Темно-серым цветом с белым ободом закрашены видимые боковые грани спиралей БК, выделенных в одном икосаэдре или в колонке из взаимопроникающих икосаэдров. Одинаковыми цифрами обозначены грани тетраэдров, принадлежащих одной спирали БК. На рис. д, р дополнительные связи между спиралями обозначены штриховыми линиями.
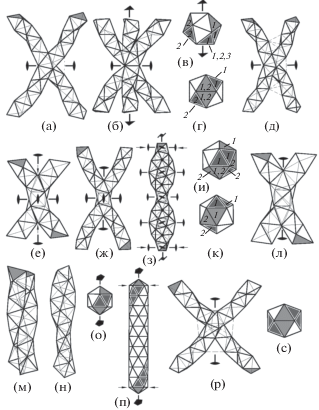
Две спирали с двумя общими СТ связаны двойной осью симметрии, проходящей через общую грань общих СТ и еще один тетраэдр, который спиралям не принадлежит, но двух разных граней которого они касаются (рис. 2а). Два СТ имеют одну общую тройную ось симметрии, поэтому через общую область в виде двух СТ могут проходить не только две, но и три правые спирали БК (рис. 2б). Они связаны той же тройной осью и тремя двойными осями симметрии, проходящими через общую грань общих СТ, а углы между их осями равны arccos(2/5). На рис. 2в показано, как эти три спирали проходят через один икосаэдр и связаны тройной осью, а на рис. 2г – как две из них проходят через один икосаэдр и связаны двойной осью.
Возможно образование до девяти дополнительных связей между вершинами двух спиралей БК, проходящих через два общих тетраэдра (рис. 2д). Это приведет к искажению тетраэдров в области пересечения спиралей и некоторому уменьшению угла между осями их прямолинейных участков, в которых нет дополнительных связей между вершинами спиралей (рис. 2а, 2д). Оценку величины изменения этого угла можно получить, сравнивая углы между осями спиралей для разных точных геометрических моделей, соответствующих этому пересечению спиралей с физически обоснованными искажениями. Это будет сделано ниже.
Две спирали БК, имеющие только один общий тетраэдр, связаны тремя двойными осями симметрии этого тетраэдра (рис. 2е). В данном случае при переходе к физически осмысленной модели в обеих парах близко расположенных вершин, указанных на рис. 2е стрелками, их нужно слить в одну, так как два атома не могут находиться на таком коротком расстоянии друг от друга. Тогда кроме общего тетраэдра у спиралей БК появятся еще две общие треугольные грани, хорошо видные на рис. 2ж.
Дополнительные связи между атомами спиралей, находящимися на расстоянии, сравнимом с длиной ребра тетраэдра, придется вводить последовательно вдоль всей длины спиралей (рис. 2з). На рис. 2з изображены две спирали из тетраэдров, связанные двойной осью, но можно достроить еще две такие же спирали, связанные между собой двойной осью, повернутые на 90° и сдвинутые на полпериода относительно первой пары спиралей. Совокупность всех четырех спиралей будет обладать винтовой симметрией с осью 42.
На рис. 2и, 2к показано два возможных взаимных расположения в икосаэдре двух спиралей БК, пересекающихся с образованием только одного общего тетраэдра.
Углы между осями правых спиралей БК, имеющих общую грань. Добавим еще точки 5 (–1/3, 4/3, 4/3), 6 (4/3, –1/3, 4/3), 7 (4/3, 4/3, –1/3) и 8 (–1/3, –1/3, –1/3), являющиеся отражением точек 1, 2, 3 и 4 относительно граней 234, 134, 124 и 123 соответственно. Тогда правыми спиралями БК, имеющими общую грань с тетраэдром 1234, но не содержащими его, будут спирали 3–6–1–4, 4–6–3–1, 1–6–4–3 и симметричные им относительно тройной оси [111] 1–7–2–4, 4–7–1–2, 2–7–4–1, 2–5–3–4, 4–5–2–3 и 3–5–4–2, а также спирали 1–8–3–2, 2–8–1–3 и 3–8–2–1, связанные той же тройной осью.
Для определения углов между осями спиралей БК, имеющих общую грань, были найдены направления осей всех правых спиралей, содержащих тетраэдр 8123, но не проходящих через грань 123, и вычислены углы между ними и осями всех правых спиралей, содержащих тетраэдр 1234, но не проходящих через грань 123. Результаты приведены в табл. 1.
Спирали БК, состоящие из правильных тетраэдров и касающиеся друг друга с углом между осями arccos(±2/3) (рис. 2л), могут существовать только в качестве бестелесной геометрической модели. При переходе к структурной модели с атомами в вершинах тетраэдров необходимо в трех местах объединить близкорасположенные вершины. В результате получится уже известная структура (рис. 2ж), где общими для двух спиралей будет один тетраэдр и две треугольные грани, каждая из которых имеет общее ребро с этим тетраэдром. Если при этом также введены дополнительные связи между спиралями, то получается структура, показанная на рис. 2з.
Спирали БК, состоящие из правильных тетраэдров и касающиеся друг друга треугольными гранями с углом между осями arccos(±14/15) (рис. 2м), также существуют только в качестве геометрической модели. При переходе к структурной модели из атомов у этих спиралей приходится объединить целую полосу из треугольных граней, и они начинают обвивать друг друга (рис. 2н). Отдельный икосаэдр (рис. 2о), а также колонку из взаимопроникающих икосаэдров, соединенных вдоль пятерной оси (рис. 2п), можно разделить на пять спиралей БК, касающихся друг друга подобным образом. На рис. 2о, 2п выделена одна из этих пяти спиралей. Последовательность ребер, выстроенных в прямую линию на пятерной оси, является общей для всех пяти спиралей.
Касание несоседних спиралей в колонке на рис. 2п будет рассмотрено в следующем разделе. Если способом, изображенным на рис. 2м, соединяются не целые спирали из атомов в вершинах тетраэдров, а половины спиралей, образуя развернутый угол, то он примет вычисленное значение arccos(±14/15), так как дополнительных связей в этом случае вводить не нужно.
Наконец, при одной общей грани и угле между осями спиралей БК arccos(±1/15) эти спирали связаны одной двойной осью, являющейся также двойной осью общей треугольной грани и одного из тетраэдров, который этим спиралям не принадлежит, но двух граней которого они касаются (рис. 2р). Между вершинами этих спиралей может образоваться еще восемь дополнительных связей (штриховые линии на рис. 2р), что также приведет к некоторому искажению тетраэдров и к незначительному изменению угла между прямолинейными участками осей спиралей, где нет дополнительных связей между вершинами спиралей. Одно из возможных взаимных расположений в икосаэдре двух подобным образом пересекающихся спиралей показано на рис. 2с.
Углы между осями правых спиралей БК, имеющих смежные грани с одним и тем же им не принадлежащим тетраэдром. В табл. 2 приведены направления осей всех правых спиралей БК, имеющих одну общую грань с тетраэдром 1234. Есть четыре различных случая, когда одного тетраэдра касаются три спирали БК, связанные тройной осью симметрии этого тетраэдра, и три случая, когда одного тетраэдра касаются две спирали БК, связанные двойной осью этого тетраэдра.
Таблица 2.
Углы между осями спиралей БК для точных геометрических моделей, когда спирали имеют по одной смежной грани с тетраэдром с вершинами 1 (1, 0, 0), 2 (0, 1, 0), 3 (0, 0, 1) и 4 (1, 1, 1)
| Спирали | Направления их осей | Углы между осями спиралей | Ось симметрии, связывающая спирали | Рисунок | |
|---|---|---|---|---|---|
| 1 | 1–8–3–2 2–8–1–3 3–8–2–1 |
[–4 5 2] [2 –4 5] [52 –4 ] |
arccos(–18/45) ≈ 113.57° | [111] | 3а |
| 2 | 1–8–3–2 4–6–3–1 2–5–3–4 |
[–4 5 2] [–2 –4 –5] [5 –24 ] |
arccos(–22/45) ≈ 119.26° | [11$\bar {1}$] | 3в |
| 3 | 1–8–3–2 3–5–4–2 4–7–1–2 |
[–4 5 2] [24 –5] [–5 –2 –4] |
arccos(2/45) ≈ 87.45° | [1$\bar {1}$1] | 3д |
| 4 | 1–8–3–2 1–7–2–4 1–6–4–3 |
[–4 5 2] [–2 4 5] [–5 2 4] |
arccos(38/45) ≈ 32.38° | [$\bar {1}$11] | 3ж, 3з |
| 5 | 1–8–3–2 2–7–4–1 |
[–4 5 2] [4 –5 2 ] |
arccos(–37/45) ≈ 145.30° | [001] | 3к, 3л |
| 6 | 1–8–3–2 3–6–1–4 |
[–4 5 2] [4 5 –2 ] |
arccos(5/45) ≈ 83.62° | [010] | 2р |
| 7 | 1–8–3–2 4–5–2–3 |
[–4 5 2] [–4 –5 –2] |
arccos(–13/15) ≈ 106.79° | [100] | 2а |
В первом случае три спирали имеют один общий тетраэдр 8123 и касаются одной и той же грани 123 тетраэдра 1234. Величина угла между осями указывает на то, что каждые две из трех рассматриваемых спиралей должны иметь еще по одному общему тетраэдру, смежному с 8123, и пересекаются как на рис. 2а. Второй тетраэдр не может быть общим для всех трех спиралей, как на рис. 2б, так как в последнем случае нет тетраэдра, которого все три спирали касались бы гранями. Пересечение трех спиралей БК, когда у каждой пары спиралей есть два общих СИТ, причем один из них принадлежит всем трем спиралям, показано на рис. 3а. Подобное пересечение спиралей БК внутри одного икосаэдра показано на рис. 3б.
Рис. 3.
Спирали БК, имеющие по одной общей грани с одним и тем же тетраэдром, который им не принадлежит, и связанные его тройной (а–з) или двойной (к, л) осью симметрии. Те же пересечения спиралей БК, что и на рис. а, в, д, но в пределах одного икосаэдра (б, г, е). Три спирали, попарно касающиеся граней одного тетраэдра как на рис. ж (после введения физически обоснованных искажений), выделенные в колонке из смежных икосаэдров, выстроенных вдоль тройной оси (з). Центральная область этой колонки (и). Две спирали, касающиеся граней одного тетраэдра как на рис. к (после введения физически обоснованных искажений), выделенные в колонке из взаимопроникающих икосаэдров, выстроенных вдоль пятерной оси (л). Серым цветом закрашены грани, к которым должны быть приставлены следующие тетраэдры спиралей. Темно-серым цветом с белым ободом закрашены боковые грани спиралей. Одинаковыми цифрами обозначены грани тетраэдров, принадлежащих одной спирали БК.
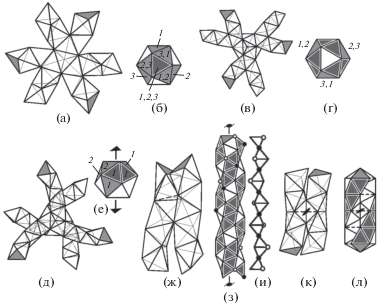
Во втором случае оси спиралей, касающихся одного тетраэдра, лежат практически в одной плоскости. При переходе от строгой геометрической модели (из идеальных тетраэдров) к физической нужно для каждой пары спиралей обобществить по два тетраэдра. Тогда спирали будут попарно пересекаться с обобществлением двух тетраэдров (как на рис. 2а), но в силу искажения тетраэдров, соответствующего искажению тетраэдров в икосаэдре, угол между осями спиралей изменится с ~66° (~114°) на 60° (120°) (рис. 3в). На рис. 3г показаны грани икосаэдра, из которых выходят три спирали 30/11, соединенные подобным образом. Взаимное расположение каждых двух из них в икосаэдре такое же, как у каждых двух на рис. 2в.
В третьем случае (рис. 3д) с учетом физически обоснованных искажений, спирали попарно касаются друг друга как на рис. 2р. На рис. 3е показано взаимное расположение таких трех спиралей в одном икосаэдре. Из-за искажения тетраэдров в икосаэдре угол между осями спиралей лишь приблизительно равен arccos(2/45).
В четвертом случае у двух спиралей 30/11, имеющих по общей грани с им не принадлежащим тетраэдром, есть также общее для них ребро (рис. 3ж). Соединять близкие вершины в одну придется последовательно по всей длине спиралей. В результате общей станет ломаная линия из ребер, идущая по всей длине спиралей, а сами спирали станут закрученными вокруг общей оси. Это хорошо видно на рис. 3з, где изображена колонка из выстроенных вдоль тройной оси смежных икосаэдров (с дополнительными тетраэдрами между ними), у которой закрашены грани трех спиралей БК, принадлежащих этой колонке. Тетраэдры, которых касаются все три спирали, лежат на тройной оси и на рис. 3з не видны. Они изображены отдельно на рис. 3и. Грани тетраэдров, которых касаются только две из трех изображенных спиралей, на рис. 3з обозначены белым цветом. Если этим способом вокруг тетраэдра соединяются не целые спирали, а их половины, образуя развернутый угол, то его значение равно arccos(‒38/45), так как в этом случае дополнительные связи между вершинами спиралей отсутствуют.
В пятом случае две спирали также имеют по общей грани с им не принадлежащим тетраэдром, а между собой общее ребро (рис. 3к). Угол между их осями равен arccos(–37/45). Спирали связаны двойной осью, проходящей через общее ребро спиралей и являющейся двойной осью смежного с ними тетраэдра. После попарного слияния близких вершин, проводимого последовательно вдоль всей длины спиралей, они закручиваются друг за друга, имея последовательность общих ребер и набор тетраэдров, смежных граней которых они касаются (рис. 3л). Таким способом касаются несоседние спирали в колонке из взаимопроникающих икосаэдров, соединенных вдоль пятерной оси (рис. 2п, 3л). Если подобным образом одного тетраэдра касаются не две целые спирали, а их половины, образуя развернутый угол, то его величина равна arccos(–37/45).
Шестой случай (табл. 3) после слияния близких вершин соответствует рис. 2р, а седьмой – рис. 2а. На обоих рисунках видны тетраэдры, граней которых спирали касаются, и указаны соответствующие двойные оси.
Таблица 3.
Углы между направлением (τ/6)[–1, –1 – τ2, τ2], описывающим положение правой спирали БК с номером 1 в идеальном икосаэдре, и направлениями, описывающими положение других правых спиралей БК, проходящих через тот же идеальный икосаэдр
| Номер и направление спирали | Угол | Рисунок | |
|---|---|---|---|
| Спирали БК, имеющие только одну общую точку | |||
| 2 | (1/6)[τ4, –τ2, –1] | arccos(0) = 90° | |
| Спирали БК, имеющие два общих тетраэдра | |||
| 3 | (τ/6)[1 + τ2, τ2, 1] | arccos(–1/2) = 120° | 2в, 3г |
| 4 | (τ/6)[–τ2, 1, –1 – τ2] | ||
| 5 | (1/6)[τ2, –1, τ4] | ||
| 6 | (1/6)[1, –τ4, –τ2] | ||
| 7 | (τ/6)[–1 – τ2, τ2, –1] | arccos(–τ/4) ≈ 113.86° | 3б |
| 8 | (1/6)[τ4, τ2, 1] | ||
| 9 | (τ/6)[τ2, –1, –1 – τ2] | ||
| 10 | (τ2/3)[–1, 1, 0] | ||
| 11 | (1/6)[τ2, 1, τ4] | arccos(–(1 + τ2)/4τ2) ≈ 110.22° | 2г |
| 12 | (τ/6)[–1, –1 – τ2, –τ2] | ||
| Спирали БК, имеющие один общий тетраэдр и две прилегающие к нему грани | |||
| 13 | (1/6)[τ4, τ2, –1] | arccos(–(1 + τ2)/4τ) ≈ 123.99° | 2и |
| 14 | (1/6)[1, τ4, τ2] | ||
| 15 | (1/6)[–τ2, 1, –τ4] | ||
| 16 | (τ2/3)[1, 0, –1] | ||
| 17 | (1/6)[–τ2, –1, τ4] | arccos(–(2 + τ2)/4τ) ≈ 135.52° | 2к |
| 18 | (τ2/3)[1, 1, 0] | ||
| Спирали БК, имеющие одну общую грань и почти перпендикулярные друг другу | |||
| 19 | (τ/6)[τ2, 1, 1 + τ2] | arccos(1/4τ) ≈ 81.11° | 3е |
| 20 | (τ/6)[1 + τ2, –τ2, –1] | ||
| 21 | (1/6)[τ4, –τ2, 1] | ||
| 22 | (τ2/3)[0, 1, 1] | ||
| 23 | (τ/6)[1, –1 – τ2, –τ2] | arccos(1/4) ≈ 75.52° | 2с |
| 24 | (τ2/3)[1, 0, 1] | ||
| Соседние спирали БК, идущие вокруг пятерной оси икосаэдра | |||
| 25 | (1/6)[1, τ4, –τ2] | arccos(–(1 + 2τ2)/4τ) ≈ 164.47° | 2о |
| 26 | (τ2/3)[0, 1, –1] | ||
| Соседние через одну спирали БК, идущие вокруг пятерной оси икосаэдра | |||
| 27 | (τ/6)[–τ2, –1, 1 + τ2] | arccos(3/4) ≈ 41.40° | 3л |
| 28 | (τ/6)[–1 – τ2, –τ2, 1] | ||
| Спирали БК, идущие вокруг тройной оси икосаэдра | |||
| 29 | (τ/6)[–1, 1 + τ2, –τ2] | arccos((1 + τ2)/4) ≈ 154.75° | 3з |
| 30 | (1/6)[–1, τ4, –τ2] | ||
ВИДЫ ПЕРЕСЕЧЕНИЙ ДВУХ СПИРАЛЕЙ БК, ПРОХОДЯЩИХ ЧЕРЕЗ ОДИН ИКОСАЭДР
Для всех рассмотренных случаев любая общая вершина пересекающихся спиралей является общей вершиной от шести до девяти СТ. Поэтому вокруг нее всегда можно достроить икосаэдр, добавив к вершинам спиралей от двух до, максимум, четырех недостающих вершин икосаэдра. Для заданного пересечения спиралей число их общих вершин, не связанных симметрией, равно числу их различных взаимных расположений в икосаэдре.
В этом разделе перечислены все возможные виды пересечений спиралей БК, проходящих через один икосаэдр. Икосаэдру, через который проходит спираль БК, принадлежат четыре последовательных тетраэдра этой спирали (рис. 2о). Так как правильный икосаэдр состоит из неправильных тетраэдров, то или икосаэдр, через который проходят две спирали БК, будет неправильным, или эти спирали будут слегка искажены.
На каждой из 20 граней икосаэдра может заканчиваться три спирали БК, причем у каждой спирали два конца, поэтому общее число спиралей БК, проходящих через один икосаэдр, равно 30. Соответственно, возможно 29 видов их пересечений.
Для определения числа различных видов пересечений спиралей БК, проходящих через один икосаэдр, будем считать этот икосаэдр идеальным. Тогда спирали БК будут содержать искаженные тетраэдры, принадлежащие икосаэдру. Пусть вершины икосаэдра имеют координаты (±τ/2, ±1/2, 0), тогда центры его граней (вершины вписанного додекаэдра) находятся в точках (0, ±τ/6, ±τ3/6) и (±τ2/6, ±τ2/6, ±τ2/6). Запишем положение спирали БК в икосаэдре как направление отрезка, соединяющего центры граней икосаэдра, из которых данная спираль БК может быть продолжена. Такие отрезки идут вдоль направлений 〈±(1 + τ2) ±τ2 ±1〉, 〈±τ4 ±τ2 ±1〉 и <0 ±1 ±1>. В табл. 3 приведены углы между этими направлениями. В силу симметрии икосаэдра число различных углов между рассматриваемыми отрезками уменьшается от 29 до 11. Далее в некоторых случаях надо проводить искажение спиралей и вне икосаэдра, сливая две вершины в одну в парах близко расположенных вершин пересекающихся спиралей. После этого число топологически различных видов пересечений двух спиралей БК уменьшается до семи (табл. 3). Таким образом, все виды пересечений двух спиралей БК, проходящих через один икосаэдр, кроме одного (когда спирали имеют всего одну общую точку), сводятся к уже рассмотренным ранее.
Отрезки, характеризующие положение спиралей 1–6, являются ребрами тетраэдра с вершинами в центрах граней икосаэдра. Спирали БК 1 и 2, имеющие только одну общую точку, проходят вдоль взаимно перпендикулярных ребер этого тетраэдра. Ребра тетраэдра и, соответственно, спирали 1–6 могут быть ориентированы двумя различными способами относительно его тройной оси (рис. 2в, 3г).
ВИДЫ ПЕРЕСЕЧЕНИЙ СПИРАЛЕЙ БК И РАССЛОЕНИЕ ХОПФА МНОЖЕСТВА ВЕРШИН ПОЛИТОПА {3, 3, 5}
В E4 замкнутую спираль симметрии 30/11 из СИТ, выделенную из политопа {3, 3, 5}, можно разрезать и распрямить таким образом, что ее ось превратится из окружности в прямую линию, причем идеальность тетраэдров не нарушится, а смежность по граням нарушится только в месте разреза (рис. 1). При этом изменится симметрия спирали: формула 30/11 будет описывать ее лишь приблизительно, так как за 30 шагов спираль будет делать не 11 полных оборотов, а на 11 × 360°– 30 × arccos(–2/3) ≈ 5.69° меньше. Такой отрезок бывшей спирали 30/11, ставший отрезком спирали БК, можно без искажений перенести из E4 в E3.
В политопе {3, 3, 5} каждая вершина является центром икосаэдра, поэтому две пересекающиеся спирали 30/11 политопа {3, 3, 5} проходят через все икосаэдры с центрами в общих вершинах этих спиралей.
Координаты вершин политопа {3, 3, 5} приведены в [7, 8]. Для каждой вершины составлены списки соседних двенадцати вершин. На их основе предложен следующий алгоритм построения последовательности вершин политопа {3, 3, 5}, образующих спираль 30/11: если известны вершины i – 3, i – 2, i – 1, i спирали 30/11, то ее вершина i + 1 будет соседней для вершин i – 2, i – 1 и i, причем отличной от вершины i – 3. Используя этот алгоритм, для каждого способа пересечения спиралей БК в политопе {3, 3, 5} выделены соответствующие пары спиралей 30/11 (а в случаях рис. 2з, 2п, 3з – четыре, пять и три спирали соответственно) и определены все дополнительные связи между их вершинами. Анализ этих данных показал, что все рассмотренные способы пересечения двух спиралей БК реализуются и со спиралями 30/11 в политопе {3, 3, 5}. Во всех случаях (рис. 2, 3) объединенным вершинам спиралей БК соответствует одна вершина политопа {3, 3, 5}, а введенным дополнительным связям между вершинами разных спиралей БК соответствуют ребра политопа {3, 3, 5}.
Так как оси спиралей 30/11 представляют собой большие окружности на сфере S3, на которой лежат все вершины политопа {3, 3, 5}, а сам политоп обладает центром симметрии, две спирали всегда пересекаются одинаковым образом в двух местах с интервалом в полупериод спирали. Например, при пересечении двух спиралей 30/11, соответствующем первой строке табл. 3, у них есть две общие точки, лежащие на разных концах диаметра сферы S3 и отстоящие друг от друга на 15 шагов спирали.
Особый интерес вызывают пересечения спиралей (после введения физически обоснованных искажений), соответствующие различным дискретным расслоениям Хопфа множества вершин политопа {3, 3, 5}.
Пусть координаты точек на сфере S3 радиуса r определены через величины θ, φ и ω как x1 = = $r\cos \theta \cos \varphi $, x2 = $r\sin \theta \cos \varphi $, x3 = $r\cos \omega \sin \varphi $, x4 = $r\sin \omega \sin \varphi $. Если фиксировать φ = φ0 и положить θ = ω + ω0, где ω0 – константа, то параметры φ0 и ω0 будут определять окружность на сфере S3 и точку с координатами y1 = $(r{\text{/}}2)\cos (2{{\varphi }_{0}})$, y2 = = $(r{\text{/}}2)\cos {{\omega }_{0}}\sin (2{{\varphi }_{0}})$ и y3 = $(r{\text{/}}2)\sin {{\omega }_{0}}\sin (2{{\varphi }_{0}})$ на сфере S2 радиуса r/2 [9]. Это классический пример расслоения Хопфа, когда каждой точке сферы S2 взаимно однозначным образом по определенному закону ставится в соответствие большая окружность сферы S3 таким образом, что любая точка сферы S3 принадлежит одной и только одной окружности [9].
Все вершины политопа {3, 3, 5} лежат на одной сфере S3. Были построены такие дискретные расслоения Хопфа множества вершин политопа {3, 3, 5}, при которых большие окружности сферы S3, проходящие через вершины политопа, соответствуют вершинам икосаэдра, додекаэдра или икосододекаэдра на сфере S2 [9]. В этих случаях все вершины политопа {3, 3, 5} лежат соответственно на двенадцати, двадцати или тридцати окружностях Хопфа по десять, шесть или четыре на каждой [9]. Для каждого из этих расслоений описано взаимное расположение вершин политопа {3, 3, 5}, лежащих на одной окружности Хопфа [9].
Во фрагменте, ограниченном на рис. 2п стрелками, каждая из пяти спиралей БК состоит из 30 тетраэдров. В политопе {3, 3, 5} такой фрагмент свернут в тор, ось которого является большой окружностью сферы S3 [9]. Эта окружность, на которой лежат десять вершин политопа {3, 3, 5}, является одной из окружностей Хопфа при расслоении на 12 окружностей, содержащих по десять вершин политопа и соответствующих вершинам икосаэдра на сфере S2 [9]. Еще пять окружностей Хопфа этого расслоения лежат на поверхности тора (рис. 2п) [9]. Для любой окружности Хопфа этого расслоения вершины политопа, лежащие на ней или ближайшие к ней, образуют такой тор из пяти спиралей 30/11. Весь политоп {3, 3, 5} можно разбить на два таких тора, при этом один тор будут составлять вершины политопа, принадлежащие окружностям Хопфа, соответствующим шести вершинам верхней половины икосаэдра, выставленного вдоль пятерной оси, а другой тор – окружностям, соответствующим шести вершинам нижней половины икосаэдра [9].
Во фрагменте, изображенном на рис. 3з, каждая указанная спираль БК состоит из 30 тетраэдров, а середина фрагмента представляет собой шесть пар тетраэдров, сдвоенных через общую грань (рис. 3и). Проверено, что в политопе {3, 3, 5} этот фрагмент (рис. 3з) свернут в тор, ось которого является большой окружностью сферы S3 и проходит через шесть вершин политопа {3, 3, 5} (черные кружки на рис. 3и). Согласно [9] именно так расположены вершины политопа, принадлежащие одной из окружностей Хопфа при расслоении на 20 окружностей, соответствующих вершинам додекаэдра на сфере S2 и содержащих по шесть вершин политопа.
Все шесть вершин, лежащих на оси тора (черные кружки на рис. 3и), принадлежат каждой из трех спиралей 30/11, выделенных на рис. 3з. В каждой из них они расположены через пять шагов спирали. В силу симметрии каждая из четырех других таких шестерок вершин спирали 30/11 должна также лежать на своей окружности Хопфа. Вершины политопа {3, 3, 5}, лежащие на одной из этих окружностей Хопфа, находятся внутри тора, развернутого на рис. 3з, и обозначены на рис. 3з, 3и белыми кружками. Как и должно быть, эта окружность проходит через шесть пар сдвоенных тетраэдров. Внутри тора таких окружностей три. Вершины политопа, обозначенные на рис. 3з черными кружками, принадлежат еще одной шестерке вершин спирали 30/11 и лежат на поверхности тора. Через них (и сквозь соответствующие шесть пар сдвоенных тетраэдров) проходит еще одна окружность Хопфа. На поверхности тора таких окружностей шесть. Пять окружностей Хопфа, проходящих через вершины одной спирали 30/11, на сфере S2 соответствуют пяти вершинам одной грани додекаэдра.
В окрестности любой окружности Хопфа рассматриваемого расслоения вершины политопа {3, 3, 5} образуют три спирали 30/11, расположенные в соответствии с рис. 3з. Весь политоп {3, 3, 5} можно разбить на два тора, подобных развернутому на рис. 3з, при этом один тор будут составлять вершины политопа, принадлежащие окружностям Хопфа, соответствующим десяти вершинам верхней половины додекаэдра, выставленного вдоль тройной оси, а другой – его нижней половины. Возможность разбиения политопа на два тора была проверена непосредственным выделением их в политопе.
Длина спиралей БК во фрагменте, ограниченном на рис. 2з стрелками, равна 30 тетраэдрам. Проверено, что в политопе {3, 3, 5} такой фрагмент (включая еще две такие же спирали, повернутые относительно первых двух на 90° и сдвинутые на полпериода) замкнут в тор, на оси которого лежат четыре вершины политопа, обозначенные на рис. 2з черными кружками; ось тора является большой окружностью сферы S3, а лежащие на ней четыре вершины политопа образуют квадрат. Согласно [9] именно так, как изображено на рис. 2з (т.е. через высоту треугольной грани, середины противоположных ребер тетраэдра и еще одну высоту треугольной грани), взаимно расположены вершины политопа {3, 3, 5}, лежащие на одной окружности Хопфа при расслоении на 30 окружностей, соответствующих вершинам икосододекаэдра на сфере S2. Таким образом, в окрестности любой окружности Хопфа этого расслоения вершины политопа {3, 3, 5} образуют четыре спирали 30/11, уложенные в соответствии с рис. 2з. Напомним, что на рис. 2з показаны только две спирали из четырех, а другие две, также связанные двойной осью, повернуты относительно первых двух на 90° и сдвинуты на полпериода.
ЗАКЛЮЧЕНИЕ
Существует семь различных видов пересечения двух спиралей 30/11 одного знака хиральности внутри политопа {3, 3, 5}, которым соответствует семь видов пересечений двух спиралей БК, проходящих через один икосаэдр. При этом спирали могут иметь только одну общую точку, или один или два общих тетраэдра, или общую грань, или касаться одного и того же им не принадлежащего тетраэдра (тогда они имеют общие ребра). В E4 для спиралей 30/11 могут выполняться одновременно несколько из последних трех условий. В E3 для спиралей БК точные геометрические модели строятся с выполнением только одного из условий, а несколько условий выполняется только при внесении физически обоснованных искажений (объединения близкорасположенных вершин спиралей БК в одну и введения дополнительных связей между вершинами спиралей БК, расположенными на расстоянии порядка длины ребра тетраэдра). Проверено, что во всех случаях введенные искажения соответствовали или одной вершине политопа {3, 3, 5}, или ребру политопа {3, 3, 5}.
Установлены следующие виды пересечения спиралей БК.
1. Спирали, имеющие только одну общую точку.
2. Спирали, имеющие два общих тетраэдра, с углом между осями от arccos(4/10) ≈ 66° (строгая геометрическая модель) до 60° в зависимости от числа дополнительных связей между их атомами (рис. 2а–2д, 3а–3г). Если эти спирали рассматривать как касающиеся граней одного правильного тетраэдра и связанные между собой его двойной осью, то для такой строгой геометрической модели угол между их осями равен arccos(13/45) ≈ 73°.
3. Спирали, имеющие общие один тетраэдр и две прилегающие к нему грани (рис. 2е–2л); угол между осями, вычисленный для строгих геометрических моделей спиралей из идеальных тетраэдров с одним общим тетраэдром (рис. 2е) или с одной общей гранью (рис. 2л), равен arccos(3/5) ≈ ≈ 53° или arccos(2/3) ≈ 48° соответственно.
4. Спирали, имеющие одну общую треугольную грань и касающиеся разных граней не принадлежащего им тетраэдра (рис. 2р, 2с, 3д, 3е). Угол между осями, вычисленный для строгих геометрических моделей с одной общей гранью или с касанием одного идеального тетраэдра с появлением двойной или тройной оси, равен arccos(1/15) ≈ 86.17°, arccos(1/9) ≈ 83.62° или arccos(2/45) ≈ 87.45° соответственно.
5. Спирали с общей треугольной гранью и углом между осями arccos(14/15) ≈ 21° (строгая модель, рис. 2м); после слияния близких вершин имеют общую боковую поверхность и закручены друг за друга (рис. 2н).
6. Спирали с углом между осями arccos(38/45) ≈ ≈ 32.38°, касающиеся разных граней одного не принадлежащего им идеального тетраэдра и не имеющие общих тетраэдров или треугольных граней (строгая модель, рис. 3ж). После слияния близких вершин закручены друг за друга и имеют общую непрерывную зигзагообразную последовательность ребер (рис. 3з).
7. Спирали с углом между осями arccos(–37/45) ≈ ≈ 145.30°, также касающиеся разных граней одного не принадлежащего им тетраэдра и не имеющие общих тетраэдров или треугольных граней (строгая модель, рис. 3к). После слияния близких вершин они имеют общую последовательность ребер, выстроенных в прямую линию, и закручены друг за друга (рис. 3л).
Для различных дискретных расслоений Хопфа множества вершин политопа {3, 3, 5} расположение вершин политопа в окрестности окружности Хопфа описано как соответствующее пересечение спиралей 30/11, образуемых вершинами политопа.
В дальнейшем полученные результаты можно перенести на спирали 30/11 из тетраэдрических атомов, регулярные пересечения между которыми возможны только для спиралей одного знака хиральности.
Автор выражает благодарность Н.А. Бульенкову за ряд ценных замечаний.
Список литературы
Лорд Э.Э., Маккей А.Л., Ранганатан С. Новая геометрия для новых материалов. М.: Физматлит, 2010. 264 с.
Li H., Eddaoudi M., O’Keeffe M., Yaghi O.M. // Nature. 1999. V. 402. P. 276. https://doi.org/10.1038/46248
Бульенков Н.А. // Кристаллография. 1988. Т. 33. Вып. 2. С. 424.
Белякова О.А., Словохотов Ю.Л. // Изв. РАН. Сер. хим. 2003. № 11. С. 2175.
Nyman H., Carroll C.E., Hyde B.G. // Z. Kristallogr. 1991. B. 196. S. 39. https://doi.org/10.1524/zkri.1991.196.1-4.39
Талис А.Л., Рабинович А.Л. // Кристаллография. 2019. Т. 64. № 3. С. 341. https://doi.org/10.1134/S0023476119030287
Mosseri R., DiVincenzo D.P., Sadoc J.F., Brodsky M.H. // Phys. Rev. B. 1985. V. 32. № 6. P. 3974. https://doi.org/10.1103/PhysRevB.32.3974
Кокстер Г.С.М. Введение в геометрию. М.: Наука, 1966. 648 с.
Sadoc J.F. // Eur. Phys. J. E. 2001. V. 5. P. 575. https://doi.org/10.1007/s101890170040
Coxeter H.S.M. // Can. Math. Bull. 1985. V. 28. № 4. P. 385. https://doi.org/10.4153/CMB-1985-045-5
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография



