Кристаллография, 2022, T. 67, № 4, стр. 561-570
Информационная сложность порождающего подмножества кристаллографических групп
А. М. Банару 1, 2, *, Д. А. Банару 3, С. М. Аксенов 2, **
1 Московский государственный университет им. М.В. Ломоносова
Москва, Россия
2 Кольский научный центр РАН
Апатиты, Россия
3 Институт геохимии и аналитической химии им. В.И. Вернадского РАН
Москва, Россия
* E-mail: banaru@phys.chem.msu.ru
** E-mail: aks.crys@gmail.com
Поступила в редакцию 16.09.2021
После доработки 10.11.2021
Принята к публикации 15.11.2021
- EDN: XEDMUM
- DOI: 10.31857/S0023476122030043
Аннотация
По аналоги с шэнноновской сложностью графов вводится сложность минимальных порождающих подмножеств конечно-порожденных дискретных групп, включая кристаллографические. Введенная величина может быть полезна при анализе молекулярных и иных структур с нечеткими структурообразующими контактами. Разработан алгоритм и приведены результаты расчета для некоторых конечных групп, в том числе кристаллических классов.
ВВЕДЕНИЕ
Теория информации представляет собой развитую область математики, заложенную в конце 40-х годов Клодом Шэнноном [1]. Наиболее широко используемым в современности способом оценки количества информации, содержащейся в каком-либо символьном сообщении, является расчет так называемой информационной энтропии по Шэннону [2]. Этот функционал имеет вид
где(2)
$L({{p}_{i}}) = \left\{ \begin{gathered} 0~\quad ({{p}_{i}} = 0), \hfill \\ - {{p}_{i}}{{\log }_{2}}{{p}_{i}}\quad ({{p}_{i}} > 0). \hfill \\ \end{gathered} \right.$Расчет количества информации еще с начала 1950-х годов стал применяться к молекулярным графам, чему посвящен большой обзор Бончева [3]. Символами молекулярного графа выступают атомы (вершины графа), а сообщением – сам молекулярный граф. Эквивалентными (i-го сорта), как правило, считаются вершины, на которых группа автоморфизмов графа действует транзитивно.
Более чем десять лет такая оценка количества информации применяется к кристаллам. Согласно [4] количество структурной информации, приходящейся в кристалле на один атом, равно
(3)
$I_{G}^{{{\text{str}}}} = - \mathop \sum \limits_{i = 1}^k \,{{p}_{i}}{{\log }_{2}}{{p}_{i}}\;({\text{бит/атом}}),$(5)
$I_{{G,~{\text{tot}}}}^{{{\text{str}}}} = - {v}\mathop \sum \limits_{i = 1}^k \,{{p}_{i}}{{\log }_{2}}{{p}_{i}}\;({\text{бит/эл}}{\text{.}}\;{\text{яч}}{\text{.}}).$По значению $I_{{G,~{\text{tot}}}}^{{{\text{str}}}}$ кристаллические структуры неорганических веществ условно разделяют на очень простые (<20), простые (20–100), средней сложности (100–500), сложные (500–1000) и очень сложные (>1000) [6]. К очень сложным относятся, в первую очередь, структуры цеолитов и микропористых каркасных материалов. Самым сложным на сегодня среди минералов считается юингит Mg8Ca8[(UO2)24(CO3)30O4(OH)12(H2O)8](H2O)130 ($I_{{G,~{\text{tot}}}}^{{{\text{str}}}}$ = 23477.5 бит/эл. яч.) [7]. По мере усложнения кристаллической структуры количество информации о ней увеличивается, а конфигурационная энтропия кристалла уменьшается на пропорциональную величину [8]. Недавно было предложено дополнить информационную сложность кристаллической структуры так называемой координационной сложностью, учитывающей число степеней свободы атома в зависимости от симметрии позиции [9].
С помощью функционала по Шэннону также было предложено [10] оценивать количество химической информации, проистекающей из состава минерала: $E_{{c1}}^{{(1)}}E_{{c2}}^{{(2)}}...E_{{ck}}^{{(k)}}$, где E(i) – i-й химический элемент, ci – индекс в простейшей формуле вещества. Функционал (1) при этом рассчитывается для pi = сi/e, где e – общее число атомов в простейшей формуле вещества. В 2020 г. с помощью статистического анализа 5349 минералов, утвержденных Международной минералогической ассоциацией (IMA), был подтвержден эмпирический закон Федорова–Грота, согласно которому более сложному химическому составу обычно отвечает более низкая симметрия кристалла. Химическая сложность продемонстрировала убывающую зависимость от порядка кристаллического класса [11].
Как показано в [12], часть элементарной ячейки, в которой содержится информация о кристалле, рассчитывается как V* = V0/M, где V0 – объем элементарной ячейки, M – порядок группы симметрии, а V* представляет собой фундаментальный объем. Заметим, что в данном случае речь идет о приведенной элементарной ячейке, а под группой симметрии понимается кристаллический класс. В пределах фундаментального объема некоторые атомы могут свободно менять свое местоположение (три степени свободы), в то время как другие могут сдвигаться только вдоль поворотной оси или плоскости зеркального отражения (одна и две степени свободы соответственно), а у третьих позиции фиксированы (нонвариантны). Согласно [12] отношение ns/np (где ns – число “оставшихся” поступательных степеней свободы, np – общее число атомов в приведенной элементарной ячейке), а также V* характеризуют стабильность кристаллической структуры. При этом, как правило, далеко не весь фундаментальный объем доступен атомам из-за того, что закрытые элементы симметрии создают вокруг себя запрещенные области (таковых нет только в существенно асимморфных пространственных группах без стационарных орбит) [13, 14]. На взаимосвязь симметрии атомных позиций и стабильности структуры также обращали внимание при анализе редких федоровских групп в структурной минералогии [15, 16].
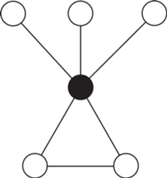
Помимо сложности, создаваемой расположением атомов в кристалле, каждая пространственная группа характеризуется своей собственной информационной сложностью [17]. Некоторые позиции Уайкова могут трансформироваться друг в друга под действием нормализатора пространственной группы, их относят к одному набору Уайкова. Если под pi понимать вероятность наугад выбранной позиции Уайкова принадлежать i-му набору Уайкова, то результатом расчета по формулам (1) и (2) становится позиционная сложность пространственной группы. Определенной сложностью обладают и кристаллографические точечные группы (кристаллические классы) [18]. Элементы точечной группы могут быть эквивалентны по действию группы автоморфизмов точечной группы, что хорошо видно на графе циклов группы и позволяет рассчитать pi. Например, у групп ${{C}_{{3{v}}}}$ и D3 (рис. 1) есть два элемента третьего порядка ($C_{3}^{1}$ и $С_{3}^{2}$), входящие в один класс эквивалентности, и три элемента второго порядка, тоже друг другу эквивалентные. Тождественное преобразование (черный кружок на рис. 1) всегда составляет отдельный класс эквивалентности. Таким образом, шесть элементов группы разбиваются на классы: {1, 2, 3}. Следовательно, согласно (1) и (2), H = –1/6log21/6 – 2/6log22/6 – ‒ 3/6log23/6 = 1.459 бит/элемент, или 8.755 бит/группа. Результаты аналогичного расчета для других кристаллических классов приведены в табл. 1.
Таблица 1.
Кристаллические классы, разбиение элементов на классы эквивалентности по группе автоморфизмов точечной группы и сложность класса в порядке увеличения Htot
| Класс (по Шенфлису) | Класс (по Геману–Могену) | Абстрактный класс | Порядок | Разбиение элементов группы | H, бит/элемент | Htot, бит/группа |
|---|---|---|---|---|---|---|
| C1 | 1 | Z1 | 1 | {1} | 0 | 0 |
| C2, Ci, Cs | 2, $\bar {1}$, m | Z2 | 2 | {1, 1} | 1.000 | 2.000 |
| C3 | 3 | Z3 | 3 | {1, 2} | 0.918 | 2.755 |
| С2h, ${{C}_{{2{v}}}}$, D2 | 2/m, mm2, 222 | Dih2 | 4 | {1, 3} | 0.811 | 3.245 |
| D2h | mmm | Dih2 × Z2 | 8 | {1, 7} | 0.544 | 4.349 |
| C4, S4 | 4, $\bar {4}$ | Z4 | 4 | {1, 1, 2} | 1.500 | 6.000 |
| ${{C}_{{{\text{3}}{v}}}}$, D3 | 3m, 32 | Dih3 | 6 | {1, 2, 3} | 1.459 | 8.755 |
| C6, S6, C3h | 6, $\bar {3}$, $\bar {6}$ | Z6 | 6 | {1, 1, 2, 2} | 1.918 | 11.510 |
| C4h | 4/m | Z4 × Z2 | 8 | {1, 1, 2, 4} | 1.750 | 14.000 |
| ${{C}_{{{\text{3}}{v}}}}$, D4, D2d | 4mm, 422, $\bar {4}2m$ | Dih4 | 8 | {1, 1, 2, 4} | 1.750 | 14.000 |
| T | 23 | A4 | 12 | {1, 3, 8} | 1.189 | 14.265 |
| C6h | 6/m | Z4 × Z2 | 12 | {1, 2, 3, 6} | 1.730 | 20.755 |
| ${{C}_{{{\text{6}}{v}}}}$, D6, D3d, D3h | 6mm, 622, $\bar {3}m$, $\bar {6}m2$ | Dih6 | 12 | {1, 1, 2, 2, 6} | 1.959 | 23.510 |
| D4h | 4/mmm | Dih4 × Z2 | 16 | {1, 1, 2, 4, 8} | 1.875 | 30.000 |
| D6h | 6/mmm | Dih6 × Z2 | 24 | {1, 2, 3, 6, 12} | 1.865 | 44.755 |
| Th | $m\bar {3}$ | A4 × Z2 | 24 | {1, 1, 6, 8, 8} | 1.939 | 46.529 |
| Td, O | $\bar {4}3m$, 432 | S4 | 24 | {1, 3, 6, 6, 8} | 2.094 | 50.265 |
| Oh | $m\bar {3}m$ | S4 × Z2 | 48 | {1, 1, 3, 8, 8, 12, 15} | 2.369 | 113.700 |
В [19] применялись формулы (1), (2) к распределениям минералов по сингониям и кристаллическим классам. Например, литосфера Земли в целом характеризуется следующей ранговой формулой: М30.3–Р21.7–К14.4–ТРИГ10.2–ТЕТР9.4–Г7.2–ТРИК6.8 (в процентах от общего числа минералов), где М – минералы моноклинной, Р – ромбической, К – кубической, ТРИГ – тригональной, Г – гексагональной, ТЕТР – тетрагональной, ТРИК – триклинной сингоний. Этой формуле отвечает H = 2.56 бит/минерал. Подобные информационные параметры можно использовать для выяснения глобальных тенденций изменения кристалло-симметрийной структуры сложных минеральных систем [19].
Итак, (1), (2) можно использовать для оценки сложности любого источника информации, если известно отношение эквивалентности на множестве символов, позволяющее рассчитать величины pi. В данной работе этот подход применяется к оценке сложности порождающих наборов кристаллографических групп. Несмотря на разнообразие таких групп [20], включая группы в пространствах высокой размерности, они все являются конечно-порожденными, а число минимальных комбинаторно-различных подмножеств порождающих элементов у них тоже является конечным.
Некоторый набор элементов (подмножество) U группы G называется порождающим (или образующим), если наименьшей подгруппой G, содержащей U и обозначаемой 〈U〉, является сама G, т.е. 〈U〉 = G. Порождающее множество U называется минимальным, если оно не содержит никакого порождающего множества G, кроме себя самого [21]. Сравнительно недавно программные алгоритмы были применены к кристаллографическим точечным группам [22], для которых выведены все возможные минимальные наборы порождающих. К сожалению, из определения минимального порождающего подмножества U не следует, что мощность |U| одинакова у всех минимальных подмножеств группы G. Некоторые порождающие подмножества кристаллографических групп не обладают наименьшей возможной мощностью min|U|, поскольку в них изначально отсутствует некоторый элемент, включение которого позволило бы еще больше минимизировать U. Например, 〈$C_{6}^{1}$〉 = C6 ⊃ $C_{6}^{2}$, но 〈$C_{6}^{2}$〉 = С3 ≠ С6 и 〈$C_{6}^{3}$〉 = С2 ≠ С6. Однако если U = {$C_{6}^{2}$, $C_{6}^{3}$}, то 〈U〉 = = C6. Такое U называется несущественно минимальным [23]. Далее в тексте под минимальным порождающим подмножеством по умолчанию понимается существенно минимальное.
У трехмерных точечных групп $G_{0}^{3}$ в существенно минимальном порождающем подмножестве два или три элемента [24], у двумерных пространственных (плоских) групп $G_{2}^{2}$ – от двух до четырех [25], у трехмерных пространственных (федоровских) групп $G_{3}^{3}$ – от двух до шести [26]. Часто эту величину называют рангом группы. Существенно минимальный набор порождающих элементов может быть выбран большим числом способов, у конечных групп оно конечно, у плоских и федоровских – бесконечно. Однако даже у последних число комбинаторно-различных вариантов выбора ограничено.
Над вероятностью порождения группы случайно выбранными элементами задумывались еще полвека назад. В [27] исследована вероятность того, что наугад выбранная пара перестановок длины n порождает группу перестановок An, и показано, что при n → ∞ эта вероятность стремится к единице. В связи с вероятностным характером порождения любой минимальный набор образующих элементов группы можно трактовать как нечеткий [22, 28–30]. Это имеет прямое отношение к молекулярным кристаллическим структурам, где, как правило, невозможно четко выявить опорные (структурообразующие) межмолекулярные контакты, порождающие конкретную пространственную группу [31–33]. В последнее время наметилась тенденция к анализу порождающих симметрических операций и у ковалентных каркасов [34], поскольку от них зависят возможные искажения каркаса и направления фазовых превращений. Кратко напомним [35]: что если U – множество элементов ui и ${{{{\mu }}}_{V}}:U \to \left[ {0,1} \right]$, то нечетким подмножеством V в U называется множество вида $\left\{ {(u,{{{{\mu }}}_{{~V}}}(u)):u \in U} \right\}$, а ${{{{\mu }}}_{{~V}}}(u)$ называют степенью принадлежности u к V. Сумму $\sum\nolimits_{i = 1}^n {{{{{\mu }}}_{V}}({{u}_{i}})} $, где n = |U|, называют массой нечеткого подмножества V. Масса нечеткого минимального порождающего подмножества группы совпадает с ее рангом [22]. Для оценки степени нечеткости множества используют функционалы, аналогичные (2), в частности энтропию S (не имеет ничего общего с термодинамической энтропией) [36]:
(6)
$S(V) = \mathop \sum \limits_{i = 1}^n \left( { - {{{{\mu }}}_{i}}\ln {{{{\mu }}}_{i}} - (1 - {{{{\mu }}}_{i}})\ln (1 - {{{{\mu }}}_{i}})} \right),$Цели настоящей работы – разработка методики, позволяющей рассчитать информационную энтропию порождающих подмножеств всякой конечно-порожденной дискретной группы; разработка программного алгоритма, реализующего данную методику для конечных групп, включая кристаллографические.
МЕТОДИКА РАСЧЕТА
Пусть конечно-порожденная дискретная группа ранга r имеет m минимальных порождающих подмножеств, а число элементов группы, встречающихся хотя бы в одном из этих подмножеств, равно s. Взаимно обратные элементы для порождающего подмножества считаются одинаковыми [22]. Обозначим за Ni число одинаковых элементов i-го сорта среди всех N = rm элементов в m подмножествах, $\sum\nolimits_{i = 1}^k {{{N}_{i}}} = N$. Тогда pi = Ni/N – вероятность того, что наугад выбранный порождающий элемент из любого минимального порождающего подмножества окажется i-го сорта. При подстановке pi в (1) и (2) получается величина H, отвечающая информационной сложности минимального порождающего подмножества в расчете на один элемент. А величина Htot = sH отвечает общей информационной сложности минимального порождающего подмножества в расчете на группу.
Можно сказать, что множеством, на котором вводится отношение эквивалентности для расчета pi, является множество комбинаторно-различимых графов Кэли для данной группы, а эквивалентность устанавливается по наличию у графов Кэли одинаковых ребер. У периодических групп можно рассматривать фактор-граф периодического графа Кэли [23].
Нетрудно показать взаимосвязь (1), (2) и (6). Так как степень принадлежности μi совпадает с вероятностью того, что в наугад выбранном минимальном порождающем наборе содержится элемент i-го сорта, то pi = μi/r. При переходе от двоичного к натуральному логарифму единица измерения количества информации также меняется с бит на нат.
В качестве примера снова рассмотрим кристаллические классы ${{C}_{{3{v}}}}$ и D3 (абстрактный класс Dih3 – диэдральная группа шестого порядка и второго ранга) с определяющими соотношениями a3 = b2 = (ab)2 = e. Порождающими являются элементы a, b, ab и aba–1 в любом парном сочетании (всего шесть подмножеств). Тогда N = 2 × 6 = = 12, pi = 3/12 = 1/4 (для всех i). Следовательно, H = 4(–1/4log2(–1/4)) = 2 бит/элемент, Htot = 4 × × 2 = 8 бит/элемент.
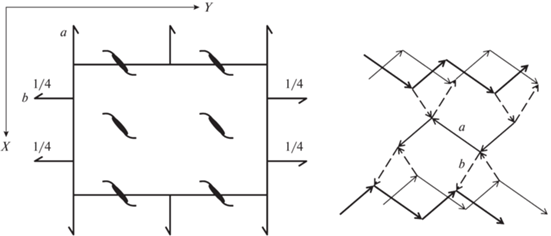
В качестве еще одного примера рассмотрим федоровскую группу P212121 второго ранга [39]. Минимальное порождающее подмножество содержит любую пару винтовых поворотов a и b вокруг осей 21 (например, вдоль X и Y) на ближайшем друг от друга расстоянии (рис. 2), ba2b–1a2 = = ab2a–1b2 = e. Третий винтовой поворот ab тоже может входить в порождающий набор. В итоге получаем три комбинаторно-различимых набора: {a, b}, {a, ab}, {b, ba}. Следовательно, N = 6, pi = = 2/6 = 1/3 (для всех i), H = 3(–1/3log2(–1/3)) = = 1.585 бит/элемент, Htot = 3 × 1.585 = 4.755 бит/ группа.
АЛГОРИТМ ДЛЯ КОНЕЧНЫХ ГРУПП
Алгоритм реализован в среде Mathematica 11.0 [40]. В нем используется изоморфизм всякой конечной группы некоторой группе перестановок (теорема Кэли [41]). На первом этапе задаются исходные порождающие перестановки, число которых равно r. При помощи перемножения выводятся все остальные перестановки в группе, за исключением e (тождественное преобразование не может входить в минимальный порождающий набор). Затем составляются все парные произведения перестановок. Если среди этих произведений оказался элемент e, одна из перестановок из соответствующей пары выбрасывается. Из списка оставшихся перестановок формируются всевозможные наборы по r в каждом. Из каждого такого набора порождается группа перестановок, и ее порядок сравнивается с порядком исходной группы. Если эти порядки равны, то данный набор является порождающим и при этом минимальным. Затем все порождающие перестановки записываются в виде слов через исходные перестановки и рассчитывается их частотность в уже найденных порождающих наборах. На последнем этапе по формулам (1), (2) рассчитывается информационная сложность. Порождающие перестановки некоторых групп были взяты из баз данных ATLAS [42] и GroupNames [43]. Всем желающим по запросу авторы предоставят программный код.
РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
В табл. 2 представлены результаты расчета информационной сложности минимального порождающего подмножества у кристаллических классов. С ростом числа элементов, способных быть порождающими, H и Htot тоже растут.
Таблица 2.
Сложность порождающих подмножеств кристаллических классов в порядке увеличения Htot
| Классы | Ранг | Порождающих элементов* | Порождающих подмножеств | H, бит/элемент | Htot, бит/группа |
|---|---|---|---|---|---|
| C1 | 0 | 0 | 0 | 0 | 0 |
| C2, Ci, Cs, C3, C4, S4, C6, S6, C3h | 1 | 1 | 1 | 0 | 0 |
| С2h, ${{C}_{{2{v}}}}$, D2 | 2 | 3 | 3 | 1.585 | 4.755 |
| C4h | 2 | 4 | 5 | 1.971 | 7.884 |
| ${{C}_{{{\text{3}}{v}}}}$, D3 | 2 | 4 | 6 | 2.000 | 8.000 |
| ${{C}_{{{\text{4}}{v}}}}$, D4, D2d | 2 | 5 | 8 | 2.311 | 11.556 |
| C6h | 2 | 6 | 9 | 2.503 | 15.020 |
| ${{C}_{{{\text{6}}{v}}}}$, D6, D3d, D3h | 2 | 7 | 12 | 2.750 | 19.250 |
| T | 2 | 7 | 18 | 2.780 | 19.460 |
| D2h | 3 | 7 | 28 | 2.807 | 19.651 |
| D4h | 3 | 12 | 136 | 3.581 | 42.967 |
| Td, O | 2 | 13 | 39 | 3.597 | 46.761 |
| Th | 2 | 14 | 54 | 3.698 | 51.775 |
| D6h | 3 | 18 | 384 | 4.151 | 74.716 |
| Oh | 2 | 22 | 78 | 4.289 | 94.364 |
У циклических групп Zn один элемент в порождающем подмножестве, но число таких элементов в общем случае не равно одному. В [44] все порождающие элементы группы Zn названы “атомом”. Если 〈a〉 = Zn, то порождающими будут все ak, где 1 ≤ k ≤ n – 1, где k и n – взаимно простые числа. Число таких k в теории групп называют функцией Эйлера φ(k). Например, у некристаллографической группы С5 из-за того, что числа 2 и 5 взаимно простые, два порождающих подмножества с точностью до обратного элемента – это {$C_{5}^{1}$} и {$C_{5}^{2}$}, следовательно, H = 1 бит/элемент и Htot = 2 бит/группа. У кристаллографических групп n = 1, 2, 3, 4 и 6, и порождающий элемент единственный, поэтому у восьми классов, изоморфных Zn, Htot = H = 0.
Наибольшая сложность у классов D6h и Oh, не являющихся подгруппами других классов. У первой порождающие подмножества кодируются 74 битами, у второй – 95 битами информации. Увеличение количества информации в порождающих наборах не вполне соответствует увеличению сложности самих классов (табл. 1). В первую очередь обращает на себя внимание группа D2h, занимающая всего лишь 9 место по первому из значений, но 5 – по второму, а среди других групп подъем еще более значительный – с 26 на 9 место. Ключом к пониманию этого может являться сравнительно большой ранг группы D2h при небольшом порядке. Также примечательно, что всего у семи классов сложность порождающего подмножества по значению Htot превышает сложность самой группы: С2h, ${{C}_{{2{v}}}}$, D2 (группа диэдра Dih2), D4h, D6h, T и Th.
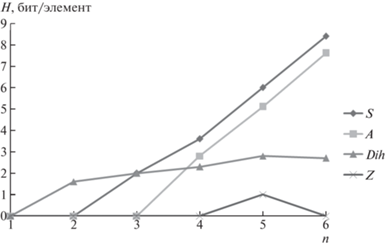
Дополнительно проанализированы серии самых известных групп, среди которых есть некристаллографические (рис. 3). По времени расчет на обычном персональном компьютере занял от нескольких секунд до нескольких минут. Группа S6 порядка 6! = 720 обсчитывалась около 10 мин, она имеет 397 порождающих элементов и 30 420 порождающих подмножеств. Ее сложность наибольшая среди всех рассмотренных групп: H = = 8.426 бит/элемент и Htot = 3345.2 бит/группа, что по сложности практически сопоставимо с таким сложным минералом, как Ba12(SiO3)6(CO3)5Cl2 ($I_{{G,~{\text{tot}}}}^{{{\text{str}}}}$ = 3913.7 бит/эл. яч.) [6]. Сложность порождающих подмножеств симметрических групп Sn и групп перестановок An быстро возрастает, начиная с n = 2 и 3 соответственно (S1 ∼ A1 ∼ A2 ∼ Z1). У диэдральных групп Dihn рост начинается раньше (Dih1 ∼ Z2, Dih3 ∼ S3), но он более медленный и, начиная с n = 5, перестает быть монотонным. Такой же немонотонный рост, зависящий от функции Эйлера, характерен для Zn. При построении зависимости m (числа минимальных порождающих подмножеств) от n в полулогарифмических координатах получается картина, практически идентичная рис. 3.
Рис. 3.
Информационная сложность симметрических групп Sn, групп перестановок An, диэдральных групп Dihn, циклических групп Zn до n = 6.
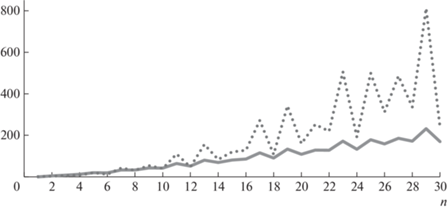
На рис. 4 представлены результаты расчета сложности диэдральных групп Dihn с немонотонным ростом. Из-за отсутствия делителей у простых n сложность соответствующих групп довольно большая, что хорошо видно на графике m (n). Точно так же при четных n сложность, как правило, меньше, чем при близких нечетных, и есть всего одно исключение из этого правила при n ≤ 30: Htot = 80.6 и 86.2 соответственно у Dih15 и Dih16.
Рис. 4.
Информационная сложность Htot, бит/группа (сплошная линия) и число минимальных порождающих наборов m (пунктирная линия) у диэдральных групп до n = 30.
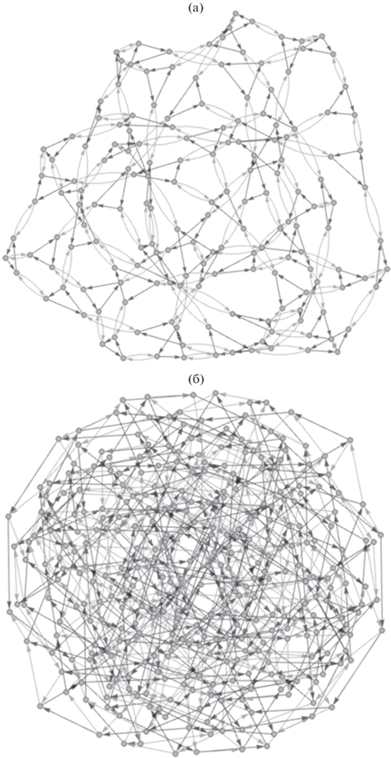
Существуют некристаллографические группы, отображающие симметрии прототипных структур в пространствах, отличающихся от трехмерного евклидова. Эти группы определяют симметрийно-возможные кристаллографические и некристаллографические структуры в E3. К таковым, например, можно отнести политоп {240} с группой автоморфизмов порядка 2880, подробно рассматриваемой в [45, 46]. Еще одним примером является строительный тетраблок для широкого круга структур, которые можно аппроксимировать цепями тетраэдров со смежными гранями [47]. Тетраблок представляет собой семивершинное объединение по граням четырех правильных тетраэдров. Линейному и плоскому вариантам тетраблока соответствуют проективная специальная линейная группа PSL(2, 7) и проективная общая линейная группа PGL(2, 7) [48], причем первая для второй является подгруппой индекса 2. У группы PSL(2, 7) порядка 168 (рис. 5a) с порождающими перестановками a = (2, 3)(3, 5), b = = (1, 2, 3)(5, 6, 7) [42] всего 94 порождающих элемента, 2814 порождающих подмножеств, H = = 6.496 бит/элемент, Htot = 610.6 бит/группа. У группы PGL(2, 7) порядка 336 (рис. 5б) с порождающими перестановками a = (1, 2, 3, 4, 5, 6, 7, 8), b = (1, 8, 2, 7, 4, 6, 5) [43] всего 192 порождающих элемента, 10 626 порождающих подмножеств, H = 7.475 бит/элемент, Htot = 1435.2 бит/группа. Весьма близкие значения у группы A6 (H = = 7.559 бит/элемент, Htot = 1526.9 бит/группа).
Оценка сложности порождающих наборов групп может иметь практический интерес не только в кристаллографии. Известно, что n независимых биполярных психологических признаков (интроверсия–экстраверсия и т.п.) порождают прямое произведение (Z2)n [49], например в трехфакторной модели Г. Айзенка n = 3 и соответствующая группа (Z2)n ∼ D2h. При n = 4 порождающих подмножеств 840, т.е. в четырехфакторной модели личности можно сконструировать 840 равноправных базисов из четырех независимых биполярных признаков. Добавление четвертого фактора увеличивает H с 2.807 до 3.907 бит/элемент и Htot – с 19.7 до 58.6 бит/группа, т.е. почти в 3 раза.
ЗАКЛЮЧЕНИЕ
Предложена методика расчета информационной энтропии порождающих подмножеств всякой конечно-порожденной дискретной группы.
Методика успешно апробирована для конечных групп, включая кристаллографические.
Для рассматриваемых групп установлены значения информационной сложности H и общей информационной сложности минимального порождающего подмножества в расчете на группу Htot, что позволило выявить соответствующую статистику.
Работа выполнена при поддержке Российского научного фонда (грант № 20-77-10065). Расчеты информационных индексов проведены Д.А. Банару в рамках госбюджетной темы № 0137-2019-0014.
Список литературы
Braverman M. // Jpn. J. Math. 2019. V. 14. № 1. P. 27. https://doi.org/10.1007/s11537-018-1727-9
Shannon C.E. // Bell Syst. Tech. J. 1948. V. 27. № 3. P. 379. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x
Bonchev D. // Complexity: Introduction and Fundamentals. London: CRC Press, 2003. P. 157.
Krivovichev S. // Acta Cryst. A. 2012. V. 68. P. 393. https://doi.org/10.1107/S0108767312012044
Klee W.E. // Cryst. Res. Technol. 2004. V. 39. № 11. P. 959. https://doi.org/10.1002/crat.200410281
Krivovichev S. V. // Angew. Chem. Int. Ed. 2014. V. 53. № 3. P. 654. https://doi.org/10.1002/anie.201304374
Krivovichev S.V. // Acta Cryst. B. 2020. V. 76. № 4. P. 618. https://doi.org/10.1107/S2052520620007131
Krivovichev S.V. // Acta Cryst. B. 2016. V. 72. № 2. P. 274. https://doi.org/10.1107/s205252061501906x
Hornfeck W. // Acta Cryst. A. 2020. V. 76. P. 534. https://doi.org/10.1107/S2053273320006634
Siidra O.I., Zenko D.S., Krivovichev S. V // Am. Mineral. 2014. V. 99. P. 817. https://doi.org/10.2138/am.2014.4723
Krivovichev S.V., Krivovichev V.G. // Acta Cryst. A. 2020. V. 76. P. 429. https://doi.org/10.1107/S2053273320004209
Borisov S.V., Magarill S.A., Pervukhina N.V. // J. Struct. Chem. 2019. V. 60. № 8. P. 1191. https://doi.org/10.1134/S0022476619080018
Somov N.V., Chuprunov E.V. // Crystallography Reports. 2018. V. 63. № 3. P. 314. https://doi.org/10.1134/S1063774518030264
Somov N.V., Chuprunov E.V. // Crystallography Reports. 2021. V. 66. № 3. P. 361. https://doi.org/10.1134/S106377452103024X
Urusov V.S., Nadezhina T.N. // J. Struct. Chem. 2009. V. 50. P. 22. https://doi.org/10.1007/s10947-009-0186-9
Shablovsky Ya.O. // Mineralogy. 2019. V. 5. № 2. P. 3. https://doi.org/10.35597/2313-545X-2019-5-2-3-9
Banaru A.M. // Ural. Geol. J. 2018. № 3. P. 84.
Banaru A.M., Aksenov S.M., Krivovichev S. V. // Symmetry (Basel). 2021. V. 13. № 8. P. 1399. https://doi.org/10.3390/sym13081399
Юшкин Н.П., Шафрановский И.И., Янулов К.П. Законы симметрии в минералогии. Л.: Наука, 1987. 335 с.
Farkas D.R. // Rocky Mt. J. Math. 1981. V. 11. № 4. P. 511. https://doi.org/10.1216/RMJ-1981-11-4-511
Halbeisen L., Hamilton M., Růžička P. // Quaest. Math. 2007. V. 30. № 3. P. 355. https://doi.org/10.2989/16073600709486205
Banaru A.M. // Crystallography Reports. 2018. V. 63. № 7. P. 1077. https://doi.org/10.1134/S1063774518070052
Banaru A.M. // Crystallography Reports. 2019. V. 64. № 6. P. 847. https://doi.org/10.1134/S1063774519050043
Галиулин Р.В. Кристаллографическая геометрия. М.: КомКнига, 2005. 136 с.
Коксетер Г.С.М., Мозер У.О.Д. Порождающие элементы и определяющие соотношения дискретных групп. М.: Наука, 1980. 240 с.
Банару А.М. // Вестн. МГУ. Сер. 2. Химия. 2009. Т. 50. № 2. С. 100. https://doi.org/10.3103/S0027131409020023
Dixon J.D. // Math. Z. 1969. B. 110. S. 199. https://doi.org/10.1007/BF01110210
Banaru A.M. // Crystallography Reports. 2018. V. 63. № 7. P. 1071. https://doi.org/10.1134/S1063774518070040
Banaru A.M., Shiroky V.R. // Crystallography Reports. 2019. V. 64. № 2. P. 201. https://doi.org/10.1134/S1063774519020044
Banaru A.M., Shiroky V.R. // Crystallography Reports. 2020. V. 65. № 3. P. 417. https://doi.org/10.1134/S1063774520030050
Банару А.М., Гридин Д.М. // Вестн. МГУ. Сер. 2. Химия. 2019. Т. 60. № 6. С. 351. https://doi.org/10.3103/S0027131419060051
Банару А.М., Гридин Д.М. // Журн. структур. химии. 2019. Т. 60. № 12. С. 1968. https://doi.org/10.1134/S0022476619120047
Гридин Д.М., Банару А.М. // Журн. структур. химии. 2020. Т. 61. № 5. С. 784. https://doi.org/10.1134/S0022476620050108
Eon J.-G. // Acta Cryst. A. 2016. V. 72. № 3. P. 268. https://doi.org/10.1107/s2053273315022950
Zadeh L.A. // Inf. Control. 1965. V. 8. № 3. P. 338. https://doi.org/10.1016/S0019-9958(65)90241-X
De Luca A., Termini S. // Inf. Control. 1972. V. 20. № 4. P. 301. https://doi.org/10.1016/S0019-9958(72)90199-4
Dumitrescu D. // J. Math. Anal. Appl. 1993. V. 176. P. 359. https://doi.org/10.1006/jmaa.1993.1220
Bhandari D., Pal N.R. // Inf. Sci. (Ny). 1993. V. 67. № 3. P. 209. https://doi.org/10.1016/0020-0255(93)90073-U
Lord E.A., Banaru A.M. // Moscow Univ. Chem. Bull. 2012. V. 67. № 2. P. 50. https://doi.org/10.3103/S0027131412020034
Wolfram Research, Inc. Mathematica 11.0, 2016.
Курош А.Г. Теория групп. М.: Наука, 1967. 648 с.
Wilson R., Walsh P., Tripp J. et al. ATLAS of Finite Group Representations – Version 3. http://brauer.maths.qmul.ac.uk/Atlas/v3/
Dokchitser T. GroupNames.org. https://people.maths. bris.ac.uk/~matyd/GroupNames/index.html
Sander J.W., Sander T. // J. Number Theory. 2013. V. 133. № 2. P. 705. https://doi.org/https://doi.org/10.1016/j.jnt.2012.08.021
Talis A.L., Rabinovich A.L. // Crystallography Reports. 2020. V. 65. № 5. P. 687. https://doi.org/10.1134/S1063774520050235
Talis A.L., Rabinovich A.L. // Crystallography Reports. 2021. V. 66. № 3. P. 367. https://doi.org/10.1134/S1063774521030275
Talis A.L., Everstov A.A., Kraposhin V.S., Simich-Lafitskii N.D. // Met. Sci. Heat Treat. 2021. V. 62. P. 725. https://doi.org/10.1007/s11041-021-00629-1
Talis A.L., Rabinovich A.L. // Crystallography Reports. 2019. V. 64. № 3. P. 367. https://doi.org/10.1134/S106377451903026X
Рейнин Г. Тайны типа. Модели. Группы. Признаки. М.: Черная белка, 2010. 295 с.
Дополнительные материалы отсутствуют.
Инструменты
Кристаллография