Кристаллография, 2023, T. 68, № 2, стр. 196-203

ВВЕДЕНИЕ

Эффект дифракции рентгеновских лучей (РЛ) в кристаллах был открыт экспериментально вскоре после открытия РЛ, т.е. в начале XX века. Как известно [1, 2], результаты экспериментов в то время не совпадали с первой теорией дифракции, развитой Дарвиным, а затем и с более общей теорией Эвальда, доведенной Лауэ до современного вида. Теория была развита для кристаллов большого размера с совершенной кристаллической решеткой, а кристаллы в то время были несовершенными. Это были поликристаллы, в которых кусочки с совершенной структурой имели малый размер, а сам материал состоял из большого числа таких кусочков с разной ориентацией. Кроме того, само излучение было некогерентным, поэтому разные части образца формировали дифрагированное излучение независимо друг от друга.

Дифракция РЛ в таких условиях была названа кинематической и расчеты проводились при условии, что дифрагированная волна имеет малую интенсивность и не влияет на падающую волну. В теории Эвальда–Лауэ это влияние учитывается и приводит к целому ряду интересных особенностей самого эффекта. Дифракцию РЛ в условиях взаимного влияния проходящей и дифрагированной волн назвали динамической. Тем не менее даже кинематическая дифракция РЛ сыграла и сейчас играет огромную роль в развитии кристаллографии [3].

Решить проблему с когерентностью удалось в 1959 г. [4] в схеме эксперимента на просвет (геометрия Лауэ) при использовании узкой щели, пропускающей пучок РЛ с поперечным размером не более 10 мкм. При этом излучение проникает в толстый кристалл внутри треугольника Бормана. В центре этого треугольника наблюдались экстинкционные полосы, т.е. был виден когерентный эффект интерференции волн с различным показателем преломления. Однако для описания этого эксперимента теорию, первоначально развитую для падающей плоской волны, пришлось модифицировать.

Впервые это сделал Като [5] в 1961 г. методом преобразования Фурье волновой функции РЛ. В следующем году Такаги [6] предложил более универсальную форму теории в виде системы дифференциальных уравнений, которые проще, чем исходные уравнения Максвелла, но учитывают динамические эффекты при дифракции РЛ в монокристаллах в полной мере. Решения уравнений он, однако, не представил. Топен в 1964 г. предложил такие же уравнения, а затем впервые применил их для численного расчета дифракции РЛ в кристалле с дислокацией [7]. В результате для этих уравнений закрепилась аббревиатура TTE (Takagi–Taupen Equations).

В последующие годы появилось много публикаций, в которых были представлены результаты численных расчетов изображений монокристаллов в форме пластины, содержащих единичные дефекты структуры, такие как дислокации, дефекты упаковки и так далее, а также при внешних воздействиях, например изгиба или точечного давления на поверхность пластины. Использовались методы численного решения TTE. Обсуждение этих работ, а также ссылки на статьи можно найти в обзорах [8–10].

Также было показано, что решение TTE для совершенного кристалла с произвольными граничными условиями можно представить в виде интегралов по границе кристалла от произведения волновой функции РЛ на границе и так называемой функции влияния, которая является решением TTE для точечного источника на границе [1, 2]. Функции влияния были получены для геометрии Лауэ с произвольной границей кристалла и для геометрии Брэгга для кристалла в форме пластины конечной толщины. Типичный пример использования таких решений опубликован в [11, 12]. Там же есть ссылки на публикации предыдущих лет.

Что касается методов численного решения TTE, то наибольшее развитие получил метод, обозначенный в [13] как HSD (half-step derivative). Он использует прямоугольную систему координат с границей на поверхности кристалла и с разными шагами по осям вдоль и перпендикулярно поверхности. В случае Лауэ волновая функция РЛ вычисляется от входной поверхности пластины кристалла (ось X) до выходной поверхности на линиях, параллельных поверхности пластины, т.е. на каждом шаге получаем решение для пластины, толщина которой равна целому числу шагов по нормали к поверхности (ось Z). Обычно исследовались только деформации кристаллической решетки.

В случае Брэгга граничные условия рассматривались как на входной поверхности, так и на боковой границе кристалла на линии вдоль направления падающего пучка. В расчетах использовались две противоположные схемы, а именно, сходящаяся (для падающей плоской волны) и расходящаяся (для источника на поверхности). В первой схеме входным был когерентный падающий пучок на большом, но конечном интервале оси X, а результат получался на меньшем интервале, так как на каждом шаге по оси Z интервал по оси X уменьшался на один шаг.

Однако получить в лаборатории когерентную волну с широким фронтом в течение многих лет было невозможно. По этой причине рассматривались узкие пучки на входе, которые засвечивали кристалл внутри треугольника Бормана. В этой схеме на каждом шаге по оси Z интервал по оси X увеличивался на один шаг, а первоначально волновая функция РЛ была отлична от нуля в малом числе точек на оси X. В остальных точках функция равнялась нулю, т.е. тоже была известна. Появление источников синхротронного излучения расширило возможности исследования эффекта дифракции в кристаллах. Стало возможно изучать кристаллы относительно небольших размеров и произвольной формы [14]. С другой стороны, появились публикации, в которых развиваются другие методы решения TTE (например, [15, 16] и ссылки в них).

Вместе с тем в 1971 г. [17] было отмечено, что разумно выделить в кристалле три области, которые можно рассматривать отдельно. Это области совершенного кристалла, области деформированного кристалла и области, в которых дифракция полностью отсутствует. Естественно развить эту идею и добавить в кристалл области, в которых может быть материал с другой плотностью и даже пустота, как это бывает в кристаллах карбида кремния [18] или в кристаллах сложной формы [19, 20].

В настоящей работе предложен и детально описан новый метод численного решения TTE, пригодный для кристаллов произвольной формы и структуры. Прямоугольная система координат и алгоритм HSD [13] доказали свою эффективность и используются, но рекуррентные формулы этого метода модифицированы. Новое состоит в том, что граничные условия устанавливаются на оси X, которая никак не привязана к форме кристалла. Решение последовательно получается при движении по оси Z, направление которой идет параллельно отражающим атомным плоскостям кристалла.

Пространство, внутри которого решаются TTE, может содержать как области с кристаллической решеткой, так и недифракционные области с разной плотностью и структурой, включая пустоту. Дифракция происходит только при очень малом отклонении межплоскостного расстояния или ориентации плоскостей от такого состояния, когда выполняется условие Брэгга. Разработана компьютерная программа, реализующая предложенный метод. В качестве примеров ее использования рассмотрены два случая дифракции в кристалле прямоугольной формы, у которого одна грань меньшего размера (торец) параллельна оси X, а боковые грани параллельны оси Z. В первом случае узкий падающий пучок входит в кристалл с торца. Первоначально получается геометрия Лауэ, а потом боковые грани кристалла вносят изменения в условия дифракции. Во втором случае широкий пучок падает на боковую грань пластины, что соответствует геометрии Брэгга. Более сложные задачи будут рассмотрены в будущих публикациях.

МЕТОД ЧИСЛЕННОГО РЕШЕНИЯ TTE

Определим полупространство как все значения координаты x и только положительные значения координаты z прямоугольной системы координат, как показано на рис. 1. В двухволновом случае дифракции от координаты y результат не зависит, если среда однородна в этом направлении. Если нет, то зависимость имеет параметрический характер и учитывается тривиально. В этом полупространстве находятся области произвольной формы, имеющие кристаллическую решетку, в которой есть атомные плоскости, параллельные оси Z, с определенным межплоскостным расстоянием. Эти плоскости могут быть представлены вектором обратной решетки h, лежащим в плоскости (XZ).

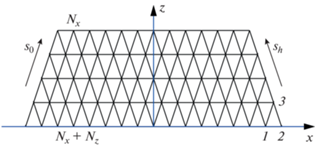
На оси X при z = 0 известны медленно меняющиеся комплексные амплитуды для плоских волн с волновыми векторами k₀ и k_h = k₀ + h. При этом параметр α = ($k_{h}^{2}{\text{/}}k_{0}^{2}$ – 1) имеет очень малое значение, сравнимое с действительной частью комплексных параметров дифракции χ₀, χ_h и χ_–h , которые равны коэффициентам ряда Фурье для периодической поляризуемости среды на векторах обратной решетки 0, h, –h. Кроме областей с указанной кристаллической решеткой в полупространстве могут существовать области с другими параметрами, т.е. в общем случае параметры χ₀, χ_h и χ_–h зависят от координат.

Зависимость от координат определяется не только деформацией кристаллической решетки, но и другими изменениями как структуры, так и электронной плотности. В частности, могут быть равны нулю параметры χ_h и χ_–h (в аморфных областях) или все параметры (в областях, где нет вещества). Деформации описываются вектором смещения u атомов из идеально периодического состояния. Смещение атомов приводит к тому, что параметр χ_h умножается на множитель exp(‒ihu), а χ_–h на комплексно сопряженный множитель. Эти множители также зависят от координат. В общем случае может меняться не только фаза, но и модуль комплексных параметров.

По этой причине исходные TTE разумно записать в более простом, чем в [20], виде, не указывая конкретный тип зависимости от координат, а именно,

где X₀, X_h, X_–h и A – новые комплексные параметры, получающиеся после умножения параметров χ₀, χ_h, χ_–h и α на множитель iKp/4. Здесь и далее K = 2π/λ, λ – длина волны РЛ. В (1) производные записаны по координатам, которые отсчитываются по направлениям векторов k₀ и k_h, как показано на рис. 1. Параметр p в этих уравнениях сокращается и не влияет на результат. Он приобретает смысл только при использовании алгоритма приближенного вычисления производных.

Вычисления проводятся на косоугольной системе координат узлов расчетной сетки, показанной на рис. 1. Ключевым параметром является шаг по оси Z. Он выбирается пользователем и равен d_z = d. Шаг по оси X не может быть произвольным и равен d_x = 2d $\operatorname{tg} {{\theta }_{{\text{B}}}}$, где θ_B – угол Брэгга, равный половине угла между векторами k₀ и k_h . Точки сетки по оси X при каждом шаге по оси Z смещаются на половину шага. Значения функций задаются и определяются в точках пересечения сетки линий вдоль направлений волновых векторов. На каждом шаге по оси Z известны все значения на оси X предыдущего ряда. В самом начале они известны из граничных условий.

Рассмотрим три точки сетки на рис. 1 в правом нижнем углу. Они имеют номера 1, 2 и 3. На каждом шаге уравнения (1) устанавливают связь между известными полями E^(old) = ($E_{0}^{{(1)}}$ , $E_{h}^{{(1)}}$, $E_{0}^{{(2)}}$, $E_{h}^{{(2)}}$) в точках 1 и 2 и неизвестными полями E^(new) = = ($E_{0}^{{(3)}}$, $E_{h}^{{(3)}}$) в точке 3. При этом оба уравнения (1) записываются для точек в середине отрезков между парой точек 1 и 3 и парой точек 2 и 3. Производная заменяется на отношение разности полей в каждой паре точек к расстоянию между точками, равному p = d/$\cos {{\theta }_{{\text{B}}}}$, а значения функций в правой части уравнений – на полусумму значений в этих же точках.

После таких замен уравнения (1) приближенно записываются в виде

Здесь и далее X₁ = X₀ – A. Верхние индексы указывают, в какой точке надо брать значения функций. Уравнения (2) определяют неизвестные значения через известные неявным образом. Решение этой системы уравнений удобно записать в матричном виде E^(new) = M_2,4 × E^(old). Матрица имеет вид где

Внутри однородной или медленно изменяющейся среды изменением параметров дифракции во всех трех точках можно пренебречь, что и делалось в предыдущих работах. Однако на границе раздела между средами, особенно на границе кристалла, различия могут быть весьма существенные. Отметим, что матрица имеет определенную симметрию. Некоторые множители повторяются как по вертикали, так и по горизонтали.

Численное решение задачи сводится к последовательному рассмотрению всех треугольников вдоль оси X. Начиная с первой линии, где заданы граничные условия в N_x + N_z +1 точках, получаем следующую линию с числом точек на единицу меньше. Через N_z шагов число точек, где известно решение, равно N_x + 1. Ответ разумно записывать в прямоугольнике с числом точек (N_x + 1) по оси X и (N_z + 1) по оси Z с пропуском нечетного числа точек, в то время как числа N_x и N_z надо брать четными. Такая сходящаяся схема предполагает, что значения волновой функции за пределами рассматриваемого отрезка при z = 0 неизвестны. Поэтому нельзя получить достоверный ответ при z = = dN_z за пределами интервала шириной d_xN_x.

В расходящейся схеме предполагается известным, что при z = 0 за пределами рассматриваемого отрезка волновая функция равна нулю. По этой причине расчет делается точно так же, но на каждом шаге по оси Z на оси X слева и справа прибавляется по одной точке с нулевыми значениями. При этом исходных точек становится на две больше, а в результате остается на одну больше. Соответственно, интервал шириной d_xN_x при z = = 0 превращается в интервал d_x(N_x + N_z) при z = = dN_z. Если считать такой вариант по сходящейся схеме, то надо прибавить к входным данным 2N_z нулей, и расчет делается дольше с тем же результатом.

Расчет внутри аморфной среды можно проводить по такой же схеме, как и в кристалле, только с нулевыми значениями параметров X_h, X_–h и A. При этом матрица принимает совсем простой вид, у нее отличны от нуля только первый элемент первой строки и последний элемент второй строки. Но решение в этом случае проще получить сразу из уравнений (2) в виде

В пустоте имеем такие же соотношения, только параметры X_0± равны единице. Расчет этих областей можно делать намного быстрее, чем в кристалле. Отметим, что в [20] для этих областей выписана матрица, но умножение комплексной матрицы на комплексный вектор в большом числе точек увеличивает время расчета и неразумно.

Самый общий способ задания формы кристалла, а также формы аморфной области состоит в том, что при каждом значении z определяются пределы x₁(z) и x₂(z), между которыми на оси X находится кристалл или аморфная область. Если пределы совпадают для какой-то координаты z, то для таких координат область отсутствует. Таким способом можно определить любую совокупность кристаллов любой формы. Более того, он приводит к уменьшению времени работы программы за счет более простого способа определения среды для расчета матрицы перехода. Если среда не меняется, то матрицу пересчитывать не нужно.

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Компьютерная программа для численного моделирования дифракции в кристаллах произвольной формы разработана в рамках более общей программы XRWP1 [21], спроектированной для решения всех (по возможности) задач когерентной рентгеновской оптики, и является ее частью. Описание работы программы можно найти на указанном сайте. В данном разделе рассмотрены два примера ее применения для расчета дифракции в кристалле прямоугольной формы. Относительно простая форма кристалла позволяет сравнить вычисленные зависимости с известными ранее решениями, полученными другим способом. Но данный метод дает больше информации уже в процессе расчета, показывая детальное распределение интенсивности излучения во всем объеме.

В обоих случаях рассматриваются кристалл кремния и отражение 220, энергия фотонов E = = 10 кэВ, угол Брэгга θ_B = 18.84°. Падающее на кристалл излучение – это плоская волна, ограниченная щелью определенного размера S по направлению, перпендикулярному вектору k₀. Шаг d сетки точек по оси Z для численных расчетов равен 0.04 мкм. Параметры дифракции получены с помощью онлайн-программы [22]. Грани кристалла параллельны осям X (ширина) и Z (длина).

Первый случай. Кристалл имеет размеры W_c = = 50 мкм в ширину и L_c = 120 мкм в длину. Падающий пучок весьма узкий, S = 0.4 мкм, и его центр находится в точке x = 0. При этом ширина основания треугольника Бормана W_B = 2Ltg(θ_B) = = 82 мкм, т.е. больше, чем ширина кристалла. Кристалл находится в точном брэгговском положении, т.е. угловое отклонение Δθ = 0. Отметим, что параметр α = –2sin(2θ_B)Δθ. В расчете использовалась расходящаяся схема. Результаты расчета показаны на рис. 2. Для узкого пучка на входе дифрагированное излучение имеет очень малую интенсивность. По этой причине контраст удобно показывать в логарифмическом масштабе.

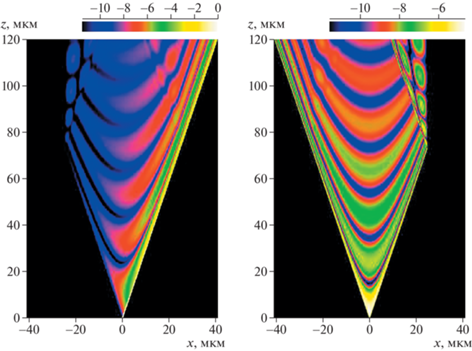
На рис. 2 слева показано распределение натурального логарифма относительной интенсивности для проходящего пучка, т.е. ln(I_T/I₀), а справа – для отраженного пучка, т.е. ln(I_R/I₀). На входной поверхности I_T = I₀ внутри щели. Чтобы получить наилучший контраст, шкала цветов показывает интервал от минимального значения I_mi/I₀ до максимального I_ma /I₀, причем I_mi = MI_ma. Все значения, меньшие, чем I_mi, заменялись на I_mi. Коэффициент M подбирался эмпирически для получения наилучшего контраста. Это необходимо по той причине, что ln(0) = –∞. Если выбрать слишком малое значение M, контраст максимальных значений будет очень слабым, а если слишком большое, пропадет контраст малых значений. Шкала цветов над картинкой показывает значения ln(I_n/I₀), где n = T, R.

Отметим, что при малых значениях z рисунок в отраженном пучке показывает известные симметричные интерференционные полосы Като [5] секционной топографии, и граница кристалла никак себя не проявляет. Начиная с z = 73 мкм, на правой стороне рис. 2 интенсивность ограничивается шириной кристалла, а на левой становится постоянной вдоль линий, параллельных вектору k_h. Для проходящего пучка картинка асимметричная, и ограничение шириной кристалла происходит слева.

Падающий узкий пучок на всей длине кристалла остается весьма сильным, намного превышая по интенсивности дифрагированное излучение. Можно сделать вывод: дифракция узкого пучка не вполне динамическая, так как дифрагированная волна слабо влияет на падающую волну, хотя интерференция и имеет место. Это совсем не так при дифракции широкого пучка. Этот факт до сих пор слабо обсуждается, хотя аналитическая теория его хорошо показывает. Максимальное относительное отражение I_R/I₀ происходит очень быстро, т.е. при малых значениях z, и равно примерно 0.01.

Второй случай. Кристалл имеет размеры W_c = = 30 мкм в ширину и L_c = 250 мкм в длину. Падающий пучок имеет относительно большую ширину, S = 100 мкм, и его центр сдвинут влево на –64.2 мкм. В результате падающий пучок освещает только левую боковую поверхность кристалла и этот случай соответствует дифракции в геометрии Брэгга. Из аналитической теории для плоских волн известно, что в этом случае имеет место полное внешнее отражение при условии |α – 2Re(χ₀)| < < |Re(χ_h)|. Поэтому было выбрано значение углового отклонения из условия α = 2Re(χ₀), а именно, Δθ = 16.088 × 10^–6 мкрад.

Использовалась сходящаяся схема таким образом, чтобы на выходе получить результат не только на торце кристалла, но и в той области, которая получается при отражении волны от боковой грани кристалла. Кристалл длиной L способен отразить пучок на ширину W = Ltg(θ_B). При L = 250 мкм имеем W = 85.3 мкм. По этой причине показан размер 2W + W_c = 200.6 мкм. Чтобы показать слабое волновое поле внутри кристалла, снова использовался логарифмический масштаб, т.е. значения ln(I_n/I₀), где n = T, R.

Результаты расчета показаны на рис. 3. На карте проходящего пучка можно заметить, что ширина падающего пучка больше, чем необходимо для того, чтобы осветить всю боковую грань кристалла. Левая часть пучка просто проходит расчетную область без изменений. А та часть пучка, которая попадает в кристалл, изменяется в нем по-разному при малых и больших значениях z. Падающий пучок достигает правой границы кристалла при z = 88 мкм. До этой точки кристалл отражает как толстый, а затем наличие его правой границы вносит коррективы в характер изменения относительной интенсивности.

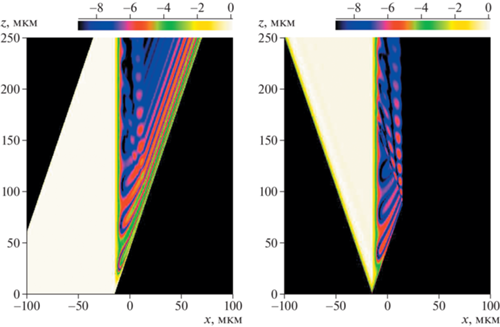
Наиболее отчетливо эти изменения проявляют себя в отраженном пучке. Соответственно, в вакууме отраженный пучок меняется на двойном расстоянии 176 мкм. Отметим две особенности, которые недостаточно наглядно представлены в логарифмическом масштабе. Первая состоит в том, что полное отражение возникает не сразу. При очень малых значениях z отражение слабое и оно возрастает постепенно. То есть полное отражение получается с задержкой. Это можно сравнить с эффектом Гуса–Хенхен, который обсуждался для нейтронов [23], но имеет место для любого излучения при отражении. Кроме того, переход в полное отражение сопровождается осцилляциями, причем в максимумах относительная интенсивность отраженного пучка может даже превышать единицу.

Вторая особенность состоит в том, что в этом же месте проходящий пучок проникает в кристалл на очень большие глубины. В рассмотренном варианте он выходит из кристалла с потерей всего половины интенсивности (частично из-за поглощения). Главным результатом расчета в данном случае является распределение относительной интенсивности на выходной плоскости, т.е. на оси X при максимальном значении координаты z. Это распределение для отраженного пучка более детально показано на рис. 4. Изменение характера кривой происходит при x = x₀ = –40 мкм. Эта точка соответствует выходу из кристалла луча, впервые отраженного от его правого края одновременно с лучом, отраженным от левого края.

Отметим, что аналитическая формула для такой кривой была впервые опубликована еще в 1971 г. [17]. В обозначениях данной статьи на начальном этапе, когда правая граница кристалла не влияет на результат, она имеет следующий вид:

где Здесь и далее J_n(z) – функция Бесселя n-го порядка.

Расчет по этой формуле полностью совпадает с кривой на рис. 4, если отсчитывать координату от левого края, соответствующего началу засветки кристалла. Совпадение происходит при x < x₀ = = 60.3 мкм. После этой точки, как показано в [17], надо добавить к функции G₀(x) дополнительную функцию

По определению эта функция равна нулю при мнимых значениях параметра η, т.е. при x < x₀. Координата x₀, как отмечалось выше, соответствует положению луча, который впервые отразился от правой грани кристалла.

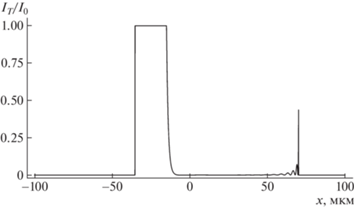
Распределение для проходящего пучка более детально показано на рис. 5. Здесь интерес представляет только узкий пик в правой части кривой. Это та часть правого края пучка, которая отразилась кристаллом очень слабо. Она показывает, как отражается очень узкий пучок. Для него эффект полного отражения отсутствует. Дифрагированное излучение такое же слабое, как и в случае Лауэ. В рассматриваемой схеме расчета вполне могут быть части пучка, которые никак не меняются, если они проходят мимо областей с кристаллической решеткой. Это тоже специально демонстрируется на графике. Тут интересно то, что левый край ограничен щелью, а правый край – кристаллом. Можно видеть, как быстро, но не мгновенно, излучение пропадает в кристалле в условиях полного отражения.

ЗАКЛЮЧЕНИЕ

Новая схема для численного моделирования эффекта когерентной динамической дифракции синхротронного излучения в кристаллах произвольной формы и структуры доказала свою эффективность. В этой схеме граничные условия для решения уравнений Такаги–Топена не привязаны к границам кристалла. Последние определяются через функции от координаты z. Такая схема позволяет решать очень большой круг задач моделирования дифракции в кристаллах сложной формы.

Представлены результаты численного решения уравнений в рамках одной и той же схемы для двух примеров: дифракции узкого пучка в геометрии Лауэ и дифракции широкого пучка в геометрии Брэгга. Результаты расчета полностью совпадают с полученными ранее аналитическими решениями, но численные решения дают больше информации, в том числе детальное распределение интенсивности во всем объеме.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 19-29-12043мк) в части разработки компьютерной программы, а также при поддержке Министерства науки и высшего образования РФ (грант № 075-15-2021-1362) в части выполнения компьютерного эксперимента.