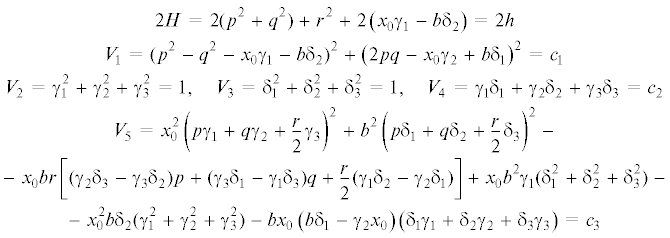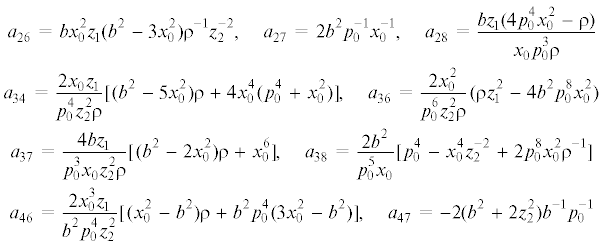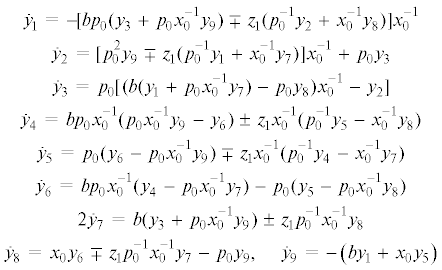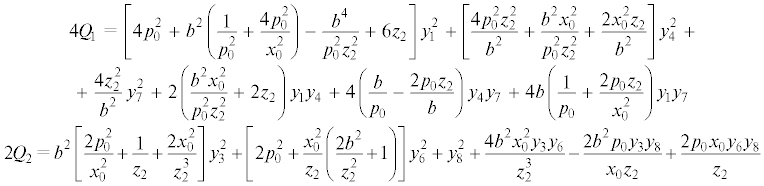Известия РАН. Механика твердого тела, 2019, № 1, стр. 101-114

О СТАЦИОНАРНЫХ ДВИЖЕНИЯХ ОБОБЩЕННОГО ВОЛЧКА КОВАЛЕВСКОЙ И ИХ УСТОЙЧИВОСТИ

В. Д. Иртегов^a, *, Т. Н. Титоренко^a

^a Институт динамики систем и теории управления им. В.М. Матросова СО РАН
Иркутск, Россия

Поступила в редакцию 20.06.2017
После доработки 26.03.2018
Принята к публикации 13.04.2018

DOI: 10.1134/S0572329919010045

Аннотация

Проводится качественный анализ уравнений движения волчка Ковалевской в двойном постоянном поле сил. В рамках данного исследования установлено, что в случае параллельных силовых полей уравнения движения тела имеют семейства перманентных вращений, в случае ортогональных – движения маятникового типа, при специальной ориентации силовых полей – семейства положений равновесия. Показано, что решения принадлежат либо одному из двух инвариантных многообразий коразмерности 2, либо их пересечению. Для найденных решений получены необходимые и достаточные условия устойчивости по Ляпунову.

Ключевые слова: твердое тело, двойное поле сил, стационарные движения, инвариантные многообразия, устойчивость

1. Введение. Изучается вращение твердого тела вокруг неподвижной точки под воздействием двух постоянных силовых полей. Геометрия масс тела соответствует интегрируемому случаю Ковалевской [1]. В такой постановке задача о движении твердого тела рассматривалась Богоявленским [2]. Им дана механическая интерпретация уравнений движения и указан частный случай их интегрируемости. К настоящему времени найден дополнительный первый интеграл задачи [3, 4]. Таким образом, исследуемая система является вполне интегрируемой по Лиувиллю. Ее изучению посвящен ряд работ, например, [5, 6]. В них выполнен топологический анализ фазового пространства системы. В данной работе проводится качественный анализ уравнений движения тела. Как известно, задача в этом случае сводится к выделению особых решений системы (положений равновесия, периодических движений) и исследованию их качественных свойств. В случае консервативных систем класс особых решений расширяется за счет стационарных множеств, состоящих из траекторий уравнений движения. Это множества любой конечной размерности, на которых первые интегралы задачи (или их комбинации) принимают стационарное значение. Обладающие указанным свойством нульмерные множества традиционно называют стационарными решениями [7], а множества ненулевой размерности будем называть стационарными инвариантными многообразиями (ИМ) [8]. В предлагаемой работе, используя метод Рауса–Ляпунова [9] и его обобщения [10], выделяются стационарные решения и ИМ уравнений движения и исследуется их устойчивость.

2. Постановка задачи. Для описания движения тела свяжем с его неподвижной точкой O инерциальную систему координат OXYZ, жестко с движущимся телом – систему координат Oxyz. Оси x, y, z направлены вдоль главных осей инерции тела для точки O. Моменты инерции тела удовлетворяют условию: $A = B = 2C$. Через $p$, $q$, $r$ обозначим проекции вектора угловой скорости на оси системы Oxyz, ${{\gamma }_{i}}$ ($i = 1,2,3$) – компоненты направляющего вектора 1-го силового поля, ${{\delta }_{i}}$ ($i = 1,2,3$) – компоненты направляющего вектора 2-го силового поля, (${{x}_{0}},0,0$) – компоненты радиус-вектора 1-го силового центра, ($0,b,0$) – компоненты радиус-вектора 2-го силового центра. Уравнения движения тела в системе координат $Oxyz$ имеют вид

(2.1)

$\begin{gathered} 2\dot {p} = qr + b{{\delta }_{3}},\quad {{{\dot {\gamma }}}_{1}} = {{\gamma }_{2}}r - {{\gamma }_{3}}q,\quad {{{\dot {\delta }}}_{1}} = {{\delta }_{2}}r - {{\delta }_{3}}q \\ 2\dot {q} = {{x}_{0}}{{\gamma }_{3}} - pr,\quad {{{\dot {\gamma }}}_{2}} = {{\gamma }_{3}}p - {{\gamma }_{1}}r,\quad {{{\dot {\delta }}}_{2}} = {{\delta }_{3}}p - {{\delta }_{1}}r \\ \dot {r} = - b{{\delta }_{1}} - {{x}_{0}}{{\gamma }_{2}},\quad {{{\dot {\gamma }}}_{3}} = {{\gamma }_{1}}q - {{\gamma }_{2}}p,\quad {{{\dot {\delta }}}_{3}} = {{\delta }_{1}}q - {{\delta }_{2}}p \\ \end{gathered} $

и допускают следующие первые интегралы:

(2.2)

где ${{V}_{1}}$ – интеграл, указанный Богоявленским [2], ${{V}_{5}}$ – дополнительный первый интеграл, найденный в [3, 4].

Отметим, что направления силовых полей в данной задаче определяются значением постоянной интеграла ${{V}_{4}} = {{c}_{2}}$. Таким образом, систему (2.1) на многообразии ${{V}_{4}} = {{c}_{2}}$ можно рассматривать как некоторое семейство систем, параметризованных ${{c}_{2}}$.

При $b = 0$ уравнения (2.1) соответствуют интегрируемому случаю Ковалевской в задаче о движении твердого тела с неподвижной точкой в поле тяжести.

Цель настоящей работы заключается в выделении стационарных решений и ИМ системы (2.1) и исследовании их устойчивости.

3. Стационарные решения и ИМ. Согласно методу Рауса–Ляпунова, стационарные решения и ИМ исследуемых дифференциальных уравнений можно получить как решение задачи на условный экстремум первых интегралов этих уравнений. Для этого из первых интегралов задачи строится их линейная или нелинейная комбинация (семейство первых интегралов) и записываются необходимые условия экстремума этого семейства относительно фазовых переменных. Тем самым, в случае систем с полиномиальными первыми интегралами, задача нахождения стационарных решений и ИМ сводится к отысканию решений некоторой системы алгебраических уравнений.

Следуя выбранной методике, образуем из первых интегралов задачи (2.2) их полную линейную комбинацию

(3.1)

$\begin{gathered} 2K = 2{{\lambda }_{0}}H - {{\lambda }_{1}}{{V}_{1}} - {{\lambda }_{2}}{{V}_{2}} - {{\lambda }_{3}}{{V}_{3}} - 2{{\lambda }_{4}}{{V}_{4}} - 4{{\lambda }_{5}}{{V}_{5}} \hfill \\ \end{gathered} $

где ${{\lambda }_{i}} = {\text{const}}$ ($i = 0,\; \ldots ,\;5$) – параметры семейства интегралов $K$, и запишем необходимые условия экстремума K по фазовым переменным

(3.2)

$\begin{gathered} \frac{{\partial K}}{{\partial p}} = 0,\quad \frac{{\partial K}}{{\partial q}} = 0,\quad \frac{{\partial K}}{{\partial r}} = 0,\quad \frac{{\partial K}}{{\partial {{\gamma }_{i}}}} = 0,\quad \frac{{\partial K}}{{\partial {{\delta }_{i}}}} = 0\quad (i = 1,2,3) \hfill \\ \end{gathered} $

Решения уравнений (3.1) позволяют определить семейства стационарных решений и ИМ дифференциальных уравнений (2.1), соответствующие семейству первых интегралов K.

Условия стационарности интеграла K (3.1) – это система 9 кубических уравнений с параметрами и ее решение относительно фазовых переменных представляет значительную вычислительную трудность даже с использованием системы аналитических вычислений. Поэтому в данной работе вначале были найдены постоянные решения дифференциальных уравнений (2.1) непосредственно из самих уравнений, а затем с помощью соотношений (3.1), (3.2) получены семейства интегралов, которые принимают стационарное значение на этих решениях. Для нахождения решений применялась система аналитических вычислений.

3.1. Перманентные вращения. Приравняем к нулю правые части дифференциаль-ных уравнений (2.1) и дополним их соотношениями ${{V}_{2}} = 1$, ${{V}_{3}} = 1$ (2.2):

(3.3)

$\begin{gathered} \begin{gathered} \begin{array}{*{20}{l}} {qr + b{{\delta }_{3}} = 0,\quad {{\gamma }_{2}}r - {{\gamma }_{3}}q = 0,\quad {{\delta }_{2}}r - {{\delta }_{3}}q = 0} \\ {{{x}_{0}}{{\gamma }_{3}} - pr = 0,\quad {{\gamma }_{3}}p - {{\gamma }_{1}}r = 0,\quad {{\delta }_{3}}p - {{\delta }_{1}}r = 0} \\ {b{{\delta }_{1}} + {{x}_{0}}{{\gamma }_{2}} = 0,\quad {{\gamma }_{1}}q - {{\gamma }_{2}}p = 0,\quad {{\delta }_{1}}q - {{\delta }_{2}}p = 0} \end{array} \hfill \\ \end{gathered} \\ {{V}_{2}} = \gamma _{1}^{2} + \gamma _{2}^{2} + \gamma _{3}^{2} = 1,\quad {{V}_{3}} = \delta _{1}^{2} + \delta _{2}^{2} + \delta _{3}^{2} = 1 \\ \end{gathered} $

Для системы полиномиальных уравнений (3.3) построим базис Гребнера [11] относительно некоторой части фазовых переменных, например, ${{\gamma }_{1}}$, ${{\gamma }_{2}}$, ${{\gamma }_{3}}$, ${{\delta }_{1}}$, ${{\delta }_{2}}$, ${{\delta }_{3}}$, $q$, $r$. Будем использовать лексикографическое упорядочение переменных (${{\delta }_{1}} > {{\gamma }_{2}} > {{\gamma }_{1}} > {{\delta }_{2}}$ > > ${{\gamma }_{3}} > {{\delta }_{3}} > r > q$). Такой способ в ряде случаев [10] позволяет получить ИМ различной размерности, в данном случае – одномерные ИМ.

В результате система уравнений (3.3) преобразуется к виду, позволяющему разделить ее на четыре подсистемы:

(3.4)

$\begin{gathered} {\text{I}})\,bp - {{x}_{0}}q = 0,\quad ({{b}^{2}} + x_{0}^{2}){{p}^{4}} + x_{0}^{2}({{p}^{2}}{{r}^{2}} - x_{0}^{2}) = 0 \\ - pr - {{x}_{0}}{{\delta }_{3}} = 0,\quad {{x}_{0}}{{\gamma }_{3}} - p{\kern 1pt} r = 0,\quad - b{{p}^{2}} - x_{0}^{2}{{\delta }_{2}} = 0 \\ {{p}^{2}} - {{x}_{0}}{{\gamma }_{1}} = 0,\quad b{{p}^{2}} - x_{0}^{2}{{\gamma }_{2}} = 0,\quad {{p}^{2}} + {{x}_{0}}{{\delta }_{1}} = 0 \\ \end{gathered} $

(3.5)

$\begin{gathered} {\text{II}})\,bp + {{x}_{0}}q = 0,\quad ({{b}^{2}} + x_{0}^{2}){{p}^{4}} + x_{0}^{2}({{p}^{2}}{{r}^{2}} - x_{0}^{2}) = 0 \\ {{x}_{0}}{{\delta }_{3}} - pr = 0,\quad {{x}_{0}}{{\gamma }_{3}} - pr = 0,\quad - b{{p}^{2}} - x_{0}^{2}{{\delta }_{2}} = 0 \\ {{p}^{2}} - {{x}_{0}}{{\gamma }_{1}} = 0,\quad b{{p}^{2}} + x_{0}^{2}{{\gamma }_{2}} = 0,\quad {{p}^{2}} - {{x}_{0}}{{\delta }_{1}} = 0 \\ \end{gathered} $

(3.6)

$\begin{gathered} {\text{III}})\,bp - {{x}_{0}}q = 0,\quad r = 0,\quad {{\gamma }_{3}} = 0,\;{{\delta }_{3}} = 0 \\ ({{b}^{2}} + x_{0}^{2})\delta _{2}^{2} - {{b}^{2}} = 0,\quad b{{\gamma }_{1}} + {{x}_{0}}{{\delta }_{2}} = 0 \\ {{\delta }_{2}} + {{\gamma }_{2}} = 0,\quad {{x}_{0}}{{\delta }_{2}} - b{{\delta }_{1}} = 0 \\ \end{gathered} $

(3.7)

$\begin{gathered} {\text{IV}})\,bp + {{x}_{0}}q = 0,\quad r = 0,\quad {{\gamma }_{3}} = 0,\;{{\delta }_{3}} = 0 \\ ({{b}^{2}} + x_{0}^{2})\delta _{2}^{2} - {{b}^{2}} = 0,\quad b{{\gamma }_{1}} + {{x}_{0}}{{\delta }_{2}} = 0 \\ {{\delta }_{2}} - {{\gamma }_{2}} = 0,\quad b{{\delta }_{1}} + {{x}_{0}}{{\delta }_{2}} = 0 \\ \end{gathered} $

Прямым вычислением по определению ИМ легко проверить, что уравнения (3.4)–(3.7) определяют четыре одномерных ИМ уравнений (2.1). Векторное поле на каждом ИМ описывается уравнением $\dot {p} = 0$, которое имеет следующее семейство решений:

(3.8)

$p = {{p}_{0}} = {\text{const}}$

С геометрической точки зрения, ИМ (3.4)–(3.7) в пространстве R⁹ соответствуют 4 кривые, каждая точка которых является неподвижной точкой в фазовом пространстве.

Уравнения (3.4), (3.5) совместно с (3.8) определяют 4 семейства решений уравнений движения (2.1):

(3.9)

$\begin{gathered} p = {{p}_{0}},\quad q = b{{p}_{0}}x_{0}^{{ - 1}},\quad r = \pm {{z}_{1}}p_{0}^{{ - 1}}x_{0}^{{ - 1}},\quad {{\gamma }_{1}} = p_{0}^{2}x_{0}^{{ - 1}},\quad {{\gamma }_{2}} = bp_{0}^{2}x_{0}^{{ - 2}} \\ {{\gamma }_{3}} = \pm {{z}_{1}}x_{0}^{{ - 2}},\quad {{\delta }_{1}} = - p_{0}^{2}x_{0}^{{ - 1}},\quad {{\delta }_{2}} = - bp_{0}^{2}x_{0}^{{ - 2}},\quad {{\delta }_{3}} = \mp {{z}_{1}}x_{0}^{{ - 2}} \\ \end{gathered} $

(3.10)

$\begin{gathered} p = {{p}_{0}},\quad q = - b{{p}_{0}}x_{0}^{{ - 1}},\quad r = \pm {{z}_{1}}p_{0}^{{ - 1}}x_{0}^{{ - 1}},\quad {{\gamma }_{1}} = p_{0}^{2}x_{0}^{{ - 1}},\quad {{\gamma }_{2}} = - bp_{0}^{2}x_{0}^{{ - 2}} \\ {{\gamma }_{3}} = \pm {{z}_{1}}x_{0}^{{ - 2}},\quad {{\delta }_{1}} = p_{0}^{2}x_{0}^{{ - 1}},\quad {{\delta }_{2}} = - bp_{0}^{2}x_{0}^{{ - 2}},\quad {{\delta }_{3}} = \pm {{z}_{1}}x_{0}^{{ - 2}} \\ \end{gathered} $

Здесь ${{p}_{0}}$ – параметр семейств, ${{z}_{1}} = {{(x_{0}^{4} - ({{b}^{2}} + x_{0}^{2})p_{0}^{4})}^{{1/2}}}$.

Условия вещественности решений: ${{p}_{0}} \ne 0$, ($p_{0}^{2} + {{x}_{0}} < 0$ или ${{x}_{0}} > p_{0}^{2}$) и ($ - \sigma \leqslant b < 0$ или $0 < b \leqslant \sigma $), где $\sigma = \left| {{{x}_{0}}} \right|{{(x_{0}^{2} - p_{0}^{4})}^{{1/2}}}p_{0}^{{ - 2}}$.

Уравнения (3.6), (3.7) и (3.8) позволяют получить следующие 4 семейства решений:

(3.11)

$\begin{gathered} p = {{p}_{0}},\quad q = b{{p}_{0}}x_{0}^{{ - 1}},\quad r = 0,\quad {{\gamma }_{1}} = \mp {{x}_{0}}z_{2}^{{ - 1}},\quad {{\gamma }_{2}} = \mp bz_{2}^{{ - 1}},\quad {{\gamma }_{3}} = 0 \\ {{\delta }_{1}} = \pm {{x}_{0}}z_{2}^{{ - 1}},\quad {{\delta }_{2}} = \pm bz_{2}^{{ - 1}},\quad {{\delta }_{3}} = 0 \\ \end{gathered} $

(3.12)

$\begin{gathered} p = {{p}_{0}},\quad q = - b{{p}_{0}}x_{0}^{{ - 1}},\quad r = 0,\quad {{\gamma }_{1}} = \mp {{x}_{0}}z_{2}^{{ - 1}},\quad {{\gamma }_{2}} = \pm bz_{2}^{{ - 1}},{{\gamma }_{3}} = 0 \\ {{\delta }_{1}} = \mp {{x}_{0}}z_{2}^{{ - 1}},\quad {{\delta }_{2}} = \pm bz_{2}^{{ - 1}},\quad {{\delta }_{3}} = 0 \\ \end{gathered} $

${{z}_{2}} = {{({{b}^{2}} + x_{0}^{2})}^{{1/2}}}$

Интеграл ${{V}_{4}}$ на решениях (3.9), (3.11) тождественно равен –1, а на решениях (3.10), (3.12) – 1. Таким образом, с механической точки зрения, элементам найденных семейств решений соответствуют перманентные вращения твердого тела в параллельных или противоположно направленных силовых полях. Эти вращения происходят вокруг совпадающих (или противоположных) направлений силовых полей с угловой скоростью ${{\omega }^{2}} = x_{0}^{2}p_{0}^{{ - 2}}$ (${{\omega }^{2}} = p_{0}^{2}({{b}^{2}}x_{0}^{{ - 2}} + 1)$), причем в случае (3.11), (3.12) ось вращения неподвижна в теле, а для движений (3.9), (3.10) ее положение зависит от значения параметра семейства p₀.

Получим семейства интегралов, которые принимают стационарное значение на найденных решениях. Рассмотрим вначале семейство решений (3.9).

Из уравнений (3.2) найдем ограничения на ${{\lambda }_{i}}$, при которых решения (3.9) удовлетворяют этим уравнениям: λ₂ = ${{\lambda }_{4}}\, - \,x_{0}^{2}\sigma p_{0}^{{ - 2}}$, λ₃ = ${{\lambda }_{4}}\, - \,{{b}^{2}}\sigma p_{0}^{{ - 2}}$, λ₅ = $x_{0}^{2}\sigma {{[({{b}^{2}}\, + \,x_{0}^{2})p_{0}^{4}\, + \,x_{0}^{4}]}^{{ - 1}}}$, где $\sigma = x_{0}^{2}{{\lambda }_{0}}{{({{b}^{2}} + x_{0}^{2})}^{{ - 1}}}$.

Подставив последние выражения в (3.1), будем иметь

(3.13)

${2{{K}_{1}} = \hat {K} - ({{V}_{2}} + {{V}_{3}} + 2{{V}_{4}}){{\lambda }_{4}}}$

$\hat {K} = \left[ {2H + \frac{{x_{0}^{2}}}{{({{b}^{2}} + x_{0}^{2})p_{0}^{2}}}\left( {x_{0}^{2}{{V}_{2}} + {{b}^{2}}{{V}_{3}} - \frac{{4x_{0}^{2}p_{0}^{2}{{V}_{5}}}}{{({{b}^{2}} + x_{0}^{2})p_{0}^{4} + x_{0}^{4}}}} \right)} \right]{{\lambda }_{0}} - {{V}_{1}}{{\lambda }_{1}}$

Семейство интегралов ${{K}_{1}}$ распадается на три подсемейства, которые соответствуют коэффициентам при ${{\lambda }_{0}}$, ${{\lambda }_{1}}$, ${{\lambda }_{4}}$. Как само семейство, так и каждое из его подсемейств принимает стационарное значение на элементах семейств решений (3.9), что проверяется прямым вычислением.

Аналогично находим семейство интегралов $2{{K}_{2}} = \hat {K} + \left( {{{V}_{2}} + {{V}_{3}} - 2{{V}_{4}}} \right){{\lambda }_{4}}$, которое, как и его подсемейства (коэффициенты при ${{\lambda }_{0}}$, ${{\lambda }_{1}}$, ${{\lambda }_{4}}$), принимает стационарное значение на элементах семейств (3.10).

В принятой в статье терминологии, многообразия, определяемые уравнениями (3.4), (3.5), являются стационарными, так как соответственно интегралы ${{V}_{1}}$, V₂ + ${{V}_{3}} + 2{{V}_{4}}$ и ${{V}_{1}}$, ${{V}_{2}} + {{V}_{3}} - 2{{V}_{4}}$ принимают стационарное значение на этих ИМ.

Изложенным выше способом получены семейства интегралов

(3.14)

${2{{K}_{3}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{K} - \left( {{{V}_{2}} + {{V}_{3}} + 2{{V}_{4}}} \right){{\lambda }_{4}},\quad 2{{K}_{4}} = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{K} + \left( {{{V}_{2}} + {{V}_{3}} - 2{{V}_{4}}} \right){{\lambda }_{4}}}$

$\begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{K} = 2\left[ {H + \left( {\frac{{p_{0}^{2}}}{{x_{0}^{2}}} \pm \frac{1}{{2{{z}_{2}}}}} \right)[x_{0}^{2}{{V}_{2}} + {{b}^{2}}{{V}_{3}}] - \frac{{{{V}_{5}}}}{{z_{2}^{2}}}} \right]{{\lambda }_{0}} - \\ - \;\left[ {{{V}_{1}} + \left( {\frac{{2p_{0}^{4}z_{2}^{2}}}{{x_{0}^{4}}} \pm \frac{{p_{0}^{2}{{z}_{2}}}}{{x_{0}^{2}}} - 1} \right)} \right.[x_{0}^{2}{{V}_{2}} + {{b}^{2}}{{V}_{3}}] - \left. {2\left( {\frac{{p_{0}^{2}}}{{x_{0}^{2}}} \pm \frac{1}{{{{z}_{2}}}}} \right){{V}_{5}}} \right]{{\lambda }_{1}} \\ \end{gathered} $

доставляющие стационарные значения элементам семейств (3.11) и (3.12) соответственно. Интегралы ${{V}_{2}} + {{V}_{3}} + 2{{V}_{4}}$ и ${{V}_{2}} + {{V}_{3}} - 2{{V}_{4}}$ принимают стационарное значение на многообразиях, которым принадлежат рассматриваемые решения, т.е. соответственно ИМ (3.6) и ИМ (3.7).

3.2. Положения равновесия. Из уравнений (3.3) при $p = q = r = 0$ найдем следующие семейства решений уравнений движения (2.1):

(3.15)

$\begin{gathered} p = 0,\quad q = 0,\quad r = 0,\quad {{\gamma }_{1}} = - {{(x_{0}^{2} - {{b}^{2}}\delta _{1}^{{{{0}^{2}}}})}^{{1/2}}}{{x}_{0}}^{{ - 1}},\quad {{\gamma }_{2}} = - b\delta _{1}^{0}x_{0}^{{ - 1}},\quad {{\gamma }_{3}} = 0 \\ {{\delta }_{1}} = \delta _{1}^{0},\quad {{\delta }_{2}} = \pm {{(1 - \delta _{1}^{{{{0}^{2}}}})}^{{1/2}}},\quad {{\delta }_{3}} = 0 \\ \end{gathered} $

(3.16)

$\begin{gathered} p = 0,\quad q = 0,\quad r = 0,\quad {{\gamma }_{1}} = {{(x_{0}^{2} - {{b}^{2}}\delta _{1}^{{{{0}^{2}}}})}^{{1/2}}}x_{0}^{{ - 1}},\quad {{\gamma }_{2}} = - b\delta _{1}^{0}x_{0}^{{ - 1}},\quad {{\gamma }_{3}} = 0 \\ {{\delta }_{1}} = \delta _{1}^{0},\quad {{\delta }_{2}} = \pm {{(1 - \delta _{1}^{{{{0}^{2}}}})}^{{1/2}}},\quad {{\delta }_{3}} = 0 \\ \end{gathered} $

Здесь $\delta _{1}^{0}$ – параметр семейства, ${\text{|}}\delta _{1}^{0}{\text{|}} \leqslant 1$ и $\left| b \right| \leqslant {\text{|}}{{x}_{0}}{\text{/}}\delta _{1}^{0}{\text{|}}$ – условия вещественности решений.

Эти решения принадлежат одномерному ИМ, уравнения которого имеют вид:

(3.17)

$\begin{gathered} p = 0,\quad q = 0,\quad r = 0,\quad {{\gamma }_{3}} = 0,\quad {{\delta }_{3}} = 0 \\ {{x}_{0}}{{\gamma }_{2}} + b{{\delta }_{1}} = 0,\quad {{b}^{2}}\delta _{1}^{2} + x_{0}^{2}(\gamma _{1}^{2} - 1) = 0,\quad \delta _{1}^{2} + \delta _{2}^{2} = 1 \\ \end{gathered} $

Интеграл ${{V}_{4}}$ на решениях (3.15), (3.16) принимает вид: $ \pm \delta _{1}^{0}x_{0}^{{ - 1}}[{{(x_{0}^{2} - {{b}^{2}}\delta _{1}^{{{{0}^{2}}}})}^{{1/2}}} \pm $ $ \pm \;b{{(1 - \delta _{1}^{{{{0}^{2}}}})}^{{1/2}}}]$ = c₂. Таким образом, с механической точки зрения, элементы семейств решений (3.15), (3.16) соответствуют положениям равновесия тела, причем каждое положение равновесия соотносится с определенным углом между направлениями силовых полей. В частности, последние соотношения обращаются в нуль при $\delta _{1}^{0} = 0$. Следовательно, при таком значении параметра $\delta _{1}^{0}$ решения (3.15), (3.16) соответствуют ортогональным силовым полям. При $\delta _{1}^{0} = \pm {{x}_{0}}{{({{b}^{2}} + x_{0}^{2})}^{{ - 1/2}}}$ второе семейство решений (3.15) и первое семейство (3.16) соответствуют параллельным силовым полям.

Описанным выше способом получим семейства интегралов, доставляющие стационарные значения элементам семейств (3.15), (3.16). Одно из таких семейств представлено ниже.

(3.18)

$\begin{gathered} 2{{K}_{5}} = \left[ {\frac{{2(({{b}^{2}} + x_{0}^{2} - 2{{z}^{2}})H + 2{{V}_{5}})}}{z} - {{V}_{1}}} \right]{{\lambda }_{1}} + \\ + \;\left[ {\frac{{({{b}^{2}} + x_{0}^{2} - 3{{z}^{2}})H + 2{{V}_{5}}}}{{x_{0}^{2}z}} - {{V}_{2}} - \frac{{{{b}^{2}}{{V}_{3}}}}{{x_{0}^{2}}}} \right]{{\lambda }_{2}} + \\ + \;\left[ {\frac{{({{b}^{2}} - 5x_{0}^{2} + 2\delta _{1}^{{{{0}^{2}}}}({{b}^{2}} + x_{0}^{2}) + {{z}^{2}})H}}{{{{x}_{0}}\delta _{1}^{0}({{b}^{2}} - x_{0}^{2})}} + \frac{{\bar {z}{{V}_{3}}}}{{{{x}_{0}}\delta _{1}^{0}}} - 2{{V}_{4}} - \frac{{2{{{(1 - \delta _{1}^{{{{0}^{2}}}})}}^{{1/2}}}{{V}_{5}}}}{{b{{x}_{0}}\delta _{1}^{0}z}}} \right]{{\lambda }_{4}} \\ \end{gathered} $

$z = b{{(1 - \delta _{1}^{{{{0}^{2}}}})}^{{1/2}}} + {{(x_{0}^{2} - {{b}^{2}}\delta _{1}^{{{{0}^{2}}}})}^{{1/2}}},\quad \bar {z} = b{{(1 - \delta _{1}^{{{{0}^{2}}}})}^{{1/2}}} - {{(x_{0}^{2} - {{b}^{2}}\delta _{1}^{{{{0}^{2}}}})}^{{1/2}}}$

Семейство интегралов ${{K}_{5}}$ и каждое из его подсемейств (коэффициенты при ${{\lambda }_{1}}$, ${{\lambda }_{2}}$, ${{\lambda }_{4}}$) принимают стационарные значения на элементах 1-го семейства решений (3.15). Соответствующие семейства интегралов для остальных решений (3.15), (3.16) аналогичны по структуре ${{K}_{5}}$.

3.3. Движения маятникового типа. Такие движения в рассматриваемой задаче можно получить из условий стационарности нелинейной комбинации первых интегралов, например, комбинации следующего вида $2\tilde {K} = 2{{H}^{2}} - {{\mu }_{1}}{{V}_{1}} - {{\mu }_{2}}{{V}_{2}} - {{\mu }_{3}}{{V}_{3}}$, где ${{\mu }_{i}}$ (i = 1, 2, 3) – некоторые величины, одновременно не равные нулю.

Запишем необходимые условия экстремума семейства интегралов $\tilde {K}$ по фазовым переменным

(3.19)

$\begin{gathered} \frac{{\partial{ \tilde {K}}}}{{\partial p}} = 0,\quad \frac{{\partial{ \tilde {K}}}}{{\partial q}} = 0,\quad \frac{{\partial{ \tilde {K}}}}{{\partial r}} = 0,\quad \frac{{\partial{ \tilde {K}}}}{{\partial {{\gamma }_{i}}}} = 0,\quad \frac{{\partial{ \tilde {K}}}}{{\partial {{\delta }_{i}}}} = 0\quad (i = 1,2,3) \hfill \\ \end{gathered} $

и построим для полиномов системы (3.19), дополненной соотношением ${{V}_{3}} = 1$, лексикографический базис Гребнера, считая неизвестными часть параметров и часть фазовых переменных $p$, $r$, ${{\gamma }_{2}}$, ${{\delta }_{1}}$, ${{\delta }_{2}}$, ${{\delta }_{3}}$, ${{\mu }_{1}}$, ${{\mu }_{2}}$. В результате система (3.19) преобразуется к виду, позволяющему разделить ее на несколько подсистем. Рассмотрим две из них:

(3.20)

$\begin{gathered} b\left( {{{\mu }_{1}} + 2} \right) \pm \left( {{{\mu }_{1}} - 2} \right)({{q}^{2}} + {{x}_{0}}{{\gamma }_{1}}) = 0,\quad {{\mu }_{2}} = 0 \\ 4b[b \mp ({{q}^{2}} + {{x}_{0}}{{\gamma }_{1}})] - {{\mu }_{3}} = 0 \\ \end{gathered} $

(3.21)

${p = 0,\quad r = 0,\quad {{\gamma }_{2}} = 0,\quad {{\delta }_{1}} = 0,\quad {{\delta }_{2}} = \pm 1,\quad {{\delta }_{3}} = 0}$

Уравнения (3.21) определяют два ИМ коразмерности 6 дифференциальных уравнений (2.1), что проверяется прямым вычислением по определению ИМ.

Уравнения векторного поля на этих ИМ

(3.22)

$\begin{gathered} 2\dot {q} = {{x}_{0}}{{\gamma }_{3}},\quad {{{\dot {\gamma }}}_{1}} = - q{{\gamma }_{3}},\quad {{{\dot {\gamma }}}_{3}} = q{{\gamma }_{1}} \hfill \\ \end{gathered} $

описывают маятникоподобные колебания тела относительно неподвижной оси динамической симметрии тела Oy. Эта ось ортогональна направляющему вектору 1-го силового поля и совпадает с направляющим вектором 2-го силового поля.

Выражения ${{\mu }_{1}} = {{ - 2[b \mp ({{q}^{2}} + {{x}_{0}}{{\gamma }_{1}})]} \mathord{\left/ {\vphantom {{ - 2[b \mp ({{q}^{2}} + {{x}_{0}}{{\gamma }_{1}})]} {[b \pm ({{q}^{2}} + {{x}_{0}}{{\gamma }_{1}})]}}} \right. \kern-0em} {[b \pm ({{q}^{2}} + {{x}_{0}}{{\gamma }_{1}})]}}$, ${{\mu }_{3}} = 4b[b \mp ({{q}^{2}} + {{x}_{0}}{{\gamma }_{1}})]$, най-денные из (3.20), являются первыми интегралами уравнений (3.22), что также нетрудно проверить прямым вычислением.

Таким же способом получены еще два ИМ коразмерности 6 дифференциальных уравнений (2.1):

(3.23)

${q = 0,\quad r = 0,\quad {{\gamma }_{1}} = \pm 1,\quad {{\gamma }_{2}} = 0,\quad {{\gamma }_{3}} = 0,\quad {{\delta }_{1}} = 0}$

Уравнения векторного поля на этих ИМ имеют вид

$\begin{gathered} 2\dot {p} = b{{\delta }_{3}},\quad\quad \quad{{{\dot {\delta }}}_{2}} = p{{\delta }_{3}},\quad {{{\dot {\delta }}}_{3}} = - p{{\delta }_{2}} \hfill \\ \end{gathered} $

и определяют маятникоподобные колебания тела относительно его неподвижной оси Ox, которая совпадает с направляющим вектором 1-го силового поля, а направляющий вектор 2-го силового поля ей ортогонален.

Рассмотрим еще одно решение уравнений (2.1) – ИМ коразмерности 4:

(3.24)

$\begin{gathered} p = 0,\quad q = 0,\quad {{\gamma }_{3}} = 0,\quad {{\delta }_{3}} = 0 \hfill \\ \end{gathered} $

Векторное поле на этом ИМ

$\begin{gathered} \dot {r} = - ({{x}_{0}}{{\gamma }_{2}} + b{{\delta }_{1}}),\quad {{{\dot {\gamma }}}_{1}} = r{{\gamma }_{2}},\quad {{{\dot {\gamma }}}_{2}} = - r{{\gamma }_{1}},\quad {{{\dot {\delta }}}_{1}} = r{{\delta }_{2}},\quad {{{\dot {\delta }}}_{2}} = - r{{\delta }_{1}} \hfill \\ \end{gathered} $

описывает маятникоподобные колебания тела относительно его неподвижной главной оси Oz. Ось вращения тела ортогональна направлениям силовых полей. Движения существуют при любом угле между направлениями силовых полей, т.е. это семейство ИМ.

Используя семейство интегралов $\tilde {K}$ нетрудно записать интегралы, принимающие стационарное значение на ИМ (3.21), (3.23). Ими соответственно будут ${{\tilde {K}}_{1}}$ = H² – V₁ + + $2b[(b \pm H){{V}_{3}} + V_{1}^{{1/2}}]$ и ${{\tilde {K}}_{2}} = {{H}^{2}} - {{V}_{1}} + 2{{x}_{0}}[({{x}_{0}} \mp H){{V}_{2}} + V_{1}^{{1/2}}]$. В случае ИМ (3.24) это будет нелинейная комбинация первых интегралов ${{\tilde {K}}_{3}} = ({{V}_{1}} - x_{0}^{2}{{V}_{2}} - {{b}^{2}}{{V}_{3}})H + 2{{V}_{5}}$.

4. Об инвариантных многообразиях коразмерности 2. Покажем, что найденные выше решения принадлежат либо одному из двух ИМ коразмерности 2 уравнений движения (2.1), либо их пересечению. Уравнения этих ИМ соответственно записываются так [12]:

(4.1)

$\begin{gathered} 2bp\left( {{{\delta }_{2}}{{\gamma }_{3}} - {{\delta }_{3}}{{\gamma }_{2}}} \right) - \left( {2p{{\gamma }_{1}} + 2q{{\gamma }_{2}} + r{{\gamma }_{3}}} \right)\left( {pr - {{x}_{0}}{{\gamma }_{3}}} \right) = 0 \\ 2{{x}_{0}}q\left( {{{\delta }_{1}}{{\gamma }_{3}} - {{\delta }_{3}}{{\gamma }_{1}}} \right) - \left( {2p{{\delta }_{1}} + 2q{{\delta }_{2}} + r{{\delta }_{3}}} \right)\left( {qr + b{{\delta }_{3}}} \right) = 0 \\ \end{gathered} $

(4.2)

$\begin{array}{*{20}{l}} {{{\sigma }_{0}}\gamma _{2}^{2} + {{\sigma }_{1}}{{\gamma }_{2}} + {{\sigma }_{2}} = 0,\quad {{{\hat {\sigma }}}_{0}}{{\delta }_{1}} + {{{\hat {\sigma }}}_{1}}{{\gamma }_{2}} + {{{\hat {\sigma }}}_{2}} = 0} \end{array}$

Здесь ${{\sigma }_{i}}$, ${{\hat {\sigma }}_{i}}$ – полиномы от $p$, $q$, $r$, ${{\delta }_{2}}$, ${{\delta }_{3}}$, ${{\gamma }_{1}}$, ${{\gamma }_{3}}$. Полиномы достаточно громоздкие и полностью приведены в [12].

При ${{x}_{0}} = \pm 1$, ${\kern 1pt} b = \mp 1$ уравнения (4.1), (4.2) эквивалентны уравнениям (3.3) и (3.5) [5] соответственно.

Как можно проверить прямым вычислением, ИМ (4.1) существует при любых углах между направлениями силовых полей. Таким образом, уравнения (4.1) совместно с интегралом ${{V}_{4}} = {{c}_{2}}$ можно рассматривать как семейство ИМ, каждый элемент которого соответствует определенной ориентации силовых полей (в зависимости от значения параметра ${{c}_{2}}$). Это справедливо и для ИМ (4.2).

Разрешим уравнения (3.4) и (3.5) относительно переменных $q$, $r$, ${{\gamma }_{i}}$, ${{\delta }_{i}}$ ($i = 1,2,3$) и подставим полученные выражения в (4.1). Последние обратятся в тождество. Откуда следует, что многообразия, определяемые уравнениями (3.4) и (3.5), являются подмногообразиями ИМ (4.1). Так как интеграл ${{V}_{4}}$ на ИМ (3.4), (3.5) тождественно равен ±1, то и ИМ (4.1) должно удовлетворять такому же условию. Иными словами речь идет об элементах семейства ИМ (4.1), соответствующих случаю ${{c}_{2}} = \pm 1$ системы (2.1) на многообразии ${{V}_{4}} = {{c}_{2}}$.

Аналогично находим, что многообразия, определяемые уравнениями (3.6), (3.7), (3.17), (3.21), (3.23), (3.24), являются подмногообразиями как ИМ (4.1), так и ИМ (4.2), т.е. принадлежат их пересечению. Причем в зависимости от значения параметра ${{c}_{2}}$ все перечисленные ИМ соответствуют различным случаям системы (2.1) на многообразии ${{V}_{4}} = {{c}_{2}}$.

Интеграл ${{V}_{4}}$ на ИМ (3.4)–(3.7) тождественно равен ±1, а на ИМ (3.21), (3.23) – 0, что соответствует параллельным и ортогональным силовым полям. На ИМ (3.17) интеграл ${{V}_{4}}$ принимает вид $ \pm [b{{(1 - \delta _{1}^{2})}^{{1/2}}} \pm {{(x_{0}^{2} - {{b}^{2}}\delta _{1}^{2})}^{{1/2}}}]{{\delta }_{1}}x_{0}^{{ - 1}} = {{c}_{2}}$. Эти соотношения определяют силовые поля специальной ориентации в зависимости от значения параметра ${{\delta }_{1}}$. На семействе ИМ (3.24) ${{\left. {{{V}_{4}}} \right|}_{0}} = {{\gamma }_{1}}{{\delta }_{1}} + {{\gamma }_{2}}{{\delta }_{2}} = {{c}_{2}}$. Следовательно, это семейство существует при любых углах между силовыми полями.

5. Об устойчивости стационарных решений и ИМ. Интегралы и их семейства, принимающие стационарное значение на найденных решениях, будем использовать при исследовании устойчивости этих решений методом Рауса–Ляпунова. Задача в этом случае сводится к проверке критерия условного экстремума – знакоопределенности второй вариации соответствующего семейства интегралов, полученной в окрестности исследуемого решения, на вариациях “условных” интегралов.

5.1. Перманентные вращения. Исследуем устойчивость элементов семейств решений (3.9). Для этого используем семейство интегралов ${{K}_{1}}$ (3.13) при следующих ограничениях на параметры: ${{\lambda }_{1}} = (2x_{0}^{2}{{\lambda }_{0}}){\text{/}}(p_{0}^{2}({{b}^{2}} + x_{0}^{2}))$ и ${{\lambda }_{4}} = 0$, которое принимает стационарное значение на этих решениях. При указанных условиях интеграл ${{K}_{1}}$ примет вид

${2{{F}_{1}} = 2H + \frac{{x_{0}^{2}}}{{({{b}^{2}} + x_{0}^{2})}}\left[ {\frac{{{{V}_{2}}x_{0}^{2} + {{b}^{2}}{{V}_{3}} - 2{{V}_{1}}}}{{p_{0}^{2}}} - \frac{{4x_{0}^{2}{{V}_{5}}}}{{p_{0}^{4}({{b}^{2}} + x_{0}^{2}) + x_{0}^{4}}}} \right]}$

Введем отклонения от элементов исследуемого семейства решений:

$\begin{gathered} {{y}_{1}} = {{\delta }_{1}} - \delta _{1}^{0},\quad {{y}_{2}} = {{\delta }_{2}} - \delta _{2}^{0},\quad {{y}_{3}} = {{\delta }_{3}} - \delta _{3}^{0},\quad {{y}_{4}} = {{\gamma }_{1}} - \gamma _{1}^{0},\quad {{y}_{5}} = {{\gamma }_{2}} - \gamma _{2}^{0} \\ {{y}_{6}} = {{\gamma }_{3}} - \gamma _{3}^{0},\quad {{y}_{7}} = q - {{q}^{0}},\quad {{y}_{8}} = r - {{r}^{0}},\quad {{y}_{9}} = p - {{p}_{0}} \\ \end{gathered} $

где ${{p}_{0}}$, ${{q}^{0}}$, ${{r}^{0}}$, $\gamma _{i}^{0}$, $\delta _{i}^{0}$ ($i = 1,2,3$) – значения переменных в невозмущенном движении (3.9).

Вторая вариация интеграла ${{F}_{1}}$ в окрестности элементов исследуемого семейства решений в отклонениях ${{y}_{j}}$ ($j = 1,\; \ldots ,\;9$) на линейном многообразии

$\begin{gathered} {}\delta H = 2p_{0}^{2}\left( {b{{y}_{7}} + {{x}_{0}}{{y}_{9}}} \right) - {{p}_{0}}{{x}_{0}}\left( {b{{y}_{2}} - {{x}_{0}}{{y}_{4}}} \right) \pm {{z}_{1}}{{y}_{8}} = 0 \\ \delta {{V}_{2}} = 2(p_{0}^{2}\left( {{{x}_{0}}{{y}_{4}} + b{{y}_{5}}} \right) \pm {{z}_{1}}{{y}_{6}}) = 0,\quad \delta {{V}_{3}} = - 2(p_{0}^{2}\left( {{{x}_{0}}{{y}_{1}} + b{{y}_{2}}} \right) \pm {{z}_{1}}{{y}_{3}}) = 0 \\ \delta {{V}_{5}} = - \rho [b{{x}_{0}}p_{0}^{2}({{b}^{2}} + z_{2}^{2}){{y}_{2}} - p_{0}^{2}x_{0}^{2}(x_{0}^{2} + z_{2}^{2}){{y}_{4}} + bp_{0}^{2}x_{0}^{2}\left( {b{{y}_{1}} - {{x}_{0}}{{y}_{5}}} \right) - \\ - \;2p_{0}^{3}z_{2}^{2}\left( {b{{y}_{7}} + {{x}_{0}}{{y}_{9}}} \right) \mp {{z}_{1}}({{p}_{0}}z_{2}^{2}{{y}_{8}} - {{x}_{0}}({{b}^{2}}{{y}_{3}} - x_{0}^{2}{{y}_{6}}))] = 0 \\ \end{gathered} $

записывается так:

(5.1)

$\begin{gathered} 2{{\delta }^{2}}{{F}_{1}} = {{a}_{{22}}}y_{2}^{2} + {{a}_{{33}}}y_{3}^{2} + {{a}_{{44}}}y_{4}^{2} + {{a}_{{66}}}y_{6}^{2} + {{a}_{{77}}}y_{7}^{2} + {{a}_{{88}}}y_{8}^{2} + {{a}_{{24}}}{{y}_{2}}{{y}_{4}} + {{a}_{{27}}}{{y}_{2}}{{y}_{7}} + \\ + \;{{a}_{{36}}}{{y}_{3}}{{y}_{6}} + {{a}_{{38}}}{{y}_{3}}{{y}_{8}} + {{a}_{{47}}}{{y}_{4}}{{y}_{7}} + {{a}_{{68}}}{{y}_{6}}{{y}_{8}} \mp \left[ {{{a}_{{23}}}{{y}_{2}}{{y}_{3}} + {{a}_{{26}}}{{y}_{2}}{{y}_{6}}} \right. + {{a}_{{28}}}{{y}_{2}}{{y}_{8}} + \\ + \;{{a}_{{34}}}{{y}_{3}}{{y}_{4}} + {{a}_{{37}}}{{y}_{3}}{{y}_{7}} + {{a}_{{46}}}{{y}_{4}}{{y}_{6}} + {{a}_{{48}}}{{y}_{4}}{{y}_{8}} + \left. {{{a}_{{67}}}{{y}_{6}}{{y}_{7}} + {{a}_{{78}}}{{y}_{7}}{{y}_{8}}} \right] \\ \end{gathered} $

$\begin{gathered} 2{{a}_{{22}}} = - \frac{{{{b}^{2}}}}{{p_{0}^{2}}}(2p_{0}^{4}x_{0}^{2}{{\rho }^{{ - 1}}} + 1),\quad {{a}_{{33}}} = \frac{{{{b}^{2}}}}{{p_{0}^{6}z_{2}^{2}\rho }}[(6p_{0}^{4}x_{0}^{2} - z_{1}^{2})\rho - 2p_{0}^{4}x_{0}^{4}(2p_{0}^{4} + 5x_{0}^{2})] \\ 2{{a}_{{44}}} = \frac{{x_{0}^{2}}}{{{{b}^{2}}p_{0}^{2}\rho }}[2x_{0}^{4}(p_{0}^{4} + x_{0}^{2}) - (x_{0}^{2} + 3z_{2}^{2})\rho ],\quad {{a}_{{66}}} = \frac{{x_{0}^{4}}}{{{{b}^{2}}p_{0}^{6}z_{2}^{2}\rho }}[2{{b}^{2}}p_{0}^{8}(x_{0}^{2} - {{b}^{2}}) - \\ - \;z_{1}^{2}(\rho + 4{{b}^{2}}p_{0}^{4})],\quad {{a}_{{77}}} = - 6({{b}^{2}}x_{0}^{{ - 2}} + 1),\quad 2{{a}_{{88}}} = 3({{b}^{2}}x_{0}^{{ - 2}} - x_{0}^{2}p_{0}^{{ - 4}}) + 5 \\ {{a}_{{23}}} = 8{{b}^{3}}x_{0}^{2}{{z}_{1}}{{\rho }^{{ - 1}}}z_{2}^{{ - 2}},\quad {{a}_{{24}}} = b{{x}_{0}}(p_{0}^{{ - 2}} + 2p_{0}^{2}x_{0}^{2}{{\rho }^{{ - 1}}}) \\ \end{gathered} $

$\begin{gathered} {{a}_{{48}}} = {{z}_{1}}(3\rho - 4p_{0}^{4}x_{0}^{2})p_{0}^{{ - 3}}{{\rho }^{{ - 1}}},\quad {{a}_{{67}}} = \frac{{4{{x}_{0}}{{z}_{1}}}}{{bp_{0}^{3}z_{2}^{2}\rho }}[(x_{0}^{2} - {{b}^{2}})\rho - {{b}^{2}}p_{0}^{4}z_{2}^{2}] \\ {{a}_{{68}}} = 2{{x}_{0}}p_{0}^{{ - 5}}[x_{0}^{2} - {{b}^{2}} + {{b}^{4}}z_{2}^{{ - 2}} - 2p_{0}^{8}(z_{2}^{2} + x_{0}^{2}){{\rho }^{{ - 1}}}] \\ {{a}_{{78}}} = 6b{{z}_{1}}p_{0}^{{ - 2}}x_{0}^{{ - 2}} \\ \end{gathered} $

Здесь и далее используются обозначения ${{z}_{1}}$, ${{z}_{2}}$, введенные в п. 3.1, $\rho = p_{0}^{4}z_{2}^{2} + x_{0}^{4}$.

Условия отрицательной определенности квадратичной формы ${{\delta }^{2}}{{F}_{1}}$ являются достаточными для устойчивости элементов исследуемого семейства решений. В форме неравенств Сильвестра они имеют вид:

$\begin{gathered} - 3({{b}^{2}}x_{0}^{{ - 2}} + 1) < 0,\quad 3x_{0}^{2}p_{0}^{{ - 4}} - 5({{b}^{2}}x_{0}^{{ - 2}} + 1) > 0 \\ {{b}^{2}}[(2x_{0}^{2}(2p_{0}^{4} + x_{0}^{2}) - 5z_{1}^{2}){{\rho }^{2}} - 24p_{0}^{4}x_{0}^{6}z_{1}^{2}]p_{0}^{{ - 6}}x_{0}^{{ - 2}}{{\rho }^{{ - 2}}} < 0 \\ x_{0}^{2}[8x_{0}^{8}(3\rho - 2x_{0}^{4}) - {{\rho }^{2}}(3\rho + 4x_{0}^{4})]p_{0}^{{ - 8}}{{\rho }^{{ - 2}}} > 0 \\ - {{b}^{2}}x_{0}^{8}[{{\rho }^{2}}[\rho (3{{b}^{2}}p_{0}^{4} - 7x_{0}^{4}) + 4x_{0}^{6}(p_{0}^{4} + 2x_{0}^{2})] + 8p_{0}^{4}x_{0}^{{10}}z_{1}^{2}]p_{0}^{{ - 10}}z_{2}^{{ - 2}}{{\rho }^{{ - 4}}} < 0 \\ {{b}^{2}}x_{0}^{{20}}(p_{0}^{4}z_{2}^{2} - x_{0}^{4})(3p_{0}^{4}z_{2}^{2} - x_{0}^{4})p_{0}^{{ - 12}}z_{2}^{{ - 4}}{{\rho }^{{ - 4}}} > 0 \\ \end{gathered} $

С учетом условий вещественности рассматриваемых решений, последние неравенства совместны при следующих ограничениях на параметры $b$, ${{x}_{0}}$, ${{p}_{0}}$:

(5.2)

${{{p}_{0}} \ne 0,\quad (\sqrt 3 p_{0}^{2} + {{x}_{0}} < 0\;{\text{и л и }}\;{{x}_{0}} > \sqrt 3 p_{0}^{2})\quad {\text{и }}\quad ( - \sigma < b < 0\;{\text{и л и }}\;0 < b < \sigma )}$

$\sigma = \left| {{{x}_{0}}} \right|{{(x_{0}^{2}{\text{/}}(3p_{0}^{{}}) - 1)}^{{1/2}}}$

Неравенства (5.2) выделяют из исследуемого семейства решений подсемейство, элементы которого устойчивы.

Необходимые условия устойчивости элементов семейств решений (3.9) получим, исходя из теоремы Ляпунова [13] об устойчивости по первому приближению.

Уравнения первого приближения в рассматриваемом случае записываются так:

(5.3)

Здесь ${{y}_{i}}$ ($i = 1,\; \ldots ,\;9$) – отклонения от элементов исследуемого семейства решений.

Характеристическое уравнение системы (5.3)

$\begin{gathered} {{\lambda }^{3}}(p_{0}^{2}{{\lambda }^{2}} + x_{0}^{2})[p_{0}^{2}x_{0}^{2}{{\lambda }^{2}} + x_{0}^{4} - p_{0}^{4}({{b}^{2}} + x_{0}^{2})][4p_{0}^{2}x_{0}^{2}{{\lambda }^{2}} + x_{0}^{4} - 3p_{0}^{4}({{b}^{2}} + x_{0}^{2})] = 0 \hfill \\ \end{gathered} $

имеет только нулевые и чисто мнимые корни при следующих ограничениях на параметры $b$, ${{x}_{0}}$, ${{p}_{0}}$:

${{{p}_{0}} \ne 0,\quad (\sqrt 3 p_{0}^{2} + {{x}_{0}} < 0\;{\text{и л и }}\;{{x}_{0}} > \sqrt 3 p_{0}^{2})\quad {\text{и }}\quad \left( { - \sigma \leqslant b < 0\;{\text{и л и }}\;0 < b \leqslant \sigma } \right)}$

Сопоставляя последние неравенства с (5.2), заключаем, что условия (5.2) являются необходимыми и достаточными для устойчивости элементов семейств решений (3.9) с точностью до границы.

Аналогичный результат будем иметь и при исследовании устойчивости элементов семейств решений (3.10), если для получения достаточных условий устойчивости использовать то же самое семейство интегралов ${{F}_{1}}$.

Далее исследуем устойчивость элементов 1-го семейства решений (3.11). Будем действовать аналогично предыдущему случаю, используя вместо ${{K}_{1}}$ семейство интегралов ${{K}_{3}}$ (3.14) при ${{\lambda }_{1}} = {{\lambda }_{4}} = 0$. При этих ограничениях семейство интегралов ${{K}_{3}}$ примет вид

(5.4)

${{{F}_{2}} = \left[ {H + \left( {\frac{{p_{0}^{2}}}{{x_{0}^{2}}} + \frac{1}{{2{{z}_{2}}}}} \right)[x_{0}^{2}{{V}_{2}} + {{b}^{2}}{{V}_{3}}] - \frac{{{{V}_{5}}}}{{z_{2}^{2}}}} \right]}$

Для уравнений возмущенного движения 2-я вариация интеграла ${{F}_{2}}$ в окрестности элементов исследуемого семейства решений на линейном многообразии

$\begin{gathered} \delta H = {{x}_{0}}\left( {{{x}_{0}}{{y}_{4}} - b{{y}_{2}}} \right) + 2{{p}_{0}}\left( {b{{y}_{7}} + {{x}_{0}}{{y}_{9}}} \right) = 0,\quad \delta {{V}_{2}} = - 2\left( {{{x}_{0}}{{y}_{4}} + b{{y}_{5}}} \right) = 0 \\ \delta {{V}_{3}} = 2\left( {{{x}_{0}}{{y}_{1}} + b{{y}_{2}}} \right) = 0,\quad \delta {{V}_{5}} = 2{{p}_{0}}{{x}_{0}}\left( {b{{y}_{7}} + {{x}_{0}}{{y}_{9}}} \right)z_{2}^{2} + 2p_{0}^{2}[{{b}^{2}}\left( {{{x}_{0}}{{y}_{1}} + b{{y}_{2}}} \right) - \\ - \;x_{0}^{2}\left( {{{x}_{0}}{{y}_{4}} + b{{y}_{5}}} \right)]{{z}_{2}} + bx_{0}^{3}\left[ {b\left( {{{y}_{1}} + {{y}_{4}}} \right) - {{x}_{0}}\left( {{{y}_{2}} + {{y}_{5}}} \right)} \right] = 0 \\ \end{gathered} $

записывается так: ${{\delta }^{2}}{{F}_{2}} = {{Q}_{1}} + {{Q}_{2}}$, где

Здесь ${{y}_{i}}$ ($i = 1,\; \ldots ,\;9$) – отклонения от невозмущенного движения.

Условия положительной определенности ${{\delta }^{2}}{{F}_{2}}$ в форме неравенств Сильвестра имеют вид:

$\begin{gathered} z_{2}^{2}x_{0}^{{ - 2}} > 0,\quad 2p_{0}^{2}z_{2}^{2}x_{0}^{{ - 2}} + {{z}_{2}}(z_{2}^{2}{{b}^{{ - 2}}} + 2) > 0,\quad z_{2}^{4}(3x_{0}^{2} + 2p_{0}^{2}{{z}_{2}}){{b}^{{ - 2}}}x_{0}^{{ - 2}} > 0 \\ p_{0}^{2}({{b}^{2}}z_{2}^{{ - 2}} + 1) + x_{0}^{2}z_{2}^{{ - 1}}(2{{b}^{2}}z_{2}^{{ - 2}} + 1) > 0,\quad {{b}^{2}}[2p_{0}^{4}x_{0}^{{ - 2}} + 3x_{0}^{2}z_{2}^{{ - 2}} + 5p_{0}^{2}z_{2}^{{ - 1}}] > 0 \\ \end{gathered} $

Эти неравенства совместны при $b \ne 0,\;$ ${{x}_{0}} \ne 0$ и ${{p}_{0}} \ne 0$. Откуда и следует устойчивость элементов исследуемого семейства решений.

Для элементов 2-го семейства перманентных вращений (3.11) из анализа линеаризованных в окрестности исследуемого решения уравнений движения (2.1) получены условия неустойчивости.

Уравнения первого приближения в отклонениях

$\begin{gathered} {{y}_{1}} = {{\delta }_{1}} + {{x}_{0}}z_{2}^{{ - 1}},\quad {{y}_{2}} = {{\delta }_{2}} + bz_{2}^{{ - 1}},\quad {{y}_{3}} = {{\delta }_{3}},\quad {{y}_{4}} = {{\gamma }_{1}} - {{x}_{0}}z_{2}^{{ - 1}},\quad {{y}_{5}} = {{\gamma }_{2}} - bz_{2}^{{ - 1}} \\ {{y}_{6}} = {{\gamma }_{3}},\quad {{y}_{7}} = p - {{p}_{0}},\quad {{y}_{8}} = q - b{{p}_{0}}x_{0}^{{ - 1}},\quad {{y}_{9}} = r \\ \end{gathered} $

здесь имеют вид:

(5.5)

$\begin{gathered} {{{\dot {y}}}_{1}} = - b({{p}_{0}}x_{0}^{{ - 1}}{{y}_{3}} + z_{2}^{{ - 1}}{{y}_{9}}),\quad {{{\dot {y}}}_{2}} = {{p}_{0}}{{y}_{3}} + {{x}_{0}}z_{2}^{{ - 1}}{{y}_{9}} \\ {{{\dot {y}}}_{3}} = {{p}_{0}}(bx_{0}^{{ - 1}}{{y}_{1}} - {{y}_{2}}) + z_{2}^{{ - 1}}\left( {b{{y}_{7}} - {{x}_{0}}{{y}_{8}}} \right),\quad {{{\dot {y}}}_{4}} = b(z_{2}^{{ - 1}}{{y}_{9}} - {{p}_{0}}x_{0}^{{ - 1}}{{y}_{6}}) \\ {{{\dot {y}}}_{5}} = {{p}_{0}}{{y}_{6}} - {{x}_{0}}z_{2}^{{ - 1}}{{y}_{9}},\quad {{{\dot {y}}}_{6}} = {{p}_{0}}(bx_{0}^{{ - 1}}{{y}_{4}} - {{y}_{5}}) + z_{2}^{{ - 1}}\left( {{{x}_{0}}{{y}_{8}} - b{{y}_{7}}} \right) \\ 2{{{\dot {y}}}_{7}} = b({{y}_{3}} + {{p}_{0}}x_{0}^{{ - 1}}{{y}_{9}}),\quad 2{{{\dot {y}}}_{8}} = {{x}_{0}}{{y}_{6}} - {{p}_{0}}{{y}_{9}},\quad {{{\dot {y}}}_{9}} = - b{{y}_{1}} - {{x}_{0}}{{y}_{5}} \\ \end{gathered} $

Характеристическое уравнение системы (5.5):

$\begin{gathered} {{\lambda }^{3}}(2{{\lambda }^{2}} - {{z}_{2}})(x_{0}^{2}{{\lambda }^{2}} + p_{0}^{2}z_{2}^{2})(x_{0}^{2}{{\lambda }^{2}} + (p_{0}^{2}{{z}_{2}} - x_{0}^{2}){{z}_{2}}) = 0 \hfill \\ \end{gathered} $

Как видно из самого уравнения, оно имеет хотя бы один положительный корень при $b \ne 0,$ ${{x}_{0}} \ne 0$ и ${{p}_{0}} \ne 0$. Откуда следует неустойчивость элементов исследуемого семейства решений.

Для семейств решений (3.12) получены аналогичные результаты.

Исследуем устойчивость многообразий, которым принадлежат семейства решений (3.9)–(3.12). Для получения достаточных условий устойчивости используем интегралы ${{V}_{2}} + {{V}_{3}} \pm 2{{V}_{4}}$.

Для уравнений возмущенного движения интеграл $F = {{V}_{2}} + {{V}_{3}} + 2{{V}_{4}}$ в окрестности ИМ (3.4) принимает вид ${{\delta }^{2}}F = ({{y}_{3}} + {{y}_{6}}{{)}^{2}} + {{({{y}_{4}} + {{y}_{7}})}^{2}} + {{({{y}_{5}} + {{y}_{8}})}^{2}}$ где ${{y}_{1}} = q - bpx_{0}^{{ - 1}}$, ${{y}_{2}} = r \pm {{z}_{1}}{{p}^{{ - 1}}}x_{0}^{{ - 1}}$, ${{y}_{3}} = {{\gamma }_{1}} - {{p}^{2}}x_{0}^{{ - 1}}$, ${{y}_{4}} = {{\gamma }_{2}} - b{{p}^{2}}x_{0}^{{ - 2}}$, ${{y}_{5}} = {{\gamma }_{3}} \pm {{z}_{1}}x_{0}^{{ - 2}}$, ${{y}_{6}} = {{\delta }_{1}} + {{p}^{2}}x_{0}^{{ - 1}}$, y₇ = = ${{\delta }_{2}} + b{{p}^{2}}x_{0}^{{ - 2}}$, ${\kern 1pt} {{y}_{8}} = {{\delta }_{3}} \mp {{z}_{1}}x_{0}^{{ - 2}}$ – отклонения от исследуемого ИМ.

Так как квадратичная форма ${{\delta }^{2}}F$ знакоопределена по переменным y₃ +y₆, y₄+y₇, y₅+y₈, то исследуемое ИМ устойчиво по переменным ${{\delta }_{1}} + {{\gamma }_{1}}$, ${{\delta }_{2}} + {{\gamma }_{2}}$, ${{\delta }_{3}} + {{\gamma }_{3}}$. Последнее означает, что ИМ устойчиво относительно возмущения направления силовых полей. Аналогично доказывается устойчивость по части переменных ИМ (3.5)–(3.7).

5.2. Положения равновесия. Исследуем устойчивость элементов 1-го семейства решений (3.15). В рамках нашего подхода используем для этого семейство нтегралов ${{K}_{5}}$ (3.18) при ${{\lambda }_{2}} = - 2{{\lambda }_{1}}x_{0}^{2}$, ${{\lambda }_{4}} = 0$. При этих ограничениях семейство интегралов примет вид

$2{{F}_{3}} = 2[zH + x_{0}^{2}{{V}_{2}} + {{b}^{2}}{{V}_{3}}] - {{V}_{1}}$

Здесь $z$, $\bar {z}$ – обозначения, введенные в п. 3.2.

Для уравнений возмущенного движения 2-я вариация интеграла ${{F}_{3}}$ в окрестности элементов исследуемого семейства решений на линейном многообразии

$\begin{gathered} \delta H = {{x}_{0}}{{y}_{4}} - b{{y}_{2}} = 0,\quad \delta {{V}_{1}} = 2[2b\delta _{1}^{0}\left( {b{{y}_{1}} - {{x}_{0}}{{y}_{5}}} \right) + \left( {b{{y}_{2}} + {{x}_{0}}{{y}_{4}}} \right)\bar {z}] = 0 \\ \delta {{V}_{2}} = - 2[{{(x_{0}^{2} - {{b}^{2}}\delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}{{y}_{4}} + b\delta _{1}^{0}{{y}_{5}}] = 0,\quad \delta {{V}_{3}} = 2[\delta _{1}^{0}{{y}_{1}} + {{(1 - \delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}{{y}_{2}}] = 0 \\ \end{gathered} $

имеет вид ${{\delta }^{2}}{{F}_{3}} = {{\bar {Q}}_{1}} + {{\bar {Q}}_{2}}$, где $2{{\bar {Q}}_{1}} = {{z}^{2}}\delta {{_{1}^{0}}^{{^{{ - 2}}}}}y_{2}^{2} + 2({{b}^{2}}y_{3}^{2} + x_{0}^{2}y_{6}^{2}) + zy_{9}^{2}$, ${{\bar {Q}}_{2}} = 2[b{{(1 - \delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}y_{7}^{2}$ + + ${{(x_{0}^{2} - {{b}^{2}}\delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}y_{8}^{2} - 2b\delta _{1}^{0}{{y}_{7}}{{y}_{8}}]$, ${{y}_{i}}$ ($i = 1,\; \ldots ,\;9$) – отклонения от невозмущенного решения.

Условия положительной определенности квадратичной формы ${{\delta }^{2}}{{F}_{3}}$

(5.6)

$z > 0,\quad \delta _{1}^{0} \ne 0,\quad b{{(1 - \delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}} > 0,\quad b[{{(1 - \delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}{{(x_{0}^{2} - {{b}^{2}}\delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}} - b\delta {{_{1}^{0}}^{{^{2}}}}] > 0$

являются достаточными для устойчивости элементов исследуемого семейства решений. С учетом условий вещественности решений (3.15), неравенства (5.6) совместны при $b > 0$, ${{x}_{0}} \ne 0$ и ($ - \sigma < \delta _{1}^{0} < 0$ или $0 < \delta _{1}^{0} < \sigma $), где $\sigma = \left| {{{x}_{0}}} \right|{{({{b}^{2}} + x_{0}^{2})}^{{ - 1/2}}}$.

Как было отмечено ранее, интеграл ${{V}_{4}}$ на элементах исследуемого семейства решений принимает вид $ - [b{{(1 - \delta _{1}^{2})}^{{1/2}}} + {{(x_{0}^{2} - {{b}^{2}}\delta _{1}^{2})}^{{1/2}}}]{{\delta }_{1}}x_{0}^{{ - 1}} = {{c}_{2}}$. Это соотношение совместно с последними неравенствами определяет границы изменения углов между направлениями силовых полей, в пределах которых элементы исследуемого семейства решений устойчивы.

Аналогично исследуется устойчивость элементов 2-го семейства решений (3.15). Достаточные условия устойчивости здесь определяются неравенствами $b < 0$, ${{x}_{0}} \ne 0$ и ($ - \sigma < \delta _{1}^{0} < 0$ или $0 < \delta _{1}^{0} < \sigma $).

Для элементов семейств решений (3.16) получены условия неустойчивости из анализа линеаризованных в окрестности элементов этих семейств уравнений (2.1).

Запишем уравнения первого приближения в окрестности элементов 1-го семейства решений (3.16):

(5.7)

$\begin{gathered} {{{\dot {y}}}_{1}} = {{(1 - \delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}{{y}_{9}},\quad {{{\dot {y}}}_{5}} = - {{(x_{0}^{2} - {{b}^{2}}\delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}x_{0}^{{ - 1}}{{y}_{9}} \\ {{{\dot {y}}}_{2}} = - \delta _{1}^{0}{{y}_{9}},\quad {{y}_{6}} = [b\delta _{1}^{0}{{y}_{7}} + {{(x_{0}^{2} - {{b}^{2}}\delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}]x_{0}^{{ - 1}}{{y}_{9}} \\ {{{\dot {y}}}_{3}} = \delta _{1}^{0}{{y}_{8}} - {{(1 - \delta {{_{1}^{0}}^{{^{2}}}})}^{{1/2}}}{\kern 1pt} {{y}_{7}},\quad 2{{{\dot {y}}}_{7}} = b{{y}_{3}} \\ {{{\dot {y}}}_{4}} = - b\delta _{1}^{0}x_{0}^{{ - 1}}{{y}_{9}},\quad 2{{{\dot {y}}}_{8}} = {{x}_{0}}{{y}_{6}},\quad {{{\dot {y}}}_{9}} = - \left( {b{{y}_{1}} + {{x}_{0}}{{y}_{5}}} \right) \\ \end{gathered} $

Характеристическое уравнение системы (5.7) имеет вид:

(5.8)

$\begin{gathered} {{\lambda }^{3}}\left[ {4{{\lambda }^{6}}\, + \,6\bar {z}{{\lambda }^{4}}\, - \,\frac{1}{2}({{b}^{2}}\, + \,x_{0}^{2}\, - \,5{{{\bar {z}}}^{2}}){{\lambda }^{2}} + } \right. \\ \left. {_{{_{{_{{_{{_{{_{{}}}}}}}}}}}}\, + {{b}^{2}}[b{{{(1 - \delta {{{_{1}^{0}}}^{{^{2}}}})}}^{{3/2}}} - \delta {{{_{1}^{0}}}^{{^{2}}}}\bar {z}]\, - \,{{{(x_{0}^{2} - {{b}^{2}}\delta {{{_{1}^{0}}}^{{^{2}}}})}}^{{3/2}}}\, + \,({{b}^{2}} - x_{0}^{2})z} \right]\, = \,0 \\ \end{gathered} $

Данное уравнение распадается на два:

$\begin{gathered} {{\lambda }^{3}} = 0,\quad 4{{\zeta }^{3}} + 6\bar {z}{{\zeta }^{2}} - \frac{1}{2}({{b}^{2}} + x_{0}^{2} - 5{{{\bar {z}}}^{2}})\zeta + {{b}^{2}}[b{{(1 - \delta {{_{1}^{0}}^{{^{2}}}})}^{{3/2}}} - \delta {{_{1}^{0}}^{{^{2}}}}\bar {z}] - \\ - \;{{(x_{0}^{2} - {{b}^{2}}\delta {{_{1}^{0}}^{{^{2}}}})}^{{3/2}}} + ({{b}^{2}} - x_{0}^{2})z = 0,\quad \zeta = {{\lambda }^{2}} \\ \end{gathered} $

Произведение корней последнего уравнения выглядит так:

(5.9)

$\begin{gathered} 4{{\zeta }_{1}}{{\zeta }_{2}}{{\zeta }_{3}} = {{b}^{2}}[b{{(1 - \delta {{_{1}^{0}}^{{^{2}}}})}^{{3/2}}} - \delta {{_{1}^{0}}^{{^{2}}}}\bar {z}] - {{(x_{0}^{2} - {{b}^{2}}\delta {{_{1}^{0}}^{{^{2}}}})}^{{3/2}}} + ({{b}^{2}} - x_{0}^{2})z \hfill \\ \end{gathered} $

Правая часть равенства (5.9) с учетом условий вещественности исследуемых решений будет положительной при $0 < b < \left| {{{x}_{0}}} \right|$ и ${\text{|}}\delta _{1}^{0}{\text{|}} \leqslant 1$. Это означает, что уравнение (5.8) имеет хотя бы один положительный корень. Таким образом, при указанном ограничении на параметры $b$, ${{x}_{0}}$ элементы исследуемого семейства решений неустойчивы на всем интервале изменения параметра $\delta _{1}^{0}$. Как следует из последних неравенств, область неустойчивости включает в себя случаи ортогональных ($\delta _{1}^{0} = 0$) и параллельных ($\delta _{1}^{0} = \pm {{x}_{0}}{{({{b}^{2}} + x_{0}^{2})}^{{ - 1/2}}}$) силовых полей.

Условия неустойчивости элементов 2-го семейства решений (3.16) определяются неравенствами $ - \left| {{{x}_{0}}} \right| < b < 0$ и ${\text{|}}\delta _{1}^{0}{\text{|}} \leqslant 1$.

5.3. Движения маятникового типа. Исследуем устойчивость 1-го ИМ (3.21), используя семейство интегралов ${{\hat {K}}_{1}} = {{H}^{2}} - {{V}_{1}} + 2b[(b + H){{V}_{3}} + V_{1}^{{1/2}}]$ для получения достаточных условий устойчивости.

Вторая вариация интеграла ${{\hat {K}}_{1}}$ в окрестности исследуемого решения на линейном многообразии $\delta {{V}_{3}} = 2{{y}_{6}} = 0$ записывается так:

$\begin{gathered} {{\delta }^{2}}{{{\hat {K}}}_{1}} = {{\sigma }_{1}}[{{\sigma }_{2}}(4\left( {{{x}_{0}}{{\gamma }_{1}} + b} \right)y_{1}^{2} - x_{0}^{2}y_{3}^{2} + 2b{{x}_{0}}{{y}_{3}}{{y}_{4}} + \\ + \;b\left. {\left( {{{\sigma }_{1}} + {{\sigma }_{2}}} \right)y_{4}^{2} + 4q{{y}_{1}}\left( {{{x}_{0}}{{y}_{3}} - b{{y}_{4}}} \right)} \right) + y_{2}^{2} + 2by_{5}^{2}] \\ \end{gathered} $

где ${{y}_{i}}$ ($i = 1,\; \ldots ,\;5$) – отклонения в возмущенном движении, ${{\sigma }_{1}} = {{q}^{2}} + {{x}_{0}}{{\gamma }_{1}}$, σ₂ = = ${{({{q}^{2}} + {{x}_{0}}{{\gamma }_{1}} + b)}^{{ - 1}}}$.

Условия отрицательной определенности квадратичной формы ${{\delta }^{2}}{{\hat {K}}_{1}}$:

$\begin{gathered} - x_{0}^{2}{{\sigma }_{1}}\sigma _{2}^{{ - 1}} < 0,\quad - x_{0}^{2}\sigma _{1}^{2}\sigma _{2}^{{ - 1}} > 0,\quad - bx_{0}^{2}\sigma _{1}^{3}\sigma _{2}^{{ - 1}} < 0 \hfill \\ \end{gathered} $

являются достаточными для устойчивости исследуемого ИМ.

Так как интеграл энергии на рассматриваемом ИМ принимает вид H|₀ = q² + + ${{x}_{0}}{{\gamma }_{1}} - b = \hat {h}$, то последние неравенства выполняются при $\hat {h} < 0$ и $0 < b < - \hat {h}{\text{/}}2$. Условие $\hat {h} < 0$ имеет простую механическую интерпретацию. При устойчивом движении маятника силовой центр первого поля сил должен совершать колебание с ограниченной амплитудой ${{\gamma }_{1}} < b{\text{/}}{{x}_{0}}$.

Исследование устойчивости остальных ИМ (3.21), (3.23) проводится аналогичным образом.

6. Заключение. На основе метода Рауса–Ляпунова и его обобщений проведен качественный анализ фазового пространства в задаче о движении твердого тела в двух постоянных силовых полях. С помощью метода базисов Гребнера найдены семейства стационарных решений и стационарные ИМ уравнений движения тела. Построены линейные и нелинейные комбинации первых интегралов задачи, доставляющие стационарные значения найденным решениям. Эти комбинации интегралов использованы в рамках метода Рауса–Ляпунова при исследовании устойчивости решений. Для ряда решений достаточные условия устойчивости сопоставлены с необходимыми.

Работа частично поддержана Советом по грантам Президента РФ для государственной поддержки ведущих научных школ РФ (НШ-8081.2016.9) и грантом РФФИ (грант 16-07-00201а).

Список литературы

Kowalewski S. Sur le probleme de la rotation d’un corps solide autour d’un point fixe // Acta Math. 1889. V. 12. P. 177–232.
Богоявленский О.И. Два интегрируемых случая динамики твердого тела в силовом поле // ДАН СССР. 1984. Т. 275. № 6. С. 1359–1363.
Рейман А.Г., Семенов-Тян-Шанский М.А. Лаксово представление со спектральным параметром для волчка Ковалевской и его обобщений // Функц. анализ и его прил. 1988. Т. 22. Вып. 2. С. 87–88.
Bobenko A.I, Reyman A.G., Semenov-Tian-Shansky M.A. The Kowalewski Top 99 Years Later: A Lax Pair, Generalizations and Explicit Solutions // Commun. Math. Phys. 1989. V. 122. P. 321–354.
Рябов П.Е., Харламов М.П. Классификация особенностей в задаче о движении волчка Ковалевской в двойном поле сил // Матем. сб. 2012. Т. 203. № 2. С. 111–142.
Харламов М.П., Рябов П.Е. Топологический атлас волчка Ковалевской в двойном поле // Фундамент. и прикл. матем. 2015. Т. 20. Вып. 2. С. 185–230.
Кузьмин П.А. Стационарные движения твердого тела и их устойчивость в центральном поле тяготения // Тр. межвуз. конф. по прикл. теории устойчивости движения и аналит. механике. Казань, 1964. С. 93–98.
Иртегов В.Д. Инвариантные многообразия стационарных движений и их устойчивость. Новосибирск: Наука, 1985. 144 с.
Ляпунов А.М. О постоянных винтовых движениях твердого тела в жидкости. Соб. соч. М.: АН СССР, 1954. Т. 1. С. 276–319.
Иртегов В.Д., Титоренко Т.Н. Об инвариантных многообразиях систем с первыми интегралами // ПММ. 2009. Т. 73. Вып. 4. С. 531–537.
Кокс Д., Литтл Дж., О’Ши Д. Идеалы, многообразия и алгоритмы. М.: Мир, 2000. 687 с.
Irtegov V., Titorenko T. Qualitative Analysis of the Reyman-Semenov-Tian-Shansky Integrable Case of the Generalized Kowalewski Top // Proc. of the 18th Int. Workshop on Computer Algebra in Scientific Computing. Springer, 2016. LNCS 9890. P. 289–304.
Ляпунов А.М. Общая задача об устойчивости движения. Соб. соч. М.; Л.: АН СССР, 1956. Т. 2. С. 7–263.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал