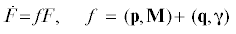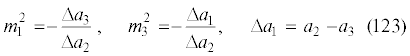Известия РАН. Механика твердого тела, 2019, № 1, стр. 88-100
ПОСТРОЕНИЕ ЛИНЕЙНЫХ ИНВАРИАНТНЫХ СООТНОШЕНИЙ УРАВНЕНИЙ КИРХГОФА
В. Ю. Ольшанский *
Институт проблем точной механики и управления РАН
Саратов, Россия
* E-mail: olshanskiy_vlad@mail.ru
Поступила в редакцию 22.06.2017
После доработки 08.12.2017
Принята к публикации 08.11.2017
Аннотация
Для уравнений Кирхгофа в общем случае, когда матрица перекрестных членов гамильтониана может быть несимметричной, получены условия существования линейного инвариантного соотношения общего вида, связывающего импульсивный момент и импульсивную силу. Показано, что уравнения с таким инвариантным соотношением могут быть преобразованы к уравнениям с инвариантным соотношением для импульсивного момента, условия существования которого при симметричной матрице перекрестных членов совпадают со случаем Чаплыгина. Дано описание семейства гамильтонианов, допускающих существование линейного инвариантного соотношения общего вида. Получена координатная форма инвариантного соотношения и условий его существования. Общее число условий равно шести, в отличие от восьми условий в случае Чаплыгина. Выполнена редукция к уравнению Риккати. Показано, что при существовании линейного интеграла уравнения Кирхгофа приводятся к случаю Кирхгофа.
1. Введение. Известно (смотри, например, [1]), что при движении по инерции твердого тела в идеальной несжимаемой жидкости, течение которой является безвихревым, уравнения движения твердого тела отделяются от дифференциальных уравнений в частных производных, описывающих движение жидкости. Система шести обыкновенных дифференциальных уравнений в форме Лагранжа была получена Г. Кирхгофом [2]. Рассмотрим уравнения Кирхгофа в гамильтоновой форме, полученной А. Клебшем [3]:
(1.1)
${\mathbf{\dot {M}}} = {\mathbf{M}} \times ({\mathbf{AM}} + {{{\mathbf{B}}}^{T}}{\mathbf{\gamma }}) + {\mathbf{\gamma }} \times ({\mathbf{BM}} + {\mathbf{C\gamma }}),\quad\quad {\mathbf{\dot {\gamma }}} = {\mathbf{\gamma }} \times ({\mathbf{AM}} + {{{\mathbf{B}}}^{T}}{\mathbf{\gamma }})$Здесь M и γ – импульсивный момент и импульсивная сила, гамильтониан H в формуле (1.2) – кинетическая энергия системы “тело плюс жидкость”.
Система (1.1) имеет три первых квадратичных интеграла:
(1.2)
${{I}_{1}} = ({\mathbf{M}},\quad{\mathbf{\gamma }}),\quad\quad {{I}_{2}} = {{{\mathbf{\gamma }}}^{2}},\quad {{I}_{3}} = 2H = ({\mathbf{AM}},\quad{\mathbf{M}}) + 2({\mathbf{BM}},\quad{\mathbf{\gamma }}) + ({\mathbf{C\gamma }},\quad{\mathbf{\gamma }})$При существовании четвертого интеграла система будет интегрируемой. Известны случай интегрируемости Кирхгофа (с дополнительным линейным интегралом), случаи Клебша, Ляпунова, Стеклова (с дополнительным квадратичным интегралом). Во всех этих случаях (описание которых смотри, например, [4]) матрицы коэффициентов уравнений (1.1) – диагональные. При B ≠ BT найден [5] полиномиальный интеграл четвертой степени.
Существование линейного инвариантного соотношения (ЛИС) порождает частный случай интегрируемости. Классическое ЛИС Чаплыгина [6] и условия его существования имеют вид
(1.3)
$F = \quad{{{\kappa }}_{3}}{{M}_{1}}\quad \mp \quad{{{\kappa }}_{1}}{{M}_{3}},\quad {{{\kappa }}_{1}} = \sqrt {{{a}_{3}} - \quad{{a}_{2}}} ,\quad {{{\kappa }}_{3}} = \sqrt {{{a}_{2}} - \quad{{a}_{1}}} $(1.4)
$\begin{array}{*{20}{c}} {{{b}_{{13}}}{{{\kappa }}_{3}}\quad \mp \left( {{{b}_{{22}}} - {{b}_{{11}}}} \right){{{\kappa }}_{1}} = \quad0,\quad {{b}_{{13}}}{{{\kappa }}_{1}}\quad \pm \left( {{{b}_{{33}}} - {{b}_{{22}}}} \right){{{\kappa }}_{3}} = 0} \\ \quad \\ {{{c}_{{13}}}{{{\kappa }}_{3}}\quad \mp \left( {{{c}_{{22}}} - {{c}_{{11}}}} \right){{{\kappa }}_{1}} = \quad0,\quad\quad {{c}_{{13}}}{{{\kappa }}_{1}}\quad \pm \left( {{{c}_{{33}}} - {{c}_{{22}}}} \right){{{\kappa }}_{3}} = 0} \\ \quad \\ {{{b}_{{12}}} = \;\quad{{b}_{{23}}} = \quad\;{{c}_{{12}}} = \quad\;{{c}_{{23}}} = 0} \end{array}$Здесь ai и ei – собственные значения и векторы оператора A; Mi и (bij), (cij) – компоненты вектора M и матрицы операторов B, C в базисе (ei), B = BT.
Для найденных новых дополнительных интегралов [5, 7–9] уравнений Пуанкаре–Жуковского, уравнений Кирхгофа и их обобщений было отмечено, что уравнения в полученных частных случаях обладают различными линейными инвариантными соотношениями, отличными от ЛИС Чаплыгина. Более того, было показано [4, 8–10], что в указанных случаях дополнительный интеграл может быть представлен в виде произведения двух инвариантных соотношений, одно из которых – линейное.
Важным для построения новых случаев интегрируемости является нахождение всех квадратичных гамильтонианов, допускающих существование ЛИС систем Пуанкаре–Жуковского, Кирхгофа и их обобщений. Для уравнений Пуанкаре–Жуковского был отмечен [11] один новый случай существования ЛИС и получено [12, 13] описание всех случаев существования ЛИС при симметричных и несимметричных матрицах гамильтониана. Найдены [14] все случаи существования ЛИС уравнений Кирхгофа при B = BT. Условия существования [14] накладывают шесть связей на коэффициенты уравнений (1.1), в отличие от восьми связей в условиях Чаплыгина (1.4). Существование инвариантных соотношений дает возможность построения новых частных решений уравнений движения [13, 15, 16].
Ниже приведено описание всех случаев существования ЛИС уравнений Кирхгофа без требования симметрии оператора B. Получено простое представление семейства гамильтонианов, допускающих ЛИС, координатная форма условий существования и явная запись самого ЛИС. Для движения с линейным инвариантным соотношением выполнена редукция к уравнению Риккати. Показано, что если при невырожденной матрице A существует линейный интеграл, то уравнения Кирхгофа приводятся к случаю Кирхгофа.
2. Основные результаты. Производная ЛИС
в силу системы (1.1) должна удовлетворять условию
При замене переменных
(2.3)
${\mathbf{M}}\quad = {\mathbf{\tilde {M}}} + {\mathbf{\rho }} \times {\mathbf{\tilde {\gamma }}},\quad {\mathbf{\gamma }} = {\mathbf{\tilde {\gamma }}}$для переменных ${\mathbf{\tilde {M}}}$ и $\tilde {\gamma }$ получим уравнения Кирхгофа с матрицами коэффициентов ${\mathbf{\tilde {A}}}$ = A и
(2.4)
${\mathbf{\tilde {B}}} = {\mathbf{B}} - {\mathbf{V}}({\mathbf{\rho }}){\mathbf{A}},\quad\quad {\mathbf{\tilde {C}}} = {\mathbf{C}} - {\mathbf{V}}({\mathbf{\rho }}){\mathbf{AV}}({\mathbf{\rho }}) + {\mathbf{BV}}({\mathbf{\rho }}) - {\mathbf{V}}({\mathbf{\rho }}){{{\mathbf{B}}}^{T}}$Здесь V(a) оператор векторного умножения на вектор a, V(a)z ≡ a × z.
Отметим, что, учитывая возможность в задаче о движении твердого тела в жидкости выбора специальной системы координат, приводящей матрицу A к диагональному, а B – к симметрическому виду, иногда договариваются считать [4], что это приведение выполнено. Тем не менее, изучение случая B ≠ BT представляет интерес как в классической задаче Кирхгофа, когда отказ от условия B = BT позволяет привести гамильтониан системы, допускающей ЛИС к наиболее простому виду (2.12), так и в связанных с наличием подвижных внутренних масс неавтономных обобщениях уравнений Кирхгофа, когда подвижную систему координат естественно зафиксировать в самом теле.
При каноническом преобразовании (2.3) ЛИС (2.1) преобразуется к виду
(2.5)
$F = ({\mathbf{m}},{\mathbf{\tilde {M}}}) + ({\mathbf{m}} \times {\mathbf{\rho }} + {\mathbf{n}},\quad{\mathbf{\tilde {\gamma }}})$Ниже (Предложение 3) показано, что для существования ЛИС (2.1) необходимо выполнение условия
где a2 – собственное значение A такое, что a1 ≤ a2 ≤ a3 или a1 ≥ a2 ≥ a3.Случай, когда оператор A вырожденный, в работе не рассматривается, а при m ≠ 0 и (m, n) = 0 можно выбрать ρ так, чтобы выполнялось равенство n = ρ × m.
Таким образом, ЛИС (2.1) при a2 ≠ 0 можно привести к виду
Здесь и всюду далее считаем |m| = 1.
Ниже, в теореме 1, приведено описание всего семейства гамильтонианов, допускающих существование ЛИС (2.7). Следствием теоремы являются условия существования линейного интеграла. Показано, что при существовании интеграла (2.1) F = const (с m ≠ 0) уравнения Кирхгофа приводятся каноническим преобразованием к известному случаю Кирхгофа [2]. Связь ЛИС общего вида с ЛИС (2.7) позволяет дать описание семейства гамильтонианов, допускающих ЛИС (2.1) и получить координатную форму ЛИС и условий существования для общего случая.
Теорема 1. Если уравнения Кирхгофа обладают линейным инвариантным соотношением (2.1) (с m ≠ 0) и среднее собственное значение матрицы A не равно нулю, то существует каноническое преобразование (2.3), приводящее матрицы коэффициентов к виду
(2.8)
${\mathbf{\tilde {A}}} = {\mathbf{A}},\quad {\mathbf{\tilde {B}}} = {{{\mu }}_{b}}{\mathbf{E}} + {\mathbf{d}}{{{\mathbf{m}}}^{T}},\quad {\mathbf{\tilde {C}}} = {{{\mu }}_{c}}{\mathbf{E}} + {{{\nu }}_{c}}{\mathbf{m}}{{{\mathbf{m}}}^{T}}$Здесь m – орт нормали кругового сечения поверхности (z, ${\mathbf{\tilde {A}}}$z) = const, μb, μc, νc, d – некоторые параметры. В базисе (ei) собственных векторов матрицы A ЛИС F и множитель f записываются в виде
(2.10)
$f = ({\mathbf{p}},{\mathbf{M}}) + \langle {\mathbf{d}},{\mathbf{m}},\quad{\mathbf{\gamma }}\rangle $Слагаемые μbE, μcE в формулах (2.8) несущественны, они не изменяют вид системы (1.1). При выполнении условий теоремы 1 существует каноническое преобразование, позволяющее записать гамильтониан в виде
(2.12)
$H = \frac{1}{2}({\mathbf{A\tilde {M}}},\quad{\mathbf{\tilde {M}}}) + ({\mathbf{m}},{\mathbf{\tilde {M}}})({\mathbf{d}},\quad{\mathbf{\tilde {\gamma }}}) + {\nu }{{({\mathbf{m}},\quad{\mathbf{\tilde {\gamma }}})}^{2}}$Если в условии (2.2) f ≡ 0, то линейная функция (2.1) является интегралом. Из теоремы 1 получаем следующий результат.
Следствие 1. Если у уравнений Кирхгофа существует линейный интеграл
(2.13)
$({\mathbf{m}},\quad{\mathbf{M}}) + ({\mathbf{n}},\quad{\mathbf{\gamma }}) = {\text{const,}}\;\;{\text{m}} \ne {\text{0}}$(2.14)
${\mathbf{\tilde {A}}} = {\text{diag}}({{a}_{1}},{{a}_{1}},{{a}_{3}}),\quad\quad {\mathbf{\tilde {B}}} = {\text{diag}}({{b}_{1}},{{b}_{1}},{{b}_{3}}),\quad\quad {\mathbf{\tilde {C}}} = {\text{diag}}({{c}_{1}},{{c}_{1}},{{c}_{3}}),\quad {{\tilde {M}}_{3}} = {\text{const}}$Отметим, что преобразование (2.3) позволяет перейти к системе с симметричными матрицами коэффициентов; достаточно потребовать, чтобы параметр ρ удовлетворял условию AV(ρ) + V(ρ)A = B – BT, которое эквивалентно системе условий для компонент ρ:
Для случая B = BT при существовании линейного интеграла указано [13] линейное преобразование, приводящее к случаю Кирхгофа. Отсюда следует, что и общем случае B = BT система с линейным интегралом также приводится к случаю Кирхгофа. Ниже следствие 1 получено из теоремы 1.
Следствие 2. Если уравнения Кирхгофа (1.1) с невырожденной матрицей A допускают существование ЛИС (2.1) с m ≠ 0, то матрицы B, C можно представить в виде
(2.15)
${\mathbf{B}} = {{{\mu }}_{b}}{\mathbf{E}} - {{a}_{2}}{\mathbf{m}}{{{\mathbf{n}}}^{T}} + {\mathbf{n}}{{({\mathbf{m}} \times {\mathbf{p}})}^{T}} + {\mathbf{r}}{{{\mathbf{m}}}^{T}} + {\alpha }{\mathbf{V}}({\mathbf{m}})$(2.16)
$\, - {\alpha }({\mathbf{m}}{{({\mathbf{m}} \times {\mathbf{n}})}^{T}} + ({\mathbf{m}} \times {\mathbf{n}}){{{\mathbf{m}}}^{T}})$Здесь m – орт нормали кругового сечения поверхности (z, Az) = const, μb, μc, νc, α, r – произвольные параметры.
Если записать равенства (2.15), (2.16) в координатной форме в базисе собственных векторов A, то получим, при несимметричной матрице B, 15 равенств, содержащих 4 параметра μb, μc, νc, α, три компонента вектора r и три компонента n, связанных условием (m, n) = 0. После их исключения получаем систему из шести необходимых и достаточных условий существования ЛИС.
Следствие 3. Для существования при невырожденном операторе A ЛИС (2.1) с m ≠ 0 необходимо и достаточно выполнения условий
(2.17)
${{m}_{3}}({{a}_{1}}{{b}_{{12}}} + {{a}_{2}}{{b}_{{21}}})\quad = {{m}_{1}}({{a}_{2}}{{b}_{{23}}} + {{a}_{3}}{{b}_{{32}}})$(2.18)
${{m}_{1}}({{c}_{{22}}} - {{c}_{{33}}}) + {{m}_{3}}{{c}_{{13}}} = {{m}_{3}}{\alpha }{{n}_{2}} + \quad2{{m}_{1}}({{n}_{2}}{{r}_{2}} - {{n}_{3}}{{r}_{3}}) + $(2.19)
${{r}_{1}} = {{m}_{1}}\left( {{{b}_{{11}}} - {{b}_{{22}}}} \right) + {{m}_{3}}{{b}_{{13}}},\quad\quad\quad\quad{{r}_{3}} = {{m}_{3}}\left( {{{b}_{{33}}} - {{b}_{{22}}}} \right) + {{m}_{1}}{{b}_{{31}}}$(2.20)
$ - \frac{1}{{{{a}_{2}}}}({{m}_{1}}{{b}_{{12}}} + {{m}_{3}}{{b}_{{32}}}){{{\gamma }}_{2}} + \frac{1}{{{{a}_{3}}}}( - {{m}_{1}}{{b}_{{13}}} + {{m}_{3}}({{b}_{{11}}} - {{b}_{{22}}})){{{\gamma }}_{3}}$(2.21)
$ + \frac{1}{{{{a}_{2}}}}({{m}_{1}}{{m}_{3}}({{a}_{1}} + {{a}_{3}})({{b}_{{33}}} - {{b}_{{11}}}) + (m_{1}^{2} - m_{3}^{2})({{a}_{3}}{{b}_{{31}}} + {{a}_{1}}{{b}_{{13}}})){{{\gamma }}_{2}}$Известны [4, 5, 7] ЛИС для случая, когда два собственных значения оператора A совпадают. Условия существования такого ЛИС получим из общих условий (2.17) – (2.21), полагая a1 = a2 ≠ a3.
Следствие 4. Если A = diag(a1, a1, a3), a1 ≠ 0, a1 ≠ a3, то для существования ЛИС (2.1) с m ≠ 0 необходимо и достаточно выполнения условий
(2.22)
${{c}_{{23}}} = - \frac{1}{{{{a}_{1}}}}({{b}_{{32}}}({{b}_{{33}}} - {{b}_{{11}}}) + {{b}_{{31}}}{{b}_{{12}}}),\quad {{c}_{{13}}} = \frac{1}{{{{a}_{1}}}}({{b}_{{12}}}{{b}_{{32}}} - {{b}_{{31}}}({{b}_{{33}}} - {{b}_{{11}}}))$(2.23)
$F = {{M}_{3}} - \frac{1}{{{{a}_{1}}}}({{b}_{{31}}}{{{\gamma }}_{1}} + {{b}_{{32}}}{{{\gamma }}_{2}})$(2.24)
$f = \left( {{{b}_{{23}}} + \frac{{{{a}_{3}}}}{{{{a}_{1}}}}{{b}_{{32}}}} \right){{{\gamma }}_{1}} - \left( {{{b}_{{13}}} + \frac{{{{a}_{3}}}}{{{{a}_{1}}}}{{b}_{{31}}}} \right){{{\gamma }}_{2}}$Приведем еще координатную форму условий существования ЛИС (2.7).
Следствие 5. Для существования ЛИС (2.7) необходимо и достаточно выполнения условий
(2.25)
${{m}_{3}}({{b}_{{11}}} - {{b}_{{22}}}) = {{m}_{1}}{{b}_{{13}}},\quad\quad {{m}_{1}}({{b}_{{33}}} - {{b}_{{22}}}) = {{m}_{3}}{{b}_{{31}}}$При этом
(2.26)
$F = {{m}_{1}}{{M}_{1}} + {{m}_{3}}{{M}_{3}} = \sqrt {{{a}_{1}} - {{a}_{2}}} {{M}_{1}} + \sqrt {{{a}_{2}} - {{a}_{3}}} {{M}_{3}}$(2.27)
$f = p{{M}_{2}} + (\quad{{m}_{1}}{{b}_{{21}}} + {{m}_{3}}{{b}_{{23}}})({{m}_{3}}{{{\gamma }}_{1}} - {{m}_{1}}{{{\gamma }}_{3}}) + ({{b}_{{31}}} - {{b}_{{13}}}){{{\gamma }}_{2}}$Отметим еще исключенный выше случай m = 0.
Предложение 1. ЛИС F = (n, γ) существует при выполнении условий
3. Условия для матриц коэффициентов. Условие (2.2) эквивалентно следующей системе тождеств:
(3.1)
$\langle {\mathbf{m}},\quad{\mathbf{M}},\quad{\mathbf{AM}}\quad\rangle \equiv \quad({\mathbf{p}},{\mathbf{M}})({\mathbf{m}},\quad{\mathbf{M}})$(3.2)
$\langle {\mathbf{m}},\quad{\mathbf{M}},\quad{{{\mathbf{B}}}^{T}}{\mathbf{\gamma }}\rangle + \langle {\mathbf{m}},\quad{\mathbf{\gamma }},\quad{\mathbf{BM}}\rangle + \langle {\mathbf{n}},\quad{\mathbf{\gamma }},\quad{\mathbf{AM}}\rangle \equiv ({\mathbf{p}},{\mathbf{M}})({\mathbf{n}},\quad{\mathbf{\gamma }}) + ({\mathbf{q}},{\mathbf{\gamma }})({\mathbf{m}},\quad{\mathbf{M}})\quad$(3.3)
$\langle {\mathbf{m}},\quad{\mathbf{\gamma }},\quad{\mathbf{C\gamma }}\rangle \quad + \quad\langle {\mathbf{n}},\quad{\mathbf{\gamma }},\quad{{{\mathbf{B}}}^{T}}{\mathbf{\gamma }}\rangle \quad \equiv \quad({\mathbf{q}},{\mathbf{\gamma }})({\mathbf{n}},\quad{\mathbf{\gamma }})$Тождество (3.1) можно записать в виде (V(m)M, AM) ≡ (M, pmTM) и это тождество выполнено, только если оператор AV(m) – pmT является кососимметрическим. Аналогично, тождество (3.3) выполнено, только если оператор CTV(m) + BV(n) – qnT – кососимметрический. Тождество (3.2) можно записать так:
Это тождество имеет вид (M, Gγ) ≡ 0 и выполнено, только если G = 0.
Таким образом, условия выполнения тождеств (3.1)–(3.3) следующие
(3.4)
${\mathbf{AV}}({\mathbf{m}}) - {\mathbf{V}}({\mathbf{m}}){\mathbf{A}} = {\mathbf{p}}{{{\mathbf{m}}}^{T}} + {\mathbf{m}}{{{\mathbf{p}}}^{T}}$(3.5)
${{{\mathbf{B}}}^{T}}{\mathbf{V}}({\mathbf{m}}) - {\mathbf{V}}({\mathbf{m}}){{{\mathbf{B}}}^{T}} + {\mathbf{AV}}({\mathbf{n}}) = {\mathbf{p}}{{{\mathbf{n}}}^{T}} + {\mathbf{m}}{{{\mathbf{q}}}^{T}}$(3.6)
${\mathbf{CV}}({\mathbf{m}}) - {\mathbf{V}}({\mathbf{m}}){\mathbf{C}} + {\mathbf{BV}}({\mathbf{n}}) - {\mathbf{V}}({\mathbf{n}}){{{\mathbf{B}}}^{T}} = {\mathbf{n}}{{{\mathbf{q}}}^{T}} + {\mathbf{q}}{{{\mathbf{n}}}^{T}}$Рассмотрим равенство (3.4). Умножая обе его части слева и справа на m, получим условие
Запишем оператор A, удовлетворяющий условию (3.4), в виде
При условии (3.7) для оператора A0 из (3.4) получим условие
(3.8)
${{{\mathbf{A}}}_{0}}{\mathbf{V}}({\mathbf{m}}) - {\mathbf{V}}({\mathbf{m}}){{{\mathbf{A}}}_{0}} = 0$Это условие выполнено, только если симметрический оператор A0 имеет вид A0 = = μaE + νammT. Следовательно, оператор A, для которого выполнено тождество (3.1), можно записать в виде
(3.9)
${\mathbf{A}}\quad = \quad{{{\mu }}_{a}}{\mathbf{E}} + \quad{{{\nu }}_{a}}{\mathbf{m}}{{{\mathbf{m}}}^{T}}\quad + \quad{\mathbf{m}}{{({\mathbf{m}} \times {\mathbf{p}})}^{T}} + ({\mathbf{m}} \times {\mathbf{p}}){{{\mathbf{m}}}^{T}}$Записывая равенство (3.9) в базисе (ei), получим формулы (2.11) для p, m и следующие выражения для параметров μa, νa :
(3.10)
${{{\mu }}_{a}}\quad = \quad{{a}_{2}},\quad {{v}_{a}}\quad = {{a}_{1}} + {{a}_{3}} - 2{{a}_{2}}\quad$Вектор m – нормаль кругового сечения поверхности (z, Az) = const.
Форма записи (3.9) оператора A оказывается удобной при анализе условий существования ЛИС уравнений Кирхгофа и уравнений Пуанкаре–Жуковского [12–14]. Отметим, что в виде (3.9) можно записать любой симметрический оператор A: ${{\mathbb{R}}^{3}}$ ⇒ ${{\mathbb{R}}^{3}}$ и, таким образом, тождество (3.1) не накладывает никаких ограничений на вид оператора A.
Предложение 2. Для существования ЛИС (2.1) необходимо выполнение условия
Доказательство. Преобразуем условие (3.5). Обозначим
Разделяя в равенстве (3.5) симметричную и кососимметричную части, получим условия
(3.12)
${{{\mathbf{B}}}_{1}}{\mathbf{V}}({\mathbf{m}}) - {\mathbf{V}}({\mathbf{m}}){{{\mathbf{B}}}_{1}} = {\mathbf{Q}},\quad {\mathbf{V}}({\mathbf{m}}){{{\mathbf{B}}}_{2}} - {{{\mathbf{B}}}_{2}}{\mathbf{V}}({\mathbf{m}}) = {\mathbf{R}}$(3.13)
$2{\mathbf{Q}} = {\mathbf{V}}({\mathbf{n}}){\mathbf{A}} - {\mathbf{AV}}({\mathbf{n}}) + {\mathbf{p}}{{{\mathbf{n}}}^{T}} + {\mathbf{n}}{{{\mathbf{p}}}^{T}} + {\mathbf{m}}{{{\mathbf{q}}}^{T}} + {\mathbf{q}}{{{\mathbf{m}}}^{T}}$(3.14)
$2{\mathbf{R}} = - {\mathbf{V}}({\mathbf{n}}){\mathbf{A}} - {\mathbf{AV}}{\text{(}}{\mathbf{n}}) + {\mathbf{p}}{{{\mathbf{n}}}^{T}} - {\mathbf{n}}{{{\mathbf{p}}}^{T}} + {\mathbf{m}}{{{\mathbf{q}}}^{T}} - {\mathbf{q}}{{{\mathbf{m}}}^{T}}$Из первого равенства (3.12) получим (m, Qm) = 0. Это условие, при учете формулы (3.13), записывается в виде
Отсюда, используя представление оператора A в виде (3.9), получим условие (3.11).
Предложение 3. Для существования ЛИС (2.1) необходимо условие (2.6).
Доказательство. Из второго равенства (3.12) следует
Так как оператор B2 – кососимметрический, то получаем (e2, R(m × e2)) = 0. Из формул (3.14), (3.9) найдем 0 = (e2, R(m × e2)) = a2(m, n).
Условие (2.6), как было отмечено в разделе 2, позволяет при a2 ≠ 0 привести общий случай существования ЛИС (2.1) к частному случаю (2.7).
4. Доказательство теоремы 1 и ее следствий. Пусть уравнения (1.1) обладают ЛИС (2.1). В соответствии с доказанным выше предложением 3 должно выполнятся условие (m, n) = 0. Выполним преобразование (2.3), где
ЛИС (2.1) при учете формулы (2.5) преобразуется к виду (2.7), так как
Множитель в формуле (2.2) запишется в виде
(4.3)
$f = ({\mathbf{p}},\quad{\mathbf{\tilde {M}}}) + ({\mathbf{\tilde {q}}},{\mathbf{\tilde {\gamma }}}),\quad {\mathbf{\tilde {q}}} = {\mathbf{q}} + {\mathbf{p}} \times {\mathbf{\rho }}$Учитывая следующее из формул (2.11) условие (p, m) = 0, получим
Так как ${\mathbf{\tilde {A}}}$ = A, то параметры p, m, μa, νa остаются прежними.
Условия (3.5), (3.6) при ${\mathbf{\tilde {n}}}$ = 0 запишутся в виде
(4.5)
${{{\mathbf{\tilde {B}}}}^{T}}{\mathbf{V}}({\mathbf{m}}) - {\mathbf{V}}({\mathbf{m}}){{{\mathbf{\tilde {B}}}}^{T}} = {\mathbf{m}}{{{\mathbf{\tilde {q}}}}^{T}}$Предложение 4. Условия (4.5), (4.6) выполнены, только если операторы ${\mathbf{\tilde {B}}}$, ${\mathbf{\tilde {C}}}$ представимы в виде
(4.7)
${\mathbf{\tilde {B}}} = {{{\mu }}_{b}}{\mathbf{E}} + {\mathbf{\tilde {d}}}{{{\mathbf{m}}}^{T}} + {\beta }{\mathbf{V}}({\mathbf{m}}),\quad {\mathbf{\tilde {C}}} = {{{\tilde {\mu }}}_{c}}{\mathbf{E}} + {{{\tilde {\nu }}}_{c}}{\mathbf{m}}{{{\mathbf{m}}}^{T}}$Доказательство. Условие (4.6) совпадает с условием (3.8), оператор ${\mathbf{\tilde {C}}}$, удовлетворяющий этому условию, записывается в виде (4.7).
Представим оператор ${\mathbf{\tilde {B}}}$, удовлетворяющий условию (4.5), в виде
(4.8)
${\mathbf{\tilde {B}}} = {{{\mathbf{\tilde {B}}}}_{0}} + ({\mathbf{m}} \times {\mathbf{\tilde {q}}}){{{\mathbf{m}}}^{T}}$Отметим, что из формул (3.11), (4.4) следует (m, ${\mathbf{\tilde {q}}}$) = 0. Для оператора ${\mathbf{\tilde {B}}}$ из формул (4.5), (4.8) получим равенство
Любой оператор ${{{\mathbf{\tilde {B}}}}_{0}}$, удовлетворяющий этому равенству, можно записать в виде
Учитывая формулу (4.8), получаем представление оператора ${\mathbf{\tilde {B}}}$ в виде (4.7), где ${\mathbf{\tilde {d}}}$ = = νbm + m × ${\mathbf{\tilde {q}}}$ и тогда
Предложение 4 доказано.
Выполним в уравнениях Кирхгофа с матрицами коэффициентов ${\mathbf{\tilde {A}}}$, ${\mathbf{\tilde {B}}}$, ${\mathbf{\tilde {C}}}$, где ${\mathbf{\tilde {B}}}$, ${\mathbf{\tilde {C}}}$ заданы формулами (4.7), каноническое преобразование (2.3) при ρ = $\tilde {\alpha }$m. ЛИС (2.7) сохранит свой вид. Новые матрицы ${\mathbf{\tilde {A}'}}$, ${\mathbf{\tilde {B}'}}$, ${\mathbf{\tilde {C}'}}$ получим из формул (2.4), (3.9), (4.7). При этом
Так как μa = a2 ≠ 0, то, полагая $\tilde {\alpha }$ = β/a2, d = d + $\tilde {\alpha }$p, получим запись ${\mathbf{\tilde {B}}}{\text{'}}$ в виде (2.8). Учитывая равенство V2(m) = mmT – E, оператор ${\mathbf{\tilde {C}}}{\text{'}}$ также запишем в виде (2.8). Таким образом, показано, что если существует ЛИС (2.1), то при a2 ≠ 0 существует каноническое преобразование (2.3), где
приводящее к уравнениям Кирхгофа с ЛИС (2.7) и матрицами коэффициентов (2.8).Выражения (2.11) для параметров m, p следуют из представления оператора A в виде (3.9). Условие $\dot {F}$ = fF тождественно выполнено, если функции F, f заданы равенствами (2.9), (2.10), а матрицы коэффициентов – формулами (2.8). Теорема 1 доказана.
Получим следствие 1. Линейный интеграл (2.13) есть частный случай ЛИС (2.1) при f ≡ 0. Как показано в теореме 1, ЛИС всегда можно каноническим преобразованием привести к виду (2.7), а матрицы коэффициентов – к виду (2.8). Из формулы (2.10) следует, что для преобразованной системы условие f ≡ 0 выполнено тогда и только тогда, когда p = 0 и d || m. Учитывая формулы (2.11), получим, что p = 0, только если у оператора A имеются два совпадающих собственных значения. Положим a1 = a2 ≠ a3, тогда m = e3 и из формул (2.8) при d || m получим равенства (2.14), то есть в точности случай Кирхгофа.
Докажем следствие 2. Каноническое преобразование (2.3) с параметром ρ, заданным равенством (4.10), приводит уравнения Кирхгофа с ЛИС (2.1) и матрицами коэффициентов A, B, C к уравнениям с ЛИС (2.7) и матрицами коэффициентов, заданными формулами (2.8). Из формул (2.4), (2.8), (3.9) получаем представления матриц B, C в виде (2.15), (2.16), где
(4.11)
${\alpha } = {{a}_{2}}{\tilde {\alpha }},\quad {\mathbf{r}} = {\mathbf{d}} - {\tilde {\alpha }}{\mathbf{p}} + ({{a}_{2}} + {{{\nu }}_{a}}){\mathbf{n}} + \langle {\mathbf{m}},{\mathbf{n}},\quad{\mathbf{p}}\rangle {\mathbf{m}}$Отметим, что условия (2.15), (2.16) не только необходимы, но и достаточны для существования ЛИС (2.1). Можно проверить, что если матрицы B, C имеют вид (2.15), (2.16), то условия (3.5), (3.6) выполнены (а тогда выполнено и условие (2.2)) при
(4.12)
${\mathbf{q}}\quad = \quad{\mathbf{r}} \times {\mathbf{m}} + ({{a}_{1}} + {{a}_{3}} - {{a}_{2}}){\mathbf{m}} \times {\mathbf{n}} - ({\mathbf{n}},\quad{\mathbf{p}}){\mathbf{m}}$Получим теперь указанную в следствии 3 координатную форму ЛИС и условий его существования.
Найдем из равенства (2.15) элементы матрицы B в базисе (ei):
(4.13)
${{b}_{{13}}} = - {{a}_{2}}{{m}_{1}}{{n}_{3}} + p{{m}_{1}}{{n}_{1}} + {{m}_{3}}{{r}_{1}},\quad {{b}_{{31}}} = - {{a}_{2}}{{m}_{3}}{{n}_{1}} - p{{m}_{3}}{{n}_{3}} + {{m}_{1}}{{r}_{3}}$Должно также выполняться равенство
Имеем 10 связей с восемью параметрами μb, α, ni, ri. Исключение параметров дает две связи (2.17). Для параметров α, ni, ri из системы равенств (4.13), (4.14) получаем выражения (2.19). Если из записи элементов матрицы C, заданной равенством (2.16), исключить параметры μc, νc, то получим условия (2.18).
Явная форма записи (2.20) ЛИС получается при подстановке в формулу (2.1) значений ni из формул (2.19). Множитель f задан равенством (2.2), где p = pe2, а компоненты q находим из равенств (4.12), (2.19).
Приведенные в следствии 4 условия (2.22) существования ЛИС, запись F и f в виде (2.23), (2.24) получаются из формул (2.17) – (2.21) при m1 = 0, m3 = 1.
При n = 0 ЛИС записывается в виде (2.7). Приведенные в следствии 5 условия (2.25) для cij, получаются сразу из последних четырех условий (2.18) при ni = 0. Если в трех последних равенствах (2.19) положить n1 = n2 = n3 = 0, то получим три условия для bij. Система, составленная из этих трех условий и двух условий (2.17), эквивалентна системе первых четырех условий (2.25). Следствие 5 доказано.
5. Сопоставление с известными условиями существования линейных инвариантных соотношений. Рассмотрим известные случаи существования ЛИС и укажем их включение в описанный выше общий случай или его следствия.
1) Условия существования (1.4) ЛИС Чаплыгина (1.3) получим из условий (2.25) при B = BT. Отметим, что, если потребовать, чтобы оператор B, заданный формулой (2.15), был симметрическим, то получим α = 0, r || m. Формулы (2.15), (2.16) при n = 0 принимают вид
(5.1)
${\mathbf{B}} = {{{\mu }}_{b}}{\mathbf{E}} + {{{\nu }}_{b}}{\mathbf{m}}{{{\mathbf{m}}}^{T}},\quad {\mathbf{C}} = {{{\mu }}_{c}}{\mathbf{E}} + {{{\nu }}_{c}}{\mathbf{m}}{{{\mathbf{m}}}^{T}}$Здесь m – нормаль кругового сечения эллипсоида A. Возможность записи, в случае B = BT, операторов в виде (5.1) является необходимой и достаточной для существования ЛИС (1.3).
2) В работе [10] указано, что для гамильтониана
(5.2)
$H = \frac{1}{2}{{m}^{2}}{{M}^{2}} + \frac{1}{2}{{({\mathbf{m}},{\mathbf{M}})}^{2}} + \langle {\mathbf{m}} \times {\mathbf{n}},\quad{\mathbf{M}},\quad{\mathbf{\gamma }}\rangle $Гамильтониан (5.2) задан матрицами
В этом случае m – собственный вектор A. Считая |m|2 = 1, обозначим m = e3, тогда
Все условия (2.22) выполнены. ЛИС (2.1) записывается в виде (2.23).
3) Для гамильтониана
(5.3)
$H = {{c}_{1}}({\mathbf{a}},{\mathbf{b}}){{M}^{2}} + {{c}_{2}}({\mathbf{a}},{\mathbf{M}})({\mathbf{b}},{\mathbf{M}}) + \langle {\mathbf{b}},\quad{\mathbf{M}},\quad{\mathbf{\gamma }}\rangle $Для сопоставления с условиями (2.25) запишем матрицы операторов в базисе собственных векторов оператора A. Для гамильтониана (5.3) имеем
(5.5)
${\mathbf{A}} = 2{{c}_{1}}({\mathbf{a}},{\mathbf{b}}){\mathbf{E}} + {{c}_{2}}({\mathbf{a}}{{{\mathbf{b}}}^{T}} + {\mathbf{b}}{{{\mathbf{a}}}^{T}}),\quad {\mathbf{B}} = {\mathbf{V}}({\mathbf{b}}),\quad {\mathbf{C}} = 0$Если векторы a и b коллинеарны, то они являются собственными векторами A. Полагая b = e3, получим
Условия (2.22) выполнены. Из формулы (2.24) следует f ≡ 0 и формула (2.23) в случае a || b задает не ЛИС, а линейный интеграл.
Рассмотрим теперь основной случай, когда векторы a, b не коллинеарны. Собственными векторами оператора A, заданного равенством (5.5), являются
(5.6)
${{{\mathbf{l}}}_{1}} = {{{\mathbf{a}}}^{0}} + {{{\mathbf{b}}}^{0}},\quad {{{\mathbf{l}}}_{2}} = {{{\mathbf{a}}}^{0}} \times {{{\mathbf{b}}}^{0}},\quad {{{\mathbf{l}}}_{3}} = {{{\mathbf{a}}}^{0}} - {{{\mathbf{b}}}^{0}}$Собственные значения заданы равенствами
(5.7)
${{a}_{{1,3}}} = ab(2{{c}_{1}}({{{\mathbf{a}}}^{0}},{{{\mathbf{b}}}^{0}}) + {{c}_{2}}(({{{\mathbf{a}}}^{0}},{{{\mathbf{b}}}^{0}}) \pm 1)),\quad {{a}_{2}} = 2ab{{c}_{1}}({{{\mathbf{a}}}^{0}},{{{\mathbf{b}}}^{0}})$Обозначив (a0, b0) = cos2α из формул (5.6), (5.7) получим
(5.8)
$\frac{{\Delta {{a}_{3}}}}{{\Delta {{a}_{2}}}} = - {\text{co}}{{{\text{s}}}^{2}}{\alpha },\quad \quad\frac{{\Delta {{a}_{1}}}}{{\Delta {{a}_{2}}}} = - {\text{si}}{{{\text{n}}}^{2}}{\alpha },\quad l_{1}^{2} = 4{\text{co}}{{{\text{s}}}^{2}}{\alpha },\quad l_{3}^{2} = 4{\text{si}}{{{\text{n}}}^{2}}{\alpha }$Пусть ei = ${\mathbf{l}}_{i}^{0}$. Из формул (5.6), (5.8) следует
Векторы a0 и b0, удовлетворяющие последним равенствам, являются нормалями круговых сечений эллипсоида A. Запись матрицы A в виде (5.5) эквивалентна следующей записи, использующей две различные нормали к плоскостям круговых сечений A:
В таком виде можно представить любую симметрическую матрицу 3 × 3.
Положим b0 = m = m1e1 + m3e3, тогда ЛИС (5.4) запишется в виде (2.26). Из формулы (5.5) следует
Учитывая приведенное в предложении 4 представление матриц B, C в виде (4.7), гамильтониан (5.3) можно дополнить следующим образом, также допускающим ЛИС (5.4):
Здесь ν, s – дополнительные произвольные параметры. Каноническим преобразованием (2.3) при ρ = κb, сохраняющим ЛИС (5.4), невозможно привести данный гамильтониан к виду (5.3).
4) Известно [5], что существует ЛИС, если матрицы коэффициентов уравнения (1.1) заданы равенствами A = diag(1, 1, 2)
Все условия следствия 4 выполнены, формулы (2.23), (2.24) дают
Этот же случай преобразуется [4] к виду со следующими ненулевыми элементами:
Условия (2.22) выполнены и F = M3, f = –αγ2.
5) Кубичный интеграл при условии (M, γ) = 0 существует, если [7]:
Условия (2.22) выполнены, F = M3 + a1γ1 + a2γ2, f = –2a2γ1 + 2a1γ2. Кубичный интеграл записывается [7] в виде произведения ЛИС и полинома второй степени.
6. Редукция к уравнению Риккати. Пусть существует ЛИС (2.1) и выполнено каноническое преобразование, приводящее матрицы коэффициентов к виду (2.8). Рассмотрим семейство частных решений, заданных инвариантным соотношением (m, ${\mathbf{\tilde {M}}}$) = 0.
Выберем базис l1 = m, l2 = e2, l3 = m × e2 и обозначим Mi = (${\mathbf{\tilde {M}}}$, li), γi = ($\tilde {\gamma }$, li). Учитывая инвариантное соотношение M1 = 0, уравнения Кирхгофа запишем в виде
(6.1)
${{\dot {M}}_{2}} = g{{M}_{3}} + {\nu }{{{\gamma }}_{1}}{{{\gamma }}_{3}},\quad {{\dot {M}}_{3}} = - g{{M}_{2}} - {\nu }{{{\gamma }}_{1}}{{{\gamma }}_{2}},\quad g = p{{M}_{3}} + ({\mathbf{d}},{\mathbf{\gamma }})$Полученная система обладает интегралами (1.2), имеющими вид
(6.2)
${{M}_{2}}{{\gamma }_{2}} + {{M}_{3}}{{\gamma }_{3}} = {{c}_{1}},\quad \gamma _{1}^{2} + \gamma _{2}^{2} + \gamma _{3}^{2} = {{c}_{2}},\quad M_{2}^{2} + M_{3}^{2} - \mu \gamma _{1}^{2} = {{c}_{3}}$Здесь μ = –ν/a2. Третий из интегралов (6.2) получен из гамильтониана (2.12), где, с учетом формулы (3.9):
Учитывая тождество
(6.3)
${{{\dot {\gamma }}}_{1}} = G({{{\gamma }}_{1}}),\quad {{G}^{2}}({{{\gamma }}_{1}}) = a_{2}^{2}({{c}_{2}} - {\gamma }_{1}^{2})({{c}_{3}} + {\mu \gamma }_{1}^{2}) - {{a}_{2}}c_{1}^{2}$Решение системы (6.2) относительно M2, M3 можно записать в виде, аналогичном записи [4] в случае Гесса для уравнений Эйлера–Пуассона
Из системы (6.1) следует
Это уравнение, полагая
Для φ(γ1) получаем уравнение
Стандартную запись уравнения Риккати получим при замене переменной
Работа выполнена при частичной финансовой поддержке РФФИ (грант № 16-01-00220).
Список литературы
Ламб Г. Гидродинамика. ОГИЗ, Гостехиздат, 1947. 928 с. Lamb H. Hydrodynamics, ed. 6-th. N.Y., Dover publ., 1945.
Кирхгоф Г. Механика. Лекции по математической физике. М.: АН СССР, 1962. 402 с. Kirchhoff G.R. Vorlesungen über mathematische Physik. Mechanik. Leipzig: Teubner, 1876.
Clebsch A. Über die Bewegung eines Körpers in einer Flüssigkeit. Math. Annalen, 1871. Bd. 3. S. 238–262.
Борисов А.В., Мамаев И.С. Динамика твердого тела. Гамильтоновы методы, интегрируемость, хаос. Москва, Ижевск: Ин-т компьют. исслед., 2005. 576 с.
Соколов В.В. Новый интегрируемый случай для уравнений Кирхгофа // Теор. и мат. физика. 2001. Т. 129. № 1. С. 31–37.
Чаплыгин С.А. О некоторых случаях движения твердого тела в жидкости. Собр. соч. Т. 1. М.; Л.: Гостехиздат. 1948. Статья первая. С. 13–193. Статья вторая. С. 194–311. (Изд. 1-е: Мат. сборник Кружка любителей мат. наук, 1987. Т. 20. Вып. 1. С. 115–170. Вып. 2. С. 173–246.)
Соколов В.В., Цыганов А.В. Пары Лакса для деформированных волчков Ковалевской и Горячева–Чаплыгина // Теор. и мат. физика. 2002. Т. 131. № 1. С. 118–125.
Борисов А.В., Мамаев И.С., Соколов В.В. Новый интегрируемый случай на so(4) // Докл. РАН. 2001. Т. 381. № 5. С. 614–615.
Borisov A.V., Mamaev I.S. Generalization of the Goryachev–Chaplygin case // Regular and Chaotic Dynamics. 2002. V. 7. № 1. P. 21–30.
Sokolov V.V., Wolf T. Integrable quadratic classical Hamiltonians on so(4) and so(3, 1) // J. Physics A: Mathematical and General. 2006. V. 39. № 8. P. 1915–1926.
Ольшанский В.Ю. Об одном новом линейном инвариантном соотношении уравнений Пуанкаре–Жуковского // ПММ. 2012. Т. 76. Вып. 6. С. 883–894.
Ольшанский В.Ю. Линейные инвариантные соотношения уравнений Пуанкаре–Жуковского // ПММ. 2014. Т. 78. Вып. 1. С. 29–45.
Ольшанский В.Ю. Частные линейные интегралы уравнений Пуанкаре–Жуковского (общий случай) // ПММ. 2017. Т. 81. Вып. 4.
Ольшанский В.Ю. Линейные инвариантные соотношения уравнений Кирхгофа // ПММ. 2015. Т. 79. Вып. 4. С. 476–497.
Горр Г.В. Инвариантные соотношения и частные решения уравнений динамики твердого тела // ПММ. 2017. Т. 81. Вып. 4.
Узбек Е.К. Полурегулярные прецессии второго типа гиростата под действием потенциальных и гироскопических сил // Изв. РАН. МТТ. 2006. № 4. С. 31–41.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела