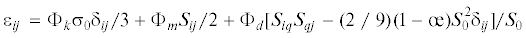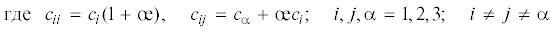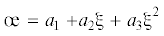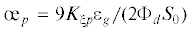Известия РАН. Механика твердого тела, 2019, № 1, стр. 50-62
О методике определения модуля объемной упругости и параметров, учитывающих разрыхление и изменение упругости композитов, основанной на тензорно-нелинейных уравнениях
К. Ф. Комков *
Военно-технический университет
Балашиха, Россия
* E-mail: 06kfk38@mail.ru
Поступила в редакцию 21.05.2017
После доработки 21.05.2017
Принята к публикации 29.01.2018
Аннотация
Проведен анализ уравнений связи девиатора деформаций с девиатором напряжений В.В. Новожилова, содержащих в себе неопределенность в виде дополнительной характеристики, названной фазой подобия девиаторов, которая является ограничением к непосредственному применению их для обработки опытных данных. Преобразование уравнений позволило придать материальным функциям физический смысл характеристик сдвига в площадках с главными касательными напряжениями и найти соотношения для обобщенного модуля сдвига и фазы, которые снимают отмеченное ограничение и дают возможность отражать влияние формоизменения на объемную деформацию и их взаимозависимость.
Преобразование исходных уравнений, включающих в себя уравнение связи средней деформации с инвариантами тензора напряжений, приведены к виду, характерному для уравнений анизотропной среды, которые дают возможность найти другой вариант уравнения для средней (объемной) деформации. Этот математический аппарат позволил разработать методику определения всех характеристик упругости, включая модули и податливости, способные отражать эффект разрыхления вследствие разрыва связей и изменения взаимодействия между элементами структуры композитных материалов, а так же изменения упругости.
По начальным значениям модулей объемной упругости, названных “кажущимися”, поскольку они характеризуют не жесткость среды, а ее изменение, определяются три параметра изменяющейся упругости. Последние являются отношением “классического” модуля, принятого величиной постоянной при изменении средней деформации, к “кажущимся” модулям. Они дают возможность оценить возникшую деформационную анизотропию и упругость, сохранившуюся и приобретенную в результате изменения состояния связей.
Удовлетворительное согласие результатов расчетов упругой части объемной деформации и дополнительной (дилатансии) по исходному уравнению и найденному после преобразования, включающему податливости объемной упругости и параметр разрыхления, с результатами испытаний явилось проверкой проведенных преобразований. Показано, что основной и единственной причиной изменения упругости, разномодульности и анизотропии является эффект разрыхления.
1. Введение. Наиболее заметной особенностью композитных материалов является их склонность к изменению структуры: размягчению и разрыхлению даже при малых нагрузках. Эти эффекты проявляют себя нелинейной зависимостью напряжений от деформации и отношением между деформациями в разных направлениях при испытаниях на растяжение и сжатие. Достаточно надежную информацию об объемной деформации дают зависимости коэффициента поперечной деформации от продольной. Проблеме связи разрыхления с характеристиками материала посвящено множество экспериментальных работ, выполненных известными исследователями, о которых можно узнать в книге Дж.Ф. Белла [1]. В более поздние годы ее изучению посвящены работы И. Баушингера, П.В. Бриджмена, Г.С. Писаренко, А.М. Жукова, В.В. Новожилова [2] и других. Общий вывод, следующий из их анализа, сводится к тому, что испытания сложных сред обнаруживают снижение начального значения коэффициента поперечной деформации при растяжении, тогда как при сжатии он растет.
2. Об обзоре работ по поставленной проблеме. Широкое внедрение композитных материалов началось в конце прошлого столетия и в те же годы появилось множество работ, освещающих их механические свойства, в том числе обзорных, среди которых достойное место занимают работы Е.В. Ломакина [3], посвященные описанию разрыхления мрамора, скальных сред и искусственных материалов, где также констатируется аналогичное поведение технических характеристик с ростом нагрузки. Эффект разрыхления может учитываться и тензорно-линейными уравнениями, как в работе [3], где все характеристики для сложных сред определяются из условия потенциальности соотношений между деформациями и напряжениями. Их выражения предопределяются выбором конкретного вида потенциала.
В данной работе для учета отмеченных эффектов найдено такое преобразование уравнений связи тензора деформаций с тензором напряжений, которое дало возможность вывода общих формул для всех характеристик упругости. Последние, представленные для главных деформаций, дали возможность не только определять объемную деформацию и согласовать результаты расчетов с опытными данными, но более отчетливо описать и представить внутренние процессы, сопровождающие деформацию композитных материалов.
Цель данной работы состоит в том, чтобы наиболее полно раскрыть возможности тензорно-нелинейных уравнений В.В. Новожилова: преобразовать их к виду, удобному для формулировки соотношений, определяющих все материальные функции для придания им физического смысла, возможности анализа и обработки результатов испытаний. На их основе разработать методику расчета всех характеристик, в том числе модулей продольной и объемной упругости и соответствующих податливостей, а так же параметров, характеризующих разрыхление структуры и изменение упругих свойств материалов с ростом нагрузки, учитывающих зависимость объемной деформации от формоизменения.
3. О деформационных свойствах зернистых композитов. Разработка методик проведена по результатам исследований двух разных композитов. Первый наполненный полимерный материал, называемый далее ВНПМ-1, является отвердевшей механической смесью минерального наполнителя с полимером, второй также является смесью, но с наполнителем в виде металлических частиц, ВНПМ-2. Результаты испытаний и сведения об их свойствах опубликованы в работах [5] и [6].
Оба материала обладают разномодульностью, которая уточняет их поведение наличием расхождения начальных продольных модулей и коэффициентов поперечных деформаций при растяжении и сжатии, определяемых при значениях деформаций близких к нулю. Кроме того, они проявляют зависимость упругих свойств от времени, поэтому в данной работе используются результаты испытаний, полученные при одной скорости деформации, чтобы освободиться далее от ошибок, связанных с временными эффектами.
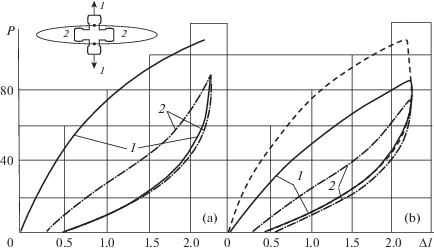
Первый композит имеет при нормальной температуре высокую податливость, разрушение его происходит при деформациях ~15%. Для исследований используются только участки диаграмм, ограниченные значением продольной деформации. Нелинейность диаграмм композита наглядно представлена результатами испытаний крестообразных образцов при повторном растяжении. Главная цель испытаний состояла в оценке изменения внутренних связей и упругих свойств от величины деформации, измеряемой тензометром. Максимальная деформация цикла составляет ~6%.
На фиг. 1,a приведена кривая 1 – восходящая ветвь диаграммы при первом цикле активной деформации по оси 1–1, которая представляет исходные свойства материала и кривая 2 – диаграмма второго цикла, где сила в H, Δl – удлинение в миллиметрах. При разгрузке кривая резко снижается, что говорит о существенном снижении количества “слабых” связей, разрушающихся при малых деформациях, меньших 2. Восходящая ветвь второго цикла иллюстрирует сопротивление оставшихся “длинных” и восстановившихся “слабых” связей. На фиг. 1,b кривая 1 является восходящей ветвью диаграммы испытания образца при первом цикле по оси 2–2. Для сравнения приведена диаграмма (штриховая), отмечающая исходные свойства композита. Разница диаграмм первых циклов по разным направлениям говорит о том, что разрыв связей происходит и в поперечном направлении. Первая кривая показывает, что “слабые” связи по направлению оси 2–2 частично сохраняются.
Разница диаграмм растяжения по оси 1–1 и 2–2 (восходящие ветви первого и второго циклов) представляют реальную, “настоящую” деформационную анизотропию, что отмечал В.В. Новожилов в работе [2]. Разрушение композита ВНПМ-2 происходит при малых деформациях, ~2%. При сжатии цилиндрического образца со сплошным сечением восходящая ветвь диаграммы первого цикла до ε = 0.4% является тоже нелинейной. Разгрузка с большой остаточной деформацией и восходящие ветви двух последующих циклов показывают меньшую нелинейность при заметно большем начальном продольном модуле упругости. Такие испытания дают возможность выявить возрастание числа связей при сжатии композита ВНПМ-2.
В настоящей работе, как и в работе [7], для второго композита используется подход, названный “экстраполяцией”. “Опытные” данные за предельными деформациями для простого растяжения и чистого сдвига принимались с помощью касательных модулей для сжатия.
4. Анализ тензорно-нелинейных уравнений В.В. Новожилова. Для описания деформации зернистых композитов, считая их изотропными, использовались тензорно-нелинейные уравнения связи девиатора деформаций De с девиатором напряжений Dσ:
(4.1)
${{\varepsilon }_{{ij}}} - \frac{1}{3}{{\hat {e}}_{1}}{{\delta }_{{ij}}} = \frac{1}{{2G}}\left[ {\frac{{{\text{cos}}\left( {2{\xi } + {\psi }} \right)}}{{{\text{cos}}3{\xi }}}{{S}_{{ij}}} + \sqrt {\frac{3}{{{{{\hat {S}}}_{2}}}}} \frac{{{sin\omega }}}{{{\text{cos}}3{\xi }}}\left( {{{S}_{{i\alpha }}}{{S}_{{\alpha j}}} - \frac{2}{3}{{{\hat {S}}}_{2}}{{{\delta }}_{{ij}}}} \right)} \right]$Покажем, что обобщенный модуль упругости G и фазу подобия девиаторов ω можно выразить через коэффициенты при тензорных аргументах
(4.2)
$X = \frac{1}{{2G}}\frac{{{\text{cos}}(2{\xi } + {\psi })}}{{{\text{cos}}3{\xi }}},\quad Y = \frac{1}{{2G}}\sqrt {\frac{3}{{{{{\hat {S}}}_{2}}}}} \frac{{{sin\omega }}}{{{\text{cos}}3{\xi }}} = \frac{1}{{2G}}\frac{3}{{{{S}_{0}}}}\frac{{{sin\omega }}}{{{\text{cos}}3{\xi }}}$Для этого воспользуемся уравнениями (4.1), представленными для главных компонент девиатора деформаций
Коэффициентам X и Y можно придать однозначный физический смысл и вывести формулы для их определения по сдвиговым характеристикам материала. Используя три сдвиговые податливости ϕi = γi/τi в площадках с главными касательными напряжениями τi = (Sj – Sα)/2, где γi = ej – eα – главные сдвиги, уравнения (4.3) позволяют найти три податливости сдвигу ϕi = 2(X – $\hat {Y}$ci) (величины обратные модулю сдвига), где $\hat {Y}$ = YS0/3. Учитывая, что сумма (c1 + c2 + c3) = 0, из соотношений для податливости находим их среднее значение:
Среднеквадратическое отклонение от средней податливости принимает вид
(4.5)
${{{\Phi }}_{d}} = {{\{ [{{\left( {{{{\Phi }}_{m}} - {{\phi }_{1}}} \right)}^{2}} + {{\left( {{{{\Phi }}_{m}} - {{\phi }_{2}}} \right)}^{2}} + {{\left( {{{{\Phi }}_{m}} - {{\phi }_{1}}} \right)}^{2}}]3{\text{/}}8\} }^{{1/2}}} = 3\hat {Y}$Таким образом, анализ уравнений (4.1) позволил, без каких-либо допущений, освободиться от неопределенности и найти подход к определению характеристик формоизменения Φm и Φd, которые уже нашли применение для разных материалов, например, серых чугунов [7], поэтому и далее будут оставаться в тех же обозначениях:
(4.6)
${{{\Phi }}_{m}} = 2X = \frac{{{\text{cos}}(2{\xi } + {\psi })}}{{G{\text{cos}}3{\xi }}}\quad {{{\Phi }}_{d}} = \frac{1}{3}\hat {Y} = \frac{{{sin\omega }}}{{2G{\text{cos}}3{\xi }}}$Для установления связи между интенсивностью деформаций и интенсивностью напряжений необходимо найти три разности главных значений девиатора деформаций:
(4.7)
${{e}_{i}} - {{e}_{j}} = \frac{{{{S}_{0}}}}{3}({{c}_{i}} - {{c}_{j}})(X - \hat {Y}{{c}_{\alpha }})$(4.8)
${{({{e}_{i}} - {{e}_{j}})}^{2}} = \frac{{S_{0}^{2}}}{9}{{({{c}_{i}} - {{c}_{j}})}^{2}}({{X}^{2}} + 2X\hat {Y}{{c}_{\alpha }} + {{\hat {Y}}^{2}}c_{\alpha }^{2})$Окончательно связь между интенсивностью деформаций и интенсивностью напряжений сводится к уравнению:
(4.9)
${{e}_{0}} = \frac{{2{{S}_{0}}}}{3}{{[({{X}^{2}} + 2X\hat {Y}{\text{sin}}3{\xi } + {{\hat {Y}}^{2}})]}^{{1/2}}}$Оно приводит к обобщенной податливости
(4.10)
${{{\Phi }}_{{\xi }}} = \frac{{3{{e}_{0}}}}{{{{S}_{0}}}} = {{[{\Phi }_{m}^{2} + (4{\text{/}}3){{{\Phi }}_{m}}{{{\Phi }}_{d}}\sin 3{\xi } + (4{\text{/}}9){\Phi }_{d}^{2}]}^{{1/2}}}$(4.11)
${\omega } = {\text{arctg}}\frac{{\hat {Y}{\text{cos}}3{\xi }}}{{X - \hat {Y}{\text{sin}}3{\xi }}} = {\text{arctg}}\frac{{2{{{\Phi }}_{d}}{\text{cos}}3{\xi }}}{{(3{{\Phi }_{m}} - 2{{\Phi }_{d}}\sin 3\xi )}}$Таким образом, уравнения (4.1) для компонент девиатора деформаций, используя соотношения (4.6), можно привести к другому виду
(4.12)
${{e}_{{ij}}} = ({{\Phi }_{m}}{\text{/}}2){{S}_{{ij}}} + {{\Phi }_{d}}({{S}_{{i\alpha }}}{{S}_{{\alpha j}}} - 2{\text{/}}9S_{0}^{2}{{\delta }_{{ij}}}){\text{/}}{{S}_{0}},\quad (i,j,\alpha = 1,2,3)$5. Определение характеристик формоизменения. Для обоих композитов диаграммы S0 ~ e0 для трех напряженных состояний представляют собой плавно возрастающие кривые. Диаграммы и данные о коэффициентах поперечных деформаций при растяжении и сжатии дают возможность подготовить дискретные значения переменных величин: S0, σ0, e0, ε0, где i = p, c. Они, а также податливости Φq = 3e0q/S0q, где q – номер опытной точки вдоль диаграммы или кривой, включены в программу для обработки результатов испытаний. Графическое отображение результатов расчетов удобно представлять в виде функций деформации ε, изменяющейся с постоянным шагом Δε. Общие формулы для определения характеристик формоизменения вытекают из соотношения (4.6)
(5.1)
${{{\Phi }}_{m}} = {{{\Phi }}_{{\xi }}}\cos (2{\xi } + {\psi }){\text{/}}\cos 3{\xi \;} = {{\phi }_{i}}{\text{/}}3$(5.2)
${{{\Phi }}_{d}} = 3{{{\Phi }}_{{\xi }}}\sin ({\xi } - {\psi }){\text{/}}(2\cos 3{\xi }) = {{\{ [{{({{\phi }_{j}} - {{\phi }_{{\alpha }}})}^{2}}]{\text{/}}8\} }^{{1/2}}}$Для упрощения расчетов принято, что обобщенная податливость ${{{\Phi }}_{{\xi }}}$ является заранее заданной функцией
(5.3)
${{{\Phi }}_{{\xi }}} = {{a}_{1}} - {{a}_{2}}{\text{sin}}3{\xi } + {{a}_{3}}{{({\text{sin}}3{\xi })}^{2}}$Ее коэффициенты определяются по значениям податливостей, вычисленным по результатам испытаний, соответствующих растяжению, чистому сдвигу и сжатию Φqp, Φqτ и Φqc. Эта функция позволяет для каждого уровня q расставить эти податливости к углам ξ равным –π/6, 0, π/6. Следует отметить, что диаграммы для чистого сдвига не всегда могут быть в наличии или они получены при испытаниях с помощью другой оснастки и способа измерения деформаций.
Для восстановления отсутствующей информации иногда можно воспользоваться приближенными соотношениями. Из соотношения (4.10) для: растяжения, сжатия и чистого сдвига, находим выражения для соответствующих податливостей: ${{{\Phi }}_{{{\xi }p}}} = {{{\Phi }}_{m}}$ + + 2/3Φd, ${{{\Phi }}_{{{\xi }c}}} = {{{\Phi }}_{m}} - 2{\text{/}}3{{{\Phi }}_{d}}$ и ${{{\Phi }}_{{{\xi \tau }}}} = {{[{\Phi }_{m}^{2} + 4{\text{/}}9{\Phi }_{d}^{2}]}^{{1/2}}}$. При условии независимости Φm и Φd от угла ξ, сумма квадратов первых двух равна удвоенному квадрату третьей податливости. Учитывая, что Φξi = 3e0i/S0i, где i = p, c, τ, из этого равенства находим формулу для определения интенсивности напряжений при сдвиге
(5.4)
${{S}_{{0\tau }}} = \sqrt 2 {{S}_{{0p}}}{{S}_{{0c}}}{\text{/}}{{[{{({{S}_{{0p}}}{{e}_{{0c}}}{\text{/}}{{e}_{{0\tau }}})}^{2}} + {{({{S}_{{0c}}}{{e}_{{0p}}}{\text{/}}{{e}_{{0\tau }}})}^{2}}]}^{{1/2}}}$Начальным шагом к определению характеристик формоизменения Φm и Φd является расчет по вторым равенствам соотношений (5.1) и (5.2) для растяжения (ξ = –π/6, приняв ϕi = Φqi по результатам испытаний, где i = p, c, τ. При всех индексах q отношение φ = Φd/Φm становится единым для любого угла ξ при использовании соотношения (5.3), поскольку такое упрощение приводит к подобию характеристик. Для других углов ξ определяется фаза подобия девиаторов по (4.11), угол ψ и средняя податливость Φm по первому равенству формулы (5.1), а среднеквадратическая податливость устанавливается по формуле Φd = φΦm.
6. Об уравнениях связи средней (объемной) деформации с инвариантами тензора напряжения. Описание общей объемной деформации, как суммы упругой ее части и дилатансии, предлагается принять в виде
где величина Kξ, используется ниже, как теоретический модуль объемной упругости. Второе равенство представлено, как отношение некоторой функции к модулю. Аргументами этой функции являются среднее напряжение и интенсивность напряжений с коэффициентами: (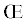 =
= 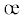 Kξ, где
Kξ, где 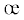 – параметр разрыхления и Φd – среднеквадратическая податливость, отражающая зависимость объемной деформации от
формоизменения.
– параметр разрыхления и Φd – среднеквадратическая податливость, отражающая зависимость объемной деформации от
формоизменения.
Второе равенство в уравнении (6.1) призвано показать, что оно не противоречит идеи В.В. Новожилова в работе [2], где объемная деформация предполагается функцией инвариантов тензора напряжений. В предложенном уравнении, объемная деформация так же зависит, от инвариантов σ0, S0 и от параметров, зависящих от угла ξ. В частном случае, при всестороннем растяжении или сжатии, уравнение (6.1) принимает выражение закона линейной теории упругости, ε0 = σ0/3K, в котором K – “классический” модуль объемной упругости, определяемый по результатам испытания на растяжение.
7. Вывод уравнений связи деформаций с напряжениями для определения технических характеристик. Математическая модель материала включает в себя тензорно-нелинейные уравнения связи деформаций с напряжениями:
где Φk = 1/Kξ. Они представляют собой сумму: уравнение связи девиатора деформаций с девиатором напряжений (4.12) и уравнение связи средней (объемной) деформации с инвариантами напряжений (6.1). Если уравнения (7.1) записать для главных деформаций, то они приводятся к виду, характерному для уравнений, описывающих деформацию анизотропной среды [8]. Для этого предварительно необходимо выразить их тензорные аргументы и инвариантные величины в главных напряжениях.В качестве примера приводим преобразование третьего слагаемого с индексом 1: Φd[$S_{1}^{2}$ – 2$S_{0}^{2}$/9]/S0 = 3Φd[σ1S1 + σ2S3 + σ3S2]/9S0. Величина 2Φd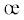 S0/9 преобразуется аналогично. Она учитывает влияние разрыхления на технические характеристики.
Принимая во внимание, что ci = 3Si/S0 преобразование приводит к системе уравнений, которые удобно представить в матричном
виде:
S0/9 преобразуется аналогично. Она учитывает влияние разрыхления на технические характеристики.
Принимая во внимание, что ci = 3Si/S0 преобразование приводит к системе уравнений, которые удобно представить в матричном
виде:
(7.2)
$\left\{ {\begin{array}{*{20}{c}} {{{{\varepsilon }}_{1}}} \\ {{{{\varepsilon }}_{2}}} \\ {{{{\varepsilon }}_{3}}} \end{array}} \right\} = \left( {\begin{array}{*{20}{c}} {{{a}_{{11}}}}&{{{a}_{{12}}}}&{{{a}_{{13}}}} \\ {{{a}_{{21}}}}&{{{a}_{{22}}}}&{{{a}_{{23}}}} \\ {{{a}_{{31}}}}&{{{a}_{{32}}}}&{{{a}_{{33}}}} \end{array}} \right)\left\{ {\begin{array}{*{20}{c}} {{{{\sigma }}_{1}}} \\ {{{{\sigma }}_{2}}} \\ {{{{\sigma }}_{3}}} \end{array}} \right\}\quad$Каждая компонента матрицы или их комбинации представляют технические характеристики для любого уровня нагрузки
(7.3)
${{a}_{{ii}}} = E_{i}^{{ - 1}} = (3{{\Phi }_{m}} + {{\Phi }_{k}} + {{\Phi }_{d}}{{c}_{{ii}}}){\text{/}}9$(7.4)
${{a}_{{ij}}} = {{\nu }_{{ij}}}E_{i}^{{ - 1}} = (3{{\Phi }_{m}}{\text{/}}2 - {{\Phi }_{k}} - {{\Phi }_{d}}{{c}_{{ij}}}){\text{/}}9$При выполнении расчетов характеристик необходимо предварительно найти тригонометрические множители, которые можно записать компактно:
В развернутой форме окончательно находим преобразованные уравнения:
(7.6)
$\begin{gathered} {{\varepsilon }_{1}} = {{\sigma }_{1}}{\text{/}}{{E}_{1}} - {{\nu }_{{21}}}{{\sigma }_{2}}{\text{/}}{{E}_{2}} - {{\nu }_{{31}}}{{\sigma }_{3}}{\text{/}}{{E}_{3}} \\ {{\varepsilon }_{2}} = - {{\nu }_{{12}}}{{\sigma }_{1}}{\text{/}}{{E}_{1}} + {{\sigma }_{2}}{\text{/}}{{E}_{2}} - {{\nu }_{{32}}}{{\sigma }_{3}}{\text{/}}{{E}_{3}} \\ {{\varepsilon }_{3}} = - {{\nu }_{{13}}}{{\sigma }_{1}}{\text{/}}{{E}_{1}} - {{\nu }_{{23}}}{{\sigma }_{2}}{\text{/}}{{E}_{2}} + {{\sigma }_{3}}{\text{/}}{{E}_{3}} \\ \end{gathered} $Из соотношений (7.3) и (7.4) следует, что каждому напряженному состоянию присущи три модуля Ei продольной упругости и шесть коэффициентов поперечных деформаций νij, которые не являются независимыми характеристиками, поскольку их значения определяются тремя функциями, Φm, Φd и Φk.
8. Об определении теоретического модуля объемной упругости и параметра разрыхления. В отличие от варианта методики, который можно найти в работах [5] и [7], базирующегося на уравнении (6.1) с постоянным модулем K, в данном варианте, как параметр разрыхления œ, так и модуль Kξ представляются квадратичными функциями угла ξ
Соотношения (7.3) и (7.4) позволяют найти для продольных модулей и коэффициентов поперечных
деформаций теоретические кривые для состояний растяжения и сжатия. При увеличении,
при нулевых значениях a1 > 0 и a3, повышаются значения параметра разрыхления 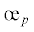 , кривая для коэффициента поперечных деформаций νp по конфигурации приближаются к опытным значениям. Затем проводится такое же сближение
коэффициента νc путем последовательного изменения a2 и a3.
, кривая для коэффициента поперечных деформаций νp по конфигурации приближаются к опытным значениям. Затем проводится такое же сближение
коэффициента νc путем последовательного изменения a2 и a3.
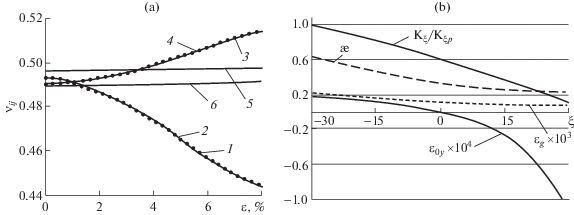
Процесс сближения кривых можно ускорить, если коэффициенты для модуля Kξ принять в соответствии со значениями углов ξ: a1 = Kτ, a2 = 3(Kc – Kτ)/π, a3 = 36(Kp – ‒ 2Kτ + Kc)/π. Определение модуля Kξ достигается после совмещения кривых путем изменения значений модулей Ki, где i = p, τ, c. На фиг. 2,a показан результат совмещения кривой 2 для коэффициента ν12 (сплошная линия) с кривой 1 (линия из точек) для коэффициента νp. И так же при сжатии, кривой 4 (сплошная линия) для коэффициента ν31 с кривой для коэффициента νc (линия из точек).
Вторым шагом для надежного совмещения и определения значений параметра 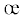 и модуля Kξ являются последующие аналогичные операции с кривыми 5 и 6, относящихся к коэффициентам
поперечных деформаций νti, найденными по формуле
и модуля Kξ являются последующие аналогичные операции с кривыми 5 и 6, относящихся к коэффициентам
поперечных деформаций νti, найденными по формуле
(8.2)
${{{\nu }}_{{ti}}} = (1 - {{{\sigma }}_{i}}{\text{/}}(3{{K}_{{{\xi }i}}}{\varepsilon })){\text{/}}2$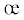 = 0, где i = p,. c; Ki – модули объемной упругости, уже найденные выше при первом шаге, для которых теоретическими
кривыми приняты коэффициенты, полученные расчетами по соотношениям (7.3) и (7.4).
Опыт использования методики показал, что форма кривых E1, E2 и E3 существенно зависит от значения модуля Kθτ, поэтому она, учитывая этот факт, заканчивается приведением в соответствующее положение
начальных значений модулей Ep, Eτ и Ec.
= 0, где i = p,. c; Ki – модули объемной упругости, уже найденные выше при первом шаге, для которых теоретическими
кривыми приняты коэффициенты, полученные расчетами по соотношениям (7.3) и (7.4).
Опыт использования методики показал, что форма кривых E1, E2 и E3 существенно зависит от значения модуля Kθτ, поэтому она, учитывая этот факт, заканчивается приведением в соответствующее положение
начальных значений модулей Ep, Eτ и Ec.
Описанный процесс совмещения коэффициентов поперечных деформаций привел к физически противоречивому результату для модуля Kξ. При растяжении и самом высоком значении параметра разрыхления, модуль увеличил свое значение более, чем в 5 раз, а при сжатии уменьшил в 0.9 раза по сравнению с “классическим”. Этот факт дал основание считать эту величину “кажущимся” модулем, отражающим собой два свойства: объемную упругость и ее изменение вследствие утраты или приобретения связей. Поэтому появилась необходимость введения параметра изменяющейся упругости, который связан с модулями объемной упругости
Кривая Kξ/Kξp показывает зависимость отношения теоретического (“кажущегося”) модуля к такому же
модулю при растяжении, которая отражает реакцию “слабых” связей на знак напряжения.
Кривая для параметра разрыхления 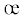 плавно снижается от растяжения к сжатию. Этот факт подтверждается плавным снижением
дилатансии, которая иллюстрируется кривой εg × 103, тогда как линейная объемная деформация ε0y × 104, как функция угла ξ имеет существенно меньшие значения. Все кривые относятся к уровню
продольной деформации ε = 2.5%. Описанное совмещение дает возможность найти связь
“кажущихся” модулей с теоретическими коэффициентами νti0 при растяжении и сжатии. На графиках коэффициенты νti0 находятся на оси ординат на фиг. 2,a, где i = p, c в вначале кривых 5 и 6.
плавно снижается от растяжения к сжатию. Этот факт подтверждается плавным снижением
дилатансии, которая иллюстрируется кривой εg × 103, тогда как линейная объемная деформация ε0y × 104, как функция угла ξ имеет существенно меньшие значения. Все кривые относятся к уровню
продольной деформации ε = 2.5%. Описанное совмещение дает возможность найти связь
“кажущихся” модулей с теоретическими коэффициентами νti0 при растяжении и сжатии. На графиках коэффициенты νti0 находятся на оси ординат на фиг. 2,a, где i = p, c в вначале кривых 5 и 6.
Продолжая анализ уравнения (6.1) после преобразования (7.1), используя результаты испытаний композита ВНПМ-2 отметим, что определение характеристик совмещением кривых для коэффициентов νi по изложенному выше первому варианту выполнить удается только для ветви νc. Точка c в конце кривой соответствует предельному значению этого коэффициента. Результат совмещения показан на фиг. 2,a кривыми 3 и 4.
Для растяжения потребовался другой вариант определения модуля Kξp, параметра ϑp и параметра разрыхления 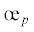 . Не привлекая соотношения (7.3) и (7.4), объемная деформация определяется по данным
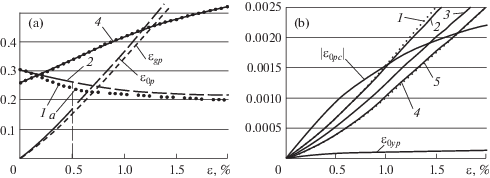
о коэффициенте поперечной деформации νp, найденной по результатам испытаний ε0p = (1 – 2νp)ε/3, а дилатансия по соотношению εgp = 2(νtp – νp)ε/3. На фиг. 3,a они (с множителем α = 200) показаны кривыми, исходящими от начала координат, сплошной
до точки a, а затем штрихами на участке “экстраполяции”. По дилатансии определяется параметр
разрыхления
. Не привлекая соотношения (7.3) и (7.4), объемная деформация определяется по данным
о коэффициенте поперечной деформации νp, найденной по результатам испытаний ε0p = (1 – 2νp)ε/3, а дилатансия по соотношению εgp = 2(νtp – νp)ε/3. На фиг. 3,a они (с множителем α = 200) показаны кривыми, исходящими от начала координат, сплошной
до точки a, а затем штрихами на участке “экстраполяции”. По дилатансии определяется параметр
разрыхления
Коэффициент νtp0 определяются последовательным приближением по значениям “кажущегося” модуля, который изменяется согласно равенству Kξp = Kk, где коэффициент k > 1. Кривая 1 (линия из точек) построена по опытным значениям νp. Объемная деформация, найденная по уравнению (6.1), постепенно приближается к опытной кривой. Для кривой 2 значения коэффициента вычисляются по соотношению для деформации ε0p. Между кривыми 1 и 2 необходимо создавать зазор, чтобы миновать точку a, в которой предельное значение коэффициента νpa свидетельствует о полной потери упругости вследствие разрушения, где модуль Kξ → ∞. Второй вариант совмещения кривых 1 и 2 позволил выяснить главную причину несовместимости.
Поведение второго композита раскрывается графиками упругой деформации и дилатансии. На фиг. 3,b деформация, представлена кривой ε0yp, которая меньше упругой деформации при сжатии. Абсолютные значения ε0yc превышают первую более, чем на порядок. Дилатансия этого композита подчеркивает его особенность, состоящую в том, что разрыхление развивается весьма интенсивно и показывает себя сразу после приложения нагрузки “стартовыми” дефектами.
Параметр разрыхления 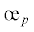 этого композита превышает значение первого почти вдвое. Кривые 2, 3 и 4 для дилатансии приведены на фиг. 3,b при состояниях с углами ξ = –30, 0 и 30°, полученные
расчетом, и опытные кривые 1 и 5 (линии из точек), рассчитанные по коэффициентам νi и νti, согласно соотношению εg = ±2(νti – νi)ε/3 (плюс для растяжения, минус для сжатия). Тогда как кривые для упругих деформаций
ε0yp и |ε0yc| существенно различаются. Второй вариант приводит к выводу, что совмещение с “экстраполяцией”
следует проводить по первому варианту, принимая для коэффициента νp за “опытные” данные, несколько меньшие реальных.
этого композита превышает значение первого почти вдвое. Кривые 2, 3 и 4 для дилатансии приведены на фиг. 3,b при состояниях с углами ξ = –30, 0 и 30°, полученные
расчетом, и опытные кривые 1 и 5 (линии из точек), рассчитанные по коэффициентам νi и νti, согласно соотношению εg = ±2(νti – νi)ε/3 (плюс для растяжения, минус для сжатия). Тогда как кривые для упругих деформаций
ε0yp и |ε0yc| существенно различаются. Второй вариант приводит к выводу, что совмещение с “экстраполяцией”
следует проводить по первому варианту, принимая для коэффициента νp за “опытные” данные, несколько меньшие реальных.
9. Преобразование уравнения (6.1) и определение параметров изменяющейся упругости. Свертка уравнений (7.6) приводит к уравнению связи средней деформации с напряжениями
(9.1)
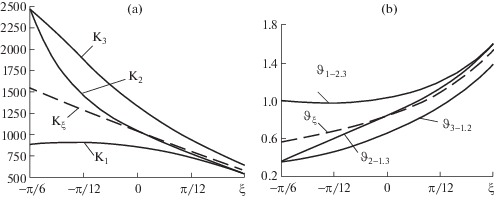
${{\varepsilon }_{0}} = ({{\sigma }_{1}}{\text{/}}{{K}_{1}} + {{\sigma }_{2}}{\text{/}}{{K}_{2}} + {{\sigma }_{3}}{\text{/}}{{K}_{3}}){\text{/}}9$На фиг. 4,a показаны графики для начальных модулей Ki и модуля Kξ. Начальными они названы потому, что определены по начальным значениям модулей Ei и коэффициентов νij для каждого значения угла ξ. По значениям этих модулей определяются три параметра изменяющейся объемной упругости ϑi, как отношение “классического” модуля к “кажущимся” модулям, согласно с соотношением (8.3). Их графики на фиг. 4,b дают представление о сохранившейся упругости для состояний с ϑi ≤ 1, а для состояний с ϑi > 1 о приобретенной, в результате возрастания связей и изменения взаимодействия частиц наполнителя. Индексы параметров означают: первый тот же, что и у модуля, второй и третий определяют плоскости элементарного объема, в которых происходит потеря или приобретение упругости. Так при простом растяжении параметр ϑ1–2, 3 = 1 означает, что в горизонтальных плоскостях элементарного объема никаких изменений упругости нет, а вдоль обоих вертикальных – самые наибольшие ϑ2–1, 3 = ϑ3–1, 2 = 0.361. Влияние же разрыхления на изменение объемной упругости, характеризуемое параметрами ϑ3–1, 2 и ϑ2–1, 3, следует считать существенным, сопоставимым с изменением коэффициента νp.
При чистом сдвиге (θ = π/6)) изменения происходят в трех плоскостях, а именно ϑ1–2, 3 = 1.03; ϑ2–1, 3 = 0.846; ϑ3–1, 2 = 0.634 число связей незначительно возрастает в площадках с наименьшим напряжением (с учетом знака), а им перпендикулярных падает. При простом сжатии (θ = π/6) при ϑ1–2, 3 = 1,6; ϑ2–1, 3 = 1,6; ϑ3–1, 2 = 1,39 во всех плоскостях наблюдается возрастание связей. Малые значения параметра ϑ3–1, 2 в начале кривой говорят о том, что коэффициент поперечных деформаций при этом приблизился к предельному значению при растяжении, то есть к полной утрате упругости. Значения параметра ϑξ = K/Kξ, как показано на фиг. 4,b изменяются в пределах 0.56 < ϑξ < 1.54, которые оценивают сохранившуюся часть упругости в среднем по трем направлениям.
Исследования с помощью математической модели показывают, что при значении параметра
разрыхления 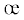 = 0 “кажущиеся” модули Ki совпадают с теоретическим модулем Kξ, поскольку значение коэффициента νtp, найденного по формуле (8.2), принято в качестве исходных данных. При незначительно изменяющихся модулях Ei коэффициенты принимают такие значения νij, что “кажущиеся” модули становятся равными между собой. Материал ведет себя, как
изотропное тело при весьма малой линейной объемной деформации и нулевой дилатансии.
При растяжении реального материала большие значения объемной деформации связаны с
коэффициентом νp, который существенно отличается от νtp тем, что он “включает” в себя дилатансию (от разрыхления), именно поэтому кривые
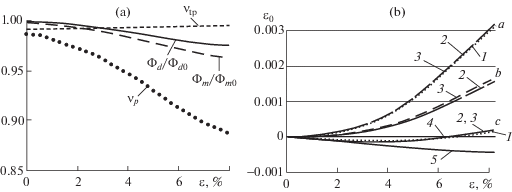
для них, представленные на фиг. 5,a значительно отличаются. Их влияние на характеристики формоизменения показано кривыми
для податливостей Φ/Φ0 и Φm/Φm0. Индекс с нулем относится к варианту
= 0 “кажущиеся” модули Ki совпадают с теоретическим модулем Kξ, поскольку значение коэффициента νtp, найденного по формуле (8.2), принято в качестве исходных данных. При незначительно изменяющихся модулях Ei коэффициенты принимают такие значения νij, что “кажущиеся” модули становятся равными между собой. Материал ведет себя, как
изотропное тело при весьма малой линейной объемной деформации и нулевой дилатансии.
При растяжении реального материала большие значения объемной деформации связаны с
коэффициентом νp, который существенно отличается от νtp тем, что он “включает” в себя дилатансию (от разрыхления), именно поэтому кривые
для них, представленные на фиг. 5,a значительно отличаются. Их влияние на характеристики формоизменения показано кривыми
для податливостей Φ/Φ0 и Φm/Φm0. Индекс с нулем относится к варианту 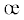 = 0.
= 0.
Кривые показывают, что различие исходных данных этих вариантов мало влияют на характеристики формоизменения, тогда как изменение объемной деформации отличается от формоизменения, как количественно, так и качественно. Второй вариант расчета показывает, что отказаться от учета разрыхления, ограничиваясь одним теоретическим модулем Kξ, приводит не только к ошибке определения объемной деформации, но и описания истинного поведения разрыхляющего материала. Для введения в модель “кажущихся” модулей Ki использовались элементы матричной механики, аналогичные тем, которые привели к созданию математической модели атома.
10. Проверка результатов расчетов объемной деформации. Таким образом, основной и единственной причиной различия модулей Ki является разрыхление, характеризуемое параметром œ. Его снижение ведет к сближению модулей Ki и уменьшению анизотропии. При отсутствии дилатансии материал, согласно модели, становится изотропным. Расчеты упругой части объемной деформации проводятся по известной формуле σ0y = σ0/(3Kξ), где модуль Kξ выражается постоянной величиной при ξ = const. Располагая значениями интенсивности напряжений S0, пользуясь формулой, вычисляются главные напряжения: σi = S0ci, i = 1, 2, 3. Общую объемную деформацию проще определять по уравнению (9.1), если “кажущиеся” модули упругости заменить на их обратные величины, податливости Φki = 1/Ki. Влияние разрыхления на объемную деформацию выясняется сравнением ее с результатами испытаний и расчетов по формулам, полученным до преобразования, которые практически совпадают. На фиг. 5,b показаны три пучка кривых: a – для растяжения, b – чистого сдвига и c – сжатия. Кривые (линии из точек) под цифрой 1 относятся к растяжению и сжатию, построены по результатам испытаний. Кривые по результатам расчета по формуле (9.1) приведены под цифрой 2 (сплошные линии), а цифрой 3 (штриховые линии) по результатам расчета по формуле (6.1). Кривая 4, практически совпадающая с линией сетки, представляет упругую часть объемной деформации при растяжении, а кривая 5 при сжатии.
11. Заключение. Исследования структурно-неоднородных материалов и, в частности композитов, с помощью предложенных выше методик показывают, что их деформация сопровождается существенным изменением, как общей, так и объемной упругости. Эти изменения вызваны ростом нелинейной деформации (дилатансии), вызванной разрывом “слабых” связей. Дилатансия влияет на формоизменение, увеличивая интенсивность деформации, а в объемной деформации она почти сравнивается с ней. Малость линейной объемной деформации можно объяснить только снижением объемной упругости при растяжении, тогда как отрицательные напряжения вызывают этот эффект в меньшей степени, который практически не влияет на “классический” модуль объемной упругости.
Выявленные три “кажущиеся” модуля Ki и их средняя величина – теоретический модуль Kξ, не характеризуют объемную упругость, они приносят новую информацию об изменении упругости с помощью параметров ϑi, позволяющих количественно оценить возникшую анизотропию с осями симметрии, совпадающими с направлениями главных напряжений. Анизотропия проявляет себя, несмотря на то, что потенциальная функция, приведшая к выводу уравнений В.В. Новожилова, является изотропной. Выполненные исследования показывают, что тензорно-нелинейные уравнения В.В. Новожилова можно применять, как для анализа поведения сложных сред, так и для решения практических задач, в частности, обработки результатов испытаний.
Благодарности. Автор выражает благодарность академику Н.Ф. Морозову, отметившему полезность и необходимость исследований по развитию идей В.В. Новожилова. Профессору Оксане Григорьевне Рыбакиной за полезные замечания, высказанные по материалам данной статьи, доценту МГТУ им. Баумана Еремичеву А.Н. за рекомендованные им результаты экспериментальных исследований, оказавшие влияние на окончательные выводы данной работы.
Список литературы
Бел Дж.Ф. Экспериментальные основы механики деформируемых твердых. тел. М.: Наука 1984, часть I–596 с. II–431 с.
Новожилов В.В. О связи между напряжениями и деформациями в нелинейно-упругой среде // ПММ. 1951. Т. 15. Вып. 2. С. 183–194.
Ломакин Е.В. Механика сред, с зависящими от вида напряженного состояния свойствами // Физическая мезомеханика. 2007. Т. 10. № 5. С. 41–52.
Надаи А. Пластичность и разрушение твердых тел. Т. 2. М.: Изд-во иностр. лит., 1969. 863 с.
Комков К.Ф. Особенности упругих свойств высоконаполненных полимерных материалов // Вестник МГТУ им. Н.Э. Баумана. Сер. “Машиностроение”. 2008. № 3. С. 3–13.
Еремичев А.Н. Комплексные испытания по определению механических свойств высоконаполненного полимерного материала. Электронный журнал, ISSN 237–0595. Инженерный вестник, № 9, 2014, с. 17–32. Режим доступа: http://engbul. bmstu.ru/doc/726797.html.
Комков К.Ф. О тензорной нелинейности сред, проявляющих существенное различие в сопротивлении растяжению и сжатию // Электрон. журн. # 10, октябрь 2013. DOI: 10.7463/0513.0571202
Лехницкий С.Г. Теория упругости анизотропного тела. М.: Наука, 1977. 415 с.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела