Известия РАН. Механика твердого тела, 2019, № 1, стр. 72-87

1. Введение. Повышенный интерес к исследованию задач термоупругости с учетом взаимодействия полей деформации и температуры получил развитие в середине прошлого века [1–3]. Новое направление исследований – связанная термоупругость – получило развитие в [3–5] и других.

Для решения задач связанной термоупругости использовались как аналитические [4, 5], так и численные [6] методы: метод конечных элементов, метод граничных и интегральных уравнений и др. Для решения связанных задач термоупругости разрабатывались в основном конечно-элементные модели в [7–11] и других. Аналитические методы решения этого класса задач были подытожены в [12].

Несвязанные задачи термоупругости о скользящем контакте жесткого тела с упругим покрытием с учетом трения и разогрева от трения на контакте рассматривались как отечественными, так и зарубежными учеными [13–23]. Исследование несвязанных задач термоупругости о скользящем контакте позволило установить наличие областей устойчивых и неустойчивых решений. Изучению свойств неустойчивых решений несвязанных задач термоупругости о скользящем контакте посвящены исследования, проводимые как аналитическими [13, 22, 23], так и численными методами [14–21].

В настоящей работе в рамках связанной термоупругости аналитическими методами в пространстве безразмерных параметров задачи изучаются границы области устойчивых и области неустойчивых решений, которую на практике часто называют областью термоупругой неустойчивости скользящего контакта. Исследуются признаки возникновения и развития термоупругой неустойчивости. Формулируются частные задачи опосредованного мониторинга основных параметров скользящего контакта и задачи управления этими параметрами.

2. Постановка основной задачи. Рассматривается контактная задача связанной термоупругости о скольжении с постоянной скоростью V жесткой теплоизолированной полуплоскости I ($h \leqslant x < \infty $) по верхней поверхности ($x = h$) упругого теплопроводящего покрытия толщины $h$ ($0 \leqslant x \leqslant h$), нижняя поверхность которого жестко сцеплена с недеформируемой, нетеплопроводной подложкой в виде полуплоскости II ($ - \infty < x < 0$)фиг. 1. Скольжение полуплоскости I по поверхности упругого покрытия происходит с учетом кулоновского трения. Поток тепла, образующийся на контакте за счет трения, направлен в покрытие. С начального момента времени движущаяся вдоль оси $y$ полуплоскость I деформирует поверхность ($x = h$) упругого покрытия, смещаясь в направлении, противоположном направлению оси x, по закону $\Delta (t)$. До начального момента покрытие находится в покое, а его температура равняется ${{T}_{0}}$.

Рассматриваемая задача предполагает, что распределения температуры, смещений и напряжений в покрытии не зависят от выбора горизонтальной координаты по оси $y$, параллельной направлению движения полуплоскости I, и являются функциями только вертикальной координаты x и времени t. В этом случае дифференциальные уравнения термоупругости [24]:

совместно с дифференциальным уравнением связанной теплопроводности [24]: составляют систему дифференциальных уравнений связанной термоупругости, описывающих поведение упругого покрытия, в которых $u(x,t)$, $w(x,t)$ – вертикальные и горизонтальные смещения материала покрытия, $T(x,t)$ – температура в покрытии, $\lambda $, $\mu $ – постоянные Ламе, $\nu $ – коэффициент Пуассона, $\alpha $ – коэффициент линейного теплового расширения материала покрытия, $\kappa $ – коэффициент температуропроводности, $K$ – коэффициент теплопроводности, ${{T}_{0}}$ – начальная температура в покрытии.

Граничные условия сформулированной задачи для дифференциальных уравнений (2.1), (2.2) имеют вид:

где $f$ – коэффициент трения, $k$ – коэффициент теплообмена, ${{\sigma }_{{xx}}}(x,t)$, ${{\sigma }_{{xy}}}(x,t)$ – нормальные и касательные напряжения в покрытии:

Начальные условия задачи на смещения $u$, $w$ – нулевые:

Начальная температура в покрытии

Следует заметить, что вертикальные смещения $u(x,t)$, нормальные напряжения ${{\sigma }_{{xx}}}(x,t)$ и температура $T(x,t)$ в упругом покрытии определяются независимо от горизонтальных смещений $w(x,t)$. Горизонтальные смещения определяются из второго уравнения в (2.1), граничных (2.3), (2.5) и начальных условий (2.8) через нормальные напряжения ${{\sigma }_{{xx}}}(h,t)$.

3. Точное решение задачи. Решение связанной контактной задачи термоупругости, поставленной в предыдущем пункте, определяется с помощью интегрального преобразования Лапласа [25] в виде сверток Лапласа для температуры $T(x,t)$, смещений $u(x,t)$ и напряжений ${{\sigma }_{{xx}}}(x,t)$ в покрытии

где

Контур интегрирования $\Gamma = \{ z{\text{:}}\; - i\infty + d{{t}_{\kappa }},i\infty + d{{t}_{\kappa }}\} $ представляет собой прямую линию в комплексной плоскости переменной интегрирования $z$, параллельную мнимой оси и отстоящую вправо от нее на величину $d{{t}_{\kappa }} > 0$. Значение $d$ подбирается таким образом, чтобы контур интегрирования проходил правее всех изолированных особых точек подынтегральных функций. Следует заметить, что при $\hat {T} = 0$ полученные формулы (3.1)–(3.10) совпадают с соответствующими формулами несвязанной задачи термоупругости о скользящем термофрикционном контакте [23].

В полученных формулах решения рассматриваемой задачи (3.1)–(3.10) для $T(x,t)$, $u(x,t)$, ${{\sigma }_{{xx}}}(x,t)$ присутствуют контурные квадратуры (3.2), (3.6), (3.9). Подынтегральные функции этих квадратур в комплексной плоскости переменной интегрирования $z$ являются функциями мероморфными, содержащими счетное множество полюсов. На бесконечности в комплексной плоскости переменной интегрирования $z$ подынтегральные функции из (3.2), (3.6), (3.9) имеют следующие асимптотические оценки

Проведенные исследования показывают, что квадратуры (3.2), (3.6), (3.9) в обычном смысле не существуют и понимаются в обобщенном смысле [26]. После регуляризации подынтегральных функций контурных квадратур на бесконечности (при $\left| z \right| \to \infty $) с учетом асимптотических соотношений (3.11)–(3.13) контурные квадратуры записываются в виде суперпозиции регулярной части обобщенной составляющей и свертки Лапласа

в которых $N_{T}^{0}(x,z)$, $N_{u}^{0}(x,z)$, $N_{\sigma }^{0}(x,z)$, $R(z)$ из формул (3.3), (3.7), (3.10), (3.4) соответственно.

Квадратуры в (3.15), (3.17), (3.19) являются регулярными, подынтегральные функции квадратур являются мероморфными и на бесконечности имеют степенное убывание

Для их вычисления можно использовать методы теории функций комплексного переменного [27]. В связи с этим возникает задача определения полюсов подынтегральных функций в квадратурах (3.15), (3.17), (3.19) в комплексной плоскости переменной интегрирования.

4. Полюсы подынтегральных функций. Полюсы подынтегральных функций в (3.15), (3.17), (3.19) совпадают с нулями $R(z)$ из (3.4) за исключением тех нулей $R(z)$, которые являются устранимыми особыми точками подынтегральных функций. Для определения нулей знаменателя подынтегральных функций $R(z)$ необходимо решить уравнение

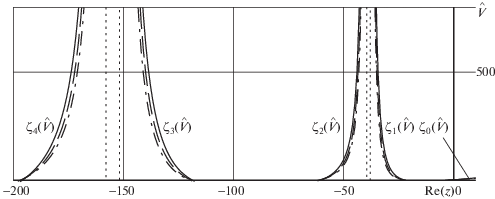
в комплексной плоскости $z = \xi + i\eta $, где ${{\beta }^{2}}$, Bi, $\hat {T}$, $\hat {V}$ даны после (3.10).

В уравнении (4.1) нули $R(z)$ зависят от трех безразмерных параметров задачи $\hat {V}$, Bi, $\hat {T}$, так как четвертый безразмерный параметр ${{\beta }^{2}}$ выражается через $\hat {T}$. Исследование поведения нулей $R(z)$ из (4.1) проводилось, используя опыт [22, 23] в зависимости от $\hat {V} \in \left[ {0,\infty } \right)$ при фиксированных Bi, $\hat {T}$. Вычисления показали, что уравнение (4.1) имеет счетное множество действительных корней ${{\zeta }_{k}}$ $k = 0,\;1,\;2,\; \ldots $, которые являются полюсами подынтегральных функций (3.15), (3.17), (3.19), На фиг. 1 показано изменение действительной части полюсов ${{\zeta }_{k}}$ $k = 0{\kern 1pt} - {\kern 1pt} 4$ для Bi = 100. Сплошной линией показана величина полюса при значении параметра связанности $\hat {T} = 0$, что соответствует несвязанной задаче термоупругости [23]; штриховая линия соответствует $\hat {T} = 0.25$, а штрихпунктирная – $\hat {T} = 0.5$.

На фиг. 1 видно, что ${{\zeta }_{k}}(\hat {V}) < 0$ k = 1, 2, 3, … при любых значениях $\hat {V} \in [0,\infty )$. Знак полюса ${{\zeta }_{0}}$ зависит от значения $\hat {V}$: при $\hat {V} < {{\hat {V}}_{{\text{c}}}}$ где

величина ${{\zeta }_{0}}(\hat {V}) < 0$, при $\hat {V} = {{\hat {V}}_{{\text{c}}}}$ полюс находится в начале координат ${{\zeta }_{0}}({{\hat {V}}_{{\text{c}}}}) = 0$, в то время как при $\hat {V} > {{\hat {V}}_{{\text{c}}}}$ полюс становится положительным ${{\zeta }_{0}}({{\hat {V}}_{{\text{c}}}}) > 0$ и при неограниченном увеличении $\hat {V}$ $\mathop {\lim }\limits_{\hat {V} \to \infty } {{\zeta }_{0}}(\hat {V}) = \infty $.

5. Эффективные решения задачи. В предположении, что полюсы подынтегральных функций ${{\zeta }_{k}}$ $k = 0,\;1,\;2,\; \ldots $ из (3.15), (3.17), (3.19) однократны и известны, формулы вычисления перечисленных квадратур принимают вид

где $R{\text{'}}(z)$ – производная от $R(z)$.

С учетом (3.14)–(3.19) и (5.2) получается, что

Решения задачи $T(x,t)$, $u(x,t)$, ${{\sigma }_{{xx}}}(x,t)$ при этом записываются в виде рядов по полюсам ${{\zeta }_{k}}$ k = 0, 1, 2, …

где ${{B}_{a}}(x,z)$ вычисляется по формуле (5/2), $D(z,t)$ по формуле

Горизонтальные смещения $w(x,t)$ определяются из (2.1) и вторых условий в (2.3), (2.5) и даются формулой

6. Анализ решений задачи. Области устойчивых и неустойчивых решений. При анализе свойств полученных решений $T(x,t)$, $u(x,t)$, ${{\sigma }_{{xx}}}(x,t)$ используются разные их формы, как в виде свертки Лапласа (3.14), (3.16), (3.18), где одна из подынтегральных функций представляется в виде контурной квадратуры (3.15), (3.17), (3.19), так и в виде функциональных рядов (5.4)–(5.6). Исследование решений задачи $T(x,t)$, $u(x,t)$, ${{\sigma }_{{xx}}}(x,t)$, представленных как формулами (3.14), (3.16), (3.18), так и формулами (5.4)–(5.6), показывает, что при ${{\zeta }_{k}} < 0$ $k = 0,\;1,\;2,\; \ldots $ решения задачи устойчивы и стремятся с увеличением времени $t$ к стационарному состоянию. Если хотя бы один из ${{\zeta }_{k}}$ $k = 0,\;1,\;2,\; \ldots $ при изменении параметров задачи становится положительным ${{\zeta }_{k}} > 0$, то амплитуда $T(x,t)$, $u(x,t)$, ${{\sigma }_{{xx}}}(x,t)$ неограниченно возрастает при $t \to \infty $, что свидетельствует о неустойчивости решения задачи, о термоупругой неустойчивости скользящего контакта. В предположении, что внедрение $\Delta (t)$ является функцией ограниченной

для интеграла (5.7) при ${{\zeta }_{k}} > 0$ $k = 0,\;1,\;2,\; \ldots $ справедлива оценка свидетельствующая о том, что при $t \to \infty $ решения задачи (5.4)–(5.6) становятся неограниченными $\mathop {\lim }\limits_{t \to \infty } \left\{ {T(x,t),p(x,t)} \right\} = \infty $, где $p(x,t) = - {{\sigma }_{{xx}}}(x,t)$.

В комплексной плоскости $z$ траектории ${{\zeta }_{0}}(\hat {V})$ для $\hat {V} \in [0,{{\hat {V}}_{{\text{c}}}})$, где ${{\hat {V}}_{{\text{c}}}}$ из (4.2), и ${{\zeta }_{k}}$ k = = 1, 2, ... для $\hat {V} \in \left[ {0,\infty } \right)$ и любых Bi и $\hat {T}$ находятся в левой полуплоскости на отрицательной части действительной оси (фиг. 1) и образуют область устойчивых решений задачи. При $\hat {V} > {{\hat {V}}_{{\text{c}}}}$ полюс ${{\zeta }_{0}}(\hat {V})$ становится положительным, и хотя все остальные полюса ${{\zeta }_{k}}$ $k = 1,\;2,\;3,\; \ldots $ отрицательны решение задачи согласно (6.1) неустойчиво.

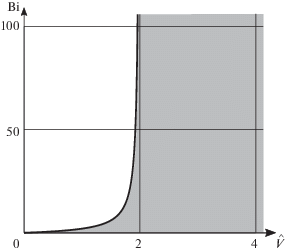
На фиг. 2 на плоскости $\hat {V}$, Bi представлены области устойчивых (не закрашена) и неустойчивых (закрашена) решений задачи. Граница между указанными областями определяется из условия обнуления ${{\zeta }_{{\text{0}}}}(\hat {V}) = 0$ или ${\text{Bi}} = 2\hat {V}{\text{/}}(2 - \hat {V})$ и не зависит от параметра термомеханической связанности $\hat {T}$.

7. Асимптотический и численный анализ полученных решений. Формулы решения рассматриваемой связанной задачи термоупругости о скользящем контакте, полученные для температуры $T(x,t)$ (3.14), смещений $u(x,t)$ (3.16) и напряжений ${{\sigma }_{{xx}}}(x,t)$ (3.18), позволяют провести сравнительный асимптотический анализ изменения этих характеристик при малых $t$ в условиях связанной и соответствующей несвязанной задачи. Формулы решения задачи (3.14), (3.16), (3.18) с учетом оценок (3.20) в области устойчивых решений записываются для малых $t$ в виде следующих асимптотических соотношений

Первый член асимптотики (7.2) для смещения $u(x,t)$ совпадает с соответствующим членом несвязанной задачи [23]. После дифференцирования $u(x,t)$ в (7.2) по $x$ и по $t$ скорость деформации на контакте ${{\dot {\varepsilon }}_{{xx}}}(h,t)$ имеет вид

Отсюда следует, что в связанной задаче интенсивность изменения температуры на контакте $\dot {T}(h,t)$ при малых $t$ пропорциональна скорости деформации ${{\dot {\varepsilon }}_{{xx}}}$ с коэффициентом пропорциональности

пропорциональном $\hat {T}$. Напряжения на контакте ${{\sigma }_{{xx}}}(x,t)$ при малых $t$ пропорциональны скорости деформации ${{\dot {\varepsilon }}_{{xx}}}$ с коэффициентом пропорциональности также зависящим от $\hat {T}$. Формулы (7.5), (7.6), как и формулы (7.1), (7.3), демонстрируют влияние связанности на основные параметры контакта и позволяют указать параметры задачи, которые способствуют усилению этого влияния.

Численный анализ полученных решений рассматриваемой связанной задачи термоупругости о скользящем контакте в условиях разогрева от трения сводится к расчетам температуры $T(h,t)$ по формуле (5.4) и контактных напряжений $p(t) = - {{\sigma }_{{xx}}}(h,t)$ (5.6) в пространстве безразмерных параметров $\hat {V}$, Bi, $\hat {T}$. Расчеты проводятся в предположении, что максимальный уровень проседания жесткой полуплоскости I в упругое покрытие равен ${{\Delta }_{0}}$. Закон $\Delta (t)$ внедрения полуплоскости I, состоящий из активной фазы (на временном интервале $0 < t < {{t}_{\varepsilon }}$) и пассивной фазы (на интервале ${{t}_{\varepsilon }} < t < \infty $) принимается в виде

где ${{t}_{\varepsilon }} = {{\varepsilon }^{{ - 1}}}\ln 2$ – время окончания активной фазы внедрения, $\varepsilon $ – параметр закона внедрения.

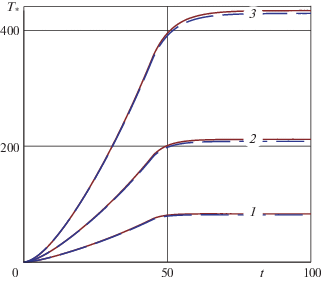
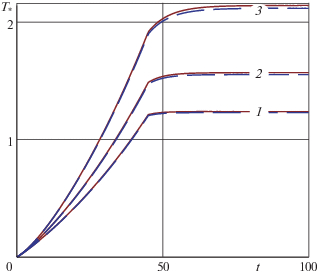
Характер неустойчивых решений связанной задачи качественно не отличается от соответствующих неустойчивых решений несвязанной задачи [23], а области неустойчивых решений связанной и несвязанной задач совпадают. Ниже исследуется влияние параметров $V$ – скорости скольжения полуплоскости I и ${{T}_{0}}$ – температуры окружающей среды на развитие температуры на контакте $T(h,t)$ и контактных напряжений $p(t) = - {{\sigma }_{{xx}}}(h,t)$, возникающих и развивающихся во времени на скользящем контакте между жесткой полуплоскостью I и покрытием из алюминиевого сплава со следующими термомеханическими $\mu = 24.8$ ГПа, $\text{v} = 0.34$, κ = 88.09 × 10^–6 м²/с, α = 22.9 × 10^–6 1/град, $K = 209.3$ Вт/(м ⋅ град), $f = 0.15$, $k = 100$ кВт/(м² ⋅ град) и геометрическими h = 25 мм, ${{\Delta }_{0}} = 0.01h = 0.25$ мм характеристиками. Рассматриваются три скорости скольжения $V$: ${{V}_{1}} = 3.5$ мм/с, ${{V}_{2}} = 7$ мм/с, ${{V}_{3}} = 10.5$ мм/с, и два значения начальной температуры ${{T}_{0}}$ : $T_{0}^{1} = 0$, $T_{0}^{2} = 525$ K, которые соответствуют следующим безразмерным параметрам $\hat {V}$ и $\hat {T}$: ${{\hat {V}}_{1}} = 0.298266$, ${{\hat {V}}_{2}} = 0.596530$, ${{\hat {V}}_{3}} = 0.894794$ и ${{\hat {T}}_{1}} = 0$, ${{\hat {T}}_{2}} = 0.000093$ из области устойчивых решений (фиг. 2). Параметр Bi фиксирован и равен 11.9446.

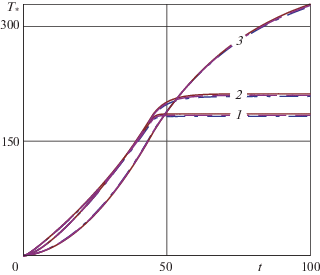
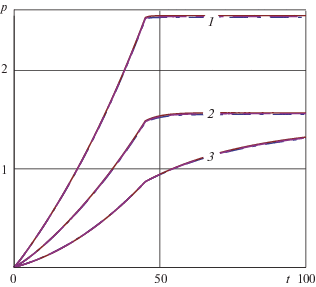
На фиг. 3 представлены графики ${{T}_{*}}(h,t) = T(h,t) - {{T}_{0}}$ (K), на фиг. 4 – графики p(t) = = $ - {{\sigma }_{{xx}}}(h,t)$ (ГПа) при $\hat {T} = {{\hat {T}}_{1}}$ (сплошной линией) и $\hat {T} = {{\hat {T}}_{2}}$ (штриховой) для различных ${{\hat {V}}_{k}}$, номера $k$ которых указаны цифрами 1–3 на кривых. По горизонтальной оси на фиг. 3 и последующих фигурах отмечено время t (с). Время окончания активной фазы внедрения ${{t}_{\varepsilon }}$ составляет 45 с.

Расчеты показали, что заметное влияние на физические характеристики контакта $T(h,t)$ и $p(t) = - {{\sigma }_{{xx}}}(h,t)$ оказывает толщина покрытия $h$ и время активной фазы внедрения ${{t}_{\varepsilon }}$. На фиг. 5–6 представлены графики ${{T}_{*}}(h,t) = T(h,t) - {{T}_{0}}$ (K) и $p(t) = - {{\sigma }_{{xx}}}(h,t)$ (ГПа) для трех значений $h = 12.5$ мм (отмечен цифрой 1), 25 мм (2), 50 мм (3) и фиксированного ${{\Delta }_{0}} = 0.25$ мм для покрытия из алюминиевого сплава. Скорость скольжения $V = 7$ мм/с. Сплошной линией изображены графики при начальной температуре $T_{0}^{1} = 0$, штриховой – $T_{0}^{2} = 525$ K. Из графиков на фиг. 6 видно, что увеличение толщины покрытия приводит к уменьшению значений контактного давления $p(t)$ (фиг. 6).

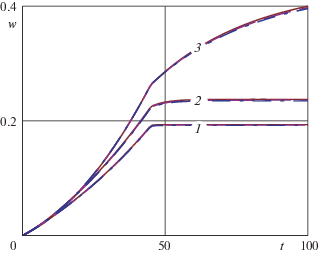
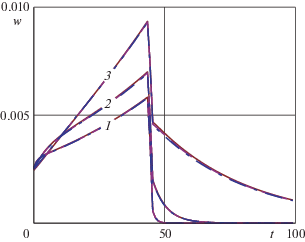
Горизонтальные смещения поверхности покрытия $w(h,t)$ и скорости $\dot {w}(h,t)$ приобретают влияние связанности через нормальные напряжения ${{\sigma }_{{xx}}}(h,t)$ на контакте согласно формулам (5.8) и асимптотики ${{\sigma }_{{xx}}}(h,t)$ (7.3). На фиг. 7–8 приведены графики $w(h,t)$ (мм) и $\dot {w}(h,t)$ (мм/с) при трех значениях $h = 12.5$ мм (отмечен цифрой 1), 25 мм (2), 50 мм (3) и тех же значениях параметров контакта, которые использовались при построении графиков на фиг. 5–6. Из фиг. 7–8 видно, что с увеличением толщины покрытия величины горизонтальных смещений и их скорости увеличиваются.

8. Мониторинг и управление параметрами контакта. Размещение пленочных наноразмерных датчиков в изделиях из композитных, функционально-градиентных и многослойных материалов вносит исчезающе малый вклад при расчетах напряженно-деформируемого состояния на макроуровне. В рамках постановки основной задачи макроисследования скользящего контакта появляется возможность решения частных задач об отслеживании основных параметров контакта по данным датчиков, расположенных на произвольной глубине контактирующих материалов. К частным задачам такого типа относятся задачи о мониторинге основных параметров скользящего контакта при эксплуатации триботехнических устройств, а также задачи управления этими параметрами с целью недопущения возникновения термоупругой неустойчивости. Полученные в результате мониторинга данные с датчиков, расположенных на глубине под скользящим контактом, пересчитываются по формулам, заранее полученным при решении соответствующих частных задач, на значения основных параметров контакта.

Частные задачи мониторинга параметров скользящего контакта формулируются следующим образом: по данным датчиков а) давления, б) температуры, установленных, к примеру, между покрытием и подложкой, определить значения основных параметров скользящего контакта – контактных напряжений, температуры разогрева контакта. При этом предполагается, что сами датчики в силу их малости не вносят искажений в напряженно-деформированное состояние изделия.

В случае а) для получения формул пересчета напряжений между покрытием и подложкой ${{\sigma }_{{xx}}}(0,t)$ на температуру $T(h,t) - {{T}_{0}}$ на контакте используются формулы (3.1)–(3.3) и (3.8)–(3.10), из которых следует

где $f_{\sigma }^{0}(0,t)$ и $f_{\sigma }^{0}(h,t)$ вычисляются по формуле (3.9), $f_{T}^{0}(h,t)$ вычисляется по формуле (3.2) через функцию $N_{T}^{0}(h,z)$ из (3.3).

Исключая $\Delta (t)$ из (8.1), (8.2) с помощью преобразования Лапласа получим соотношение для пересчета ${{\sigma }_{{xx}}}(0,t)$ на $T(h,t) - {{T}_{0}}$ в виде

Вычисляя интеграл в (8.4), получим соотношение (8.3) в новой форме

где ${{\zeta }_{k}}$ k = 0, 1, 2, … являются корнями уравнения $\tilde {N}_{\sigma }^{0}(0,z) = 0$, причем $\operatorname{Re} ({{\zeta }_{k}}) < 0$, k = 0, 1, 2, …

В случае б) для получения формулы пересчета температуры $T(0,t) - {{T}_{0}}$ между покрытием и подложкой на контактные напряжения ${{\sigma }_{{xx}}}(h,t)$ воспользуемся формулами (3.1)–(3.3) и (3.8)–(3.10), из которых следует, что

где $f_{T}^{0}(0,t)$ вычисляется по формуле (3.2) через $N_{T}^{0}(0,z)$ из (3.3).

Исключая из (8.5) и (8.2) функцию $\Delta (t)$ с помощью преобразования Лапласа, получим формулу пересчета $T(0,t) - {{T}_{0}} = {{T}_{0}}(t)$ на ${{\sigma }_{{xx}}}(h,t)$

После вычисления интеграла в (8.8) получим формулу пересчета в более простой форме

где ${{\zeta }_{k}}$ k = 0, 1, 2, … являются корнями уравнения $\tilde {N}_{T}^{0}(h,z) = 0$, а $\operatorname{Re} ({{\zeta }_{k}}) < 0$, k = 0, 1, 2, ….

Управление параметрами скользящего контакта – напряжениями и температурой – может достигаться, в том числе, за счет подбора закона внедрения штампа $\Delta (t)$ в упругое покрытие. Пусть требуется подобрать закон внедрения $\Delta (t)$ таким образом, чтобы: в) напряжения ${{\sigma }_{{xx}}}(h,t)$ на контакте изменялись по заранее заданному закону ${{\sigma }_{{xx}}}(h,t)$ = = –p(t), в том числе и при $p(t) = {\text{const}}$; г) на контакте температура $T(h,t)$ изменялась бы по заранее заданному закону $T(h,t) - {{T}_{0}} = {{T}_{h}}(t)$ или была бы постоянной заранее установленной величиной ${{T}_{h}}(t) = T = {\text{const}}$.

В случае в) для определения $\Delta (t)$ при заданном ${{\sigma }_{{xx}}}(h,t) = - p(t)$ решение задачи с помощью формулы (3.8) сводится к интегральному уравнению Вольтерры [28]

где $N_{\sigma }^{0}(h,z)$ определена в (3.10), а $R(z)$ в (3.4).

Для обращения интегрального уравнения (8.9) используется преобразование Лапласа, с помощью которого определяется

где ${{\zeta }_{k}}$ k = 0, 1, 2, … – все корни уравнения $\tilde {N}_{\sigma }^{0}(h,z) = {{\beta }^{2}}r(z) = 0$, причем $\operatorname{Re} ({{\zeta }_{k}}) < 0$ k = 0, 1, 2, …

При $p(t) = {{p}_{0}} = {\text{const}}$, когда напряжение на контакте при $t > 0$ удерживается постоянным, $\Delta (t)$ принимает вид

где $H(t)$ – функция Хевисайда.

В случае г) для определения $\Delta (t)$ по заданному $T(h,t) - {{T}_{0}} = {{T}_{h}}(t)$ решение задачи с помощью формулы (3.1) сводится к интегральному уравнению Вольтерры

где $f_{T}^{0}(h,t)$ вычисляется по формуле (3.2) через функцию $N_{T}^{0}(h,z)$ из (3.3).

Обращение интегрального уравнения (8.13) определяется с помощью преобразования Лапласа

где $r(z)$ из (3.4).

После вычисления интеграла в (8.15) и подстановки результата в (8.14) получим формулу

где ${{\zeta }_{k}}$ k = 0, 1, 2, … – все корни уравнения $\tilde {N}_{T}^{0}(h,z) = 0$, причем $\operatorname{Re} ({{\zeta }_{k}}) < 0$ k = 0, 1, 2, …

Для поддержания на скользящем контакте постоянной температуры ${{T}_{h}}(t) = {{T}_{h}}$ = const получается следующая зависимость внедрения $\Delta (t)$ от ${{T}_{h}}$

9. Заключение. Точные решения связанной задачи термоупругости о скользящем термофрикционном контакте позволяют:

– установить области устойчивых и неустойчивых решений в области безразмерных параметров задачи;

– установить влияние связанности задачи на изменение границы областей устойчивых и неустойчивых решений, на собственные числа задачи, на основные параметры контакта – температуру и напряжения;

– решить частные задачи опосредованного мониторинга основных параметров скользящего контакта;

– решить частные задачи управления параметрами контакта за счет подбора закона внедрения жесткого тела.

Работа выполнена при финансовой поддержке Минобрнауки РФ (госзадание 9.1481.2017/4.6) и РФФИ (гранты 16-07-00929-а, 17-07-01376-а).