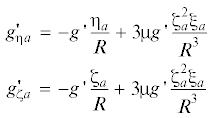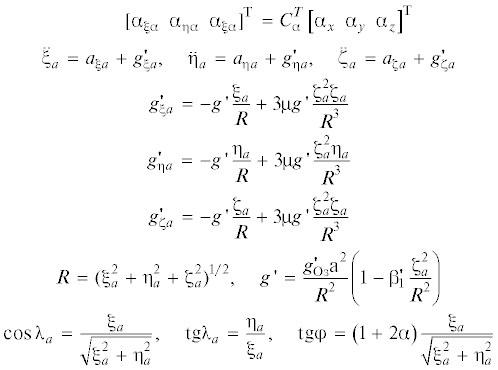Известия РАН. Механика твердого тела, 2019, № 2, стр. 48-62

1. Постановка задачи. К компьютерной механике будем относить теорию механических моделей, которые в природе и технике, относящиеся к инерциальной навигации, не созданы, а которые описываются аналитически и представлены в виде компьютерных программ функционирования, а также их решений. Как в составе действующих систем, так и на стадии математического или полунатурного моделирования. Одной из первых решенных задач компьютерной механики является открытое М. Шулером свойство невозмущаемости физического (математического) маятника к действию ускорений, точка подвеса которого перемещается по поверхности Земли. Это условие гласит, что плечо маятника должно равняться радиусу Земли, что физически невыполнимо. Еще до этого открытия он разработал физическую модель маятника Шулера в виде гиромаятниковой вертикали, а совместно с Аншютцем – в виде физически (технически) реализованных двухроторных гирокомпасов. Указанные широко применяемые приборы обладают свойством невозмущаемости к действию горизонтальных ускорений подвижного объекта, на котором устанавливаются. Следовательно, они не имеют так называемых баллистических погрешностей.

Развитие науки и техники привело к созданию платформенных инерциальных навигационных систем (ИНС) аналитического (АИНС), полуаналитического (ПИНС) и геометрического (ГИНС) типов, и во всех из них основу составляет та или иная модель маятника с периодом Шулера. При этом в АИНС применена виртуальная, т.е. компьютерная модель маятника Шулера, реализованного в БК, где использовались также и другие компьютерные вычисления. В ПИНС и ГИНС применялись физические гиромаятниковые модели, имеющие период Шулера [1–3].

Позже были созданы бесплатформенные инерциальные навигационные системы (БИНС) [4–8]. В процессе их создания разработаны элементы теории компьютерной механики БИНС, в которой наряду с реальными элементами, например, в виде датчиков первичной информации, были применены виртуальные, компьютерные модели систем с новыми, нереализуемыми на практике механическими принципами. В первую очередь, вместо гиростабилизированных платформ со сложными электромеханическими системами стабилизации и коррекции применены бортовые компьютеры, алгоритмы и программы работы которых базируются на кинематических дифференциальных уравнениях Эйлера, Пуассона, кватернионных или других, коэффициентами которых являются сигналы трехкомпонентных гироскопических измерителей угловых скоростей (ТГИУС) и трехкомпонентных измерителей кажущихся ускорений (ТИКУ). Их решениями являются кинематические параметры, с помощью которых определяются углы ориентации ПО, а также координаты местоположения его некоторой точки. Появились безгироскопные акселерометрические БИНС, в которых источниками первичной инерциальной информации выступают ТИКУ. Появились БИНС на основе ТГИУС и ТИКУ в качестве датчиков первичной информации, а вторичной – компьютерные модели разных гироприборов c коррекцией от маятников [6]. Принципиально новый тип БИНС предложен и описан в [7, 8] – в этих трудах в качестве датчика первичной информации использован пространственный осциллятор, а в тракте алгоритмов ориентации БК используются конечные соотношения.

Итак, к настоящему времени известны три типа платформенных инерциальных навигационных систем: ПИНС – полуаналитические, АИНС – аналитические, ГИНС – геометрические [1–3], а также три типа БИНС [4–8]: на основе ТГИУС или двухкомпонентных гироскопических измерителей угловых движений в совокупности с трехкомпонентными измерителями кажущихся ускорений (ТИКУ) [1–6], различающиеся между собой алгоритмами функционирования, на основе пространственных осцилляторов [7, 8], на основе акселерометрических (безгироскопных) датчиков [9]. В статье рассматриваются новые БИНС на основе пространственных осцилляторов [7, 8], чувствительным элементам которых аналогов в платформенных ИНС и БИНС нет; ИНС и БИНС на основе гироскопов и акселерометров [1–6]. Акселерометрические безгироскопные БИНС [9] не рассматриваются. Известно, что БИНС дешевле, чем платформенные ИНС; в производстве – не менее, чем на 25%, а в эксплуатации – на 75% [10].

В статье ставится задача: выявить и систематизировать вопросы использования компьютерной механики, в первую очередь, в теории нового класса БИНС [7, 8]. Проанализировать соотношение свойств этого класса БИНС со свойствами ИНС и БИНС, степень использования в них компьютерной механики, их достоинства. Дать сопоставительной анализ теории ПИНС и АИНС с аналогичными им по свойствам БИНС. Выделить в них элементы компьютерной механики и проанализировать их функционирование, соотношение погрешностей, а также достоинства, которые они обеспечивают.

2. БИНС на основе пространственного осциллятора. В [7] описана схема, представлены уравнения движения и алгоритмы управления эллиптической траекторией движения принимаемого за точку осциллятора БИНС МТ, подвешенного на объекте с помощью одинаковых по жесткости пружинок. В [8] наряду с осциллятором стержневого типа предложено использовать также либо сферическое тело, либо сферический гироскоп Эйлера на бесконтактном электростатическом подвесе (ЭСП). В последнем случае чувствительный элемент представляет собой вращательно-осциллирующее тело. Показано, что прибор определяет полную первичную инерциальную информацию. Особенность БИНС МТ состоит в том, что матрица ориентации находится не путем интегрирования уравнений Пуассона, а в виде конечных соотношений по приращениям амплитуд поступательных колебаний тела и, как следствие, компонентов указанной матрицы за короткие промежутки времени. Этот подход изложен ниже. Если предположить вначале, что подвижный объект совершает только вращение вокруг неподвижной точки, то любое свободное движение этого осциллятора представляет собой эллиптическую траекторию, не меняющую свою ориентацию в инерциальной системе координат.

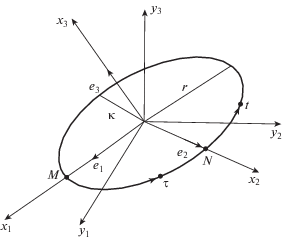
При съеме информации о положении осциллятора в момент его нахождения в максимально удаленной от точки подвеса точки эллипса M, фиг. 1, и в ближайшей к центру точке N и если вычислить векторное произведение соответствующих единичных векторов ${{e}_{1}} \times {{e}_{2}} = {{e}_{3}}$, то матрица $A = \left\| {{{e}_{1}},{{e}_{2}},{{e}_{3}}} \right\|$, составленная из этих векторов, и является искомой матрицей поворота. С ее помощью переводят подвижную систему отсчета у в инерциальную х. В общем случае ускоренного движения ПО центр рассматриваемого эллипса будет смещаться в сторону, противоположную ускорению, и перед выполнением указанных выше процедур следует выделить из показаний осциллятора ${{x}_{u}} = x + \Delta x$ гармоническую часть x. Оставшаяся медленно изменяющаяся часть информации Δx пропорциональна кажущемуся ускорению и используется далее для построения алгоритмов определения координат местоположения ПО, т.е. навигационных алгоритмов.

Уравнения движения и алгоритмы функционирования БИНС МТ имеют вид [7, 8]:

где A – матрица поворота; x, y – векторы поступательных колебательных составляющих движения осциллятора в инерциальной системе координат и в объектовой системе координат. При этом y – вектор измеренных датчиками переменных. Для обеспечения устойчивости эллиптической траектории в уравнение (2.3) вводится управляющее воздействие, в силу чего оно приобретает вид: где ${{k}_{0}},k$ – начальная и текущая квадратуры; ${\varepsilon },{\mu }$ – коэффициенты. Уравнение (2.4) рассматривается на интервале, где матрица A = const. Эта матрица определяется в бортовом вычислителе непрерывно с учетом настройки отсчетного генератора на асимптотически устойчивый режим согласно уравнению (2.4). Решение уравнения (2.4) представляется в форме: где угол t определяет мгновенное положение точки на эллипсе фиг. 1; u, $v$ – трехмерные векторы произвольных постоянных. Так как r и k – длины большой и малой полуосей эллипса, имеет место r = |u|, k = |$v$|, ${\tau }$ = 0, и алгоритм определения матрицы поворота A имеет вид:

Навигационный алгоритм имеет вид (в реальном масштабе)

где ${\ddot {I}}$$,{{a}_{k}}$ – векторы абсолютного и кажущегося ускорений ПО, g – ускорение силы тяготения. По аналогии с [3, 15] ${\;}{{a}_{k}}$ определяется как сила реакции деформации подвеса по алгоритму:

Здесь k – коэффициент жесткости подвеса, m – масса осциллятора, $\Delta x$ – медленно изменяющаяся часть деформации подвеса осциллятора. Должны быть учтены начальные координаты и скорости ПО. Пересчет переменных производится по формуле:

Проанализируем процесс функционирования БИНС МТ. Создание режима осцилляции точки по заданным инерциальным осям аналогично режиму стабилизации платформы трехосного гиростабилизатора, чему соответствуют соотношения для АИНС [3]. Это – принцип классической механики. В БИНС МТ этот режим описывается дифференциальными уравнением и алгоритмами (2.1)–(2.5). Формирование матрицы поворота А, пересчет измеренной информации к осям инерциальной системы координат о соотношения (2.5)–(2.6) – это элементы компьютерной механики, что отсутствует в АИНС. И, наконец, определение координат местоположения ПО по алгоритмам (2.7)–(2.8) – это принцип компьютерной механики, что имеет место и в АИНС [3]. Нетрудно видеть, что по функционированию БИНС МТ аналогична АИНС: в них физически моделируется не вращающийся в инерциальном пространстве трехгранник, и по его трем осям также физически определяются три компонента кажущегося ускорения. Что касается отличия АИНС от БИНС МТ, то в последней матрица поворота определяется аналитически, на основе измерений параметров эллипса движения осциллирующей точки. Это производится по конечным соотношения (2.6). В БИНС интегрируется система дифференциальных кинематических уравнений Пуассона 9-го порядка (или других параметрах), что сопровождается накоплением погрешностей ориентации. Следует отметить, что в теории данного типа БИНС подлежит более глубокой проработке задача по определению свойств осциллятора при действии возмущающих сил и моментов сил.

3. Свойства полуаналитической инерциальной навигационной системы и ее бесплатформенного аналога – БИНС. 3.1. Схема ПИНС [1, 13] представлена на фиг. 2.

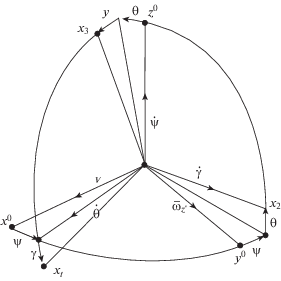
На фиг. 4 представлены повороты подвижного объекта, с которым связана система координат $o{{x}_{1}},{{x}_{2}}{{x}_{3}}$, относительно системы координат oxyz, связанной с платформой 2, на углы рыскания $\quad{\psi }$, тангажа θ и крена ${\gamma }$, измеряемые датчиками углов 13, 14, 15. При этом ось $o{{x}_{2}}$ – продольная, $o{{x}_{3}}$ – нормальная, $o{{x}_{1}}$ – поперечная, направленная на правый борт ПО. На фиг. 5 изображены повороты платформы 2 на углы ошибок стабилизации. Моменты сил коррекции M_i $(i = 1,2,3)$ в ПИНС определяются выражениями [2]:

На фиг. 5 изображены повороты платформы ПИНС на углы погрешностей. Формулы для определения угловых скоростей платформы 2 – реальные сигналы, соответствующие уравнениям прецессионного движения:

где K – коэффициент передачи интегральной коррекции; H – кинетический момент; ${{{\omega }}_{x}},{{{\omega }}_{y}},{{{\omega }}_{z}}$ – угловые скорости трехгранника oxyz; ${{V}_{x}}\left( 0 \right),{{V}_{y}}\left( 0 \right)$ – начальные значения абсолютной скорости точки О по осям Ox, Oy; ${{a}_{x}},{{a}_{y}}$ – кажущиеся ускорения, измеряемые ньютонометрами по соответствующим осям платформы 2, причем при отсутствии у них погрешностей оценки сигналов ньютонометров ${{\hat {W}}_{x}},{{\hat {W}}_{y}}$ совпадают с истинными кажущимися ускорениями (${{a}_{x}},{{a}_{y}}$): ${{a}_{x}} = {{W}_{x}};{{a}_{y}} = {{W}_{y}}$.

Навигационные алгоритмы ПИНС [1, 2] имеют вид

где ${{\phi }_{0}},{{{\lambda }}_{0}},{{{\chi }}_{0}}$ – начальные значения географических широты, долготы и угла ${\chi }$ между осями $o{\xi }$ и $ox'$ (фиг. 2). Уравнения (3.4) описывают навигационные параметры ПО. Высота ПО может быть определена по сигналам ТИКУ. Решается навигационная задача с помощью бортового компьютера. Это – принцип компьютерной механики. Для ПИНС, после проведения точной начальной выставки по углам и угловым скоростям платформы 2, обеспечиваются условия настройки параметров горизонтальной коррекции и гироскопов на частоту Шулера [1, 2]

В данном случае применен принцип физического моделирования маятника Шулера в горизонтной системе координат с помощью гироскопов и акселерометров.

Рассмотрим уравнения ошибок стабилизации платформы 2 в системе координат, одна из осей которых направлена по вектору абсолютной скорости ПО [1]

Итак, система ориентации на основе ТГС и маятник Шулера на основе гироскопов и акселерометров – это устройства электромеханики, отражением которых являются формулы (1), (2), а уравнения навигации (5) – это алгоритмы функционирования БК – признак компьютерной механики.

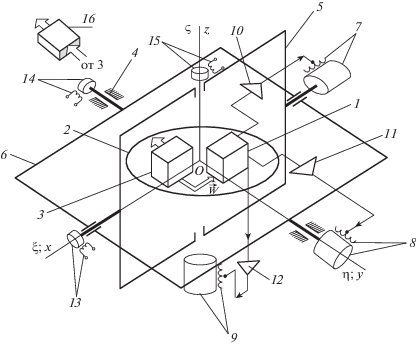
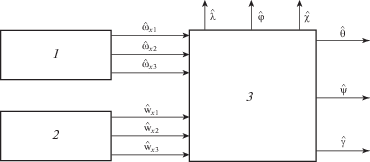
3.2. Схема и свойства БИНС – аналога ПИНС. Функциональная схема БИНС представлена на фиг. 6; базируется (кроме ТГИУС и ТИКУ) на принципах компьютерной механики [8]. На фиг. 6 введены обозначения: 1 – трехкомпонентный гироскопический измеритель угловой скорости; 2 – трехкомпонентный измеритель кажущегося ускорения; 3 – бортовой компьютер.

По решаемым задачам и свойствам аналогична рассмотренной в предыдущем параграфе ПИНС.

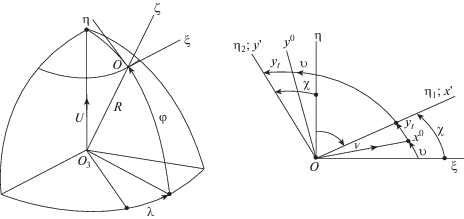
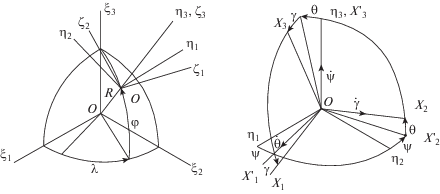
В ее состав входят трехкомпонентный гироскопический измеритель угловой скорости (ТГИУС) и трехкомпонентный измеритель кажущегося ускорения (ТИКУ) центра масс подвижного объекта (ПО). Предполагается, что ТГИУС и ТИКУ состоят из установленных на борту ПО датчиков высокой точности, характерной для БИНС. Параметры ориентации ПО определяются в бортовом компьютере (БК) по приведенным ниже алгоритмам в виде оценок углов рыскания ${\hat {\psi }}$, тангажа ${\hat {\theta }}$ и крена ${\hat {\gamma }}$, а также по навигационным параметрам, аналогичным приведенным в предыдущем параграфе. В данном параграфе сохранены обозначения переменных и констант, принятые в статье [11]. Вводятся в рассмотрение следующие правые ортогональные системы координат (фиг. 7): ξ – инерциальная; η – азимутально-свободная горизонтная [1, 2], ось ${{O}_{{{{\eta }_{2}}}}}$ которой направлена по вертикали места, а оси ${{O}_{{{{\eta }_{1}}}}}$ и ${{O}_{{{{\eta }_{3}}}}}$ лежат в плоскости горизонта; X – система координат, связанная с ПО, причем ось ОХ1 – продольная, ОХ2 – нормальная, OX3 – поперечная, направленная на правый борт. Точку О совмещаем с центром масс ПО; X' – система координат, поворачивающаяся относительно η на угол рыскания; ξ – географическая сопровождающая система координат; ψ, η, γ – углы рыскания, тангажа и крена; Ψ – угол курса (не показан).

Здесь λ, φ – углы географических долготы и широты места; R – радиус Земли, принятой за сферу; Оз – центр Земли;, ω_ηi, W_ηi (i = 1, 2, 3) компоненты переносной угловой скорости системы координат η и кажущегося ускорения точки О по ее осям; ω_xi, W_xi (i = 1, 2, 3) – компоненты переносной угловой скорости ПО и кажущегося ускорения точки О по осям $O{{X}_{i}}$ (i = 1, 2, 3) соответственно – сигналы реальных ТГИУС и ТИКУ. Переносные угловые скорости трехгранника η в проекциях на его оси определяются по формулам:

Здесь V_η1, V_η2 – компоненты абсолютной скорости точки О ПО.

Рассмотрим алгоритмы блока ориентации

Отметим, что БК по алгоритмам (3.7)–(3.9) для БИСО моделирует работу горизонтальной свободной в азимуте платформы, аналогичной платформе гиростабилизатора ПИНС. Навигационный алгоритм имеет такой же вид, что и (3.4) с заменой в угловых скоростях индексов хi на индексы ηi (i = 1, 2, 3).

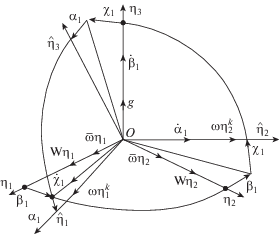
Ниже дан анализ уравнений ошибок БИСО. На фиг. 8 представлена схема поворотов моделируемой в БК горизонтной смстемы координат на углы ошибок. После выкладок получаем следующие уравнения ошибок БИСО относительно трехгранника ${\eta }$ А.Ю. Ишлинского, не вращающегося по азимуту (для установившегося режима, когда члены позиционной коррекции отключены и выполнены условия Шулера):

Данный случай можно с геометрической точки зрения сопоставить с размещением БИСО на горизонтальной площадке, т.е. уравнениям движения платформы 2 гиростабилизатора ПИНС. В [11], как и в [1, 2] для ПИНС, учтены абсолютные погрешности ТГИУС и ТИКУ, и уравнения (3.12) аналогичны уравнениям (3.1)–(3.3) движения платформы ПИНС с учетом раскрытия в них выражений для угловых скоростей.

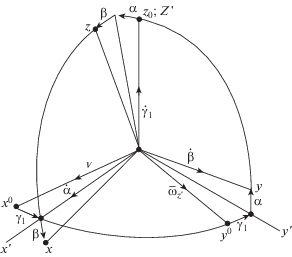
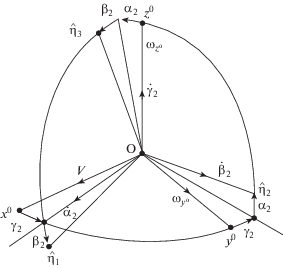
Следует отметить, что в БИНС имеет место принцип компьютерной механики. Показано также, что для БИНС по фиг. 6 уравнения ошибок в системе координат, одна из горизонтальных осей которой совпадает с вектором скорости ПО, с точностью до обозначений совпадают с уравнениями (3.6) для ПИНС, свидетельствуя об общности свойств ПИНС и БИНС. Рассмотрим уравнения ошибок в системе координат, одна из горизонтальных осей которой совпадает с вектором скорости. Выведем уравнения ошибок для углов α₂, β₂, γ₂ для БИНС (вместо углов α, β, γ для фиг. 5 для ПИНС) в горизонтной системе координат Оx⁰y⁰z⁰, одна ось которой направлена по вектору V скорости ПО – фиг. I . Имеют место формулы [1, 2]:

Для кажущегося ускорения $W_{{z0}}^{K}$ имеем: $W_{{z0}}^{K} = g\quad - \frac{{{{V}^{2}}}}{R}$.

Приняв обозначения по [1, 2] для условий Шулера

и положив, что после проведения начальной выставки отключается позиционная коррекция, так что K_θ = K_γ = 0, будем иметь следующие дифференциальные уравнения горизонтальных каналов и по азимуту (φ ≡ θ ≡ γ ≡ 0) платформы 2:

Согласно фиг. 9, на которой представлены повороты модели платформы на углы ошибок в СК $o{{x}^{0}}{{y}^{0}}{{z}^{0}}$, после преобразований, для случая отсутствия угловых скоростей дрейфов, получаем выражения:

Выражения для ускорений точки О ПО:

После этого уравнениям придаем форму:

С точностью до обозначений данные дифференциальные уравнения ошибок “платформы” БИНС совпадают с аналогичными уравнениями (3.6) платформы 2 ПИНС. Это свидетельствует об аналогии свойств ПИНС и БИНС.

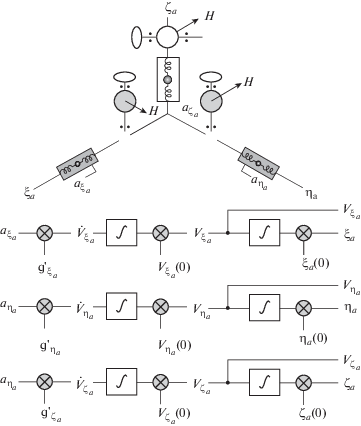
4. Сопоставление свойств АИНС и БИНС. 4.1. Аналитическая инерциальная навигационная система. Схема размещения на платформе трехосного гиростабилизатора АИНС, оси которой направлены по осям инерциальной системы координат и на которой размещены тройка двухстепенных гироскопов и тройка акселерометров, представлена на фиг. 10 [3] (реальные приборы и платформа). Полная кинематическая схема АИНС почти такая же как ПИНС на фиг. 1, но в ней отсутствуют связи коррекции от акселерометров к гироскопам. На фиг. 10 представлены кинематика платформы и структурная схема БК по введению поправочных гравитационных ускорений в сигналы акселерометров, а также вычисления скоростей и координат ПО с помощью трех сумматоров и двух интеграторов в каждом канале. Трехосный гиростабилизатор с ТИКУ есть физико-техническая реализация АИНС. Его уравнения по [3]:

– угловые скорости реальной платформы. Блок БК по схеме фиг. 10 – это компьютерная модель маятника Шулера и счисления скоростей и координат ПО.

Алгоритмы функционирования БК АИНС имеют вид:

Уравнения ошибок АИНС имеют вид:

4.2. БИНС – аналог АИНС. В рассматриваемом случае ориентация трехгранника XYZ определяется по проекциям его абсолютной угловой скорости ω_x, ω_y, ω_z на оси X, Y, Z, которые измеряются тремя гироскопическими датчиками абсолютной угловой скорости, ${{{\omega }}_{x}} = {{{\omega }}_{x}}(t);\quad$ ${{{\omega }}_{y}} = {{{\omega }}_{y}}(t);$ ${{{\omega }}_{z}} = {{{\omega }}_{z}}(t)$ – сигналы реального ТГИУС.

Алгоритмы функционирования БИНС – аналога АИНС

Уравнения ошибок ориентации БИНС

Уравнения по координатам поступательных движений совпадают с (4.6). Кроме уравнений (4.1)–(4.2) физической платформы АИНС, остальные алгоритмы и уравнения ошибок АИНС и БИНС совпадают, что подтверждает аналогию свойств этих систем. Сопоставление свойств АИНС и БИНС, произведенное по [3], показало, что, кроме уравнений физической платформы АИНС, оси которой ориентированы по осям инерциальной системы координат, или моделируемой в БК БИНС аналогичной платформы, остальные алгоритмы и уравнения ошибок АИНС и БИНС совпадают, что подтверждает аналогию свойств этих систем.

Заключение. 1. Выдвинуто положение о компьютерной механике в ИНС, подтвержденное примерами.

2. По степени использования принципов компьютерной механики ИНС можно расположить в такой последовательности: БИНС МТ, БИНС, ПИНС, АИНС, ГИНС.

3. В бесплатформенных системах наименее сложные алгоритмы присущи БИНС МТ, а также БИНС на основе трехстепенных гироскопов (электростатических и других). Это объясняется тем, что в них отсутствует процедура интегрирования дифференциальных кинематических уравнений – матрица поворота определяется по конечным соотношениям. Поэтому отсутствуют погрешности из-за расходимости их решений.

4. Компьютерная механика обеспечивает возможность моделирования в БК БИНС инерциальных системы координат, а также маятника Шулера; обеспечивает моделирование функций трехосных гиростабилизаторов по кинематическим уравнениям Эйлера (по кватернионным, по уравнениям Пуассона), а также на основе второго закона Ньютона – по сигналам гироскопов и акселерометров. При этом, для горизонтально ориентированных платформ ИНС дифференциальные уравнения маятника Шулера – это системы по два уравнения второго порядка – (3.6) для ПИНС, (3.11) и (3.16) для БИНС, а при ориентированных в инерциальных системах координат – это системы по три уравнения второго порядка – (4.6) как для АИНС, так и для БИНС.