Известия РАН. Механика твердого тела, 2019, № 2, стр. 29-47

1. Введение. Нелинейное определяющее соотношение (ОС) Работнова [1–19] описывает одномерные изотермические процессы деформирования структурно-стабильных (нестареющих) реономных материалов, связывая истории напряжения $\sigma (t)$ и деформации $\varepsilon (t)$ в данной точке тела:

Здесь $\Pi (t)$, $R(t)$ – функции ползучести и релаксации, а $\varphi (u)$ – дополнительная материальная функция (МФ), введенная Ю.Н. Работновым [1–3]. Входные процессы ($\sigma (t)$ или $\varepsilon (t)$) предполагаются кусочно непрерывными и кусочно-гладкими на любом отрезке. ОС (1.1) обобщает линейное ОС вязкоупругости (получающееся при $\varphi (u) = u$):

Если $\Pi (0 + ) \ne 0$ (модель регулярна), то $R(0 + ) < \infty $ и на линеале непрерывных кусочно гладких при $t \geqslant 0$ функций (взаимно обратные) операторы (1.1) представимы в виде

ОС (1.3) с регулярной ФП было предложено Ю.Н. Работновым еще в 1948 г. [1]. В [1–3] ОС (1.3) называлось “соотношением наследственной теории ползучести” и “пластичности”, в [4] было дано название “нелинейная теория наследственности”. В англоязычных публикациях ОС (1.1) называется уравнением квазилинейной вязкоупругости (“QLV”) [20–37], а его автором считается Y.C. Fung со ссылками на его работы 1970–1990-х годов [20, 25]. В [1–19] ОС (1.1) прилагались к описанию поведения металлов и сплавов, стеклопластиков, графита, а в [20–37] – связок, сухожилий и др. биологических тканей. В работах [1–19] авторы рассматривали случай малых деформаций (и номинальных напряжений), выбирали ядро ползучести степенным или дробно-экспоненциальным ядром Работнова, его параметры (3–4 штуки) находили по кривым ползучести в линейной области (где $\varphi (u) = u$), а затем МФ φ(u) определяли численно в отдельных точках по экспериментальным кривым ползучести и деформирования – без использования аналитических представлений для $\varphi $ (за исключением полинома четвертого порядка в [5, 9] и степенной функции $\varphi (u) = c{{u}^{{0.75}}}$ в [17]), “при помощи программ Maple и Excel” [17]. Тщательное аналитическое изучение общих свойств основных квазистатических кривых (кривых ползучести и релаксации с произвольной начальной стадией нагружения до заданного уровня, ползучести при ступенчатых нагружениях, диаграмм деформирования при постоянных и кусочно постоянных скоростях нагружения, при циклическом нагружении и др.), порождаемых ОС (1.1) с произвольными МФ $\Pi (t)$ и φ(u), систематическое исследование комплекса моделируемых (и не моделируемых) эффектов в зависимости от характеристик МФ и необходимых феноменологических ограничений на МФ $\varphi $ не проводились в [1–37 ]; границы области применимости ОС (1.1) и их маркёры (за исключением требования подобия изохронных кривых ползучести в [1–9] и подобия кривых релаксации в [31–33]) выявлены не были. Аналитическое исследование этих свойств в общем виде (даже при малых деформациях в одноосном случае) или хотя бы краткий перечень отсутствуют в литературе по вязкоупругости, вязкопластичности, ползучести и механике полимеров, в частности, в монографиях [3, 9, 32, 38–48]).

Цель данной статьи (и всего цикла работ [49–52], посвященных анализу ОС (1.1)) – восполнить указанные пробелы, выявить возможности и преимущества ОС (1.1) (как по сравнению с линейным ОС (1.2), так и с более сложными нелинейными ОС) и способствовать расширению и уточнению сферы его обоснованного применения в моделировании поведения реономных материалов с выраженной нелинейной наследственностью и скоростной чувствительностью (полимеров, композитов, пен, керамик, асфальтобетонов, твердых топлив, алюминиевых и титановых сплавов, нержавеющих сталей, связок, сухожилий, стенок сосудов и других биологических тканей). Задача данной статьи – изучение общих свойств диаграмм деформирования (ДД) при постоянных скоростях нагружения, порожденных ОС (1.1) с произвольными МФ $\Pi $ и $\varphi $, – как унаследованных от ДД линейного ОС (1.2), так и новых, специфичных для нелинейного ОС (1.1).

К ОС (1.1) применяется технология качественного анализа определяющих соотношений для реономных материалов, разработанная ранее автором в цикле работ [53–63]. В них изучены два новых нелинейных ОС, учитывающие историю деформирования (или нагружения) и старение материала [53–55], линейное ОС вязкоупругости (1.2) [56–59] и нелинейная модель типа Максвелла с двумя МФ [60–63]. Все эти ОС, как и (1.1), нацелены на описание комплекса основных реологических эффектов, типичных для материалов, обладающих наследственностью и высокой чувствительностью к скорости деформирования (нагружения).

В статье приняты следующие сокращения и обозначения: МФ – материальные функции; (${{\omega }_{ - }}$; ${{\omega }_{ + }}$) и ($\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} $; $\bar {x}$) – области определения и значений МФ $\varphi (u)$, $\bar {x}: = \sup \varphi (x)$; ω – краткое обозначение для ${{\omega }_{ + }}$; ${{D}_{\varphi }}: = \left[ {0;\omega } \right)$; $\Phi = {{\varphi }^{{ - 1}}}$, ${{D}_{\Phi }}: = \left[ {0;\bar {x}} \right)$; ДД – диаграмма деформирования $\sigma (\varepsilon ,b)$ при постоянной скорости нагружения (СН) b; ФР и ФП (КР, КП) – функции (кривые) релаксации и ползучести; $\operatorname{h} (t)$ – функция Хевисайда, δ(t) – дельта-функция; РеМ – регулярные модели (с $\Pi (0) \ne 0$); СиМ – сингулярные модели (ФР содержит слагаемое $\eta \delta (t)$); $y(0): = y(0 + )$ – предел функции y(t) справа в т. t = 0.

2. Материальные функции соотношения Работнова. Линейное ОС вязкоупругости (1.2), инвариантное относительно сдвигов по времени, получается из (1.1) при $\varphi (u) = u$ и содержит лишь одну независимую МФ, так как ФП и ФР связаны условием взаимной обратности интегральных операторов (1.2) (“the interconversion relation”):

Зная ФР, можно найти ФП из уравнения (2.1), и обратно. Поэтому из трех МФ φ, Π, R в ОС (1.1) лишь две независимы, а тождество (2.1) является условием взаимной обратности операторов (1.1), отображающих друг в друга функции σ(t) и $e(t) = \varphi (\varepsilon (t))$.

На ФП и ФР в ОС (1.1) наложим априори те же минимальные ограничения, что и в линейной теории: Π(t) и R(t) должны быть положительными и дифференцируемыми на интервале $(0;\infty )$, Π(t) – возрастающей, выпуклой вверх, а ФР R(t) – убывающей и выпуклой вниз на $(0;\infty )$ (ФР может иметь интегрируемую особенность или δ-сингулярность в точке t = 0). Из этих условий следует, в частности, существование пределов $\Pi (0 + ) \geqslant 0$, $\dot {\Pi }( + \infty ) \geqslant 0$ и $R( + \infty ) \geqslant 0$ [57].

Свойства основных теоретических кривых, порождаемых линейным ОС вязкоупругости (1.2) с произвольной ФП, и необходимые феноменологические ограничения на ФП и ФР проанализированы в цикле работ [56–59] и др. Анализ, в частности, показал, что среди моделей, описываемых ОС (1.2) с различными ФР и ФП, необходимо различать (как минимум) три основных класса, поскольку качественные свойства базовых кривых моделей этих классов (а также особенности постановки и решения краевых задач) заметно отличаются: 1) регулярные модели (РеМ) – у которых $\Pi (0) \ne 0$ (тогда мгновенный модуль $E = R(0 + ) = 1{\text{/}}\Pi (0 + )$ конечен, а ОС (1.2) и первое уравнение (2.1) сводятся к уравнениям Вольтерры второго рода (1.3) с $\varphi (u) = u$ и (2.1)); 2) сингулярные (СиМ) – с ФР, содержащей слагаемое $\eta \delta (t)$, $\eta > 0$ (ФР $R = \eta \delta (t)$ задает ньютоновскую жидкость с ОС $\sigma = \eta \dot {\varepsilon }$ и входит слагаемым в ФР “половины” реологических моделей из пружин и демпферов), тогда Π(0) = 0 и $\dot {\Pi }(0) = {{\eta }^{{ - 1}}}$; 3) нерегулярные модели с неограниченной ФР (НеМ), не содержащей слагаемого $\eta \delta (t)$, но имеющей интегрируемую особенность в т. t = 0 ($R(0 + ) = + \infty $). Третий класс занимает промежуточное положение между первыми двумя. К нему относится, например, ФР R(t) = $A{{t}^{{ - u}}}$, $u \in (0;1)$, A > 0, задающая “фрактальный” элемент “фрактальных” моделей (“fractional models”); соответствующая ФП имеет вид $\Pi (t) = {{A}^{{ - 1}}}C(u){{t}^{u}}$, C(u) = = ${{(u\pi )}^{{ - 1}}}{\text{sin}}u\pi $, и обладает не только свойством Π(0) = 0, как и СиМ, но и свойством $\dot {\Pi }(0) = \infty $, переходным к $\Pi (0) \ne 0$, характеризующему РеМ.

Линейным ОС (1.2) задаются, в частности, все модели, собранные из линейных пружин и демпферов посредством параллельных и последовательных соединений (ФП классических реологических моделей будут использованы для иллюстрации общих свойств ДД ОС (1.1)). Можно доказать, что множество всех несократимых n-звенных моделей распадается ровно на два класса эквивалентности: РеМ-n и СиМ-n (структурно различные модели эквивалентны, если задаются одинаковыми семействами ФП или ФР). В частности, эквивалентны друг другу трехзвенные РеМ Пойнтинга–Томсона и Кельвина ([57], фиг. 1а), а все четыре РеМ-4 ([57], фиг. 1в) эквивалентны модели стандартного тела (последовательному соединению моделей Максвелла и Фойгта, т.е. РеМ-2 и СиМ-2). Например, семейство

удовлетворяет всем ограничениям на ФП. Оно порождает все РеМ-4 при $\gamma \in (0;\beta )$, $\alpha ,\beta > 0$, а при α = 0 – все РеМ-3. Так как $\Pi (0) = \beta - \gamma $, то ФП (2.2) порождает СиМ, когда γ = β: при $\lambda \beta = 0$ – ньютоновскую жидкость, при α = 0 – модель Фойгта (СиМ-2), при α > 0 – все СиМ-3. При γ = 0 семейство (2.2) дает модель Максвелла.

На МФ φ(u) в ОС (1.1) наложим следующие минимальные априорные требования (анализ покажет, нужно ли дополнить их список): функция φ(u), $u \in ({{\omega }_{ - }};{{\omega }_{ + }})$, непрерывно дифференцируема и строго возрастает на $({{\omega }_{ - }};0) \cup (0;{{\omega }_{ + }})$ (где ${{\omega }_{ - }}{{\omega }_{ + }} < 0$), причем $\varphi (0 + ) = \varphi (0 - ) = 0$ (иначе процессу $\varepsilon (t) \equiv 0$ соответствует ненулевой отклик σ(t)). Формально возможны случаи ${{\omega }_{ - }} = - \infty $ и ${{\omega }_{ + }} = + \infty $, и случай $\varphi {\text{'}}(0) = + \infty $. Для материалов с одинаковым поведением при растяжении и сжатии МФ $\varphi (u)$ нечетна, ${{\omega }_{ - }} = - {{\omega }_{ + }}$. Из возрастания φ(u) следует существование обратной функции $\Phi : = {{\varphi }^{{ - 1}}}$ на промежутке ${{D}_{\Phi }} = (\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} ;\bar {x})$, где $\bar {x}: = \sup \varphi (u) = \varphi ({{\omega }_{ + }} - 0)$, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} : = \inf \varphi (u) = \varphi ({{\omega }_{ - }} + 0)$, и обратимость ОС (1.1). Величины $\bar {x}$ и $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} $ – важные характеристики МФ φ и Φ, существенно влияющие на поведение теоретических кривых ОС (1.1) [49–52].

Конечность ${{\omega }_{ + }}$ или $\bar {x}$ (или ${{\omega }_{ - }}$ и $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} $) означает, что, благодаря такому выбору МФ, в ОС (1.1) встроен критерий разрушения при растяжении (при сжатии), обеспечивающий обрыв теоретических кривых (ползучести, деформирования и др.) в некоторый момент времени. В этом случае их можно интерпретировать как материальные параметры, через которые выражаются предел прочности, предельная деформация, время разрушения [49]. Например, задача моделирования с помощью ОС (1.1) дробно-линейной зависимости Шестерикова-Юмашевой [64] для скорости ползучести от напряжения $r(x) = Ax{\text{/}}({{\sigma }_{*}} - x)$, $x \in \left[ {0;{{\sigma }_{*}}} \right)$, приводит к МФ

с ${{\omega }_{ + }} = + \infty $ и с конечным $\bar {x} = {{\sigma }_{*}}$ [49].

Для задания МФ φ или Φ удобно, например, пятипараметрическое семейство (оно будет использовано для иллюстрации свойств диаграмм деформирования ОС (1.1))

При любых значениях параметров (кроме $\vartheta = 0;\,1$) $y(0) = 0$, $y{\text{'}}(0) = \infty $, $y(C) = A$, функция y(x) возрастает и имеет точку перегиба

Весовой параметр $\vartheta \in (0;1)$ позволяет совместить точку перегиба (2.5) с любой точкой x > 0 и описать кривые ползучести со всеми тремя стадиями [49]. Семейство (2.4) убывает по ϑ на интервале $x \in (0;C)$ и возрастает на $(C;\infty )$. В случае $m = 1{\text{/}}n$ семейство (2.4) стремится при $n \to 1 + 0$ к линейной функции $y = A{{C}^{{ - 1}}}x$, то есть МФ $\varphi $ или $\Phi $ в ОС (1.1) “исчезает” и нелинейное ОС превращается в линейное ОС (1.2).

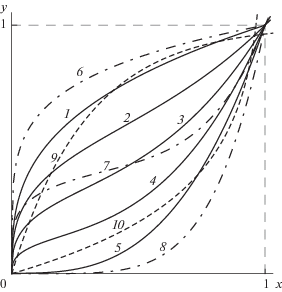
На фиг. 1 приведены графики функций (2.4) с $m = 1{\text{/}}n$, n = 3, $A = C = 1$ и $\vartheta = 0$; 0.25; 0.5; 0.75; 1 (линии 1–5) и графики при n = 5 и $\vartheta = 0;\;0.5;\;1$ (штрих-пунктирные линии 6–8). С ростом $n$ $\varphi {\text{'}}(x)$ в окрестностях точек x = 0 и x = 1 возрастают. Штриховые линии 9, 10 – графики взаимно обратных МФ (2.3) с ${{\sigma }_{*}} = 1$, $A = 0.25$.

При u < 0 можно определить φ(u) формулой $\varphi (u) = - y( - u)$, причем для материала с разными свойствами при растяжении и сжатии можно взять разные наборы пяти параметров функции (2.4) при u < 0 и u > 0 (условия $y(0) = 0$, $y{\text{'}}(0) = \infty $ обеспечивают гладкую склейку МФ $\varphi $ в точке u = 0 при любом выборе параметров).

3. Семейства кривых релаксации и ползучести ОС Работнова. Кривые релаксации (КР), порождаемые ОС (1.1) при мгновенном деформировании $\varepsilon (t) = \bar {\varepsilon }h(t)$ до уровня $\bar {\varepsilon } \in ({{\omega }_{ - }};{{\omega }_{ + }})$, имеют вид

КР с $\bar {\varepsilon } > 0$ убывают и выпуклы вниз по t и возрастают по $\bar {\varepsilon }$ (т.е. ОС (1.1) воспроизводит основные качественные свойства типичных экспериментальных КР), ибо R(t) убывает и выпукла вниз, а φ(u) возрастает. КР (3.1) подобны и имеют точно такую же форму, как и у линейного ОС (1.2), но зависимость КР от $\bar {\varepsilon }$ уже не линейна, а задается МФ φ. Существенно, что МФ φ не влияет на форму КР и на время (спектр, скорость) релаксации. Подобие КР материала – важный индикатор применимости ОС (1.1). Разделение переменных в уравнении (3.1) позволяет, в принципе, определить обе МФ по нескольким КР материала для разных $\bar {\varepsilon }$ (если наблюдается их подобие).

Кривые ползучести ОС (1.1) при мгновенном нагружении $\sigma (t) = \bar {\sigma }\,h(t)$ имеют вид:

где $\bar {x}: = \sup \varphi (u)$, $\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x} : = \inf \varphi (u)$. Семейство КП (3.2) возрастает по $\bar {\sigma }$ (ибо Φ возрастает), а при любом $\bar {\sigma } > 0$ (будем рассматривать этот случай) КП возрастает по t на всем промежутке, где $\bar {\sigma }\,\Pi (t) < \bar {x}$. Если $\bar {x} = \infty $ (как для линейного ОС (1.2)), то КП с $\bar {\sigma } > 0$ определены при всех $t \geqslant 0$. Если же $\bar {x} < \infty $, то $\bar {\sigma }\Pi (t) \in {{D}_{\Phi }}$ только при $\bar {\sigma } < \bar {x}{\text{/}}\Pi (0)$ и $\Pi (t) < \bar {x}{\text{/}}\bar {\sigma }$; это означает, что КП (3.2) существует только для напряжений $\bar {\sigma } < {{\sigma }_{ + }}$, ${{\sigma }_{ + }}: = \bar {x}{\text{/}}\Pi (0)$ и обрывается в момент ${{t}_{*}}$, удовлетворяющий уравнению $\Pi ({{t}_{*}}) = \bar {x}{\text{/}}\bar {\sigma }$, если $\bar {\sigma } > \bar {x}{\text{/}}\Pi (\infty )$ (если $\Pi (\infty ) < \infty $, то КП (3.2) с $\bar {\sigma } < \bar {x}{\text{/}}\Pi (\infty )$ не обрывается).

Таким образом, если $\bar {x} < \infty $ и $\Pi (0) \ne 0$, то параметр ${{\sigma }_{ + }}: = \bar {x}{\text{/}}\Pi (0) = E\bar {x}$ имеет смысл предела (мгновенной) прочности при растяжении, и в ОС (1.1) уже встроен критерий разрушения. Если ${{\omega }_{ + }} < \infty $, разрушение при растяжении происходит по достижению критической деформации: ${{\varepsilon }_{*}}: = \Phi (\bar {x}) = {{\omega }_{ + }}$ (такой физический смысл можно придать параметру ω₊). Уравнение кривой длительной прочности при растяжении:

где p(x) – обратная функция к Π(t), $E: = 1{\text{/}}\Pi (0)$, ${{E}_{\infty }}: = 1{\text{/}}\Pi (\infty )$ – мгновенный и длительный модули диаграмм деформирования линейного ОС (1.2) [56, 57].

Изохронные КП $\sigma = \varphi (\varepsilon ){\text{/}}\Pi (t)$ подобны; это один из необходимых признаков применимости ОС (1.1). В работах [1–19] подобие изохронных КП материала трактовалось как достаточное условие применимости ОС (1.3).

Подробный анализ свойств кривых релаксации, ползучести и длительной прочности, порождаемых ОС (1.1), проведен в работах [49–52].

4. Свойства диаграмм деформирования с постоянной скоростью нагружения. Найдем отклик ОС (1.1) на процессы вида $\sigma = bt$, t > 0, где b > 0 – скорость нагружения:

то есть $\varepsilon (t) = \Phi (bQ(t))$ при $bQ(t) \in {{D}_{\Phi }}$. Это параметрическое задание ДД. Удобно переписать его в форме $\varepsilon (t) = \Phi (\sigma \Theta (t))$, где $\Theta (t): = {{t}^{{ - 1}}}Q(t)$ (свойства усреднения ФП $\Theta (t)$ смотри в [56, 57]). Очевидно, Q(0) = 0, $\Theta (0 + ) = \Pi (0)$, $Q(\infty ) = \infty $, $\Theta (\infty ) = \Pi (\infty )$, а при t > 0: $Q(t) > 0$, $\dot {Q}(t) = \Pi (t) > 0$, $\ddot {Q}(t) = \dot {\Pi }(t) > 0$, $\dddot Q(t) = \ddot {\Pi }(t) < 0$. Для ФП вида (2.2), например, $Q(t) = 0.5\alpha {{t}^{2}} + \beta t - \gamma {{\lambda }^{{ - 1}}}(1 - {{e}^{{ - \lambda t}}})$.

Исключив параметр $t = \sigma {\text{/}}b$ (или $t = F(\varphi (\varepsilon ){\text{/}}b)$, $F = {{Q}^{{ - 1}}}$) из тождества $\varphi (\varepsilon (t)) = bQ(t)$, получим семейство ДД в виде $\varepsilon = \varepsilon (\sigma ,b)$ и в явной форме $\sigma = \sigma (\varepsilon ,b)$:

где $\omega $ – краткое обозначение для ${{\omega }_{ + }}$. Так как $Q(0) = 0$ и $Q(\infty ) = \infty $, то обратная к $Q$ функция $F(x)$ определена на всем луче $x \geqslant 0$, $F(0) = 0$, $F(\infty ) = \infty $.

Уравнение (4.1) можно записать в виде

Для исследования семейства ДД в общем виде установим свойства МФ F(x), вытекающие из ограничений, наложенных на ФП $\Pi (t)$ в п. 2 (за исключением $\ddot {\Pi }(t) \leqslant 0$).

Лемма. Если $\Pi (t)$ положительна, дифференцируема и строго возрастает на (0; ∞), то функция $F = {{Q}^{{ - 1}}}$ определена на [0; ∞) и при x > 0 обладает следующими свойствами:

1) F положительна, дважды дифференцируема и строго возрастает, F(0) = 0, $F(\infty ) = \infty $;

2) $F{\kern 1pt} {\text{'}}(x) = 1{\text{/}}\dot {Q}(F(x)) = 1{\text{/}}\Pi (F(x)) > 0$, $F{\kern 1pt} {\text{'}}(x)$ строго убывает, $F{\kern 1pt} {\text{'}}(0 + ) = 1{\text{/}}\Pi (0) = $ $ = \sup F{\kern 1pt} {\text{'}}(x)$ (в частности, $F{\kern 1pt} {\text{'}}(0 + ) = \infty $ для нерегулярных моделей), $F{\kern 1pt} {\text{'}}(\infty ) = 1{\text{/}}\Pi (\infty ) = $ $ = \inf F{\kern 1pt} {\text{'}}(x)$;

3) $F{\kern 1pt} {\text{''}}(x) = - \ddot {Q}(F(x)){{[\dot {Q}(F(x))]}^{{ - 3}}} = - \dot {\Pi }(F(x)){{\left[ {\Pi (F(x))} \right]}^{{ - 3}}} \leqslant 0$;

в частности, $F{\kern 1pt} {\text{''}}(x) < 0$, если нет точек с $\dot {\Pi }(t) = 0$;

4) $F(x){\text{/}}x > F{\kern 1pt} {\text{'}}(x)$ при x > 0;

5) функция $F(x){\text{/}}x$ убывает при x > 0;

6) при $x \to 0$ $F(x){\text{/}}x \to 1{\text{/}}\Pi (0)$ (для нерегулярных моделей $F(x){\text{/}}x \to \infty $), а при $x \to \infty $: $F(x){\text{/}}x \to 1{\text{/}}\Pi (\infty )$;

7) Если ФП дважды дифференцируема и $\ddot {\Pi }(t) \leqslant 0$, то $\dddot Q(t) \leqslant 0$ и F'''(x) = = $ - \ddot {\Pi }(F(x)){{[\Pi (F(x))]}^{{ - 4}}}$ + $3{{[\dot {\Pi }(F(x))]}^{2}}{{\left[ {\Pi (F(x))} \right]}^{{ - 5}}}$ (и потому $F{\text{'''}}(x) > 0$ на $(0;\infty )$).

Доказательство. Пункты 1–3 леммы следуют из свойств $Q(t)$ и обратной функции. В частности, строгое убывание $F{\kern 1pt} {\text{'}}(x)$ могло бы быть нарушено лишь на тех интервалах, где $\Pi (t) = const$ (но в предпосылке требуется строгое возрастания ФП); $\ddot {Q}(t) = \dot {\Pi }(t) > 0$ и $F{\kern 1pt} {\text{''}}(x) < 0$, а равенство $F{\kern 1pt} {\text{''}}(x) = 0$ возможно лишь в тех точках, где $\dot {\Pi }(F(x)) = 0$; если $\ddot {\Pi }(t) \leqslant 0$, то наличие точки, в которой $\dot {\Pi }({{t}_{0}}) = 0$, означает, что $\Pi (t) = const$ при t > t₀.

Пункты 4 и 5 справедливы для любой функции с $F{\kern 1pt} {\text{''}}(x) < 0$ и $F(0) \geqslant 0$. В самом деле, по теореме Лагранжа $y: = F(x){\text{/}}x - F{\text{'}}(x) = F{\text{'}}(\xi ) - F{\text{'}}(x)$ + F(0)/x, $\xi \in (0;x)$, $F{\kern 1pt} {\text{'}}(\xi ) > F{\kern 1pt} {\text{'}}(x)$, так как $F{\kern 1pt} {\text{'}}(x)$ строго убывает (если бы в некоторой точке достигалось равенство $y({{x}_{0}}) = 0$, то было бы $F{\text{'}}(x) = {\text{const}}$ на некотором отрезке $\left[ {\xi ,{{x}_{0}}} \right]$ и $\Pi (t) = {\text{const}}$ на соответствующем отрезке $\left[ {{{t}_{0}},\zeta } \right]$, что противоречит строгому неравенству $F{\kern 1pt} {\text{''}}(x) < 0$ и строгой монотонности ФП). Итак, $y(x) > 0$. Отсюда следует и п.  5: $(F(x){\text{/}}x){\text{'}} = F{\kern 1pt} {\text{'}}(x){{x}^{{ - 1}}} - F(x){{x}^{{ - 2}}} = - {{x}^{{ - 1}}}y(x) < 0$.

Пункт 6 следует из дифференцируемости F и предельных равенств $F{\kern 1pt} {\text{'}}(0 + ) = 1{\text{/}}\Pi (0)$ и $F{\kern 1pt} {\kern 1pt} {\text{'}}(\infty ) = 1{\text{/}}\Pi (\infty )$ по правилу Лопиталя.

Пункт 7 получается дифференцированием равенства из п. 3:

$F{\kern 1pt} {\text{'''}}(x) \geqslant 0$, так как $\ddot {\Pi }(t) \leqslant 0$ при всех t > 0; равенство $F{\kern 1pt} {\text{'''}}(x) = 0$ возможно в некоторой точке x₀ > 0 только если существует точка t₀ > 0, в которой одновременно $\dot {\Pi }({{t}_{0}}) = 0$ и $\ddot {\Pi }({{t}_{0}}) = 0$, но в силу ограничений $\dot {\Pi }(t) \geqslant 0$ и $\ddot {\Pi }(t) \leqslant 0$, наличие такой точки означает, что $\dot {\Pi }(t) \equiv 0$ и $\Pi (t) = const$ при $t \geqslant {{t}_{0}}$. Если такие модели с финитной ползучестью исключить из рассмотрения (требованием строгого возрастания ФП – смотри предпосылку леммы), то справедливо строгое неравенство $F{\kern 1pt} {\text{'''}}(x) > 0$ при x > 0.

Из представления ДД в виде (4.2) и пунктов 5, 6 леммы сразу следуют два важных свойства: 1) семейство ДД возрастает по b при любом фиксированном $\varepsilon \in (0;\omega )$, т.е. с ростом $b$ ДД (4.1) целиком смещается вверх вдоль оси $\sigma $ (ОС моделирует материалы с положительной скоростной чувствительностью); 2) для любой ДД с b > 0, порожденной ОС (1.1) с произвольной допустимой ФП, справедливы (точные) оценки:

Оценка сверху содержательна, если ${{\Pi }_{0}} \ne 0$, то есть для регулярных моделей. Ниже будет показано, что верхняя и нижняя границы имеют механический смысл: $\varphi (\varepsilon ){\text{/}}{{\Pi }_{0}} = \sigma (\varepsilon , + \infty )$ – “мгновенная” ДД, а $\varphi (\varepsilon ){\text{/}}{{\Pi }_{\infty }} = \sigma (\varepsilon ,0)$ – “равновесная” ДД. Дифференцируя (4.1) по $\varepsilon $, найдем касательный модуль

Так как $\varphi {\text{'}}(\varepsilon ) > 0$ и $F{\kern 1pt} {\text{'}}(x) > 0$, то всегда $\sigma _{\varepsilon }^{'}(\varepsilon ,b) > 0$, и ДД $\sigma = \sigma (\varepsilon ,b)$ возрастает по $\varepsilon $.

Если $\bar {x}: = \varphi (\omega ) = \infty $ (как для линейного ОС (1.2), например), то ${{D}_{\Phi }} = \left[ {0;\infty } \right)$, ДД (4.1) определены при всех $\sigma \geqslant 0$ и $t \geqslant 0$, и напряжение σ = bt формально может нарастать неограниченно. Если $\omega = \infty $ ДД (4.2) определены на всем луче $\varepsilon \geqslant 0$. Если же $\omega < \infty $ (т.е. $\varphi (\varepsilon )$ имеет асимптоту $\varepsilon = \omega $), то ДД $\sigma (\varepsilon ,b)$ имеют общую вертикальную асимптоту ε = ω (если рабочий диапазон деформаций при моделировании лежит внутри $[0;\omega {\text{/}}2]$ наличие этой асимптоты и предельной деформации ε = ω не проявляются).

Рассмотрим случай $\bar {x} < + \infty $. Тогда $bQ(t) \in {{D}_{\Phi }}$ только при $Q(t) < \bar {x}{\text{/}}b$; это означает, что каждая ДД обрывается в момент времени $t = {{t}_{\omega }}$, такой, что $Q({{t}_{\omega }}) = \bar {x}{\text{/}}b$, т.е. ${{t}_{\omega }} = F(\bar {x}{\text{/}}b)$. В силу п.1 леммы ${{t}_{\omega }}(b)$ убывает с ростом b и ${{t}_{\omega }}(b) \to 0$ при $b \to + \infty $. ДД ведут себя по-разному в двух случаях. 1) Если $\omega < + \infty $, то есть $\,\Phi (\bar {x}) < \infty $, то обрыв любой ДД (разрушение) происходит (как и при ползучести) по достижению критической деформации: $\varepsilon ({{t}_{\omega }}) = {{\varepsilon }_{*}}$, где ${{\varepsilon }_{*}}: = \Phi (\bar {x}) = \omega $ – постоянная, не зависящая от b и ФП $\Pi (t)$. Напряжение в момент разрушения зависит от b и ФП: ${{\sigma }_{\omega }} = b{{t}_{\omega }} = bF(\bar {x}{\text{/}}b)$, причем ${{\sigma }_{\omega }}(b)$ возрастает (т.к. $\sigma _{\omega }^{'}(b) > 0$ в силу п. 4 леммы) и ${{\sigma }_{\omega }}(b) \to {{\sigma }_{ + }}: = \bar {x}{\text{/}}\Pi (0)$ (см. п. 2) при $b \to \infty $ в силу п. 6 леммы (в частности, ${{\sigma }_{\omega }}(b)$ меньше предела прочности ${{\sigma }_{ + }}$ при любых СН и ${{\sigma }_{ + }} = \sup {{\sigma }_{\omega }}(b)$).

2) Если же $\omega = + \infty $, то есть $\Phi (\bar {x}) = \infty $, то деформация $\varepsilon (t) = \Phi (bQ(t))$ обладает вертикальной асимптотой t = t_ω; это означает, что любая ДД обрывается в момент времени t = t_ω из-за неограниченного нарастания деформации и ее скорости (можно интерпретировать это как свидетельство зарождения и роста шейки в образце), а каждая ДД в форме $\sigma (\varepsilon ,b)$ имеет горизонтальную асимптоту $\sigma = \bar {\sigma }(b)$, где $\bar {\sigma } = bF(\varphi (\infty ){\text{/}}b) = bF(\bar {x}{\text{/}}b)$. “Напряжение течения” (или “шейкообразования”) $\bar {\sigma }(b)$ возрастает с ростом СН (так как $\bar {\sigma } = \bar {x}F(x){\text{/}}x$, $x: = \bar {x}{\text{/}}b$, а функция $F(x){\text{/}}x$ убывает), $\inf \bar {\sigma }(b) = \bar {\sigma }(0 + ) = \bar {x}{\text{/}}\Pi (\infty )$, $\sup \bar {\sigma }(b) = \bar {\sigma }(\infty ) = \bar {x}{\text{/}}\Pi (0)$ (для регулярных моделей $\bar {\sigma }(\infty ) < \infty $, для нерегулярных $\bar {\sigma }(\infty ) = \infty $). Верно и обратное: если хотя бы одна ДД (4/1) имеет горизонтальную асимптоту, то ее имеет и МФ φ (т.е. $\omega = \infty $ и $\bar {x} < \infty $), а значит, и все ДД (ДД при постоянной СН линейного ОС (1.2) никогда не имеют горизонтальной асимптоты). Существенно, что зависимости времени разрушения ${{t}_{\omega }}(b) = F(\bar {x}{\text{/}}b)$ и “напряжения течения” $\bar {\sigma }(b) = bF(\bar {x}{\text{/}}b)$ от СН определяются только ФП $\Pi (t)$, а МФ φ влияет на них только через скалярный параметр $\bar {x}: = \varphi (\omega )$.

Касательный модуль (4.3) зависит от СН (возрастает по b при любом фиксированном $\varepsilon $, так как Π(t) и F(x) возрастают). Мгновенный модуль при ε = 0 не зависит от СН: $E: = \sigma _{\varepsilon }^{'}(0 + ,b) = F{\kern 1pt} {\text{'}}(\varphi (0){\text{/}}b)\varphi {\text{'}}(0) = F{\kern 1pt} {\text{'}}(0)\varphi {\text{'}}(0) = \varphi {\text{'}}(0){\text{/}}\Pi (0)$. Для регулярных моделей он конечен, если $\varphi {\text{'}}(0) < \infty $, для нерегулярных (с Π(0) = 0) он бесконечен, если $\varphi {\text{'}}(0) \ne 0$. Если же $\varphi {\text{'}}(0) = 0$ или $\varphi {\text{'}}(0) = \infty $, то предел $\sigma _{\varepsilon }^{'}(0 + ,b)$ зависит от соотношений порядков асимптотик $\varphi {\text{'}}(\varepsilon )$ и $\Pi (F(\varphi (\varepsilon ){\text{/}}b))$ при $\varepsilon \to 0$.

Длительный модуль ${{E}_{\infty }}: = \sigma _{\varepsilon }^{'}(\infty ,b)$ определен лишь в случае ${{D}_{\varphi }} = \left[ {0;\infty } \right)$, то есть когда $\omega = \infty $: ${{E}_{\infty }} = \varphi {\text{'}}(\infty ){\text{/}}\Pi (F(\bar {x}{\text{/}}b))$. Если $\bar {x} = \infty $, то ${{E}_{\infty }} = \varphi {\text{'}}(\infty ){\text{/}}\Pi (\infty )$ (так как $F(\infty ) = \infty $), и конечность предела ${{E}_{\infty }} = \varphi {\text{'}}(\infty ){\text{/}}\Pi (\infty )$ зависит от того, конечны ли $\varphi {\text{'}}(\infty )$ и $\Pi (\infty )$; в частности, если $\varphi {\text{'}}(\infty ) < \infty $, то E_∞ конечен (и ${{E}_{\infty }} = 0$ при $\Pi (\infty ) = \infty $). Если $\bar {x} < \infty $ (т.е. $\varphi (\varepsilon )$ имеет горизонтальную асимптоту), то ${{E}_{\infty }} = 0$, так как $\varphi {\text{'}}(\infty ) = 0$, $\Pi (F(\varphi (\infty ){\text{/}}b)) < \infty $ (это верно для любой ФП с любым пределом $\Pi (\infty )$). В случае линейного ОС (1.2) (при $\varphi (u)$ = u) касательный модуль убывает по $\varepsilon $ и все ДД $\sigma (\varepsilon ,b)$ выпуклы вверх [56, 57], мгновенный модуль – максимальный касательный модуль, а длительный модуль – минимальный. Для ОС (1.1) с произвольной МФ $\varphi $ это не обязательно так, ибо ДД не обязана быть выпуклой вверх.

Так как $\sigma _{\varepsilon }^{{''}}(\varepsilon ,b) = [F{\kern 1pt} {\text{'}}(\varphi (\varepsilon ){\text{/}}b)\varphi {\text{'}}(\varepsilon )]{\text{'}} = {{b}^{{ - 1}}}F{\kern 1pt} {\text{''}}(\varphi (\varepsilon ){\text{/}}b)\varphi {\text{'}}{{(\varepsilon )}^{2}} + F{\kern 1pt} {\text{'}}(\varphi (\varepsilon ){\text{/}}b)\varphi {\text{''}}(\varepsilon )$, выпуклость ДД зависит от знака и величины $\varphi {\text{''}}(x)$: первое слагаемое отрицательно (ибо $F{\text{''}}(x) < 0$ по п. 3 леммы); если $\varphi {\text{''}}(\varepsilon ) < 0$, то второе слагаемое в скобке тоже отрицательно, $\sigma _{\varepsilon }^{{''}}(\varepsilon ,b) < 0$ и ДД выпукла вверх. Таким образом, если φ(x) выпукла вверх, то ДД выпукла вверх, а если у $\varphi (x)$ есть участки выпуклости вниз, то у ДД они тоже могут быть (см. фиг. 2а).

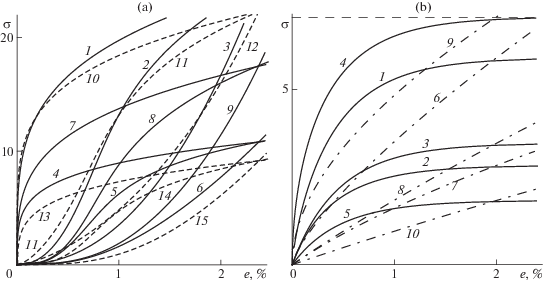
Фигуры 2а, 2b демонстрируют разнообразие форм (свойств) ДД ОС (1.1). На фиг. 2а приведены ДД при постоянной СН b = 1 моделей с тремя разными МФ $\Phi (x)$ (Φ = ${{(x{\text{/}}10)}^{3}}$, $\Phi = {{x}^{{1/3}}}$ и МФ $\Phi (x)$ вида (2.4) с $m = 1{\text{/}}n$, n = 3, $\vartheta = 0.001$, A = 0.5, C = 1) для ФП $\Pi (t) = 0.25{{t}^{{1/3}}}$ (ДД 1–3) и четырех классических ФП вида (2.2): кривые 4–6 – ДД для ФП РеМ-4 (с λ = 0.1, $\alpha = 0.1$, $\beta = 1$, γ = 0.5 и временем ретардации ${{\tau }_{c}} = 1{\text{/}}\lambda = 10$), кривые 7–9 – ДД для ФП РеМ-3 (с $\alpha = 0$, $\lambda = 0.1$, $\beta = 1$, $\gamma = 0.5$; тогда ${{\tau }_{c}} = 10$, а время релаксации $\tau = {{\tau }_{c}}(1 - \gamma {\text{/}}\beta ) = 5$), штриховые кривые 10–12 – ДД для ФП модели Фойгта (с $\lambda = 0.1$, $\gamma = \beta = 1$), штриховые кривые 13–15 – ДД для ФП модели Максвелла (с γ = 0, $\alpha = 0.1$, $\beta = 0.5$ и $\tau = \beta {\text{/}}\alpha = 5$). ДД моделей с $\Phi = {{(x{\text{/}}10)}^{3}}$ выпуклы вверх, с Φ = ${{x}^{{1/3}}}$ выпуклы вниз, а с $\Phi (x)$ вида (2.4) имеют точку перегиба. На фиг. 2b приведены ДД 1–5 моделей с МФ (2.3) для $A = 0.5$, ${{\sigma }_{*}} = 2$ и теми же пятью ФП (нумерация ДД – в порядке перечисления ФП). У МФ $\varphi $ вида (2.3) есть горизонтальная асимптота, и потому каждая ДД $\sigma (\varepsilon ,b)$ имеет горизонтальную асимптоту $\sigma = \bar {\sigma }$ c $\bar {\sigma } = bF({{\sigma }_{*}}{\text{/}}b)$. Штрих-пунктирные линии 6–10 – ДД линейного ОС (1.2) ($\varphi (u) = u$) с теми же ФП.

Основные обнаруженные выше общие свойства всех ДД (4.2), порождаемых ОС (1.1) при фиксированной СН, соберем в теореме.

Теорема 1. Пусть $\Pi (t)$ положительна, дифференцируема и строго возрастает на $(0;\infty )$, а $\varphi (x)$ непрерывно дифференцируема и строго возрастает на $(0;\omega )$ и $\varphi (0) = 0$. Тогда любая ДД $\sigma = \sigma (\varepsilon ,b)$ с фиксированной СН b > 0 обладает следующими свойствами.

1) Все ДД $\sigma (\varepsilon ,b)$ возрастают по $\varepsilon $ на всей области определения, $\sigma (0,b) = 0$.

2) Если $\bar {x}: = \varphi (\omega ) = \infty $ то ДД (4.1) определены при всех $\varepsilon \in (0,\omega )$ и напряжение $\sigma = bt$ формально может нарастать неограниченно; в случае $\omega < \infty $ (когда МФ $\varphi (\varepsilon )$ имеет асимптоту $\varepsilon = \omega $) все ДД $\sigma = \sigma (\varepsilon ,b)$ имеют общую вертикальную асимптоту $\varepsilon = \omega $.

2) Если $\bar {x} < + \infty $, каждая ДД обрывается в момент ${{t}_{\omega }} = F(\bar {x}{\text{/}}b)$; в случае $\omega < + \infty $ обрыв ДД (разрушение) происходит по достижению критической деформации: $\varepsilon ({{t}_{\omega }}) = {{\varepsilon }_{*}}$, где ${{\varepsilon }_{*}}: = \Phi (\bar {x}) = \omega $ не зависит от СН $b$; в случае $\omega = + \infty $ каждая ДД $\sigma (\varepsilon ,b)$ имеет горизонтальную асимптоту $\sigma = \bar {\sigma }(b)$, где $\bar {\sigma } = bF(\bar {x}{\text{/}}b)$ – напряжение течения, а деформация $\varepsilon (t) = \Phi (bQ(t))$ обладает вертикальной асимптотой $t = {{t}_{\omega }}$ (и $\dot {\varepsilon }(t) \to \infty $).

3) Касательный модуль ДД выражается формулой (4.3), он не обязан убывать по $\varepsilon $.

4) Мгновенный модуль (при ε = 0) равен $E: = \sigma _{\varepsilon }^{'}(0 + ,b) = \varphi {\text{'}}(0){\text{/}}\Pi (0)$ (не зависит от СН), для регулярных моделей $E < \infty $, если $\varphi {\text{'}}(0) < \infty $, для нерегулярных $E = \infty $, если $\varphi {\text{'}}(0) \ne 0$.

5) Длительный модуль ${{E}_{\infty }}: = \sigma _{\varepsilon }^{'}(\infty ,b)$ определен лишь в случае $\omega = \infty $ и равен ${{E}_{\infty }} = \varphi {\text{'}}(\infty ){\text{/}}\Pi (F(\bar {x}{\text{/}}b))$; для его равенства нулю достаточно одного из условий: а) $\bar {x} < \infty $ или б) $\bar {x} = \infty $ и $\Pi (\infty ) = \infty $ и $\varphi {\text{'}}(\infty ) < \infty $.

6) Для любой ДД справедливы (точные) оценки: $\varphi (\varepsilon ){\text{/}}{{\Pi }_{\infty }} < \sigma (\varepsilon ,b) < \varphi (\varepsilon ){\text{/}}{{\Pi }_{0}}$, $\varepsilon \in (0,\omega )$.

5. Зависимость диаграмм деформирования от скорости нагружения. Все доказанные утверждения опираются на общие предпосылки – ограничения на МФ ОС (1.1), наложенные в теореме 1 (см. также п. 2). В предыдущем пункте уже доказана

Теорема 2. В предпосылках теоремы 1 справедливы следующие утверждения:

1) При любом $\varepsilon \in (0;\omega )$ семейство ДД (4.2) $\sigma (\varepsilon ,b)$, $b > 0$, возрастает по $b$ (с ростом СН ДД смещается вверх); для всех ДД справедлива оценка снизу $\sigma (\varepsilon ,b) > \varphi (\varepsilon ){\text{/}}{{\Pi }_{\infty }}$ ($\sigma > 0$, если ${{\Pi }_{\infty }} = \infty $), а если ${{\Pi }_{0}} \ne 0$, то верна и оценка сверху $\sigma (\varepsilon ,b) < \varphi (\varepsilon ){\text{/}}{{\Pi }_{0}}$, $\varepsilon \in (0;\omega )$.

2) Касательный модуль (4.3) возрастает по b при любом $\varepsilon \in (0;\omega )$, а его предельные значения при $\varepsilon \to 0$ и $\varepsilon \to \infty $ (мгновенный и длительный модули) не зависят от СН.

3) Если $\bar {x} < \infty $, то ДД (4.1) обрывается в момент ${{t}_{\omega }} = F(\bar {x}{\text{/}}b)$, ${{t}_{\omega }}$ убывает с ростом СН $b$, напряжение разрушения ${{\sigma }_{\omega }}(b) = b{{t}_{\omega }} = bF(\bar {x}{\text{/}}b)$ возрастает по $b$, ${{\sigma }_{\omega }}(b) < {{\sigma }_{ + }}$, где ${{\sigma }_{ + }}: = \bar {x}{\text{/}}\Pi (0)$ – предел прочности, а при $b \to + \infty $ ${{\sigma }_{\omega }}(b) \to {{\sigma }_{ + }} = \sup {{\sigma }_{\omega }}(b)$ и ${{t}_{\omega }}(b) \to 0$.

Исследуем, существуют ли пределы семейства ДД (4.2) при $b \to \infty $ и $b \to 0$, то есть ДД при “мгновенном” нагружении и равновесная ДД.

Теорема 3. 1) При $b \to \infty $ (для любого фиксированного $\varepsilon \in \left[ {0;\omega } \right)$) семейство ДД (4.2) сходится (снизу) к кривой $\sigma = \varphi (\varepsilon ){\text{/}}{{\Pi }_{0}}$ (мгновенной ДД), если ${{\Pi }_{0}} \ne 0$. Если же Π₀ = 0 (модель нерегулярна), то при $b \to \infty $ семейство ДД (в форме $\varepsilon (\sigma ,b) = \Phi (\sigma \Theta (\sigma {\text{/}}b))$) сходится к вертикальной прямой ε = 0 для любого допустимого $\sigma \geqslant 0$, т.е. такого, что $\sigma \Theta (\sigma {\text{/}}b) \in {{D}_{\Phi }}$, или $\sigma \Theta (\sigma {\text{/}}b) < \bar {x}$ (если $\bar {x} = \infty $, то сходимость имеет место на всем луче $\sigma \geqslant 0$, а если $\bar {x} < \infty $, то с ростом СН $b$ область сходимости неограниченно расширяется, т.к. $\sigma {\text{/}}b \to 0$ и $\Theta (\sigma {\text{/}}b) \to 0$ при $b \to \infty $).

2) При $b \to 0$ (для любого $\varepsilon \in \left[ {0;\omega } \right)$) семейство ДД (4.1) сходится (сверху) к кривой $\sigma = \varphi (\varepsilon ){\text{/}}\Pi (\infty )$ (“равновесной” ДД), ибо $F(x){\text{/}}x \to 1{\text{/}}\Pi (\infty )$ при $x \to \infty $. Если ФП не ограничена (${{\Pi }_{\infty }} = \infty $), то семейство ДД (4.1) сходится к прямой σ = 0.

Доказательство. По (4.2) $\sigma (\varepsilon ,b) = \varphi (\varepsilon )F(x){\text{/}}x$, где $x = \varphi (\varepsilon ){\text{/}}b$. Но для любой допустимой ФП $F(x){\text{/}}x < 1{\text{/}}{{\Pi }_{0}}$ и $F(x){\text{/}}x \to 1{\text{/}}{{\Pi }_{0}}$ при $x \to 0$ (п. 6 леммы); при $\varepsilon = 0$ сходимость имеет место, так как $\sigma (0,b) = 0$ и $\varphi (0) = 0$. Если же ${{\Pi }_{0}} = 0$, то при $b \to \infty $ семейство ДД $\varepsilon (\sigma ,b) = \Phi (\sigma \Theta (\sigma {\text{/}}b))$ сходится к прямой ε = 0 для любого фиксированного $\sigma \geqslant 0$, так как $\Theta (0 + ) = {{\Pi }_{0}} = 0$ и $\Phi (0) = 0$ (и для любого фиксированного $\sigma \geqslant 0$ найдется достаточно большое b, при котором $\sigma \Theta (\sigma {\text{/}}b) < \bar {x}$).

Докажем, что сходимость семейства ДД (4.2) к мгновенной и к равновесной ДД равномерна внутри области определения (на любом отрезке).

Теорема 4. 1) Если модель регулярна (${{\Pi }_{0}} \ne 0$), то при $b \to + \infty $ семейство ДД (4.2) $\sigma (\varepsilon ,b)$ сходится к функции $\sigma = \varphi (\varepsilon ){\text{/}}{{\Pi }_{0}}$ равномерно на любом отрезке $[0,\tilde {\varepsilon }]$ с $\tilde {\varepsilon } < \omega $.

2) Семейство ДД любой модели в форме $\varepsilon = \varepsilon (\sigma ,b)$ сходится при $b \to + \infty $ к функции $\varepsilon (\sigma ) = \Phi ({{\Pi }_{0}}\sigma )$ равномерно на любом отрезке $S = [{{\sigma }_{1}},{{\sigma }_{2}}]$ с ${{\sigma }_{1}} > 0$, ${{\sigma }_{2}} < \bar {x}{\text{/}}{{\Pi }_{0}}$; если $\Phi {\text{'}}(0 + ) < \infty $ (т.е. $\varphi {\text{'}}(0 + ) \ne 0$), это верно и для отрезков с ${{\sigma }_{1}} = 0$.

3) Если ${{\Pi }_{0}} = 0$, то семейство $\varepsilon (\sigma ,b)$ сходится при $b \to + \infty $ к функции ε = 0 на любом отрезке вида $[0,{{\sigma }_{2}}]$ с ${{\sigma }_{2}} > 0$.

4) При $b \to 0$ семейство ДД $\sigma = \sigma (\varepsilon ,b)$ любой модели сходится к функции σ = $\varphi (\varepsilon ){\text{/}}{{\Pi }_{\infty }}$ равномерно на любом отрезке $[0,\tilde {\varepsilon }]$ с $\tilde {\varepsilon } < \omega $ (в случае ${{\Pi }_{\infty }} = \infty $ – к функции $\sigma \equiv 0$).

5) Если $\bar {x} < \infty $ и ${{\Pi }_{0}} \ne 0$, то равномерная сходимость семейства ДД $\sigma (\varepsilon ,b)$ при $b \to \infty $ и $b \to 0$ имеет место не только внутри D_φ, но и на ее замыкании: если $\omega < \infty $, то сходимость равномерна на $[0,\omega ]$, а если $\omega = \infty $, то – на всем луче $\left[ {0,\infty } \right)$.

6) Если $\bar {x} = \infty $, то равномерной сходимости на всем интервале $[0,\omega )$ при $b \to + \infty $ нет.

Доказательство. 1) Уклонение ДД (4.2) с фиксированной СН от предельной функции $y(\varepsilon ): = \left| {\sigma (\varepsilon ,b) - \varphi (\varepsilon ){\text{/}}{{\Pi }_{0}})} \right| = \varphi (\varepsilon )[\Pi _{0}^{{ - 1}} - F(x){{x}^{{ - 1}}}]$ – возрастающая функция ε на D_φ (как произведение возрастающих функций: ведь второй множитель возрастает в силу п. 5 леммы), и потому его норма в пространстве $C[0,\tilde {\varepsilon }]$ совпадает со значением уклонения на правом конце отрезка $E = [0,\tilde {\varepsilon }]$: $\Delta (b) = \mathop {\sup }\limits_{\varepsilon \in E} \left| {y(\varepsilon )} \right| = \varphi (\tilde {\varepsilon })[\Pi _{0}^{{ - 1}} - F(\tilde {x}){{\tilde {x}}^{{ - 1}}}]$, где $\tilde {x} = \varphi (\tilde {\varepsilon }){\text{/}}b$. При $b \to + \infty $, очевидно, $\tilde {x} \to 0$, $F(\tilde {x}){{\tilde {x}}^{{ - 1}}} \to \Pi _{0}^{{ - 1}}$ (в силу п. 6 леммы) и $\Delta (b) \to 0$, то есть сходимость равномерна на $[0,\tilde {\varepsilon }]$.

2) Норма уклонения ДД $\varepsilon (\sigma ,b)$ от предельной функции на отрезке S:

где $\xi = \xi (\sigma ,b) \in (\sigma {{\Pi }_{0}};\sigma \Theta (\sigma {\text{/}}b)) \subset I$, $I: = \left[ {{{\sigma }_{1}}{{\Pi }_{0}},{{\sigma }_{2}}\Theta ({{\sigma }_{2}}{\text{/}}b)} \right]$. Если ${{\Pi }_{0}} \ne 0$, то ${{\sigma }_{1}}{{\Pi }_{0}} > 0$ и $\Phi {\text{'}}(x)$ ограничена на отрезке I (как непрерывная функция), поэтому $\Delta (b)\, \leqslant \,M{{\sigma }_{2}}{\text{|}}\Theta ({{\sigma }_{2}}{\text{/}}b)$ – Π₀| → 0 при $b \to \infty $ (так как $\dot {\Theta }(t) > 0$ и $\Theta (0 + ) = {{\Pi }_{0}}$).

3) Если ${{\Pi }_{0}} = 0$, то $\Theta (0 + ) = 0$, условие ${{\sigma }_{2}}\Theta (0) \in {{D}_{\Phi }}$ выполнено для всех ${{\sigma }_{2}} \geqslant 0$, а отклонение $\varepsilon (\sigma ,b)$ от предельной функции ε = 0 на отрезке $S = \left[ {0,{{\sigma }_{2}}} \right]$ можно оценить без использования $\Phi {\text{'}}$: $\Delta (b) = \mathop {\sup }\limits_{\sigma \in S} \left| {\Phi (\sigma \Theta (\sigma {\text{/}}b)) - 0} \right| = \Phi ({{\sigma }_{2}}\Theta ({{\sigma }_{2}}{\text{/}}b))$ (в силу возрастания функции от $\sigma $). При фиксированном ${{\sigma }_{2}} \geqslant 0$ $\Delta (b) \to 0$ при $b \to \infty $, так как $\Theta (0 + ) = 0$.

4) Уклонение $z(\varepsilon ): = {\text{|}}\sigma (\varepsilon ,b) - \Pi _{\infty }^{{ - 1}}\varphi (\varepsilon )){\text{|}} = bF(\varphi (\varepsilon ){\text{/}}b) - \Pi _{\infty }^{{ - 1}}\varphi (\varepsilon ) = \varphi (\varepsilon )[F(x){{x}^{{ - 1}}} - \Pi _{\infty }^{{ - 1}}]$ является возрастающей функцией $\varepsilon $ на D_φ (хотя второй множитель убывает в силу п. 5 леммы): ведь $z{\text{'}}(\varepsilon ) = \varphi {\text{'}}(\varepsilon )[F{\kern 1pt} {\text{'}}(\varphi (\varepsilon ){\text{/}}b) - \Pi _{\infty }^{{ - 1}}] > 0$, ибо $F{\kern 1pt} {\text{'}}(x) > F{\kern 1pt} {\text{'}}(\infty ) = \Pi _{\infty }^{{ - 1}}$ в силу п. 2 леммы. Поэтому норма уклонения $z(\varepsilon )$ в пространстве $C[0,\tilde {\varepsilon }]$ совпадает со значением уклонения на правом конце отрезка $E = [0,\tilde {\varepsilon }]$: $\Delta (b) = \varphi (\tilde {\varepsilon })[F(\tilde {x}){{\tilde {x}}^{{ - 1}}} - \Pi _{\infty }^{{ - 1}}]$, где $\tilde {x} = \varphi (\tilde {\varepsilon }){\text{/}}b$. При $b \to 0$, очевидно, $\tilde {x} \to \infty $, $F(\tilde {x}){{\tilde {x}}^{{ - 1}}} \to \Pi _{\infty }^{{ - 1}}$ (в силу п. 6 леммы) и $\Delta (b) \to 0$, то есть сходимость равномерна на любом отрезке $[0,\tilde {\varepsilon }]$ с $\tilde {\varepsilon } < \omega $. Доказательство сохраняет силу и в случае $\Pi _{\infty }^{{}} = \infty $, т.е. $\Pi _{\infty }^{{ - 1}} = 0$.

5) Если $\omega < \infty $ и $\bar {x} < \infty $ (т.е. МФ определена и непрерывна на отрезке $[0,\omega ]$), то можно положить $\tilde {\varepsilon } = \omega $ и сходимость равномерна на всем $[0,\omega ]$. Если $\omega = \infty $ и $\bar {x} < \infty $ (т.е. МФ $\varphi $ имеет горизонтальную асимптоту, а обратная функция Φ – вертикальную), то сходимость равномерна на всем луче $\left[ {0,\infty } \right)$, так как Δ(b) = $\mathop {\sup }\limits_{\varepsilon \in [0,\infty )} {\text{|}}z(\varepsilon ){\text{|}}$ = = $\varphi (\infty )[F(\tilde {x}){{\tilde {x}}^{{ - 1}}} - \Pi _{\infty }^{{ - 1}}]$, где $\tilde {x} = \varphi (\infty ){\text{/}}b$, и, по-прежнему, при $b \to 0$ будет $\tilde {x} \to \infty $ и $F(\tilde {x}){{\tilde {x}}^{{ - 1}}} \to \Pi _{\infty }^{{ - 1}}$ и $\Delta (b) \to 0$. Аналогично ведет себя и норма уклонения при $b \to + \infty $, если $\Pi _{0}^{{}} \ne 0$: $\Delta (b) = \mathop {\sup }\limits_{\varepsilon \in [0,\infty )} \left| {y(\varepsilon )} \right| = \varphi (\infty )[\Pi _{0}^{{ - 1}} - F(\tilde {x}){{\tilde {x}}^{{ - 1}}}]$, где $\tilde {x} = \varphi (\infty ){\text{/}}b$, и, по-прежнему, при $b \to + \infty $ будет $\tilde {x} \to 0$ и $F(\tilde {x}){{\tilde {x}}^{{ - 1}}} \to \Pi _{0}^{{ - 1}}$ и $\Delta (b) \to 0$.

6) Если же $\bar {x} = \infty $, то при $\tilde {\varepsilon } \to \omega $ (и фиксированном $b$) будет $\tilde {x} \to \infty $, $F(\tilde {x}){{\tilde {x}}^{{ - 1}}} \to \Pi _{\infty }^{{ - 1}}$ и норма уклонения на отрезке $[0,\tilde {\varepsilon }]$ равна $\Delta (b) = \sup \left| {y(\varepsilon )} \right| \to \varphi (\omega )[\Pi _{0}^{{ - 1}} - \Pi _{\infty }^{{ - 1}}] = \infty $, уклонение Δ(b) не ограничено на $\left[ {0,\omega } \right)$ и равномерной сходимости при $b \to + \infty $ нет.

Математические результаты данной статьи о свойствах диаграмм деформирования ОС (1.1) справедливы как для случая малых деформаций в ОС (1.1), так и для случая, когда ОС (1.1) связывает логарифмическую деформацию $\varepsilon = \ln \left[ {l(t){\text{/}}{{l}_{0}}} \right]$ и истинное напряжение. Но от выбора меры деформации и напряжения, конечно, зависит физический смысл этих результатов, сопоставление с данными испытаний и методика идентификации. Специфике ОС Работнова в случае конечных деформаций и трехмерного напряженного состояния (как результатам испытаний, так и используемому понятийному аппарату, включая выбор мер деформаций и напряжений и объективных производных в ОС (1.1) будут посвящены отдельные работы.

6. Примеры диаграмм деформирования конкретных моделей. Для степенной ФП $\Pi (t) = B{{t}^{u}}$, $B > 0$, $u \in \left( {0;1} \right]$, имеем $Q(t) = B{{(u + 1)}^{{ - 1}}}{{t}^{{u + 1}}}$, $F(x) = H{{x}^{w}}$, где $w: = {{(u + 1)}^{{ - 1}}} \in $ ∈ [0.5; 1), $H: = {{(wB)}^{{ - w}}}$, и ДД (4.1) имеет вид:

В этом случае переменные разделяются, ДД с разными СН b подобны, форма всех ДД определяется функцией $\varphi {{(\varepsilon )}^{w}}$, зависимость от СН – степенная с показателем $1 - w \in \left( {0;0.5} \right]$ (при $u \to 0$ имеем $w \to 1$, $\sigma (\varepsilon ,b) \to \varphi (\varepsilon ){\text{/}}B$, т.е. ДД становится слабо чувствительной к СН при малых u). Касательный и мгновенный модули:

$E = \infty $, если $\varphi {\text{'}}(0) \ne 0$ (ибо $\varphi (0) = 0$), а если $\varphi {\text{'}}(0) = 0$, то все зависит от асимптотики произведения $\varphi {\text{'}}(\varepsilon )\varphi {{(\varepsilon )}^{{w - 1}}}$ при $\varepsilon \to 0$ (в частности, при u < 1 из существования $\varphi {\text{''}}(0) \ne 0$ следует, что E = 0). При $b \to \infty $ семейство ДД модели с любым $u \in \left( {0;1} \right]$ и любой МФ $\varphi (\varepsilon )\,$сходится к вертикальной прямой ε = 0, так как $\Pi (0) = 0$; при $b \to 0$ семейство ДД сходится к прямой σ = 0, так как ${{b}^{{1 - w}}} \to 0$. Абсцисса точки перегиба (если она есть) не зависит от СН и совпадает с абсциссой точки перегиба функции $\varphi {{(\varepsilon )}^{w}}$, поскольку

Для степенной ФП и любой МФ $\varphi $ с $\omega = \infty $ и $\bar {x} < \infty $ зависимости времени разрушения и напряжения течения от СН имеют степенной вид: ${{t}_{\omega }} = F(\bar {x}{\text{/}}b) = H{{\bar {x}}^{w}}{{b}^{{ - w}}}$, $w \in \left[ {0.5;1} \right)$, и $\bar {\sigma }(b) = bF(\bar {x}{\text{/}}b) = H{{\bar {x}}^{w}}{{b}^{{1 - w}}}$, $1 - w \in \left( {0;0.5} \right]$. В частности, для МФ (2.3) ДД (6.1) имеют вид $\sigma (\varepsilon ,b) = H{{b}^{{1 - w}}}\sigma _{*}^{w}{{(1 - {{e}^{{ - \varepsilon /A}}})}^{w}}$, $\varepsilon \geqslant 0$. Каждая ДД обладает горизонтальной асимптотой $\sigma = \bar {\sigma }$, $\bar {\sigma } = H\sigma _{*}^{w}{{b}^{{1 - w}}}$, время разрушения ${{t}_{\omega }} = F(\bar {x}{\text{/}}b) = H\sigma _{*}^{w}{{b}^{{ - w}}}$.

Для МФ $\varphi (\varepsilon ) = C(1 - \cos (\varepsilon {\text{/}}A))$, возрастающей на отрезке $\varepsilon \in \left[ {0,\pi A} \right]$, имеем $\omega = \pi A$, $\Phi (x) = A\left[ {\arcsin (x{\text{/}}C - 1) + 0.5\pi } \right]$, $x \in \left[ {0,2C} \right]$, $\bar {x} = 2C$, а семейство ДД (6.1) имеет вид: $\sigma (\varepsilon ,b) = H{{b}^{{1 - w}}}{{C}^{w}}{{(1 - \cos (\varepsilon {\text{/}}A))}^{w}}$, $\varepsilon \in \left[ {0,\pi A} \right]$. Обрыв любой ДД происходит по достижению критической деформации: $\varepsilon ({{t}_{\omega }}) = {{\varepsilon }_{*}}$, где ${{\varepsilon }_{*}} = \omega = \pi A$ (не зависит от СН b и ФП), время разрушения ${{t}_{\omega }} = F(\bar {x}{\text{/}}b) = H(2C)_{{}}^{w}{{b}^{{ - w}}}$. Мгновенный модуль E равен нулю для всех $u \in (0;1)$: в самом деле, при $\varepsilon \to 0$ $\varphi (\varepsilon ) \sim 0.5C{{A}^{{ - 2}}}{{\varepsilon }^{2}}$, φ'(ε)φ(ε)^{w – 1} ~ ~ ${{(0.5C{{A}^{{ - 2}}}{{\varepsilon }^{2}})}^{{w - 1}}}C{{A}^{{ - 2}}}\varepsilon $ = cε^2w – 1; но для $u \in (0;1)$ всегда $w > 0.5$, и потому E = 0 (а для u = 1 имеем $w = 0.5$ и $E = c \in (0;\infty )$). ДД с этой МФ всегда имеет точку перегиба $\tilde {\varepsilon } = A\arccos u > 0$ (и еще одну в т. ε = 0). При $u \to 0$ $\tilde {\varepsilon } \to 0.5\pi A$, при $u \to 1$ $\tilde {\varepsilon } \to 0$.

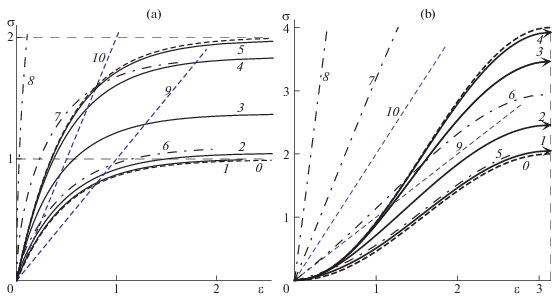
На фиг. 3а приведены ДД $\sigma (\varepsilon ,b)$ с разными СН $b = 0.001;\;0.01;\;0.1;\;1;\;10$ (кривые 1–5) для модели с МФ (2.3) (она дает дробно-линейную зависимость Шестерикова-Юмашевой [64] для скорости ползучести), A = 0.5, ${{\sigma }_{*}} = 1$, и ФП РеМ-3, т.е. ФП (2.2) с α = 0, $\lambda = 0.1$, β = 1, γ = 0.5 (тогда $\Pi (0) = \beta - \gamma \ne 0$, время ретардации ${{\tau }_{c}} = 1{\text{/}}\lambda = 10$, время релаксации $\tau = {{\tau }_{c}}(1 - \gamma {\text{/}}\beta ) = 5$). У всех ДД мгновенный модуль E = = $\varphi {\text{'}}(0){\text{/}}\Pi (0)\, = \,{{A}^{{ - 1}}}{{\sigma }_{*}}{{(\beta \, - \,\gamma )}^{{ - 1}}}$, а длительный модуль ${{E}_{\infty }} = 0$. Так как у МФ $\varphi $ вида (2.3) есть горизонтальная асимптота $\sigma = {{\sigma }_{*}}$, то каждая ДД обрывается в момент ${{t}_{\omega }} = F({{\sigma }_{*}}{\text{/}}b)$ ($\varepsilon ({{t}_{\omega }} - 0) = \infty $) и имеет горизонтальную асимптоту $y = \bar {\sigma }(b)$, где напряжение течения $\bar {\sigma } = bF({{\sigma }_{*}}{\text{/}}b)$ – возрастающая функция СН ($\bar {\sigma }(\infty ) = {{\sigma }_{*}}{\text{/}}\Pi (0) = {{\sigma }_{*}}{\text{/}}(\beta - \gamma )$, $\bar {\sigma }(0 + ) = {{\sigma }_{*}}{\text{/}}\Pi (\infty ) = {{\sigma }_{*}}{\text{/}}\beta $). При $b \to \infty $ семейство ДД (монотонно) сходится к кривой $\sigma = {{(\beta - \gamma )}^{{ - 1}}}\varphi (\varepsilon )$, то есть $\sigma (\varepsilon ) = {{\sigma }_{*}}{{(\beta - \gamma )}^{{ - 1}}}(1 - {{e}^{{ - \varepsilon /A}}})$, а при $b \to 0$ семейство ДД сходится к кривой $\sigma = \varphi (\varepsilon ){\text{/}}\beta $, т.е. $\sigma (\varepsilon ) = {{\sigma }_{*}}{{\beta }^{{ - 1}}}(1 - {{e}^{{ - \varepsilon /A}}})$ (штриховые кривые с маркерами ∞ и 0); в секторе между ними лежат все ДД с b > 0. Три штрих-пунктирные кривые 6–8, выходящие за пределы описанного криволинейного сектора, – ДД модели с той же МФ φ, но с ФП Фойгта (ФП (2.2) с $\beta = \gamma = 1$) для СН $b = 0.01;\;0.1;\;1$. При $b \to 0$ семейство ДД модели с ФП Фойгта сходится к той же кривой $\sigma = \varphi (\varepsilon ){\text{/}}\beta $ (ибо значение $\beta $ такое же). Отличие от РеМ-3 (с $\gamma < \beta $) состоит в том, что $\Pi (0) = 0$ (модель Фойгта сингулярна) и потому $E = \infty $ (касательные к ДД в т. $\varepsilon = 0$ вертикальны), а при $b \to \infty $ семейство ДД сходится к вертикальной прямой $\varepsilon = 0$. Штриховые прямые 9, 10 – предельные ДД для $b \to \infty $ и $b \to 0$ ($\sigma = \varepsilon {\text{/}}(\beta - \gamma )$ и $\sigma = \varepsilon {\text{/}}\beta $) в случае линейного ОС (когда $\varphi (u) = u$).

На фиг. 3b приведены ДД с разными СН $b = 0.01;\;0.1;\;1;\;10$ (кривые 1–4) для модели с той же ФП РеМ-3, что и на фиг. 3а, и МФ $\Phi (x) = A\left[ {\arcsin (x{\text{/}}C - 1) + 0.5\pi } \right]$, $x \in [0,2C]$ ($\varphi (\varepsilon ) = C(1 - \cos (\varepsilon {\text{/}}A))$, $\omega = \pi A$, $\bar {x} = 2C$) с $A = 1$, $C = 1$. Все ДД имеют нулевой мгновенный модуль $E = \varphi {\text{'}}(0){\text{/}}\Pi (0)$, так как $\varphi {\text{'}}(0) = 0$, а $\Pi (0) \ne 0$. Поскольку $\bar {x} < \infty $ и $\Phi (\bar {x}) < \infty $, то любая ДД обрывается (происходит разрушение) по достижению критической деформации ${{\varepsilon }_{*}} = \omega = \pi A$ (постоянная не зависит от СН b и ФП $\Pi (t)$), время разрушения ${{t}_{\omega }} = F(\bar {x}{\text{/}}b)$ и предельное напряжение ${{\sigma }_{\omega }} = bF(\bar {x}{\text{/}}b)$ зависят от СН b и ФП. При $b \to \infty $ семейство ДД (монотонно) сходится к кривой $\sigma = {{(\beta - \gamma )}^{{ - 1}}}\varphi (\varepsilon )$, то есть $\sigma = 2(1 - \cos \varepsilon )$, а при $b \to 0$ семейство ДД сходится к кривой $\sigma = \varphi (\varepsilon ){\text{/}}\beta $, то есть $\sigma = 1 - \cos \varepsilon $ (штриховые кривые с маркерами ∞ и 0); в секторе между ними лежат все ДД с b > 0. Четыре штрих-пунктирные кривые 5–8, выходящие за пределы описанного криволинейного сектора, – ДД модели с ФП Фойгта (при $\beta = \gamma = 1$) и той же МФ Φ(x) для тех же СН $b = 0.01;\;0.1;\;1;\;10$. При $b \to 0$ семейство ДД модели с ФП Фойгта сходится к той же кривой $\sigma = \varphi (\varepsilon ){\text{/}}\beta $ (поскольку значение $\beta $ то же самое), а при $b \to \infty $ – к вертикальной прямой ε = 0.

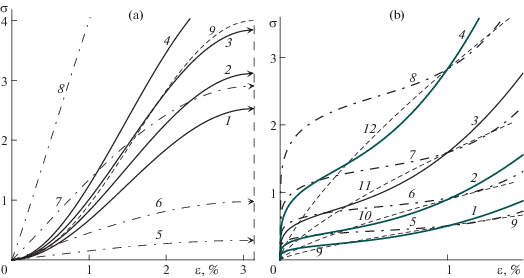
На фиг. 4а приведены ДД для двух моделей с МФ $\Phi (x) = A\left[ {\arcsin (x{\text{/}}C - 1) + 0.5\pi } \right]$, $x \in [0,2C]$ (той же самой, что и на фиг. 3b) и ФП $\Pi (t) = B{{t}^{u}}$ с $B = 0.5$ и двумя значениями показателя: $u = 0.1$ (ДД 1–4) и $u = 0.9$ (ДД 5–8). СН пробегают 3 порядка: $b = 0.01$; 0.1; 1; 10. Для $\Pi (t) = B{{t}^{u}}$ имеем $F(x) = H{{x}^{w}}$, где $w: = {{(u + 1)}^{{ - 1}}} \in \left[ {0.5;1} \right)$, $H: = {{(wB)}^{{ - w}}}$, и ДД (4.1): $\sigma (\varepsilon ,b) = bH{{(\varphi (\varepsilon ){\text{/}}b)}^{w}} = H{{b}^{{1 - w}}}\varphi {{(\varepsilon )}^{w}}$. ДД с разными СН подобны, форма всех ДД определяется функцией $\varphi {{(\varepsilon )}^{w}}$, абсцисса точки перегиба $\tilde {\varepsilon } = A\arccos u$ не зависит от СН, мгновенный модуль E равен нулю для всех $u \in (0;1)$. Так как $\bar {x} < \infty $ и $\Phi (\bar {x}) < \infty $, то любая ДД обрывается по достижению критической деформации ${{\varepsilon }_{*}} = \omega = \pi A$. Зависимость ДД от СН – степенная с показателем $1 - w \in \left( {0;0.5} \right]$. При $b \to \infty $ семейство ДД модели с любым $u \in \left( {0;1} \right]$ монотонно сходится к вертикальной прямой ε = 0, так как $\Pi (0) = 0$; при $b \to 0$ семейство ДД сходится к прямой σ = 0, так как $\Pi (\infty ) = \infty $. При малых u модель становится слабо чувствительной к СН (ДД 1–4 для модели с $u = 0.1$ лежат в заметно более узком секторе, чем ДД модели с u = 0.9), а при $u \to 0$ имеем $w \to 1$, $\tilde {\varepsilon } \to 0.5\pi A$, $\sigma (\varepsilon ,b) \to \varphi (\varepsilon ){\text{/}}B$ (см. штриховую кривую 9).

На фиг. 4b приведены ДД при $b = 0.001;\;0.01;\;0.1;\;1$ для двух моделей с ФП Π(t) = = ${{t}^{{1/3}}}{\text{/}}3$ (тогда $w = 3{\text{/}}4$, $F(s) = {{2}^{{3/2}}}{{s}^{{3/4}}}$) и двумя МФ $\varphi (x) = \vartheta {{x}^{n}} + (1 - \vartheta ){{x}^{{1/n}}}$ вида (2.4), $x \geqslant 0$, $n > 1$, $\vartheta \in (0;1)$, с разными значениями $n$ и $\vartheta $: ДД 1–4 – для $n = 3$, $\vartheta = 0.5$, ДД  5–8 – для n = 5, $\vartheta = 0.1$. Уравнение ДД имеет вид $\sigma = H{{b}^{{1 - w}}}\varphi {{(\varepsilon )}^{w}}$, т.е. σ(ε, b) = ${{2}^{{3/2}}}{{b}^{{1/4}}}{{(\vartheta {{\varepsilon }^{n}} + (1 - \vartheta ){{\varepsilon }^{{1/n}}})}^{{3/4}}}$. Все ДД имеют вертикальную касательную в нуле ($E = \infty $), точку перегиба (ее абсцисса не зависит от СН b, так как для степенных ФП ДД подобны) и ${{E}_{\infty }} = \infty $. С ростом n ДД приобретает “площадку текучести”. При $b \to \infty $ семейство ДД сходится к прямой ε = 0 (так как $\Pi (0) = 0$); при $b \to 0$ семейство ДД сходится к прямой σ = 0. Штриховые кривые 9–12 – ДД линейного ОС (1.2) с той же ФП при тех же скоростях $b = 0.001;\;0.01;\;0.1;\;1$.

Формы ДД на фиг. 3а и 4b типичны для многих полимеров, асфальтобетонов, металлов и сплавов со скоростной чувствительностью [7–10, 32, 38–46, 63, 65–73]. ДД на фиг. 4а и 3b (с малым, но быстро растущим при очень малых деформациях касательным модулем и точкой перегиба) качественно воспроизводят поведение ДД эластомеров (каучуков, резин и т.п.), пенопластов и биологических тканей (связок, сухожилий, сосудов) [20–22, 25–27, 30–33, 63, 74, 75].

Заключение. В работе продолжен качественный анализ определяющего соотношения Работнова (1.1): при минимальных ограничениях на две МФ выведены в общем виде уравнения семейств теоретических кривых деформирования при постоянных скоростях нагружения, детально изучены их общие качественные свойства в зависимости от свойств МФ (см. теоремы 1–4). На основе их сравнения с типичными свойствами кривых испытаний реономных материалов выявлены необходимые ограничения на МФ, обеспечивающие адекватное описание комплекса основных реологических эффектов, наблюдаемых при нагружениях с постоянной скоростью, сферы влияния обеих МФ и ряд индикаторов применимости ОС. Обнаружены те эффекты, которые ОС (1.1) принципиально не может описать ни при каких МФ (например, зависимость формы кривых релаксации от уровня деформации, отрицательная скоростная чувствительность ДД и др.), и те, которые могут быть описаны при определенных дополнительных ограничениях, наложенных на МФ (например: выпуклость ДД или наличие у них точек перегиба, подобие ДД, существование мгновенной ДД, конечность мгновенного модуля, равенство нулю или отличие от нуля длительного модуля, разрушение при деформировании с постоянной СН, зависимость времени разрушения от уровня напряжения или СН и т.п.).

Проведенный анализ позволил сопоставить круг реологических явлений, которые ОС (1.1) может адекватно описывать, с арсеналом возможностей линейного ОС вязкоупругости, которое оно обобщает, указать как наследуемые свойства, так и дополнительные возможности нелинейного ОС по сравнению с линейным. Например, доказано, что: при любых МФ все ДД с постоянными скоростями нагружения $\sigma (\varepsilon ,b)$ возрастают по $\varepsilon $ и по параметру $b$ (то есть ДД смещаются вверх с ростом СН); однако их мгновенный и длительный (касательные) модули не зависят от скоростей; если модель регулярна, то при стремлении СН к бесконечности семейство ДД сходится на луче $\varepsilon \geqslant 0$ к кривой $\sigma = \varphi (\varepsilon ){\text{/}}\Pi (0)$ (мгновенной ДД), а при стремлении СН к нулю они сходятся (сверху) к кривой $\sigma = \varphi (\varepsilon ){\text{/}}\Pi (\infty )$ (см. теоремы 1–4). Все перечисленные свойства ДД нелинейного ОС (1.1) унаследованы от линейного ОС вязкоупругости (1.2) [56, 57] (в этом случае мгновенная и равновесная ДД прямолинейны). Но, в отличие от ДД линейного ОС, которые всегда выпуклы вверх, ДД ОС (1.1) могут иметь участки выпуклости вниз (в частности, в окрестности нуля) и точки перегиба, если они имеются у МФ $\varphi (u)$, и горизонтальную асимптоту, если она есть у $\varphi $.

В последующих работах будут исследованы качественные свойства остальных квазистатических кривых, порождаемых ОС (1.1): кривых деформирования при постоянных и кусочно-постоянных скоростях деформации, кривых релаксации и ползучести с произвольной начальной стадией нагружения, условий описания немонотонности и знакопеременности коэффициента Пуассона, влияния гидростатического давления на кривые ползучести и деформирования, эффекта Маллинза, циклической ползучести, рэтчетинга, приспособляемости и других эффектов. На основе этого анализа будут составлены более полные списки индикаторов применимости ОС (1.1) и его возможностей по моделированию комплексного поведения классов реономных материалов, проявляющих нелинейную наследственность, скоростную чувствительность и разносопротивляемость.

Работа выполнена при финансовой поддержке РФФИ (грант № 17-08-01146_а).