Известия РАН. Механика твердого тела, 2019, № 3, стр. 86-99

1. Введение. Известно, что использование кусочно-линейных условий пластического течения часто упрощает математический аппарат решаемой задачи [1, 2]. Однако в случае неустановившихся напряжений это может приводить к разделению области пластического течения на части, в которых необратимое деформирование подчинено разным системам уравнений в зависимости от принадлежности напряженных состояний в материале разным граням или ребрам условия пластичности. Впервые на данное обстоятельство обратил внимание Д. Бленд [3], решая задачу о деформировании полого цилиндра за счет термомеханического воздействия на его боковые поверхности. В [4] на примере посадки на вал нагретой муфты показано, что подобные перемены в условиях пластического течения могут быть многократными.

С различными подходами в теории температурных напряжений в упругопластических телах можно познакомиться в обзорной работе [5]. Решению краевых задач теории посвящены работы [6–11]. По своей постановке задача, моделирующая сборку цилиндрических деталей способом горячей посадки, является простейшей, поэтому рассматривалась неоднократно как в условиях плоского напряженного состояния [12–14], так и при плоских деформациях [4, 15, 16]. В этих работах элементы сборки полагались упругопластическими с пределом текучести, зависимым от температуры.

Здесь рассмотрим классическую сборку “труба в трубе”, проводя ее таким образом, чтобы все характерные особенности в решении задачи, связанные с возникновением и исчезновением всех возможных областей пластического течения проявились. В целом ряде других случаев, отличных от рассмотренного размерами сопрягающихся элементов сборки, свойствами их материалов, начальной температурой нагрева, охватывающей детали, некоторые области течения могут не появиться. Главное, иных особенностей решения, отличных от рассмотренных здесь, не может проявиться. В этом состоит общность приведенного ниже решения. Следует заметить, что в любом случае проявляет себя обратное (повторное) пластическое течение, оказывающееся неотъемлемым эффектом технологической операции посадки.

2. Исходные модельные зависимости. Постановка задачи. Система уравнений теории температурных напряжений в упругопластических телах в системе прямоугольных декартовых координат имеет вид

Согласно (2.1) , где ${{e}_{{ij}}}$, $e_{{ij}}^{e}$, $e_{{ij}}^{p}$ – полные деформации и их обратимая и необратимая составляющие, $\lambda $, $\mu $, $K = \lambda + \frac{2}{3}\mu $ – упругие постоянные, a – коэффициент температуропроводности, $T$, ${{T}_{0}}$ – текущая и начальная температуры, k – предел текучести, пренебрегается взаимозависимостью деформационных и температурных процессов, то есть задача полагается несвязанной. Для поверхности $f\left( {{{\sigma }_{{ij}}},k} \right) = 0$ далее принимаем

В пространстве главных напряжений ${{\sigma }_{i}}$ соотношения (2.2) задают поверхность наклонной призмы, которую далее будем называть призмой Треска (призма Кулона–Треска [17]). Соответствующее этой поверхности нагружения условие пластического течения является [2] условием максимальных касательных напряжений или условием Треска–Сен-Венана. Зависимости (2.3) также задают поверхность наклонной призмы [1, 2], называемой призмой Ивлева, а соответствующие данной поверхности нагружения условие пластичности называется условием максимальных приведенных касательных напряжений или условием Ишлинского–Ивлева.

Для предела текучести $k$ принимаем следующую его зависимость от температуры

Здесь ${{k}_{0}}$ – предел текучести при начальной температуре ${{T}_{0}}$, ${{T}_{p}}$ – температура плавления материала.

Простейшая постановка задачи горячей посадки труб заключается в следующем: охватывающая труба нагревается до температуры ${{T}_{*}}$ и в нее помещается охватываемая. В момент времени t = 0 внешний радиус ${{R}_{1}}$ охватываемой оказывается равным внутреннему радиусу ${{R}_{1}}$ охватывающей. Распределение температуры в них оказываются однородными: T = T₀ для охватываемой и $T = {{T}_{*}}$ для охватывающей. Дальнейшее распределение температуры связываем при t > 0 с процессом теплопроводности. Полагая трубы достаточно длинными и пренебрегая краевыми эффектами на торцах, приходим к одномерной задаче теории температурных напряжений. Распределение температуры по элементам сборки в такой теории рассчитывается (2.1) независимо от деформирования согласно следующей краевой задачи теории теплопроводности в цилиндрической системе координат $r$, $\varphi $, z:

В (2.5) $r = {{R}_{0}}$, $r = {{R}_{2}}$ – внутренняя свободная поверхность охватываемой трубы и внешняя такая же поверхность охватывающей трубы соответственно, ${{\psi }_{1}}$, ${{\psi }_{2}}$ – их коэффициенты теплопроводности, знаками “+” и “–” обозначены безразмерная температура перед поверхностью контакта и сразу за ней, ${{\chi }_{1}}$, ${{\chi }_{2}}$ – безразмерные коэффициенты теплоотдачи в окружающую среду. Последние зависят от свойств материалов труб, их размера, свойств окружающей среды; далее их считаем постоянными. В данном простом случае задача (2.5) имеет аналитическое решение [19 ] , но из-за того, что далее проводятся численные расчеты, удобно на каждом шаге таких расчетов иметь также численные значения в решении задачи (2.5), что также не встречает дополнительных трудностей. Будем считать, что распределение температуры по деталям сборки нам известным и перейдем к расчету напряженно-деформированных состояний.

Первоначально, вслед за моментом времени $t = 0$, материалы сборки деформируются обратимо. Вследствие одномерности задачи в цилиндрических координатах, следуя (2.1), имеем

Подстановка (2.6) в уравнение равновесия

приводит к дифференциальному уравнению относительно компоненты перемещения ${{u}_{r}}$

Интегрируя (2.8), найдем

Зависимость (2.9) справедлива для всей сборки, необходимо только считать в ней для обхватываемой $l = {{R}_{0}}$, а для охватывающей $l = {{R}_{1}}$. При этом упругие постоянные $\lambda $, $\mu $, K также принимают соответствующие разные значения. Эти же условия следует учитывать при вычислении напряжений

Зависимости (2.9) и (2.10), где $\beta = 1,2$ в зависимости от принадлежности материала охватываемой или охватывающей детали сборки, решают задачу, если в них в каждый рассчитываемый момент времени $t$ вычислены постоянные в этот момент времени функции $С _{1}^{{(\beta )}}$, $С _{2}^{{(\beta )}}$. Их следует определить согласно граничным условиям

3. Развитие необратимого деформирования. Проводя отмеченные последовательные пошаговые вычисления со временем, замечаем, что в некоторый момент времени ${{t}_{1}} > 0$ на поверхности контакта $r = {{R}_{1}}$ в материале охватывающей трубы выполнится условие ${{\sigma }_{r}} - {{\sigma }_{\varphi }} = - 2k$. С этого момента времени в материале развивается область ${{R}_{1}} < r \leqslant {{m}_{1}}(t)$ пластического течения с продвигающейся упругопластической границей $r = {{m}_{1}}(t)$. Здесь и далее используем условие пластичности (2.2).

Следуя зависимостям закона Дюамеля–Неймана и ассоциированному закону пластического течения для напряжений и необратимых деформаций в области течения, получаем

Уравнение равновесия (2.8) для данного случая пластического течения снова удается записать в перемещениях

Проинтегрировав уравнение (3.2), для области течения найдем

Зависимости (3.3) решали бы задачу по расчетам напряженно-деформированного состояния в рассматриваемый момент времени t в области течения ${{R}_{1}} < r \leqslant {{m}_{1}}(t)$ при известном (предварительно рассчитанном) распределении температуры $\theta \left( {r,t} \right)$ и, следовательно, $k\left( {r,t} \right)$, когда бы в них были известны еще и постоянные в этот момент времени $С _{1}^{{(3)}}\left( t \right)$ и $С _{2}^{{(3)}}\left( t \right)$ и положение упругопластической границы ${{m}_{1}}\left( t \right)$. Последние определяются при выполнении граничных условий (2.11), условий непрерывности ${{u}_{r}}$ и ${{\sigma }_{r}}$ и условия обращения в ноль пластических деформаций на упругопластической границе $r = {{m}_{2}}\left( t \right)$. Продолжая расчеты, то есть производя последующие шаги по времени, приходим к тому, что в момент времени ${{t}_{2}} > {{t}_{1}}$ пластическое течение начнется в соответствии грани ${{\sigma }_{r}} - {{\sigma }_{z}} = 2k$ призмы Треска на свободной поверхности $r = {{R}_{0}}$ охватываемой трубы. По материалу этой детали сборки будет продвигаться упругопластическая граница $r = {{m}_{2}}\left( t \right)$ и в сборке будут присутствовать две области пластического течения ${{R}_{0}} \leqslant r \leqslant {{m}_{2}}(t)$ и ${{R}_{1}} \leqslant r \leqslant {{m}_{1}}(t)$ и две области ${{m}_{2}}(t) \leqslant r \leqslant {{R}_{1}}$ и ${{m}_{1}}(t) \leqslant r \leqslant {{R}_{2}}$ обратимого деформирования.

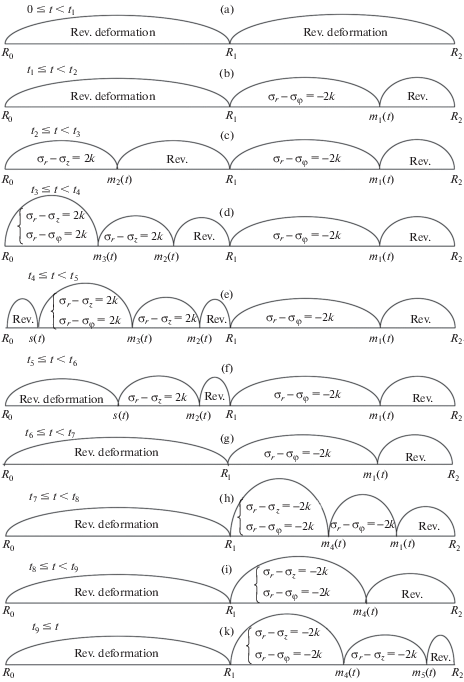
Момент возникновения и исчезновения различных областей пластического течения схематически представлен на фиг. 1, где а) – обратимое деформирование до момента времени $t = {{t}_{1}}$ зарождения первой области пластического течения, b) – $t = {{t}_{2}}$ и так далее. Последующие моменты времени этой схемы далее будут специально оговариваться. Важно заметить, что данная схема, где указываются соответствующие областям пластического течения грани и ребра призмы Треска, является общей в том смысле, что иных, не указанных на схеме областей течения не возникает, хотя некоторые из обозначенных в других условиях теплового воздействия могут отсутствовать.

Используя зависимости закона Дюамеля–Неймана и ассоциированного с гранью ${{\sigma }_{r}} - {{\sigma }_{z}} = 2k$ призмы Треска закона пластического течения, также как и ранее уравнение равновесия в материале охватываемого элемента сборки запишется в каждый момент времени в форме обыкновенного дифференциального уравнения относительно перемещения ${{u}_{r}}\left( r \right)$

После интегрирования уравнения (3.4) для перемещения ${{u}_{r}}$, напряжений и необратимых деформаций можно записать

Теперь на каждом временном шаге следует определить согласно граничным условиям и условиям на продвигающихся упругопластических границах уже десять чисел: ${{С }_{1}}$, ${{С }_{2}}$ (в каждой из четырех областей деформирования) и положение $r = {{m}_{1}}(t)$ и r = ${{m}_{2}}(t)$ в этот момент времени упругопластических границ. Продолжая расчеты (производя последующие шаги по времени) с использованием зависимостей (3.3) для области пластического течения ${{R}_{1}} < r \leqslant {{m}_{1}}(t)$ и зависимостей (3.5) в области ${{R}_{0}} < r \leqslant {{m}_{2}}(t)$, замечаем, что в некоторый последующий момент времени $t = {{t}_{3}} > {{t}_{2}}$ на поверхности $r = {{R}_{0}}$ охватываемой трубы наряду с условием ${{\sigma }_{r}} - {{\sigma }_{z}} = 2k$ выполняется еще и условие ${{\sigma }_{r}} - {{\sigma }_{\varphi }} = 2k$. Таким способом напряженное состояние выходит на ребро призмы Треска (состояние полной пластичности [1, 17]). Далее при $t > {{t}_{3}}$ развивается новая область пластического течения (фиг. 1) с продвигающейся границей $r = {{m}_{3}}(t)$, разделяющей область течения на части, в которых необратимое деформирование подчинено различным системам уравнений. В области ${{m}_{3}}\left( t \right) \leqslant r \leqslant {{m}_{2}}\left( t \right)$ остаются справедливыми зависимости (3.5), а области ${{R}_{0}} < r \leqslant {{m}_{3}}(t)$ подобные зависимости следует получить. Согласно закону Дюамеля–Неймана и ассоциированному с данным ребром призмы Треска законом пластического течения можно записать

Соотношение (3.6) позволяет переписать уравнение равновесия (2.7) в перемещениях

Подстановка результата интегрирования (3.7) в (3.6) приводит к окончательным зависимостям, справедливым в каждый рассчитываемый момент времени в области ${{R}_{0}} < r \leqslant {{m}_{3}}(t)$

Постоянные C₁, C₂ (теперь их десять) вместе с положением границ $r = {{m}_{1}}(t)$, r = = ${{m}_{2}}(t)$, $r = {{m}_{3}}(t)$ в каждый рассчитываемый момент времени находится решением системы алгебраических уравнений, следующей из граничных условий (2.11) и условий на продвигающихся границах областей деформирования.

4. Пластическое течение в процессе разгрузки и остывания. При дальнейшем остывании сборки конструкция разгружается. В некоторый момент времени $t = {{t}_{4}} > {{t}_{3}}$ от граничной поверхности $r = {{R}_{0}}$ отделяется и распространяется по материалу охватываемой трубы разгружающая упругопластическая граница $r = {{s}_{1}}(t)$ (фиг. 1, е). Область пластического течения ${{R}_{1}} < r \leqslant {{m}_{1}}(t)$ в охватывающей детали сборки при этом продолжает развиваться: ${{m}_{1}}(t) > {{m}_{1}}\left( {{{t}_{4}}} \right)$ при $t > {{t}_{4}}$. Несмотря на то, что в области ${{R}_{0}} < r \leqslant {{s}_{1}}\left( t \right)$ материал деформируется необратимо, но воспользоваться ранее записанными зависимостями (2.9) и (2.10) невозможно из-за присутствия в этой области ранее накопленных, неизменяющихся со временем пластических деформаций. Такие деформации ${{p}_{r}}(r)$, ${{p}_{\varphi }}(r)$ и ${{p}_{z}}(r)$ фиксируются моментом прихода в точку с текущей координатой $r$ разгружающей упругопластической границы $r = {{s}_{1}}(t)$. Иначе, если обозначить такой момент времени через ${{t}_{*}}$, то ${{p}_{r}}(r) = e_{r}^{p}(r,{{t}_{*}})$; ${{p}_{\varphi }}(r) = e_{\varphi }^{p}(r,{{t}_{*}})$; ${{p}_{z}}\left( r \right) = e_{z}^{p}(r,{{t}_{*}})$. Только для каждого $r$ из области ${{R}_{0}} < r \leqslant {{s}_{1}}(t)$ момент ${{t}_{*}}$ индивидуален. Уравнение равновесия, записанное в перемещениях, теперь принимает форму

Подстановка решения обыкновенного дифференциального уравнения (4.1) в соотношения закона Дюамеля–Неймана приводит к зависимостям

На каждом временном шаге теперь приходится решением системы алгебраических уравнений, следующей при выполнении граничных условий и условий на продвигающихся граничных поверхностях разделяющих область деформирования на шесть частей, вычислить двенадцать постоянных C₁ и C₂ (для каждой из областей) и четыре положения обозначенных поверхностей разделения (фиг. 1, е).

Следующим характерным моментом времени, появляющимся при последовательном проведении расчетов, оказывается момент времени $t = {{t}_{5}} > {{t}_{4}}$, когда $s\left( t \right) = {{m}_{3}}\left( t \right)$, то есть область с состоянием полной пластичности (на ребре призмы Треска) исчезнет. При $t > {{t}_{5}}$ в охватываемой трубе останется лишь одна пластическая область, соответствующая грани ${{\sigma }_{r}} - {{\sigma }_{z}} = 2k$ призмы Треска (фиг. 1, f). Дальнейшие расчеты показывают, что наступает момент времени $t = {{t}_{6}} > {{t}_{5}}$ такой, что ${{s}_{1}}\left( t \right) = {{m}_{2}}\left( t \right)$ (фиг. 1, g). При $t > {{t}_{6}}$ весь охватываемый элемент сборки деформируется обратимо, в соответствии с зависимостями (4.2).

Обратимая разгрузка охватываемой трубы приводит к изменению пластического течения в охватывающем элементе сборки. Обнаруживается последующий рассчитываемый момент времени $t = {{t}_{7}} > {{t}_{6}}$, после которого развивается область пластического течения ${{R}_{1}} < r \leqslant {{m}_{4}}\left( t \right)$ в соответствие ребру призмы Треска: ${{\sigma }_{r}} - {{\sigma }_{\varphi }} = - 2k$ и ${{\sigma }_{r}} - {{\sigma }_{z}}$ = = –2k (фиг. 1, h). Для расчетов напряженно-деформируемых состояний последней области следует воспользоваться зависимостями (3.8), соответственно изменив в них значения постоянных материала, положив $l = {{R}_{1}}$ и изменив знак предела текучести. Иные постоянные задачи, также как и всюду до этого, вычисляются на каждом шаге вычислений, следуя граничным условиям и условиям на продвигающихся границах областей.

Появление и исчезновение последующих областей необратимого деформирования представляет фиг. 1 со следующими со временем состояниями i, k. Последние следуют с необходимостью при дальнейших временных шагах расчетов. Перемещения, напряжения и необратимые деформации в каждой из вновь возникающих областей пластического течения в их зависимости от распределения температуры $\theta \left( {r,t} \right)$ вычисляются соответствующими выше выписанными зависимостями при необходимых в них изменениях: $\lambda $, $\mu $, ${{k}_{0}}$, $\alpha $ теперь соответствуют материалу охватывающей трубы, предел текучести $k(t)$ меняет знак. Также в этих зависимостях в качестве l следует принять минимальное значение r для рассматриваемой области необратимого деформирования.

Последующие расчеты приводят к возникновению на контактной поверхности $r = {{R}_{1}}$ и продвигающихся далее по материалу охватывающей трубы разгружающей упругопластической границы $r = {{s}_{2}}(t)$ (см. фиг. 1, состояния l, m, n). В образующейся области обратимого деформирования будут справедливы зависимости (4.2) с теми же оговоренными изменениями в них, приспособляющими их к расчету обратимого деформирования охватывающей трубы, а не охватываемой, как ранее. Ниже приведем результаты расчетов согласно описанному здесь алгоритму их проведения последовательными шагами по времени для итогового распределения остаточных напряжений по элементам сборки.

Следует еще раз заметить, что рассмотренный выше процесс посадки является общим, демонстрирующим все возможные особенности расчетов. При других начальных условиях и иных толщинах труб некоторые из областей необратимого деформирования могут не состояться. Возможно также, что процесс закончится без исчезновения областей пластического течения (чаще всего в охватывающей трубе). Тогда в таких областях реализуются условия нейтрального нагружения без дальнейшего роста термоупругих и пластических деформаций.

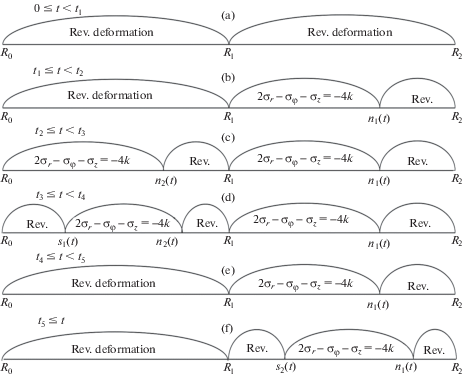
5. Условие максимальных приведенных касательных напряжений. Рассмотрим тот же процесс сборки при условии пластичности Ишлинского–Ивлева (2.3). Возникновение и исчезновение областей пластического течения в этом случае иллюстрирует фиг. 2. Сравнивая ее с аналогом для условия пластического течения Треска–Сен-Венана (фиг. 1), отмечаем значительное упрощение из-за того, что все необратимое деформирование в этом случае осуществляется в соответствии напряженных состояний двум противоположным граням призмы Ивлева. Именно: $2{{\sigma }_{r}} - {{\sigma }_{\varphi }} - {{\sigma }_{z}} = \pm 4k$. Также как и всюду здесь уравнение равновесия (2.7) удается, следуя ассоциированному закону пластического течения и зависимостям закона Дюамеля–Неймана, записать в перемещениях и проинтегрировать. Итоговые зависимости для перемещения, напряжений и необратимых деформаций следуют в виде

Совершенно аналогично предыдущему теперь на каждом шаге расчетов вычисляем постоянные интегрирования в рассматриваемый момент времени вместе с положением упругопластических границ. В расчетах напряжений за разгружающими упругопластическими границами следует использовать зависимости (4.2).

Рассмотрим некоторые результаты проведенных численных экспериментов. Пусть внешняя труба изготовлена из дюралюминия (Д16т), обладающего следующими характеристиками: плотность $\rho = 2.8 \cdot {{10}^{3}}$ кг/м³, теплопроводность ${{\chi }_{2}} = 130$ Вт/(мК), изобарная удельная теплоемкость ${{с }_{p}} = 0.922$ кДж/(кг ⋅ К), коэффициент отдачи нагретого материала в окружающую среду ${{\chi }_{2}} = 10$ Вт/(м² ⋅ К), коэффициент линейного температурного расширения $\alpha = 22.9 \cdot {{10}^{{ - 6}}}$, предел текучести материала при комнатной температуре $k_{0}^{{(2)}} = 255$ МПа, температура плавления материала ${{T}_{p}} = 660^\circ {\text{C}}$, модуль Юнга $E = 72$ ГПа, коэффициент Пуассона $v = 0.3$. Внутренняя труба выполнена из алюминия (АД6): $\rho = 2.7 \cdot {{10}^{3}}$ кг/м³, $\chi = 188$ Вт/мК, $с _{p}^{{(1)}} = 0.903$ кДж/(кг ⋅ К), ${{\chi }_{1}} = 10$ Вт/(м² ⋅ К), $\alpha = 23.4 \cdot {{10}^{{ - 6}}}$, $k_{0}^{{(1)}} = 210$ МПа, ${{T}_{p}} = 660^\circ {\text{C}}$, $E = 70$ ГПа, $v = 0.3$.

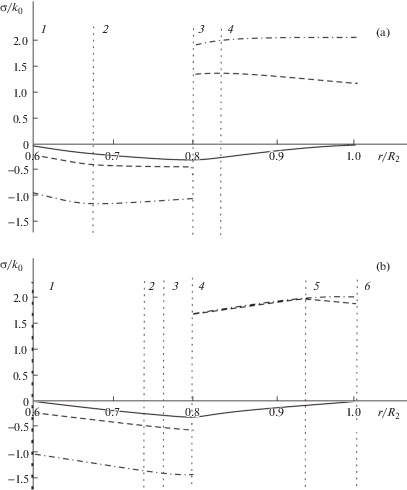
На фиг. 3 и фиг. 4 изображены распределения остаточных напряжений в материале сборки, за $k_{0}^{{(2)}} = 255$ МПа. На фиг. 3, а результаты, полученные при использовании критерия Ишлинского-Ивлева, а на фиг. 3, b результаты, полученные при использовании Треска. При этом начальная температура внешней трубы $300^\circ {\text{C}}$, эта температура не превышает температуры рекристаллизации металла. Сплошной линией показано радиальное напряжение ${{\sigma }_{r}}$, пунктирной – ${{\sigma }_{\varphi }}$, штрих-пунктирной – ${{\sigma }_{z}}$. Границы зон пластического течения отмечены вертикальными штриховыми линиями, зоны (1–2) и (4–5) соответствуют ребрам призмы Треска, зона (2–3) и (5–6) граням. Натяг при этом составляет для случая Ишлинского–Ивлева 83 МПа, для случая Треска 84.6 МПа.

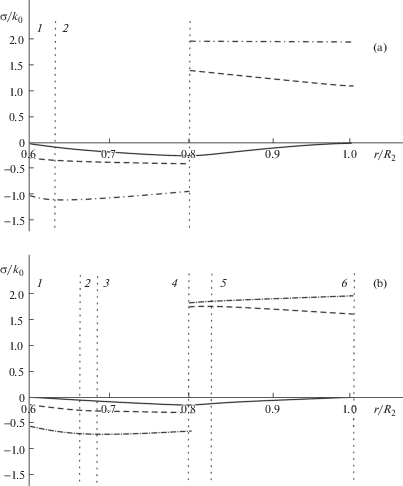
Расчеты, приведенные на фиг. 3, произведены с начальной температурой внешней трубы $300^\circ {\text{C}}$, если произвести эти расчеты и принять, что температура внешней трубы будет $280^\circ {\text{С }}$, то получим результат, изображенный на фиг. 4. Они характерны отсутствием пластического течения в материале внешнего цилиндра при условии Ишлинского–Ивлева.

Важно заметить, что несмотря на различия в распределении остаточных напряжений итоговый натяг практически одинаков в обоих таких случаях (с точностью до погрешности вычислений). Данное обстоятельство позволяет рекомендовать в качестве нормативного расчета операции посадки именно вычисления согласно критерию Ишлинского–Ивлева, поскольку в этом случае объем таких вычислений существенно сокращается.

Работа выполнена при поддержке государственного задания № 075-00414-19-00.