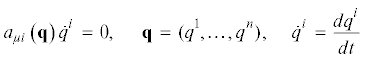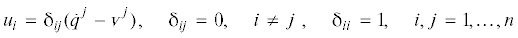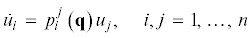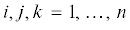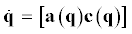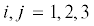Известия РАН. Механика твердого тела, 2019, № 3, стр. 124-135

О МЕТОДАХ ПОСТРОЕНИЯ УРАВНЕНИЙ ДИНАМИКИ С УЧЕТОМ СТАБИЛИЗАЦИИ СВЯЗЕЙ

И. Е. Каспирович^a, *, Р.Г. Мухарлямов^a

^a Российский университет дружбы народов
Москва, Россия

Поступила в редакцию 25.03.2018
После доработки 25.03.2018
Принята к публикации 19.11.2018

DOI: 10.1134/S0572329919030115

Аннотация

Построение уравнений динамики системы по известным уравнениям связей, основанное на методах классической механики, связано с накоплением ошибок при численном решении и требует определенной модификации, направленной на стабилизацию связей. Проблема стабилизации связей может быть решена изменением динамических показателей системы, что позволяет определить множители Лагранжа в уравнениях движения, учитывающие возможные отклонения от уравнений связей. В системах с линейными неголономными связями оказывается возможным выражение проекций скоростей через функции координат системы. В этом случае удается составить систему дифференциальных уравнений второго порядка и представить их в форме уравнений Лагранжа. Используя обобщенные условия Гельмгольца можно составить уравнения Лагранжа с диссипативной функцией и обеспечить выполнение условий стабилизации связей.

Ключевые слова: уравнения, связи, стабилизация, условия Гельмгольца, устойчивость

1. Введение. Для построения уравнений динамики механических систем со связями обычно используются два подхода. В случае, когда кинематическое состояние системы может быть определено обобщенными координатами и скоростями, решение соответствующих уравнений динамики позволяет описать изменение состояния системы. Если уравнения связей не позволяют описать динамику системы через обобщенные координаты и скорости или это оказывается нецелесообразным, приходится использовать множители Лагранжа, которые определяются дифференцированием уравнений связей.

Традиционный метод определения множителей Лагранжа основан на предположении о том, что связи, наложенные на систему, представляют собой первые интегралы уравнений движения. При этом численное интегрирование уравнений динамики с множителями Лагранжа приводит к неустойчивости множества траекторий, соответствующих уравнениям связей. Ограничить накопление ошибок численного интегрирования уравнений динамики позволяет стабилизация связей [1], основанная на применении линейной комбинации уравнений связей и их производных для определения выражений множителей Лагранжа. Метод стабилизации связей оказался эффективным при решении задач моделирования динамики и управления механическими системами [2–5] и системами различной физической природы [6–8]. Были предложены различные модификации этого метода, которые сводились к подбору коэффициентов комбинации уравнений связей с их производными первого и второго порядка [9–12].

По существу, процесс определения произвольных множителей сводится к достраиванию уравнений динамики в окончательном виде и относится к обратным задачам динамики [13–21]. Общее решение обратной задачи динамики сводится к построению множества систем дифференциальных уравнений, решения которых обладают заданными свойствами [22–25]. В [23] определена структура систем дифференциальных уравнений, имеющих заданные частные интегралы, в [24] сформулированы условия устойчивости соответствующего множества траекторий, метод построения уравнений динамики механических систем и определения множителей Лагранжа, обеспечивающих стабилизацию связей, предложен в [26]. В работе [27] исследуется задача управления динамикой системы в предположении, что цели управления задаются уравнениями связей.

Условия, необходимые для приведения системы дифференциальных уравнений к форме уравнений Эйлера–Лагранжа, были сформулированы в [28]. Было доказано [29, 30], что эти условия являются также и достаточными. Для приведения дифференциальных уравнений к форме уравнений Лагранжа с учетом стабилизации связей необходимо обеспечить асимптотическую устойчивость множества траекторий, соответствующих уравнениям связей. Обобщенные условия Гельмгольца, полученные в [31], позволяют построить уравнения Эйлера–Лагранжа с диссипативной функцией. В настоящей работе предлагается метод построения уравнений Лагранжа и диссипативной функции, которые могли бы обеспечить стабилизацию линейных неголономных связей при численном решении.

2. Построение дифференциальных уравнений по уравнениям связей. Рассматривается динамическая система, состояние которой определяется координатами ${{q}^{1}},\; \ldots ,\;{{q}^{n}}$, и на которую наложены линейные дифференциальные связи, заданные уравнениями

(2.1)

Здесь, как и в дальнейшем, предполагается суммирование по одинаковым индексам. Если строки матрицы $A = {{a}_{{\mu i}}}\left( q \right)$ линейно независимы при всех допустимых значениях $q$, то система уравнений (2.1) допускает выражение скоростей через координаты системы

(2.2)

${{\dot {q}}^{i}} = {{\text{v}}^{i}}\left( q \right),\quad i = 1, \ldots ,n$

Правые части равенства (2.2) с точностью до произвольного множителя c определяются компонентами векторного произведения $\quad{\mathbf{v}}\left( q \right) = с \left[ {{{a}_{1}} \ldots {{a}_{m}}{{c}_{{m + 1}}} \ldots {{c}_{{n - 1}}}} \right]$, где ${{a}_{\mu }}$ – строки матрицы A, ${{c}_{{m + 1}}},\; \ldots ,\;{{c}_{{n - 1}}}$ – произвольные векторы. Полагая, что множитель c и произвольные векторы являются функциями координат: $с = с \left( q \right)$, $\quad{{c}_{{m + 1}}} = {{c}_{{m + 1}}}(q)$, …, $\quad{{c}_{{n - 1}}} = {{c}_{{n - 1}}}(q)$, равенства (2.2) можно рассматривать как систему дифференциальных уравнений, определяющих закон изменения вектора состояния системы: $q = q\left( t \right)$, соответствующий начальному значению $q\left( {{{t}_{0}}} \right) = {{q}_{0}}$. Принимая равенство $q = q\left( t \right)$ за невозмущенное решение системы уравнений (2.2), будем определять отклонения от этого решения возмущениями скоростей

(2.3)

Составим уравнения возмущений связей в виде линейной системы дифференциальных уравнений относительно отклонений с коэффициентами, зависящими от переменных ${{q}^{1}},\; \ldots ,\;{{q}^{n}}$:

(2.4)

Если коэффициенты $p_{i}^{j}\left( q \right)$ системы (2.4) при всех допустимых значениях вектора состояния q удовлетворяют условиям асимптотической устойчивости тривиального решения ${{u}_{i}} = 0$, 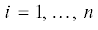, то решение $q = q\left( t \right)$, системы (2.2), соответствующее начальному условию $q\left( {{{t}_{0}}} \right) = {{q}_{0}}$, будет устойчиво асимптотически. Равенствам (2.4) с учетом обозначений (2.3) соответствует система дифференциальных уравнений второго порядка

(2.5)

$\begin{gathered} {{{\ddot {q}}}^{i}} - (\text{v}_{j}^{i}\left( q \right) + p_{j}^{i}\left( q \right)){{{\dot {q}}}^{j}} + p_{j}^{i}\left( q \right){{\text{v}}^{j}}\left( q \right) = 0,\quad \quad\text{v}_{j}^{i}\left( q \right) = \frac{{\partial {{\text{v}}^{i}}\left( q \right)}}{{\partial {{q}^{j}}}}\quad\quad \\ i,j = 1,\; \ldots ,\;n \\ \end{gathered} $

3. Представление дифференциальных уравнений второго порядка в форме уравнений Лагранжа. Система дифференциальных уравнений (2.5) составляет зависимости между обобщенными координатами, скоростями и ускорениями динамической системы:

(3.1)

$\begin{gathered} {{f}^{i}}\left( {q,\dot {q},\ddot {q}{\text{,}}t} \right) \equiv {{{\ddot {q}}}^{i}} - (\text{v}_{j}^{i}\left( q \right) + p_{j}^{i}\left( q \right)){{{\dot {q}}}^{j}} + p_{j}^{i}\left( q \right){{\text{v}}^{j}}\left( q \right) = 0 \\ i,j = 1,\; \ldots ,\;n \\ \end{gathered} $

Соотношения (3.1) могут быть представлены в форме уравнений Лагранжа, что возможно при выполнении необходимых и достаточных условий [6], накладываемых на функции ${{f}^{i}}(q,\dot {q},{\mathbf{\ddot {q}}},t) = 0$:

(3.2)

$\frac{{\partial {{f}^{i}}}}{{\partial {{{\ddot {q}}}^{k}}}} = \frac{{\partial {{f}^{k}}}}{{\partial {{{\ddot {q}}}^{i}}}}$

(3.3)

$\frac{{\partial {{f}^{i}}}}{{\partial {{{\dot {q}}}^{k}}}} + \frac{{\partial {{f}^{k}}}}{{\partial {{{\dot {q}}}^{i}}}} = 2\frac{d}{{dt}}\frac{{\partial {{f}^{i}}}}{{\partial {{{\ddot {q}}}^{k}}}}$

(3.4)

$\frac{{\partial {{f}^{i}}}}{{\partial {{q}^{k}}}} - \frac{{\partial {{f}^{k}}}}{{\partial {{q}^{i}}}} = \frac{1}{2}\frac{d}{{dt}}\left( {\frac{{\partial {{f}^{i}}}}{{\partial {{{\dot {q}}}^{k}}}} - \frac{{\partial {{f}^{k}}}}{{\partial {{{\dot {q}}}^{i}}}}} \right)$

(3.5)

$\begin{gathered} \frac{{{{\partial }^{2}}{{f}^{i}}}}{{\partial {{{\ddot {q}}}^{j}}\partial {{{\ddot {q}}}^{k}}}} = 0 \\ i,j,k = 1, \ldots ,n \\ \end{gathered} $

Из выражений (3.1) непосредственно следует, что условия (3.2), (3.5) выполняются. Условия (3.3) принимают вид:

(3.6)

$\begin{gathered} \text{v}_{k}^{i} + p_{k}^{i} + \text{v}_{i}^{k} + p_{i}^{k} = 0 \\ i,k = 1, \ldots ,n \\ \end{gathered} $

Очевидно, если коэффициенты уравнений системы (2.4) выбрать в соответствии с равенством 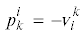, то будут выполнены условия (3.6) и справедливы равенства

$\frac{{\partial p_{j}^{i}}}{{\partial {{q}^{k}}}} - \frac{{\partial p_{j}^{k}}}{{\partial {{q}^{i}}}} = 0,\quad p_{j}^{i}\text{v}_{k}^{j} - p_{j}^{k}\text{v}_{i}^{j} = 0\quad$

Условиям (3.4) соответствуют равенства

(3.7)

$\begin{gathered} \left( {\frac{{\partial \text{v}_{j}^{k}}}{{\partial {{q}^{i}}}} + \frac{{\partial p_{j}^{k}}}{{\partial {{q}^{i}}}} - \frac{{\partial \text{v}_{j}^{i}}}{{\partial {{q}^{k}}}} - \frac{{\partial p_{j}^{i}}}{{\partial {{q}^{k}}}}} \right){{{\dot {q}}}^{j}} + \left( {\frac{{\partial p_{j}^{i}}}{{\partial {{q}^{k}}}} - \frac{{\partial p_{j}^{k}}}{{\partial {{q}^{i}}}}} \right){{\text{v}}^{j}} + (p_{j}^{i}\text{v}_{k}^{j} - p_{j}^{k}\text{v}_{i}^{j}) = \\ = \;\frac{1}{2}\frac{d}{{dt}}((\text{v}_{i}^{k} + p_{i}^{k}) - (\text{v}_{k}^{i} + p_{k}^{i})) \\ i,j,k = 1, \ldots ,n \\ \end{gathered} $

Легко убедиться, что равенство (3.7) также обращается в тождество. Левая часть принимает вид

$\frac{{\partial {{f}^{i}}}}{{\partial {{q}^{k}}}} - \frac{{\partial {{f}^{k}}}}{{\partial {{q}^{i}}}} = \left( {\frac{{\partial \text{v}_{j}^{k}}}{{\partial {{q}^{i}}}} - \frac{{\partial \text{v}_{j}^{i}}}{{\partial {{q}^{k}}}}} \right){{\dot {q}}^{j}} = \frac{d}{{dt}}\left( {\frac{{\partial {{\text{v}}^{k}}}}{{\partial {{q}^{i}}}} - \frac{{\partial {{\text{v}}^{i}}}}{{\partial {{q}^{k}}}}} \right)$

что совпадает с правой частью

$\frac{1}{2}\frac{d}{{dt}}((\text{v}_{i}^{k} + p_{i}^{k}) - (\text{v}_{k}^{i} + p_{k}^{i})) = \frac{1}{2}\frac{d}{{dt}}((\text{v}_{i}^{k} - \text{v}_{k}^{i}) - (\text{v}_{k}^{i} - \text{v}_{i}^{k})) = \frac{d}{{dt}}\left( {\frac{{\partial {{\text{v}}^{k}}}}{{\partial {{q}^{i}}}} - \frac{{\partial {{\text{v}}^{i}}}}{{\partial {{q}^{k}}}}} \right)$

Следовательно, условия Гельмгольца будут выполнены и система дифференциальных уравнений

(3.8)

${{\ddot {q}}^{i}} + g_{j}^{i}\left( q \right){{\dot {q}}^{j}} + p_{j}^{i}\left( q \right){{\text{v}}^{j}}\left( q \right) = 0,\quad i,j = 1, \ldots ,n$

$g_{j}^{i}\left( q \right) = \text{v}_{i}^{j}\left( q \right) - \text{v}_{j}^{i}\left( q \right),\quad p_{j}^{i}\left( q \right) = - \text{v}_{i}^{j}\left( q \right)$

может быть представлена в виде системы уравнений Лагранжа

$\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial {{{\dot {q}}}^{i}}}}} \right) - \frac{{\partial L}}{{\partial {{q}^{i}}}} = \frac{{\partial G}}{{\partial {{{\dot {q}}}^{i}}}},\quad i = 1, \ldots ,n$

Здесь $L = T - P$ – лагранжиан, $T = \left( {1{\text{/}}2} \right){{\dot {q}}^{i}}{{{\delta }}_{{ij}}}{{\dot {q}}^{j}}$ – кинетическая энергия, P = = $(1{\text{/}}2){{\text{v}}^{i}}{{{\delta }}_{{ij}}}{{\text{v}}^{j}}$ – потенциальная энергия, $\partial G{\text{/}}\partial {{\dot {q}}^{i}} = g_{j}^{i}\left( q \right){{\dot {q}}^{j}}$ – гироскопические силы, G = $(1{\text{/}}2){{\dot {q}}^{i}}{{{\delta }}_{{ik}}}g_{j}^{k}(q){{\dot {q}}^{j}}$, $g_{j}^{i}(q) = - g_{i}^{j}(q)$.

4. Уравнения динамики системы единичных масс с диссипативными силами. Система дифференциальных уравнений (3.8) содержит коэффициенты $p_{j}^{i}\left( q \right)$ уравнений возмущений связей (2.4), выбором которых определяется устойчивость тривиального решения уравнений системы (2.4). Необходимым условием стабилизации связей, представленных уравнениями (2.2), при численном решении системы уравнений (3.8), является асимптотическая устойчивость тривиального решения системы (2.4), что приводит к необходимости введения диссипативных сил. Условия приведения системы дифференциальных уравнений к форме уравнений Лагранжа

$\frac{d}{{dt}}\frac{{\partial L}}{{\partial {{{\dot {q}}}^{i}}}} - \frac{{\partial L}}{{\partial {{q}^{i}}}} = - \frac{{\partial D}}{{\partial {{{\dot {q}}}^{i}}}},\quad i = 1, \ldots ,n$

с диссипативной функцией Рэлея $D = \left( {1{\text{/}}2} \right){{d}_{{ik}}}\left( q \right){{\dot {q}}^{i}}{{\dot {q}}^{k}}$ определяются обобщенными условиями Гельмгольца [9]:

(4.1)

$\frac{{\partial {{f}^{i}}}}{{\partial {{{\ddot {q}}}^{k}}}} = \frac{{\partial {{f}^{k}}}}{{\partial {{{\ddot {q}}}^{i}}}}$

(4.2)

$\frac{1}{2}\left( {\frac{{\partial {{f}^{i}}}}{{\partial {{{\dot {q}}}^{k}}}} + \frac{{\partial {{f}^{k}}}}{{\partial {{{\dot {q}}}^{i}}}}} \right) - \frac{d}{{dt}}\frac{{\partial {{f}^{i}}}}{{\partial {{{\ddot {q}}}^{k}}}} = {{{\delta }}^{{ij}}}{{d}_{{jk}}}$

(4.3)

$\frac{{\partial {{f}^{i}}}}{{\partial {{q}^{k}}}} - \frac{{\partial {{f}^{k}}}}{{\partial {{q}^{i}}}} - \frac{1}{2}\frac{d}{{dt}}\left( {\frac{{\partial {{f}^{i}}}}{{\partial {{{\dot {q}}}^{k}}}} - \frac{{\partial {{f}^{k}}}}{{\partial {{{\dot {q}}}^{i}}}}} \right) = r_{k}^{i}$

(4.4)

$\frac{{{{\partial }^{2}}{{f}^{i}}}}{{\partial {{{\ddot {q}}}^{j}}\partial {{{\ddot {q}}}^{k}}}} = 0$

$r_{k}^{i} = \frac{{{{\partial }^{2}}D}}{{\partial {{{\dot {q}}}^{i}}\partial {{q}^{k}}}} - \frac{{{{\partial }^{2}}D}}{{\partial {{{\dot {q}}}^{k}}\partial {{q}^{i}}}},\quad i,j,k = 1, \ldots ,n$

Легко видеть, что условия (4.1)–(4.4) переходят в условия (3.2)–(3.5) при отсутствии диссипативной функции $D$. Очевидно, что для системы уравнений (3.1) условия (4.1) и (4.4) выполняются. Условия (4.2) и (4.3) накладывают ограничения на выбор коэффициентов 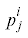уравнений возмущений связей (2.4) и коэффициентов $d_{k}^{i} = d_{i}^{k}$, $d_{k}^{i}\, = \,{{\delta }^{{ij}}}{{d}_{{jk}}}$, диссипативной функции $D.$ Условия (4.2) приводятся к виду:

(4.5)

$\text{v}_{j}^{i} + p_{j}^{i} + d_{j}^{i} = - (\text{v}_{i}^{j} + p_{i}^{j} + d_{i}^{j})$

Условия (4.3) с учетом выражения $\quad2D = {{d}_{{ik}}}\left( q \right){{\dot {q}}^{i}}{{\dot {q}}^{k}}$ записываются в виде:

(4.6)

$\begin{gathered} - \frac{\partial }{{\partial {{q}^{k}}}}(\text{v}_{j}^{i} + p_{j}^{i}){{{\dot {q}}}^{j}} + \frac{\partial }{{\partial {{q}^{k}}}}(p_{j}^{i}{{\text{v}}^{j}}) + \frac{\partial }{{\partial {{q}^{i}}}}(\text{v}_{j}^{k} + p_{j}^{k}){{{\dot {q}}}^{j}} - \frac{\partial }{{\partial {{q}^{i}}}}(p_{j}^{k}{{\text{v}}^{j}}) - \quad \\ - \frac{1}{2}\frac{d}{{dt}}((\text{v}_{i}^{k} + p_{i}^{k}) - (\text{v}_{k}^{i} + p_{k}^{i})) = \frac{{\partial d_{j}^{i}}}{{\partial {{q}^{k}}}}{{{\dot {q}}}^{j}} - \frac{{\partial d_{j}^{k}}}{{\partial {{q}^{i}}}}{{{\dot {q}}}^{j}} \\ i,j,k = 1,\; \ldots ,\;n \\ \end{gathered} $

Равенство (4.6) может быть переписано с учетом условий (4.5):

$\begin{gathered} \frac{\partial }{{\partial {{q}^{i}}}}(\text{v}_{j}^{k} + p_{j}^{k}){{{\dot {q}}}^{j}} - \frac{\partial }{{\partial {{q}^{k}}}}(\text{v}_{j}^{i} + p_{j}^{i}){{{\dot {q}}}^{j}} + \frac{\partial }{{\partial {{q}^{k}}}}(p_{j}^{i}{{\text{v}}^{j}}) - \frac{\partial }{{\partial {{q}^{i}}}}(p_{j}^{k}{{\text{v}}^{j}}) - \frac{d}{{dt}}(\text{v}_{i}^{k} + p_{i}^{k}) = \\ = \;\left( {\frac{{\partial d_{j}^{i}}}{{\partial {{q}^{k}}}} + \frac{{\partial d_{k}^{i}}}{{\partial {{q}^{j}}}} - \frac{{\partial d_{j}^{k}}}{{\partial {{q}^{i}}}}} \right){{{\dot {q}}}^{j}} \\ \end{gathered} $

и после несложных преобразований принимает вид:

(4.7)

$\begin{gathered} \frac{\partial }{{\partial {{q}^{i}}}}(\text{v}_{j}^{k} + p_{j}^{k} + d_{j}^{k}){{{\dot {q}}}^{j}} - \frac{\partial }{{\partial {{q}^{k}}}}(\text{v}_{j}^{i} + p_{j}^{i} + d_{j}^{i}){{{\dot {q}}}^{j}} - \frac{\partial }{{\partial {{q}^{j}}}}(\text{v}_{i}^{k} + p_{i}^{k} + d_{j}^{k}){{{\dot {q}}}^{j}} + \\ \quad + \;\frac{\partial }{{\partial {{q}^{k}}}}(p_{j}^{i}{{\text{v}}^{j}}) - \frac{\partial }{{\partial {{q}^{i}}}}(p_{j}^{k}{{\text{v}}^{j}}) = 0 \\ \end{gathered} $

Очевидно, что, если определить коэффициенты уравнений системы (2.4) равенствами

(4.8)

$p_{j}^{i} = - \frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{i}}}} - d_{j}^{i},\quad i,j = 1, \ldots ,n$

соответствующими (4.5), и из равенства (4.7) следуют условия:

$\frac{\partial }{{\partial {{q}^{k}}}}(p_{j}^{i}{{\text{v}}^{j}}) = \frac{\partial }{{\partial {{q}^{i}}}}(p_{j}^{k}{{\text{v}}^{j}}),\quad i,j,k = 1,\; \ldots ,\;n$,

С учетом выражений (4.8) условия (4.3) сводятся к равенствам

(4.9)

$\begin{gathered} \left( {\frac{\partial }{{\partial {{q}^{k}}}}\left( {\frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{i}}}} + d_{j}^{i}} \right)} \right){{\text{v}}^{j}} + \left( {\frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{i}}}} + d_{j}^{i}} \right)\frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{k}}}} = \left( {\frac{\partial }{{\partial {{q}^{i}}}}\left( {\frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{k}}}} + d_{j}^{k}} \right)} \right){{\text{v}}^{j}} + \left( {\frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{k}}}} + d_{j}^{k}} \right)\frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{i}}}} \\ i,j,k = 1,\; \ldots ,\;n \\ \end{gathered} $

Из выражений (4.9) следует, что условия (4.3) будут выполнены, если коэффициенты диссипативной функции удовлетворяют условиям

(4.10)

$\frac{\partial }{{\partial {{q}^{k}}}}(d_{j}^{i}{{\text{v}}^{j}}) = \frac{\partial }{{\partial {{q}^{i}}}}(d_{j}^{k}{{\text{v}}^{j}}),\quad i,j,k = 1,\; \ldots ,\;n$

Следовательно, система дифференциальных уравнений

${{\ddot {q}}^{i}} - \left( {\frac{{\partial {{\text{v}}^{i}}}}{{\partial {{q}^{j}}}} - \left( {\frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{i}}}} + d_{j}^{i}} \right)} \right){{\dot {q}}^{j}} - \left( {\frac{{\partial {{\text{v}}^{j}}}}{{\partial {{q}^{i}}}} + d_{j}^{i}} \right){{\text{v}}^{j}} = 0,\quad i,j = 1,\; \ldots ,\;n$

приводится к системе уравнений Лагранжа

$\frac{d}{{dt}}\frac{{\partial L}}{{\partial {{{\dot {q}}}^{i}}}} - \frac{{\partial L}}{{\partial {{q}^{i}}}} = \frac{{\partial G}}{{\partial {{{\dot {q}}}^{i}}}} - \frac{{\partial D}}{{\partial {{{\dot {q}}}^{i}}}},\quad i,j,k = 1,\; \ldots ,\;n$

где $L = T - P$, $T = \left( {1{\text{/}}2} \right){{\dot {q}}^{i}}{{{\delta }}_{{ij}}}{{\dot {q}}^{j}}$ – кинетическая энергия, $P = \left( {1{\text{/}}2} \right){{\text{v}}^{i}}{{{\delta }}_{{ij}}}{{\text{v}}^{j}}\quad$ – потенциальная энергия, $\partial G{\text{/}}\partial {{\dot {q}}^{i}} = g_{j}^{i}\left( q \right){{\dot {q}}^{j}}$ – гироскопические силы, $G = \left( {1{\text{/}}2} \right){{\dot {q}}^{i}}{{{\delta }}_{{ik}}}g_{j}^{k}\left( q \right){{\dot {q}}^{j}}$, $g_{j}^{i}(q) = - g_{i}^{j}(q) = \partial {{\text{v}}^{j}}{\text{/}}\partial {{q}^{i}} - \partial {{\text{v}}^{i}}{\text{/}}\partial {{q}^{j}}$.

5. Построение уравнений динамики механической системы с неголономными связями. Для построения уравнений динамики механической системы, на которую наложены связи, описываемые уравнениями (2.1), и кинетическая энергия которой определяется квадратичной формой $T = \left( {1{\text{/}}2} \right){{m}_{{ij}}}{{\dot {q}}^{i}}{{\dot {q}}^{j}}$, ${{m}_{{ij}}} = {{m}_{{ji}}} = {{m}_{{ij}}}\left( q \right)$, $i,j = 1,\; \ldots ,\;n$, примем величины

(5.1)

${{u}_{i}} = {{m}_{{ij}}}{{\dot {q}}^{j}} - {{\text{v}}_{i}}$

${{\text{v}}_{i}} = {{m}_{{ij}}}\left( q \right){{\text{v}}^{j}}\left( q \right),$

за отклонения от уравнений связей (2.2). Составим уравнения возмущений связей также в виде линейной системы (2.4). Тогда из (5.1), (2.4) следует система дифференциальных уравнений

(5.2)

${{m}_{{ij}}}{{\ddot {q}}^{j}} + \frac{{\partial {{m}_{{ij}}}}}{{\partial {{q}^{k}}}}{{\dot {q}}^{j}}{{\dot {q}}^{k}} - \frac{{\partial {{\text{v}}_{i}}}}{{\partial {{q}^{j}}}}{{\dot {q}}^{j}} = p_{i}^{k}({{m}_{{kj}}}{{\dot {q}}^{j}} - {{\text{v}}_{k}}),$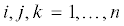

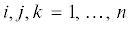
которая может быть представлена в форме уравнений Лагранжа, если функции

${{f}^{i}}\left( {q,\dot {q},{\mathbf{\ddot {q}}},t} \right) \equiv {{m}_{{ij}}}{{\ddot {q}}^{j}} + \frac{1}{2}\left( {\frac{{\partial {{m}_{{ij}}}}}{{\partial {{q}^{k}}}} + \frac{{\partial {{m}_{{ik}}}}}{{\partial {{q}^{j}}}}} \right){{\dot {q}}^{j}}{{\dot {q}}^{k}} - \left( {\frac{{\partial {{\text{v}}_{i}}}}{{\partial {{q}^{j}}}} + {{p}_{{ij}}}} \right){{\dot {q}}^{j}} + p_{i}^{j}{{\text{v}}_{j}} = 0$

${{p}_{{ij}}} = p_{i}^{k}{{m}_{{kj}}},$

удовлетворяют условиям Гельмгольца (3.2)–(3.5). Очевидно, что условия (3.2), (3.5) выполняются. Условиям (3.3) соответствуют равенства

$\frac{{\partial {{m}_{{ij}}}}}{{\partial {{q}^{k}}}}{{\dot {q}}^{j}} - \left( {\frac{{\partial {{\text{v}}_{i}}}}{{\partial {{q}^{k}}}} + {{p}_{{ik}}}} \right) + \frac{{\partial {{m}_{{kj}}}}}{{\partial {{q}^{i}}}}{{\dot {q}}^{j}} - \left( {\frac{{\partial {{\text{v}}_{k}}}}{{\partial {{q}^{i}}}} + {{p}_{{ki}}}} \right) = 0,$

из которых следуют выражения коэффициентов $p_{i}^{k}$ уравнений возмущений связей:

(5.3)

${{p}_{{ik}}} = - \frac{{\partial {{\text{v}}_{k}}}}{{\partial {{q}^{i}}}} + \frac{{\partial {{m}_{{kj}}}}}{{\partial {{q}^{i}}}}{{\dot {q}}^{j}},$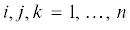

Выполнение условий (5.3) возможно за счет произвольных векторов ${{{\mathbf{c}}}_{{m + 1}}} = {{{\mathbf{c}}}_{{m + 1}}}({\mathbf{q}})$, …, ${{{\mathbf{c}}}_{{n - 1}}} = {{{\mathbf{c}}}_{{n - 1}}}({\mathbf{q}})$ и функции $с = с (q)$.

Условия (3.4) накладывают дополнительные ограничения на коэффициенты $p_{i}^{k}$. Вычисление правых частей условий (3.4) с учетом выражений (5.3) приводит к следующему результату:

(5.4)

$\frac{1}{2}\frac{d}{{dt}}\left( {\frac{{\partial {{f}_{i}}}}{{\partial {{{\dot {q}}}^{j}}}} - \frac{{\partial {{f}_{j}}}}{{\partial {{{\dot {q}}}^{i}}}}} \right) \equiv \frac{d}{{dt}}\left( {\left( {\frac{{\partial {{m}_{{ik}}}}}{{\partial {{q}^{j}}}} - \frac{{\partial {{m}_{{jk}}}}}{{\partial {{q}^{i}}}}} \right){{{\dot {q}}}^{k}} + \frac{{\partial {{\text{v}}_{j}}}}{{\partial {{q}^{i}}}} - \frac{{\partial {{\text{v}}_{i}}}}{{\partial {{q}^{j}}}}} \right),$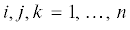

Левые части равенств (5.4) принимают вид:

(5.5)

$\begin{gathered} \frac{{\partial {{f}_{i}}}}{{\partial {{q}^{j}}}} - \frac{{\partial {{f}_{j}}}}{{\partial {{q}^{i}}}} \equiv \left( {\frac{{\partial {{m}_{{is}}}}}{{\partial {{q}^{j}}}} - \frac{{\partial {{m}_{{js}}}}}{{\partial {{q}^{i}}}}} \right){{{\ddot {q}}}^{s}} + \left( {\frac{\partial }{{\partial {{q}^{k}}}}\left( {\frac{{\partial {{m}_{{is}}}}}{{\partial {{q}^{j}}}} - \frac{{\partial {{m}_{{js}}}}}{{\partial {{q}^{i}}}}} \right) + \frac{\partial }{{\partial {{q}^{s}}}}\left( {\frac{{\partial {{m}_{{ik}}}}}{{\partial {{q}^{j}}}} - \frac{{\partial {{m}_{{jk}}}}}{{\partial {{q}^{i}}}}} \right)} \right){{{\dot {q}}}^{s}}{{{\dot {q}}}^{k}} - \\ - \frac{\partial }{{\partial {{q}^{s}}}}\left( {\frac{{\partial {{\text{v}}_{i}}}}{{\partial {{q}^{j}}}} - \frac{{\partial {{\text{v}}_{j}}}}{{\partial {{q}^{i}}}}} \right){{{\dot {q}}}^{s}} + \frac{\partial }{{\partial {{q}^{j}}}}({{p}_{{is}}}{{\text{v}}^{s}}) - \frac{\partial }{{\partial {{q}^{i}}}}({{p}_{{js}}}{{\text{v}}^{s}}) \\ \end{gathered} $

Сравнение выражений (5.4), (5.5) показывает, что условия (3.4) будут выполнены при соблюдении равенств

(5.6)

$\frac{\partial }{{\partial {{q}^{j}}}}({{p}_{{is}}}{{\text{v}}^{s}}) - \frac{\partial }{{\partial {{q}^{i}}}}({{p}_{{js}}}{{\text{v}}^{s}}) = 0$,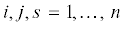

Используя равенства (5.3), условия (5.6) можно представить в виде:

(5.7)

$\frac{{\partial {{m}_{{sk}}}}}{{\partial {{q}^{i}}}}\frac{{\partial {{\text{v}}^{s}}}}{{\partial {{q}^{j}}}} - \frac{{\partial {{m}_{{sk}}}}}{{\partial {{q}^{j}}}}\frac{{\partial {{\text{v}}^{s}}}}{{\partial {{q}^{i}}}} = 0,$ $i,j,k,s = 1,\; \ldots ,\;n$

В случае, когда элементы матрицы кинетической энергии являются постоянными, условия (5.7) выполняются тождественно.

Рассуждая аналогично, можно убедиться, что уравнения (5.2) будут удовлетворять обобщенным условиям Гельмгольца, если коэффициенты $p_{i}^{k}$ уравнений возмущений связей выбраны в виде:

${{p}_{{ik}}} = - \frac{{\partial {{\text{v}}_{k}}}}{{\partial {{q}^{i}}}} + \frac{{\partial {{m}_{{kj}}}}}{{\partial {{q}^{i}}}}{{\dot {q}}^{j}} - {{d}_{{ik}}},$ $i,j,k,s = 1, \ldots ,\;n$

где ${{d}_{{ik}}}$ – коэффициенты функции Рэлея: $D = (1{\text{/}}2){{d}_{{ik}}}{{\dot {q}}^{i}}{{\dot {q}}^{k}}$.

6. Уравнения движения тележки по горизонтальной плоскости. В качестве примера рассматривается типовая задача динамики неголономных систем [32]. Качение тележки по плоскости с идеально тонким ведущим колесом в виде заостренного лезвия происходит в соответствии с уравнением связи

(6.1)

${{\dot {q}}^{1}}\sin {{q}^{3}} - {{\dot {q}}^{2}}\cos {{q}^{3}} = 0$

где ${{q}^{1}} = x$, ${{q}^{2}} = y$ – координаты центра масс, ${{q}^{3}} = {\varphi }$ – угол между продольной осью симметрии тележки и осью Ox. Выражения составляющих скорости $\dot {q} = ({{\dot {q}}^{1}},{{\dot {q}}^{2}},{{\dot {q}}^{3}})\quad$ центра масс $\quad\dot {x}\quad$, $\dot {y}$ и угловой скорости ${\dot {\varphi }}$ определяются как общее решение

$a\left( q \right) = (\sin {{q}^{3}},\quad - \cos {{q}^{3}},0),$ $c(q) = ({{c}^{1}}(q),\quad{{c}^{2}}(q),\quad{{c}^{3}}(q))$

уравнения связи (6.1):

${{\dot {q}}^{1}} = - {{c}^{3}}\left( q \right)\cos {{q}^{3}},\quad {{\dot {q}}^{2}} = - {{c}^{3}}\left( q \right)\sin {{q}^{3}}$

${{\dot {q}}^{3}} = {{c}^{2}}\left( q \right)\sin {{q}^{3}} + {{c}^{1}}\left( q \right)\cos {{q}^{3}}$

где c¹(q), c²(q), c³(q) – произвольные функции координат. Полагая

${{c}^{3}}\left( q \right) = - \quad\text{v},\quad\quad \quad\text{v}\; - \;{\text{const,}}$ ${{c}^{2}}\left( q \right) = \quad{\omega }\sin {{q}^{3}}$

${{c}^{1}}\left( q \right) = {\omega cos}{{q}^{3}},\quad \quad{\omega }\; - \;{\text{const}}$

получим уравнения кинематики

${{\dot {q}}^{1}} = {{\text{v}}^{1}}\left( q \right),\quad {{\dot {q}}^{2}} = {{\text{v}}^{2}}\left( q \right),\quad \quad{{\dot {q}}^{3}} = {{\text{v}}^{3}}\left( q \right)$

${{\text{v}}^{1}}\left( q \right) = \text{v}\cos {{q}^{3}},\quad {{\text{v}}^{2}}\left( q \right) = \text{v}\sin {{q}^{3}},\quad {{\text{v}}^{3}}\left( q \right) = {\omega }$

Вводя отклонения от уравнений связей

(6.2)

${{u}_{i}} = {{\delta }_{{ij}}}{{\dot {q}}^{j}} - {{\text{v}}_{i}}$

${{\text{v}}_{i}} = {{\delta }_{{ij}}}\left( q \right){{\text{v}}^{j}}\left( q \right),$

составим уравнения возмущений связей

(6.3)

${{\dot {u}}_{i}} = p_{i}^{j}\left( q \right){{u}_{j}},\quad i,j = 1,2,3$

с коэффициентами $p_{i}^{j}\left( q \right) = - \text{v}_{j}^{i}\left( q \right)$:

$p_{i}^{j}\left( q \right) = 0,\quad j = 1,2,\quad p_{1}^{3}\left( q \right) = \text{v}{\text{sin}}{{q}^{3}},\quad p_{2}^{3}\left( q \right) = - \text{v}\cos {{q}^{3}},\quad p_{3}^{3}\left( q \right) = 0$

Очевидно, тривиальное решение системы (6.3) не является устойчивым асимптотически. Из выражений (6.2), (6.3) следует система уравнений движения тележки:

(6.4)

$\left\{ {\begin{array}{*{20}{l}} {{{{\ddot {q}}}^{1}} + (\text{v}\sin {{q}^{3}}){{{\dot {q}}}^{3}} = 0} \\ {{{{\ddot {q}}}^{2}} - (\text{v}\cos {{q}^{3}}){{{\dot {q}}}^{3}} = 0} \\ {{{{\ddot {q}}}^{3}} - (\text{v}\sin {{q}^{3}}){{{\dot {q}}}^{1}} + (\text{v}\cos {{q}^{3}}){{{\dot {q}}}^{2}} = 0} \end{array}} \right.$

которая может быть представлена в виде уравнений Лагранжа:

$\frac{d}{{dt}}\left( {\frac{{\partial L}}{{\partial {{{\dot {q}}}^{i}}}}} \right) - \frac{{\partial L}}{{\partial {{q}^{i}}}} = \frac{{\partial G}}{{\partial {{{\dot {q}}}^{i}}}},$ $i = 1,2,3$

$L = T - P,$ $T = \frac{1}{2}{{\dot {q}}^{i}}{{{\delta }}_{{ij}}}{{\dot {q}}^{j}},$ $P = 0,$ $G = \frac{1}{2}{{\dot {q}}^{i}}{{{\delta }}_{{ik}}}g_{j}^{k}\left( q \right){{\dot {q}}^{j}}$

$g_{i}^{i} = 0,\quad g_{2}^{1} = g_{1}^{2} = 0,\quad g_{3}^{1} = - g_{1}^{3} = \text{v}\sin {{q}^{3}},\quad g_{3}^{2} = - g_{2}^{3} = - \text{v}\cos {{q}^{3}}$

Уравнения движения тележки с диссипативной функцией записываются следующим образом:

(6.5)

${{\ddot {q}}^{i}} + g_{j}^{i}\left( q \right){{\dot {q}}^{j}} + p_{j}^{i}\left( q \right){{\text{v}}^{j}}\left( q \right) = - d_{j}^{i}{{\dot {q}}^{j}}$, $i = 1,2,3$

$d_{j}^{i} = {{{\delta }}^{{ik}}}{{d}_{{kj}}},$ $D = \left( {1{\text{/}}2} \right){{d}_{{ik}}}{{\dot {q}}^{i}}{{\dot {q}}^{k}}$

Здесь все $p_{j}^{i}\left( q \right) = - d_{j}^{i}$, за исключением случаев $i = 3$, 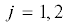, , 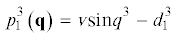$p_{2}^{3}\left( q \right) = - \text{v}\cos {{q}^{3}} - d_{2}^{3}$. Равенства (4.10) накладывают следующие условия на коэффициенты диссипативной функции

$\frac{\partial }{{\partial {{q}^{1}}}}(d_{1}^{2}\text{v}\cos {{q}^{3}} + d_{2}^{2}\text{v}\sin {{q}^{3}} + d_{3}^{2}{\omega }) = \frac{\partial }{{\partial {{q}^{2}}}}(d_{1}^{1}\text{v}\cos {{q}^{3}} + d_{2}^{1}\text{v}\sin {{q}^{3}} + d_{3}^{1}{\omega })$

$\frac{\partial }{{\partial {{q}^{2}}}}(d_{1}^{3}\text{v}\cos {{q}^{3}} + d_{2}^{3}\text{v}\sin {{q}^{3}} + d_{3}^{3}{\omega }) = \frac{\partial }{{\partial {{q}^{3}}}}(d_{1}^{2}\text{v}\cos {{q}^{3}} + d_{2}^{2}\text{v}\sin {{q}^{3}} + d_{3}^{2}{\omega })$

$\frac{\partial }{{\partial {{q}^{3}}}}(d_{1}^{1}\text{v}\cos {{q}^{3}} + d_{2}^{1}\text{v}\sin {{q}^{3}} + d_{3}^{1}{\omega }) = \frac{\partial }{{\partial {{q}^{1}}}}(d_{1}^{3}\text{v}\cos {{q}^{3}} + d_{2}^{3}\text{v}\sin {{q}^{3}} + d_{3}^{3}{\omega })$

которые выполняются, если

$d_{1}^{2} = d_{2}^{1} = 0,$ $d_{3}^{2} = d_{2}^{3} = - \frac{\text{v}}{\omega }d_{2}^{2}\sin {{q}^{3}},$ $d_{3}^{1} = d_{1}^{3} = - \frac{\text{v}}{\omega }d_{1}^{1}\cos {{q}^{3}}$

Квадратичная форма $D$ с матрицей коэффициентов

$(d_{j}^{i}) = \left( {\begin{array}{*{20}{c}} {d_{1}^{1}}&0&{ - \frac{\text{v}}{{\omega }}d_{1}^{1}\cos {{q}^{3}}} \\ 0&{d_{2}^{2}}&{ - \frac{\text{v}}{{\omega }}d_{2}^{2}\sin {{q}^{3}}} \\ { - \frac{\text{v}}{{\omega }}d_{1}^{1}\cos {{q}^{3}}}&{ - \frac{\text{v}}{{\omega }}d_{2}^{2}\sin {{q}^{3}}}&{d_{3}^{3}} \end{array}} \right)$

будет определенно положительной при выполнении условий Сильвестра:

$d_{1}^{1} > 0,$ $d_{2}^{2} > 0,$ $d_{3}^{3} > {{\left( {\frac{\text{v}}{{\omega }}} \right)}^{2}}(d_{1}^{1}{{(\cos {{q}^{3}})}^{2}} + d_{2}^{2}{{(\sin {{q}^{3}})}^{2}})$

Уравнения возмущений связей имеют следующий вид:

(6.6)

${{\dot {u}}_{i}} = p_{i}^{j}\left( q \right){{u}_{j}},\quad p_{i}^{j} = - \text{v}_{j}^{i} - d_{j}^{i},\quad i,j = 1,2,3$

Для определения условий устойчивости тривиального решения используем метод функций Ляпунова, полагая $2V = \quad{{{\delta }}^{{ij}}}{{u}_{i}}{{u}_{j}}$. Производная функции Ляпунова, вычисленная в силу уравнений системы (6.6) также является квадратичной формой $\dot {V} = \,\quad{{{\delta }}^{{ik}}}p_{k}^{j}{{u}_{i}}{{u}_{j}}$ с матрицей коэффициентов $(p_{i}^{j})$. Следовательно, тривиальное решение системы уравнений (6.6) устойчиво асимптотически, если диагональные миноры определителя матрицы

$( - p_{i}^{j}) = \left( {\begin{array}{*{20}{c}} {d_{1}^{1}}&0&{\quad - \quad\frac{\text{v}}{{\omega }}d_{1}^{1}\cos {{q}^{3}}} \\ 0&{d_{2}^{2}}&{\quad - \quad\frac{\text{v}}{{\omega }}d_{2}^{2}\sin {{q}^{3}}} \\ { - \text{v}{\text{sin}}{{q}^{3}} - \frac{\text{v}}{{\omega }}d_{1}^{1}\cos {{q}^{3}}}&{\text{v}\cos {{q}^{3}} - \frac{\text{v}}{{\omega }}d_{2}^{2}\sin {{q}^{3}}}&{d_{3}^{3}} \end{array}} \right)$

являются положительными. Так как $d_{1}^{1} > 0$, $d_{2}^{2} > 0$, то остается проверить знак определителя ${\text{|}}{\kern 1pt} - {\kern 1pt} p_{i}^{j}\quad{\text{|}}$, который может быть представлен суммой двух определителей: ${\text{|}}{\kern 1pt} - {\kern 1pt} p_{i}^{j}\quad{\text{|}} = {\text{|}}d_{j}^{i}\quad{\text{|}} + \,{\text{|}}s_{j}^{i}\quad{\text{|}},$

$\left| {s_{j}^{i}\quad} \right| = \frac{{{{{\left( \text{v} \right)}}^{2}}}}{\omega }\left| {\begin{array}{*{20}{c}} 1&0&{\quad\cos {{q}^{3}}} \\ 0&1&{\quad\sin {{q}^{3}}} \\ {\sin {{q}^{3}}}&{ - \cos {{q}^{3}}}&0 \end{array}} \right|$

первый из которых $\left| {d_{j}^{i}\quad} \right|$ является положительным, а второй $\quad\left| {s_{j}^{i}\quad} \right|$ равен нулю. Следовательно, производная функции Ляпунова $\dot {V}$ является знакоопределенной отрицательной, и тривиальное решение уравнений возмущений связей (6.3) устойчиво асимптотически.

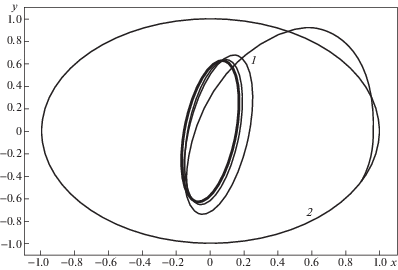
Решение уравнений динамики (6.5) c длиной шага ${{t}_{{k + 1}}} - {{t}_{k}} = {\tau } = 0.01$ на интервале $0 \leqslant t \leqslant 10$ проведено методом Эйлера при начальных условиях

(6.7)

$x\left( 0 \right) = 0,\quad y\left( 0 \right) = - 1,\quad \quad\varphi \left( 0 \right) = 0,\quad \dot {x}\left( 0 \right) = \text{v},\quad \dot {y}\left( 0 \right) = 0,\quad \dot {\varphi }\left( 0 \right) = {\omega }$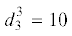

удовлетворяющих уравнениям связей (6.1). Результаты численного интегрирования представлены на фигуре. Случай (1) соответствует устойчивому численному решению при значениях коэффициентов диссипативной функции $d_{1}^{1} = 10$, $d_{2}^{2} = 5$, $d_{3}^{3} = 11$. При значениях коэффициентов $d_{1}^{1} = 10$, $d_{2}^{2} = 50$,

условия устойчивости не выполняются, и движение по окружности оказывается неустойчивым (случай (2)).

6. Заключение. Метод построения уравнений динамики непосредственно по уравнениям дифференциальных связей относится к обратным задачам динамики. Удается определить выражения действующих сил, обеспечивающих выполнение заданных уравнений связей. Использование модифицированных условий Гельмгольца позволяет ввести диссипативные силы, за счет которых можно обеспечить стабилизацию связей. Моделирование движения тележки с тонким ведущим колесом иллюстрирует возможность использования простейших численных методов решения уравнений динамики с требуемой точностью выполнения уравнений связей.

Работа выполнена при поддержке РФФИ (проект 19-08-00261 А).

Фиг. 1

Список литературы

Baumgarte J. Stabilization of constraints and integrals of motion in dynamical systems // Computer Methods in Applied Mechanics and Engineering. 1972. № 1. P. 1–16.
Нугманова Ш.С. Об уравнениях движения управляемых систем // Тр. Казанского авиац. ин-та. 1953. Т. 27. С. 23–40.
Витенбург Й. Динамика систем твердых тел. М.: Мир, 1980. 294 с.
Amirouche F. Fundamentals of Multibody Dynamics: Theory and Applications. Boston: Birkh user, 2006. P. 684.
Буров А.А., Косенко И.И. О дифференциально-алгебраических уравнениях Лагранжа // ПММ. 2014. Т. 78. № 6. С. 818–832.
Layton R.A. Principles of Analytical System Dynamics. N.-Y.: Springer, 1998. P. 158.
Meiser P., Enge O., Freudenberg H., Kielau G. Electromechanical Interactions in Multibody Systems Containing Electromechanical Drives // Multibody System Dynamics. 1997. № 1. P. 281–302.
Gonzales F., Kovecses J. Use of Penalty Formulation in Dynamic Simulation and Analysis of Redundantly Constrained Multibody Systems // Multibody System Dynamics. 2012. P. 57–76.
Ascher U.M., Hongsheng Chin, Petzold L.R., Reich S. Stabilization of constrained Mechanical systems with DAEs and invariant manifolds // J. Mechanics Structures and Machines. 1995. V. 23. P. 135–158.
Ascher U., Chin H., Reich S. Stabilization of DAEs and invariant manifolds // Numer. Math. 1994. V. 67. P. 131–149.
Ascher U. Stabilization of invariant of discretized differential systems // Numerical Algorithms. 1997. V. 14. Issue 1. P. 1–24.
Shih-Tin Lin, Jiann-Nan Huang. Numerical integration of multibody mechanical systems using Baumgarte’s constraint stabilization method // J. Chin. Inst. Engineers. 2002. V. 25. № 2. P. 243–252.
Bertrand M.G. Theoreme relatife au mouvement d’un point attire vers un centre fixe // Compte rendus. 1873. V. 77. T. LXXVII. № 16. P. 849–853.
Darboux M.G. Recherche de la loi que dois suivre une force centrale pour que la trajectoire quellle determine soit toujour une conique // Compte rendus. 1877. T. LXXXIV. № 16. P. 760–762.
Имшенецкий В.Г. Определение силы, движущей по коническому сечению материальную точку, в функции ее координат // Сообщения Харьковского математического общества. 1879. Вып. 1. С. 5–15.
Суслов Г.К. О силовой функции, допускающей заданные интегралы. Киев: Изд-во Киевского университета, 1890. С. 114.
Жуковский Н.Е. Определение силовой функции по данному семейству траекторий // Полное собр. соч. Т. I. М.-Л.: Главная редакция авиационной литературы, 1937. С. 293–308.
Леви-Чивита, У. Амальди. Курс теоретической механики. Т. 2. Ч. 2. М.: Изд-во ИЛ, 1952. 544 с.
Галиуллин А.С. Методы решения обратных задач динамики. М.: Наука, 1986. С. 224.
Bozis G., Ichtiaroglou S. Existence and construction of dynamical systems having a prescribed integral of motion-an inverse problem // Inverse Problems. 1987. V. 3. P. 213–227.
Галиуллин А.С., Гафаров Г.Г., Малайшка Р.П., Хван А.М. Аналитическая динамика систем Гельмгольца, Биркгофа, Намбу. М.: Успехи физических наук, 1997. С. 324.
Еругин Н.П. Построение всего множества систем дифференциальных уравнений, имеющих заданную интегральную кривую // ПММ. 1952. Т. 21. № 6. С. 659–670.
Мухарлямов Р.Г. О построении дифференциальных уравнений оптимального движения по заданному многообразию // Дифференц. уравнения. 1971. Т. 7. № 10. С. 1825–1834.
Мухарлямов Р.Г. О построении множества систем дифференциальных уравнений устойчивого движения по интегральному многообразию // Дифференц. уравнения. 1969. Т. 5. № 4. С. 688–699.
Jaume Llibre, Rafael Ramirez. Inverse Problems of Ordinary Differential Equations and Applications. Springer Int. Publ. Switzerland, 2016. P. 266.
Мухарлямов Р.Г. Дифференциально-алгебраические уравнения программных движений лагранжевых динамических систем // Известия РАН. Механика твердого тела. 2011. № 4. С. 50–61.
Мухарлямов Р.Г. Моделирование процессов управления, устойчивость и стабилизация систем с программными связями // Известия РАН. Теория и системы управления. 2015. № 1. С. 15–28.
Helmholtz H. Über die physikalische Bedeutung des Prinicips der kleinsten Wirkung // Journal fur die reine und angewandte Mathematik. 1887. № 100. P. 137–166.
Суслов Г.К. О кинетическом потенциале Гельмгольца // Матем. сб. 1896. Т. 19. № 1. С. 197–210.
Mayer A. Die Existenbedingungen eines kinetischen Potentials. Berl. Ges. Wiss., Leipzig, 1896. P. 519–529.
Kielau G., Maisser P. A generalization of the Helmholtz conditions for the existence of a first-order Lagrangian // Z. Angew. Math. Mech. 2006. № 86(9). P. 722–735.
Неймарк Ю.И., Фуфаев Н.А. Динамика неголономных систем. М.: Наука, 1967. С. 520.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал