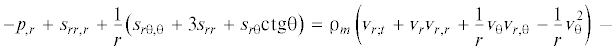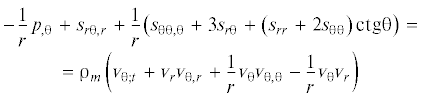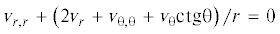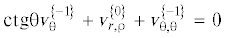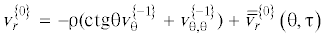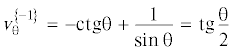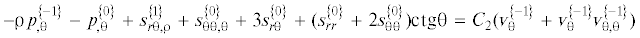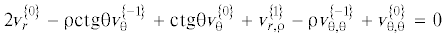1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 2, 2020

Известия РАН. Механика твердого тела, 2020, № 2, стр. 22-27

Динамические эффекты деформирования при сжатии-стоке асимптотически тонкого идеально жесткопластического сферического слоя

Р. Р. Шабайкин *

Московский государственный университет им. М.В. Ломоносова
Москва, Россия

* E-mail: rr.shabaykin@outlook.com

Поступила в редакцию 07.04.2019
После доработки 30.05.2019
Принята к публикации 06.06.2019

Полный текст (PDF)

Аннотация

В данной работе получено решение аналога задачи Прандтля о сжатии-стоке идеально жесткопластического материала в асимптотически тонком сферическом слое с учетом инерционных эффектов. Рассмотрены различные режимы сдавливания, характеризующие переход от квазистатического процесса к динамическому.

Ключевые слова: идеально жесткопластическое тело, задача Прандтля, сжатие, растекание, асимптотические разложения, осесимметричная задача, число Эйлера, динамика

1. Введение. Ввиду своей применимости в теории обработки металлов давлением, классическая задача Прандтля [1] получила многочисленные обобщения. Например, в [2] обобщено решение Прандтля на случай линейной зависимости максимального касательного напряжения от среднего давления и случай сжатия слоя наклонными шероховатыми плитами, а также плитами, изогнутыми в виде концентрических окружностей. В монографии [3] предложено решение задачи о вдавливании стержня из сжимающейся шероховатой втулки, в статье [4] проанализированы процессы течения пластического материала по упруго деформируемым поверхностям. Решение с учетом многослойности и термодиффузии приведено в работе [5], а случай сжимаемого материала рассмотрен в [6].

Отдельно выделим обобщения, связанные с динамической постановкой. Так в [7] установлена важность учета инерционных сил при моделировании высокоскоростных пластических течений. В работах [8–10] построено аналитическое решение динамической задачи Прандтля. В работе [11] рассмотрена задача о сдавливании идеально-пластического диска шероховатыми плитами при учете инерционных сил. В [12] получено решение плоской динамической задачи теории пластичности при условии степенного упрочнения.

Подробный обзор можно найти в монографиях и учебниках [2, 3, 13].

2. Постановки задачи. Пусть течение происходит в области ${{{\Omega }}_{t}}$, представляющей собой тонкий слой между абсолютно жесткими концентрическими сферами. Данная область занята несжимаемым идеально жесткопластическим материалом с пределом текучести ${{{\sigma }}_{s}}$.

В сферической системе координат $\left( {r,{\theta },{\varphi }} \right)$ (θ – полярный угол), связанной с центром сфер координаты точек ${{{\Omega }}_{t}}$ описываются неравенствами

(2.1)
${{{\Omega }}_{t}} = \left\{ {R(t) < r < R(t) + h(t);0 \leqslant {\theta } < {\pi };0 \leqslant {\varphi } < 2{\pi }} \right\},\quad h \ll R$

Внешняя сфера неподвижна, а внутренняя радиально расширяется с постоянной скоростью V, выдавливая материал через сток ${\theta } = {\pi }$. Условие непротекания имеет вид:

(2.2)
${{\left. {{{{v}}_{r}}} \right|}_{{r = R}}} = V,\quad {{\left. {{{{v}}_{r}}} \right|}_{{r = R + h}}} = 0$

Как известно [14], условия на касательную компоненту скорости на указанных в (2.2) границах не задаются.

Система уравнений осесимметричной теории идеальной пластичности включает два уравнения равновесия, критерий пластичности Мизеса–Генки, два независимых условия соосности девиаторов напряжений и скоростей деформации, а также условие несжимаемости:

$s_{{rr}}^{2} + s_{{{\theta \theta }}}^{2} + {{s}_{{rr}}}{{s}_{{{\theta \theta }}}} + s_{{r{\theta }}}^{2} = {\sigma }_{s}^{2}{\text{/}}2 \equiv {\tau }_{s}^{2}$
${{s}_{{rr}}}\left( {{{{v}}_{{{\theta },{\theta }}}} + {{{v}}_{r}}} \right){\text{/}}r = {{s}_{{{\theta \theta }}}}{{{v}}_{{r,r}}},\quad {{s}_{{rr}}}\left( {{{{v}}_{{{\theta },r}}} + \left( {{{{v}}_{{r,{\theta }}}} - {{{v}}_{{\theta }}}} \right){\text{/}}r} \right) = 2{{s}_{{r{\theta }}}}{{{v}}_{{r,r}}}$
(2.3)

Помимо выполнения кинематических условий (2.2) на границах контакта потребуем достижение касательным напряжением своего максимального вдоль радиального направления значения:

(2.4)
${{\left| {{{s}_{{r{\theta }}}}} \right|}_{{r = R}}} = {{\left| {{{s}_{{r{\theta }}}}} \right|}_{{r = R + h}}} = m\left( {\theta } \right){{{\tau }}_{s}},\quad ~0 < m \leqslant 1$
где m – шероховатость пресса. Обозначим через ${\alpha } = h{\text{/}}R \ll 1$ малый геометрический параметр и проведем разложение всех входящих в систему (2.3) функций в степенные ряды по α, рассматривая безразмерные коэффициенты рядов как функции безразмерных координат θ, ${\rho } = \left( {r - R} \right){\text{/}}h$ и ${\tau } = V \cdot t{\text{/}}h$.

${{{v}}_{{\theta }}}\left( {r,{\theta },t} \right) = V({{{\alpha }}^{{ - 1}}}{v}_{{\theta }}^{{\left\{ { - M} \right\}}} + \ldots + {v}_{{\theta }}^{{\left\{ 0 \right\}}} + {\alpha }{v}_{{\theta }}^{{\left\{ 1 \right\}}} + \ldots )$
(2.5)
${{{v}}_{r}}(r,{\theta },t) = V({v}_{r}^{{\left\{ 0 \right\}}} + {\alpha }{v}_{r}^{{\left\{ 1 \right\}}} + \ldots ),~\quad {{s}_{{{\beta \gamma }}}}\left( {r,{\theta },t} \right) = {{{\tau }}_{s}}(s_{{{\beta \gamma }}}^{{\left\{ 0 \right\}}} + {\alpha }s_{{{\beta \gamma }}}^{{\left\{ 1 \right\}}} + \ldots )$
$p\left( {r,{\theta },t} \right) = {{{\tau }}_{s}}({{{\alpha }}^{{ - 1}}}{{p}^{{\left\{ { - N} \right\}}}} + \ldots + {{p}^{{\left\{ 0 \right\}}}} + {\alpha }{{p}^{{\left\{ 1 \right\}}}} + \ldots )$

Наличие в (2.5) членов с N и M связано со стремлением ${{{v}}_{{\theta }}}$ и p к бесконечности при ${\alpha } \to 0$. Система (2.3) с граничными условиями (2.2), (2.4) допускает последовательное асимптотическое интегрирование [10]. Учитывая ${{{v}}_{{x;t}}} = {{{v}}_{{x,{\alpha }}}}{\dot {\alpha }} + {{{v}}_{{x,{\rho }}}}{\dot {\rho }} + {{{v}}_{{x,{\tau }}}}{\dot {\tau }}$, и принимая во внимание, что производные по времени выражены как эволюционные функции следующим образом:

${\dot {\alpha }} = - \frac{V}{h}{\alpha }\left( {{\alpha } + 1} \right),\quad {\dot {\rho }} = - V\frac{{1 - {\rho }}}{h},\quad {\dot {\tau }} = \frac{V}{h}\left( {1 + {\tau }} \right)$
получаем что в уравнениях движения возникнет величина ${{{\rho }}_{m}}{{V}^{2}}{\text{/}}{{{\tau }}_{s}}$ равная обратному числу Эйлера. Как и геометрический параметр она полагается малой, но в отличие от последнего не изменяется в процессе прессования. Это позволяет разбить процесс на стадии с учетом соизмеримости представленных параметров:

(2.6)
${\text{E}}{{{\text{u}}}^{{ - 1}}} = O({{{\alpha }}^{{\beta }}}) = {{C}_{{\beta }}}{{{\alpha }}^{{\beta }}},\quad {{C}_{{\beta }}} = O\left( 1 \right)$

Для показателя ${\beta }$ интерес представляет следующий диапазон: $0 < {\beta } \leqslant 2$. Он включает в себя два целочисленных значения ${\beta } = \left\{ {1;2} \right\}$, для которых ниже будет производится поиск решения.

Также нетрудно показать, что первые значащие члены разложения по степеням ${\alpha }$ возникнут при α–1. Таким образом, можно положить $M = N = 1$, а система, соответствующая данной степени, будет иметь вид:

$p_{{,{\rho }}}^{{\left\{ { - 1} \right\}}} = 0,\quad {v}_{{{\theta },{\rho }}}^{{\left\{ { - 1} \right\}}} = 0$
откуда следует независимость данных функций от радиальной координаты

${{p}^{{\left\{ { - 1} \right\}}}} = {{\bar {\bar {p}}}^{{\left\{ { - 1} \right\}}}}\left( {{\theta },{\tau }} \right),\quad {v}_{{\theta }}^{{\left\{ { - 1} \right\}}} = {\bar {\bar {v}}}_{{\theta }}^{{\left\{ { - 1} \right\}}}\left( {{\theta },{\tau }} \right)$

3. Случай ${\mathbf{\beta }} = 2$. При данном значении β система, составленная из коэффициентов при α0, не отличается от квазистатического случая и имеет следующий вид:

$ - p_{{,{\rho }}}^{{\left\{ 0 \right\}}} + s_{{rr,{\rho }}}^{{\left\{ 0 \right\}}} = 0$
$ - p_{{,{\theta }}}^{{\left\{ { - 1} \right\}}} + s_{{r{\theta },{\rho }}}^{{\left\{ 0 \right\}}} = 0$
${{(s_{{rr}}^{{\left\{ 0 \right\}}})}^{2}} + {{(s_{{{\theta \theta }}}^{{\left\{ 0 \right\}}})}^{2}} + s_{{rr}}^{{\left\{ 0 \right\}}}s_{{{\theta \theta }}}^{{\left\{ 0 \right\}}} + {{(s_{{r{\theta }}}^{{\left\{ 0 \right\}}})}^{2}} = 1$
$s_{{rr}}^{{\left\{ 0 \right\}}}{v}_{{{\theta },{\theta }}}^{{\left\{ { - 1} \right\}}} = s_{{{\theta \theta }}}^{{\left\{ 0 \right\}}}{v}_{{r,{\rho }}}^{{\left\{ 0 \right\}}}$
$s_{{rr}}^{{\left\{ 0 \right\}}}{v}_{{{\theta },{\rho }}}^{{\left\{ 0 \right\}}} - s_{{rr}}^{{\left\{ 0 \right\}}}{v}_{{\theta }}^{{\left\{ { - 1} \right\}}} = 2s_{{r{\theta }}}^{{\left\{ 0 \right\}}}{v}_{{r,{\rho }}}^{{\left\{ 0 \right\}}}$
(3.1)

Из второго и шестого уравнений системы (3.1) получаем выражение для касательных напряжений и скорости:

$s_{{r{\theta }}}^{{\left\{ 0 \right\}}} = {\rho }~p_{{,{\theta }}}^{{\left\{ { - 1} \right\}}} + \bar {\bar {s}}_{{r{\theta }}}^{{\left\{ 0 \right\}}}\left( {{\theta },{\tau }} \right)$

Подставив данные выражения в граничные условия (2.2), (2.4), найдем

${{p}^{{\left\{ { - 1} \right\}}}} = {{\bar {p}}^{{\left\{ { - 1} \right\}}}}\left( {\tau } \right) - 2\mathop \smallint \limits_0^{\theta } {{k}_{1}} \cdot {\mu }\left( {\varepsilon } \right)d{\varepsilon }$
$s_{{r{\theta }}}^{{\left\{ 0 \right\}}} = {{k}_{1}}\left( {1 - 2{\rho }} \right){\mu }\left( {\theta } \right)$
(3.2)
${v}_{r}^{{\left\{ 0 \right\}}} = 1 - {\rho }$
где ${{k}_{1}} = \pm 1$. Остальные функции находятся из системы (3.1) с точностью до констант интегрирования:

$s_{{rr}}^{{\left\{ 0 \right\}}} = {{k}_{2}}\frac{{{{{\sin }}^{2}}{\theta }\sqrt {1 - {{{\left( {1 - 2{\rho }} \right)}}^{2}}{{{\mu }}^{2}}\left( {\theta } \right)} }}{{\sqrt {(1 - \cos {\theta })(1 - {{{\cos }}^{3}}{\theta })} }}$
$s_{{{\theta \theta }}}^{{\left\{ 0 \right\}}} = - {{k}_{2}}\frac{{\sqrt {1 - \cos {\theta }} \sqrt {1 - {{{\left( {1 - 2{\rho }} \right)}}^{2}}{{{\mu }}^{2}}\left( {\theta } \right)} }}{{\sqrt {1 - {{{\cos }}^{3}}{\theta }} }}$
(3.3)
${v}_{{\theta }}^{{\left\{ 0 \right\}}} = \frac{{ - {{k}_{1}}}}{{{{k}_{2}}{{{\sin }}^{2}}{\theta \mu }\left( {\theta } \right)}}\sqrt {\left( {1 - \cos {\theta }} \right)(1 - {{{\cos }}^{3}}{\theta })} \sqrt {1 - {{{\left( {1 - 2{\rho }} \right)}}^{2}}{{{\mu }}^{2}}\left( {\theta } \right)} + {\rho tg}\frac{{\theta }}{2} + {\bar {\bar {v}}}_{{\theta }}^{{\left\{ 0 \right\}}}\left( {{\theta },{\tau }} \right)$
(3.4)
${{p}^{{\left\{ 0 \right\}}}} = s_{{rr}}^{{\left\{ 0 \right\}}} + {{\bar {\bar {p}}}^{{\left\{ 0 \right\}}}}\left( {{\theta },{\tau }} \right)$

Процессу растекания соответствует ${{k}_{2}} = - 1$, а для правильной выпуклости профиля скорости следует положить ${{k}_{1}} = 1.$

Чтобы найти неизвестные функции ${{\bar {\bar {p}}}^{{\left\{ 0 \right\}}}}$ и ${\bar {\bar {v}}}_{{\theta }}^{{\left\{ 0 \right\}}}$ рассмотрим следующее по ${\alpha }$ приближение для второго и шестого уравнений системы (2.3) (заведомо нулевые слагаемые опущены):

Поскольку явное аналитическое выражение неизвестных функций представляет значительные сложности, исследуем лишь их “отклонение” от решения в квазистатическом случае (верхний индекс ks), которое удовлетворяет однородной системе. Почленно вычитая уравнения, учитывая, что все найденные до этого функции совпадают с квазистатическим случаем, получим что

$s_{{r{\theta },{\rho }}}^{{\left\{ 1 \right\}}} - s_{{r{\theta },{\rho }}}^{{{\text{ks}}\left\{ 1 \right\}}} = \bar {\bar {p}}_{{,{\theta }}}^{{\left\{ 0 \right\}}} - \bar {\bar {p}}_{{,{\theta }}}^{{{\text{ks}}\left\{ 0 \right\}}} + {{C}_{2}}({v}_{{\theta }}^{{\left\{ { - 1} \right\}}} + {v}_{{\theta }}^{{\left\{ { - 1} \right\}}}{v}_{{{\theta },{\theta }}}^{{\left\{ { - 1} \right\}}})$
откуда с учетом теперь уже нулевых граничных условий получим выражение

(3.5)
$\begin{gathered} {{{\bar {\bar {p}}}}^{{\left\{ 0 \right\}}}} = {{{\bar {\bar {p}}}}^{{{\text{ks}}\left\{ 0 \right\}}}} - \frac{{{{C}_{2}}}}{2}\int {{{\left( {2\sin \frac{{\theta }}{2}{{{\cos }}^{2}}\frac{{\theta }}{2} + \sin \frac{{\theta }}{2}} \right)} \mathord{\left/ {\vphantom {{\left( {2\sin \frac{{\theta }}{2}{{{\cos }}^{2}}\frac{{\theta }}{2} + \sin \frac{{\theta }}{2}} \right)} {{{{\cos }}^{3}}\frac{{\theta }}{2}~d{\theta }}}} \right. \kern-0em} {{{{\cos }}^{3}}\frac{{\theta }}{2}~d{\theta }}}} = \\ = \;{{{\bar {\bar {p}}}}^{{{\text{ks}}\left\{ 0 \right\}}}} + {{C}_{2}}\left( {2\ln \cos \frac{{\theta }}{2} - \frac{1}{2}{{{\sec }}^{2}}\frac{{\theta }}{2}} \right) + {{{\bar {p}}}^{{\left\{ 0 \right\}}}}\left( {\tau } \right) \\ \end{gathered} $

Выражение для скорости ${\bar {\bar {v}}}_{{\theta }}^{{\left\{ 0 \right\}}}$ совпадет с квазистатическим случаем, с точностью до функции ${\bar {v}}_{{\theta }}^{{\left\{ 0 \right\}}}\left( {\tau } \right)$, возникающие при интегрировании.

4. Случай β = 1. При таком параметре β система, соответствующая α0, будет отличаться от (3.1) уравнениями движения, в правой части которых возникнут инерционные слагаемые (заведомо нулевые слагаемые опущены):

$ - p_{{,{\rho }}}^{{\left\{ 0 \right\}}} + s_{{rr,{\rho }}}^{{\left\{ 0 \right\}}} = {{C}_{1}}{{({v}_{{\theta }}^{{\left\{ { - 1} \right\}}})}^{2}}$
(4.1)
$ - p_{{,{\theta }}}^{{\left\{ { - 1} \right\}}} + s_{{r{\theta },{\rho }}}^{{\left\{ 0 \right\}}} = {{C}_{1}}({v}_{{\theta }}^{{\left\{ { - 1} \right\}}} + {v}_{{\theta }}^{{\left\{ { - 1} \right\}}}{v}_{{{\theta },{\theta }}}^{{\left\{ { - 1} \right\}}} + \left( {1 + {\tau }} \right){v}_{{{\theta },{\tau }}}^{{\left\{ { - 1} \right\}}})$

Поскольку уравнение неразрывности не изменилось, выражения для ${v}_{{\theta }}^{{\left\{ { - 1} \right\}}}$ и ${v}_{r}^{{\left\{ 0 \right\}}}$ останутся прежними. Из второго уравнения (4.1) получим

$s_{{r{\theta }}}^{{\left\{ 0 \right\}}} = {\rho }\left( {p_{{,{\theta }}}^{{\left\{ { - 1} \right\}}} + \frac{{{{C}_{1}}}}{2}{{\left( {2\sin \frac{{\theta }}{2}{{{\cos }}^{2}}\frac{{\theta }}{2} + \sin \frac{{\theta }}{2}} \right)} \mathord{\left/ {\vphantom {{\left( {2\sin \frac{{\theta }}{2}{{{\cos }}^{2}}\frac{{\theta }}{2} + \sin \frac{{\theta }}{2}} \right)} {{{{\cos }}^{3}}\frac{{\theta }}{2}}}} \right. \kern-0em} {{{{\cos }}^{3}}\frac{{\theta }}{2}}}~} \right) + \bar {\bar {s}}_{{r{\theta }}}^{{\left\{ 0 \right\}}}\left( {{\theta },{\tau }} \right)$
откуда с учетом граничного условия (2.4) найдем

(4.2)
${{p}^{{\left\{ { - 1} \right\}}}} = {{\bar {p}}^{{\left\{ { - 1} \right\}}}}\left( {\tau } \right) + {{C}_{1}}\left( {2\ln \cos \frac{{\theta }}{2} - \frac{1}{2}{{{\sec }}^{2}}\frac{{\theta }}{2}} \right) - 2\mathop \smallint \limits_0^{\theta } {{k}_{1}} \cdot {\mu }\left( {\varepsilon } \right)d{\varepsilon }$
(4.3)
$s_{{r{\theta }}}^{{\left\{ 0 \right\}}} = {{k}_{1}}\left( {1 - 2{\rho }} \right){\mu }\left( {\theta } \right).$

Также не изменятся функции $s_{{rr}}^{{\left\{ 0 \right\}}}$, $s_{{{\theta \theta }}}^{{\left\{ 0 \right\}}}$ и ${v}_{{\theta }}^{{\left\{ 0 \right\}}}$, а выражение для давления примет вид:

(4.4)
${{p}^{{\left\{ 0 \right\}}}} = s_{{rr}}^{{\left\{ 0 \right\}}} - {{C}_{1}}{\rho t}{{{\text{g}}}^{2}}\frac{{\theta }}{2} + {{\bar {\bar {p}}}^{{\left\{ 0 \right\}}}}\left( {{\theta },{\tau }} \right)$

На данной стадии сжатия, для вычисления величины ${{\bar {\bar {p}}}^{{\left\{ 0 \right\}}}}$ необходим явный вид функции ${v}_{{\theta }}^{{\left\{ 0 \right\}}}$, который как было сказано выше, в общем случае аналитически не выражается.

5. Анализ результатов. Полученные решения (3.2)–(3.4), (4.3) не отличаются от квазистатического случая [15], за исключением функции давления, где возникает слагаемое ${{C}_{{\beta }}}\left( {2\ln \cos \frac{{\theta }}{2} - \frac{1}{2}{{{\sec }}^{2}}\frac{{\theta }}{2}} \right) + {{\bar {p}}^{{\left\{ {{\beta } - 2} \right\}}}}\left( {\tau } \right)$ в членах при ${{{\alpha }}^{{ - 1}}}$ и α0 в режимах β = 1 и β = 2 соответственно. Естественно требовать, чтобы давление на границах слоя совпадало с атмосферным $p_{{{\text{atm}}}}^{{\left\{ 0 \right\}}}$ (здесь полагается, что ${{p}_{{{\text{atm}}}}}$ – величина порядка α0), однако данное слагаемое при ${\theta } \to {\pi }$ стремится к бесконечности. Таким образом, если слой полностью занимает область, невозможно удовлетворить данное граничное условие, не нарушив асимптотичность ряда в смысле Пуанкаре [16]. Напротив, если слой (1.1) лежит в секторе ${\theta } \in \;~\left[ {0;~{{{\theta }}_{0}}} \right]$, то с учетом граничного условия уравнения (4.2) и (3.4, 3.5) примут вид:

(5.1)
${{p}^{{\left\{ { - 1} \right\}}}} = {{C}_{1}}\left( {2\ln \left( {{{\cos \frac{{\theta }}{2}} \mathord{\left/ {\vphantom {{\cos \frac{{\theta }}{2}} {\cos \frac{{{{{\theta }}_{0}}}}{2}}}} \right. \kern-0em} {\cos \frac{{{{{\theta }}_{0}}}}{2}}}} \right) - \frac{1}{2}\left( {{{{\sec }}^{2}}\frac{{\theta }}{2} - {{{\sec }}^{2}}\frac{{{{{\theta }}_{0}}}}{2}} \right)} \right) - 2\mathop \smallint \limits_{{{{\theta }}_{0}}}^{\theta } {\mu }\left( {\varepsilon } \right)d{\varepsilon },$
(5.2)
$\begin{gathered} {{p}^{{\left\{ 0 \right\}}}} = s_{{rr}}^{{\left\{ 0 \right\}}} - {{\left. {s_{{rr}}^{{\left\{ 0 \right\}}}} \right|}_{{{\theta } = {{{\theta }}_{0}}}}} + {{{\bar {\bar {p}}}}^{{{\text{ks}}\left\{ 0 \right\}}}} - \bar {\bar {p}}{{\left. {^{{{\text{ks}}\left\{ 0 \right\}}}} \right|}_{{{\theta } = {{{\theta }}_{0}}}}} + \\ + \;{{C}_{2}}\left( {2\ln \left( {{{\cos \frac{{\theta }}{2}} \mathord{\left/ {\vphantom {{\cos \frac{{\theta }}{2}} {\cos \frac{{{{{\theta }}_{0}}}}{2}}}} \right. \kern-0em} {\cos \frac{{{{{\theta }}_{0}}}}{2}}}} \right) - \frac{1}{2}\left( {{{{\sec }}^{2}}\frac{{\theta }}{2} - {{{\sec }}^{2}}\frac{{{{{\theta }}_{0}}}}{2}} \right)} \right) + p_{{{\text{atm}}}}^{{\left\{ 0 \right\}}}. \\ \end{gathered} $

При этом область ${\theta } = {{{\theta }}_{0}}$ представляет собой зону краевого эффекта, где найденное решение не применимо.

Уравнения (5.1), (5.2) отличаются от квазистатического случая наличием выпуклого вверх слагаемого $2\ln \left( {{{\cos \frac{{\theta }}{2}} \mathord{\left/ {\vphantom {{\cos \frac{{\theta }}{2}} {\cos \frac{{{{{\theta }}_{0}}}}{2}}}} \right. \kern-0em} {\cos \frac{{{{{\theta }}_{0}}}}{2}}}} \right) - \frac{1}{2}\left( {{{{\sec }}^{2}}\frac{{\theta }}{2} - {{{\sec }}^{2}}\frac{{{{{\theta }}_{0}}}}{2}} \right)$, которое увеличивает суммарную силу, действующую на сферы со стороны слоя.

Уравнение (2.6) устанавливает критерий применимости квазистатического приближения: $\frac{{{{{\rho }}_{m}}{{V}^{2}}}}{{{{{\tau }}_{s}}}} \ll \frac{{{{h}^{2}}}}{{{{R}^{2}}}} \ll 1.$

Список литературы

  1. Prandtl L. Anwendungsbeispiele zu einem Henckyschen Satz über das plastiche Gleichgewicht // ZAMM. 1923. Bd. 3. H. 6. S. 401–406. = Прандтль Л. Примеры применения теоремы Генки к равновесию пластических тел // Теория пластичности. М.: Изд-во иностр. лит., 1948. С. 102–113.

  2. Nadai A. Theory of Flow and Fracture of Solids. N.Y.: Wiley, 1950. = Надаи А. Пластичность и разрушение твердых тел. М.: Изд-во иностр. лит., 1954. 648 с.

  3. Hill R. The Mathematical Theory of Plasticity. Oxford: ClarendonPress, 1950. = Хилл Р. Математическая теория пластичности. М.: Гостехиздат, 1956. 408 с.

  4. Кийко И.А. О воздействии сжатого пластического тонкого слоя на упругие поверхности // Изв. АН СССР, ОТН, Мех. и машиностр. 1961. № 6. С. 1082–1085.

  5. Победря Б.Е., Гузей И.Л. Математическое моделирование деформирования композитов с учетом термодиффузии // Математическое моделирование систем и процессов. 1998. № 6. С. 82–91.

  6. Кийко И.А. Обобщение задачи Л. Прандтля об осадке полосы на случай сжимаемого материала // Вестн. МГУ. Сер. 1. Математика, механика. 2002. № 4. С. 47–52.

  7. Ильюшин А.А. Труды. Т. 4. Моделирование динамических процессов в твердых телах и инженерные приложения. М.: Физматлит, 2009. 526 с.

  8. Быковцев Г.И. О сжатии пластического слоя жесткими шероховатыми плитами с учетом сил инерции // Изв. АН СССР. ОТН. Механика и машиностроение. 1960. № 6. С. 140–142.

  9. Кийко И.А., Кадымов Б.А. Обобщения задачи Л. Прандтля о сжатии полосы // Вестник МГУ. Сер. 1. Математика, механика. 2003. № 4. С. 50–56.

  10. Георгиевский Д.В. Асимптотическое интегрирование задачи Прандтля в динамической постановке // Изв. РАН. МТТ. 2013. № 1. С. 97–105.

  11. Георгиевский Д.В., Шабайкин Р.Р. Квазистатическое и динамическое сдавливание плоского круглого идеальнопластического слоя жесткими плитами // Изд-во ТвГТУ Тверь. Математическое моделирование и экспериментальная механика деформируемого твердого тела. 2017. С. 56–63.

  12. Задоян М.А. Пространственные задачи теории пластичности. М.: Наука, 1992. 384 с.

  13. Ишлинский А.Ю., Ивлев Д.Д. Математическая теория пластичности. М.: Физматлит, 2001. 704 с.

  14. Победря Б.Е. Численные методы в теории упругости и пластичности. М.: Изд-во МГУ, 1995. 366 с.

  15. Георгиевский Д.В. Сжатие-сток асимптотически тонкого идеально жесткопластического сферического слоя // Вестник Московского университета. Серия 1: Математика. Механика. 2011. № 6. С. 65–68.

  16. Кравченко В.Ф., Несененко Г.А., Пустовойт В.И. Асимптотики Пуанкаре решений задач нерегулярного тепло- и массопереноса. М.: Физматлит, 2006. 419 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал