1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 5, 2020

Известия РАН. Механика твердого тела, 2020, № 5, стр. 107-119

МОДЕЛЬ НЕСТАЦИОНАРНЫХ УПРУГО-ДИФФУЗИОННЫХ КОЛЕБАНИЙ ШАРНИРНО ОПЕРТОЙ БАЛКИ ТИМОШЕНКО

А. В. Вестяк a, А. В. Земсков a, b, *

a Московский авиационный институт (национальный исследовательский университет)
Москва, Россия

b НИИ механики МГУ имени М.В. Ломоносова
Москва, Россия

* E-mail: azemskov1975@mail.ru

Поступила в редакцию 11.12.2019
После доработки 12.02.2020
Принята к публикации 03.03.2020

Полный текст (PDF)

Аннотация

Исследуются нестационарные колебания шарнирно опертой балки Тимошенко с учетом массопереноса, находящейся под действием распределенной поперечной нагрузки. Для постановки задачи используется модель балки Тимошенко, полученная с помощью принципа Даламбера из уравнений упругой диффузии для сплошной среды. Для решения полученной задачи применяется интегральное преобразование Лапласа по времени и разложение в ряды Фурье. Путем перехода к классической задаче о нестационарных колебаниях упругой балки проанализировано влияние массопереноса на поле перемещений внутри балки.

Ключевые слова: упругая диффузия, балка Тимошенко, нестационарные колебания, интегральные преобразования

Введение. Примерно с середины 20-го столетия значительное внимание в научной литературе уделяется процессам деформации упругих тел при взаимном влиянии полей различной физической природы, в том числе с учетом диффузии. Несмотря на большие математические трудности, связанные с решением соответствующих начально-краевых задач, существует множество научных работ, посвященных этой тематике. Применительно к задачам механодиффузии с возможным учетом температурных и электромагнитных факторов здесь можно отметить публикации [1–10], где рассматриваются связанные задачи в основном для канонических областей: пространства, полупространства или слоя.

При этом следует отметить, что реальные элементы конструкций имеют, как правило, конечные размеры и моделируются с помощью стержней, пластин или оболочек. Публикаций, посвященных изучению механодиффузионных процессов в телах с указанной геометрией крайне мало. В качестве наиболее известных на сегодняшний день можно указать работы [11–13], где рассматривается постановка контактной задачи термоупругой диффузии для слоистой оболочки и исследуется влияние диффузионных процессов на несущую способность пологой трансверсально-изотропной оболочки в случае статических нагрузок. В статьях [14, 15] рассматриваются квазистатические контактные задачи для стержня с упругим полупространством, а в [16, 17] обсуждаются вопросы, связанные с постановкой задачи механодиффузии для пластины. Вопросы, связанные с построением аналитических решений указанных задач в нестационарной постановке, на сегодняшний день не рассматриваются.

В данной работе исследуются нестационарные механодиффузионные колебания балки Тимошенко. Модель колебаний балки строится на основе вариационных принципов с использованием известных уравнений упругой диффузии для сплошных сред [1–10, 18–21]. Предлагается аналитический метод решения данной задачи, основанный на использовании интегрального преобразования Лапласа и разложений в ряды по собственным функциям упругодиффузионного оператора.

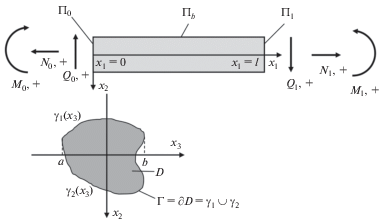
1. Постановка задачи. Рассматривается задача о нестационарных колебаниях балки Тимошенко с учетом явлений массопереноса. В общем случае балка находится под действием растягивающих усилий, изгибающих моментов и перерезывающих сил, заданных на ее концах. Схема приложенных усилий, ориентация координатных осей и геометрия балки изображены на рис 1.

Рис. 1

Для постановки задачи используем упругодиффузионную модель сплошной среды, записанную в декартовой системе координат ($\left( {{{x}_{1}},{{x}_{2}},{{x}_{3}}} \right) \in G \subset {{\Re }^{3}}$, $\partial G = {{\Pi }_{\sigma }} \cup {{\Pi }_{J}}$)

(1.1)
$\begin{gathered} {{{\ddot {u}}}_{i}} = \frac{{\partial {{\sigma }_{{ij}}}}}{{\partial {{x}_{j}}}} + {{F}_{i}},\quad \left( {1 + {{\tau }_{q}}\frac{\partial }{{\partial \tau }}} \right)\left( {\frac{{\partial {{\eta }^{{\left( q \right)}}}}}{{\partial \tau }} + \frac{{\partial J_{i}^{{\left( q \right)}}}}{{\partial {{x}_{i}}}} - {{Y}^{{\left( q \right)}}}} \right) = 0\quad \left( {q = \overline {1,N} } \right) \\ {{\left. {{{\sigma }_{{ij}}}{{\nu }_{j}}} \right|}_{{{{\Pi }_{\sigma }}}}} = {{P}_{i}},\quad {{\left. {\left( {J_{i}^{{\left( q \right)}} + {{\tau }_{q}}\frac{{\partial J_{i}^{{\left( q \right)}}}}{{\partial \tau }}} \right)} \right|}_{{{{\Pi }_{J}}}}} = I_{i}^{{\left( q \right)}},\quad {{\left. {{{u}_{i}}} \right|}_{{\tau = 0}}} = {{\left. {\frac{{\partial {{u}_{i}}}}{{\partial \tau }}} \right|}_{{\tau = 0}}} = {{\left. {{{\eta }^{{\left( q \right)}}}} \right|}_{{\tau = 0}}} = {{\left. {\frac{{\partial {{\eta }^{{\left( q \right)}}}}}{{\partial \tau }}} \right|}_{{\tau = 0}}} = 0 \\ \end{gathered} $
где ${{\sigma }_{{ij}}}$ и $J_{i}^{{\left( q \right)}}$ – компоненты тензора напряжений и вектора диффузионного потока, которые определяются следующим образом [18–21]:

(1.2)
$\begin{gathered} {{\sigma }_{{ij}}} = {{C}_{{ijkl}}}\frac{{\partial {{u}_{k}}}}{{\partial {{x}_{l}}}} - \sum\limits_{q = 1}^N {\alpha _{{ij}}^{{(q)}}{{\eta }^{{(q)}}}} , \\ J_{i}^{{(q)}} + {{\tau }_{q}}\frac{{\partial J_{i}^{{(q)}}}}{{\partial \tau }} = - \sum\limits_{t = 1}^N {D_{{ij}}^{{(q)}}{{g}^{{\left( {qt} \right)}}}\frac{{\partial {{\eta }^{{(t)}}}}}{{\partial {{x}_{j}}}}} + \Lambda _{{ijkl}}^{{(q)}}\frac{{{{\partial }^{2}}{{u}_{k}}}}{{\partial {{x}_{j}}\partial {{x}_{l}}}}\quad \left( {q = 1 \div N} \right) \\ \end{gathered} $

Здесь все величины являются безразмерными и для них приняты следующие обозначения

(1.3)
$\begin{gathered} {{x}_{i}} = \frac{{x_{i}^{*}}}{l},\quad {{u}_{i}} = \frac{{u_{i}^{*}}}{l},\quad \tau = \frac{{Ct}}{l},\quad {{C}_{{ijkl}}} = \frac{{C_{{ijkl}}^{*}}}{{C_{{1111}}^{ * }}},\quad {{C}^{2}} = \frac{{C_{{1111}}^{*}}}{\rho },\quad \alpha _{{ij}}^{{\left( q \right)}} = \frac{{\alpha _{{ij}}^{{*\left( q \right)}}}}{{C_{{1111}}^{*}}} \\ D_{{ij}}^{{\left( q \right)}} = \frac{{D_{{ij}}^{{*\left( q \right)}}}}{{Cl}},\quad \Lambda _{{ijkl}}^{{\left( q \right)}} = \frac{{{{m}^{{\left( q \right)}}}D_{{ij}}^{{ * \left( q \right)}}\alpha _{{kl}}^{{*\left( q \right)}}n_{0}^{{\left( q \right)}}}}{{\rho R{{T}_{0}}Cl}},\quad {{F}_{i}} = \frac{{\rho lF_{i}^{*}}}{{C_{{1111}}^{*}}},\quad {{Y}^{{\left( q \right)}}} = \frac{{l{{Y}^{{*\left( q \right)}}}}}{C},\quad {{\tau }_{q}} = \frac{{C{{\tau }^{{\left( q \right)}}}}}{l} \\ \end{gathered} $
где $t$ – время; $x_{i}^{*}$ – прямоугольные декартовы координаты; $u_{i}^{*}$ – компоненты вектора перемещений; l – длина балки; ${{\eta }^{{\left( q \right)}}} = {{n}^{{\left( q \right)}}} - n_{0}^{{\left( q \right)}}$ – приращение концентрации q-й компоненты вещества в составе N – компонентной среды; ${{n}^{{\left( q \right)}}}$ и $n_{0}^{{\left( q \right)}}$ – актуальная и начальная концентрации q-го вещества; $C_{{ijkl}}^{*}$ – компоненты тензора упругих постоянных; $\rho $ – плотность; $\alpha _{{ij}}^{{*\left( q \right)}}$ – коэффициенты, характеризующие объемное изменение среды за счет диффузии; $D_{{ij}}^{{*\left( q \right)}}$ – коэффициенты самодиффузии; $R$ – универсальная газовая постоянная; ${{T}_{0}}$ – температура среды; ${{m}^{{\left( q \right)}}}$ – молярная масса q-го вещества, ${{P}_{i}}$, $I_{i}^{{\left( q \right)}}$ – поверхностные возмущения, $F_{i}^{*}$, $Y_{i}^{{*\left( q \right)}}$ – объемные возмущения; ${{\nu }_{i}}$ – компоненты вектора нормали к поверхности балки; ${{\tau }^{{\left( q \right)}}}$ – время релаксации диффузионных потоков.

Уравнения упругодиффузионных колебаний балки получаем на основе вариационного принципа Даламбера. Используя начально-краевую задачу (1.1), имеем [18–20]

(1.4)
$\begin{gathered} \int\limits_G {\left( {{{{\ddot {u}}}_{i}} - \frac{{\partial {{\sigma }_{{ij}}}}}{{\partial {{x}_{j}}}} - {{F}_{i}}} \right)\delta {{u}_{i}}dG} + \sum\limits_{q = 1}^N {\int\limits_G {\left( {1 + {{\tau }_{q}}\frac{\partial }{{\partial \tau }}} \right)\left( {\frac{{\partial {{\eta }^{{\left( q \right)}}}}}{{\partial \tau }} + \frac{{\partial J_{i}^{{\left( q \right)}}}}{{\partial {{x}_{i}}}} - {{Y}^{{\left( q \right)}}}} \right)\delta {{\eta }^{{\left( q \right)}}}dG} } + \\ \, + \iint\limits_{{{\Pi }_{\sigma }}} {\left( {{{\sigma }_{{ij}}}{{\nu }_{j}} - {{P}_{i}}} \right)\delta {{u}_{i}}dS} + \sum\limits_{q = 1}^N {\iint\limits_{{{\Pi }_{J}}} {\left( {J_{i}^{{\left( q \right)}} - I_{i}^{{\left( q \right)}}} \right){{\nu }_{i}}\delta {{\eta }^{{\left( q \right)}}}dS}} = 0 \\ \end{gathered} $

Здесь $\delta {{u}_{i}}$ – виртуальные перемещения, $\delta {{\eta }^{{\left( q \right)}}}$ – виртуальные приращения концентраций.

Далее, для построения уравнений изгиба балки в плоскости $O{{x}_{1}}{{x}_{2}}$ принимаем, что:

– материал является изотропным ($\lambda $ и $\mu $ – коэффициенты Ламе, ${{\delta }_{{ij}}}$ – символ Кронекера)

(1.5)
${{C}_{{ijkl}}} = \lambda {{\delta }_{{ij}}}{{\delta }_{{kl}}} + \mu \left( {{{\delta }_{{ik}}}{{\delta }_{{jl}}} + {{\delta }_{{il}}}{{\delta }_{{jk}}}} \right),\quad \Lambda _{{\alpha \alpha \beta \beta }}^{{\left( q \right)}} = {{\Lambda }_{q}},\quad \alpha _{{\alpha \alpha }}^{{\left( q \right)}} = {{\alpha }_{q}},\quad D_{{\alpha \alpha }}^{{\left( q \right)}} = {{D}_{q}}$
– прогибы балки малы и сечения, перпендикулярные к оси балки до деформации, остаются плоскими и после деформации (гипотеза плоских сечений). Тогда, линеаризуя искомые величины по переменной ${{x}_{2}}$, получаем [18–21]
(1.6)
$\begin{gathered} {{u}_{1}}\left( {{{x}_{1}},{{x}_{2}},\tau } \right) = u\left( {{{x}_{1}},\tau } \right) + {{x}_{2}}\chi \left( {{{x}_{1}},\tau } \right),\quad {{u}_{2}}\left( {{{x}_{1}},{{x}_{2}},\tau } \right) = v\left( {{{x}_{1}},\tau } \right) + {{x}_{2}}\psi \left( {{{x}_{1}},\tau } \right) \\ {{\eta }^{{\left( q \right)}}}\left( {{{x}_{1}},{{x}_{2}},\tau } \right) = {{N}_{q}}\left( {{{x}_{1}},\tau } \right) + {{x}_{2}}{{H}_{q}}\left( {{{x}_{1}},\tau } \right) \\ \end{gathered} $
– деформации в поперечном направлении отсутствуют. Тогда $\psi \left( {{{x}_{1}},\tau } \right) \equiv 0$ и соотношения (1.6) записываются так

(1.7)
$\begin{gathered} {{u}_{1}}\left( {{{x}_{1}},{{x}_{2}},\tau } \right) = u\left( {{{x}_{1}},\tau } \right) - {{x}_{2}}\chi \left( {{{x}_{1}},\tau } \right),\quad {{u}_{2}}\left( {{{x}_{1}},{{x}_{2}},\tau } \right) = v\left( {{{x}_{1}},\tau } \right) \\ {{\eta }^{{\left( q \right)}}}\left( {{{x}_{1}},{{x}_{2}},\tau } \right) = {{N}_{q}}\left( {{{x}_{1}},\tau } \right) + {{x}_{2}}{{H}_{q}}\left( {{{x}_{1}},\tau } \right) \\ \end{gathered} $

С учетом (1.5) и (1.7), компоненты тензора напряжений и вектора диффузионного потока (1.2) будут иметь вид [20] (здесь штрих обозначает производную по переменной ${{x}_{1}}$, точка – производную по времени $\tau $)

(1.8)
$\begin{gathered} {{\sigma }_{{11}}} = \left( {u{\text{'}} - {{x}_{2}}\chi {\text{'}}} \right) - \sum\limits_{q = 1}^N {{{\alpha }_{q}}\left( {{{N}_{q}} + {{x}_{2}}{{H}_{q}}} \right)} ,\quad {{\sigma }_{{22}}} = \lambda \left( {u{\text{'}} - {{x}_{2}}\chi {\text{'}}} \right) - \sum\limits_{q = 1}^N {{{\alpha }_{q}}\left( {{{N}_{q}} + {{x}_{2}}{{H}_{q}}} \right)} \\ {{\sigma }_{{12}}} = \mu \left( {v{\text{'}} - \chi } \right),\quad J_{1}^{{\left( q \right)}} + {{\tau }_{q}}\dot {J}_{1}^{{\left( q \right)}} = - {{D}_{q}}(N_{q}^{'} + {{x}_{2}}H_{q}^{'}) + {{\Lambda }_{q}}\left( {u{\text{''}} - {{x}_{2}}\chi {\text{''}}} \right) \\ J_{2}^{{\left( q \right)}} + {{\tau }_{q}}\dot {J}_{2}^{{\left( q \right)}} = - {{D}_{q}}{{H}_{q}} - {{\Lambda }_{q}}\chi {\text{'}}\quad \left( {q = 1 \div N} \right) \\ \end{gathered} $

Подставляя (1.7) и (1.8) в (1.4) и используя необходимое условие стационарности функционалов, получаем модель нестационарного плоского изгиба упругодиффузионной балки Тимошенко, которая состоит из двух задач:

– задача об одноосном растяжении-сжатии стержня с учетом диффузии

$\begin{gathered} \ddot {u}\left( {{{x}_{1}},\tau } \right) - u{\text{''}}\left( {{{x}_{1}},\tau } \right) + \sum\limits_{q = 1}^N {{{\alpha }_{q}}N_{q}^{'}\left( {{{x}_{1}},\tau } \right)} - n\left( {{{x}_{1}},\tau } \right) = 0 \\ {{{\dot {N}}}_{q}}\left( {{{x}_{1}},\tau } \right) + {{\tau }_{q}}{{{\ddot {N}}}_{q}}\left( {{{x}_{1}},\tau } \right) - {{D}_{q}}N_{q}^{{''}}\left( {{{x}_{1}},\tau } \right) + {{\Lambda }_{q}}u{\text{'''}}\left( {{{x}_{1}},\tau } \right) - {{y}^{{\left( q \right)}}}\left( {{{x}_{1}},\tau } \right) = 0 \\ \end{gathered} $
${{\left. {\left[ {u{\text{'}}\left( {{{x}_{1}},\tau } \right) - \sum\limits_{q = 1}^N {{{\alpha }_{q}}{{N}_{q}}\left( {{{x}_{1}},\tau } \right)} } \right]} \right|}_{{{{x}_{1}} = 0}}} = \frac{{{{N}_{0}}\left( \tau \right)}}{F},\quad {{\left. {\left[ {u{\text{'}}\left( {{{x}_{1}},\tau } \right) - \sum\limits_{q = 1}^N {{{\alpha }_{q}}{{N}_{q}}\left( {{{x}_{1}},\tau } \right)} } \right]} \right|}_{{{{x}_{1}} = 1}}} = \frac{{{{N}_{1}}\left( \tau \right)}}{F}$
${{\left. {[{{\Lambda }_{q}}u{\text{''}}\left( {{{x}_{1}},\tau } \right) - {{D}_{q}}N_{q}^{'}\left( {{{x}_{1}},\tau } \right)]} \right|}_{{{{x}_{1}} = 0}}} = \frac{{\Gamma _{0}^{{\left( q \right)}}\left( \tau \right)}}{F},\quad {{\left. {[{{\Lambda }_{q}}u{\text{''}}\left( {{{x}_{1}},\tau } \right) - {{D}_{q}}N_{q}^{'}\left( {{{x}_{1}},\tau } \right)]} \right|}_{{{{x}_{1}} = 1}}} = \frac{{\Gamma _{1}^{{\left( q \right)}}\left( \tau \right)}}{F}$
– задача относительно прогибов балки с учетом диффузии
(1.9)
$\begin{gathered} \ddot {v}\left( {{{x}_{1}},\tau } \right) - \mu \left[ {v{\text{''}}\left( {{{x}_{1}},\tau } \right) - \chi {\text{'}}\left( {{{x}_{1}},\tau } \right)} \right] - \frac{{q\left( {{{x}_{1}},\tau } \right)}}{F} = 0 \\ \ddot {\chi }\left( {{{x}_{1}},\tau } \right) - \chi {\text{''}}\left( {{{x}_{1}},\tau } \right) - \eta \mu \left[ {v{\text{'}}\left( {{{x}_{1}},\tau } \right) - \chi \left( {{{x}_{1}},\tau } \right)} \right] - \sum\limits_{q = 1}^N {{{\alpha }_{q}}H_{q}^{'}} \left( {{{x}_{1}},\tau } \right) - \frac{{m\left( {{{x}_{1}},\tau } \right)}}{{{{J}_{3}}}} = 0 \\ {{{\dot {H}}}_{q}}\left( {{{x}_{1}},\tau } \right) + {{\tau }_{q}}{{{\ddot {H}}}_{q}}\left( {{{x}_{1}},\tau } \right) - {{D}_{q}}H_{q}^{{''}}\left( {{{x}_{1}},\tau } \right) - {{\Lambda }_{q}}\chi {\text{'''}}\left( {{{x}_{1}},\tau } \right) - \frac{{{{z}^{{\left( q \right)}}}\left( {{{x}_{1}},\tau } \right)}}{{{{J}_{3}}}} = 0 \\ \end{gathered} $
${{\left. {\left[ {v{\text{'}}\left( {{{x}_{1}},\tau } \right) - \chi \left( {{{x}_{1}},\tau } \right)} \right]} \right|}_{{{{x}_{1}} = 0}}} = \frac{{{{Q}_{0}}\left( \tau \right)}}{{\mu F}},\quad {{\left. {\left[ {v{\text{'}}\left( {{{x}_{1}},\tau } \right) - \chi \left( {{{x}_{1}},\tau } \right)} \right]} \right|}_{{{{x}_{1}} = 1}}} = \frac{{{{Q}_{1}}\left( \tau \right)}}{{\mu F}}$
(1.10)
$\begin{gathered} {{\left. {\left[ {\chi {\text{'}}\left( {{{x}_{1}},\tau } \right) + \sum\limits_{q = 1}^N {{{\alpha }_{q}}{{H}_{q}}\left( {{{x}_{1}},\tau } \right)} } \right]} \right|}_{{{{x}_{1}} = 0}}} = - \frac{{{{M}_{0}}\left( \tau \right)}}{{{{J}_{3}}}} \\ {{\left. {\left[ {\chi {\text{'}}\left( {{{x}_{1}},\tau } \right) + \sum\limits_{q = 1}^N {{{\alpha }_{q}}{{H}_{q}}\left( {{{x}_{1}},\tau } \right)} } \right]} \right|}_{{{{x}_{1}} = 1}}} = - \frac{{{{M}_{1}}\left( \tau \right)}}{{{{J}_{3}}}} \\ \end{gathered} $
$\begin{gathered} {{\left. {[{{\Lambda }_{q}}\chi {\text{''}}\left( {{{x}_{1}},\tau } \right) + {{D}_{q}}H_{q}^{'}\left( {{{x}_{1}},\tau } \right)]} \right|}_{{{{x}_{1}} = 0}}} = - \frac{{\Omega _{0}^{{\left( q \right)}}\left( \tau \right)}}{{{{J}_{3}}}} \\ {{\left. {[{{\Lambda }_{q}}\chi {\text{''}}\left( {{{x}_{1}},\tau } \right) + {{D}_{q}}H_{q}^{'}\left( {{{x}_{1}},\tau } \right)]} \right|}_{{{{x}_{1}} = 1}}} = - \frac{{\Omega _{1}^{{\left( q \right)}}\left( \tau \right)}}{{{{J}_{3}}}} \\ \end{gathered} $
где $F$ – площадь сечения, ${{J}_{3}}$ – момент инерции поперечного сечения балки относительно оси $O{{x}_{3}}$, $\eta = {F \mathord{\left/ {\vphantom {F {{{J}_{3}}}}} \right. \kern-0em} {{{J}_{3}}}}$, n – распределенная погонная продольная нагрузка, $m$ – распределенный погонный момент, q – распределенная погонная поперечная нагрузка, остальные силовые факторы определяются следующим образом

$\left\{ \begin{gathered} {{y}^{{\left( q \right)}}}\left( {{{x}_{1}},\tau } \right) \hfill \\ {{z}^{{\left( q \right)}}}\left( {{{x}_{1}},\tau } \right) \hfill \\ \end{gathered} \right\} = \iint\limits_D {\left\{ \begin{gathered} {{Y}^{{\left( q \right)}}} + {{\tau }_{q}}{{{\dot {Y}}}^{{\left( q \right)}}} \hfill \\ \left( {{{Y}^{{\left( q \right)}}} + {{\tau }_{q}}{{{\dot {Y}}}^{{\left( q \right)}}}} \right){{x}_{2}} \hfill \\ \end{gathered} \right\}d{{x}_{2}}d{{x}_{3}}},\quad \left\{ \begin{gathered} {{N}_{0}}\left( \tau \right) \hfill \\ {{N}_{1}}\left( \tau \right) \hfill \\ \end{gathered} \right\} = \iint\limits_D {\left\{ \begin{gathered} {{P}_{1}}\left( {0,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ {{P}_{1}}\left( {1,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ \end{gathered} \right\}d{{x}_{2}}d{{x}_{3}}}$
$\left\{ \begin{gathered} {{M}_{0}}\left( \tau \right) \hfill \\ {{M}_{1}}\left( \tau \right) \hfill \\ \end{gathered} \right\} = \iint\limits_D {\left\{ \begin{gathered} {{P}_{1}}\left( {0,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ {{P}_{1}}\left( {1,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ \end{gathered} \right\}{{x}_{2}}d{{x}_{2}}d{{x}_{3}}},\quad \left\{ \begin{gathered} {{Q}_{0}}\left( \tau \right) \hfill \\ {{Q}_{1}}\left( \tau \right) \hfill \\ \end{gathered} \right\} = \iint\limits_D {\left\{ \begin{gathered} {{P}_{2}}\left( {0,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ {{P}_{2}}\left( {1,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ \end{gathered} \right\}d{{x}_{2}}d{{x}_{3}}}$
$\left\{ \begin{gathered} \Gamma _{0}^{{\left( q \right)}}\left( \tau \right) \hfill \\ \Gamma _{1}^{{\left( q \right)}}\left( \tau \right) \hfill \\ \end{gathered} \right\} = \iint\limits_D {\left\{ \begin{gathered} I_{1}^{{\left( q \right)}}\left( {0,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ I_{1}^{{\left( q \right)}}\left( {1,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ \end{gathered} \right\}d{{x}_{2}}d{{x}_{3}}},\quad \left\{ \begin{gathered} \Omega _{0}^{{\left( q \right)}}\left( \tau \right) \hfill \\ \Omega _{1}^{{\left( q \right)}}\left( \tau \right) \hfill \\ \end{gathered} \right\} = \iint\limits_D {\left\{ \begin{gathered} I_{1}^{{\left( q \right)}}\left( {0,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ I_{1}^{{\left( q \right)}}\left( {1,{{x}_{2}},{{x}_{3}},\tau } \right) \hfill \\ \end{gathered} \right\}{{x}_{2}}d{{x}_{2}}d{{x}_{3}}}$

В более точных моделях (для этого надо учесть слагаемые более высокого порядка малости в (1.6)) уравнения (1.9) записываются так

(1.11)
$\begin{gathered} \ddot {v}\left( {{{x}_{1}},\tau } \right) - \mu {{k}^{2}}\left[ {v{\text{''}}\left( {{{x}_{1}},\tau } \right) - \chi {\text{'}}\left( {{{x}_{1}},\tau } \right)} \right] - \frac{{q\left( {{{x}_{1}},\tau } \right)}}{F} = 0 \\ \ddot {\chi }\left( {{{x}_{1}},\tau } \right) - \chi {\text{''}}\left( {{{x}_{1}},\tau } \right) - \eta \mu {{k}^{2}}\left[ {v{\text{'}}\left( {{{x}_{1}},\tau } \right) - \chi \left( {{{x}_{1}},\tau } \right)} \right] - \sum\limits_{q = 1}^N {{{\alpha }_{q}}H_{q}^{'}} \left( {{{x}_{1}},\tau } \right) - \frac{{m\left( {{{x}_{1}},\tau } \right)}}{{{{J}_{3}}}} = 0 \\ {{{\dot {H}}}_{q}}\left( {{{x}_{1}},\tau } \right) + {{\tau }_{q}}{{{\ddot {H}}}_{q}}\left( {{{x}_{1}},\tau } \right) - {{D}_{q}}H_{q}^{{''}}\left( {{{x}_{1}},\tau } \right) - {{\Lambda }_{q}}\chi {\text{'''}}\left( {{{x}_{1}},\tau } \right) - \frac{{{{z}^{{\left( q \right)}}}\left( {{{x}_{1}},\tau } \right)}}{{{{J}_{3}}}} = 0 \\ \end{gathered} $
где k – коэффициент, учитывающий неравномерность распределения касательных напряжений по сечению балки.

Если касательные напряжения распределены по формуле Журавского, то для балки прямоугольного сечения высотой h и единичной толщины ${{k}^{2}} = 5{\text{/}}6$ [22, 23].

Будем далее рассматривать задачу об изгибе шарнирно опертой балки под действием нестационарной распределенной поперечной нагрузки. Математическая постановка задачи включает в себя уравнения (1.11) и граничные условия (1.10), в которых полагаем

${{M}_{0}}\left( \tau \right) = {{M}_{1}}\left( \tau \right) = 0$

Для получения замкнутой постановки задачи используем дополнительно следующие кинематические граничные условия

(1.12)
${{\left. {v\left( {{{x}_{1}},\tau } \right)} \right|}_{{{{x}_{1}} = 0}}} = 0,\quad {{\left. {v\left( {{{x}_{1}},\tau } \right)} \right|}_{{{{x}_{1}} = 1}}} = 0\quad {{\left. {{{H}_{q}}\left( {{{x}_{1}},\tau } \right)} \right|}_{{{{x}_{1}} = 0}}} = 0,\quad {{\left. {{{H}_{q}}\left( {{{x}_{1}},\tau } \right)} \right|}_{{{{x}_{1}} = 1}}} = 0$

Начальные условия полагаем нулевыми.

2. Метод решения. Решение задачи (1.11), (1.10), (1.12) представляем в виде (k = = $1 \div N$ + 1) [20]:

(2.1)
$\begin{gathered} v\left( {x,\tau } \right) = \sum\limits_{k = 1}^{N + 2} {\int\limits_0^\tau {\int\limits_0^1 {{{G}_{{1k}}}\left( {x,\xi ,\tau - t} \right){{F}_{k}}\left( {\xi ,t} \right)d\xi } dt} } , \\ \chi \left( {x,\tau } \right) = \sum\limits_{k = 1}^{N + 2} {\int\limits_0^\tau {\int\limits_0^1 {{{G}_{{2k}}}\left( {x,\xi ,\tau - t} \right){{F}_{k}}\left( {\xi ,t} \right)d\xi } dt} } \\ {{H}_{q}}\left( {x,\tau } \right) = \sum\limits_{k = 1}^{N + 2} {\int\limits_0^\tau {\int\limits_0^1 {{{G}_{{q + 2,k}}}\left( {x,\xi ,\tau - t} \right){{F}_{k}}\left( {\xi ,t} \right)d\xi } dt} } \\ \end{gathered} $

Здесь $x = {{x}_{1}}$, ${{F}_{k}}\left( {x,\tau } \right)$ – объемные силовые факторы, входящие в уравнения (1.11), ${{G}_{{mk}}}$ – объемные функции Грина, удовлетворяющие уравнениям [20]

(2.2)
$\begin{gathered} {{{\ddot {G}}}_{{1k}}}\left( {x,\xi ,\tau } \right) - \mu {{k}^{2}}[G_{{1k}}^{{''}}\left( {x,\xi ,\tau } \right) - G_{{2k}}^{'}\left( {x,\xi ,\tau } \right)] - {{\delta }_{{1k}}}\delta \left( {x - \xi } \right)\delta \left( \tau \right) = 0 \\ {{{\ddot {G}}}_{{2k}}}\left( {x,\xi ,\tau } \right) - G_{{2k}}^{{''}}\left( {x,\xi ,\tau } \right) - \eta \mu {{k}^{2}}[G_{{1k}}^{'}\left( {x,\xi ,\tau } \right) - {{G}_{{2k}}}\left( {x,\xi ,\tau } \right)] + \\ \, - \sum\limits_{q = 1}^N {{{\alpha }_{q}}G_{{q + 2,k}}^{'}\left( {x,\xi ,\tau } \right)} - {{\delta }_{{2k}}}\delta \left( {x - \xi } \right)\delta \left( \tau \right) = 0 \\ {{{\dot {G}}}_{{q + 2,k}}}\left( {x,\xi ,\tau } \right) + {{\tau }_{q}}{{{\ddot {G}}}_{{q + 2,k}}}\left( {x,\xi ,\tau } \right) - {{D}_{q}}G_{{q + 2,k}}^{{''}}\left( {x,\xi ,\tau } \right) - {{\Lambda }_{q}}G_{{2k}}^{{'''}}\left( {x,\xi ,\tau } \right) - \\ \, - {{\delta }_{{q + 2,k}}}\delta \left( {x - \xi } \right)\delta \left( \tau \right) = 0 \\ \end{gathered} $
и следующим однородным граничным условиям

(2.3)
$\begin{gathered} {{\left. {{{G}_{{1k}}}\left( {x,\xi ,\tau } \right)} \right|}_{{x = 0}}}\, = \,0,\quad {{\left. {{{G}_{{1k}}}\left( {x,\xi ,\tau } \right)} \right|}_{{x = 1}}}\, = \,0,\quad {{\left. {{{G}_{{q + 1,k}}}\left( {x,\xi ,\tau } \right)} \right|}_{{x = 0}}}\, = \,0,\quad {{\left. {{{G}_{{q + 1,kl}}}\left( {x,\xi ,\tau } \right)} \right|}_{{x = 1}}}\, = \,0 \\ {{\left. {\left[ {G_{{2k}}^{'}\left( {x,\xi ,\tau } \right) + \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{G}_{{j + 1,k}}}\left( {x,\xi ,\tau } \right)} } \right]} \right|}_{{x = 0}}} = 0,\quad {{\left. {\left[ {G_{{2k}}^{'}\left( {x,\xi ,\tau } \right) + \sum\limits_{j = 1}^N {{{\alpha }_{j}}{{G}_{{j + 1,k}}}\left( {x,\xi ,\tau } \right)} } \right]} \right|}_{{x = 1}}} = 0 \\ \end{gathered} $

Для нахождения объемных функций Грина вначале применяем преобразование Лапласа к задаче (2.2), (2.3) (верхний индекс “$L$” обозначает трансформанту Лапласа, $s$ – параметр преобразования Лапласа)

${{s}^{2}}G_{{1k}}^{L}\left( {x,\xi ,s} \right) - \mu {{k}^{2}}[G_{{1k}}^{{''L}}\left( {x,\xi ,s} \right) - G_{{1k}}^{{'L}}\left( {x,\xi ,s} \right)] - {{\delta }_{{1k}}}\delta \left( {x - \xi } \right) = 0$
$\begin{gathered} {{s}^{2}}G_{{2k}}^{L}\left( {x,\xi ,s} \right) - G_{{2k}}^{{''L}}\left( {x,\xi ,s} \right) - \mu \eta {{k}^{2}}[G_{{1k}}^{{'L}}\left( {x,\xi ,s} \right) - G_{{2k}}^{L}\left( {x,\xi ,s} \right)] + \\ \, - \sum\limits_{q = 1}^N {{{\alpha }_{q}}G_{{q + 2,k}}^{{'L}}\left( {x,\xi ,s} \right)} - {{\delta }_{{2k}}}\delta \left( {x - \xi } \right) = 0 \\ \end{gathered} $
$(s + {{\tau }_{q}}{{s}^{2}})G_{{q + 2,k}}^{L}\left( {x,\xi ,s} \right) - {{D}_{q}}G_{{q + 2,k}}^{{''L}}\left( {x,\xi ,s} \right) - {{\Lambda }_{q}}G_{{2k}}^{{'''L}}\left( {x,\xi ,s} \right) - {{\delta }_{{q + 2,k}}}\delta \left( {x - \xi } \right) = 0$
$\begin{gathered} {{\left. {G_{{1k}}^{L}\left( {x,\xi ,s} \right)} \right|}_{{x = 0}}} = 0,\quad {{\left. {G_{{1k}}^{L}\left( {x,\xi ,s} \right)} \right|}_{{x = 1}}} = 0,\quad {{\left. {G_{{q + 2,k}}^{L}\left( {x,\xi ,s} \right)} \right|}_{{x = 0}}} = 0,\quad {{\left. {G_{{q + 2,k}}^{L}\left( {x,\xi ,s} \right)} \right|}_{{x = 1}}} = 0 \\ {{\left. {\left[ {G_{{2k}}^{{'L}}\left( {x,\xi ,s} \right) + \sum\limits_{j = 1}^N {{{\alpha }_{j}}G_{{j + 2,k}}^{L}\left( {x,\xi ,s} \right)} } \right]} \right|}_{{x = 0}}} = 0,\quad {{\left. {\left[ {G_{{2k}}^{{'L}}\left( {x,\xi ,s} \right) + \sum\limits_{j = 1}^N {{{\alpha }_{j}}G_{{j + 2,k}}^{L}\left( {x,\xi ,s} \right)} } \right]} \right|}_{{x = 1}}} = 0 \\ \end{gathered} $

Затем трансформанты функций Грина $G_{{mk}}^{L}\left( {x,\xi ,s} \right)$ представляем в виде рядов Фурье:

$\begin{gathered} \left\{ \begin{gathered} G_{{1k}}^{L}\left( {x,\xi ,s} \right) \hfill \\ G_{{q + 2,k}}^{L}\left( {x,\xi ,s} \right) \hfill \\ \end{gathered} \right\} = \sum\limits_{n = 1}^\infty {\left\{ \begin{gathered} G_{{1k}}^{{Ls}}\left( {{{\lambda }_{n}},\xi ,s} \right) \hfill \\ G_{{q + 2,k}}^{{Ls}}\left( {{{\lambda }_{n}},\xi ,s} \right) \hfill \\ \end{gathered} \right\}\sin {{\lambda }_{n}}x} ,\quad {{\lambda }_{n}} = \pi n \\ G_{{2k}}^{L}\left( {x,\xi ,s} \right) = \frac{{G_{{2k}}^{{Lc}}\left( {0,\xi ,s} \right)}}{2} + \sum\limits_{n = 1}^\infty {G_{{2k}}^{{Lc}}\left( {{{\lambda }_{n}},\xi ,s} \right)\cos {{\lambda }_{n}}x} \\ \end{gathered} $

В результате получаем систему линейных алгебраических уравнений для определения функций $G_{{1k}}^{{Ls}}$, $G_{{q + 1,k}}^{{Ls}}$ и $G_{{2k}}^{{Lc}}$ $\left( {k = 1 \div N + 2,\;q = 1 \div N} \right)$:

(2.4)
$\begin{gathered} {{k}_{1}}\left( {{{\lambda }_{n}},s} \right)G_{{1k}}^{{Ls}}\left( {{{\lambda }_{n}},s} \right) - \mu {{\lambda }_{n}}{{k}^{2}}G_{{2k}}^{{Lc}}\left( {{{\lambda }_{n}},s} \right) = 2{{\delta }_{{1k}}}\sin {{\lambda }_{n}}\xi \\ - \mu \eta {{k}^{2}}{{\lambda }_{n}}G_{{1k}}^{{Ls}}\left( {{{\lambda }_{n}},s} \right) + {{k}_{2}}\left( {{{\lambda }_{n}},s} \right)G_{{2k}}^{{Lc}}\left( {{{\lambda }_{n}},s} \right) - {{\lambda }_{n}}\sum\limits_{q = 1}^N {{{\alpha }_{q}}G_{{q + 2,k}}^{{Ls}}\left( {{{\lambda }_{n}},s} \right)} = 2{{\delta }_{{2k}}}\cos {{\lambda }_{n}}\xi \\ - {{\Lambda }_{q}}\lambda _{n}^{3}G_{{2k}}^{{Lc}}\left( {{{\lambda }_{n}},s} \right) + {{k}_{{q + 2}}}\left( {{{\lambda }_{n}},s} \right)G_{{q + 2,k}}^{{Ls}}\left( {{{\lambda }_{n}},s} \right) = 2{{\delta }_{{q + 2,k}}}\sin {{\lambda }_{n}}\xi \\ \end{gathered} $
где

(2.5)
${{k}_{1}}\left( {{{\lambda }_{n}},s} \right) = {{s}^{2}} + \mu {{k}^{2}}\lambda _{n}^{2},\quad {{k}_{2}}\left( {{{\lambda }_{n}},s} \right) = {{s}^{2}} + \lambda _{n}^{2} + \mu \eta {{k}^{2}},\quad {{k}_{{q + 2}}}\left( {{{\lambda }_{n}},s} \right) = s + {{\tau }_{q}}{{s}^{2}} + {{D}_{q}}\lambda _{n}^{2}$

Решение системы (2.4) имеет вид [20] ($i = 1,2$, $k,l = 1 \div N + 2$, $l \ne 2$, $p,q = 1 \div N$)

(2.6)
$\begin{gathered} \left\{ \begin{gathered} G_{{il}}^{{Ls}}\left( {{{\lambda }_{n}},\xi ,s} \right) \hfill \\ G_{{q + 2,1}}^{{Ls}}\left( {{{\lambda }_{n}},\xi ,s} \right) \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} {{P}_{{il}}}\left( {{{\lambda }_{n}},s} \right) \hfill \\ {{P}_{{q + 2,1}}}\left( {{{\lambda }_{n}},s} \right) \hfill \\ \end{gathered} \right\}\frac{{2\sin {{\lambda }_{n}}\xi }}{{P\left( {{{\lambda }_{n}},s} \right)}},\quad G_{{k2}}^{{Ls}}\left( {{{\lambda }_{n}},\xi ,s} \right) = \frac{{2{{P}_{{k2}}}\left( {{{\lambda }_{n}},s} \right)\cos {{\lambda }_{n}}\xi }}{{P\left( {{{\lambda }_{n}},s} \right)}} \\ G_{{q + 2,p + 2}}^{{Ls}}\left( {{{\lambda }_{n}},s} \right) = 2\left[ {\frac{{{{\delta }_{{pq}}}}}{{{{k}_{{q + 2}}}}} + \frac{{{{P}_{{q + 2,p + 2}}}\left( {{{\lambda }_{n}},s} \right)}}{{{{Q}_{q}}\left( {{{\lambda }_{n}},s} \right)}}} \right]\sin {{\lambda }_{n}}\xi ,\quad G_{{2k}}^{{Lc}}\left( {0,\xi ,s} \right) = \frac{{2{{\delta }_{{2k}}}}}{{{{s}^{2}}}} \\ \end{gathered} $
где

$\begin{gathered} P\left( {{{\lambda }_{n}},s} \right) = [{{k}_{1}}\left( {{{\lambda }_{n}},s} \right){{k}_{2}}\left( {{{\lambda }_{n}},s} \right) - {{\mu }^{2}}\eta {{k}^{4}}\lambda _{n}^{2}]\Pi \left( {{{\lambda }_{n}},s} \right) - \lambda _{n}^{4}{{k}_{1}}\left( {{{\lambda }_{n}},s} \right)\sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\Lambda }_{j}}{{\Pi }_{j}}\left( {{{\lambda }_{n}},s} \right)} \\ {{Q}_{q}}\left( {{{\lambda }_{n}},s} \right) = {{k}_{{q + 2}}}\left( {{{\lambda }_{n}},s} \right)P\left( {{{\lambda }_{n}},s} \right) \\ {{P}_{{11}}}\left( {{{\lambda }_{n}},s} \right) = {{k}_{2}}\left( {{{\lambda }_{n}},s} \right)\Pi \left( {{{\lambda }_{n}},s} \right) - \lambda _{n}^{4}\sum\limits_{j = 1}^N {{{\alpha }_{j}}{{\Lambda }_{j}}{{\Pi }_{j}}\left( {{{\lambda }_{n}},s} \right)} \\ \end{gathered} $
(2.7)
$\begin{gathered} {{P}_{{12}}}\left( {{{\lambda }_{n}},s} \right) = \mu {{k}^{2}}{{\lambda }_{n}}\Pi \left( {{{\lambda }_{n}},s} \right),\quad {{P}_{{1,q + 2}}}\left( {{{\lambda }_{n}},s} \right) = \mu {{k}^{2}}\lambda _{n}^{2}{{\alpha }_{q}}{{\Pi }_{q}}\left( {{{\lambda }_{n}},s} \right) \\ {{P}_{{21}}}\left( {{{\lambda }_{n}},s} \right) = \mu \eta {{k}^{2}}{{\lambda }_{n}}\Pi \left( {{{\lambda }_{n}},s} \right) \\ \end{gathered} $
$\begin{gathered} {{P}_{{22}}}\left( {{{\lambda }_{n}},s} \right) = {{k}_{1}}\left( {{{\lambda }_{n}},s} \right)\Pi \left( {{{\lambda }_{n}},s} \right),\quad {{P}_{{2,q + 2}}}\left( {{{\lambda }_{n}},s} \right) = {{\alpha }_{q}}{{\lambda }_{n}}{{k}_{1}}\left( {{{\lambda }_{n}},s} \right){{\Pi }_{q}}\left( {{{\lambda }_{n}},s} \right) \\ {{P}_{{q + 2,i}}}\left( {{{\lambda }_{n}},s} \right) = \frac{{{{\Lambda }_{q}}\lambda _{n}^{3}{{P}_{{2i}}}\left( {{{\lambda }_{n}},s} \right)}}{{{{k}_{{q + 2}}}}},\quad {{P}_{{q + 2,p + 2}}}\left( {{{\lambda }_{n}},s} \right) = {{\Lambda }_{q}}\lambda _{n}^{3}{{P}_{{2,p + 2}}}\left( {{{\lambda }_{n}},s} \right)\quad \left( {i = 1,2} \right) \\ \Pi \left( {{{\lambda }_{n}},s} \right) = \prod\limits_{j = 1}^N {{{k}_{{j + 1}}}\left( {{{\lambda }_{n}},s} \right)} ,\quad {{\Pi }_{j}}\left( {{{\lambda }_{n}},s} \right) = \prod\limits_{r = 1,r \ne j}^N {{{k}_{{r + 1}}}\left( {{{\lambda }_{n}},s} \right)} \\ \end{gathered} $

Оригиналы функций Грина в (2.6) определяются следующим образом [20]

(2.8)
$\begin{gathered} \left\{ \begin{gathered} G_{{il}}^{s}\left( {{{\lambda }_{n}},\xi ,\tau } \right) \hfill \\ G_{{q + 2,1}}^{s}\left( {{{\lambda }_{n}},\xi ,\tau } \right) \hfill \\ \end{gathered} \right\} = 2\sum\limits_{j = 1}^{2N + 4} {\left\{ \begin{gathered} A_{{il}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right) \hfill \\ A_{{q + 1,1}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right) \hfill \\ \end{gathered} \right\}{{e}^{{{{s}_{j}}\left( {{{\lambda }_{n}}} \right)\tau }}}\sin {{\lambda }_{n}}\xi } \quad \left( {i = 1,2,\;l = 1 \div N + 2,\;l \ne 2} \right) \\ G_{{k2}}^{s}\left( {{{\lambda }_{n}},\tau } \right) = 2\sum\limits_{j = 1}^{2N + 4} {A_{{k2}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right){{e}^{{{{s}_{j}}\left( {{{\lambda }_{n}}} \right)\tau }}}\cos {{\lambda }_{n}}\xi } ,\quad G_{{2k}}^{c}\left( {0,\xi ,s} \right) = 2{{\delta }_{{2k}}}\tau \quad \left( {k = 1 \div N + 2} \right) \\ G_{{q + 2,p + 2}}^{s}\left( {{{\lambda }_{n}},\tau } \right) = 2\left[ {{{\delta }_{{pq}}}\sum\limits_{i = 1}^2 {\frac{{{{e}^{{{{s}_{{2N + 4 + i}}}\left( {{{\lambda }_{n}}} \right)\tau }}}}}{{1 + 2{{\tau }_{q}}{{s}_{{2N + 4 + i}}}\left( {{{\lambda }_{n}}} \right)}}} + \sum\limits_{j = 1}^{2N + 6} {A_{{q + 2,p + 2}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right){{e}^{{{{s}_{j}}\left( {{{\lambda }_{n}}} \right)\tau }}}} } \right]\sin {{\lambda }_{n}}\xi \\ \end{gathered} $
(2.9)
$A_{{q + 2,i}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right) = \frac{{{{P}_{{q + 2,i}}}\left( {{{\lambda }_{n}},{{s}_{j}}} \right)}}{{P'\left( {{{\lambda }_{n}},{{s}_{j}}} \right)}},\quad A_{{q + 2,p + 2}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right) = \frac{{{{P}_{{q + 2,p + 2}}}\left( {{{\lambda }_{n}},{{s}_{j}}} \right)}}{{{{{Q'}}_{q}}\left( {{{\lambda }_{n}},{{s}_{j}}} \right)}},\quad A_{{ik}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right) = \frac{{{{P}_{{ik}}}\left( {{{\lambda }_{n}},{{s}_{j}}} \right)}}{{P'\left( {{{\lambda }_{n}},{{s}_{j}}} \right)}}$

Здесь ${{s}_{j}}\left( {{{\lambda }_{n}}} \right)$ $\left( {j = 1 \div 2N + 4} \right)$ – нули полинома $P\left( {{{\lambda }_{n}},s} \right)$, остальные ${{s}_{j}}\left( {{{\lambda }_{n}}} \right)$ являются дополнительными нулями многочлена ${{Q}_{q}}\left( {{{\lambda }_{n}},s} \right)$

${{s}_{{2N + 5}}}\left( {{{\lambda }_{n}}} \right) = \frac{{ - 1 - \sqrt {1 - 4{{\tau }_{q}}D_{1}^{{\left( q \right)}}\lambda _{n}^{2}} }}{{2{{\tau }_{q}}}},\quad {{s}_{{2N + 6}}}\left( {{{\lambda }_{n}}} \right) = \frac{{ - 1 + \sqrt {1 - 4{{\tau }_{q}}D_{1}^{{\left( q \right)}}\lambda _{n}^{2}} }}{{2{{\tau }_{q}}}}$

Подставляя найденные выражения для функций Грина (2.8) и (2.9) в свертки (2.1) получаем решение задачи об изгибе балки Тимошенко (1.11), (1.10), (1.12).

3. Расчетный пример. Для расчетного примера возьмем дюралюминиевый стержень длины $l = {{10}^{{ - 1}}}$ м, прямоугольного сечения $h \times b = 0.1l \times 0.05l$. Дюралюминий рассматриваем как двухкомпонентный материал, (N = 2) физические характеристики которого [24] после применения процедуры обезразмеривания (1.3) следующие:

(3.1)
$\begin{gathered} \lambda = 4.92 \times {{10}^{{ - 1}}},\quad \mu = 2.54 \times {{10}^{{ - 1}}},\quad {{\alpha }_{1}} = 1.50 \times {{10}^{{ - 4}}},\quad {{\alpha }_{2}} = 5.92 \times {{10}^{{ - 4}}} \\ {{D}_{1}} = 1.27 \times {{10}^{{ - 16}}},\quad {{D}_{2}} = 5.02 \times {{10}^{{ - 21}}},\quad {{\Lambda }_{1}} = 2.77 \times {{10}^{{ - 18}}},\quad {{\Lambda }_{2}} = 5.50 \times {{10}^{{ - 23}}} \\ \end{gathered} $

Обезразмеренные геометрические характеристики сечения равны:

$F = 5.00 \times {{10}^{{ - 3}}},\quad {{J}_{3}} = 4.16 \times {{10}^{{ - 6}}}$

В уравнениях (1.11) полагаем

(3.2)
${{F}_{1}}\left( {x,\tau } \right) = \frac{{q\left( {x,\tau } \right)}}{F} = H\left( x \right)H\left( \tau \right),\quad {{F}_{2}}\left( {x,\tau } \right) = \frac{{m\left( {x,\tau } \right)}}{{{{J}_{3}}}} = 0,\quad {{F}_{{q + 2}}}\left( {x,\tau } \right) = \frac{{{{z}^{{\left( q \right)}}}}}{{{{J}_{3}}}} = 0$

Вычисляя свертки (2.1) с учетом равенств (2.8), получаем

$\begin{gathered} {v}\left( {x,\tau } \right) = \int\limits_0^\tau {\int\limits_0^1 {{{G}_{{11}}}\left( {x,\xi ,\tau - t} \right){{F}_{1}}\left( {\xi ,t} \right)d\xi } dt} = \\ \, = 2\sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^{2N + 4} {[1 - {{{\left( { - 1} \right)}}^{n}}]\frac{{({{e}^{{{{s}_{j}}\left( {{{\lambda }_{n}}} \right)\tau }}} - 1)A_{{11}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right)}}{{{{\lambda }_{n}}{{s}_{j}}\left( {{{\lambda }_{n}}} \right)}}} } \sin {{\lambda }_{n}}x \\ \end{gathered} $
(3.3)
$\begin{gathered} \chi \left( {x,\tau } \right) = \int\limits_0^\tau {\int\limits_0^1 {{{G}_{{21}}}\left( {x,\xi ,\tau - t} \right){{F}_{1}}\left( {\xi ,t} \right)d\xi } dt} = \\ \, = 2\sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^{2N + 4} {[1 - {{{\left( { - 1} \right)}}^{n}}]\frac{{({{e}^{{{{s}_{j}}\left( {{{\lambda }_{n}}} \right)\tau }}} - 1)A_{{21}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right)}}{{{{\lambda }_{n}}{{s}_{j}}\left( {{{\lambda }_{n}}} \right)}}} } \cos {{\lambda }_{n}}x \\ \end{gathered} $
$\begin{gathered} {{H}_{q}}\left( {x,\tau } \right) = \int\limits_0^\tau {\int\limits_0^1 {{{G}_{{q + 2,1}}}\left( {x,\xi ,\tau - t} \right){{F}_{1}}\left( {\xi ,t} \right)d\xi } dt} = \\ \, = 2\sum\limits_{n = 1}^\infty {\sum\limits_{j = 1}^{2N + 4} {[1 - {{{\left( { - 1} \right)}}^{n}}]\frac{{({{e}^{{{{s}_{j}}\left( {{{\lambda }_{n}}} \right)\tau }}} - 1)A_{{q + 2,1}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right)}}{{{{\lambda }_{n}}{{s}_{j}}\left( {{{\lambda }_{n}}} \right)}}} } \sin {{\lambda }_{n}}x \\ \end{gathered} $

Полагая коэффициенты ${{\alpha }_{q}}$, связывающие механическое и диффузионные поля, равными нулю, приходим к решению классической упругой задачи для балки Тимошенко. В этом случае равенства (2.7) с учетом (2.5) запишутся так

$P\left( {{{\lambda }_{n}},s} \right) = {{s}^{4}} + (\lambda _{n}^{2} + \mu {{k}^{2}}\lambda _{n}^{2} + \mu \eta {{k}^{2}}){{s}^{2}} + \mu {{k}^{2}}\lambda _{n}^{4},\quad {{P}_{{11}}}\left( {{{\lambda }_{n}},s} \right) = {{s}^{2}} + \lambda _{n}^{2} + \mu \eta {{k}^{2}}$
${{P}_{{12}}}\left( {{{\lambda }_{n}},s} \right) = \mu {{k}^{2}}{{\lambda }_{n}},\quad {{P}_{{21}}}\left( {{{\lambda }_{n}},s} \right) = \mu \eta {{k}^{2}}{{\lambda }_{n}},\quad {{P}_{{22}}}\left( {{{\lambda }_{n}},s} \right) = {{s}^{2}} + \mu {{k}^{2}}\lambda _{n}^{2}$

Многочлен $P\left( {{{\lambda }_{n}},s} \right)$ является биквадратным относительно параметра $s$ и его нули определяются по формулам

${{s}_{j}}\left( {{{\lambda }_{n}}} \right) = \frac{{ - \lambda _{n}^{2} + \mu {{k}^{2}}\lambda _{n}^{2} + \mu \eta {{k}^{2}} \pm \sqrt {{{{(\lambda _{n}^{2} + \mu {{k}^{2}}\lambda _{n}^{2} + \mu \eta {{k}^{2}})}}^{2}} - 4\mu {{k}^{2}}\lambda _{n}^{4}} }}{2}$

Тогда, в соответствии с (2.9) для коэффициентов $A_{{ik}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right)$ получаем

(3.4)
$A_{{ik}}^{{\left( j \right)}}\left( {{{\lambda }_{n}}} \right) = {{\left. {\frac{{{{P}_{{ik}}}\left( {{{\lambda }_{n}},s} \right)}}{{2s(2{{s}^{2}} + \lambda _{n}^{2} + \mu \eta {{k}^{2}} + \mu {{k}^{2}}\lambda _{n}^{2})}}} \right|}_{{s = {{s}_{j}}}}}\quad (j = \overline {1,4} )$

Прогибы ${v}$ и повороты сечений χ по-прежнему определяются с помощью формул (3.3) с учетом поправочных равенств (3.4), при N = 0.

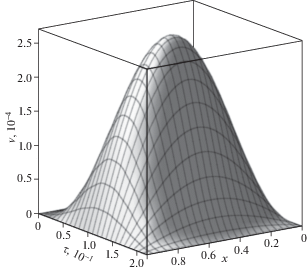
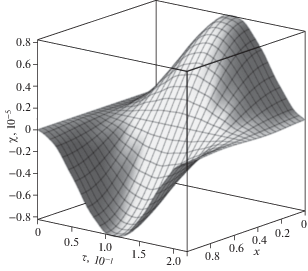
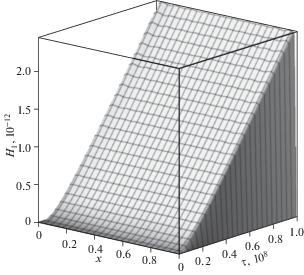
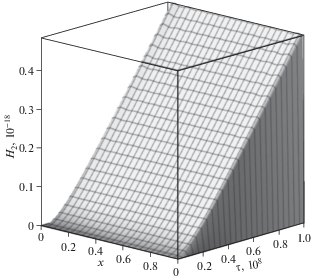
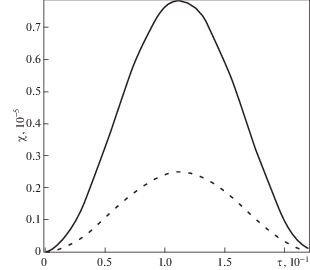
Результаты вычислений продемонстрированы на рисунках 2–7. На рис. 2 изображено пространственно-временное распределение прогибов балки под действием распределенной поперечной нагрузки (3.2). На следующих рисунках показаны зависимости от времени и продольной координаты поворотов сечений (рис. 3) и приращений концентраций первого компонента (рис. 4) и второго (рис. 5) в составе двухкомпонентной среды (3.1).

Рис. 2
Рис. 3
Рис. 4
Рис. 5
Рис. 6
Рис. 7

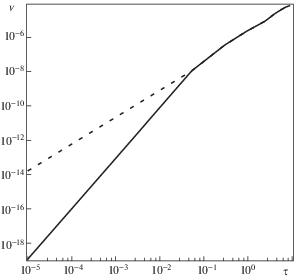
На рисунках 6 и 7 проиллюстрировано сравнение решений упругодиффузионной задачи (3.3) с решением чисто упругой задачи при x = 0.1. Сплошная линия на обоих рисунках соответствует решению (3.3), пунктирная – решению упругой задачи. На рис. 6 видно, что в рамках построенной модели упругодиффузионных колебаний балки Тимошенко массоперенос влияет на прогибы только в самые начальные моменты времени $\tau \sim {{10}^{{ - 1}}}$. В противоположность этому, диффузионные процессы существенно влияют на повороты сечений. Продемонстрированное на рис. 7 отличие сохраняется для сколь угодно больших временных промежутков.

Заключение. Таким образом, в работе получена связанная нестационарная упругодиффузионная модель балки Тимошенко. Предложен алгоритм построения объемных функций Грина и решена задача о нестационарных упругодиффузионных колебаниях балки под действием распределенной поперечной нагрузки. На основе разработанной модели и рассмотренного примера исследовано взаимодействие механического и диффузионного полей. Сравнительный анализ показывает влияние массопереноса на поле перемещений внутри балки в сторону увеличения углов поворотов поперечных сечений при изгибе.

Работа выполнена при финансовой поддержке Российского научного фонда (проект 20-19-00217).

Список литературы

  1. Afram A.Y., Khader S.E. 2D Problem for a Half-Space under the Theory of Fractional Thermoelastic Diffusion // American journal of scientific and industrial research, 2014. V. 6. № 3. P. 47–57.

  2. Aouadi M.A generalized thermoelastic diffusion problem for an infinitely long solid cylinder // Intern. J. Mathem. and Mathem. Sci. 2006. V. 2006. P. 1–15.

  3. Atwa S.Y., Egypt Z. Generalized Thermoelastic Diffusion With Effect of Fractional Parameter on Plane Waves Temperature-Dependent Elastic Medium // Journal of Materials and Chemical Engineering. 2013. V. 1. Is. 2. P. 55–74.

  4. Belova I.V., Murch G.E. Thermal and diffusion-induced stresses in crystalline solids // Journal of Applied Physics. 1995. V. 77. № 1. P. 127–134.

  5. Deswal S., Kalkal K. A two-dimensional generalized electro-magneto-thermoviscoelastic problem for a half-space with diffusion // International Journal of Thermal Sciences. 2011. V. 50. № 5. P.  749–759.

  6. Elhagary M.A. Generalized thermoelastic diffusion problem for an infinitely long hollow cylinder for short times // Acta Mech. 2011. V. 218. P. 205–215.

  7. Indeitsev D.A., Semenov B.N., Sterlin M.D. The Phenomenon of Localization of Diffusion Process in a Dynamically Deformed Solid // Doklady Physics. 2012. V. 57. № 4. P. 171–173.

  8. Knyazeva A.G. Model of medium with diffusion and internal surfaces and some applied problems // Mater. Phys. Mech. 2004. V. 7. № 1. P. 29–36.

  9. Kumar R., Chawla V. A Study of Fundamental Solution in Orthotropic Thermodiffusive Elastic Media // International Communication in Heat and Mass Transfer. 2011. V. 38. P. 456–462.

  10. Sherief H.H., El-Maghraby N.M. A Thick Plate Problem in the Theory of Generalized Thermoelastic Diffusion // Int. J. Thermophys. 2009. V. 30. P. 2044–2057.

  11. Раврик М.С. Об одной вариационной формуле смешанного типа для контактных задач термодиффузийной теории деформации слоистых оболочек // Мат. мет. та фіз.-мех. поля. 1985. Т. 22. С. 40–44.

  12. Раврик М.С., Бичуя А.Л. Осесимметричное напряженное состояние нагретой трансверсально-изотропной сферической оболочки с круговым отверстием при диффузионном насыщении // Мат. методи і фіз.-мех. поля. 1983. Вып. 17. С. 51–54.

  13. Швец Р.Н., Флячок В.М. Вариационный подход к решению динамических задач механотермодиффузии анизотропных оболочек // Мат. физ. и нелинейн. мех. 1991. № 16. С. 39–43. Shvets R.N., Flyachok V.M. The equations of mechanothermodiffusion of anisotropic shells taking account of transverse strains // Mat. Met. Fiz.-Mekh. Polya. 1984. № 20. P. 54–61.

  14. Aouadi M., Copetti M.I.M. Analytical and numerical results for a dynamic contact problem with two stops in thermoelastic diffusion theory // ZAMM Z. Angew. Math. Mech. 2015. P. 1–24.

  15. Copetti M.I.M., Aouadi M. A quasi-static contact problem in thermoviscoelastic diffusion theory // Applied Numerical Mathematics. 2016. V. 109. P. 157–183

  16. Aouadi M. On thermoelastic diffusion thin plate theory // Appl. Math. Mech.-Engl. Ed. 2015. V. 36. № 5. P. 619–632.

  17. Aouadi M., Miranville A. Smooth attractor for a nonlinear thermoelastic diffusion thin plate based on Gurtin–Pipkin’s model // Asymptotic Analysis. 2015. V. 95. P. 129–160

  18. Zemskov A.V., Tarlakovskii D.V. Unsteady Vibration Model of the Euler-Bernoulli Beam Taking into Account Diffusion // Journal of Physics: Conference Series. 2019. V. 1158. 042043.

  19. Tarlakovskii D.V., Zemskov A.V. An Elastodiffusive Orthotropic Euler-Bernoulli Beam with Considering Diffusion Flux Relaxation // Math. Comput. Appl. 2019. V. 24. Is. 1. 23.

  20. Gafurov U.S., Afanasieva O.A., Zemskov A.V. Unsteady elastic diffusion oscillations of a Timoshenko beam with considering the diffusion relaxation effects // Proceedings of the second International Conference on Theoretical, Applied and Experimental Mechanics. Springer Nature Switzerland AG. 2019. P. 193–199.

  21. Davydov S.A., Zemskov A.V. Unsteady One-dimensional Perturbations in Multicomponent Thermoelastic Layer with Cross-diffusion Effect. Journal of Physics: Conference Series. 2018. V. 1129. 012009.

  22. Михайлова Е.Ю., Тарлаковский Д.В., Федотенков Г.В. Общая теория упругих оболочек. М.: МАИ, 2018. 112 с.

  23. Горшков А.Г., Медведский А.Л., Рабинский Л.Н., Тарлаковский Д.В. Волны в сплошных средах. М.: Физматлит, 2004. 472 с.

  24. Физические величины: Справочник / Бабичев А.П., Бабушкина Н.А., Братковский А.М. и др. Под общей редакцией Григорьева И.С., Мелихова И.З. М.: Энергоатомиздат, 1991. 1232 с.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал