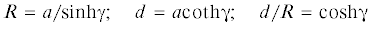1. На главную
  2. Электронные версии
  3. Известия РАН. Механика твердого тела
  4. № 5, 2020

Известия РАН. Механика твердого тела, 2020, № 5, стр. 95-106

ВЛИЯНИЕ ПОВЕРХНОСТНЫХ ЭФФЕКТОВ В ЗАДАЧАХ ТЕОРИИ УПРУГОСТИ ДЛЯ ОБЛАСТЕЙ, ОГРАНИЧЕННЫХ НЕКОНЦЕНТРИЧЕСКИМИ ОКРУЖНОСТЯМИ

Д. В. Гандилян a, *, К. Б. Устинов a, **

a Институт проблем механики им. А.Ю. Ишлинского РАН
Москва, Россия

* E-mail: david.ghandilyan@mail.ru
** E-mail: ustinov@ipmnet.ru

Поступила в редакцию 03.02.2020
После доработки 10.03.2020
Принята к публикации 20.04.2020

Полный текст (PDF)

Аннотация

В работе рассмотрены некоторые задачи теории упругости для областей, ограниченных неконцентрическими окружностями, с учетом поверхностных эффектов, таких как поверхностная упругость и поверхностные напряжения. Решения получены путем разложения в ряды Фурье переменных, записанных в биполярной системе координат. Интересующие величины поверхностных напряжений и концентраций напряжений получены с использованием рекуррентных соотношений. Рассмотрен вклад, вносимый поверхностными эффектами.

Ключевые слова: поверхностная упругость, поверхностное напряжение, биполярная система координат, ряды Фурье

Введение. Механические свойства тел вблизи поверхности могут существенно отличаться от свойств вещества вдали от поверхности в силу ряда причин – начиная от отличия в химических связях для приповерхностных атомов и наличия свободных радикалов, до присутствия оксидных пленок (напр., [1–3]). При рассмотрении объектов малых размеров (порядка микро- и нанометров) роль поверхностных эффектов возрастает. Удобным способом учета поверхностных явлений является использование наряду с уравнениями теории упругости уравнений поверхностной упругости [4]. Достаточно общий метод решения задач теории упругости с учетом поверхностных эффектов заключается в использовании специфических граничных условий, соответствующих уравнениям поверхностной упругости. Данный метод для двумерного случая в сочетании с применением методов теории функции комплексного переменного был развит в работах [5, 6]. Следует отметить, что количество полученных аналитических решений для конкретных задач ограничено, что может быть связано с довольно неудобным видом граничных условий. Большинство полученных решений ограничено достаточно простыми геометриями, такими как сферическая пора [7–10], плоскость с одиночным круговым отверстием [11], одиночная пластина [12]. Однако рассмотрение одиночных круговых (в двумерном случае) и сферических (в трехмерном) отверстий наименее интересно с точки зрения влияния поверхностных эффектов, поскольку в этих случаях их вклад минимален. В данной работе рассмотрены задачи: о двух равных круговых отверстиях в плоскости и об эксцентрической трубе под действием равномерного давления. Несмотря на достаточно простую геометрию, из-за малого расстояния между границами можно ожидать более существенного вклада от поверхностных эффектов.

Для всех рассматриваемых случаев среды предполагаются линейно упругими, свойства которых определяются постоянными Ламе: λ, μ при этом ${{{\lambda }}_{{\text{s}}}}$, ${{{\mu }}_{{\text{s}}}}$ – постоянные, характеризующие аналогичные поверхностные свойства.

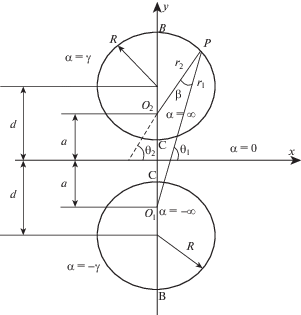
1. Задача о двух круглых отверстиях в плоскости. 1.1. Биполярная система координат. Основные уравнения. Задача о пластине с двумя отверстиями в случае классической упругости была решена Лингом [14] с использованием общего решения Джеффри [13]. Ниже будет получено обобщение данного решения, учитывающее поверхностные эффекты. Следуя [13], введем биполярные координаты (α, β), связанные с декартовыми координатами (x, y) следующим образом:

(1.1)
$x + iy = - a\coth \left( {i\frac{{{\alpha } + i{\beta }}}{2}} \right);\quad {\alpha } + i{\beta } = \ln \left( {\frac{{x + i\left( {y + a} \right)}}{{x + i\left( {y - a} \right)}}} \right)$

Полюсы O1, O2 расположены на расстоянии 2a друг от друга. Масштабный коэффициент определяется как

(1.2)
$g = 1{\text{/}}\sqrt {{{{\left( {\frac{{\partial x}}{{\partial {\alpha }}}} \right)}}^{2}} + {{{\left( {\frac{{\partial y}}{{\partial {\alpha }}}} \right)}}^{2}}} = \frac{{\cosh {\alpha } - \cos {\beta }}}{a}$

Для любой точки P, расположенной на расстоянии r1, r2 от точек O1, O2, так что их радиус-векторы образуют углы ${{{\theta }}_{1}},~{{{\theta }}_{2}}$ с осью x биполярные координаты суть

(1.3)
${\alpha } = \ln \frac{{{{r}_{1}}}}{{{{r}_{2}}}};\quad {\beta } = {{{\theta }}_{1}} - {{{\theta }}_{2}}$

Линии ${\alpha } = {\text{const}}$ представляют собой набор окружностей с центрами на оси Oy. Окружности, соответствующие положительным значениям α, лежат выше оси Ox, а отрицательным – ниже оси Ox, сама ось Ox соответствует значению α = 0 (рис. 1).

Рис. 1

Линии ${\beta } = {\text{const}}$ представляют собой дуги окружностей, проходящих через точки O1, O2 и ортогональные окружностям ${\alpha } = {\text{const}}$. С правой стороны от оси Oy ${\beta } > 0$, а с левой стороны – ${\beta } < 0$, ось Oy соответствует значению β = 0, за исключением сегмента O1, O2, где ${\beta } = \pm \pi $. В точках O1, O2 – ${\alpha } = \pm \infty $, а β неопределенно.

Будем полагать, что постоянное значение ${\alpha } = \pm {\gamma }$ соответствует контурам отверстий, тогда для радиуса отверстий R и расстояния между центрами отверстий 2d имеют место следующие соотношения

(1.4)

Компоненты тензора напряжений σij выражаются через бигармоническую функцию напряжений Φ(α, β) следующим образом:

(1.5)
${{\Delta }^{2}}{\Phi } = 0;\quad \left[ {\frac{{{{\partial }^{4}}}}{{\partial {{{\alpha }}^{4}}}} + 2\frac{{{{\partial }^{4}}}}{{\partial {{{\alpha }}^{2}}\partial {{{\beta }}^{2}}}} + \frac{{{{\partial }^{4}}}}{{\partial {{{\beta }}^{4}}}} - 2\frac{{{{\partial }^{2}}}}{{\partial {{{\alpha }}^{2}}}} + 2\frac{{{{\partial }^{2}}}}{{\partial {{{\beta }}^{2}}}} + 1} \right]\left( {g{\Phi }} \right) = 0$
$a{{{\sigma }}_{{{\alpha \alpha }}}} = \left[ {\left( {\cosh {\alpha } - \cos {\beta }} \right)\frac{{{{\partial }^{2}}}}{{\partial {{{\beta }}^{2}}}} - \sinh {\alpha }\frac{\partial }{{\partial {\alpha }}} - \sin {\beta }\frac{\partial }{{\partial {\beta }}} + \cosh {\alpha }} \right]\left( {g{\Phi }} \right)$
(1.6)
$a{{{\sigma }}_{{{\beta \beta }}}} = \left[ {\left( {\cosh {\alpha } - \cos {\beta }} \right)\frac{{{{\partial }^{2}}}}{{\partial {{{\alpha }}^{2}}}} - \sinh {\alpha }\frac{\partial }{{\partial {\alpha }}} - \sin {\beta }\frac{\partial }{{\partial {\beta }}} + \cos {\beta }} \right]\left( {g{\Phi }} \right)$
$a{{{\sigma }}_{{{\alpha \beta }}}} = - \left( {\cosh {\alpha } - \cos {\beta }} \right)\frac{{{{\partial }^{2}}}}{{\partial {\alpha }\partial {\beta }}}\left( {g{\Phi }} \right)$

Функция напряжения Φ(α,β) представляется в виде суммы [14]

$g{\Phi } = g{{{\Phi }}_{0}} + apgF$
где функция Φ0 соответствует заданным напряжениям на бесконечности, а функция F снимает усилия, возникающие от функции Φ0 на контурах отверстий. В частности, в случае всестороннего растяжения функция Φ(α, β) имеет вид

(1.7)
$\frac{{g{\Phi }}}{{ap}} = \frac{1}{2}(\cosh {\alpha } + \cos {\beta }) + K(\cosh {\alpha } - \cos {\beta })\ln (\cosh {\alpha } - \cos {\beta }) + \mathop \sum \limits_{n = 1}^\infty {{f}_{n}}\left( {\alpha } \right)\cos n{\beta }$
(1.8)
${{f}_{n}}({\alpha }) = {{A}_{n}}\cosh (n + 1){\alpha } + {{B}_{n}}\cosh (n - 1){\alpha }$

В дополнении к (1.7) должно выполняться условие

(1.9)
$\mathop \sum \limits_{n = 1}^\infty \left( {{{A}_{n}} + {{B}_{n}}} \right) = 0$
что соответствует условию gF на бесконечности (т.е. при ${\alpha } = {\beta } = 0$).

Для удовлетворения граничных условий на контуре (из-за симметрии достаточно рассмотреть только один контур α = γ) представим напряжения на контуре в виде рядов Фурье, которые в случае указанной симметрии имеют вид

$a{{{\sigma }}_{{{\alpha \alpha }}}} = {{c}_{0}} + \mathop \sum \limits_{n = 1}^\infty {{c}_{n}}\cos n{\beta }$
(1.10)
$a{{{\sigma }}_{{{\alpha \beta }}}} = \mathop \sum \limits_{n = 1}^\infty {{b}_{n}}\sin n{\beta }$
$a{{{\sigma }}_{{{\beta \beta }}}} = {{d}_{0}} + \mathop \sum \limits_{n = 1}^\infty {{d}_{n}}\cos n{\beta }$
где коэффициенты ck, bk, dk выражаются через параметры An, Bn, K.

1.2. Постановка задачи. Граничные условия. В общем случае граничные условия описываются обобщенным законом Лапласа–Юнга и имеют вид [16]

(1.11)
${\mathbf{\sigma }} \cdot {\mathbf{n}} = - {{\nabla }_{s}}{{{\mathbf{\sigma }}}^{s}}$
где σ – тензор объемных напряжений, n – вектор нормали к поверхности, ${{{\mathbf{\sigma }}}^{s}}$ – тензор поверхностных напряжений, ${{\nabla }_{s}}$ – поверхностный градиент [16]. В случае криволинейной поверхности ${{\nabla }_{s}}{{{\mathbf{\sigma }}}^{s}}$ выражается следующим образом
${{\nabla }_{s}}{{{\mathbf{\sigma }}}^{s}} = - \left[ {\frac{{{\sigma }_{{11}}^{s}}}{{{{R}_{1}}}} + \frac{{{\sigma }_{{22}}^{s}}}{{{{R}_{2}}}}} \right] + $
(1.12)
$ + \frac{{{{{\mathbf{e}}}_{1}}}}{{{{h}_{1}}{{h}_{2}}}}\left[ {\frac{{\partial ({{h}_{2}}{\sigma }_{{11}}^{s})}}{{\partial {{{\alpha }}_{1}}}} + \frac{{\partial ({{h}_{1}}{\sigma }_{{21}}^{s})}}{{\partial {{{\alpha }}_{2}}}} + \frac{{\partial {{h}_{1}}}}{{\partial {{{\alpha }}_{2}}}}{\sigma }_{{12}}^{s} - \frac{{\partial {{h}_{2}}}}{{\partial {{{\alpha }}_{1}}}}{\sigma }_{{22}}^{s}} \right] + $
$ + \frac{{{{{\mathbf{e}}}_{2}}}}{{{{h}_{1}}{{h}_{2}}}}\left[ {\frac{{\partial ({{h}_{1}}{\sigma }_{{22}}^{s})}}{{\partial {{{\alpha }}_{2}}}} + \frac{{\partial ({{h}_{2}}{\sigma }_{{12}}^{s})}}{{\partial {{{\alpha }}_{1}}}} + \frac{{\partial {{h}_{2}}}}{{\partial {{{\alpha }}_{1}}}}{\sigma }_{{21}}^{s} - \frac{{\partial {{h}_{1}}}}{{\partial {{{\alpha }}_{2}}}}{\sigma }_{{11}}^{s}} \right]~$
где R1, R2 – радиусы кривизны, h1, h2 – метрические коэффициенты, e1, e2 – орты криволинейной системы координат (α1, α2), также α1, α2 являются двумя параметрами, определяющими поверхность так, что при ${{{\alpha }}_{1}} = {\text{const}}$, ${{{\alpha }}_{2}} = {\text{const}}$ получаем два набора взаимно ортогональных кривых на поверхности. Для рассматриваемого случая, когда поверхность образована окружностью (цилиндром), при α = γ в биполярной (бицилиндрической) системе координат (1.11), имеем [17]

(1.13)
${{{\alpha }}_{1}} = {\alpha };\quad {{{\alpha }}_{2}} = z;\quad {{R}_{1}} = R;\quad 1{\text{/}}{{R}_{2}} = 0;\quad {{h}_{1}} = 1{\text{/}}g;\quad {{h}_{2}} = 1{\text{\;}}~$
(1.14)
$\begin{gathered} {{{\sigma }}_{{{\alpha \alpha }}}} = \frac{1}{R}{\sigma }_{{{\beta \beta }}}^{s} \\ {{{\sigma }}_{{{\alpha \beta }}}} = \frac{1}{R}\frac{{\cosh {\alpha } - \cos {\beta }}}{{\sinh {\alpha }}}\frac{{\partial {\sigma }_{{{\beta \beta }}}^{s}}}{{\partial {\beta }}} \\ \end{gathered} $

Второе уравнение (1.14) с помощью первого уравнения представляется в виде

(1.15)
${{{\sigma }}_{{{\alpha \beta }}}} = \frac{{\cosh {\alpha } - \cos {\beta }}}{{\sinh {\alpha }}}\frac{{\partial {{{\sigma }}_{{{\alpha \alpha }}}}}}{{\partial {\beta }}}$

Однако поверхностное напряжение ${\sigma }_{{{\beta \beta }}}^{s}$ все еще неизвестно. Чтобы получить граничные условия, выразим поверхностное напряжение через определяющие соотношения (Законы Гука и Шаттлворса):

(1.16)
${\sigma }_{{{\beta \beta }}}^{s} = C_{{{\beta \beta \beta \beta }}}^{s}{{\epsilon }_{{{\beta \beta }}}};\quad {{\epsilon }_{{{\beta \beta }}}} = \frac{1}{E}\left[ {{{{\sigma }}_{{{\beta \beta }}}} - {\nu }{{{\sigma }}_{{{\alpha \alpha }}}}} \right]$
где $C_{{{\beta \beta \beta \beta }}}^{s}$ – модуль поверхностной упругости, ${{\epsilon }_{{{\beta \beta }}}}$ – окружная поверхностная деформация, E, ν – модуль Юнга и коэффициент Пуассона. Отсюда следует

(1.17)
$\frac{{{\sigma }_{{{\beta \beta }}}^{s}}}{R} = {\varepsilon }[{{{\sigma }}_{{{\beta \beta }}}} - {\nu }{{{\sigma }}_{{{\alpha \alpha }}}}];\quad {\varepsilon } = \frac{{C_{{{\beta \beta \beta \beta }}}^{s}}}{{ER}}$

С учетом (1.17) граничные условия (1.14), (1.15) переписываются следующим образом

(1.18)
${{{\sigma }}_{{{\alpha \alpha }}}} = {\varepsilon }\left[ {{{{\sigma }}_{{{\beta \beta }}}} - {\nu }{{{\sigma }}_{{{\alpha \alpha }}}}} \right]$
(1.19)
${{{\sigma }}_{{{\alpha \beta }}}} = {\varepsilon }\frac{{\cosh {\alpha } - \cos {\beta }}}{{\sinh {\alpha }}}\frac{\partial }{{\partial {\beta }}}\left[ {{{{\sigma }}_{{{\beta \beta }}}} - {\nu }{{{\sigma }}_{{{\alpha \alpha }}}}} \right]$

Решение указанной задачи может быть получено путем приравнивания коэффициентов при синусах и косинусах β, что однако приводит к довольно сложным манипуляциям с рядами. Альтернативный способ заключается в разложении всех функций по малому параметру ε:

(1.20)
${{{\sigma }}_{{ij}}} = \mathop \sum \limits_{m = 1}^N {{{\varepsilon }}^{m}}{{{\sigma }}_{{ij}}};\quad b = \mathop \sum \limits_{m = 1}^N {{{\varepsilon }}^{m}}{{b}^{m}};\quad c = \mathop \sum \limits_{m = 1}^N {{{\varepsilon }}^{m}}{{c}^{m}};\quad d = \mathop \sum \limits_{m = 1}^N {{{\varepsilon }}^{m}}{{d}^{m}}$

Теперь, приравнивая члены с равными степенями при ε, получаем рекуррентные системы для граничных условий

${\sigma }_{{{\alpha \alpha }}}^{{\left( 0 \right)}} = 0;\quad {\sigma }_{{{\alpha \beta }}}^{{\left( 0 \right)}} = 0$
(1.21)
${\sigma }_{{{\alpha \alpha }}}^{{\left( 1 \right)}} = {\sigma }_{{{\beta \beta }}}^{{\left( 0 \right)}};\quad {\sigma }_{{{\alpha \beta }}}^{{\left( 1 \right)}} = \frac{{\cosh {\alpha } - \cos {\beta }}}{{\sinh {\alpha }}}\frac{\partial }{{\partial {\beta }}}{\sigma }_{{{\beta \beta }}}^{{\left( 0 \right)}}$
${\sigma }_{{{\alpha \alpha }}}^{{\left( m \right)}} = [{\sigma }_{{{\beta \beta }}}^{{\left( {m - 1} \right)}} - {\nu \sigma }_{{{\alpha \alpha }}}^{{\left( {m - 1} \right)}}];\quad {\sigma }_{{{\alpha \beta }}}^{{\left( m \right)}} = \frac{{\cosh {\alpha } - \cos {\beta }}}{{\sinh {\alpha }}}\frac{\partial }{{\partial {\beta }}}[{\sigma }_{{{\beta \beta }}}^{{\left( {m - 1} \right)}} - {\nu \sigma }_{{{\alpha \alpha }}}^{{\left( {m - 1} \right)}}],\quad m \geqslant 1$

1.3. Нулевое приближение (классическая упругость). В случае нулевых правых частей в (1.11), что соответствует случаю классической упругости, решение [14] имеет вид

$A_{n}^{{\left( 0 \right)}} = 2{{K}^{{\left( 0 \right)}}}\frac{{({{e}^{{ - n{\gamma }}}}\sinh \left( {n{\gamma }} \right) + n{{e}^{{ - {\gamma }}}}\sinh {\gamma })}}{{n\left( {n + 1} \right)\left( {n\sinh 2{\gamma } + \sinh \left( {2n\gamma } \right)} \right)}},\quad n \geqslant 1$
(1.22)
$\begin{gathered} B_{n}^{{\left( 0 \right)}} = - 2{{K}^{{\left( 0 \right)}}}\frac{{({{e}^{{ - n{\gamma }}}}\sinh \left( {n{\gamma }} \right) + n{{e}^{{\gamma }}}\sinh {\gamma })}}{{n\left( {n - 1} \right)\left( {n\sinh 2{\gamma } + \sinh \left( {2n\gamma } \right)} \right)}},\quad n \geqslant 2 \\ B_{1}^{{\left( 0 \right)}} = - 1 + \frac{{{{K}^{{\left( 0 \right)}}}}}{2}\tanh {\gamma }\cosh 2{\gamma } \\ \end{gathered} $
${{K}^{{\left( 0 \right)}}} = {{\left( {\frac{1}{2} + \tanh {\gamma }{{{\sinh }}^{2}}{\gamma } - 4\mathop \sum \limits_{n = 2}^{ + \infty } \frac{{{{e}^{{ - n{\gamma }}}}\sinh \left( {n{\gamma }} \right) + n\sinh {\gamma }\left( {n\sinh {\gamma } + \cosh {\gamma }} \right)}}{{n({{n}^{2}} - 1)\left( {n\sinh 2{\gamma } + \sinh \left( {2n\gamma } \right)} \right)}}} \right)}^{{ - 1}}}$

Здесь коэффициенты отмечены верхним индексом 0 соответствуют классическому решению при отсутствии поверхностной упругости. Они также служат нулевым приближением в разложении по параметру ε соответствующих решений задачи, учитывающей поверхностную упругость.

1.4. Рекуррентное решение. В разделе 1.2 посредством (1.21) рассматриваемая задача сводится к набору последовательных задач для каждого члена разложения по малому параметру ε.

Действительно, зная (m – 1)-е решение для компонент напряжения (т.е. зная $A_{n}^{{\left( {m - 1} \right)}}$, $B_{n}^{{\left( {m - 1} \right)}}$, ${{K}^{{\left( {m - 1} \right)}}}$), аналогично (1.10) с помощью (1.6), (1.7) получаем

(1.23)
$a{\sigma }_{{{\alpha \alpha }}}^{{\left( {m - 1} \right)}} = c_{0}^{{\left( {m - 1} \right)}} + \mathop \sum \limits_{n = 1}^\infty c_{n}^{{\left( {m - 1} \right)}}\cos n{\beta };\quad a{\sigma }_{{{\beta \beta }}}^{{\left( {m - 1} \right)}} = d_{0}^{{\left( {m - 1} \right)}} + \mathop \sum \limits_{n = 1}^\infty d_{n}^{{\left( {m - 1} \right)}}\cos n{\beta }$
где $c_{n}^{{\left( {m - 1} \right)}}$, $d_{n}^{{\left( {m - 1} \right)}}$ имеют вид
$c_{0}^{{(m - 1)}} = B_{1}^{{(m - 1)}} + A_{1}^{{(m - 1)}}\cosh 2{\gamma } - \frac{1}{2}{{K}^{{(m - 1)}}}\cosh 2{\gamma }$
$c_{n}^{{(m - 1)}} = {{\delta }_{{n,1}}}{{K}^{{(m - 1)}}}\cosh {\gamma } - \frac{1}{2}{{\delta }_{{n,2}}}{{K}^{{(m - 1)}}} - $
(1.24)
$\begin{gathered} - \,A_{n}^{{\left( {m - 1} \right)}}[({{n}^{2}} - 1)\cosh {\gamma }\cosh \left( {n + 1} \right){\gamma } + \left( {n + 1} \right)\sinh {\gamma }\sinh \left( {n + 1} \right){\gamma }] - \\ - \,B_{n}^{{\left( {m - 1} \right)}}[({{n}^{2}} - 1)\cosh {\gamma }\cosh \left( {n - 1} \right){\gamma } + \left( {n - 1} \right)\sinh {\gamma }\sinh \left( {n - 1} \right){\gamma }] + \\ \end{gathered} $
$ + \frac{1}{2}\left( {n + 2} \right)\left( {n + 1} \right)[A_{{n + 1}}^{{\left( {m - 1} \right)}}\cosh \left( {n + 2} \right){\gamma } + B_{{n + 1}}^{{\left( {m - 1} \right)}}\cosh n{\gamma }] + $
$ + \frac{1}{2}\left( {n - 2} \right)\left( {n - 1} \right)[A_{{n - 1}}^{{\left( {m - 1} \right)}}\cosh n{\gamma } + B_{{n - 1}}^{{\left( {m - 1} \right)}}\cosh \left( {n - 2} \right){\gamma }],\quad n \geqslant 1$
$d_{0}^{{\left( {m - 1} \right)}} = B_{1}^{{\left( {m - 1} \right)}} - A_{1}^{{\left( {m - 1} \right)}}\cosh 2{\gamma } + \frac{1}{2}{{K}^{{\left( {m - 1} \right)}}}\cosh 2{\gamma }$
$d_{n}^{{\left( {m - 1} \right)}} = - {{\delta }_{{n,1}}}{{K}^{{\left( {m - 1} \right)}}}\cosh {\gamma } + \frac{1}{2}{{\delta }_{{n,2}}}{{K}^{{\left( {m - 1} \right)}}} + $
(1.25)
$\begin{gathered} + \,A_{n}^{{\left( {m - 1} \right)}}[{{\left( {n + 1} \right)}^{2}}\cosh {\gamma }\cosh \left( {n + 1} \right){\gamma } - \left( {n + 1} \right)\sinh {\gamma }\sinh \left( {n + 1} \right){\gamma }] + \\ + \,B_{n}^{{\left( {m - 1} \right)}}[{{\left( {n - 1} \right)}^{2}}\cosh {\gamma }\cosh \left( {n - 1} \right){\gamma } - \left( {n - 1} \right)\sinh {\gamma }\sinh \left( {n - 1} \right){\gamma }] - \\ \end{gathered} $
$ - \frac{1}{2}A_{{n + 1}}^{{\left( {m - 1} \right)}}\left[ {\left( {n + 2} \right)\left( {n + 1} \right)\cosh \left( {n + 2} \right){\gamma }} \right] - \frac{1}{2}A_{{n - 1}}^{{\left( {m - 1} \right)}}\left[ {\left( {n - 1} \right)\left( {n + 2} \right)\cosh n{\gamma }} \right] - $
$ - \frac{1}{2}B_{{n + 1}}^{{\left( {m - 1} \right)}}\left[ {\left( {n - 2} \right)\left( {n + 1} \right)\cosh n{\gamma }} \right] - \frac{1}{2}B_{{n - 1}}^{{\left( {m - 1} \right)}}\left[ {\left( {n - 1} \right)\left( {n - 2} \right)\cosh \left( {n - 2} \right){\gamma }} \right],\quad ~n \geqslant 1$
где δn,m – символ Кронекера.

Граничные условия (последние два уравнения в (1.21)) могут быть записаны следующим образом

(1.26)
$a{\sigma }_{{{\alpha \alpha }}}^{{\left( m \right)}} = \mathop \sum \limits_{n = 0}^\infty s_{n}^{{\left( m \right)}}\cos n{\beta };\quad a{\sigma }_{{{\alpha \beta }}}^{{\left( m \right)}} = \mathop \sum \limits_{n = 1}^\infty t_{n}^{{\left( m \right)}}\sin n{\beta }$
где

$s_{n}^{{\left( m \right)}} = d_{n}^{{\left( {m - 1} \right)}} - {\nu }c_{n}^{{\left( {m - 1} \right)}}$
(1.27)
$t_{n}^{{\left( m \right)}} = \frac{1}{{2\sinh {\gamma }}}[\left( {n - 1} \right)d_{{n - 1}}^{{\left( {m - 1} \right)}} + \left( {n + 1} \right)d_{{n + 1}}^{{\left( {m - 1} \right)}} - 2nd_{n}^{{\left( {m - 1} \right)}}\cosh {\gamma }] - $
$ - \frac{{\nu }}{{2\sinh {\gamma }}}[\left( {n - 1} \right)c_{{n - 1}}^{{\left( {m - 1} \right)}} + \left( {n + 1} \right)c_{{n + 1}}^{{\left( {m - 1} \right)}} - 2nc_{n}^{{\left( {m - 1} \right)}}\cosh {\gamma }]$

Граничные условия дополняются условием, аналогичным (1.9)

(1.28)
$\mathop \sum \limits_{n = 1}^\infty (A_{n}^{{\left( m \right)}} + B_{n}^{{\left( m \right)}}) = 0$

Данные уравнения образуют систему для получения $f_{n}^{{\left( m \right)}}$, $f_{n}^{{'(m)}}$, K(m) через $A_{n}^{{\left( m \right)}}$, $B_{n}^{{\left( m \right)}}$, ${{K}^{{\left( {m - 1} \right)}}}$ следующим образом

$a{\sigma }_{{{\alpha \alpha }}}^{{\left( m \right)}} = \mathop \sum \limits_{n = 0}^\infty s_{n}^{{\left( m \right)}}\cos n{\beta } = - \frac{{{{K}^{{\left( m \right)}}}}}{2}\left( {\cosh 2{\gamma } - 2\cosh {\gamma }\cos {\beta } + \cos 2{\beta }} \right) + $
$ + f_{1}^{{\left( m \right)}}\left( {\gamma } \right) + \frac{1}{2}\mathop \sum \limits_{n = 1}^\infty [\left( {n - 1} \right)\left( {n - 2} \right)f_{{n - 1}}^{{\left( m \right)}}\left( {\gamma } \right) + \left( {n + 1} \right)\left( {n + 2} \right)f_{{n + 1}}^{{\left( m \right)}}\left( {\gamma } \right) - $
(1.29)
$ - 2({{n}^{2}} - 1)\cosh {\gamma }f_{n}^{{\left( m \right)}}\left( {\gamma } \right) - 2\sinh {\gamma }f_{n}^{{'\left( m \right)}}\left( {\gamma } \right)]\cos n{\beta }$
$a{\sigma }_{{{\alpha \beta }}}^{{\left( m \right)}} = \mathop \sum \limits_{n = 1}^\infty t_{n}^{{\left( m \right)}}\sin n{\beta } = - {{K}^{{\left( m \right)}}}\sinh {\gamma }\sin {\beta } - $
$ - \frac{1}{2}\mathop \sum \limits_{n = 1}^\infty [\left( {n - 1} \right)f_{{n - 1}}^{{'\left( m \right)}}\left( {\gamma } \right) - 2n\cosh {\gamma }f_{n}^{{'\left( m \right)}}\left( {\gamma } \right) + \left( {n + 1} \right)f_{{n + 1}}^{{'\left( m \right)}}\left( {\gamma } \right)]\sin n{\beta }$

Приравнивая коэффициенты при синусах и косинусах (в дальнейшем опуская верхний индекс (m)), получаем

$2{{s}_{0}} = 2{{f}_{1}}\left( {\gamma } \right) - K\cosh 2{\gamma }$
(1.30)
$2n{{s}_{n}} = {{{\psi }}_{{n - 1}}} + {{{\psi }}_{{n + 1}}} - 2{{{\psi }}_{n}}\cosh {\gamma } - 2{\psi }_{n}^{'}\sinh {\gamma } + 2K\left( {{{{\delta }}_{{1,n}}}\cosh {\gamma } - {{{\delta }}_{{2,n}}}} \right)$
$ - 2{{t}_{n}} = {\psi }_{{n - 1}}^{'} + {\psi }_{{n + 1}}^{'} - 2{\psi }_{n}^{'}\cosh {\gamma } + 2K{{{\delta }}_{{1,n}}}\sinh {\gamma }$
где

(1.31)
${{{\psi }}_{n}} = \left( {n - 1} \right)n\left( {n + 1} \right){{f}_{n}}\left( {\gamma } \right);\quad {\psi }_{n}^{'} = nf_{n}^{'}\left( {\gamma } \right)$

Предполагая временно K известным и применяя процедуру [13], а именно, умножая уравнение (1.30) на ${{e}^{{ - n{\gamma }}}}$ и суммируя для всех n, получаем

${\psi }_{1}^{'} = 2K{{e}^{{ - {\gamma }}}}\sinh {\gamma } + 2\mathop \sum \limits_{n = 1}^\infty {{t}_{n}}{{e}^{{ - n{\gamma }}}}$

При выводе данного уравнения также используется условие сходимости рядов $\mathop {\lim }\limits_{n \to \infty } {\psi }_{n}^{'}$ = 0. Из первого уравнения (1.30) непосредственно следует, что

${{f}_{1}}\left( {\gamma } \right) = \frac{K}{2}\cosh 2{\gamma } + {{s}_{0}}$

При n > 1 значения ψn, ${\psi }_{n}^{'}$ вычисляются непосредственно

(1.32)
${\psi }_{n}^{'} = p_{n}^{{\left( 1 \right)}}K + p_{n}^{{\left( 2 \right)}};\quad {{{\psi }}_{n}} = p_{n}^{{\left( 3 \right)}}K + p_{n}^{{\left( 4 \right)}},\quad n > 1$
где

$p_{n}^{{\left( 1 \right)}} = 2{{e}^{{ - {\gamma }}}}\sinh n{\gamma } - 2\sinh \left( {n - 1} \right){\gamma }$
$p_{n}^{{\left( 2 \right)}} = 2\sinh n{\gamma }{{\sinh }^{{ - 1}}}{\gamma }\mathop \sum \limits_{k = 1}^\infty {{t}_{k}}{{e}^{{ - k{\gamma }}}} - 2{{\sinh }^{{ - 1}}}{\gamma }\mathop \sum \limits_{k = 1}^{n - 1} {{t}_{k}}\sinh \left( {n - k} \right){\gamma }$
(1.33)
$\begin{gathered} p_{n}^{{\left( 3 \right)}} = 2{{e}^{{ - {\gamma }}}}\left( {n\cosh n{\gamma } - \coth {\gamma }\sinh n{\gamma }} \right) + \\ + {{\sinh }^{{ - 1}}}{\gamma }\left[ {\left( {n + 1} \right)\sinh \left( {n - 2} \right){\gamma } - \left( {n - 1} \right)\sinh n{\gamma }} \right] \\ \end{gathered} $
$p_{n}^{{\left( 4 \right)}} = 2\left( {n\cosh n{\gamma } - \coth {\gamma }\sinh n{\gamma }} \right){{\sinh }^{{ - 1}}}{\gamma }\mathop \sum \limits_{k = 1}^\infty {{t}_{k}}{{e}^{{ - k{\gamma }}}} + $
$ + 2{{\sinh }^{{ - 1}}}{\gamma }\mathop \sum \limits_{k = 1}^{n - 1} \left[ {\left( {n - k} \right){{t}_{k}}\cosh \left( {n - k} \right){\gamma } - \left( {k{{s}_{k}} + {{t}_{k}}\coth {\gamma }} \right)\sinh \left( {n - k} \right){\gamma }} \right]$

Используя уравнения (1.31), (1.8), находим

${{A}_{1}} = \frac{{{\psi }_{1}^{'}}}{{2\sinh 2{\gamma }}};\quad {{B}_{1}} = {{f}_{1}}\left( {\gamma } \right) - \frac{{{\psi }_{1}^{'}}}{2}\coth 2{\gamma }$
(1.34)
${{A}_{n}} = q_{n}^{{\left( 1 \right)}}{\psi }_{n}^{'} + q_{n}^{{\left( 2 \right)}}{{{\psi }}_{n}} = [q_{n}^{{\left( 1 \right)}}p_{n}^{{\left( 1 \right)}} + q_{n}^{{\left( 2 \right)}}p_{n}^{{\left( 3 \right)}}]K + q_{n}^{{\left( 1 \right)}}p_{n}^{{\left( 2 \right)}} + q_{n}^{{\left( 2 \right)}}p_{n}^{{\left( 4 \right)}}$
${{B}_{n}} = q_{n}^{{\left( 3 \right)}}{\psi }_{n}^{'} + q_{n}^{{\left( 4 \right)}}{{{\psi }}_{n}} = [q_{n}^{{\left( 3 \right)}}p_{n}^{{\left( 1 \right)}} + q_{n}^{{\left( 4 \right)}}p_{n}^{{\left( 3 \right)}}]K + q_{n}^{{\left( 3 \right)}}p_{n}^{{\left( 2 \right)}} + q_{n}^{{\left( 4 \right)}}p_{n}^{{\left( 4 \right)}},\quad n > 1$
где

(1.35)
$\begin{gathered} q_{n}^{{\left( 1 \right)}} = \frac{{\cosh \left( {\left( {n - 1} \right){\gamma }} \right)}}{{n\left( {n\sinh 2{\gamma } + \sinh \left( {2n{\gamma }} \right)} \right)}};\quad q_{n}^{{\left( 2 \right)}} = - \frac{{\sinh \left( {\left( {n - 1} \right){\gamma }} \right)}}{{n\left( {n + 1} \right)\left( {n\sinh 2{\gamma } + \sinh \left( {2n{\gamma }} \right)} \right)}} \\ q_{n}^{{\left( 3 \right)}} = \frac{{\cosh \left( {\left( {n + 1} \right){\gamma }} \right)}}{{n\left( {n\sinh 2{\gamma } + \sinh \left( {2n{\gamma }} \right)} \right)}};\quad q_{n}^{{\left( 4 \right)}} = \frac{{\sinh \left( {\left( {n + 1} \right){\gamma }} \right)}}{{n\left( {n - 1} \right)\left( {n\sinh 2{\gamma } + \sinh \left( {2n{\gamma }} \right)} \right)}} \\ \end{gathered} $

В итоге, используя условие (1.28), находим коэффициент K

(1.36)
$K = {{\left( {\frac{{\tanh {\gamma }\sum\limits_{k = 1}^\infty {({{t}_{k}}{{e}^{{ - k{\gamma }}}})} - {{s}_{0}} - \sum\limits_{k = 2}^\infty {[p_{k}^{{\left( 2 \right)}}(q_{k}^{{\left( 1 \right)}} + q_{k}^{{\left( 3 \right)}}) + p_{k}^{{\left( 4 \right)}}(q_{k}^{{\left( 2 \right)}} + q_{k}^{{\left( 4 \right)}})]} }}{{(\cosh 2{\gamma } - 2{{e}^{{ - {\gamma }}}}\sinh {\gamma }\tanh {\gamma }){\text{/}}2 + \sum\limits_{k = 2}^\infty {[p_{k}^{{\left( 1 \right)}}(q_{k}^{{\left( 1 \right)}} + q_{k}^{{\left( 3 \right)}}) + p_{k}^{{\left( 3 \right)}}(q_{k}^{{\left( 2 \right)}} + q_{k}^{{\left( 4 \right)}})]} }}} \right)}^{{ - 1}}}$

Таким образом, полученное решение можно рассматривать как обобщение решения [14].

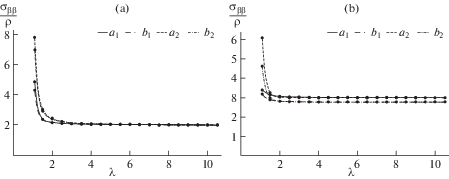
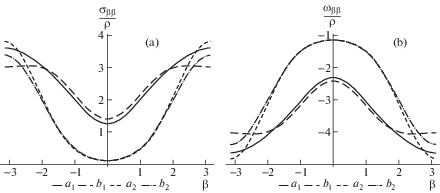
1.5. Результаты. Концентрации напряжений на контурах отверстий при всестороннем и одноосном растяжении представлены на рис. 2, 3, а непосредственно сами поверхностные напряжения – на рис. 4, 5 соответственно. Здесь и далее принято, что упругие постоянные материала соответствуют константам алюминия: $E = 70.3$ ГПа, ${\nu } = 0.345$, а соответствующие свойства поверхности – упругими постоянными, взятыми из [5]:

${{{\lambda }}_{s}} = 6.8511~\,\,{\text{Н/м}},\quad {{{\mu }}_{s}} = - 0.376~\,\,{\text{Н/м}}$
Рис. 2
Рис. 3
Рис. 4
Рис. 5

Соответственно модуль поверхностной упругости имеет вид

$C_{{{\beta \beta \beta \beta }}}^{s} = {{{\lambda }}_{s}} + 2{{{\mu }}_{s}} = 6.0991~\,\,{\text{Н/м}}$

Радиус отверстий полагался равным R = 2 нм. Концентрации напряжений в точках B, C (рис. 1) вычислялись для различных значений относительного расстояния между отверстиями λ = d/R.

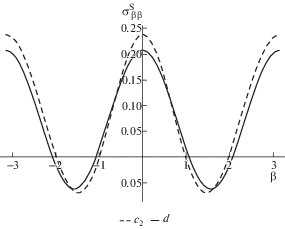
На рис. 2a, рис. 2b линии b1, a1 соответствуют значениям концентрации напряжения с и без учета поверхностного напряжения в точке B, а линии b2, a2 – в точке C. На рис. 3a, рис. 3b линии c1, c2 соответствуют значению поверхностного напряжения на всем контуре при малом (λ = 1.1) и большом (λ = 10.5) расстоянии между отверстиями.

На рис. 4 линия d соответствует решению задачи для одного отверстия [5].

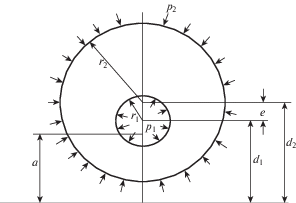
2. Эксцентрическая труба под равномерным давлением. 2.1. Общее решение. Рассмотрим эксцентрическую трубу, где по контуру ${\alpha } = {{{\alpha }}_{1}}$ действует равномерное нормальное давление, равное ${{p}_{1}}$, а по контуру ${\alpha } = {{{\alpha }}_{2}}$ – давление равное ${{p}_{2}}$ (рис. 5). В биполярных координатах, радиусы контуров r1, r2, расстояния d1, d2 от начала координат до центров соответствующих окружностей, расстояние e между центрами (эксцентриситет) выражаются следующим образом

${{d}_{1}} = a\coth {{{\alpha }}_{1}},\quad {{d}_{2}} = a\coth {{{\alpha }}_{2}},\quad e = {{d}_{2}} - {{d}_{1}}$
$2e{{d}_{1}} = r_{2}^{2} - r_{1}^{2} - {{e}^{2}},\quad 2e{{d}_{2}} = r_{2}^{2} - r_{1}^{2} + {{e}^{2}}$

Общее решение данной задачи, без учета поверхностной упругости получено в [15]

(2.1)
$g{\Phi } = J{\alpha }\left( {\cosh {\alpha } - \cos {\beta }} \right) + \left( {A\cosh 2{\alpha } + B + C\sinh 2{\alpha }} \right)\cos \beta $

Особенностью данного решения является отсутствие рядов, что сильно облегчает дальнейший анализ. Согласно (1.14)–(1.20), граничные условия для ${\alpha } = {{{\gamma }}_{1}}$, ${\alpha } = {{{\gamma }}_{2}}$, соответственно, записываются как

(2.2)
${\sigma }_{{{\alpha \alpha }}}^{{\left( 0 \right)}} = - {{p}_{1}},\quad {\sigma }_{{{\alpha \beta }}}^{{\left( 0 \right)}} = 0$
(2.3)
${\sigma }_{{{\alpha \alpha }}}^{{\left( 0 \right)}} = - {{p}_{2}},\quad {\sigma }_{{{\alpha \beta }}}^{{\left( 0 \right)}} = 0$
в результате которого получаем рекуррентные соотношения, идентичные с (1.21).

2.2. Нулевое приближение (классическая упругость). В случае нулевого приближения (т.е. классической упругости), решение [15] имеет следующий вид

${{A}^{{\left( 0 \right)}}} = \frac{{a\left( {{{p}_{1}} - {{p}_{2}}} \right)}}{{\sinh \left( {{{{\alpha }}_{1}} - {{{\alpha }}_{2}}} \right)\left( {\cosh 2{{{\alpha }}_{1}} + \cosh 2{{{\alpha }}_{2}} - 2} \right)}}\sinh \left( {{{{\alpha }}_{1}} + {{{\alpha }}_{2}}} \right)$
${{B}^{{\left( 0 \right)}}} = \frac{a}{{\sinh \left( {{{{\alpha }}_{1}} - {{{\alpha }}_{2}}} \right)\left( {\cosh 2{{{\alpha }}_{1}} + \cosh 2{{{\alpha }}_{2}} - 2} \right)}}(({{p}_{1}} + {{p}_{2}})\sinh ({{{\alpha }}_{1}} - {{{\alpha }}_{2}}) + $
(2.4)
$ + \cosh ({{{\alpha }}_{1}} - {{{\alpha }}_{2}})({{p}_{1}}\sinh 2{{{\alpha }}_{2}} - {{p}_{2}}\sinh 2{{{\alpha }}_{1}}))$
${{C}^{{\left( 0 \right)}}} = \frac{{a\left( {{{p}_{1}} - {{p}_{2}}} \right)}}{{\sinh \left( {{{{\alpha }}_{1}} - {{{\alpha }}_{2}}} \right)\left( {\cosh 2{{{\alpha }}_{1}} + \cosh 2{{{\alpha }}_{2}} - 2} \right)}}\cosh \left( {{{{\alpha }}_{1}} + {{{\alpha }}_{2}}} \right)$
${{J}^{{\left( 0 \right)}}} = \frac{{2a\left( {{{p}_{1}} - {{p}_{2}}} \right)}}{{\sinh \left( {{{{\alpha }}_{1}} - {{{\alpha }}_{2}}} \right)\left( {\cosh 2{{{\alpha }}_{1}} + \cosh 2{{{\alpha }}_{2}} - 2} \right)}}\cosh \left( {{{{\alpha }}_{1}} - {{{\alpha }}_{2}}} \right)$

Здесь как и ранее коэффициенты отмечены верхним индексом 0 соответствуют случаю отсутствия поверхностной упругости. Применяя непосредственно рекуррентные соотношения (1.21), вычисляем компоненты напряжения.

2.3. Результаты. Рассматривалось два случая:

• Эксцентрическая труба под внутренним давлением, т.е. при ${{p}_{1}} = p = 1$, ${{p}_{2}} = 0$.

• Эксцентрическая труба под внешним давлением, т.е. при ${{p}_{1}} = 0$, ${{p}_{2}} = p = 1$.

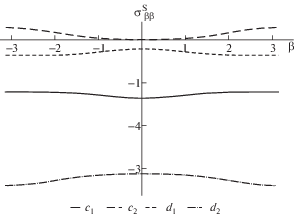
Концентрации напряжений на контурах трубы при внутреннем и внешнем давлении представлены на рис. 6a, b, а непосредственно сами поверхностные напряжения – на рис. 7 соответственно. Полагалось, что расстояния от начала координат до центров соответствующих окружностей ${{d}_{1}} = 3$ нм, ${{d}_{2}} = 4$ нм, радиусы ${{r}_{1}} = 1.5$ нм, ${{r}_{2}}$ = 3.04 нм.

Рис. 6
Рис. 7

На рис. 6a, b линии a1, b1 соответствуют значениям концентрации напряжения с и без учета поверхностного напряжения на контуре ${\alpha } = {{{\alpha }}_{1}}$, а линии a2, b2 – на контуре ${\alpha } = {{{\alpha }}_{2}}$. На рис. 7 линии c1, c2 соответствуют значению поверхностного напряжения на контурах ${\alpha } = {{{\alpha }}_{1}}$ и ${\alpha } = {{{\alpha }}_{2}}$ трубы под внутренним давлением, а линии d1, d2 – под внешним давлением соответственно.

Заключение. Получено и исследовано решение задач теории упругости для областей, ограниченных неконцентрическими окружностями, с учетом поверхностных эффектов, а именно, поверхностной упругости и поверхностного напряжения. Путем разложения в ряды Фурье переменных, записанных в биполярной системе координат и с использованием рекуррентных соотношений посчитаны величины поверхностных напряжений и концентрации напряжений. Показано, что несмотря на достаточно простую геометрию, но из-за малого расстояния между границами значения концентрации напряжений с и без учета поверхностного напряжения значительно отличаются друг от друга, по причине существенного вклада от поверхностных эффектов.

Работа выполнена при поддержке Программы Президиума РАН № 7 “Новые разработки в перспективных направлениях энергетики, механики и робототехники”.

Список литературы

  1. Ibach H. The role of surface stress in reconstruction, epitaxial growth and stabilization of mesoscopic structures // Surf. Sci. Rep. 1997. V. 29. P. 195–263.

  2. Подстригач Я.С., Повстенко Ю.З. Введение в механику поверхностных явлений в деформируемых твердых телах. Киев: Наук. думка, 1985. 200 с.

  3. Гращенко А.С., Кукушкин С.А., Осипов А.В., Редьков А.В. Исследование физико-механических характеристик наномасштабных пленок методом наноиндентирования // Изв. РАН. МТТ. 2018. № 5. С. 5–14.

  4. Shuttleworth R. The surface tension of solids // Proc. Phys. Soc. 1950. V. A63. P. 444–457.

  5. Греков М.А., Язовская А.А. Эффект поверхностной упругости и остаточного поверхностного напряжения в упругом теле с эллиптическим наноотверстием // ПММ. 2014. Т. 78. Вып. 2. С. 249–261.

  6. Vikulina Y.I., Grekov M.A., Kostyrko S.A. Model of film coating with weakly curved surface // Mechanics of Solids. 2010. V. 45. № 6. P. 778–788.

  7. Duan H.L., Wang J., Huang Z.P., Karihaloo B.L. Eshelby formalism for nanoinhomogeneities // Proc. Roy. Soc. L., A. 2005. V. 461. № 2062. P. 3335–3353.

  8. Гольдштейн Р.В., Городцов В.А., Устинов К.Б. Влияние поверхностных остаточных напряжений и поверхностной упругости на деформирование шарообразных включений нанометровых размеров в упругой матрице // Физ. мезомех. 2010. Т. 13. № 5. С. 127–138.

  9. Устинов К.Б. О влиянии поверхностных остаточных напряжений и поверхностной упругости на деформирование шарообразных включений нанометровых размеров в упругой матрице // Вестник ННГУ. 2011. № 4(5). С. 2541–2542.

  10. Городцов В.А., Лисовенко Д.С., Устинов К.Б. Шарообразное включение в упругой матрице при наличии собственных деформаций с учетом влияния свойств поверхности раздела, рассматриваемой как предел слоя конечной толщины // Изв. РАН. МТТ. 2019. № 3. С. 30–40.

  11. Duan H.L., Wang J., Karihaloo B.L., Huang Z.P. Nanoporous materials can be madee stiffer than non-porous counterparts by surface modification // Acta materiala. 2006. V. 54. P. 2983–2990.

  12. Altenbach H., Eremeyev V.A. On the shell and plate theories with surface stresses. Shell Structures. Theory and Applications // W. Pietraszkiewicz, I. Kreja (Eds). Boca Raton, CRC Press. 2010. V. 2. P. 47–50.

  13. Jeffery G.B. Plane stress and plane strain in bipolar coordinates // Phil. Trans of the Roy Soc of London ser. A. 1921. V. 221. P. 265–293.

  14. Chin-Bing Ling. On the stresses in a plate containing two circular holes // J. Appl. Phys. 1948. V. 19. № 1. P. 77–82.

  15. Уфлянд Я.С. Биполярные координаты в теории упругости. М.; Л.: Гостехиздат, 1950. 232 с.

  16. Gurtin M.E., Murdoch A.I. A continuum theory of elastic material surfaces // Arch. Ration. Mech. and Analysis. 1975. V. 57. № 4. P. 291–323.

  17. Spiegel M., Lipschutz S., Spellman D. Vector Analysis (2nd Edition). McGraw Hill, 2009. 254 p.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал