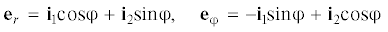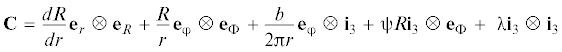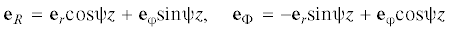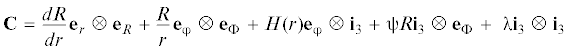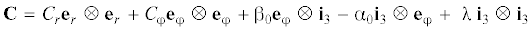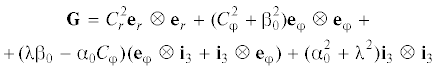Известия РАН. Механика твердого тела, 2020, № 5, стр. 120-130

УНИВЕРСАЛЬНЫЕ РЕШЕНИЯ НЕЛИНЕЙНОЙ ТЕОРИИ ДИСЛОКАЦИЙ ДЛЯ УПРУГОГО ЦИЛИНДРА

Л. М. Зубов^*

Южный федеральный университет
Ростов-на-Дону, Россия

Поступила в редакцию 18.03.2020
После доработки 25.03.2020
Принята к публикации 02.05.2020

DOI: 10.31857/S0572329920050177

Аннотация

Для упругого изотропного несжимаемого материала общего вида найден ряд точных решений о больших деформациях кручения и растяжения–сжатия сплошного кругового цилиндра с учетом распределенных дислокаций. Получены явные формулы, определяющие влияние дислокаций на зависимости крутящего момента и продольной силы от угла закручивания и осевого удлинения. Основные результаты сформулированы в виде, допускающем экспериментальную проверку.

Ключевые слова: нелинейная упругость, винтовые дислокации, большие деформации, растяжение и кручение, наноструктурные материалы, плотность дислокаций, точное решение

1. Введение. Дислокации являются важным элементом структуры твердых тел. Они играют существенную роль в таких явлениях, как пластическое течение, внутреннее трение, усталость и разрушение, ползучесть, рост кристаллов и др. [1–3]. Дислокационные модели позволяют описывать различные свойства современных наноструктурных материалов [4]. Прямолинейные винтовые дислокации влияют на механическое поведение нитевидных кристаллов, нанотрубок, нанострежней и других элементов конструкций. Изолированные дислокации, а также дисклинации [5] можно рассматривать как топологические дефекты, поскольку они обусловливают многозначность смещений точек упругого тела. Отметим, что применению топологических методов в нелинейной теории упругости большое внимание уделено в трудах И.И. Воровича, в том числе в его монографии [6]. Во многих случаях число дислокаций в ограниченном объеме тела бывает весьма велико. В этих случаях целесообразно перейти от дискретного набора дислокаций к их непрерывному распределению и использовать континуальную теорию распределенных дислокаций. Используя распределение дислокаций, можно моделировать различные другие дефекты в кристаллических и наноструктурных материалах. Классическая нелинейная теория непрерывно распределенных дислокаций построена в работах [7–9] и базируется на трактовке упругого тела как дифференциально-геометрического многообразия с определенными свойствами. Из-за значительной сложности общих уравнений континуальной теории дислокаций в настоящее время известно лишь ограниченное число [10–14] точных решений краевых задач пространственной нелинейной теории упругости для тел с дислокациями, распределенными с заданной тензорной плотностью. На важность таких задач обращено внимание, в частности, в работе [9]. Точные решения нелинейной континуальной теории дислокаций позволяют, в числе прочего, выявить новые количественные и качественные эффекты деформирования твердых тел с дислокациями. В представленной работе найдены новые точные решения нелинейной континуальной теории дислокаций. Эти решения описывают большие деформации раcтяжения–сжатия и кручения сплошного кругового цилиндра и являются общими для всех изотропных несжимаемых материалов.

2. Исходные соотношения. Пусть ${\mathbf{r}} = {{x}_{k}}{{{\mathbf{i}}}_{k}}$ и ${\mathbf{R}} = {{X}_{k}}{{{\mathbf{i}}}_{k}}$ – радиусы-векторы точки упругого тела соответственно в отсчетной и деформированной конфигурациях, x_k и X_k, k = 1, 2, 3 – декартовы координаты отсчетного и конечного состояний тела, i_k – координатные орты, ϑ – область, занимаемая телом в отсчетной конфигурации. В дальнейшем будем использовать операторы градиента, ротора и дивергенции в отсчетной конфигурации

${\text{grad}}{\mathbf{\Psi }} = {{{\mathbf{r}}}^{s}} \otimes \frac{{\partial {\mathbf{\Psi }}}}{{\partial {{q}^{s}}}},\quad {\text{rot}}{\mathbf{\Psi }} = {{{\mathbf{r}}}^{s}} \times \frac{{\partial {\mathbf{\Psi }}}}{{\partial {{q}^{s}}}}~$

(2.1)

${\text{div}}{\mathbf{\Psi }} = {\text{\;}}{{{\mathbf{r}}}^{s}} \cdot \frac{{\partial {\mathbf{\Psi }}}}{{\partial {{q}^{s}}}},\quad {{{\mathbf{r}}}^{s}} = {{{\mathbf{i}}}_{k}}\frac{{\partial {{q}^{s}}}}{{\partial {{x}_{k}}}},\quad s,k = 1,2,3~$

Здесь q^s – некоторые криволинейные лагранжевы координаты, Ψ – произвольное дифференцируемое тензорное поле.

Рассмотрим задачу об определении положения R(r) точки упругого тела после деформации по заданному в области ϑ дифференцируемому и однозначному полю тензора дисторсии C = gradR. В случае многосвязной области векторное поле R(r), вообще говоря, определяется неоднозначно, что означает существование в теле трансляционных дислокаций, каждая из которых характеризуется вектором Бюргерса [5]. Следуя [15–18], перейдем от дискретного набора дислокаций к их непрерывному распределению и определим плотность дислокаций как тензорное поле второго ранга α, поток которого через любую поверхность дает суммарный вектор Бюргерса дислокаций, пересекающих эту поверхность. Данное определение приводит к следующему уравнению относительно тензора дисторсии:

(2.2)

${\text{rot}}{\mathbf{C}} = {\mathbf{\alpha }}~$

Если тензорное поле плотности дислокаций α(r), которое должно удовлетворять условию соленоидальности

(2.3)

${\text{div}}{\mathbf{\alpha }} = 0$

считается заданным, то тензорное уравнение (2.2), называемое уравнением несовместности, вместе с векторным уравнением равновесия

(2.4)

${\text{div}}{\mathbf{D}} = 0$

и определяющими соотношениями упругого материала позволяет определить тензорное поле дисторсии, а следовательно, и поле напряжений в теле. В (2.4) D – несимметричный тензор напряжений Пиолы [19] и принято допущение об отсутствии массовых сил. Заметим, что при α ≠ 0 векторное поле R(r) и поле перемещений среды не существуют.

Упругий материал в дальнейшем будем считать изотропным и несжимаемым. В этом случае определяющие соотношения, т.е. связь напряжений и деформаций, имеют вид [19]

(2.5)

${\mathbf{D}} = {\mathbf{D}}{\text{*}} - p{{{\mathbf{C}}}^{{ - {\text{T}}}}}$

(2.6)

${\mathbf{D}}{\text{*}} = \left[ {{{{\tau }}_{1}}\left( {{{I}_{1}},{{I}_{2}}} \right) + {{I}_{1}}{{{\tau }}_{2}}\left( {{{I}_{1}},{{I}_{2}}} \right)} \right]{\mathbf{C}} - {{{\tau }}_{2}}\left( {{{I}_{1}},{{I}_{2}}} \right){\mathbf{G}} \cdot {\mathbf{C}}$

(2.7)

${\mathbf{G}} = {\mathbf{C}} \cdot {{{\mathbf{C}}}^{{\text{T}}}},~\quad {{I}_{1}} = {\text{tr}}{\mathbf{G}},\quad {{I}_{2}} = {\text{tr}}{{{\mathbf{G}}}^{{ - 1}}}$

(2.8)

${{{\tau }}_{1}} = 2\frac{{\partial W}}{{\partial {{I}_{1}}}},\quad {{{\tau }}_{2}} = 2\frac{{\partial W}}{{\partial {{I}_{2}}}}~$

Здесь G – метрический тензор, называемый также мерой деформации Коши, W(I₁, I₂) – удельная энергия деформации, τ₁, τ₂ – скалярные функции отклика материала, p – давление в несжимаемом теле, не выражаемое через деформацию, I₁, I₂ – первый и второй инварианты деформации. Третий инвариант равен единице в силу условия несжимаемости

(2.9)

$\det {\mathbf{C}} = 1~$

Уравнение несовместности первого порядка (2.2) можно преобразовать [20] к нелинейным уравнениям несовместности второго порядка относительно компонент метрического тензора G. Эти уравнения составляют основу классической континуальной теории дислокаций [7–9] и с дифференциально-геометрической точки зрения устанавливают связь тензора плотности дислокаций с картановым кручением пространства метрической связности. Уравнения несовместности второго порядка значительно сложнее, чем уравнения (2.2), и в данной работе не будут использоваться.

3. Растяжение и кручение кругового цилиндра с винтовыми дислокациями осевого направления. Рассмотрим упругое тело в форме сплошного кругового цилиндра, ось которого имеет направление орта i₃. Введем в недеформированном состоянии цилиндрические координаты $0 \leqslant r \leqslant {{r}_{0}}$, $0 \leqslant {\varphi } \leqslant 2{\pi }$, $0 \leqslant z \leqslant L$ по формулам 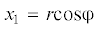, , 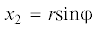${{x}_{3}} = z$ и обозначим через e_r, e_φ, i₃ орты, касательные к координатным линиям. Имеют место соотношения

Предположим, что в цилиндре задано осесимметричное распределение прямолинейных винтовых дислокаций, параллельных оси цилиндра. Тензор плотности дислокаций в этом случае имеет только одну ненулевую компоненту:

(3.1)

${\mathbf{\alpha }} = {\beta }\left( r \right){{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}~$

Требование соленоидальности (2.3) выполняется для произвольной функции β(r) в (3.1). Как известно [5], решение задачи о больших деформациях растяжения–сжатия и кручения цилиндра с одиночной винтовой дислокацией, сосредоточенной на оси цилиндра, дается выражением

(3.2)

$R = R(r),\quad {\Phi } = {\varphi } + {\psi }z,\quad Z = \frac{b}{{2{\pi }}}{\varphi } + {\lambda }z~$

Здесь R, Φ, Z – цилиндрические координаты точек цилиндра после деформации, т.е. эйлеровы координаты, b – длина вектора Бюргерса изолированной дислокации, ψ – угол закручивания, λ – кратность осевого удлинения. Постоянные b и ψ могут принимать любые действительные значения, а постоянная λ – только положительные. Соответствующий (3.2) тензор дисторсии имеет вид [5]

(3.3)

(3.4)

Слагаемое (2π)^–1bφ в (3.2) описывает депланацию сечения цилиндра, которая является многозначной функцией координат x₁, x₂. При наличии непрерывно распределенных дислокаций, как было сказано выше, поле перемещений упругой среды не существует. Однако в данном частном случае, когда тензор плотности дислокаций содержит только одну компоненту, перемещения в плоскости сечения цилиндра существуют, а несуществующей является только функция депланации. Это означает, что величины R и Φ сохраняют смысл полярных координат точек цилиндра в деформированном состоянии, если плотность дислокаций описывается формулой (3.1).

Исходя из сказанного и выражения (3.3), решение уравнения несовместности (2.2) будем искать в виде

(3.5)

При помощи (3.1), (3.4), (3.5) можно проверить, что уравнение несовместности будет выполнено тогда и только тогда, когда функция H(r) удовлетворяет уравнению

(3.6)

$\frac{{dH}}{{dr}} + \frac{H}{r} = {\beta }\left( r \right)~$

В качестве граничного условия для уравнения (3.6) примем требование отсутствия сосредоточенной дислокации в центре цилиндра:

(3.7)

$\lim (r{{{\mathbf{e}}}_{{\varphi }}} \cdot {\mathbf{C}} \cdot {{{\mathbf{i}}}_{3}}) = 0\quad {\text{при}}\quad r \to 0~$

Из (3.6) и (3.7) находим

(3.8)

$H\left( r \right) = \frac{1}{r}\mathop \smallint \limits_0^r {\beta }\left( {\rho } \right){\rho }d{\rho }~$

Для определения функции R(r) в выражении дисторсии воспользуемся условием несжимаемости (2.9), которое дает уравнение

(3.9)

$R\frac{{dR}}{{dr}} = \frac{r}{{{\lambda } - {\psi }rH\left( r \right)}}~$

Предполагая, что сплошной цилиндр остается сплошным и после деформации, т.е. считая, что $R(0) = 0$, находим решение уравнения (3.9) для произвольной плотности винтовых дислокаций β(r):

(3.10)

${{R}^{2}}\left( r \right) = 2\mathop \smallint \limits_0^r \frac{{{\rho }~d{\rho }}}{{\lambda - {\psi \rho }H\left( {\rho } \right)}}~$

Приведем примеры определения функции R(r) для некоторых частных случаев распределения винтовых дислокаций. Пусть ${\beta }(r) = {{{\beta }}_{0}}{{r}^{{ - 1}}}$, ${{{\beta }}_{0}} = {\text{const}}$. Тогда в силу (3.8) имеем $H\left( r \right) = {{{\beta }}_{0}}$ и формула (3.10) дает такой результат

(3.11)

${{R}^{2}} = - \frac{{2\lambda }}{{{{{\beta }}_{0}}^{2}{{{\psi }}^{2}}}}\ln \left( {1 - \frac{{{{{\beta }}_{0}}{\psi }r}}{{\lambda }}} \right) - \frac{{2r}}{{{{{\beta }}_{0}}{\psi }}}~$

Влияние дислокаций на функцию R(r) при малых значениях произведения ${{{\beta }}_{0}}{\psi }$ хорошо видно из степенного разложения правой части (3.11)

(3.12)

${{R}^{2}} = \frac{{{{r}^{2}}}}{{\lambda }} + \frac{{2{{{\beta }}_{0}}{\psi }{{r}^{3}}}}{{3{{{\lambda }}^{2}}}} + \frac{{{{{\beta }}_{0}}^{2}{{{\psi }}^{2}}{{r}^{4}}}}{{2{{{\lambda }}^{3}}}} + \cdots ~$

В качестве второго примера рассмотрим дислокации, равномерно распределенные по цилиндрической поверхности $r = {{r}_{*}}$. Плотность дислокаций в этом случае имеет вид ${\beta }(r) = a{\delta }(r - {{r}_{*}})$, где $a = {\text{const}}$, ${\delta }(r - {{r}_{*}})$ – дельта-функция Дирака. На основании (3.8), (3.10) получаем

(3.13)

$H(r) = \left\{ \begin{gathered} a,\quad ~0 \leqslant r \leqslant {{r}_{*}}~ \hfill \\ \frac{{a{{r}_{*}}}}{r},\quad {{r}_{*}} \leqslant r \leqslant {{r}_{0}}~ \hfill \\ \end{gathered} \right.$

(3.14)

${{R}^{2}}(r) = \left\{ \begin{gathered} \frac{{{{r}^{2}}}}{{\lambda }},\quad 0 \leqslant r \leqslant {{r}_{*}}~~ \hfill \\ \frac{{r_{*}^{2}}}{{\lambda }} + \frac{{{{r}^{2}} - r_{*}^{2}}}{{{\lambda } - {\psi }a{{r}_{*}}}},\quad {{r}_{*}} \leqslant r \leqslant {{r}_{0}}~ \hfill \\ \end{gathered} \right.$

Если в (3.14) выполнить предельный переход ${{r}_{*}} \to 0$, $a \to \infty $ при условии, что 2πa${{r}_{*}}$ = b, то получим известное [21] решение для одиночной дислокации в центре цилиндра

(3.15)

$R = \frac{r}{{\sqrt {{\lambda } - {{{\left( {2{\pi }} \right)}}^{{ - 1}}}b{\psi }} }}~$

Кроме уравнений несовместности и условия несжимаемости, должны быть выполнены уравнения равновесия для напряжений (2.4). При помощи (3.5) вычислим тензоры и инварианты деформации, участвующие в определяющих соотношениях (2.5)–(2.7). Имеем

(3.16)

${{{\mathbf{C}}}^{{ - {\text{T}}}}} = {{\left( {\frac{{dR}}{{dr}}} \right)}^{{ - 1}}}{{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{R}} + {\lambda }\frac{{dR}}{{dr}}{{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\Phi }}} - H\frac{{dR}}{{dr}}{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\Phi }}} - {\psi }R\frac{{dR}}{{dr}}{{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{i}}}_{3}} + {\text{\;}}\frac{R}{r}\frac{{dR}}{{dr}}{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}$

(3.17)

$\begin{gathered} {\mathbf{G}} = {{\left( {\frac{{dR}}{{dr}}} \right)}^{2}}{{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{r}} + \left( {\frac{{{{R}^{2}}}}{{{{r}^{2}}}} + {{H}^{2}}} \right){{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\varphi }}} + \\ + \left( {\frac{{{\psi }{{R}^{2}}}}{r} + {\lambda }H} \right)({{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{i}}}_{3}} + {{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\varphi }}}) + ({{{\psi }}^{2}}{{R}^{2}} + {{{\lambda }}^{2}}){{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}} \\ \end{gathered} $

${{I}_{1}} = {{\left( {\frac{{dR}}{{dr}}} \right)}^{2}} + \frac{{{{R}^{2}}}}{{{{r}^{2}}}} + {{H}^{2}} + {{{\psi }}^{2}}{{R}^{2}} + {{{\lambda }}^{2}}$

(3.18)

${{I}_{2}} = {{\left( {{\lambda } - {\psi }rH} \right)}^{2}}\frac{{{{R}^{2}}}}{{{{r}^{2}}}} + {{\left( {\frac{{dR}}{{dr}}} \right)}^{2}}\left( {\frac{{{{R}^{2}}}}{{{{r}^{2}}}} + {{H}^{2}} + {{{\psi }}^{2}}{{R}^{2}} + {{{\lambda }}^{2}}} \right)$

Из (2.6), (3.16)–(3.18) вытекает представление тензора D*, компоненты которого не зависят от координат φ и z,

(3.19)

$\begin{gathered} {\mathbf{D}}{\text{*}} = D_{{rR}}^{*}(r){{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{R}} + D_{{{\varphi \Phi }}}^{*}(r){{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\Phi }}} + \\ + \,D_{{{\varphi }Z}}^{*}(r){{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{i}}}_{3}} + D_{{z{\Phi }}}^{*}(r){{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\Phi }}} + D_{{zZ}}^{*}(r){{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}~ \\ \end{gathered} $

Поскольку функции H(r) и R(r) найдены и выражаются формулами (3.8), (3.10), то компоненты тензора D* в (3.19) – известные функции радиальной координаты r, определяемые при помощи (2.6), (3.5), (3.17), (3.18). Неизвестной остается функция давления p(r). При помощи (3.4), (3.16), (3.19) находим

${\text{div}}{\mathbf{D}}{\text{*}} = \left( {\frac{{dD_{{rR}}^{*}}}{{dr}} + \frac{{D_{{rR}}^{*} - D_{{{\varphi \Phi }}}^{*}}}{r} - {\psi }D_{{z{\Phi }}}^{*}} \right){{{\mathbf{e}}}_{R}}$

(3.20)

${\text{div}}(p{{{\mathbf{C}}}^{{ - {\text{T}}}}}) = \left[ {{{{\left( {\frac{{dR}}{{dr}}} \right)}}^{{ - 1}}}\frac{{dp}}{{dr}} - {\psi \beta }(r)R(r)p} \right]{{{\mathbf{e}}}_{R}}~$

В силу (2.5), (3.20) векторное уравнение (2.4) сводится к одному скалярному относительно функции p(r)

(3.21)

$\frac{{dp}}{{dr}} + L(r)p = F(r)$

$L(r) = \frac{{{\psi }r{\beta }(r)}}{{{\psi }rH(r) - {\lambda }}},\quad F(r) = \left( {\frac{{dD_{{rR}}^{*}}}{{dr}} + \frac{{D_{{rR}}^{*} - D_{{{\varphi \Phi }}}^{*}}}{r} - {\psi }D_{{z{\Phi }}}^{*}} \right)\frac{{dR}}{{dr}}~$

Решение уравнения (3.21) имеет вид

(3.22)

$p\left( r \right) = \exp \left( {\mathop \smallint \limits_r^{{{r}_{0}}} L\left( {\rho } \right)d{\rho }} \right)\left[ {p\left( {{{r}_{0}}} \right) - \mathop \smallint \limits_r^{{{r}_{0}}} F\left( {r{\kern 1pt} '} \right){\text{exp}}\left( { - \mathop \smallint \limits_{r{\kern 1pt} '}^{{{r}_{0}}} L\left( {\rho } \right)d{\rho }} \right)dr{\kern 1pt} '} \right]~$

Постоянная p(r₀) в (3.22) находится из условия незагруженности боковой поверхности цилиндра ${{D}_{{rR}}}\left( {{{r}_{0}}} \right) = 0$ и выражается так

(3.23)

$p\left( {{{r}_{0}}} \right) = \frac{{D_{{rR}}^{*}\left( {{{r}_{0}}} \right){{r}_{0}}}}{{R\left( {{{r}_{0}}} \right)\left[ {{\lambda } - {\psi }{{r}_{0}}H\left( {{{r}_{0}}} \right)} \right]}}~$

Таким образом, найдено точное решение в квадратурах задачи о больших деформациях растяжения–сжатия и кручения кругового цилиндра, содержащего произвольное осесимметричное распределение прямолинейных винтовых дислокаций. Это решение пригодно для любых изотропных несжимаемых упругих материалов, т.е. универсально в указанном классе материалов.

Из представлений (2.5), (3.19) вытекает, что в каждом поперечном сечении цилиндра напряжения приводятся к результирующей продольной силе

(3.24)

$Q = 2{\pi }\mathop \smallint \limits_0^{{{r}_{0}}} {{D}_{{zZ}}}rdr$

и результирующему крутящему моменту

(3.25)

$M = 2{\pi }\mathop \smallint \limits_0^{{{r}_{0}}} {{D}_{{z{\Phi }}}}Rrdr~$

Величины Q и M не зависят от координаты z, т.е. одинаковы во всех сечениях цилиндра. Таким образом, реализация описанной выше деформации кручения и растяжения–сжатия цилиндрического стержня конечной длины с дислокациями требует приложения к концам стержня продольной силы Q и крутящего момента M. Можно показать справедливость формул

(3.26)

$\begin{gathered} Q({\lambda },{\psi }) = {\pi }\mathop \smallint \limits_0^{{{r}_{0}}} \left( {{{{\tau }}_{1}}\frac{{\partial {{I}_{1}}}}{{\partial {\lambda }}} + {{{\tau }}_{2}}\frac{{\partial {{I}_{2}}}}{{\partial {\lambda }}}} \right)rdr \\ M({\lambda },{\psi }) = {\pi }\mathop \smallint \limits_0^{{{r}_{0}}} \left( {{{{\tau }}_{1}}\frac{{\partial {{I}_{1}}}}{{\partial {\psi }}} + {{{\tau }}_{2}}\frac{{\partial {{I}_{2}}}}{{\partial {\psi }}}} \right)rdr~ \\ \end{gathered} $

После определения функций H(r) и R(r) по формулам (3.8), (3.10) и применения соотношений (3.18) сила и момент при заданном распределении дислокаций становятся согласно (3.26) известными функциями угла закручивания и осевого удлинения.

4. Равномерно распределенные винтовые дислокации радиального и азимутального направления. Рассмотрим кручение и растяжение–сжатие сплошного кругового цилиндра в случае, когда тензор плотности дислокаций задан выражением

(4.1)

${\mathbf{\alpha }} = {{{\alpha }}_{0}}({{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{R}} + {{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\Phi }}}),\quad {{{\alpha }}_{0}} = {\text{const}}$

где векторы ${{{\mathbf{e}}}_{R}}$ и ${{{\mathbf{e}}}_{{\Phi }}}$ определены соотношениями (3.4). Легко проверить, что тензор (4.1) подчиняется требованию соленоидальности (2.3), а решение уравнения несовместности (2.2), удовлетворяющее условию несжимаемости (2.9), имеет вид

(4.2)

${\mathbf{C}} = {{{\lambda }}^{{ - 1/2}}}({{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{R}} + {{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\Phi }}}) + {\eta }r{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\Phi }}} + {\lambda }{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}$

${\eta } = {\psi }{{{\lambda }}^{{ - 1/2}}} - {{{\alpha }}_{0}}~$

На основании (4.2) находим обратный тензор дисторсии, метрический тензор и инварианты деформации

(4.3)

${{{\mathbf{C}}}^{{ - 1}}} = {{{\lambda }}^{{1/2}}}({{{\mathbf{e}}}_{R}} \otimes {{{\mathbf{e}}}_{r}} + {{{\mathbf{e}}}_{{\Phi }}} \otimes {{{\mathbf{e}}}_{{\varphi }}}) - {{{\lambda }}^{{ - \frac{1}{2}}}}{\eta }r{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\varphi }}} + \,{{{\lambda }}^{{ - 1}}}{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}$

(4.4)

${\mathbf{G}} = {{{\lambda }}^{{ - 1}}}({{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{r}} + {{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\varphi }}}) + {{{\lambda }}^{{ - \frac{1}{2}}}}{\eta }r({{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{i}}}_{3}} + {{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\varphi }}}) + {\text{\;}}({{{\lambda }}^{2}} + {{{\eta }}^{2}}{{r}^{2}}){{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}$

(4.5)

${{I}_{1}} = 2{{{\lambda }}^{{ - 1}}} + {{{\lambda }}^{2}} + {{{\eta }}^{2}}{{r}^{2}},\quad {{I}_{2}} = 2{\lambda } + {{{\lambda }}^{{ - 2}}} + {{{\lambda }}^{{ - 1}}}{{{\eta }}^{2}}{{r}^{2}}~$

Как и в разд. 3, материал считается изотропным и несжимаемым, т.е. описывается определяющими соотношениями (2.5), (2.6) с произвольной функцией удельной энергии W(I₁, I₂). Поэтому для тензора напряжений Пиолы в силу (4.3)–(4.5) будут справедливы представления (2.5), (3.19). Из (4.3) вытекает равенство div(C^–T) = 0, что приводит к такому уравнению равновесия:

(4.6)

$\sqrt {\lambda } \frac{{dp}}{{dr}} = \frac{{dD_{{rR}}^{*}}}{{dr}} + \frac{{D_{{rR}}^{*} - D_{{{\varphi \Phi }}}^{*}}}{r} - {\psi }D_{{z{\Phi }}}^{*}~$

Решая уравнение (4.6) с учетом граничного условия ${{D}_{{rR}}}\left( {{{r}_{0}}} \right) = 0$, находим

(4.7)

$\sqrt {\lambda } p\left( r \right) = D_{{rR}}^{*}\left( {{{r}_{0}}} \right) - \mathop \smallint \limits_r^{{{r}_{0}}} \left( {\frac{{D_{{rR}}^{*} - D_{{{\varphi \Phi }}}^{*}}}{r} - {\psi }D_{{z{\Phi }}}^{*}} \right)dr~$

При помощи (2.5), (2.6), (4.2)–(4.5), (4.7) вычисляется поле напряжений в цилиндре и выводятся следующие универсальные в классе изотропных несжимаемых тел и явные формулы для продольной силы и крутящего момента, действующих на торцах цилиндра, содержащего дислокации, распределенные с плотностью (4.1)

(4.8)

$\begin{gathered} Q({\lambda },{\psi }) = 2{\pi }\mathop \smallint \limits_0^{{{r}_{0}}} \left[ {\left( {{\lambda } - {{{\lambda }}^{{ - 2}}} - \frac{1}{2}{{{\lambda }}^{{ - 3/2}}}{\psi \eta }{{r}^{2}}} \right){{{\tau }}_{1}}({{I}_{1}},{{I}_{2}}) + } \right. \\ \left. { + \left( {1 - {{{\lambda }}^{{ - 3}}} - \frac{1}{2}{{{\lambda }}^{2}}{{{\eta }}^{2}}{{r}^{2}} - \frac{1}{2}{{{\lambda }}^{{ - 5/2}}}{\psi \eta }{{r}^{2}}} \right){{{\tau }}_{2}}({{I}_{1}},{{I}_{2}})} \right]rdr \\ \end{gathered} $

(4.9)

$M\left( {{\lambda },{\psi }} \right) = 2{\pi }\mathop \smallint \limits_0^{{{r}_{0}}} [{{{\lambda }}^{{ - 1/2}}}{{{\tau }}_{1}}\left( {{{I}_{1}},{{I}_{2}}} \right) + {{{\lambda }}^{{ - 3/2}}}{{{\tau }}_{2}}\left( {{{I}_{1}},{{I}_{2}}} \right)]{\eta }{{r}^{3}}dr~$

Поскольку ${\eta } = {\psi }{{{\lambda }}^{{ - 1/2}}} - {{{\alpha }}_{0}}$, из (4.9) видно, что при отсутствии внешнего крутящего момента (M = 0) происходит закручивание стержня, обусловленное дислокациями, при этом угол закручивания равен ${{{\alpha }}_{0}}\sqrt {\lambda } $.

Исследуем величину продольной силы для неогуковского [19] материала, в котором ${{{\tau }}_{2}} = 0$, а τ₁ – положительная постоянная. Согласно (4.8) при λ = 1, т.е. при сохранении длины стержня имеем

$Q = - \frac{1}{4}{\pi }{{{\tau }}_{1}}r_{0}^{4}{\psi }\left( {{\psi } - {{{\alpha }}_{0}}} \right)~$

Возникновение продольной силы для стержня с неизменной длиной – это проявление эффекта Пойнтинга при кручении [19, 22]. При ${{{\alpha }}_{0}} = 0$ сила отрицательна, т.е. сжимающая, а при ${{{\alpha }}_{0}} > 0$ сила отрицательна, если ${\psi } > {{{\alpha }}_{0}}$, и положительна, если $0 < {\psi }~ < {{{\alpha }}_{0}}$. Это означает, что наличие дислокаций может изменить знак эффекта Пойнтинга.

5. Растяжение–сжатие цилиндрического стержня с комбинированным распределением дислокаций. Поскольку в нелинейной теории дислокаций неприменим принцип суперпозиции, эффекты, обусловленные комбинированным распределением дислокаций, нельзя получить суммированием эффектов от отдельных видов дислокаций. Это существенно затрудняет решение задач в случаях, когда тензор плотности дислокаций имеет несколько независимых компонент. Тем не менее, как показано ниже, удается найти точное решение нелинейной задачи о растяжении–сжатии сплошного кругового цилиндра, изготовленного из произвольного несжимаемого материала и содержащего дислокации, распределенные с плотностью

(5.1)

${\mathbf{\alpha }} = \frac{1}{r}\left( {{{{\alpha }}_{0}}{{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{r}} + {{{\beta }}_{0}}{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}} + {{{\gamma }}_{0}}{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\varphi }}}} \right)$

Здесь α₀, β₀, γ₀ – безразмерные постоянные. Выражение (5.1) удовлетворяет требованию соленоидальности (2.3). Первое слагаемое в (5.1) соответствует винтовым дислокациям радиального направления, второе и третье описывают прямолинейные винтовые и краевые дислокации, оси которых параллельны оси цилиндра.

Оказывается, уравнению несовместности (2.2) с плотностью дислокаций (5.1) удовлетворяет такой тензор дисторсии, компоненты которого в базисе цилиндрических координат постоянны. Этот тензор имеет вид

(5.2)

${{C}_{{\varphi }}} = {{C}_{r}} + {{{\gamma }}_{0}},\quad {{C}_{r}} = {\text{const}}~$

Параметр осевого удлинения λ считается заданной положительной постоянной. Постоянство компонент тензора дисторсии в криволинейной системе координат не означает, что цилиндр испытывает однородную деформацию. При отсутствии дислокаций (${{{\alpha }}_{0}} = {{{\beta }}_{0}} = {{{\gamma }}_{0}} = 0$) из (5.2) имеем ${\mathbf{C}} = {{C}_{r}}({{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{r}} + {{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\varphi }}}) + {\lambda }{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}$, что соответствует однородной деформации цилиндрического стержня.

Постоянную C_r в (5.2) найдем из условия несжимаемости (2.9)

(5.3)

${{C}_{r}} = \frac{1}{{2{\lambda }}}( - \Delta + \sqrt {{{\Delta }^{2}} + 4{\lambda }} ),\quad \Delta = {\lambda }{{{\gamma }}_{0}} + {{{\alpha }}_{0}}{{{\beta }}_{0}}~$

При отсутствии дислокаций выражение (5.3) дает кратность удлинения в поперечном направлении для однородной деформации несжимаемого цилиндра: ${{C}_{r}} = {{{\lambda }}^{{ - 1/2}}}$.

Таким образом, для несжимаемого материала тензор дисторсии полностью определяется заданными скалярными плотностями дислокаций и параметром осевого удлинения. Используя (5.2), находим обратный тензор дисторсии, метрический тензор и инварианты деформации

(5.4)

${{{\mathbf{C}}}^{{ - 1}}} = C_{r}^{{ - 1}}{{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{r}} + {{C}_{r}}({\lambda }{{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\varphi }}} - {{{\beta }}_{0}}{{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{i}}}_{3}} + {{{\alpha }}_{0}}{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\varphi }}} + {{C}_{{\varphi }}}{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}})$

(5.5)

(5.6)

${{I}_{1}} = C_{r}^{2} + C_{{\varphi }}^{2} + {\alpha }_{0}^{2} + {\beta }_{0}^{2} + {{{\lambda }}^{2}},~\quad {{I}_{2}} = {{({{{\alpha }}_{0}}{{{\beta }}_{0}} + {\lambda }{{C}_{{\varphi }}})}^{2}} + C_{r}^{2}({\alpha }_{0}^{2} + {{{\lambda }}^{2}} + C_{{\varphi }}^{2} + {\beta }_{0}^{2})~$

Из (5.5), (5.6) видно, что распределение дислокаций (5.1) порождает сдвиговые деформации между вертикальным и азимутальным направлениями, а инварианты деформации – постоянные величины.

Чтобы определить поле вращений элементарных объемов растягиваемого цилиндра с дислокациями, построим полярное разложение тензора дисторсии ${\mathbf{C}} = {\mathbf{U}} \cdot {\mathbf{A}}$, где ${\mathbf{U}} = {{{\mathbf{G}}}^{{1/2}}}$ – положительно определенный тензор растяжения, A – собственно ортогональный тензор вращения. Извлекая квадратный корень из тензора (5.4), получим

$\begin{gathered} {\mathbf{U}} = {{C}_{r}}{{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{r}} + {{K}^{{ - 1}}}[{{C}_{{\varphi }}}({{C}_{{\varphi }}} + {\lambda }) + {{{\beta }}_{0}}\left( {{{{\alpha }}_{0}} + {{{\beta }}_{0}}} \right)]{{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\varphi }}} + \\ + \,{{K}^{{ - 1}}}({{{\beta }}_{0}}{\lambda } - {{{\alpha }}_{0}}{{C}_{{\varphi }}})({{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{i}}}_{3}} + {{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\varphi }}}) + {{K}^{{ - 1}}}[{\lambda }({{C}_{{\varphi }}} + {\lambda }) + {{{\alpha }}_{0}}\left( {{{{\alpha }}_{0}} + {{{\beta }}_{0}}} \right)]{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}} \\ \end{gathered} $$K = \sqrt {{{{\left( {{{C}_{{\varphi }}} + {\lambda }} \right)}}^{2}} + {{{\left( {{{{\alpha }}_{0}} + {{{\beta }}_{0}}} \right)}}^{2}}} $

(5.7)

${\mathbf{A}} = {{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{r}} + \cos {\chi }({{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\varphi }}} + {{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}) + \sin {\chi }({{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{i}}}_{3}} - {{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\varphi }}})$

$\cos {\chi } = {{K}^{{ - 1}}}\left( {{{C}_{{\varphi }}} + {\lambda }} \right),\quad \sin {\chi } = {{K}^{{ - 1}}}\left( {{{{\alpha }}_{0}} + {{{\beta }}_{0}}} \right)~$

Выражение (5.7) означает, что поворот элементарных объемов цилиндра происходит вокруг радиальной оси e_r на постоянный угол χ.

Обратимся к анализу напряжений и решению уравнений равновесия (2.4). На основании (2.5), (2.6), (5.2), (5.4) имеем

$D_{{rr}}^{*} = {{C}_{r}}\left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right) - {{{\tau }}_{2}}C_{r}^{3}$

$D_{{{\varphi \varphi }}}^{*} = {{C}_{{\varphi }}}\left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right) - {{{\tau }}_{2}}[{{C}_{{\varphi }}}(C_{{\varphi }}^{2} + \beta _{0}^{2}) - {{{\alpha }}_{0}}\left( {{\lambda }{{{\beta }}_{0}} - {{{\alpha }}_{0}}{{C}_{{\varphi }}}} \right)]$

$D_{{{\varphi }z}}^{*} = {{{\beta }}_{0}}\left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right) - {{{\tau }}_{2}}[{{{\beta }}_{0}}(C_{{\varphi }}^{2} + {\beta }_{0}^{2}) + {\lambda }\left( {{\lambda }{{{\beta }}_{0}} - {{{\alpha }}_{0}}{{C}_{{\varphi }}}} \right)]$

$D_{{z{\varphi }}}^{*} = - {{{\alpha }}_{0}}\left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right) - {{{\tau }}_{2}}[{{C}_{{\varphi }}}\left( {{\lambda }{{{\beta }}_{0}} - {{{\alpha }}_{0}}{{C}_{{\varphi }}}} \right) - {{{\alpha }}_{0}}({\alpha }_{0}^{2} + {{{\lambda }}^{2}})]$

(5.8)

$D_{{zz}}^{*} = {\lambda }\left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right) - {{{\tau }}_{2}}[{{{\beta }}_{0}}\left( {{\lambda }{{{\beta }}_{0}} - {{{\alpha }}_{0}}{{C}_{{\varphi }}}} \right) + {\lambda }(\alpha _{0}^{2} + {{{\lambda }}^{2}})]~$

Представляет интерес также симметричный тензор напряжений Коши

${\mathbf{T}} = {{{\mathbf{C}}}^{{\text{T}}}} \cdot {\mathbf{D}} = {{{\sigma }}_{r}}{{{\mathbf{e}}}_{r}} \otimes {{{\mathbf{e}}}_{r}} + {{{\sigma }}_{{\varphi }}}{{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{e}}}_{{\varphi }}} + {{\tau }_{{{\varphi }z}}}({{{\mathbf{e}}}_{{\varphi }}} \otimes {{{\mathbf{i}}}_{3}} + {{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{e}}}_{{\varphi }}}) + {{{\sigma }}_{z}}{{{\mathbf{i}}}_{3}} \otimes {{{\mathbf{i}}}_{3}}~$

Его компоненты имеют вид

${{{\sigma }}_{r}} = \left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right)C_{r}^{2} - {{{\tau }}_{2}}C_{r}^{4} - p\left( r \right)$

${{{\sigma }}_{{\varphi }}} = \left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right)l - {{{\tau }}_{2}}({{l}^{2}} + {{q}^{2}}) - p\left( r \right)$

${{\tau }_{{{\varphi }z}}} = \left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right)q - {{{\tau }}_{2}}q\left( {s + l} \right)$

${{{\sigma }}_{z}} = \left( {{{{\tau }}_{1}} + {{I}_{1}}{{{\tau }}_{2}}} \right)s - {{{\tau }}_{2}}({{q}^{2}} + {{s}^{2}}) - p\left( r \right)$

(5.9)

$l = C_{{\varphi }}^{2} + {\alpha }_{0}^{2},\quad s = {\alpha }_{0}^{2} + {\beta }_{0}^{2},\quad q = {{{\beta }}_{0}}{{C}_{{\varphi }}} - {{{\alpha }}_{0}}{\lambda }~$

Из (5.9) следует, что компоненты девиатора напряжений Коши в цилиндрических координатах и инварианты девиатора – постоянные величины.

Дифференциальное уравнение для давления p(r), вытекающее из (2.5), уравнений равновесия (2.4) и соотношения (5.4), будет таким:

(5.10)

$C_{r}^{{ - 1}}\frac{{dp}}{{dr}} + \frac{\Delta }{r}p = \frac{{D_{{rr}}^{*} - D_{{{\varphi \varphi }}}^{*}}}{r}~$

Здесь постоянные величины $D_{{rr}}^{*}$ и $D_{{{\varphi \varphi }}}^{*}$ определяются выражениями (5.8). Решая уравнение (5.10) при граничном условии ${{D}_{{rr}}}\left( {{{r}_{0}}} \right) = 0$, получим

(5.11)

$p\left( r \right) = \left( {D_{{rr}}^{*}{{C}_{r}} - \frac{{D_{{rr}}^{*} - D_{{{\varphi \varphi }}}^{*}}}{r}} \right){{\left( {\frac{{{{r}_{0}}}}{r}} \right)}^{{\Delta {{C}_{r}}}}} + \frac{{D_{{rr}}^{*} - D_{{{\varphi \varphi }}}^{*}}}{r}~$

Таким образом, построено универсальное в классе изотропных несжимаемых упругих тел решение задачи о растяжении-сжатии кругового цилиндра с трехпараметрическим распределением дислокаций (5.1). Из (5.11) видно, что при Δ > 0, где величина Δ определена формулой (5.3), напряжения имеют особенность на оси цилиндра r = 0. При Δ < 0 напряжения ограничены во всем цилиндре.

Уравнение (5.10) имеет очевидное постоянное решение $p = {{\Delta }^{{ - 1}}}(D_{{rr}}^{*} - D_{{{\varphi \varphi }}}^{*})$. Этому решению можно придать смысл, если рассматривать неограниченную упругую среду.

Продольная сила, действующая в каждом поперечном сечении цилиндрического стержня, определяется при помощи (5.8), (5.11) и выражается так:

(5.12)

$Q = 2{\pi }\mathop \smallint \limits_0^{{{r}_{0}}} {{D}_{{zz}}}rdr = {\pi }r_{0}^{2}\left[ {D_{{zz}}^{*} - \frac{{C_{r}^{2}{{C}_{{\varphi }}}(D_{{rr}}^{*} + D_{{{\varphi \varphi }}}^{*})}}{{2 - \Delta {{C}_{r}}}}} \right]~$

Используя (5.3), можно доказать, что $\Delta {{C}_{r}} < 1$. Поэтому знаменатель в (5.12) всегда отличен от нуля.

6. Заключение. В этой статье с точки зрения нелинейной теории дислокаций исследована задача о больших деформациях растяжения–сжатия и кручения сплошного кругового цилиндра, содержащего распределенные дислокации. Для распределенных винтовых дислокаций осевого, радиального и азимутального направлений найдены точные и универсальные в классе изотропных несжимаемых материалов решения задач о напряженно-деформированном состоянии цилиндра. Универсальное решение построено также для задачи о растяжении-сжатии цилиндрического стержня в случае, когда тензор плотности дислокаций имеет три независимые компоненты. Основные результаты сформулированы в терминах величин, доступных измерению в эксперименте: продольное удлинение, угол закручивания, осевая сила и крутящий момент. Получены явные формулы, характеризующие влияние дислокаций на нелинейное сопротивление цилиндра растяжению и кручению.

Работа выполнена при поддержке РНФ (проект 18-11-00069).

Список литературы

Clayton J.D. Nonlinear Mechanics of Crystals. Dordrecht: Springer, 2011. 700 p.
Арутюнян Р.А. Высокотемпературная ползучесть и длительная прочность металлических материалов // Изв. РАН. МТТ. 2018. № 6. С. 103–109.
Дудко О.В., Рагозина В.Е. О динамике разгрузки и упругих волнах в среде с предварительно накопленными пластическими деформациями // Изв. РАН. МТТ. 2019. № 3. С. 41–53.
Gutkin M.Y, Ovid’ko I.A Plastic Deformation in Nanocrystalline Materials. B.: Springer, 2004. 194 p.
Zubov L.M. Nonlinear Theory of Dislocations and Disclinations in Elastic Bodies. B.: Springer, 1997. 205 p.
Vorovich I.I. Nonlinear Theory of Shallow Shells. New York: Springer, 1999. 390 p.
Kondo K. On the geometrical and physical foundations in the theory of yielding. // In: Proc. 2nd Jap. Nat. Congress of Appl. Mechanics, Tokyo, 1952. P. 41–47.
Bilby B.A, Bullough R., Smith E. Continuous distributions of dislocations: a new application of the methods of non-Riemannian geometry // Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences. A, 1955.231. P. 263–273.
Kröner E. Allgemeine Kontinuumstheorie der Versetzungen und Eigenspannungen // Arch Ration Mech Anal. 1960. V. 4. P. 273–334.
Зеленина А.А., Зубов Л.М. Изгиб и кручение нелинейно упругих тел с непрерывно распределенными дислокациями // Вестник Южного научного центра РАН. 2009. Т. 5. № 4. С. 15–22.
Yavary A., Goriely A. Riemann–Cartan geometry of nonlinear dislocation mechanics // Arch. Ration. Mech. Anal. 2012. V. 205. P. 59–118.
Зеленина А.А., Зубов Л.М. Нелинейные эффекты при растяжении, изгибе и кручении упругих тел с распределенными дислокациями // ДАН. 2013. Т. 451. № 5. С. 516–519.
Зубов Л.М. Сферически симметричные решения нелинейной теории дислокаций // ДАН. 2014. Т. 458. № 2. С. 161–164.
Goloveshkina E.V., Zubov L.M. Universal spherically symmetric solution of nonlinear dislocation theory for incompressible isotropic elastic medium // Arch. Appl. Mech. 2019. V. 89. № 3. P. 409–424.
Nye J.F. Some geometrical relations in dislocated crystals // Acta Metall. 1953. V. 1. № 2. P. 153–162.
Эшелби Дж. Континуальная теория дислокаций. М.: ИЛ, 1963. 248 с.
Ландау Л.Д., Лифшиц Е.М. Теоретическая физика. Т. 7. Теория упругости. М.: Наука, 1987. 248 с.
Вакуленко А.А. Связь микро- и макросвойств в упругопластических средах // Итоги науки и техники. Сер. Механика деформируемого твердого тела. М.: ВИНИТИ. 1991. Т. 22. С. 3–54.
Лурье А.И. Нелинейная теория упругости. М.: Наука, 1980. 512 с.
Derezin S.V., Zubov L.M. Disclinations in nonlinear elasticity // Ztsch. Angew. Math. und Mech. 2011. V. 91. P. 433–442.
Галаско А.А., Зубов Л.М. Нелинейная теория кручения упругих цилиндров с винтовой дислокацией // Изв. вузов. Северо-Кавказ. регион. Естеств. науки. 2015. № 4. С. 35–43.
Зубов Л.М. О прямом и обратном эффектах Пойнтинга в упругих цилиндрах // ДАН. 2001. Т. 380. № 2. С. 194–196.

Дополнительные материалы отсутствуют.

Инструменты

следующая статья выпуска предыдущая статья выпуска содержание выпуска

Известия РАН. Механика твердого тела

Архивы выпусков Информация о журнале Отправить рукопись в журнал