Известия РАН. Механика твердого тела, 2020, № 5, стр. 87-94

1. Введение. Динамическое распространение трещины в хрупком материале – сложный процесс, для изучения которого необходимы модели разрушения, учитывающие структурно-временные особенности процессов разрушения материала.

Классическим подходом к задачам о динамическом распространении трещин является метод, основанный на квазистатическом критерии разрушении Ирвина, интерполированного на случай динамики. Так, в работе [1] предполагается, что трещина распространяется при условии равенства текущего коэффициента интенсивности напряжений значению некоторого функционала ${{K}_{{ID}}}({v})$, где ${v}$ – текущая скорость трещины. Соответственно, функционал ${{K}_{{ID}}}({v})$ предполагается параметром материала, который должен определяться из экспериментов. Однако в экспериментальных работах [2–5] отмечается, что разные конфигурации образцов и нагрузки могут существенно влиять на характер зависимости коэффициента интенсивности от скорости трещины: например, при высокоскоростном нагружении значительному изменению текущего коэффициента интенсивности напряжений может соответствовать постоянная скорость трещины.

В работе [6] отмечается, что инициация движения трещины при воздействии на образцы короткими импульсами не всегда происходит при максимальных значениях коэффициента интенсивности напряжений. Основываясь на своих экспериментальных результатах, авторы выдвинули концепцию минимального времени – временного параметра, зависящего от истории и способа воздействия и определяющего минимальную длительность нагрузок, необходимую для инициации разрушения. К распространенным подходам к задачам динамики трещин также стоит отнести метод зоны сцепления [7]. Также стоит отметить работы Шемякина и Никифоровского [8], в которых подчеркивалась важность учета интегральных временных характеристик локального поля напряжений для предсказания развития разрушения.

В настоящей работе вопросы динамики трещин исследовались при помощи структурно-временного критерия, основанного на понятии инкубационного времени разрушения. Данный подход, предложенный в работах [9, 10], заключается в структурно-временной дискретизации процесса динамического разрушения: вводится понятие пространственной ячейки разрушения с конечными размерами, которая определяет масштабный уровень, на котором регистрируется событие разрушения, а также характерное время разрушения, являющееся константой материала и связанное с релаксационными процессами, происходящими на более низких масштабных уровнях. Условие разрушения в точке пространства $x'$ в момент времени $t'$ записывается в виде следующего неравенства:

В (1.1) ${{{\sigma }}_{c}}$ – статическое критическое напряжение в материале, ${\sigma }\left( {x,t} \right)$ – зависящее от времени напряжение в точке x, d – пространственный размер, определяющий масштабный уровень регистрации разрушения. Так, в задачах о продвижении трещины параметр d может быть трактован как минимально возможное продвижение трещины, связанное с событием элементарного разрушения на данном масштабном уровне. Данный параметр вычисляется согласно формуле

содержащей критический коэффициент интенсивности напряжений ${{K}_{{Ic}}}$ и обеспечивающей предельный переход к классическому критерию в квазистатическом случае медленного воздействия [10, 11]. В (1.1) также входит инкубационное время ${\tau }$, которое считается параметром материала. Инкубационное время позволяет учесть релаксационные процессы, протекающие на более низких масштабных уровнях (в сравнении с данным масштабным уровнем, определяемым параметром d), к которым можно отнести возникновение, развитие и слияние микротрещин, дефектов и пор, приводящие, в конечном счете, к регистрируемому разрушению на данном макроскопическом масштабе.

Подход на основе критерия (1.1) был успешно применен для исследования разрушения в различных материалах [11, 12], при различных условиях нагружения, а также для исследования самых разнообразных физических процессов [13, 14].

В настоящей работе структурно-временная модель разрушения (1.1) используется для исследования нестационарных процессов, сопровождающих динамическое распространение трещины.

2. Численная реализация подхода. Для численного исследования и предсказания динамического распространения трещины критерий разрушения (1.1) используется в сочетании с методом конечных элементов. Критерий (1.1) внедряется в расчетный комплекс ANSYS в качестве внешней процедуры, созданной для контроля над процессом распространения трещины. Интегрирование по пространственной координате и по времени в (1.1) производится численно. Процедура сохраняет историю напряжений в узлах, лежащих на траектории трещины, что позволяет вычислить интеграл по времени на каждом шаге решения задачи. Пространственное интегрирование производится по нескольким узлам, лежащим в интервале [0, d], считая от вершины трещины. Данная расчетная схема позволяет решать задачи о прямолинейном распространении трещин в симметричных образцах и при симметричном способе приложения нагрузки, причем траектория трещины должна совпадать с линией симметрии.

Задача решается в упругой постановке и в предположении малых деформаций. Таким образом, математическая постановка задачи выглядит следующим образом:

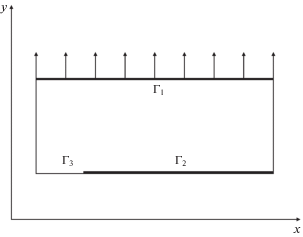
В (2.1) U – вектор перемещений, ρ – плотность материала, λ и μ – константы Лямэ. Считалось, что в начальный момент времени перемещения и скорости равны нулю. При квазистатическом нагружении к точкам одной из границ тела медленно прикладывались перемещения. В случае динамической нагрузки к берегам начальной трещины прикладывался импульс давления трапециевидной формы. В (2.2) приведены начальные краевые условия для задачи о квазистатическом нагружении пластины с трещиной, нагрузка (перемещение) прикладывается к верхнему краю пластины. Схема нагружения и используемых краевых условий представлена на рис. 1.

${{U}_{2}}\left( {{\mathbf{X}} = {{{\Gamma }}_{1}},t} \right) = {v}t$, где ${v}$ – скорость движения захвата растягивающей машины

В (2.2) ${\mathbf{X}} = \left( {{{x}_{1}},~{{x}_{2}}} \right)$, вектор перемещений ${\mathbf{U}}\left( {{\mathbf{X}},t} \right) = \left( {{{U}_{1}}\left( {{\mathbf{X}},t} \right),~{{U}_{2}}\left( {{\mathbf{X}},t} \right)} \right)$. Разработанная расчетная схема была применена для исследования осцилляций скорости трещины при квазистатическом нагружении пластин из ПММА, а также для исследования зависимости текущего коэффициента напряжений от скорости трещины для модельного материала в двух режимах нагружения – квазистатическом и высокоскоростном.

3. Результаты численных исследований. Исследования осцилляций скорости трещины. В работе [15] исследовалось распространение трещины в пластинах из ПММА под воздействием перемещений, прикладываемых к верхней и нижней границам образцов. Исследователи регистрировали позицию вершины трещины и текущую скорость трещины. При этом авторы отмечают заметные осцилляции скорости трещины.

Структурно-временной критерий разрушения подразумевает дискретизацию процесса разрушения по времени и пространству, так как вводится минимальное продвижение трещины, определяемое параметром d. Введение же характерного времени разрушения – инкубационного времени τ – приводит к дискретизации процесса разрушения по времени.

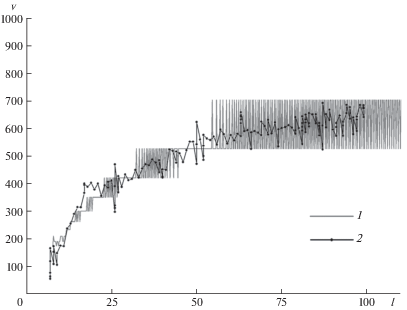
На рис. 2 приведены экспериментальные данные из [15], а также результаты расчетов с использованием критерия (1.1). Выбор характерного размера $d = 0.2$ мм согласно формуле (1.2) позволяет численно получить осцилляции скорости трещины, амплитуды которых хорошо соответствуют экспериментально наблюдаемому явлению. По горизонтальной оси отложена длина трещины l (мм), по вертикальной – скорость трещины ${v}$ (м/с). Результаты моделирования представлены линией 1, экспериментальные данные из [15] – линией 2.

Таким образом, дискретизация процесса разрушения согласно структурно-временному критерию разрушения (1.1) позволяет качественно и количественно исследовать нестационарный характер скорости движущейся трещины. Феномен осцилляций скорости трещин также был исследован экспериментально и численно в работе [16].

Исследование зависимости коэффициента интенсивности напряжений от скорости трещины. Зависимость коэффициента интенсивности K_I (рассматривается нагружение по первой моде) от скорости трещины ${v}$ имеет определяющее значение для одного из распространенных подходов к задаче предсказания движения трещины. В ряде работ утверждается [1], что данная зависимость должна рассматриваться как свойство материала и должна определяться экспериментально для дальнейшего использования в соответствующих критериях разрушения. Однако, как видно из исследований [2–4], высокоскоростное нагружение может приводить к ситуации, когда практически постоянной скорости трещины соответствуют значительные изменения значений K_I, что может служить подтверждением нестационарности данной зависимости. Таким образом, ставится под сомнение единственность зависимости ${{K}_{I}} - {v}$ для данного материала и, соответственно, возможность трактовать данную зависимость как свойство материала.

Для исследования данной проблемы было проведено моделирование поведения одинаковых образцов (квадратные пластины 20 × 20 см с боковым вырезом 10 см) из материала со свойствами, схожими со свойствами ПММА. В одном случае нагружение проводилось квазистатически – берега трещины медленно раздвигались, во втором случае к берегам трещины прикладывается импульс давления. Дискретизация процесса разрушения согласно применяемому структурно-временному подходу привела к наличию дискретного набора скоростей. Каждой скорости из этого набора сопоставляются значения текущего КИН, вычисляемого при помощи J-интеграла.

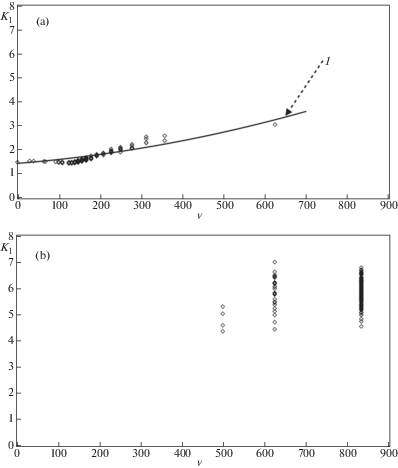
Результаты расчетов на основе структурно-временного подхода для обоих типов нагружения приведены на рис. 3. Динамическое нагружение привело к практически мгновенному ускорению трещины до максимальных скоростей – (b) на рис. 3. При этом разброс значений для одного определенного значения КИН достаточно велик, что не позволяет построить классическую зависимость ${{K}_{I}} - {v}$. Напротив, для случая приложения квазистатической нагрузки разброс значений КИН меньше, что позволяет построить кривую зависимости ${{K}_{I}} - {v}$, используя приближение гладкой функцией (рис. 3a, гладкая аппроксимация 1 указана стрелкой).

В данном случае разброс значений коэффициента интенсивности напряжений является естественным следствием пространственной и временной дискретизации процесса разрушения. Полученный сильный разброс значений КИН качественно соответствует результату, полученному в экспериментальных работах [2–4].

4. Заключение. В представленной работе были проанализированы нестационарные эффекты, сопровождающие динамическое распространение трещины в хрупких материалах. Численные исследования проводились при помощи метода конечных элементов и структурно-временного критерия разрушения. Структурно-временная модель разрушения подразумевает пространственную и временную дискретизацию процесса разрушения, так как в рамках данной модели используется минимальный объем разрушающегося материала (в случае движения трещины – минимальный возможный проскок трещины), а также характерное время разрушения – инкубационное время.

Дискретизация процесса разрушения в рамках структурно-временного подхода позволяет получить ряд принципиальных результатов, согласующихся с экспериментами. Во-первых, внедрение минимального продвижения трещины согласно структурно-временному критерию разрушения позволяет численно исследовать нестационарное поведение скорости движущейся трещины: так, были получены экспериментально наблюдаемые осцилляции скорости трещины, распространяющейся в пластинах из ПММА в условиях разгона динамической трещины, вызванного квазистатическим нагружением [15]. Амплитуда осцилляций скорости трещины, полученная при помощи расчетов, хорошо совпадает с экспериментальными значениями.

Также использование структурно-временного подхода позволяет исследовать вопрос единственности зависимости коэффициента интенсивности напряжений от скорости трещины (${{K}_{I}} - {v}$ зависимость). Вследствие дискретного характера распространения трещины при использовании структурно-временной модели и метода конечных элементов наблюдается заметный разброс значений КИН, соответствующих выбранным значениям скорости трещины. При этом разброс значений КИН для случая квазистатического нагружения относительно невелик, и классическая зависимость ${{K}_{I}} - {v}$ “в среднем” может быть построена. В случае же высокоскоростного нагружения значительный разброс значений КИН не позволяет построить такую зависимость: трещина может двигаться с практически постоянной скоростью, тогда как соответствующий ее значению коэффициент интенсивности изменяется в широком диапазоне. Такое поведение соответствует экспериментам [2–4].

Таким образом, с одной стороны, использование структурно-временного подхода позволяет разрешить противоречия, возникшие относительно единственности зависимости ${{K}_{I}} - {v}$ для данного материала, а с другой стороны обойтись без априорного знания данной зависимости для прикладных расчетов динамики трещин. Это определяет существенное преимущество развитого подхода по сравнению с традиционными, так как экспериментальное определение зависимости КИН от скорости трещины – весьма трудоемкий процесс, приводящий к неоднозначным результатам.

Работа выполнена при поддержке РФФИ (20-01-00291, 18-51-80008). Н.А. Казаринов благодарит фонд РНФ (18-71-00107) за поддержку при создании секций 2 и 3.1.