Известия РАН. Механика твердого тела, 2020, № 5, стр. 13-20
ТРЕЩИНЫ НОВОГО ТИПА И МОДЕЛИ НЕКОТОРЫХ НАНОМАТЕРИАЛОВ
В. А. Бабешко a, b, *, О. М. Бабешко b, О. В. Евдокимова a
a Южный научный центр РАН
Ростов-на-Дону, Россия
b Кубанский государственный университет
Краснодар, Россия
* E-mail: babeshko41@mail.ru
Поступила в редакцию 10.03.2020
После доработки 23.04.2020
Принята к публикации 30.04.2020
Аннотация
В статье доказано, что недавно выявленные трещины нового типа, которые имеют иной механизм разрушения среды, чем трещины Гриффитса, не могут быть получены в результате сближения сторон клиновидной полости в пластине. Таким образом, трещины нового типа получаются как результат виртуального сближения боковых сторон прямоугольной полости в пластине. Для доказательства применен метод блочного элемента. Этот же метод использован для моделирования некоторых видов нано частиц, материалов мозаичной структуры и исследования образования трещин нового типа в таких материалах.
Введение. Построенная Гриффитсом теория трещин [1] в дальнейшем усовершенствованная Ирвиным [2] получила и продолжает получать развитие в ряде работ отечественных и зарубежных исследователей. Среди них следует отметить работу [3], в которой исследовалась физическая сторона проблемы трещин, а в работе [4] дана строгая математическая теория этих объектов, открывшая путь к многочисленным приложениям. В условиях кажущегося исчерпания теоретических проблем в теории трещин, при изучении скрытых дефектов в материалах и разломов литосферных плит в сейсмологии [5, 6] пришлось столкнуться с ситуацией, которая никак не вкладывалась в теорию трещин Гриффитса, хотя и казалась происходящей из нее. Именно, в граничных задачах, описывающих поведение скрытых дефектов в материалах с покрытиями, а также в сейсмологии, в зоне разломов литосферных плит [5], было выявлено возникновение сингулярных концентраций контактных напряжений при сближении плит, что приводит к стартовым землетрясениям. В этих граничных задачах изучалось напряженно-деформированное состояние блочной структуры, состоящей из трех блоков: двух двумерных, моделируемых полубесконечными пластинами Кирхгофа, которые без трения лежали на третьем, моделируемым трехмерным упругим слоем. Внешнее воздействие осуществлялось вертикальными усилиями, действующими на плиты, включающими и их вес [5]. В работе [6] подтверждено существование трещин нового типа в трехмерной среде. В дополнение к выполненным исследованиям, в настоящей работе доказано, что трещина, образующаяся в результате сближения берегов клиновидной полости в пластине, представляет трещину Гриффитса, а не нового типа [7, 8]. Этот результат опровергает высказывания некоторых исследователей, утверждающих, что трещины нового типа ранее уже изучались. Математический аппарат метода блочного элемента, использованный при исследовании ряда прикладных задач [9, 10], а также трещин нового типа оказалось возможным применить для изучения некоторых видов нано материалов, их самоорганизации или самосборки и трещин в них. В частности, в настоящей работе, предпринята попытка объяснений явления самосборки некоторых типов нано материалов как результат ряда механических процессов, происходящих с нано частицами, моделируемыми блочными элементами. Имеющиеся в многочисленных публикациях объяснения самосборки нано материалов, в большинстве случаев относят самосборку к категории физических свойств, присущих нано частицам, и не подлежащих детализации, подобно спинам в квантовой механике, связанным со свойствами элементарных частиц. Развиваемое в статье использование блочных элементов, как моделей некоторого типа нано частиц, остающихся нано частицами после объединения, объясняет явление самосборки как результат механической локализации наночастиц, их перемешивания, происходящих постоянно, и последующего склеивания по границам. Математическое описание процесса склейки демонстрируется на примере одного типа блочных элементов. Здесь нано частицы рассматриваются как двумерные многоугольники, описываемые уравнениями мембран, подобно трехмерному представлению [11]. Изучается этап склеивания нано частиц, как объединение блочных элементов, представляющих топологические объекты. Склеивание блочных элементов вновь приводит к блочным элементам, что формирует дискретное топологическое пространство [12]. Так может формироваться материал, в том числе, нано, имеющий мозаичную структуру. В таком материале возможно возникновение трещин нового типа.
1. О трещинах нового типа. Для правильного понимания математических построений, необходимых в дальнейшем, приведем простейший вариант формирования трещины нового типа, основываясь на результатах работы [6], где рассматривалась антиплоская граничная задача для блочной структуры. Возьмем три блочных элемента, состоящих из полупространства с симметрично расположенными на нем прямоугольными неограниченными клиньям первого и второго квадрантов [6].
Для простоты рассмотрим в каждом из них антиплоскую граничную задачу для уравнений Ламе, которая сводится к уравнению Гельмгольца [6].
Считаем, что на границах задаются напряжения вида
Применением метода блочного элемента, получим
$F_{2}^{{ - 1}}({{x}_{2}},{{x}_{3}})$ – двумерный оператор обращения Фурье.
Положим во всех этих формулах
Это означает, что все три блока представлены однотипным материалом,
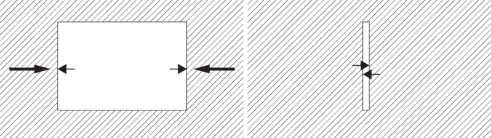
содержащим трещину нового типа, а между верхними блоками и нижним основанием имеется полное сцепление. Тогда в результате сближения клиньев до встречи, будет сформирована трещина нового типа, представленная на рис. 1 и продолженная вверх до бесконечности.
Контактные напряжения в случае не сблизившихся клиновидных блоков описываются вблизи краев формулами вида
Здесь ${{\sigma }_{{1b}}}({{x}_{2}},{{x}_{3}})$, $b = \lambda ,r$ непрерывные по обеим координатам функции при достаточно гладких ${{f}_{{bn}}}$, $b = \lambda ,r$ [6]. Решение оказывается энергетическим.
При сблизившихся блоках, концентрация контактных напряжений в зоне сближения приобретает в общем случае сингулярную особенность вида
Образуются трещины нового типа с кусочно-гладкой границей.
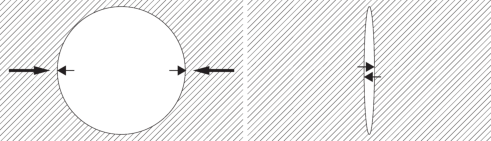
Решение оказывается не энергетическим. В частном случае специальной нагрузки на вертикальные границы клиновидных блоков эта особенность может отсутствовать, и решение окажется энергетическим. Этой особенностью трещины нового типа существенно отличаются от трещин Гриффитса [6], которые образуются сжатием с боков полости в виде эллипса или окружности, рис 2, и имеют гладкую границу.
2. О свойствах клиновидных полостей и трещин Гриффитса. В обзоре работ о сингулярностях в клиновидных областях [7, 8] рассмотрены случаи вырождения клиновидных полостей в трещины при стремлении угла клина к нулю. Высказывается мнение, что в процессе такой трансформации косочно-гладкая граница клиновидной полости остается кусочно-гладкой, и в пределе образуются трещины нового типа. Ниже показано, что это мнение ошибочно. Во всех случаях преобразования клиновидной полости в трещину, когда угол стремится к нулю, получается только трещина Гриффитса.
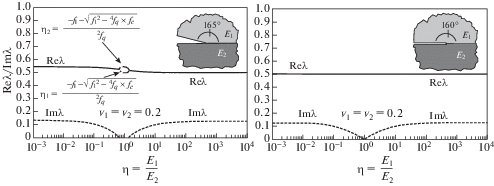
Мы используем результаты автора одной из таких работы [8], Рисунок 3, хотя примеров много. Он применил бесспорно строгий математический подход и получил значения особенностей в окрестности вершины полости и образовавшейся трещины, когда угол равен нулю. Запишем интегральное уравнение полубесконечной трещины в безразмерном виде и воспользуемся вычисленной в настоящей работе сингулярностью в окрестности вершины трещины [13]. Оно имеет вид
Здесь q(x) являются напряжениями, действующими на берега трещин; $f(x)$ описывает поведение берегов трещины, которое определяет ее форму.
K(u) – преобразование Фурье ядра интегрального уравнения [14]. Мы предполагаем, что берега трещины симметричны и одинаковые напряжения действуют на оба берега. Для простоты рассмотрим случай одного и того же материала для каждой полуплоскости берегов. В настоящей форме ядро интегрального уравнения является обобщенной функцией, так как аналитическая функция K(u) растущей.
В статическом случае будем считать, что функция K(u) не имеет нулей и полюсов на вещественной оси [6] с учетом результата работы [8], показанного на рис. 3, мы находим, что напряжения, приближающиеся к вершине трещины справа, $x \to 0$, $x > 0$, например, описывается функцией
Его преобразование Фурье имеет вид
Мы предполагаем, что задана непрерывно дифференцируемая функция $q(x) \in L( - \infty ,0)$
По теореме Лебега-Римана ее преобразования Фурье Q(u) убывают на бесконечности.
Продолжим интегральное уравнение на всю ось, имеем
Применяя преобразование Фурье к интегральному уравнению на всей оси, получаем функциональное уравнение вида
Отсюда мы находим
илиПроизводная имеет выражение
Простой анализ интеграла при таких условиях для заданных функций позволяет доказать непрерывность производной везде, кроме точки x = 0, обладающей свойством
Это означает, что касательная на вершине горизонтальной трещины занимает вертикальное положение. Интегрируя это отношение в окрестности нуля с учетом непрерывности производной на интервале $ - \infty < x < 0$, мы приходим к выводу, что функция $f(x)$ является гладкой, без угла в вершине трещины и ведет себя вблизи нуля как…
Это означает, что берега трещины непрерывно сходятся, имея гладкую форму трещины Гриффитcа [1].
Таким образом, получается трещина Гриффитса, несмотря на то, что она возникла из полости с кусочно-гладкой границей. Последнее означает, что в рассмотренных работах [7, 8] трещины нового типа не появлялись и никем ранее не описывались.
3. О сопряжении блочных элементов и модели некоторых типов наночастиц. В работе предпринята попытка объяснений явления самосборки некоторых типов наноматериалов как результат ряда механических процессов, происходящих с моделями нано частиц, рассматриваемыми как блочные элементы, введенные и исследованные авторами в ряде публикаций. Вопросам объяснения сомоорганизации или самосборки нано материалов, посвящены достаточно интересные работы [15]. Однако имеются публикации, в которых относят самосборку к категории физических свойств, присущих нано частицам, и не подлежащих детализации, подобно спинам в квантовой механике. Развиваемое в статье использование метода блочного элемента объясняет явление самосборки как результат механической локализации нано частиц, их перемешивания, происходящих постоянно, и последующего склеивания по границам. В настоящей работе в качестве примера нано частицы рассматриваются как двумерные многоугольники, описываемые уравнениями мембран. Изучается этап склеивания нано частиц, показывающий, что такие объекты представляют математическую группу, и присоединение новой нано частицы, описываемой с помощью средств внешней алгебры, порождает вновь блочный элемент, способный соединяться с другими блочными элементами, моделируя этот процесс с нано частицами.
Для исследования этих процессов вновь обратимся к уже примененным при построении трещины нового типа блочным элементам в виде прямоугольных клиньев, занимающих области первого и второго квадрантов. Однако, блочный элемент, занимающий область нижнего полупространства исключается. Ради краткости, рассматриваем простейший случай, когда граничные задачи, описывающие нано частицы, даются уравнениями Гельмгольца антиплоской задачи, что также совпадает с уравнениями мембран. Технически более сложно рассматривать случаи уравнений пластин Кирхгофа или уравнений Ламе.
В предыдущих пунктах рассматривались два блочных элемент расположенные на блочном элементе в виде полупространства, либо отстоящими друг от друга по горизонтали, либо сблизившимися, создав трещину нового типа, берега которой могут быть нагружены напряжениями. В настоящем пункте рассматриваем сблизившиеся блочные элементы, но уже без полупространства. Предположим, что эти блочные элементы полностью соединяются, то есть уходят от наличия трещины, и превращаются в единое целое. Для рассматриваемой модели должны выполняться требования совпадения границ блочных элементов, ${{b}_{1}} = {{b}_{2}} = 0$, и выполняться условия на напряжения, состоящие в равенство действий напряжений на каждый берег трещины. В упакованном виде блочные элементы имеют вид
Взяв левый и правый блочные элементы в упакованном виде, обеспечив совпадение границ, приходим при принятых предположениях относительно перемещений к взаимному сокращению первых членов справа и сохранению вторых во внешних формах ωλ, ${{\omega }_{r}}$. Получившийся новый упакованный блочный элемент имеет, как не трудно вычислить, имеет вид
Как и ожидалось, он представляет блочный элемент в форме верхнего полупространства, в результате соединения первого и второго квадрантов, и после упрощения с учетом свойств “нулей-отсикаторов” ${{\alpha }_{2}}$, ${{\alpha }_{{2 + }}}$, ${{\alpha }_{{3 + }}}$ принимает вид
Добавив во внешние формы ${{\omega }_{{\lambda 0}}}$, ${{\omega }_{{r0}}}$ члены, сокращенные справа в формулах ωλ, ${{\omega }_{r}}$, получаем разделение верхнего полупространства на два упакованных блочных элемента с носителями в первом и втором квадрантах. Таким образом, продемонстрированы свойства алгебраической группы Абеля на примере рассмотренных блочных элементов, которые могут служить моделями нано частиц. Рассмотрены простейшие примеры областей, занятых блочными элементами. Их можно усложнять, применив соответствующие алгоритмы построения блочных элементов.
Рассматривая блочные элементы, отвечающие разным граничным задачам, диктуемым дифференциальными уравнениями с переменными коэффициентами, объединяя их в блоки, занимающие области, в которых поставлена граничная задача, можем строить материалы, мозаичной структуры, диктуемые этой граничной задачей. Введя на образовавшейся границе между блочными элементами разнотипные, взаимно не сокращаемые напряжения, получим трещины нового типа, если эти блочные элементы поставить сверху на упругое полупространство.
Выводы. Таким образом, изучая методом блочного элементного прогноз землетрясений, а также скрытые дефекты в телах с покрытиями, авторы неожиданно обнаружили существование трещин нового типа. Они дополняют трещины Гриффитса-Ирвина. Существование трещин нового типа расширяет понимание процессов разрушения сред и материалов. В сейсмологии это позволяет дать новое объяснение форшокам и афтершокам. При изучении трещин нового типа обнаружилось, что развиваемый математический аппарат позволяет исследовать класс граничных задач, открывающих возможность получать определенные результаты в области нанотехнологий и дефектов в них. В настоящее время продолжается изучение свойств трещин нового типа и, возможно, будут выявлены их новые свойства.
Отдельные фрагменты работы выполнены в рамках реализации Госзадания ЮНЦ РАН на 2020 г., проекта (00-19-13) № 01201354241, программ президиума РАН №7, проект (00-19-03) и №20 проект (00-19-10), и при поддержке грантов РФФИ (19-41-230003), (19-41-230004), (19-48-230014), (18-08-00465), (18-01-00384), (18-05-80008).
Список литературы
Griffith A. The Phenomena of Rupture in Solids // Trans. R. Soc. London, 221A. 1920. P. 163–197.
Irwin G. Fracture dynamics // Fracture of metals, ASM, Cleveland. 1948. P. 147–166.
Черепанов Г.П. Механика хрупкого разрушения. М.: Наука, 1974. 640 с.
Морозов Н.Ф. Математические вопросы теории трещин. М.: Наука, 1984. 256 с.
Babeshko V.A., Evdokimova O.V., Babeshko O.M. On the possibility of predicting some types of earthquake by a mechanical approach // Acta Mechanica 2018. V. 229. № 5. P. 2163–2175. https://doi.org/10.1007/s00707-017-2092-0
Бабешко В.А., Евдокимова О.В., Бабешко О. М. Об одном новом типе трещин, дополняющих трещины Гриффитса-Ирвина // ДАН. 2019. Т. 485. № 2. С. 34–38.
Sinclair G.B. Stress singularities in classical elasticity I; II, Appl. Mechanics Reviews. 2004. V. 57. P. 251–298; 2004. V. 57. P. 385–439. Reviews. 2004. V. 57. P. 385–439.
Sator C., Becker W. Closed-form solutions for stress singularities at plane bi- and trimaterial junctions // Arch. Appl. Mech. 2012. V. 82. P. 643–658.
Бабешко В.А., Бабешко О.М., Евдокимова О.В.,Зарецкая М.В., Павлова А.В., Уафа С.Б., Шестопалов В.Л. О мониторинге состояния параллельных штолен в зоне горизонтального движения литосферных плит // Изв. РАН. МТТ. 2017. № 4. С. 42–49.
Бабешко В.А., Евдокимова О.В., Бабешко О.М. Елецкий1, Ю.Б. Уафа1 С.Б. О прочностных свойствах смазываемых подшипников с дефектными покрытиями // Изв. РАН. МТТ. 2019. № 6. С. 48–54. https://doi.org/10.1134/S0572329919060035
Ovid’ko I.A. Deformation of nanostructures // Science. 2002. T. 295. № 5564. C. 2386–2398.
Голованов Н.Н., Ильютко Д.П., Носовский Г.В., Фоменко А.Т. Компьютерная геометрия. М.: Академия, 2006. 512 с.
Glushkov EV, Glushkova N.V., Lapina O.N. Singularity exponents of elastic stresses at the point where the crack reaches the surface // Mechanics of Solids. 1998. V. 33. № 5. P. 117–122.
Ворович И.И., Бабешко В.А. Динамические смешанные задачи теории упругости для неклассических областей. М.: Наука, 1979. 320 с.
Кукушкин С.А., Осипов А.В. Самоорганизация при зарождении многокомпонентных пленок // Физика твердого тела. 1995. Т. 37. № 7. С. 2127–2132.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела