Известия РАН. Механика твердого тела, 2020, № 5, стр. 151-160
АЭРОУПРУГАЯ УСТОЙЧИВОСТЬ ЦИЛИНДРИЧЕСКИХ ОБОЛОЧЕК С ЭЛЛИПТИЧЕСКИМ ПОПЕРЕЧНЫМ СЕЧЕНИЕМ
С. А. Бочкарёв a, *, С. В. Лекомцев a, В. П. Матвеенко a
a Институт механики сплошных сред УрО РАН
Пермь, Россия
* E-mail: bochkarev@icmm.ru
Поступила в редакцию 14.04.2020
После доработки 25.05.2020
Принята к публикации 23.06.2020
Аннотация
Представлена математическая постановка и алгоритм ее численной реализации, предназначенные для исследования аэроупругой устойчивости цилиндрических оболочек произвольного поперечного сечения. Решение задачи осуществляется в трехмерной постановке с использованием метода конечных элементов. Достоверность полученных результатов подтверждена сравнением с известными решениями для круговых оболочек. Проанализированы зависимости статического давления в невозмущенном потоке газа, при котором происходит потеря устойчивости, полученные при разных отношениях полуосей эллипса и вариантах кинематических граничных условий. Продемонстрирована возможность повышения границ аэроупругой устойчивости цилиндрической оболочки с эллиптическим поперечным сечением по сравнению с круговой конфигурацией в случае консольного закрепления.
1. Введение. Интерес к изучению аэроупругих явлений, возникающих в тонкостенных телах при их взаимодействии со сверхзвуковым потоком газа, не ослабевает уже более полувека [1–4], начиная с момента, когда для решения таких задач был предложен простой и надежный инструмент в виде аналитического выражения для аэродинамического давления, построенного на основе поршневой теории [5]. Библиографические обзоры, представленные в недавних публикациях [6–11], демонстрируют тенденцию к усложнению используемых моделей. В современных исследованиях принимается во внимание не только комбинированное воздействие статических и динамических нагрузок и оценивается их влияние на неустойчивость тонкостенных оболочек, выполненных из перспективных функциональных материалов, но и анализируются возможности активного или пассивного управления порогом устойчивости с помощью материалов, обладающих пьезоэлектрическими свойствами.
В технических приложениях находят применение оболочечные конструкции, в которых эллиптический или овальный профиль применяется в качестве инженерного решения. Кроме этого, незначительное отклонение от кругового поперечного сечения может рассматриваться как неправильность формы, возникающая в процессе использования изделия [12]. Очевидно, что анализ динамического поведения таких систем при их взаимодействии с газообразной средой требует тщательного изучения с целью определения эксплуатационных характеристик, влияющих на их жизненный цикл. Несмотря на данный факт, значительная часть представленных в литературе исследований посвящена цилиндрическим или коническим оболочкам, имеющим круговое поперечное сечение. Лишь в немногих из них затронуты аспекты аэроупругой устойчивости оболочек, сечение которых отлично от кругового. Исследование панельного флаттера параболических оболочек, моделирующих обтекатель ракет-носителей, выполнено в работе [13], а цилиндрических оболочек с эллиптическим поперечным сечением – в [14–16]. В пионерской работе [14] для определения флаттерных характеристик эллиптического цилиндра конечной длины применяется метод Ритца. Показано, что критическая скорость потока газа незначительно меняется при малом изменении эксцентриситета эллипса и существенно падает с его ростом. В статьях [15, 16] с помощью метода Бубнова–Галёркина исследуется влияние эксцентриситета на критические характеристики ненагруженных и нагруженных оболочек, имеющих различные геометрические параметры. Отметим, что сведения о других исследованиях эллиптических оболочек, помимо обзорной работы [12], также приводится в статье авторов [17]. В перечисленных публикациях [14–16] используется теория пологих оболочек с пренебрежением инерцией в срединной поверхности, а решение задачи ищется в виде тригонометрических рядов с незначительным количеством удерживаемых членов. Современные конечно-элементные подходы для описания оболочек позволяют с достаточной достоверностью моделировать поведение тонкостенных конструкций в общем случае произвольного поперечного сечения [18, 19]. Существующие методы решения задач на собственные значения [20, 21], технологии разреженных матриц и параллельных вычислений предоставляют возможность использования традиционного подхода для изучения панельного флаттера в случае матриц больших размерностей. Несмотря на всю свою простоту, он все еще является эффективным инструментом для проведения параметрического исследования и получения качественных оценок в задачах аэроупругости. Разработка такого алгоритма и выполнение численных экспериментов на его основе является целью настоящей работы. Это позволит получить, по крайней мере, качественное подтверждение зависимостей, приведенных в численно-аналитических работах [14–16], которое, насколько известно авторам, в настоящий момент в литературе не представлено.
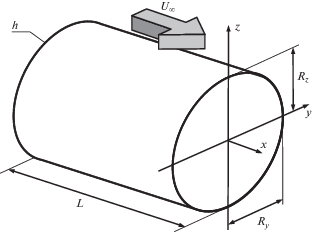
2. Математическая постановка задачи и ее численная реализация. Рассматривается тонкостенная изотропная эллиптическая цилиндрическая оболочка длиной L, полуосями Rz и Ry, толщиной h, которая взаимодействует с внешним сверхзвуковым потоком газа, текущим со скоростью ${{U}_{\infty }}$. Геометрические параметры конструкции приведены на рис. 1. Полагается, что криволинейная поверхность оболочки представляет собой совокупность плоских сегментов [22]. Деформации в каждом из них считаются малыми и вычисляются с помощью классической теории тонких пластин [23–25] в декартовых координатах ($\bar {x},\bar {y},\bar {z}$), связанных с боковой поверхностью тела
(2.1)
$\bar {\varepsilon } = {{\left\{ {{{\varepsilon }_{{\bar {x}\bar {x}}}},{{\varepsilon }_{{\bar {y}\bar {y}}}},{{\gamma }_{{\bar {x}\bar {y}}}}} \right\}}^{{\text{т}}}} = {{\left\{ {\frac{{\partial u}}{{\partial{ \bar {x}}}},\frac{{\partial {v}}}{{\partial{ \bar {y}}}},\frac{{\partial u}}{{\partial{ \bar {y}}}} + \frac{{\partial {v}}}{{\partial{ \bar {x}}}}} \right\}}^{{\text{т}}}} + \bar {z}{{\left\{ { - \frac{{{{\partial }^{2}}w}}{{\partial {{{\bar {x}}}^{2}}}}, - \frac{{{{\partial }^{2}}w}}{{\partial {{{\bar {y}}}^{2}}}}, - 2\frac{{\partial w}}{{\partial{ \bar {x}}\partial{ \bar {y}}}}} \right\}}^{{\text{т}}}}$Здесь и далее прямой чертой сверху обозначены величины, записанные в координатах $\left( {\bar {x},\bar {y},\bar {z}} \right)$, а u, ${v}$ и w – компоненты перемещений срединной поверхности в направлении этих осей.
Физические соотношения, связывающие вектор усилий и моментов s с вектором деформаций ε, записываются в виде
(2.2)
${\mathbf{s}} = {{\left\{ {{{T}_{{\bar {x}\bar {x}}}},{{T}_{{\bar {y}\bar {y}}}},{{T}_{{\bar {x}\bar {y}}}},{{M}_{{\bar {x}\bar {x}}}},{{M}_{{\bar {y}\bar {y}}}},{{M}_{{\bar {x}\bar {y}}}}} \right\}}^{{\text{т}}}} = {\mathbf{D\varepsilon }}$Матрица упругих констант D для изотропного материала определяется следующим образом
(2.3)
${\mathbf{D}} = \left[ {\begin{array}{*{20}{l}} {{{{\mathbf{D}}}_{m}}}&{\mathbf{0}} \\ {\mathbf{0}}&{{{{\mathbf{D}}}_{b}}} \end{array}} \right]{\text{,}}\quad {{{\mathbf{D}}}_{m}} = \int\limits_{ - h/2}^{h/2} {{\mathbf{Q}}d\bar {z}} {\text{,}}\quad {{{\mathbf{D}}}_{b}} = \int\limits_{ - h/2}^{h/2} {{\mathbf{Q}}{{{\bar {z}}}^{2}}d\bar {z}} ,\quad {\mathbf{Q}} = \frac{E}{{1 - {{\nu }^{2}}}}\left[ {\begin{array}{*{20}{c}} 1&\nu &0 \\ \nu &1&0 \\ 0&0&{\frac{{1 - \nu }}{2}} \end{array}} \right]$Давление, действующее со стороны внешнего сверхзвукового потока газа на поверхность оболочки, вычисляется согласно квазистатической аэродинамической теории [2] с поправкой Крумхаара на кривизну оболочки [26]
(2.4)
${{p}_{a}} = - \left( {q\frac{{\partial w}}{{\partial{ \bar {x}}}} + {{q}_{1}}\frac{{\partial w}}{{\partial t}} - {{q}_{2}}w} \right)$Здесь: q – модифицированное динамическое давление; ${{\rho }_{\infty }}$, ${{p}_{\infty }}$ и ${{c}_{\infty }}$ – плотность, статическое давление и скорость звука в невозмущенном потоке газа; ${{{\text{M}}}_{\infty }} = {{{{U}_{\infty }}} \mathord{\left/ {\vphantom {{{{U}_{\infty }}} {{{c}_{\infty }}}}} \right. \kern-0em} {{{c}_{\infty }}}}$ – число Маха в газе; κ – показатель адиабаты; $\beta = {{({\text{M}}_{\infty }^{2} - 1)}^{{1/2}}}$, R = R(φ) – функция, которая описывает изменение радиуса оболочки в зависимости от угла φ в окружном направлении.
В дополнении к выражению (2.4) рассматривается соотношение, в котором не принимается во внимание поправка на кривизну [27]
(2.5)
${{p}_{a}} = - \left( {q\frac{{\partial w}}{{\partial{ \bar {x}}}} + {{q}_{1}}\frac{{\partial w}}{{\partial t}}} \right)$(2.6)
${{p}_{a}} = - \kappa {{p}_{\infty }}\left( {{{{\text{M}}}_{\infty }}\frac{{\partial w}}{{\partial{ \bar {x}}}} + \frac{1}{{{{с}_{\infty }}}}\frac{{\partial w}}{{\partial t}}} \right)$Математическая формулировка задачи динамики тонкостенной оболочки основывается на вариационном принципе возможных перемещений, который записывается в матричном виде
(2.7)
$\int\limits_S {\delta {{{\bar {\varepsilon }}}^{{\text{т}}}}{\mathbf{D}}\bar {\varepsilon }dS} + \int\limits_V {\delta {{{{\mathbf{\bar {u}}}}}^{{\text{т}}}}{{\rho }_{s}}{\mathbf{\ddot {\bar {u}}}}dV} - \int\limits_{{{S}_{\sigma }}} {\delta {{{{\mathbf{\bar {u}}}}}^{{\text{т}}}}{\mathbf{t}}dS} = 0$Решение задачи осуществляется с помощью метода конечных элементов (МКЭ). После применения его известных процедур с учетом (2.1)–(2.3) и представления для давления, например, в виде (2.4), получим из (2.7) матричное соотношение
(2.8)
${\mathbf{M\ddot {u}}} + {\mathbf{C\dot {u}}} + \left( {{\mathbf{K}} + {\mathbf{A}} + {{{\mathbf{A}}}_{k}}} \right){\mathbf{u}} = 0$Типовые матрицы отдельно взятого конечного элемента формируются в координатах ($\bar {x},\bar {y},\bar {z}$), связанных с боковой поверхностью оболочки, следующим образом:
Здесь: B – матрица градиентов, связывающая вектор деформаций с вектором узловых перемещений оболочечного конечного элемента; N и Nw – функции формы обобщенного вектора узловых перемещений оболочки и его нормальной составляющей.
Преобразование узловых перемещений к глобальным декартовым координатам (x, y, z), в которых записано уравнение (2.8), осуществляется для каждого конечного элемента с помощью матрицы направляющих косинусов известным образом. Мембранные перемещения оболочки (u, ${v}$) аппроксимируются линейными функциями формы, а изгибные перемещения w – неконформными функциями формы Эрмита. Дискретизация поверхности конструкции осуществляется плоскими четырехугольными конечными элементами, в общем случае произвольно ориентированными в пространстве. Более подробно аспекты численной реализации изложены в предыдущих работах авторов [17, 28].
Движение оболочки представляется в виде ${\mathbf{u}}({\mathbf{x}},t) = {\mathbf{\tilde {u}}}({\mathbf{x}})\exp (\lambda t)$, где λ = δ + iω – характеристический показатель, ω – собственная частота колебаний, δ – величина, отвечающая за демпфирование системы, $i = \sqrt { - 1} $. Подставляя это выражение в уравнение (2.8) и сокращая на экспоненту, получим
(2.9)
$({{\lambda }^{2}}{\mathbf{M}} + \lambda {\mathbf{C}} + {\mathbf{K}} + {\mathbf{A}} + {{{\mathbf{A}}}_{k}}){\mathbf{\tilde {u}}} = 0$Оценка устойчивого состояния системы основывается на анализе характеристических чисел λ, получаемых при последовательно возрастающем значении варьируемого параметра, в качестве которого выступает статическое давление в невозмущенном потоке газа ${{p}_{\infty }}$. Для этого уравнение (2.9) преобразуется к обобщенной задаче на собственные значения (2.10), которая решается с помощью алгоритма на основе неявно перезапускаемого метода Арнольди [20]
(2.10)
$\lambda \left[ {\begin{array}{*{20}{c}} {\mathbf{M}}&{\mathbf{0}} \\ {\mathbf{0}}&{\mathbf{I}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\lambda {\mathbf{\tilde {u}}}} \\ {{\mathbf{\tilde {u}}}} \end{array}} \right\} + \lambda \left[ {\begin{array}{*{20}{c}} {\mathbf{C}}&{{\mathbf{K}} + {{{\mathbf{A}}}_{0}}} \\ { - {\mathbf{I}}}&{\mathbf{0}} \end{array}} \right]\left\{ {\begin{array}{*{20}{c}} {\lambda {\mathbf{\tilde {u}}}} \\ {{\mathbf{\tilde {u}}}} \end{array}} \right\} = {\mathbf{0}}$3. Результаты. 3.1. Верификация конечно-элементного алгоритма. Достоверность полученных с помощью разработанного конечно-элементного алгоритма результатов подтверждена асимптотическим поведением решения при увеличении числа узловых неизвестных (табл. 1) и сравнением с известными данными, представленными в литературе (табл. 2). Для этой цели рассмотрена задача о панельном флаттере свободно опертой на обоих краях (${v} = w = 0$, ${{\theta }_{{\bar {x}}}} = 0$) круговой цилиндрической оболочки со следующими параметрами геометрии и материала: R = 0.2032 м, L = 0.39116 м, R/h = 2000, E = 110.32 ГПа, ν = 0.35, ρs = 8902.27 кг/м3. Поток воздуха имел характеристики: ${{{\text{M}}}_{\infty }} = 3$, κ = 1.4, температура торможения в невозмущенном потоке газа ${{T}_{\infty }} = 48.89$°C. В пространственной постановке при большом количестве окружных полуволн j необходимо увеличивать число конечных элементов Nθ в этом направлении, чтобы корректно описать форму колебаний. Значения статического давления в невозмущенном потоке газа ${{p}_{\infty }}$, при которых наступает потеря устойчивости (pcr), приведены в табл. 1 при разной дискретизации в окружном направлении. В этих расчетах количество конечных элементов по длине оставалось неизменным и было равно двадцати. Во всех последующих примерах использовалась сетка, удовлетворяющая условию
Таблица 1
| Число элементов Nθ | Число степеней свободы | pcr, Па | δ, % | jcr |
|---|---|---|---|---|
| 100 | 37 200 | 4648 | – | 23 |
| 120 | 44 640 | 4069 | –14.22% | 24 |
| 140 | 52 080 | 3862 | –5.36% | 24 |
| 168 | 62 496 | 3755 | –2.86% | 25 |
| 180 | 66 960 | 3737 | –0.48% | 25 |
| 200 | 74 400 | 3721 | –0.44% | 25 |
Сравнение критических номеров окружных полуволн jcr и соответствующих им минимальных значений статического давления в невозмущенном потоке газа pcr приведено в табл. 2. Из представленной информации можно заключить, что полученные с помощью разработанного конечно-элементного алгоритма данные достаточно хорошо согласуются с представленными в литературе результатами. Имеющиеся отличия обусловлены использованием в перечисленных работах как двумерных (осесимметричных) формулировок, так и различных оболочечных теорий.
3.2. Анализ аэроупругой устойчивости. Рассматриваются цилиндрические оболочки с эллиптическим поперечным сечением, которое характеризуется отношением α = Rmax/Rmin, где Rmax и Rmin – наибольшая и наименьшая полуоси эллипса. При варьировании величины α значения Rmax и Rmin подбираются таким образом, чтобы площадь поперечного сечения оставалась неизменной и была равной площади круга радиуса R. В численных расчетах использовались следующие параметры геометрии и материала: R = 0.07725 м, L = 0.231 м, R/h = 515, E = 2.05 ГПа, ν = 0.3, ρs = 7850 кг/м3. Поток воздуха имел характеристики как в п. 3.1. Рассмотрено два варианта кинематических граничных условий, задаваемых на краях конструкции: жесткое защемление (u = ${v}$ = w = 0, ${{\theta }_{{\bar {x}}}} = {{\theta }_{{\bar {y}}}} = {{\theta }_{{\bar {z}}}} = 0$) и свободный край.
Известно [34], что потеря устойчивости круговых цилиндрических оболочек, обдуваемых снаружи сверхзвуковым потоком газа, осуществляется в виде связанного флаттера. Его критерием в постановке (2.10) является существование двух форм колебаний, у которых собственные значения λ имеют одинаковые мнимые части (частоту колебаний ω), а действительная часть одного из них (демпфирование δ) положительна. Решение задачи аэроупругой устойчивости круговой оболочки распадается на симметричную и антисимметричную составляющие. В этом случае кратным собственным частотам соответствуют две формы колебаний, отличающиеся поворотом в окружном направлении. Потеря устойчивости по каждой из них наступает при одинаковом значении критического давления. У эллиптической цилиндрической оболочки существуют формы с идентичным числом полуволн по окружности. Они имеют разные частоты в спектре и по своей сути не являются симметричными и антисимметричными, поскольку могут быть сильно искажены. В рассмотренных примерах это различие оказалось весьма мало (<0.1%), поэтому связанный флаттер наступает сначала по одной форме, а затем практически сразу же по другой, но с таким же числом полуволн по окружности. В связи с этим, в следующих примерах критическим номером окружных полуволн jcr для эллиптических цилиндрических оболочек будем считать тот, при котором потеря устойчивости наступает раньше.
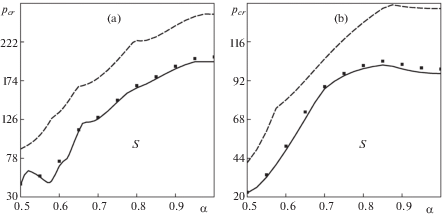
На рис. 2 представлены зависимости критического давления pcr (кПа), при котором происходит потеря устойчивости, от параметра эллиптичности α. Рассмотрены жестко закрепленные на обоих краях (рис. 2a) и консольные оболочки (рис. 2b) при R/h = 515. Здесь и далее на рисунках символом S обозначена область устойчивости. Сплошные линии соответствуют случаю, когда давление от потока газа вычислялось по квазистатической аэродинамической теории с поправкой Крумхаара на кривизну оболочки (выражение (2.4)). Символами обозначены результаты, где данная поправка отсутствует (выражение (2.5)). Поведение обеих кривых качественно совпадает, а количественное различие на одинаковой конечно-элементной сетке не превышает 5%. Вычисление аэродинамического давления согласно поршневой теории (выражение (2.6), на фигуре отмечено пунктирной линией) приводит не только к завышенным относительно этих значений результатам, но и к качественно другому виду границы устойчивости. Отметим, что аналогичное отличие в критических параметрах, получаемых по различным аэродинамическим теориям, выявлено и в случае оболочек с круговым поперечным сечением [32, 35]. Немонотонное поведение кривых объясняется сменой моды, по которой осуществляется потеря устойчивости. В частности, для жестко закрепленных на обоих краях оболочек количество окружных полуволн jcr при малых α меняется достаточно часто (рис. 2a). В качестве примера на рис. 3 изображены формы колебаний, полученные при критических значениях статического давления для разных отношений полуосей эллипса α R/h = 515. Цветовая шкала соответствует безразмерным нормальным перемещениям ${{\tilde {w}}_{n}} = {{{{w}_{n}}} \mathord{\left/ {\vphantom {{{{w}_{n}}} {\max ({{w}_{n}})}}} \right. \kern-0em} {\max ({{w}_{n}})}}$. Во всех примерах потеря устойчивости происходит в виде связанного флаттера. Она наступает в результате слияния двух форм колебаний с одинаковым числом окружных полуволн j, но с их разным количеством по длине оболочки (m = 1 и m = 2).
В ходе исследования консольно защемленной оболочки обнаружено, что при уменьшении отношения полуосей эллипса α с 1 до 0.85 происходит повышение критического давления примерно на 5%, после чего следует его убывание (рис. 2b). Таким образом формируется некоторый интервал изменения параметра α, при котором оболочка с эллиптическим поперечным сечением будет устойчивее аналогичной круговой конфигурации. Данное явление стабилизации сохраняется при всех рассмотренных вариантах вычисления аэродинамического давления.
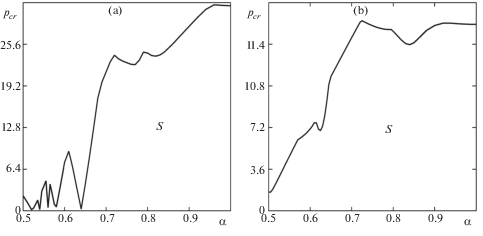
При уменьшении толщины оболочки до R/h = 1000 критическое давление pcr (кПа), вычисляемое согласно выражению (2.4), снижается в разы, а его поведение в зависимости от параметра эллиптичности приобретает существенно немонотонный характер (рис. 4). Причиной этого является уже упоминавшаяся смена моды, по которой осуществляется потеря устойчивости. Наиболее активно этот процесс происходит у жестко закрепленных оболочек при значениях параметра эллиптичности α < 0.67 (рис. 4a). Пилообразный вид кривой потребовал более тщательного анализа, поэтому построение зависимостей на таких участках осуществлялось с переменным шагом по α и со сгущением в области резкого изменения критического давления. Такое поведение можно объяснить тем, что часть конструкции с большим радиусом кривизны обладает меньшей жесткостью и работает подобно сегменту пологой оболочки или пластине, закрепленной вдоль двух длинных сторон. По этой же причине при α < 0.67 потеря устойчивости наступает при более низком давлении.
С уменьшением толщины консольно закрепленной эллиптической оболочки повышение границы флаттера относительно круговой конфигурации наблюдается в меньшей степени. В отличие от случая R/h = 515, при отношении R/h = 1000 существует два небольших участка стабилизации, разделенных пологим провалом критического давления.
4. Заключение. Аэроупругая устойчивость цилиндрических оболочек с эллиптическим поперечным сечением, обтекаемых снаружи сверхзвуковым потоком газа, исследована в трехмерной постановке с помощью изложенной математической модели и ее численной реализации на основе метода конечных элементов. С использованием разработанной программы проанализировано влияние кинематических граничных условий, геометрических размеров и параметра эллиптичности на критические характеристики потери устойчивости в виде флаттера. Продемонстрировано, что в случае консольного закрепления существуют такие отношения полуосей эллипса, которые обеспечивают более высокие границы аэроупругой устойчивости по сравнению с аналогичной круговой конфигурацией. Указанная особенность допускает возможность внесения незначительных изменений в оболочечную конструкцию, приводящих к повышению ее эксплуатационных характеристик.
Работа выполнена в рамках государственного задания; номер гос. регистрации темы АААА-А19-119012290100-8.
Список литературы
Новичков Ю.Н. Флаттер пластин и оболочек // Итоги науки и техники. Т. 11: Механика деформируемого твердого тела. М.: ВИНИТИ, 1978. С. 67–122.
Bismarck-Nasr M.N. Finite element analysis of aeroelasticity of plates and shells // Appl. Mech. Rev. 1992. V. 45. № 12. P. 461–482.
Bismarck-Nasr M.N. Finite elements in aeroelasticity of plates and shells. Pt. 2 // Appl. Mech. Rev. 1996. V. 49. № 10. P. S17–S24.
Алгазин С.Д., Кийко И.А. Флаттер пластин и оболочек. М.: Наука, 2006. 247 с.
Ильюшин А.А. Закон плоских сечений в аэродинамике больших сверхзвуковых скоростей // ПММ. 1956. Т. 20. № 6. С. 733–755.
Bochkarev S.A., Lekomtsev S.V., Matveenko V.P. Aeroelastic stability of heated functionally graded cylindrical shells containing fluid // Mech. Adv. Mater. Struct. 2017. V. 24. № 16. P. 1391–1400.
Lin H., Cao D., Shao C. An admissible function for vibration and flutter studies of FG cylindrical shells with arbitrary edge conditions using characteristic orthogonal polynomials // Compos. Struct. 2018. V. 185. P. 748–763.
Mahmoudkhani S. Aerothermoelastic analysis of imperfect FG cylindrical shells in supersonic flow // Compos. Struct. 2019. V. 225. 111160.
Li X., Li Y.H., Xie T.F. Vibration characteristics of a rotating composite laminated cylindrical shell in subsonic air flow and hygrothermal environment // Int. J. Mech. Sci. 2019. V. 150. P. 356–368.
Бочкарёв С.А., Лекомцев С.В. Устойчивость функционально-градиентных круговых цилиндрических оболочек при комбинированном нагружении // Механика композитных материалов. 2019. Т. 55. № 3. С. 501–518.
Muc A., Flis J., Augustyn M. Optimal design of plated/shell structures under flutter constraints-A literature review // Materials. 2019. V. 12. № 24. 4215.
Soldatos K.P. Mechanics of cylindrical shells with non-circular cross section: A survey // Appl. Mech. Rev. 1999. V. 52. P. 237–274.
Динамическая неустойчивость обтекателей ракет-носителей в полете / М.В. Чернобрывко [и др.] // Проблемы машиностроения. 2014. Т. 7. № 2. С. 9–16.
Шандаров Л.Г. Флаттер цилиндрической оболочки эллиптического поперечного сечения // МТТ. 1968. Т. 2. № 1. С. 122–126.
Kozarov M., Vodenitcharova T. Linear panel flutter of an elliptic cylindrical shell // Arch. Appl. Mech. 1991. V. 61. № 8. P. 505–516.
Kozarov M., Vodenitcharova T. On the linear panel flutter and divergence of an elliptic cylindrical shell // J. Constr. Steel Res. 1992. V. 21. № 1–3. P. 235–253.
Bochkarev S.A., Lekomtsev S.V., Matveenko V.P. Natural vibrations of prestressed noncircular cylindrical shells, containing quiescent fluid // Thin-Walled Struct. 2015. V. 90. P. 12–22.
Бате К.Ю. Методы конечных элементов. М: Физматлит, 2010. 1024 с.
Bathe K.J., Dvorkin E.N. A formulation of general shell elements – the use of mixed interpolation of tensorial components // Int. J. Numer. Methods Eng. 1986. V. 22. P. 697–722.
Lehoucq R.B., Sorensen D.C. Deflation techniques for an implicitly restarted Arnoldi iteration // SIAM J. Matrix Anal. Appl. 1996. V. 17. № 4. P. 789–821.
Jarlebring E., Michiels W., Meerbergen K. A linear eigenvalue algorithm for the nonlinear eigenvalue problem // Numer. Math. 2012. V. 122. P. 169–195.
Зенкевич О.С. Метод конечных элементов в технике. М.: Мир, 1975. 544 с.
Вольмир А.С. Устойчивость деформируемых систем. М.: Наука, 1967. 984 с.
Ворович И.И. Математические проблемы нелинейной теории пологих оболочек. М.: Наука, 1989. 376 с.
Reddy J.N. An introduction to nonlinear finite element analysis. New York: Oxford University Press, 2004. 488 p.
Krumhaar H. The accuracy of linear piston theory when applied to cylindrical shells // AIAA J. 1963. V. 1. C. 1448–1449.
Voss H.M. The effect of an external supersonic flow on the vibration characteristics of thin cylindrical shells // J. Aerospase Sci. 1961. V. 3. P. 945–956.
Hydroelastic stability of partially filled coaxial cylindrical shells / S.A. Bochkarev [et al.] // Acta Mech. 2019. V. 230. № 11. P. 3845–3860.
Olson M.D., Fung Y.C. Comparing theory and experiment for the supersonic flutter of circular cylindrical shells // AIAA J. 1967. V. 5. № 10. P. 1849–1856.
Hasheminejad S.M., Aghayi Motaaleghi M. Supersonic flutter control of an electrorheological fluid-based smart circular cylindrical shell // Int. J. Struct. Stab. Dynam. 2014. V. 14. № 2. 1350064.
Ganapathi M., Varadan T.K., Jijen J. Field-consistent element applied to flutter analysis of circular cylindrical shells // J. Sound Vib. 1994. V. 171. № 4. P. 509–527.
Sabri F., Lakis A.A. Finite element method applied to supersonic flutter of circular cylindrical shells // AIAA J. 2010. V. 48. № 1. P. 73–81.
Бочкарёв С.А., Лекомцев С.В. Аэроупругая устойчивость круговых цилиндрических оболочек, содержащих текущую жидкость // Вестн. Сам. гос. техн. ун-та. Сер. Физ.-мат. науки. 2015. Т. 19. № 4. С. 750–767.
Болотин В.В. Неконсервативные задачи теории упругой устойчивости. М.: Гос. изд. физ.-мат. литературы, 1961. 341 с.
Amabili M., Pellicano F. Nonlinear supersonic flutter of circular cylindrical shells // AIAA J. V. 39. 2001. P. 564–573.
Дополнительные материалы отсутствуют.
Инструменты
Известия РАН. Механика твердого тела